Analysis and Inter-Calibration of Wet Path Delay Datasets to Compute the Wet Tropospheric Correction for CryoSat-2 over Ocean
Abstract
:1. Introduction
2. WTC Estimation from Microwave Radiometers
2.1. Introduction
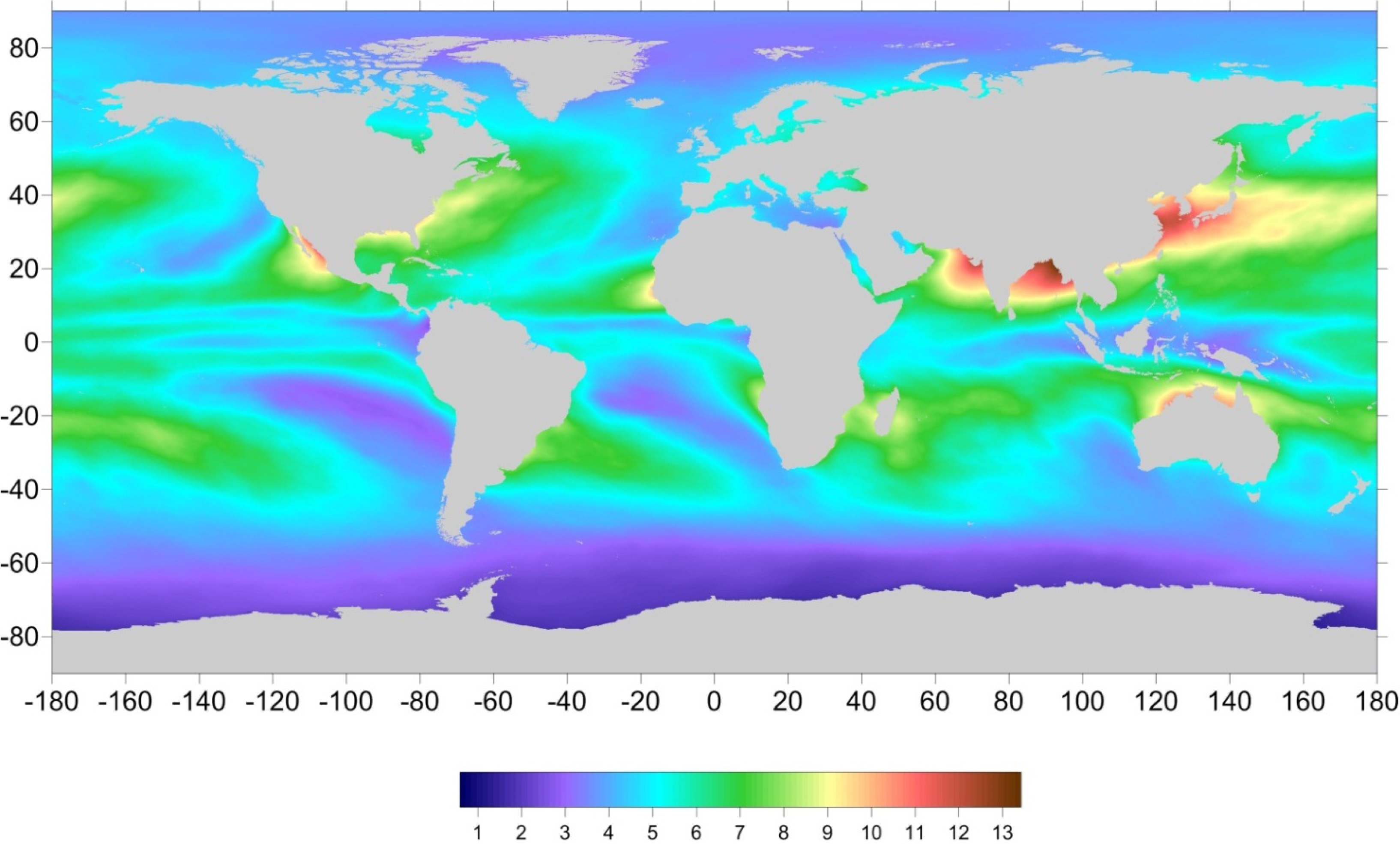
2.2. From TCWV to WTC
2.3. WTC from ERA Interim
2.4. WTC from SI-MWR Water Vapor Products
3. MWR Imaging Sensors
3.1. Data Description
- (1)
- The Advanced Microwave Sounding Unit A (AMSU-A) on board the National Oceanic and Atmospheric Administration (NOAA) satellite series (NOAA-15, -16, -17, -18, -19) and on board the European Organization for the Exploitation of Meteorological Satellites (EUMETSAT) MetOp-A satellite;
- (2)
- The Advanced Microwave Scanning Radiometer-Earth Observing System (AMSR-E) on board the National Aeronautics Space Administration (NASA) Aqua satellite;
- (3)
- The Tropical Rain Measuring Mission (TRMM) Microwave Imager (TMI) on board the joint NASA and Japan Aerospace Exploration Agency TRMM satellite;
- (4)
- The Special Sensor Microwave Imager (SSM/I) and Special Sensor Microwave Imager/Sounder (SSM/IS) on board the Defense Meteorological Satellite Program (DMSP) satellite series (F15, F16, F17, and F18);
- (5)
- The WindSat Polarimetric Radiometer developed by the Naval Research Laboratory (NRL) aboard Coriolis, a satellite of the US Department of Defense.
- (1)
- AMSU-A Level-2 swath products are made available by NOAA through its Comprehensive Large Array-Data Stewardship System (CLASS): http://www.class.ngdc.noaa.gov. The Microwave Surface and Precipitation Products System (MSPPS) Orbital Global Data products (MSPPS_ORB) have been used. In addition, CLASS also provides similar products for SSM/I (F15), although it was found that these products are not suitable for use in the WTC computation (see Section 3.3).
- (2)
- For the AMSR-E, the Level-2B ocean swath (AE_Ocean) dataset was downloaded from the National Snow and Ice Data Center (ftp://n4ftl01u.ecs.nasa.gov/SAN/AMSA/AE_Ocean.002/).
- (3)
- For TMI, the Level-2 product swath dataset was acquired from the Global Hydrology Resource Center (ftp://ghrc.nsstc.nasa.gov/pub/data/tmi-op/).
- (4)
- SSM/I and SSM/IS data are available through Remote Sensing Systems (RSS) ( http://www.ssmi.com/ssmi/ssmi_browse.html), which provide ocean data products for the DSMP satellites from F08 to F18. According to information in February 2013, products for F18 were not yet available. According to RSS information, after August 2006, F15 products are affected by RADCAL beacon interference. The released F15 Version 7 products from RSS have been corrected for this effect. Due to the required calibration and correction, F15 Version 7 products are provided with some delay; thus, for this study only data until the end of 2011 were available. In spite of the fact that RSS recommends that, after August 2006, F15 products should not be used for climate studies, it will be shown in Section 3.3 that the corrected (Version 7) RSS F15 products seem to be adequate for use in the WTC computations.
- (5)
- WindSat data are available through RSS (ftp://ftp.remss.com/windsat) also in the form of grid binary files; as for DMSP-F15 (see point 4 above) WindSat Version 7 products are being generated with some delay, and for the present study they were only available until the end of 2011—for the remaining period the near real time products are available. RSS also provides similar gridded products for AMSR-E.
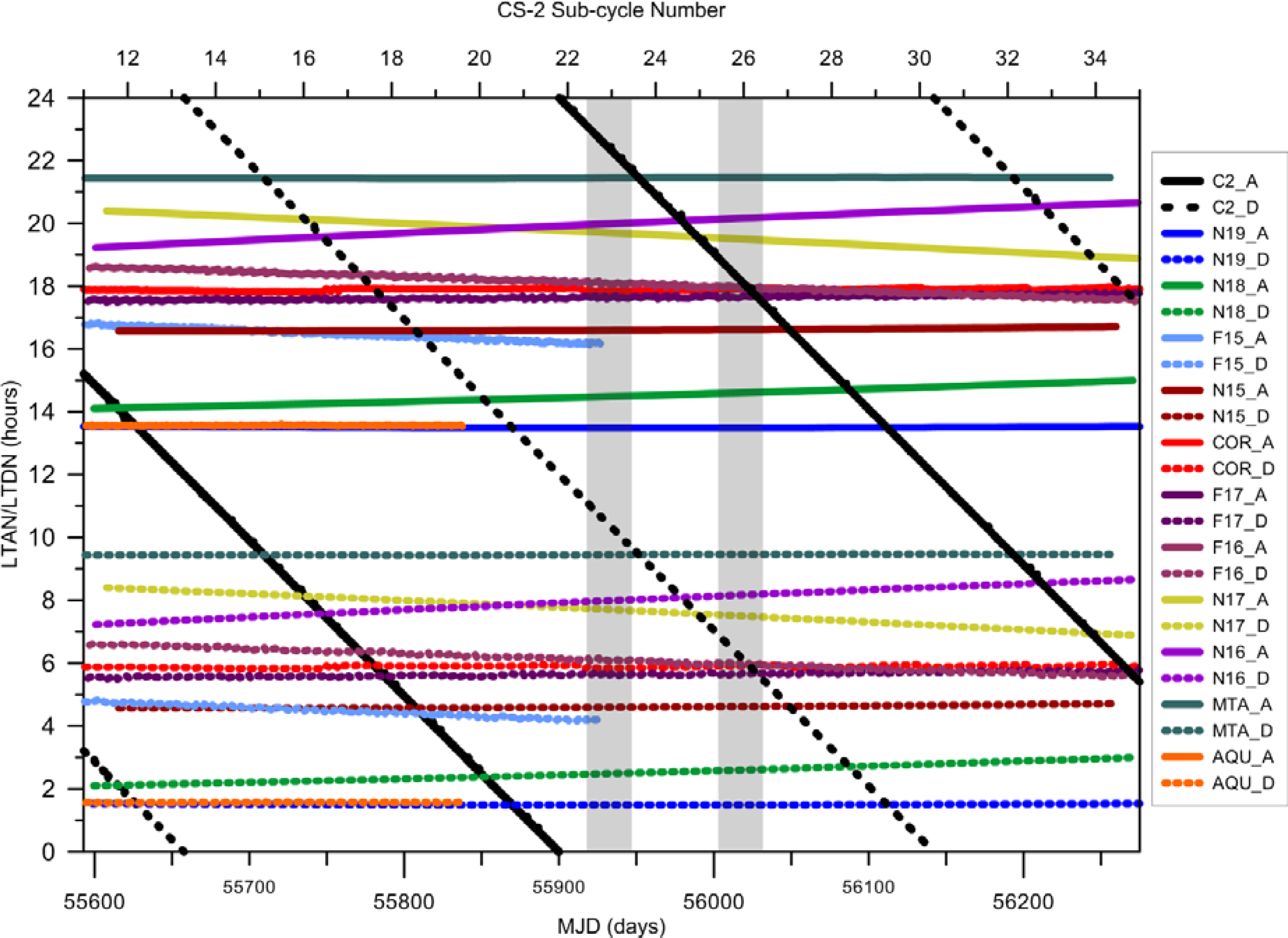
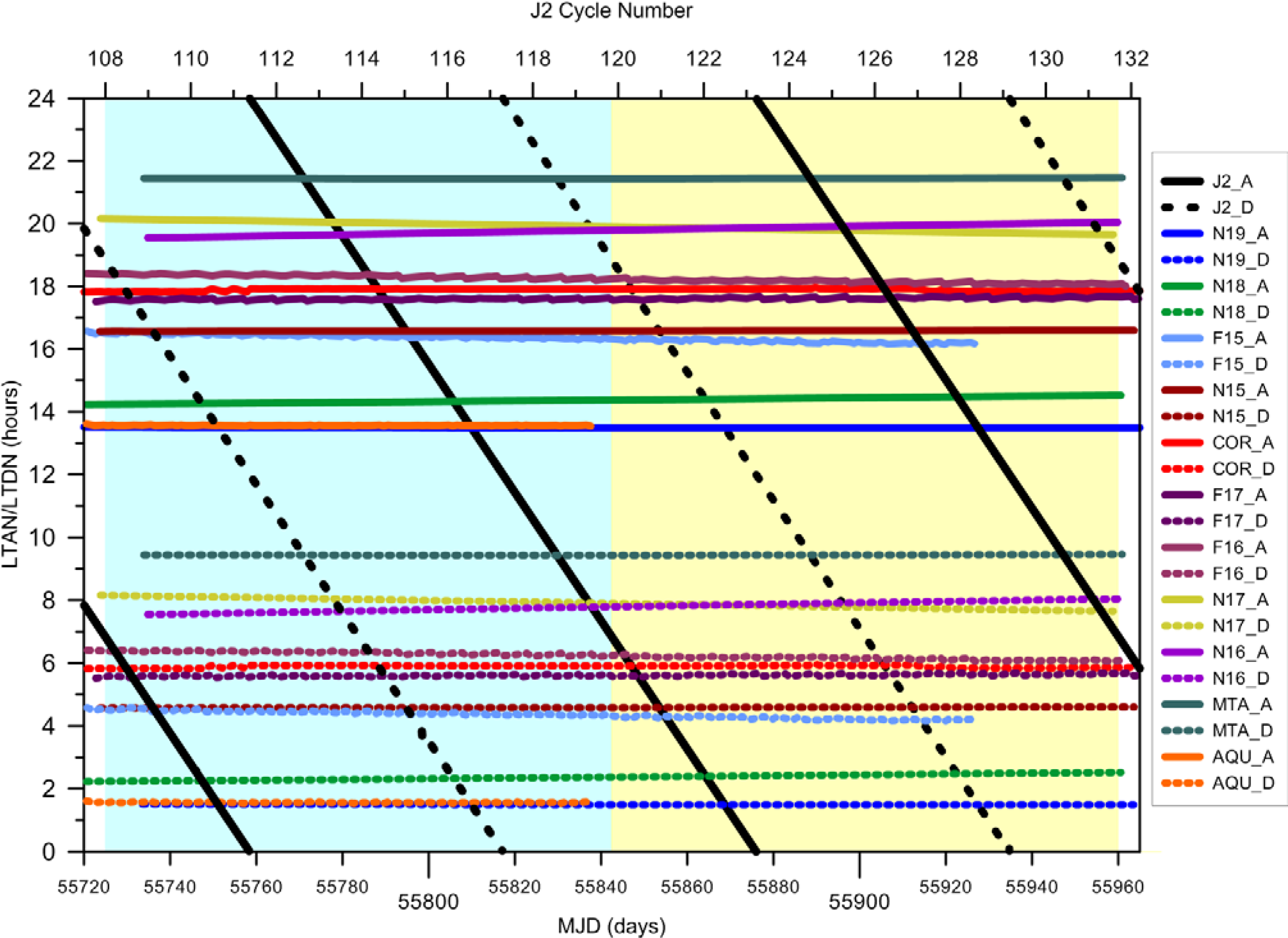
3.2. Orbit Configuration
- (1)
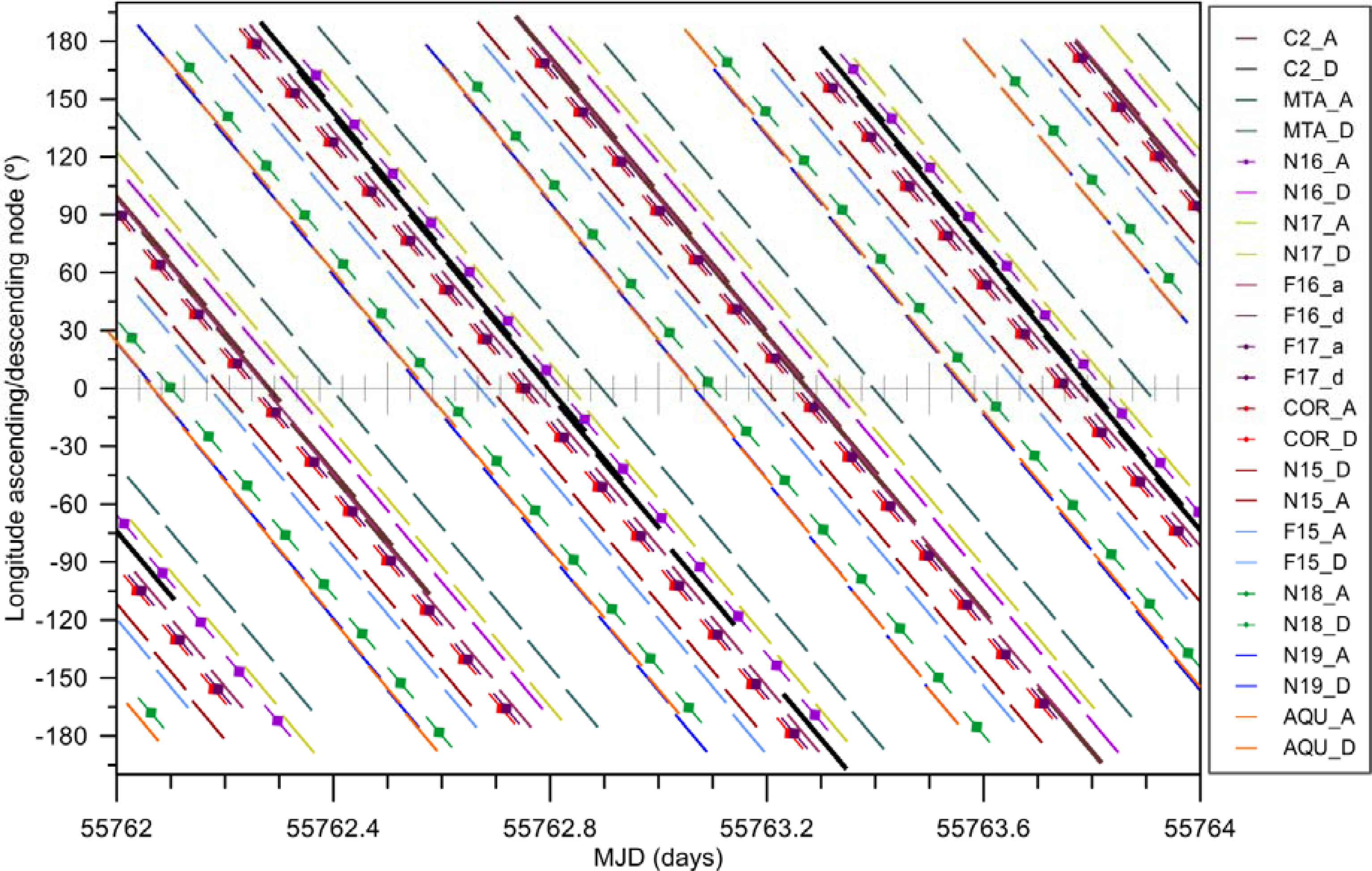
- When an ascending CS-2 pass is in phase with an ascending pass of the RS satellite, which is collecting the SI-MWR images, i.e., both satellites have close LTAN and close LTDN, since both passes are nearly parallel. This happens for the middle of CS-2 sub-cycle 26 and satellites Coriolis, F16 and F17 (Figure 7).
- (2)
- When an ascending CS-2 pass is in phase with a descending pass of the RS satellite, i.e. the CS-2 LTAN is close to the LTDN of the sun-synchronous satellite, or vice versa, when a fraction of the SI-MWR images will be within an acceptable space/time range for the WTC computation. This happens for the middle of CS-2 sub-cycle 18 and satellites Coriolis, F16 and F17 (Figure 7).
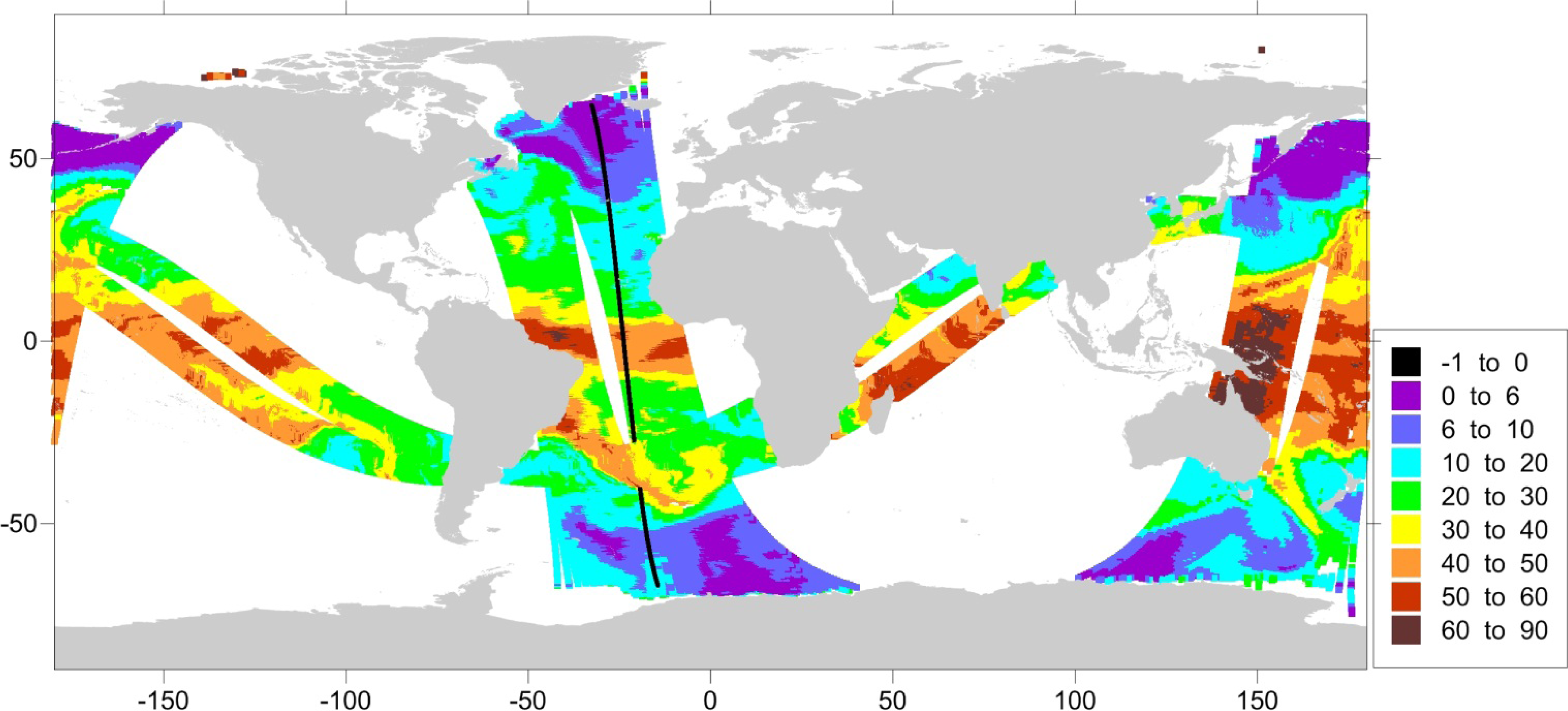
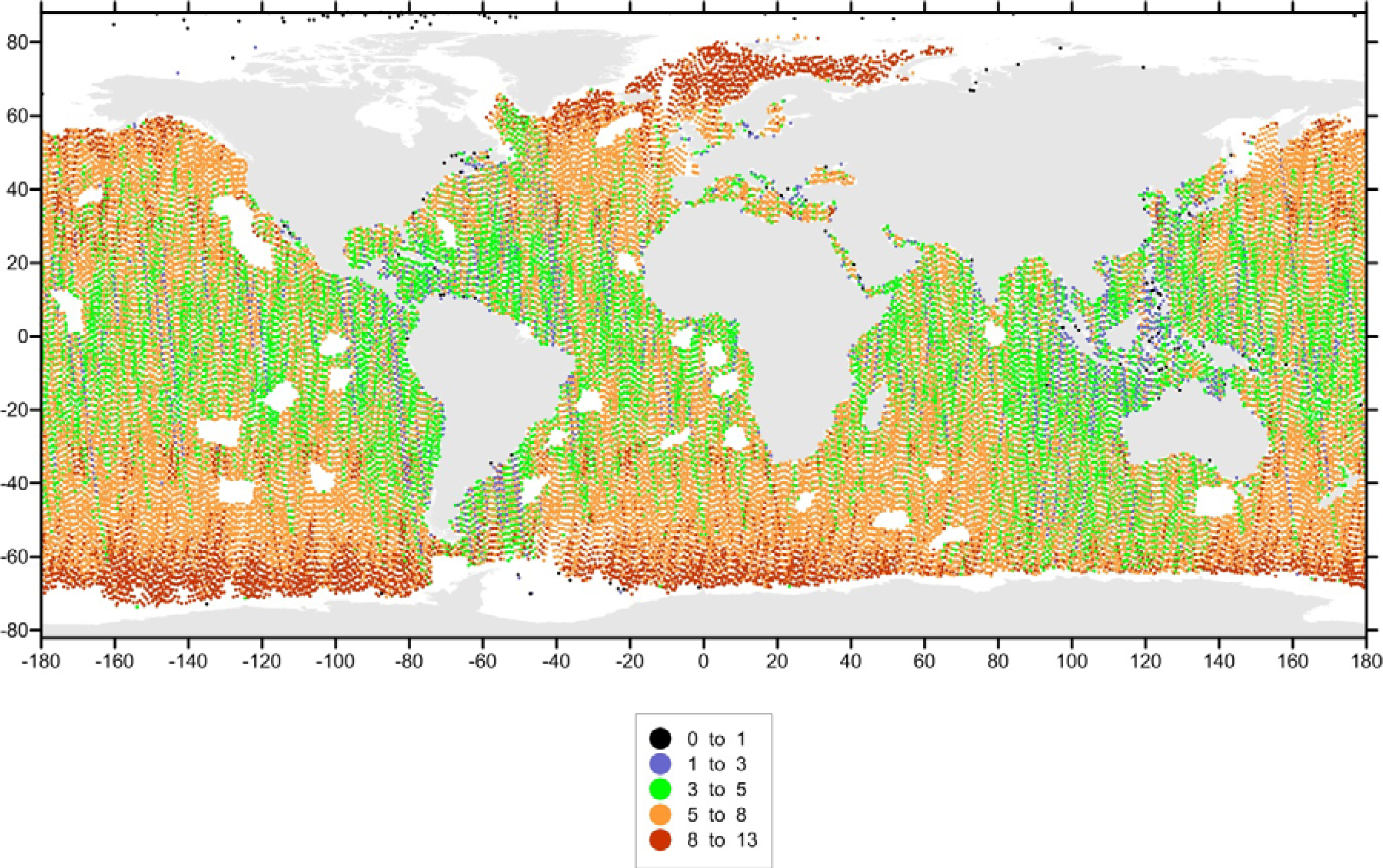
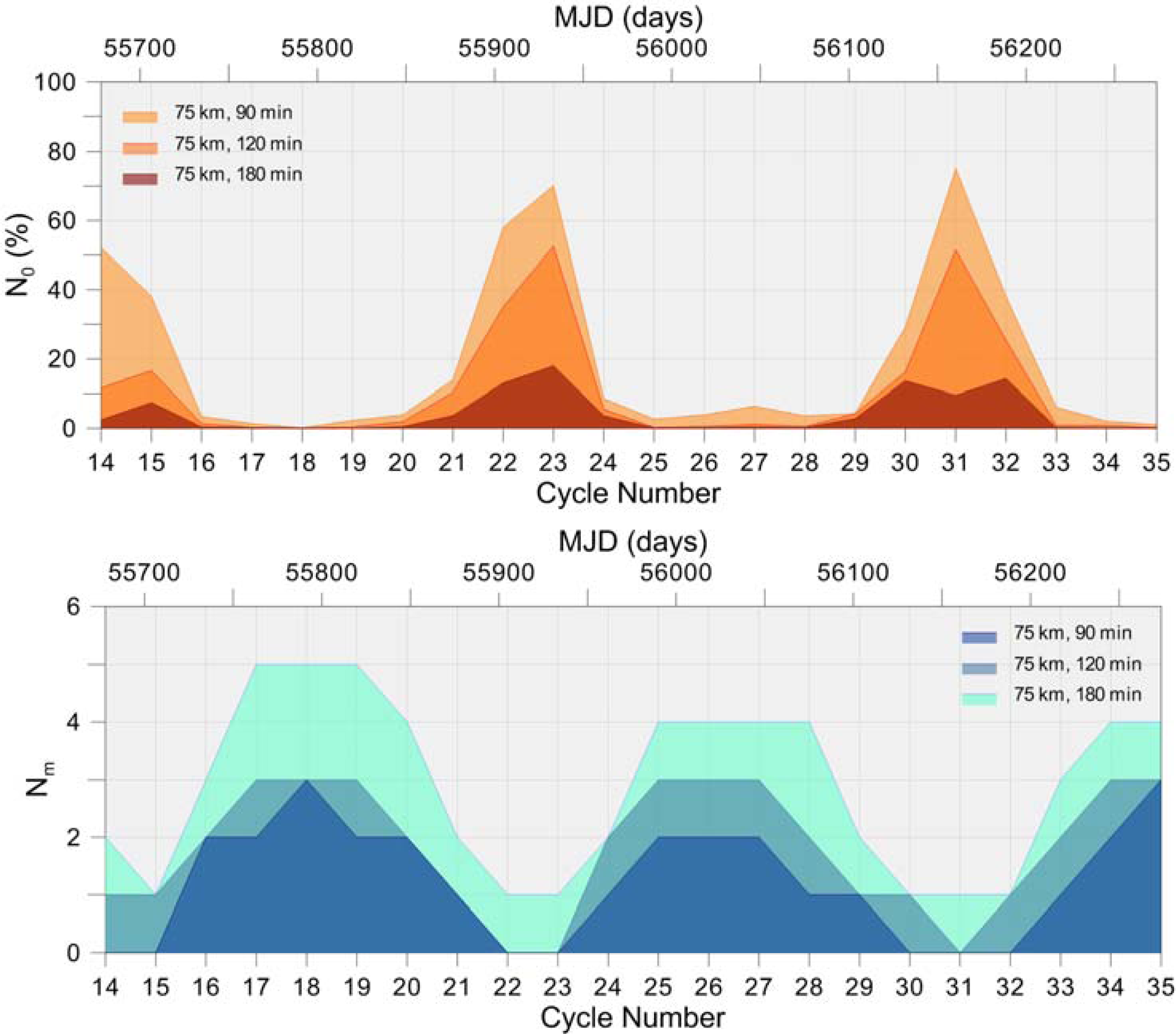
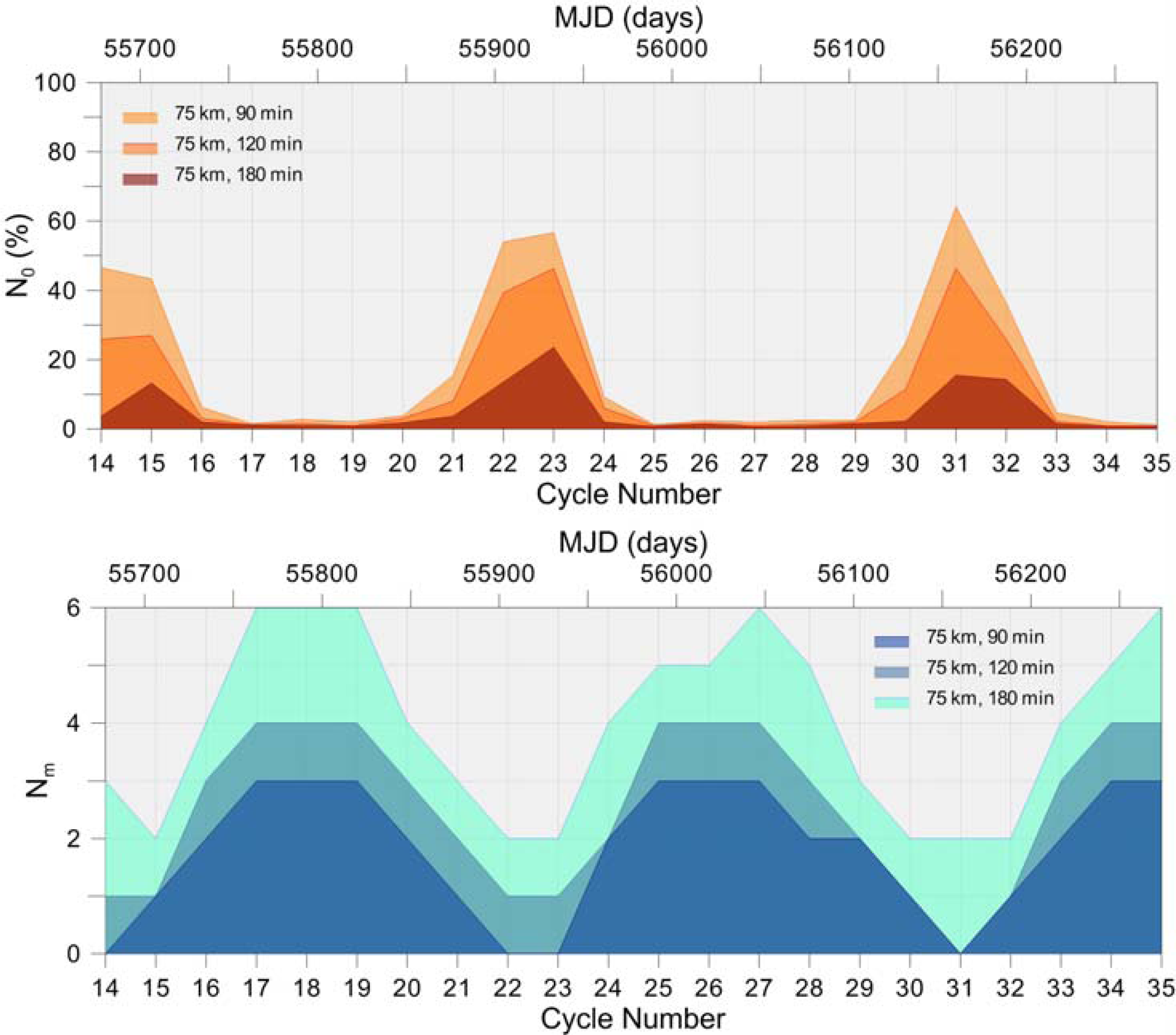
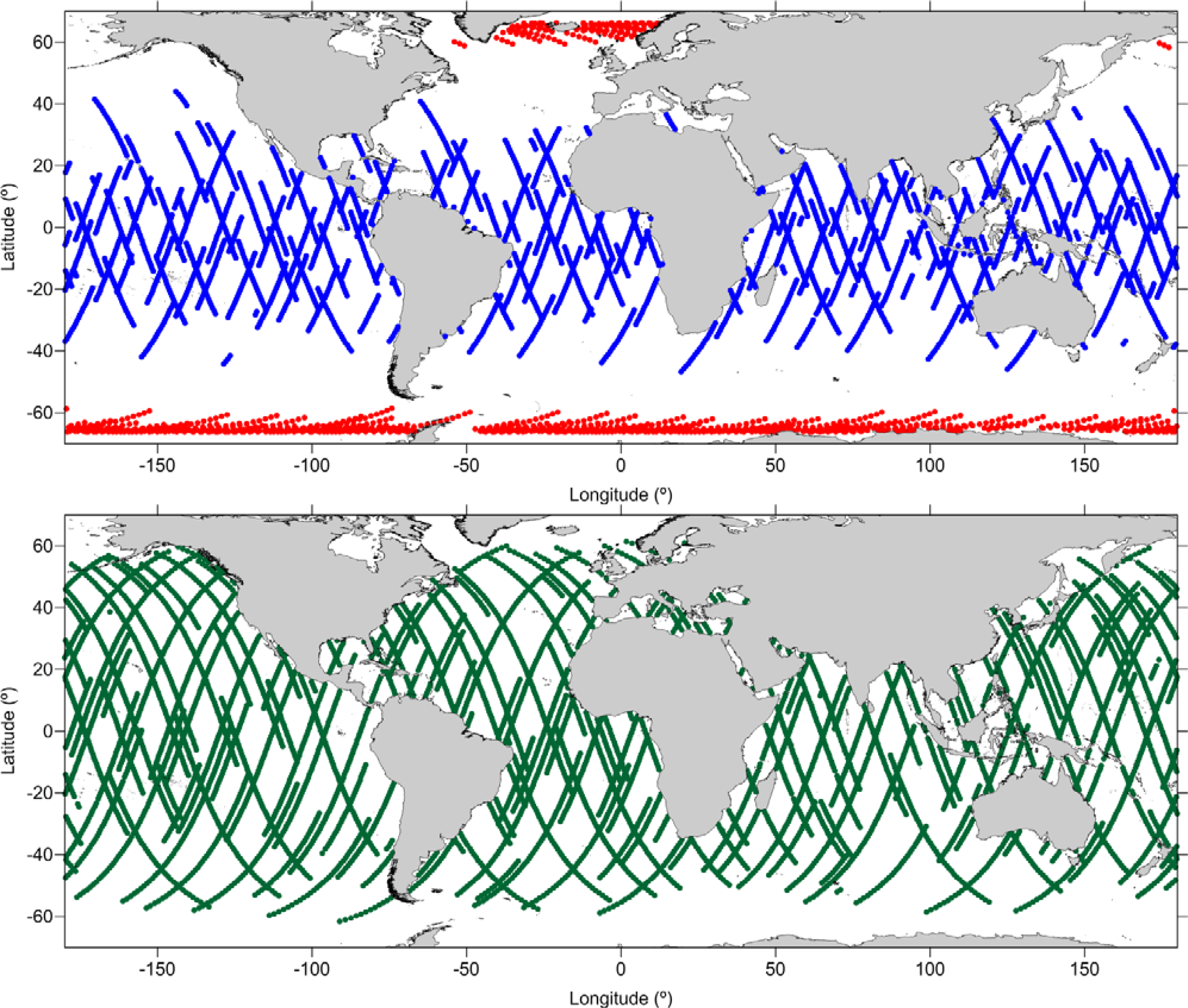
3.3. Spatial and Temporal Coverage with Respect to CryoSat-2
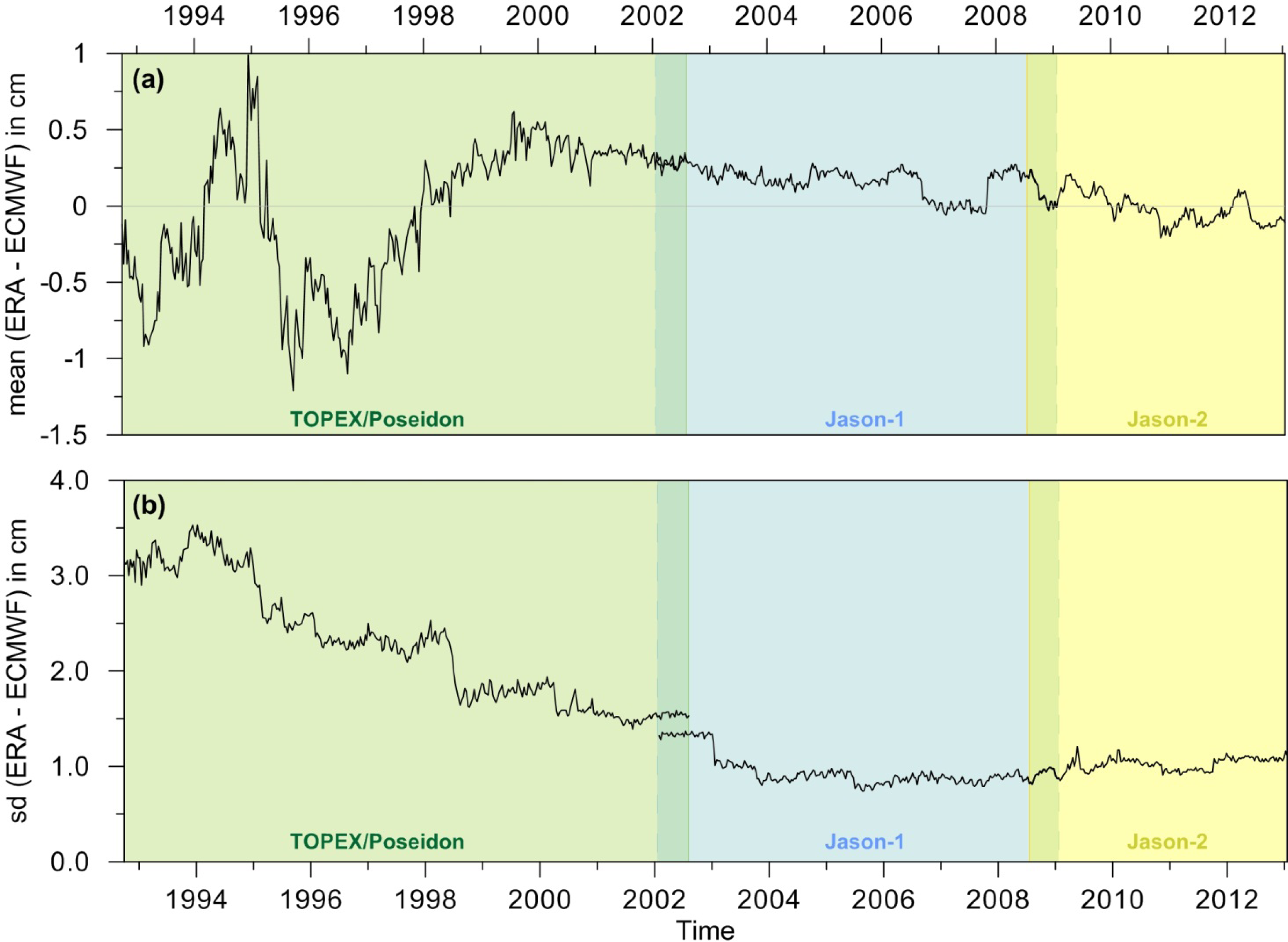
3.4. Sensor Calibration
4. Discussion and Conclusions
Acknowledgments
Conflict of Interest
References and Notes
- Cotton, D.; Benveniste, J.; Clarizia, M.-P.; Roca, M.; Gommenginger, C.; Naeije, M.; Labroue, S.; Picot, N.; Fernandes, J.; Andersen, O.; et al. CryoSat Plus For Oceans: An ESA Project for CryoSat-2 Data Exploitation Over Ocean. Proceedings of EGU General Assembly 2013, Vienna, Austria, 27 April–2 May 2013.
- Fernandes, M.J.; Lazaro, C.; Nunes, A.L.; Pires, N.; Bastos, L.; Mendes, V.B. GNSS-Derived path delay: An approach to compute the wet tropospheric correction for coastal altimetry. IEEE Geosci. Remote Sens. Lett 2010, 7, 596–600. [Google Scholar]
- Fernandes, M.J.; Pires, N.; Lázaro, C.; Nunes, A.L. Tropospheric delays from GNSS for application in coastal altimetry. Adv. Space Res 2013, 51, 1352–1368. [Google Scholar]
- Stum, J.; Sicard, P.; Carrere, L.; Lambin, J. Using objective analysis of scanning radiometer measurements to compute the water vapor path delay for altimetry. IEEE Trans. Geosci. Remote Sens 2011, 49, 3211–3224. [Google Scholar]
- Miller, M.; Buizza, R.; Haseler, J.; Hortal, M.; Janssen, P.; Untch, A. Increased resolution in the ECMWF deterministic and ensemble prediction systems. ECMWF Newslett 2010, 124, 10–16. [Google Scholar]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Quart. J. Royal Meteorol. Soc 2011, 137, 553–597. [Google Scholar]
- Eymard, L.; Obligis, E. The Altimetric Wet Troposheric Correction: Progress since the ERS-1 Mission. Proceedings of 15 Years of Progress in Radar Altimetry, Venice, Italy, 13–18 March 2006.
- Brown, S. A novel near-land radiometer wet path-delay retrieval algorithm: Application to the Jason-2/OSTM advanced microwave radiometer. IEEE Trans. Geosci. Remote Sens 2010, 48, 1986–1992. [Google Scholar]
- Tournadre, J. Improved level-3 oceanic rainfall retrieval from dual-frequency spaceborne radar altimeter systems. J.Atmos. Ocean. Technol 2006, 23, 1131–1149. [Google Scholar]
- Tournadre, J.; Lambin-Artru, J.; Steunou, N. Cloud and rain effects on AltiKa/SARAL Ka-band radar altimeter—Part I: Modeling and mean annual data availability. IEEE Trans. Geosci. Remote Sens 2009, 47, 1806–1817. [Google Scholar]
- Verron, J.; Steunou, N. ALTIKA: A Micro-Satellite Ka-band Altimetry Mission. Proceedings of 15 Years Progress in Satellite Altimetry, Venice, Italy, 13–18 March 2006.
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote-sensing of atmospheric water-vapor using the global positioning system. J. Geophys. Res.-Atmos 1992, 97, 15787–15801. [Google Scholar]
- Keihm, S.J.; Janssen, M.A.; Ruf, C.S. TOPEX/Poseidon microwave radiometer (TMR), III, Wet troposphere range correction algorithm and pre-launch error budget. IEEE Trans. Geosci. Remote Sens 1995, 33, 147–161. [Google Scholar]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS meteorology—Mapping zenith wet delays onto precipitable water. J.Appl. Meteorol 1994, 33, 379–386. [Google Scholar]
- Mendes, V.B.; Prates, G.; Santos, L.; Langley, R.B. An Evaluation of the Accuracy of Models of the Determination of the Weighted Mean Temperature of the Atmosphere. Proceedings of ION 2000 National Technical Meeting, Anaheim, CA, USA, 26–28 January 2000.
- Mendes, V.B. Modeling the Neutral-Atmosphere Propagation Delay in Radiometric Space Techniques. 1999. [Google Scholar]
- Wang, J.H.; Zhang, L.Y.; Dai, A. Global estimates of water-vapor-weighted mean temperature of the atmosphere for GPS applications. J. Geophys. Res.-Atmos 2005, 110, 1–17. [Google Scholar]
- Ross, R.J.; Rosenfeld, S. Estimating mean weighted temperature of the atmosphere for Global Positioning System applications. J. Geophys. Res.-Atmos 1997, 102, 21719–21730. [Google Scholar]
- Keihm, S.J.; Zlotnicki, V.; Ruf, C.S. TOPEX Microwave radiometer performance evaluation, 1992–1998. IEEE Trans. Geosci. Remote Sens 2000, 38, 1379–1386. [Google Scholar]
- Wentz, F.J. A well-calibrated ocean algorithm for special sensor microwave/imager. J.Geophys. Res.-Ocean 1997, 102, 8703–8718. [Google Scholar]
- Wentz, F.J.; Meissner, T. AMSR Ocean Algorithm, Version 2; Remote Sensing Systems: Santa Rosa, CA, USA, 2000. [Google Scholar]
- Viltard, N.; Burlaud, C.; Kummerow, C.D. Rain retrieval from TMI brightness temperature measurements using a TRMM PR-based database. J. Appl. Meteorol. Clim 2006, 45, 455–466. [Google Scholar]
- Meissner, T.; Wentz, F. Ocean Retrievals for WindSat—Radiative Transfer Model, Algorithm, Validation. Proceedings of OCEANS 2005 MTS/IEEE, Washington, DC, USA, 18–23 September 2005.
- Weng, F.; Ferraro, R.R.; Grody, N.C. Effects of AMSU Cross-Scan Asymmetry of Brightness Temperatures on Retrieval of Atmospheric and Surface Parameters. In Microwave Radiometry & Remote Sensing of the Earth’s Surface and Atmosphere; Pampaloni, P., Paloscia, S., Eds.; VSP: Leiden, The Netherlands, 2000; pp. 255–262. [Google Scholar]
- Ignatov, A.; Laszlo, I.; Harrod, E.D.; Kidwell, K.B.; Goodrum, G.P. Equator crossing times for NOAA, ERS and EOS sun-synchronous satellites. Int. J. Remote Sens 2004, 25, 5255–5266. [Google Scholar]
- Brown, S. Maintaining the long-term calibration of the Jason-2/OSTM advanced microwave radiometer through intersatellite calibration. IEEE Trans. Geosci. Remote Sens 2013, 51, 1531–1543. [Google Scholar]
- Cao, C.Y.; Chen, R.Y.; Miller, L. Monitoring the Jason-2/AMR stability using SNO observations from AMSU on MetOp-A. Mar. Geod 2011, 34, 431–446. [Google Scholar]






| Sensor | Pixel Size (km) | Swath Width (km) | Number of (Lines, Pixels) | Name of Product | Scale Factor of Product | Channels Used to Retrieve TCWV (GHz) |
|---|---|---|---|---|---|---|
| AMSR-E | 9 km | 1,625 | (variable, 243) | Med_res_vapor | 0.01 | 18.7/23.8/36.5 |
| AMSU-A | 50 km *** | 2,200 | (variable, 30) | TPW | 0.1 | 23.8/31.4 |
| TMI | 10 km | 878 | (variable,104) | Columnar_water_vapor | 0.01 | 19.35/21.3/37.0 |
| SSM/I * | 25 km | 1,420 | (variable,64) | TPW | 0.1 | 19.35/22.235/37.0 |
| SSM/I, SSM/IS ** | 0.25° | 1,790–1,850 | (720, 1440) | VAPOR | 0.3 | 19.35/22.235/37.0 |
| WindSat | 0.25° | 1,400 | (720, 1440) | VAPOR | 0.3 | 18.7/23.8/37.0 |
| Satellite | Sensor | Height (km) | Inclination (°) | Period (min) | Sun-synch. Orbit | LTAN Jan 2011 (hh:mm) | LTAN Jan 2012 (hh:mm) | Data Availability for Cryosat-2 |
|---|---|---|---|---|---|---|---|---|
| CryoSat-2 | - | 717 | 92.0 | 93.2 | No | N/A | N/A | since April 2010 |
| AQUA | AMSR-E | 705 | 98.0 | 99.0 | Yes | 13:36 | - | until Oct 2011 |
| NOAA-19 | AMSU-A | 870 | 98.7 | 102.1 | Yes | 13:32 | 13:32 | until present |
| NOAA-18 | AMSU-A | 854 | 98.7 | 102.1 | Yes | 14:07 | 14:30 | until present |
| DMSP-F15 | SSM/I | 850 | 98.8 | 102.0 | Yes | 16:44 | 16:05 | * |
| NOAA-15 | AMSU-A | 807 | 98.5 | 101.1 | Yes | 16:35 | 16:35 | until present |
| Coriolis | WindSat | 830 | 98.8 | 101.6 | Yes | 17:54 | 17:54 | ** |
| DMSP-F17 | SSM/IS | 850 | 98.8 | 102.0 | Yes | 17:30 | 18:06 | until present |
| DMSP-F16 | SSM/IS | 845 | 98.9 | 101.8 | Yes | 19:12 | 18:30 | until present |
| NOAA-17 | AMSU-A | 810 | 98.7 | 101.2 | Yes | 20:20 | 19:40 | until present |
| NOAA-16 | AMSU-A | 849 | 99.0 | 102.1 | Yes | 19:16 | 20:00 | until present |
| MetOp-A | AMSU-A | 817 | 98.7 | 101.4 | Yes | 21:26 | 21:27 | until present |
| TRMM | TMI | 402 | 35.0 | 93.0 | No | N/A | N/A | until present |
| ΔT\ΔD | 50 km | 75 km | 100 km |
|---|---|---|---|
| 60 min | 65.2 | 62.5 | 61.3 |
| 90 min | 54.0 | 50.7 | 49.2 |
| 120 min | 39.9 | 36.2 | 34.6 |
| 150 min | 24.9 | 21.3 | 19.8 |
| 180 min | 13.6 | 10.2 | 9.0 |
| ΔT\ΔD | 50 km | 75 km | 100 km |
|---|---|---|---|
| 60 min | 8.9 | 7.2 | 6.6 |
| 90 min | 2.9 | 2.0 | 1.6 |
| 120 min | 1.0 | 0.5 | 0.3 |
| 150 min | 0.9 | 0.4 | 0.3 |
| 180 min | 0.8 | 0.3 | 0.2 |
| Satellite | Solution Type | Scale Factor | Offset (cm) | RMS (cm) | |
|---|---|---|---|---|---|
| Before | After | ||||
| AQUA | Bevis | 0.980 | −0.74 | 1.41 | 0.85 |
| Stum | 1.012 | −1.01 | 1.14 | 0.80 | |
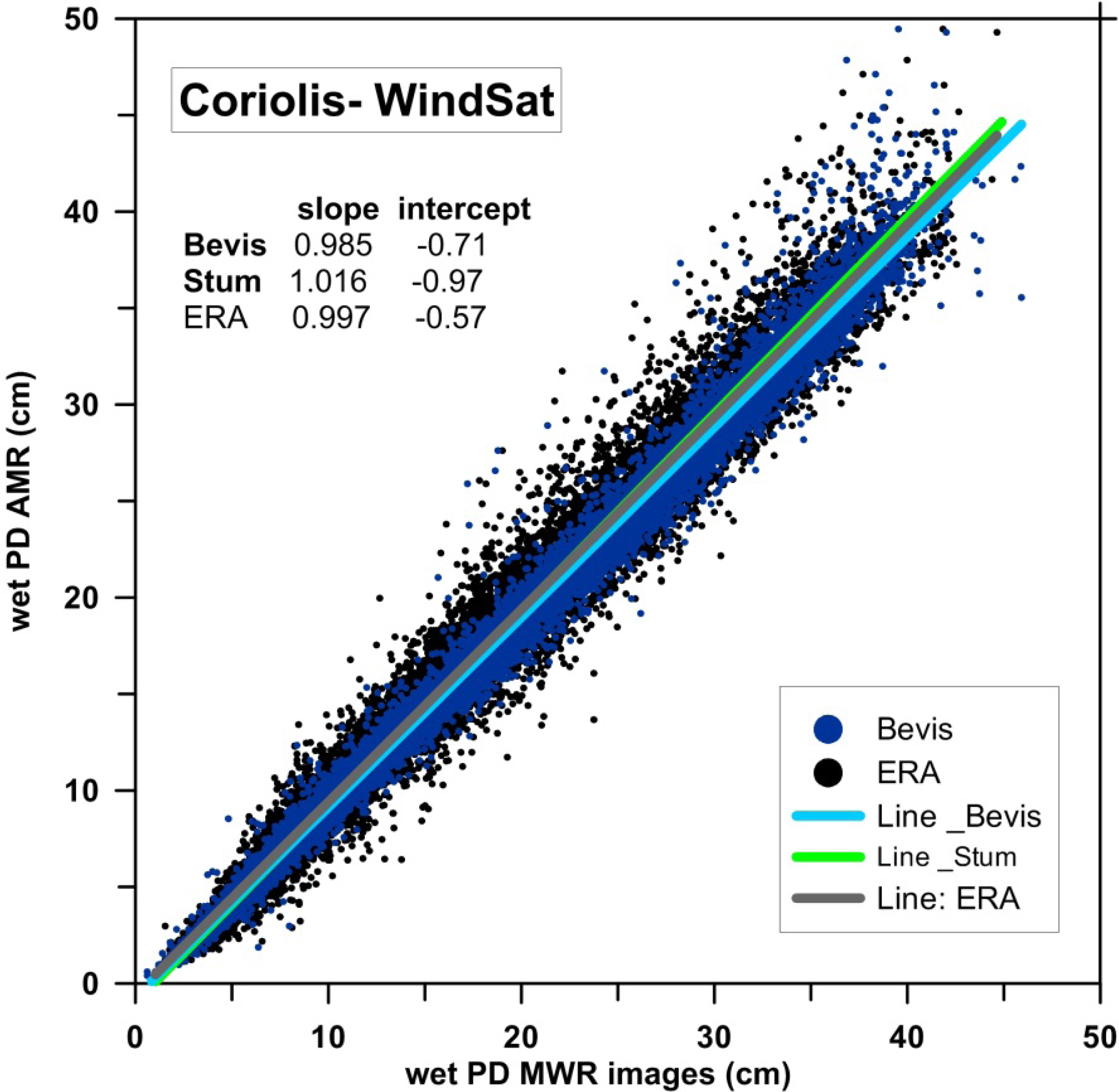
| COR | Bevis | 0.985 | −0.71 | 1.33 | 0.88 |
| Stum | 1.016 | −0.97 | 1.11 | 0.86 | |
| F15 | Bevis | 0.986 | −0.63 | 1.35 | 1.01 |
| Stum | 1.018 | −0.91 | 1.18 | 1.01 | |
| F16 | Bevis | 0.985 | −0.63 | 1.34 | 0.98 |
| Stum | 1.016 | −0.89 | 1.16 | 0.97 | |
| F17 | Bevis | 0.982 | −0.59 | 1.35 | 1.01 |
| Stum | 1.012 | −0.81 | 1.17 | 1.00 | |
| MTA | Bevis | 0.992 | 0.01 | 1.14 | 1.13 |
| Stum | 1.024 | −0.26 | 1.09 | 1.06 | |
| N15 | Bevis | 0.999 | 0.12 | 1.22 | 1,21 |
| Stum | 1.032 | −0.18 | 1.23 | 1.15 | |
| N16 | Bevis | 0.997 | 0. 10 | 1.14 | 1.14 |
| Stum | 1.029 | −0.17 | 1.14 | 1.07 | |
| N17 | Bevis | 0.978 | 0.13 | 1.24 | 1.20 |
| Stum | 1.010 | −0.14 | 1.13 | 1.13 | |
| N18 | Bevis | 0.996 | −0.09 | 1.20 | 1.19 |
| Stum | 1.029 | −0.37 | 1.13 | 1.10 | |
| N19 | Bevis | 0.993 | 0.06 | 1.17 | 1.17 |
| Stum | 1.026 | −0.21 | 1.12 | 1.08 | |
| TRM | Bevis | 1.004 | −0. 93 | 1. 38 | 1. 09 |
| Stum | 1.041 | −1.40 | 1.21 | 1.09 | |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fernandes, M.J.; Nunes, A.L.; Lázaro, C. Analysis and Inter-Calibration of Wet Path Delay Datasets to Compute the Wet Tropospheric Correction for CryoSat-2 over Ocean. Remote Sens. 2013, 5, 4977-5005. https://doi.org/10.3390/rs5104977
Fernandes MJ, Nunes AL, Lázaro C. Analysis and Inter-Calibration of Wet Path Delay Datasets to Compute the Wet Tropospheric Correction for CryoSat-2 over Ocean. Remote Sensing. 2013; 5(10):4977-5005. https://doi.org/10.3390/rs5104977
Chicago/Turabian StyleFernandes, M. Joana, Alexandra L. Nunes, and Clara Lázaro. 2013. "Analysis and Inter-Calibration of Wet Path Delay Datasets to Compute the Wet Tropospheric Correction for CryoSat-2 over Ocean" Remote Sensing 5, no. 10: 4977-5005. https://doi.org/10.3390/rs5104977





