1. Introduction
During the last decade, airborne laser scanning (ALS) data have been established as a standard data source for high precision topographic data acquisition and have also been used for estimation of forest variables [
1]. For forestry applications, the most commonly used method is to derive measures from the ALS data in raster cells approximately the size of a field plot, 100–200 m
2, and use the measures as independent variables in regression models to estimate forest variables such as mean tree height and stem volume [
2–
4].
The measures derived from the ALS data may be height percentiles and measures of the density of the vegetation as the fraction of ALS reflections from vegetation relative to the total amount of ALS reflections [
5]. In that case the regression models are based on an assumption that the stem volume is proportional to one or several height measures (e.g., percentiles of the height above the ground) multiplied by a density measure (e.g., the fraction of ALS data above a threshold height above the ground). Usually a log-log regression model is used. The regression model is often selected with best subset regression that selects the set of independent variables that result in the highest correlation with the dependent variable or with stepwise regression where independent variables are included or excluded in the regression model depending on their significance. The estimation of the regression model parameters is based on reference data from one study area [
6]. Another approach for stem volume or biomass estimation is to use a model based on the structure of the forest by calculating the canopy volumes for different height layers and using those measures as independent variables in a linear regression model [
7]. As defined in [
7], the canopy volume is the entire volume between the canopy and the terrain surface. Furthermore, the different canopy height layers account for height-dependent differences in canopy structure. The forest canopy can either be described by the first echoes directly or by a rasterized digital surface model (DSM) calculated from the first echoes. As the input for the canopy volume estimation, the canopy height normalization with respect to the digital terrain model (DTM) of the first echoes and the DSM, respectively, is required. For the calibration of the linear regression model, reference data is needed, for example, from a forest inventory. Depending on its sampling design (e.g., angle count sampling, fully callipered sample plot area, stand-based), the spatial unit used to extract the ALS-based measures can vary.
If the ALS data are dense enough, individual tree crowns may be identified from the data [
8–
12]. The identification is usually done by deriving a normalized digital surface model (nDSM) from the ALS data and defining local maxima in the nDSM as treetops. The nDSM is calculated by subtracting the DTM from the DSM and commonly has a pixel size of 0.5 m to 1.0 m. As a second step, segmentation of the nDSM around the local maxima can be done to derive more information about the tree crowns. Commonly used raster-based segmentation methods are, for example, the watershed segmentation [
13], the multi resolution segmentation [
14] or an edge-based segmentation [
15]. A common problem with identification of individual trees is that there is an underestimation in the result, especially for smaller trees below the dominant tree layer [
16].
The analyses based on nDSMs are faster and more robust than those based directly on ALS returns. However, the nDSMs still provide information about local variations in the forest that are related to individual trees. As demonstrated in [
17], the canopy volume regression model can also be applied to the rasterized ALS data. Derivation of measures from ALS data in smaller raster cells (e.g., 0.5 m to 1.0 m) could also be a way to compensate for the varying density of the ALS data [
18]. The density may vary, for example, due to the pattern of the laser scanner or overlapping strips. If measures are derived from the ALS from a 100–200 m
2 raster cell, these measures are largely influenced by the parts of the raster cell with the highest pulse density.
The purpose of this study is to compare methods to estimate stem volume, stem number and basal area. The first comparison is between measures derived from ALS data in 0.5 m raster cells and variables derived from larger raster cells corresponding to the size of the field plots for estimation of forest variables. The second comparison is between the canopy volume model [
7] and a model based on height percentiles and density of ALS data [
3] for estimation of stem volume in hemi-boreal forest. The third comparison is between area-based regression models and individual tree-based models for estimation of stem number and basal area.
2. Material
2.1. Study Area
The study area is located in the southwest of Sweden (Lat. 58°N, Long. 13°E). The most common tree species are Norway spruce (Picea abies) (38.5% of basal area), Scots pine (Pinus sylvestris) (28.0% of basal area), birch (Betula pendula and Betula pubescens) (18.0% of basal area), oak (Quercus robur) (6.0% of basal area), and other broadleaved trees (9.5% of basal area).
2.2. Field Data
In total sixty-eight circular field plots with 12 m radius were allocated during July and August 2009 (
Figure 1). The positions of the center of the field plots were measured using a DGPS with a few dm accuracy after post-processing. Within the field plots, the diameter at breast height (DBH) of all trees with DBH ≥ 40 mm were measured using a caliper and the tree species were recorded. For a sub‐sample of trees, the heights were also measured using a hypsometer. The sub-sample was randomly selected with inclusion probability proportional to the basal area of the trees.
The stem number
N in each field plot was calculated as the number of trees divided by the area
A of the field plot. The stem volume of each tree in the sub-sample, where the height was measured, was calculated with specific functions for pine, spruce [
19] and oak [
20]. For other species, the function for birch was used [
19]. To estimate the stem volume of all trees, species specific log-linear regression models were created for pine, spruce, oak, and other species based on the subsample of trees where the height was measured in all field plots simultaneously (
Equation (1)).
The root mean square error (RMSE) at tree level of the regression models was 137 dm3 (19.1%) for pine, 102 dm3 (15.9%) for spruce, 389 dm3 (7.7%) for oak, and 90 dm3 (25.9%) for other species. The stem volume of all trees was estimated with the respective regression models.
The stem volume
V in each field plot was calculated as the sum of the stem volume of all trees in the field plot divided by the area
A of the field plot. The basal area
BA was calculated in each field plot using
Equation (2):
2.3. ALS Data
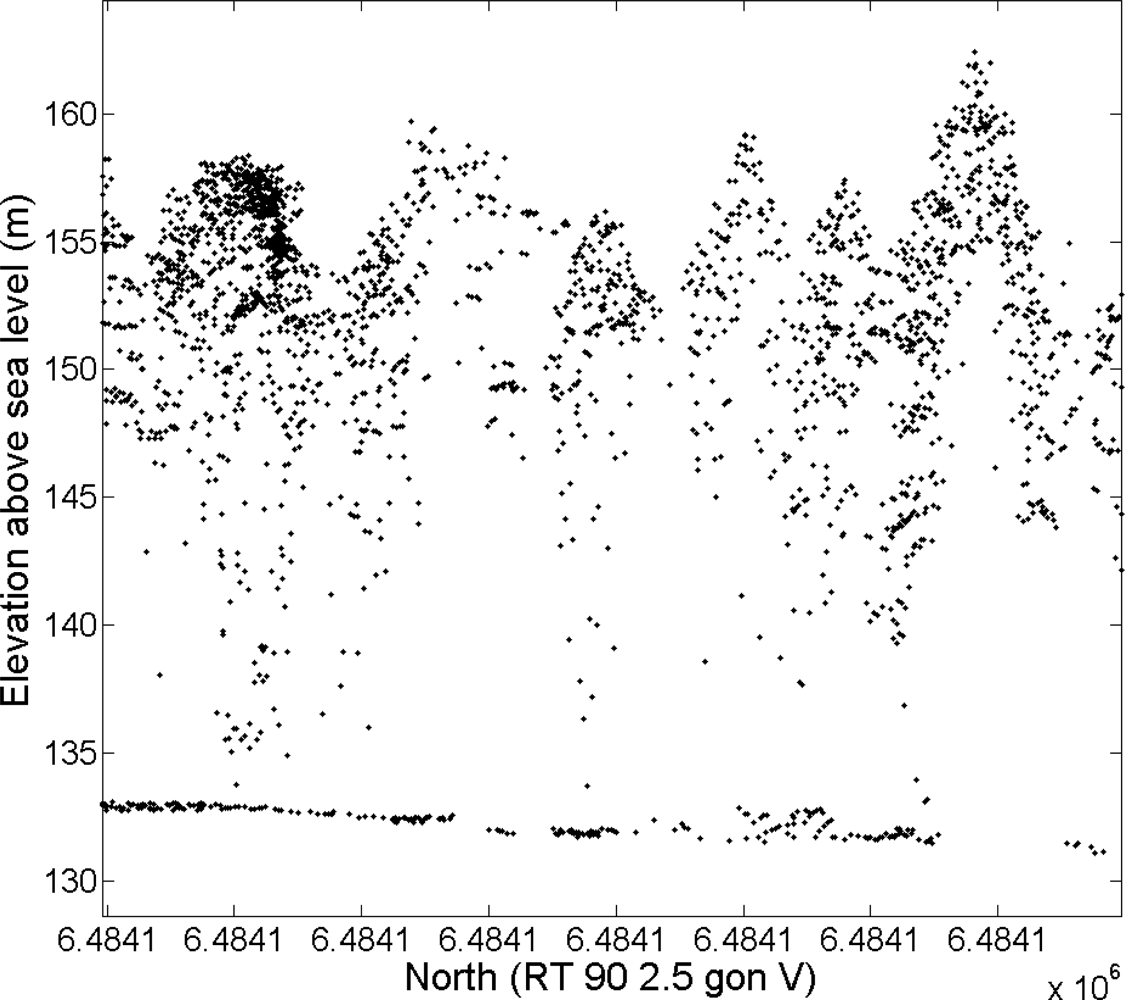
The ALS data were acquired on 4 September 2008 using a TopEye MKII ALS system with a wavelength of 1064 nm carried by a helicopter. The flying altitude was 250 m above ground and the average emitted pulse density was 7 m
−2. The first and last returns were saved for each laser pulse and the average return density was 11 m
−2 (
Figure 2).
3. Methods
3.1. Derivation of DTM from ALS Data
ALS returns were classified as ground or non-ground using the progressive Triangular Irregular Network (TIN) densification method [
21] in the TerraScan software [
22]. A DTM was derived as the mean value of the ground returns in 0.5 m raster cells. TIN interpolation was used for raster cells with no data.
3.2. Statistical ALS Measures
The
z-values of the ALS returns were normalized with respect to the DTM (
Equation (3)).
The following measures were derived from the ALS returns in each circular field plot with 12 m radius.
The 10th, 20th, ..., 100th percentiles of the normalized z-values from the ALS returns ≥ 2 m above the DTM in each field plot: p10, p20, ..., p100.
The total number of ALS returns: Ntot.
The number of ALS returns in intervals I1, I2, I3, and I4: N1, N2, N3, and N4.
The number of ALS returns ≥ 2 m and < 34 m above the DTM: Nveg.
The total number of first ALS returns: Nf,tot.
The number of first ALS returns in intervals I1, I2, I3, and I4: Nf,1, Nf,2, Nf,3, and Nf,4.
where
I1 was 2 ≤
z < 10,
I2 was 10 ≤
z < 18,
I3 was 18 ≤
z < 26, and
I4 was 26 ≤
z < 34 m above the DTM.
The vegetation ratio in each field plot was calculated as rveg = Nveg/Ntot. The fractions of ALS returns in intervals Ij were calculated as rhj=Nj/Ntot.
The following measures were derived from the ALS returns in raster cells of 0.5 m.
The mean normalized z-value of all ALS returns ≥ 2 m and < 34 m above the DTM: zmean. The mean of this value in all raster cells inside each field plot: hmean.
The mean normalized z-value of all first ALS returns in intervals I1, I2, I3, and I4: zf,mn,1, zf,mn,2, zf,mn,3, and zf,mn,4. The mean of this value in all raster cells inside each field plot: hf,mn,1, hf,mn,2, hf,mn,3, and hf,mn,4.
The maximum normalized z-value of all first ALS returns < 34 m above the DTM (i.e., a first return nDSM): zf,max.
The maximum normalized z-value of all ALS returns < 34 m above the DTM (i.e., an nDSM): zmax. The 99th percentile of this value in all raster cells inside each field plot: h99.
To calculate the canopy volume for each interval Ij, the relative proportion (between 0 and 1) of first return DSM raster cells, whose heights fell within the interval, was used: Nf,j,raster/Nf,tot,raster. The maximum height of 34 m was chosen based on the maximum tree height in the field data and on the observation that ALS returns ≥ 34 m above the DTM were all erroneous returns high above the tree tops, found in a few field plots. Raster cells without ALS returns were excluded when calculating mean values and percentiles.
3.3. Canopy Volume Estimation
The canopy volume was calculated for four different height classes
j = 1, 2, 3 and 4 using
Equation (4) [
7].
where
aj=
A ×
Nf,j/Nf,tot and
A is the total area of each field plot. For the calculation of the canopy volume, it is assumed that
A is represented by the total number of first echoes
Nf,tot. The canopy volume was also calculated for rasterized ALS data with
aj,raster=
A ×
Nf,j,raster/Nf,tot,raster.
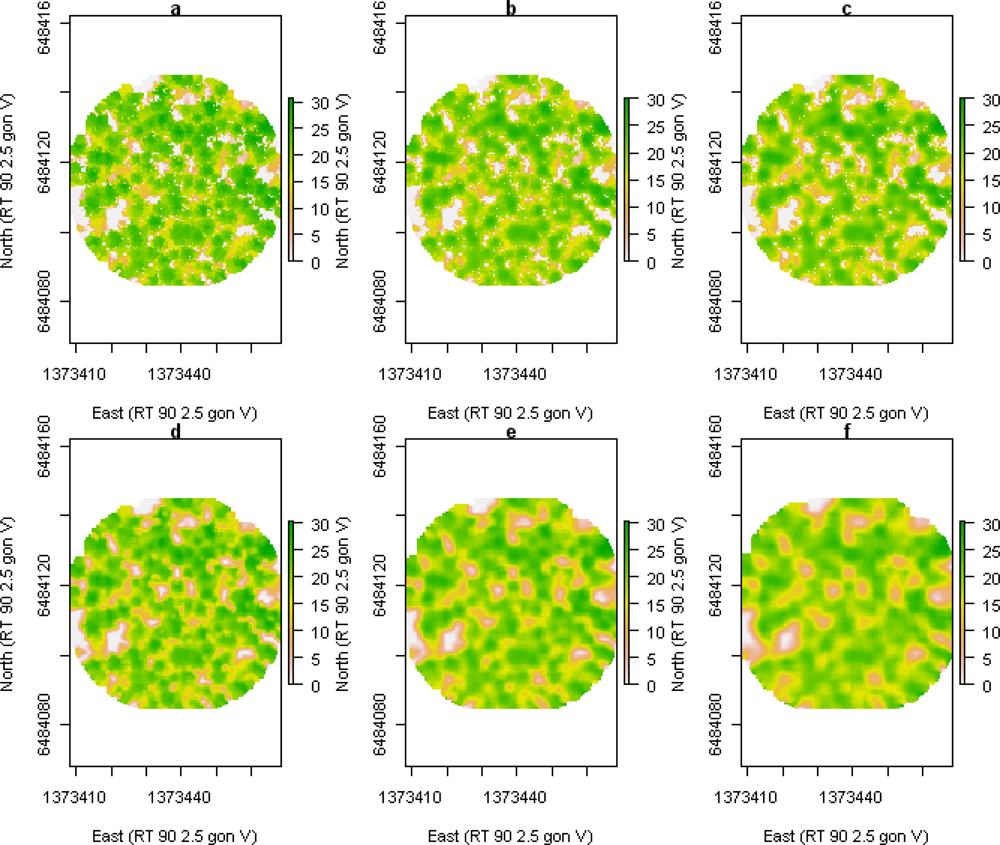
3.4. Local Maxima Detection
Local maxima detection was used to find individual tree tops in the raster of
zmax. Raster cells without ALS data were iteratively filled with the mean value of the eight surrounding raster cells. Before the local maxima detection was done, different filtering approaches were applied to the raster of
zmax to remove small variations in the surface model. Three different approaches were tested: in the first case, an m × m mean filter was applied to all raster cells, in the second case, the filter was applied only if
h99 ≥
hlim, and in the third case, the filter was applied only for local
zmax ≥
hlim, otherwise
zmax was used without mean filtering. This was done for
hlim = 15 and 20 m and for filter sizes m × m = 3 × 3, 5 × 5, and 7 × 7 (
Figure 3). For the local maxima detection, a 3 × 3 max filter was applied to the original and the filtered raster, respectively. Local maxima were defined where the raster values were equal in the raster before and after max filtering. Those raster cells represent the local maxima in the 3 × 3 windows. If several adjacent raster cells fulfilled the criterion, only the midmost raster cell was used as a local maximum. For each detected local maximum, the height of the corresponding raster cell was extracted:
hloc.
3.5. Stem Volume Estimation
The stem volume was estimated with five different regression models. The independent variables of the regression models were derived from the ALS returns in each circular field plot with 12 m radius in two cases (
Equations (5) and
(8)) and from the ALS returns in raster cells of 0.5 m in the other cases (
Equations (6),
(7) and
(9)).
The models in
Equations (5–
7) were selected with best subset regression. For the models in
Equations (5–
7), the stem volume was calculated as the exponential function of the estimated values. This introduces a bias (e.g., [
23,
24]). Due to this, the estimates were corrected for logarithmic bias by multiplying the result with the mean value of the stem volumes from the dataset on which the regression models were based, divided by the mean value of the stem volume estimates using the dataset on which the regression models were based [
25].
3.6. Stem Number and Basal Area Estimation
The stem number and the basal area were estimated with two methods: (i) an area-based approach and (ii) an individual tree-based approach.
In the area-based approach, the stem number (
Equations (10) and
(11)) and the basal area (
Equations (12) and
(13)) were estimated with different regression models. The independent variables of the regression models were derived from the ALS returns in each circular field plot with 12 m radius in two cases (
Equations (10) and
(12)) and from the ALS returns in raster cells of 0.5 m in two cases (
Equations (11) and
(13)).
The models were selected with best subset regression. The models in
Equations (12) and
(13) were corrected for logarithmic bias [
25].
In the individual tree-based approach, values of DBH were calculated using a relationship between DBH and tree height based on a regression model for the subsample of trees where the heights were measured (
Equation (14)):
where
DBHj is the DBH of tree
j and
hj is the height of tree
j and assuming that the heights of the local maxima
hloc were the tree heights. The regression model was based on all tree species since the tree species was not determined from the ALS data. The stem number was derived as the number of local maxima in a field plot divided by the area, and the basal area was calculated from the estimated DBH values.
3.7. Validation
The accuracy of the estimates from ALS data was validated using leave-one-out cross-validation for one field plot at a time: one field plot was excluded; the parameters of the models were estimated based on the remaining field plots and then applied to the excluded field plot to estimate forest variables. The accuracy was validated with the field-measured values using the RMSE and the bias (
Equations (15) and
(16)).
where
Yi is the stem volume, stem number or basal area in plot
i, and
n is the number of field plots. Furthermore, scatter plots were generated. The validation was done by both including all field plots as well as excluding field plots with > 80% basal area from oak, which were five field plots out of 68.
4. Results
The RMSE of the estimated stem volume was largest for the regression model in
Equation (5) and smallest for the regression model in
Equation (7) (
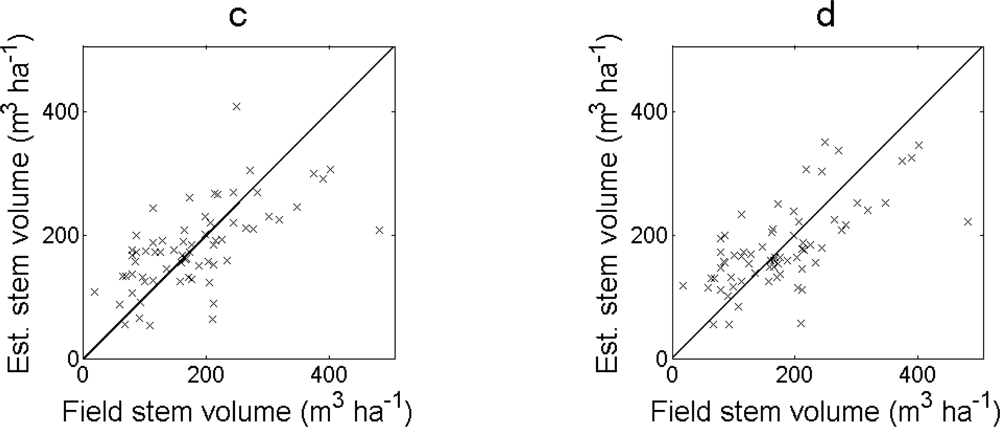
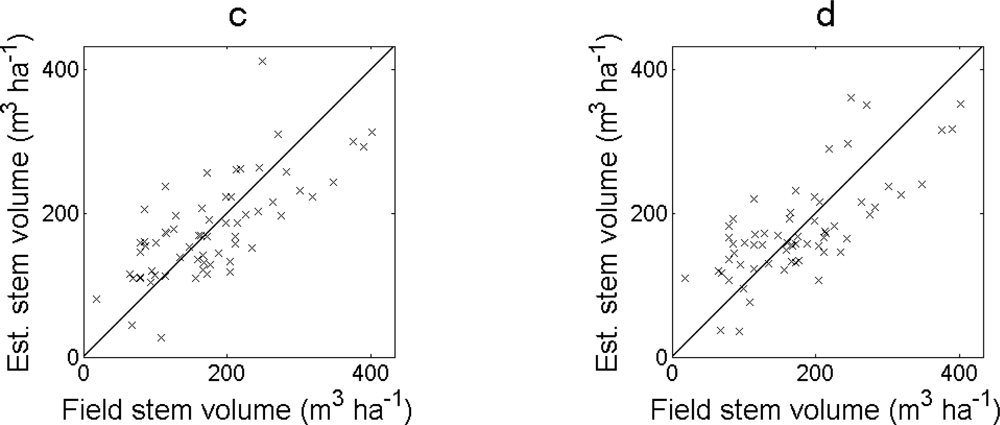
Table 1). The bias was less than 2% for all regression models. For larger field-measured values, the deviation between estimated and field-measured values was larger and a few outliers were observed (
Figure 4).
The RMSE of the estimated stem volume was smaller when excluding field plots with > 80% basal area from oak (
Table 2). The regression model in
Equation (7) had the smallest RMSE also in this case. The bias was still less than 2%. The estimated values showed fewer obvious outliers (
Figure 5).
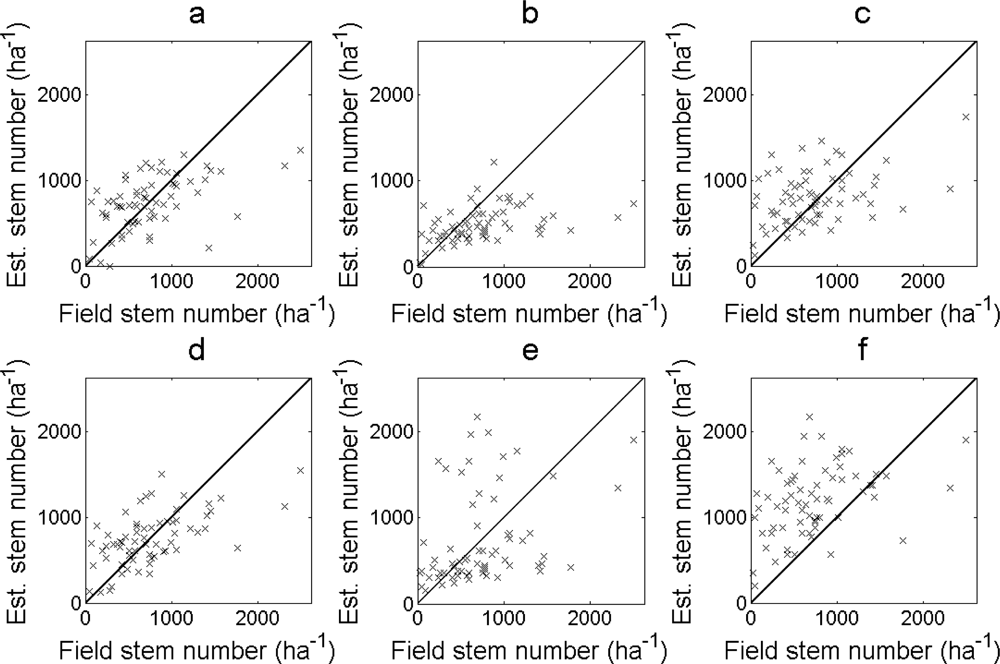
The RMSE of the estimated stem number was smallest for the regression model in
Equation (11) and second smallest for the regression model in
Equation (10). The bias was close to zero in both cases (
Table 3). When tree tops were identified from local maxima in the nDSM, the RMSE of the estimated stem number was in general larger for larger filter sizes and smaller for conditions when
zmax was filtered more often (
i.e., always filtered or lower
hlim). The bias was in general lower the more
zmax was filtered (
i.e., larger filter sizes or filtered more often). All cases showed outliers for large field-measured values and low estimated values (
Figure 6).
The RMSE of the estimated stem number was slightly larger for the regression model when excluding field plots with > 80% basal area from oak (
Table 4 and
Figure 7). When tree tops were identified from local maxima in the nDSM, the RMSE was larger when
zmax was always mean filtered or mean filtered if
h99 ≥ 15 m, and smaller for the other cases. The bias changed in a negative direction for all cases. The relative order of the RMSE and bias was the same as when all field plots were included.
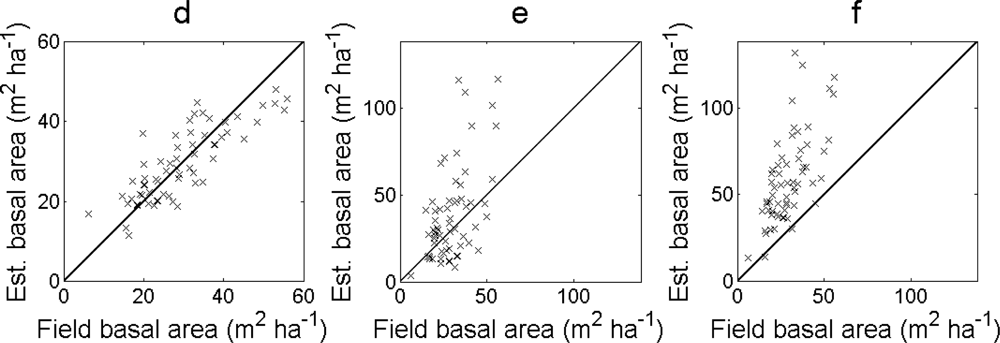
The RMSE and bias of the estimated basal area was smallest for the regression model in
Equation (13) and
Equation (12) (
Table 5). When the basal area was calculated from the DBH derived from the local maxima, the RMSE of the estimated basal area was in general smaller for larger filter sizes and for conditions when
zmax was filtered more often (
i.e., always filtered or lower
hlim). The bias was in general lower the more
zmax was filtered (
i.e., larger filter sizes or filtered more often). The estimated values deviated more from the field-measured values for the basal area calculated from the DBH derived from the local maxima than for the regression model (
Figure 8). In the first case, the basal area was overestimated for larger field-measured values.
The RMSE of the estimated basal area was smaller for the regression model in
Equations (12) and
(13) when excluding field plots with > 80% basal area from oak (
Table 6). When the basal area was calculated from the DBH derived from the local maxima, the RMSE was larger and the bias was higher. The relative order of the RMSE and bias was the same as when all field plots were included. The estimated values showed a similar pattern as when all field plots were included (
Figure 9).
5. Discussion
The most accurate estimates of stem volume, stem number and basal area were achieved with regression models that used rasterized (0.5 m raster cells) ALS data as input instead of 3D point cloud data directly. This suggests that the raster cells can compensate for the varying density of the ALS data and the variability of the forest properties within the field plots. For the two stem volume models that used input measures calculated at plot level from the normalized 3D point cloud directly, the canopy volume regression model was more accurate than the log-log regression model including the vegetation ratio and measures of the height of the ALS returns. However, the most accurate estimate was achieved with a log-log regression model including the vegetation ratio and a measure of the maximum height of the ALS returns derived from 0.5 m raster cells. Apart from the canopy volume models, the final models were selected with best subset regression, which means that the selection of independent variables was based on the reference data. Since the parameters of the regression model are also estimated based on the reference data, the model can be fitted very well to the reference data. However, it requires that the local reference dataset is large enough to base the models on. The canopy volume model is stable in the sense that the independent variables are not selected based on the local reference data, which might have advantages for estimation of stem volume for large areas. The stem volume used as ground truth was estimated with regression models with a comparatively high RMSE, which was around 20% for most of the trees. This makes the validation more uncertain. Excluding field plots with > 80% basal area from oak resulted in fewer outliers since most of the outliers were oak dominated field plots. Previous studies have reported larger errors for estimation of stem volume and basal area in mixed forest than in coniferous dominated forest [
2,
17,
26] since field plots with different properties are included in the same model. The stem volume of oak is generally higher than that of most other tree species having the same tree height. In this study, only five out of 68 field plots were oak dominated. This means that the models where all field plots were included were mainly based on forest with a smaller fraction of oak and resulted in large errors when they were applied to oak dominated forest.
The estimation of the basal area showed fewer outliers for large field-measured values than the estimation of stem volume. The reason may be that the outliers for stem volume were mostly oak dominated field plots and that the relationship between DBH and tree height is more similar for oak and other tree species than the relationship between stem volume and tree height. The RMSE of the regression estimates decreased slightly when excluding oak dominated field plots in the same way as for the estimation of stem volume. However, the RMSE and the bias of the basal area derived from local maxima increased when excluding oak dominated field plots. This may be because the regression model used for calculating DBH from the heights of the local maxima underestimated DBH for tall trees and the oaks were taller than the average tree. This negative contribution to the bias disappeared when excluding the oak dominated field plots and the result was a higher bias.
The bias of the estimated stem number changed in the negative direction when excluding oak dominated field plots. The reason was that the excluded field plots were outliers with an overestimated stem number. This may be due to the canopy of oak having more small variations than other species, which gives rise to several local maxima within the same tree crown. A few other field plots were outliers with an underestimated stem number for large field-measured values. This is expected when identifying trees from local maxima since trees below the dominant tree layer are not visible in the nDSM.
The estimates of stem number and basal area were more accurate for the regression models then when identifying tree tops from local maxima in the nDSM. The advantage of the latter is that a list of DBH estimates is produced at the same time. Distributions of DBH have previously been estimated from height and density measures from ALS data and theoretical diameter distribution models [
27] and as percentiles of DBH [
28]. The advantage of using local maxima in the nDSM is that they also describe the horizontal distribution of the ALS data that percentiles and density do not.
When tree tops were identified from local maxima in the nDSM, the RMSE of the estimated stem number was smallest when the nDSM was mean filtered for local zmax ≥ 15 m and largest when the nDSM was mean filtered for local zmax ≥ 20 m. The bias was large and positive when the nDSM was mean filtered for local zmax ≥ 20 m, and closer to zero when the nDSM was mean filtered for local zmax ≥ 15 m. The large positive bias in the first case was probably caused by small variations that gave rise to local maxima then identified as tree tops since the nDSM was filtered less often than for the other cases. The nDSM was filtered more often with the condition h99 ≥ 15 m than local zmax ≥ 15 m and the result was a lower bias in the first case. The same effect was visible for h99 ≥ 20 m and local zmax ≥ 20 m. The accuracy was similar when the nDSM was always mean filtered and when the nDSM was mean filtered if h99 ≥ 15 m. This is probably because h99 was rarely below 15 m, so in the second case the nDSM was almost always filtered.
For the estimated basal area derived from local maxima, the RMSE was smallest when the nDSM was always mean filtered or mean filtered if h99 ≥ 15 m, and largest when the nDSM was mean filtered for local zmax ≥ 20 m. The bias was lowest in the first case and highest in the second case. An adaptive filtering may improve the identification of local maxima corresponding to tree tops but the method may also be very sensitive to parameter settings. Additionally, the filter sizes are limited to odd multiples of the size of the raster cells. This means that the conditions for setting different parameters must be chosen carefully. In future work, definition of the conditions that can be applied to different forest types will be needed.
The RMSE of the estimated stem number was smallest when the nDSM was mean filtered with a 3 × 3 filter and the bias was highest. The RMSE of the estimated stem number was larger when a 5 × 5 and 7 × 7 filter was used and the bias was lower. This suggests that the larger filter sizes removed small variations in the nDSM that would otherwise have given rise to local maxima. However, the RMSE of the estimated basal area was smallest when a 7 × 7 filter was used and the bias was lowest. The bias was large and positive for the filter size 3 × 3 (i.e., the basal area was overestimated) and the basal area was overestimated for larger field-measured values for all filter sizes. Since the basal area was calculated from the DBH and the DBH was derived from the heights of the local maxima in the nDSM, this suggests that the heights of the local maxima overestimated the tree heights. The reason may be that not all local maxima corresponded to tree tops. Tree tops below the dominant tree layer do not give rise to local maxima in the nDSM. This means that the stem number will be underestimated if the nDSM is filtered so that only tree tops give rise to local maxima. If the number of local maxima is equal to the stem number, some of the local maxima do not correspond to tree tops and the heights of the local maxima overestimate the heights of the trees below the dominant tree layer. This may explain why the basal area was overestimated with a 3 × 3 filter size even though the estimate of the stem number was most accurate.
6. Conclusions
This study has compared estimation of forest variables from regression models based on measures derived from ALS data in small (0.5 m) raster cells and based on variables derived from the 3D point cloud. The RMSE of the results achieved from regression models based on 0.5 m raster cells were approximately 2–5% lower than those achieved from the 3D point cloud, which suggests that the smaller raster cells can compensate for the varying density of the ALS data. Once the ALS data have been rasterized, the raster cells may be aggregated to any area unit suitable for the application, which means that the approach is easy to integrate in operational work flows and may have advantages in terms of computational issues. Only one raster cell size was used in the study. The size of the raster cells could be optimized or the varying density of the ALS data could be compensated for in other ways, for example, by weighting the ALS returns depending on local density. This study has also compared a canopy volume model for estimation of stem volume in hemi-boreal forest with a model based on height percentiles and density of ALS data selected with best subset regression. The most accurate estimate was achieved with a log-log regression model including the vegetation ratio and a measure of the maximum height of the ALS returns, although the RMSE was only 1% lower. Hence, both model types may be used for estimation of stem volume. However, the selection of model type can be based on many considerations, for example, if the local reference dataset is large enough for best subset regression. Finally, the study has compared area-based regression models and individual tree-based models with different filtering conditions for estimation of stem number and basal area. The most accurate results were achieved from the regression models (7–11% lower RMSE for stem number; 39–40% lower RMSE for basal area compared to the best filtering conditions). However, an advantage of the individual tree-based models is that a list of DBH is estimated at the same time. When individual trees are derived from local maxima in an nDSM, the filter sizes and the conditions for filtering the nDSM must be carefully selected. Criteria for selection of filter sizes and conditions still remain to be defined for different forest types.