1.1. Semantics, Definitions, Conception and Standardizations
A landform peak can be defined as a point higher in elevation than the adjacent area. The shape is a geometric property of the peak point on an arbitrarily selected surrounding area (depending on the scale or level of detail) that is morphologically expressed as being sharp, blunt, oblong, circular, conical, or other. Both definitions are vague and subject to further discussion.
Professional mountaineers have perhaps the best knowledge of the peaks and other characteristics of the mountains from different regions worldwide, but it partly depends on their subjective perception and experiences. Researchers have been trying to measure and standardize mountain peaks for at least the past 120 years [
1–
6]. Defining a peak is a conceptual problem that requires a certain level of abstraction which is an essential part of the model, and which should have subsequent feasibility for the applicable automation process. The concept of a peak is contextually associated with several other concepts, such as the concept of the whole mountain, its roughness, locations of prominence and others, all of which are important for an enriched understanding of the problem in question. Size and shape (in context) are important criteria for the definition of peaks as a landform category or even for the construction of the landform taxonomy [
7]. Until now, definitions of peaks have been based mostly on tradition, experience and visual appreciations—on a subjective perception of the natural appearance of the peaks [
1]. The different views of the problem studied in this research can serve as sources of a comprehensive definition of a mountain peak, which can be further used as a source for an enhanced ontology of mountain peaks.
The concepts and definitions of the term “peak” must be considered in association with the wider topography (regional and global) and its relation to the term “mountain”, considering the entire mountain or range. The concept of a peak as a topographic and morphologic extreme in a specific geographical space has several other meanings in a semantic sense. However, our aim here is not to find absolute definitions, but merely to discuss the complexity of the subject of our study.
Just as the most significant peaks are visible from a distance, in the immediate neighborhood the peaks on the lower rising ground are also visible. The peaks may appear different when viewed from various distances (e.g., the peak appears oblong from 100 m, but circular from 1 km), from different directions—oblique or vertical views (e.g., sharp from one valley and blunt from another), when view at different times of the day (
Figure 1), and also in different weather conditions (including the visibility phenomenon) with different snow cover or during different seasons. Furthermore, peaks are conceived in different ways worldwide, which impacts on the terminology. For instance, the characteristics of the Alps, Carpathians, Himalayas or even the Pannonian Plain are quite distinctive. These factors depend on physical and environmental properties, such as the elevation above sea level, geological properties, the shapes of peaks, the illumination (
Figure 1), vegetation, and on the particular perception of an individual observer. These findings may lead to mentally various perceptions and consequently to different identification, conceptualization and classification by the observer. In order to provide a proper description of the peaks, the landscape in question and its properties has to be considered.
The relation of the peak to the roughness concept of the relief refers to the irregularity of a terrain, which may even be defined with self-similar fractals. The terrain roughness is geomorphometrically related to the periodic functions, where a texture is used to refer to the shortest wavelength in topography, and the grain used to refer to the longest significant wavelength [
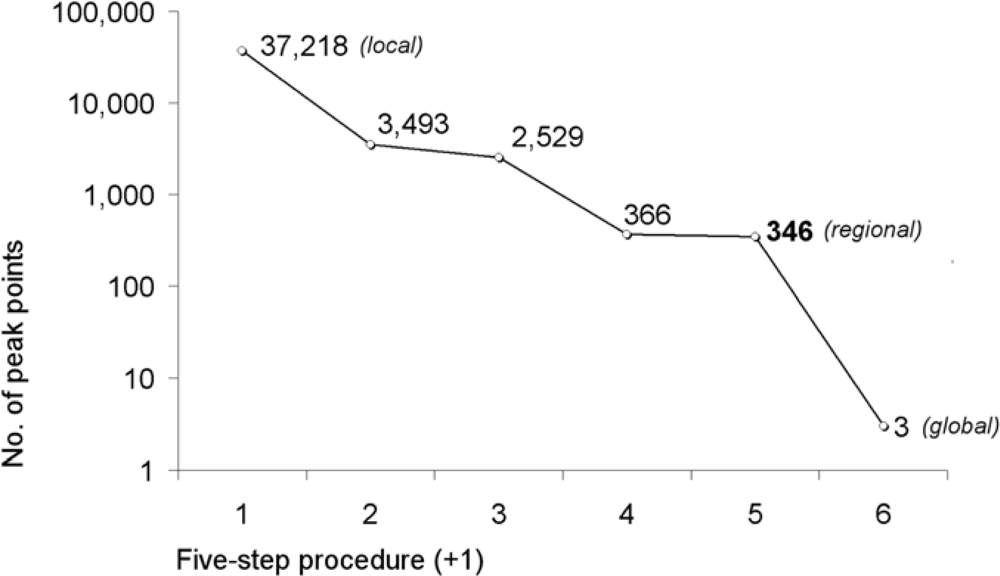
5]. Three types of peaks will be discussed according to their different size-scale (and level of detail): local, regional and global. The local peaks represent significant maximum points of the texture, while the regional and global peaks are related to the grain. The concept of roughness raises the many further complexities of the peaks e.g., the relation to aesthetic quantification.
Within common concepts, the peak is defined as being any point on a surface that is elevated by a certain difference in height with respect to its surroundings. A peak must be autonomous in the sense of possessing individuality, interest and other characteristics. The peaks might be considered in addition to the features that satisfy the especially subjective criterion of a “well defined morphology”. These primary criteria are referred to as topographic, morphologic and mountaineering [
2].
According to dictionary definitions, standards, and encyclopedias, e.g., [
7,
9,
10], the term peak is less technically defined,
i.e., mostly with reference to the morphologic properties of the surface that surrounds the higher point. These definitions may therefore be vastly dissimilar. Possible peak definitions are: “any rising ground that splits the mountain in its higher part”; “upper, usually folded part of the mountain”; “the highest point of the mountain”; “the point on a surface that is higher in elevation than all points immediately adjacent to it”. More precise definitions of this phenomenon concern size and shape and distinguish between the terms “peak” and “summit”. The summit means the highest elevation on a profile, whilst the concept of a peak depicts part of a summit with moderate to very steep sides [
11]. However, this last definition already reflects a corresponding ontology and cultural semantic aspects (e.g., concepts are not the same in English and the Slovenian language) [
1,
12]. The term “peak” is used in the study to correspond to a point.
The concepts of regional and global peaks should also be discussed. Regional peaks are complex features which occur in the most common definitions of peaks that are found in basic dictionaries, described by the UIAA, and defined by people who live in the mountains. This term is defined by a broader range of topographic, morphologic and other so-called mountaineering properties on a regional scale [
2]. Global peaks are a subset of regional peaks. Global peaks are limited to the most prominent or salient peaks of a given mountain (range), e.g., the entire Kamnik Alps. Global peaks have acquired cultural importance and have been of immense interest to humans over centuries or millennia. Therefore, they are defined according to the mountain range and/or according to their prominent location.
Peaks are also defined by referencing topographically related mountain ranges (
i.e., groups of mountains), mountains, massifs, hills, or hill-like features [
7]. Similarly, the terms “mountain” and “hill” also vary in definition worldwide. Thus, only the term “mountain” is discussed here in order to support its wider geo-connoted conception. The concept of a mountain is more complicated and subjective than the concept of a peak, and it involves aesthetical, ecological, chronological, and other factors. The term mountain is not a real physical (bona fide) object. It can even be interpreted as a fiat object, which only exists in the human understanding and division of the landscape [
12–
15]. However, it is clear that mountains exist as real correlations of everyday human thought and action, and that they form the archetype for geographic objects [
12].
A mountain can be defined as a natural rise in the Earth's surface that usually has a peak (or a summit) [
8]. Similarly, the term mountain is defined as a landform that sufficiently extends above the surrounding terrain over a limited area with comparatively steep sides and a peak. A peak (a highest point or a highest ridge) and the mountainside (part of a mountain between the peak and the foot) are considered to be the main sections of a mountain [
16].
The mountain as an object comprises the following morphometrical parameters: size, perimeter length, maximum elevation, slope, mean or average slope, slope gradient, relative or local relief, relative massiveness (according to stage of erosion), shape, roughness, texture and grain,
etc. [
5,
17,
18]. The following are those definitions that contain quantitative operational definitions: mountains are usually steeper and taller than hills; they are often considered to be hills that rise over 600 m (a.s.l.) in height; another study utilizes the higher vegetation zones as the important criterion for defining it as a mountain [
4]; a mountain is defined with an altitude (height), slope and relative height distinction; the lowest limit is 300 m in the altitudes of 65°N and 55°S and up to 1,000 m at the equator. A team of Kapos [
19] used criteria based on altitude and slope in combination with a depiction of the world’s mountain environments to form their definition. They proposed seven classes based on slope and local elevation range. The most important for the definition of a mountain are: (classes 1 to 3) elevations >2,500 m; (class 4) elevations 1,500 to 2,500 m and slope ≥2°; (class 5) elevations 1,000 to 1,500 m and slope ≥ 5° or local elevation range >300 m (radius of 7 km); and (class 6) elevations 300 to 1,000 m and local elevation range >300 m outside 23°N to 19°S (radius of 7 km).
1.2. Appropriate Data Sources
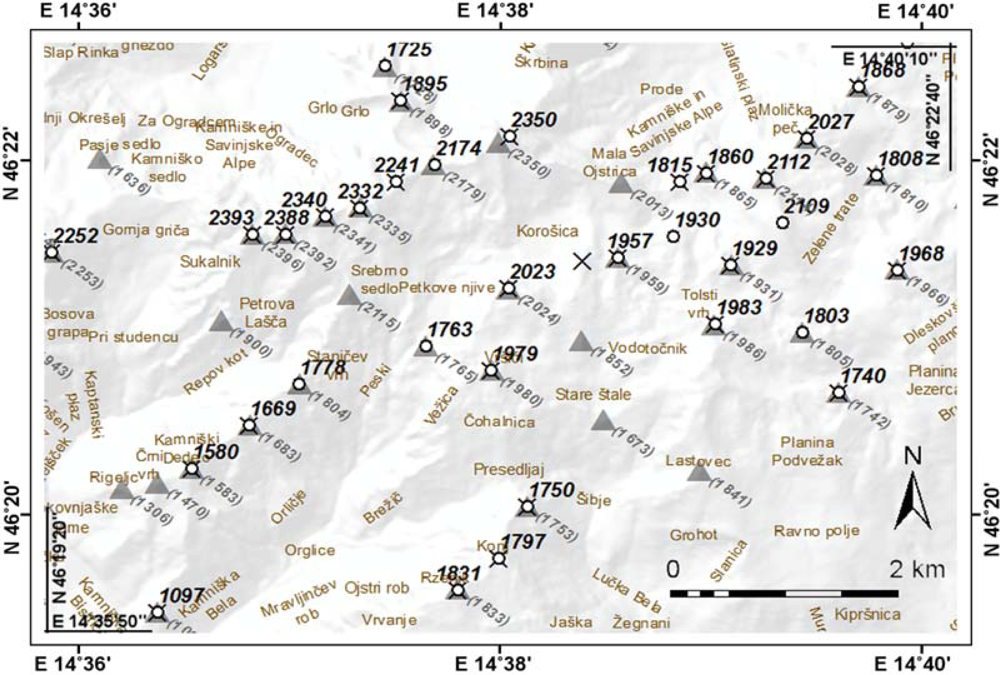
The mapping of peaks and mountains has generally been performed manually through fieldwork and the visual interpretation of topographic maps, aerial photographs and satellite images. An example (
Figure 2) presents an old Josephine military topography (scale 1:28,800) from the end of 18th century that was verified with an overlaid modern topographic map demonstrating that the peak positions are in this case considered to be correct (scale 1:25,000, DTK 25). On the old map, some peaks are clearly detected but with their positions have been incorrectly mapped. One of the reasons for this is that some peaks had not been climbed yet when this old map was produced.
The problem of the remote sensing techniques that use aerial photographs and satellite images, from which modern maps are produced, is that a large amount of semantic information is inherently hidden in these data sources. Moreover, the detection and interpretation of topographic peaks is problematic in forest areas.
Another potential data source for studying topographic peaks is a digital elevation model—DEM (or digital terrain model—DTM). The DEM allows a very high level of automation for the study of geomorphologic features [
20]. Its geomorphological quality and appropriate (high) scale/resolution (
Table 1) are crucial for successful applications [
21,
22]. However, the lack of both properties is a distinctive problem for real data sources application. Typical sources of the DEM are maps, aerial photographs and satellite images, as mentioned before, which is not encouraged. Fortunately, more independent and higher quality data sources are available nowadays based on LIDAR or SAR technologies as important remote sensing techniques for topographic data collection.
A geomorphologically higher quality DEM would be required in order to study the peaks of flatter areas, compared to the requirements in the hilly areas, such as the Pannonian Plain. The resolution of the DEM controls an optimal scale and the level of detail of the peak determination, particularly local peaks. It should reflect the discussed topographically-relevant terrain roughness. The integrative study of more alternative datasets (and techniques) in a geographical information systems (GIS) environment can improve the judgments in morphologically enhanced studies [
22].
1.3. Morphometric Algorithms Based on a Digital Elevation Model (DEM)
The extraction techniques of peaks have evolved considerably—from manual in the past, through computer assisted, to various automated methods over the last decades. The automated application of the detection of peaks and the delineation of their shape is discussed through morphometric algorithms based on a geomorphologically accurate DEM. The algorithms for local peak detection are considered as an ordinary problem, while the algorithms for topographic (regional and global) peak detection demand more complex solutions to the problem of feature extraction and recognition, all based on morphometric image processing or spatial analysis techniques.
Local peaks are computed using the most elementary numerical (computer-based) peak detection approach from the DEM. The algorithms are based on an assessment of local extremes, e.g., the Peucker and Douglas method [
23] that detects every rise in ground elevation. The problem can be resolved with tools as part of both: standard remote sensing (image processing) and GIS (spatial analysis).
The existing solutions for the numerical implementation of regional peaks incorporate mostly only topographic criteria, e.g., an algorithm to extract the number of peaks based on a morphological smoothing method [
24], and an algorithm based on the minimum drop surrounding peak criterion [
29].
The procedures for global peak detection use a considerably larger surrounding area than the procedures for regional peak detection. Their definition is either related to (A) the entire mountain range, or (B) a prominent location.
(A) Most of the developed automated techniques concentrate on the detection or classification of whole mountains or mountain ranges, e.g., the algorithms for feature-matching [
3], the component-labeling algorithm applied to the mountain terrain class [
17], a local histograms analysis [
25], and mathematical-morphological based algorithms [
16].
(B) A number of studies have attempted to establish prominent locations (peaks) using numerical algorithms. Their characteristic technique is to study specifically cultural responses that influence human behavior, including beliefs, taboos, and rituals,
etc. Prominent peaks are explored by analyzing their properties according to their wider surroundings. This includes: an exposure index, cumulative viewsheds, defining location hierarchies (nested peaks), taking into account the fuzziness of general multi-scale landscape morphometry, a comparative evaluation according to a multi-scale prototypicality of peaks identified, a computation of horizon lines based on a viewshed analysis, and the identification of the salient points on the horizon based on a hierarchical decomposition of the projected horizon,
etc. [
14,
26–
30]. A comparison of the automated implementation of local, regional and global peaks can be seen in
Table 1.
The comprehensive peak detection procedure should also consider the morphological shape of peaks. The topographic shape delineation of a peak is a more complex conceptual and implementational problem than its detection. The algorithms that touch on the problem of shape analysis relate to the issue of peak prominence discussed in the previous paragraph. The automated shape analysis procedures can additionally improve the strategy for detecting peaks.