Abstract
Quantification of biophysical parameters of urban trees is important for urban planning, and for assessing carbon sequestration and ecosystem services. Airborne lidar has been used extensively in recent years to estimate biophysical parameters of trees in forested ecosystems. However, similar studies are largely lacking for individual trees in urban landscapes. Prediction models to estimate biophysical parameters such as height, crown area, diameter at breast height, and biomass for over two thousand individual trees were developed using best subsets multiple linear regression for a study area in central Oklahoma, USA using point cloud distributional metrics from an Optech ALTM 2050 lidar system. A high level of accuracy was attained for estimating individual tree height (R2 = 0.89), dbh (R2 = 0.82), crown diameter (R2 = 0.90), and biomass (R2 = 0.67) using lidar-based metrics for pooled data of all tree species. More variance was explained in species-specific estimates of biomass (R2 = 0.68 for Juniperus virginiana to 0.84 for Ulmus parviflora) than in estimates from broadleaf deciduous (R2 = 0.63) and coniferous (R2 = 0.45) taxonomic groups—or the data set analysed as a whole (R2 = 0.67). The metric crown area performed particularly well for most of the species-specific biomass equations, which suggests that tree crowns should be delineated accurately, whether manually or using automatic individual tree detection algorithms, to obtain a good estimation of biomass using lidar-based metrics.
1. Introduction
Urban trees perform ecosystem functions such as sequestering carbon, improving air quality and providing general amenities [1,2]. Urban trees in the USA store 700 million tonnes of carbon (tC) with a gross carbon sequestration rate of 22.8 million tC/yr [3]. The quantification of urban tree carbon storage can lead to a better understanding of the role of urban trees in global carbon accounting for greenhouse gas emissions [4]. However, uncertainties exist in such quantification due to a lack of direct measurements of urban tree allometry and biomass [5].
Only 10% of the trees in urban areas in the USA are publicly-owned; the remaining 90% are on private property [6]. Thus the management of urban trees varies immensely. At the same time, urban trees are subjected to different stresses—they often grow on compacted soil, are subjected to intense pruning, have very little space in which to grow, are improperly staked, etc. [7]. These factors affect the rate of growth as well as the shape and form of the trees, which makes the ability to predict biophysical parameters such as tree height, biomass, and crown dimensions more difficult than with forests, where trees are more homogenous in their growth and form for a particular locality and species. Unlike traditional forests, where trees experience a change in growth and allocation after certain events like thinning, low density of trees in urban environments reduces potential competition for light and other resources [8].
Urban tree inventories can provide estimates of trees’ biophysical parameters. But urban tree inventories are labor intensive, and thus expensive, because they often place emphasis on measuring individual trees [9]. Cost-effective approaches such as using optical remote sensing and airborne lidar data may provide alternatives for urban tree inventories. Additional cost-savings may occur in urban tree inventories because they are more complex and often take into account a wider range of parameters at the individual tree level.
High resolution to moderate or coarser resolution satellite images and airborne hyperspectral data have been widely used to estimate forest biophysical parameters [10,11]. Some examples include estimating forest biomass using moderate resolution Landsat Thematic Mapper [12], estimating leaf area index using hyperspectral HyMap data [13], and estimating several forest inventory parameters using high resolution IKONOS imagery [14]. Issues on using remote sensing for estimation of forest biophysical parameters have been reviewed by [15] and [16].
Because of their ability to record vertical structure, airborne lidar data are more useful than two-dimensional optical images in estimating forest biophysical parameters like tree height, aboveground biomass, leaf area index, crown, etc. ([17–25]). Lidar based estimation of forest biophysical parameters has been implemented at the grid level [26,27], stand level [28–30], sub-stand segment level [31], plot level [32–34], tree cluster level [35], and individual tree level [36–38]. Only a few parameters, such as height and crown diameter, can be measured directly from the lidar data (e.g., [39,40]). For most biophysical parameters, lidar-based estimation generally involves establishing the relationship between the metrics describing the distribution of lidar-derived heights in a given area and metrics measured (or derived from) in situ measurements [26,41].
The synergistic integration of vertical structure information from lidar data with spectral information from optical remote sensing data improves forest canopy characterization [42]. Such integration has been used to increase accuracy for species classification [43,44], height estimation [45], and biomass/volume estimation [34].
The estimation of biophysical parameters, such as biomass, using lidar relies on a strong relationship between the amount of foliage and the various tree components since foliage normally is the main element blocking laser pulses [41]. Despite a growing body of studies using small-footprint discrete return lidar for forest parameter estimation, studies using distributional approaches, which exploit the relationships between distributional height metrics (e.g., mean, range, skewness, percentiles, etc.) and forest biophysical parameters, are rare [26,35,46,47] at the individual tree level [38,48]. Furthermore, there are few to no related studies for individual trees in urban landscapes. Our assumption is that metrics computed directly from the lidar point cloud, rather than from an interpolated raster surface which represents the outer canopy return data and misses the returns from the inner foliage, will improve the estimation of the biophysical parameters.
This study evaluates the potential of height distribution metrics derived from normalized lidar point clouds to estimate total height, diameter, crown radius, and biomass for individual urban trees (defined as vegetation 1 m or greater in height). The study also evaluates the potential improvements to urban tree biomass estimation when high-resolution spectral remote sensing is combined with airborne lidar data.
2. Biomass Estimation Using Airborne Lidar
Forest biomass estimation using lidar data is dependent on how well the height of the tree is related to diameter. Naesset [49] found bias of the difference between predicted and actual diameter at the stand level to be 0.15–0.74 cm, which was better than using methods based on field inventory and photo interpretation. Biomass is estimated based on height metrics obtained from lidar data [26,50,51] or based on lidar-measured crown variables, e.g., crown width [40] or canopy cover density [49]. Table 1 shows the results of recent biomass/volume studies in primarily coniferous forests (with some deciduous forests) conducted using lidar data. Because these studies were conducted using different sensors in different forest types, the root mean square error (RMSE) values may not be directly comparable, but in general less of the overall variance is explained in deciduous stands.

Table 1.
Studies using small footprint lidar to estimate aboveground biomass/volume in forests.
Popescu et al. [40] found the explanatory power of the lidar-derived metrics for predicting biomass for deciduous plots lower than that for pines. One factor contributing to this may be the deliquescent tree forms of hardwoods which result in greater amounts of woody biomass into lateral branches, thereby making the height-volume or height-biomass relationship noisier [23,52,55]. But, additional differences between coniferous and deciduous species related to (1) crown material (leaves versus needles) and (2) branch size and structure may also affect the lidar penetration depth and resulting precision of stand characteristics derived from laser data [49]. Naesset [49] found that only 2–3% of pulses reached an area of the canopy 2 m or less above ground in a young deciduous forest plot, and 20–25% of pulses reached the same portion of the canopy in a mature conifer stand. The difference in penetration rates may affect the residuals for stand variables that are related to canopy density. Difference in crown shape between hardwoods and softwoods has an effect on the height estimation from lidar data, and hence on the prediction of biomass or volume. Nelson [56] found that as the crown shape changes from conical (most softwood) to spherical (most hardwoods) the estimates of lidar-based forest height tend to be 16–25% higher with elliptical and spherical canopies than with a conical canopy.
Later studies [41,49] reported a higher biomass and volume for spruce compared to deciduous trees of similar size. The narrow and conical-shaped crown of spruce trees allows for a relatively large portion of the laser pulses to hit low in the tree crowns, whereas more rounded crown shapes of deciduous trees normally will result in laser point clouds located higher up in the canopy.
A mixture of coniferous and deciduous trees within stands degrades the precision of lidar-based biomass estimation and presents a major challenge in practical applications [49]. There is a relative scarcity of component biomass equations, along with substantial variation in the observed estimates from existing equations [57]. Jenkins et al. [57] compiled component biomass equations for several hardwood and softwood species and developed equations to estimate component biomass as a proportion of total above ground biomass, which shows that hardwoods distribute more biomass in the branches than the stem as compared to softwoods, especially for trees with smaller diameters. Contrary to assumption, the hardwood trees distribute less biomass in foliage than the softwood trees.
Naesset [58] estimated stand volume of Norway spruce and Scots pine using various tree lidar-based metrics of canopy height and canopy cover density. Two test sites were used, one with 97% pine and the other with 69% spruce and 28% pine. The pine site had a coefficient of determination (for stand volume estimation) of 0.4 and the spruce site 0.8. Norway spruce is usually taller (24–30 m), with a relatively compact crown spread (8–12 m). Scots pine is usually shorter (9–12 m) with a large crown spread (8–9 m). Even though both are conifers, the Norway spruce has a greater height to spread ratio. According to the “apical-deliquescent” hypothesis, a spruce distributes its biomass more to stem than to branches. This might explain the difference in the coefficient of determination, though Naesset [58] points out several other factors—such as a larger footprint size and lack of stratification—that may also have contributed to the low R2 in pine.
Biomass is dependent on site properties, management regime, and stand age. Thinning changes the distribution of biomass within the crown. Gary [59] found a strongly skewed distribution of needles and branch wood in the top half of the canopy of unthinned 80-year old lodgepole pine stand compared to a normal distribution in thinned stands. Within species, the distribution of aboveground biomass among the various components changes with stand age. Peichl and Arain [60] found the relative proportion of stem biomass to total tree biomass increased from 25% for a 2 year old stand to 69% for a 65 year old stand of white pine, while the relative contribution of foliage and branches decreased with stand age.
3. Methodology
3.1. Study Area
The study area is on Tinker Air Force Base in central Oklahoma, USA (latitude: 35°25′35.43″N; longitude: 97°24′37.73″W) (Figure 1). The area represents a typical suburban residential area with detached and row houses with trees, both broadleaves and conifers, growing along the road and in the yards and parks. The base is around 20 km2 (5,000 acres) in area and has 472 buildings [61]. There are about 6,600 trees, the most common species being Eastern red cedar (Juniperus virgiana), Austrian pine (Pinus nigra) and Siberian elm (Ulmus pumila) [62].
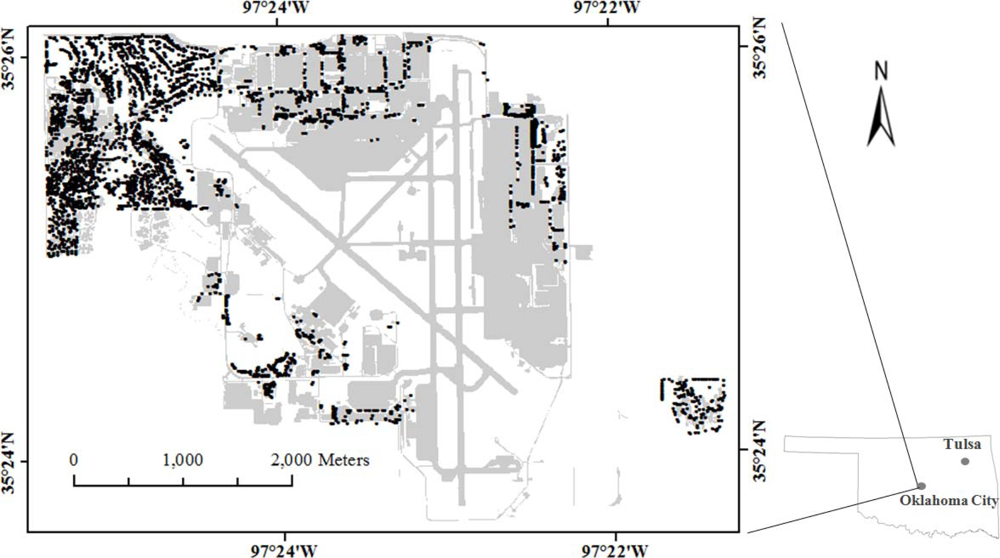
Figure 1.
Study area at Tinker Air Force Base, Oklahoma. Trees measured are shown in darker shades.
3.2. Lidar Data
Lidar data were acquired using an Optech ALTM 2050 lidar system in July 2004 in leaf-on condition. The Optech ALTM 2050 is a small-footprint multiple-return lidar system which uses a 1,064 nm laser. The provided lidar data did not have any return numbers. There were about 8 pulses per m2. The system was flown at a 640 m flight height with a swath overlap of 40%. The pulse repetition frequency was 50 KHz and the scan frequency 45 Hz. The scan angle was less than 15 degrees.
To do away with any complications arising from classifying lidar data using height-filtering algorithms in urban areas, a 2 m-resolution bare-earth digital elevation model (DEM) delivered by the vendor (Tobin Aerial Surveys, Texas) was used. The DEM was evaluated by the vendor using ground control points and vertical accuracy within ±15 cm was reported. A normalized point cloud was computed by subtracting the digital elevation model (DEM) of the area from the elevation of lidar returns. In the normalized point cloud, all points with less than 1 m height were filtered out, which resulted in retaining only the lidar returns from trees and other urban objects. With the help of the normalized point cloud and a color orthophoto (acquired 17 February 2004 with a spatial resolution of 10.2 cm), lidar points within each tree with distinctly separable crowns (3,564 in total) were manually selected. The boundary of each crown was delineated by computing the planimetric convex hull around the lidar points within each tree in ArcGIS. We opted for a manual approach to avoid the discrepancies common when using an automated crown-delineation algorithm, especially in cases where tree crowns are overlapping with other trees or with buildings. Only a few individual tree crown delineating algorithms have been tested in urban landscapes (e.g., [63]), where conditions are different than forested environments. Various lidar metrics were computed for lidar returns within each individual tree (Table 2).

Table 2.
Candidate predictor variables computed using normalized point clouds from individual trees.
3.3. High-Resolution Satellite Image
High-resolution satellite data of the area was obtained from a Quickbird satellite image (DigitalGlobe Inc., USA) acquired 17 May 2005. The image was radiometrically corrected, sensor corrected, and geometrically corrected. The image consisted of a panchromatic image with 0.6 m spatial resolution and a 4-band multispectral image with 2 m resolution. The spectral resolution of the Quickbird image is shown in Table 3.

Table 3.
Spectral resolution of the Quickbird image.
Subsequent to preprocessing, three vegetation indices were computed as follows: normalized difference vegetation index (NDVI) [64], soil-adjusted vegetation index (SAVI) [65], and modified soil-adjusted vegetation index (MSAVI) [66]. For each of these three indices, and for spectral bands one through four, tree-specific descriptive statistics (minimum, maximum, mean, and standard deviation) were calculated (Table 4). NDVI enhances vegetation but is sensitive to optical properties of soil background, especially in areas with considerable soil-brightness variation. SAVI minimizes the effect of soil by introducing an adjustment factor to NDVI to account for first-order soil variation and differential red and near-infrared flux extinction through vegetation [65]. Unlike NDVI, SAVI vegetation isolines do not converge to the origin and are independent of soil background [67]. The constant factor varies from 0 to infinity depending on the vegetation density. A factor of 0.5 was used for this study as it has been found optimal in a wide range of conditions. MSAVI replaces the constant factor of SAVI with an iterative self-adjusting factor.

Table 4.
Predictor variables computed from Quickbird imagery 1.
3.4. Field Measurement
Field measurements of the urban trees used for this study were made in 2006. The coordinates of each individual tree were recorded using a GPS unit. A high resolution digital orthoimage was used in the field to verify the location of each tree. Various tree attributes were recorded including species, diameter at breast height, tree height, condition of tree, crown radius, age class, etc. [62]. Diameter at breast height (dbh) was measured to the nearest inch using a logger’s tape. If the tree was co-dominant, the largest leader at breast height (1.37 m) was measured and recorded. Tree height was measured to the nearest foot (0.3048 m) using an Opti-Logic 100 LH Laser Rangefinder Hypsometer. On windy days several measurements were taken and averaged. Crown radius was measured at two directions perpendicular to each other with a logger’s tape to the nearest foot from the center of the trunk to the drip line of the canopy by using a nail to secure the tape to the trunk. For this study, a total of 3,562 trees, 60 broadleaf species and 12 conifer species, were used (Table 5). Most of the conifers are shorter than the broadleaf trees. Among broadleaf species, Platanus occidentalis and Acer saccharinum are, in general, taller than the other species. The descriptive statistics for diameter at breast height and crown size are shown in Table 6. Ulmus pumila, Acer saccharinum, and Platanus occidentalis are among those having larger diameter and crown widths. Conifers generally have smaller dbh and crown size than broadleaf trees.

Table 5.
Number of trees measured in the field by height class.

Table 6.
Statistics for diameter at breast height and crown radius of the trees measured in the field.
3.5. Variables Predicted
The biophysical parameters of the trees, including tree height, diameter at breast height, mean crown radius, and biomass were estimated. Tree biomass is usually estimated either through direct measurement such as destructive sampling, or through use of biomass equations and tables [68]. Because the direct method of biomass measurement is often impractical, allometric equations developed for specific tree species and localities are often used to estimate biomass. As there are few allometric equations developed specifically for urban trees (e.g., [69]), most studies rely on the equations based on forest trees. Allometric equations developed for a tree species in different parts of the world differ little in the values of the parameters [70,71]. This suggests that biomass equations developed for certain tree species in one part of the world can satisfactorily predict the biomass of the species in another part of the world, albeit with some bias in the predictions [72]. The USDA Forest Service has developed and evaluated models to quantify the benefit of urban trees—namely i-Tree Streets ( http://www.itreetools.org/streets) and Urban Forest Effects Model ( http://nrs.fs.fed.us/tools/ufore). These models also use allometric equations from urban trees of the specific region where available.
For the present study, due to lack of availability of urban tree allometry, forest-derived aboveground biomass equations were used in most cases. The species-specific allometric equations were chosen such that they represent the climatic conditions of the study area, where available, and were based on trees with sufficient range of dbh. Equations used to estimate above ground biomass for major species are listed in Table 7. McHale et al. [8] compared biomass equations derived from terrestrial lidar scanning of urban trees to equations developed from traditional forests and found that variability ranged from 60–300%, but when a variety of equations are used for the entire urban forest community, variability was reduced to 10%. In the present study, we used multiple species-specific biomass equations, rather than one or two general biomass equations for all the trees in the area, as this should reduce the potential errors associated with using forest-based allometry.

Table 7.
Biomass equations used to estimate individual tree aboveground biomass.
Once all significant variables were identified among the lidar descriptive statistics (Table 3), best subsets regression was used in Minitab version 16.1.1 software (Minitab Inc., Pennsylvania, USA) to select the best subset of candidate predictor variables to be included in each final model. Multicollinearity of all the independent variables were tested using variance inflation factors (VIF) [79]. If any of the variables had VIF value >10, then the variables with the highest VIF was removed, and the VIF computed again with the new set of variables. This process was repeated until all the variables had VIF of ≤10. The best subsets regression was performed with the remaining independent variables that were significant (α = 0.05). The regression models were evaluated using the following three criteria to select the best model [80]: (1) maximum adjusted coefficient of determination (R2adj), (2) minimum Mallows Cp, and (3) minimum mean square error (MSE). In this study, the most parsimonious models with Cp ≤ (p + 1), where p is the number of variables in the model, were chosen.
Each resulting model was subjected to residual and influential analysis. While selecting the final model, the parsimony principle was employed whereby fewer variables were preferred over slightly better values of R2adj or Cp. The predictive capability of the selected model was assessed using cross-validation multiple-correlation [81] and prediction sum of squares (PRESS) [82]. Outliers in the model were identified using jackknife residuals [83], where the multivariate distance for each observation is calculated using means, variances, and covariances that do not include the observation itself. Each outlier, as defined by jacknife residuals, was investigated carefully to determine the cause of the outlier. Only when the outlier was due to unnatural causes, such as lidar returns from power wires or dead trees, or anomalous measurements, was it discarded from the data analysis. Outlier removal was particularly important for this study because there was a lapse of two years between the lidar flight and the field data collection. In the two years between lidar data collection in 2004 and field data collection in 2006, some trees had growth in height and crown diameter, others were pruned, and some were completely removed.
4. Results and Discussion
4.1. Relationship between Tree Height and HMAX
The lidar return with maximum height (HMAX) from an individual tree is representative of the return coming from the topmost branch of the tree, and is most often related to the field-measured height of the tree. The mean field-measured height was higher compared to mean HMAX in both conifers (field measured 7.2 m, HMAX 7. 1 m) and broadleaf trees (field measured 10.1 m, HMAX 9.6 m). The height underestimation may have become compounded because of the two year lapse between the lidar flight (2004) and field data collection (2006), in which time the height of tree could have increased.
Previous studies (e.g. [84]) using individual tree height with lidar have found similar underestimation in forested environments. Hyyppä et al. [85] and Persson et al. [36] found an underestimation of 0.14 m and 1.73 m respectively in Norway spruce and Scots pine forests. The difference in bias between the two studies was attributed to lidar point density. Hyyppä et al. [85] used a point density of 24 points/m2, which was considerably denser than the present study. Using fairly dense lidar data (10 points/m2) in a mixed Bavarian forest, Heurich et al. [86] obtained similar underestimation of 0.42 m for deciduous trees, but a much larger underestimation of 0.65 m for coniferous trees. The smaller underestimation of conifers in the present study can be attributed to lower growth during the two year lapse period compared to broadleaf trees.
The distribution of the field-measured total height and HMAX for broadleaf trees shows a larger number of trees in taller height classes having lower HMAX than field-measured height, while for shorter trees fewer numbers of trees had lower HMAX (Figure 2). This positive shift in height distribution of field-measured broadleaf trees is likely due to growth during the two year lapse. In conifers, however, the total number of trees was lower for most of the trees in the middle height range (Figure 2). For very tall and very short trees, HMAX overestimated the total height. This result does not conform to the findings by other studies showing lidar underestimates the tree height consistently. In mixed temperate forests of Northern Idaho, Falkowski et al. [87] found that lidar underestimated high tree height and overestimated low tree height, which is similar to the results obtained for broadleaf trees by the present study. Brandtberg et al. [19] also found similar results in an oak-dominated forest in West Virginia using leaf-off lidar data. Since the overall height growth for the conifers over two years’ period was minimal, the height underestimation in the upper height class may also be due to lidar pulses missing the conifer top or to random errors in field measurement where it is sometimes harder to locate the tree-tops, leading to over- or under-estimation of tree heights [25,88].
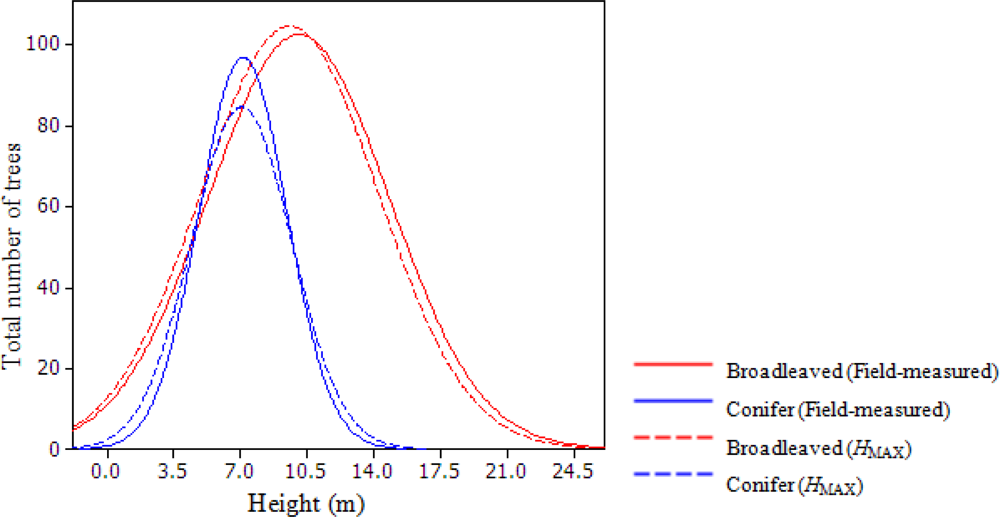
Figure 2.
Distribution of trees in each class showing field measured total height (solid line) and lidar measured maximum height HMAX (dotted line) of conifers and broad leaves.
The field-measured tree height and HMAX of 3562 total trees had an R2 of 0.887 and RMSE of 1.34 m (Figure 3). Conifers (R2 = 0.789), had a poorer relationship with HMAX than the broadleaf trees (R2 = 0.889) (Figure 4). The increased probability that lidar pulses missed the conical and pointed tip of the conifers may have contributed to the lower R2 than in broadleaf trees, whose tips are not as pronounced as that of conifers.
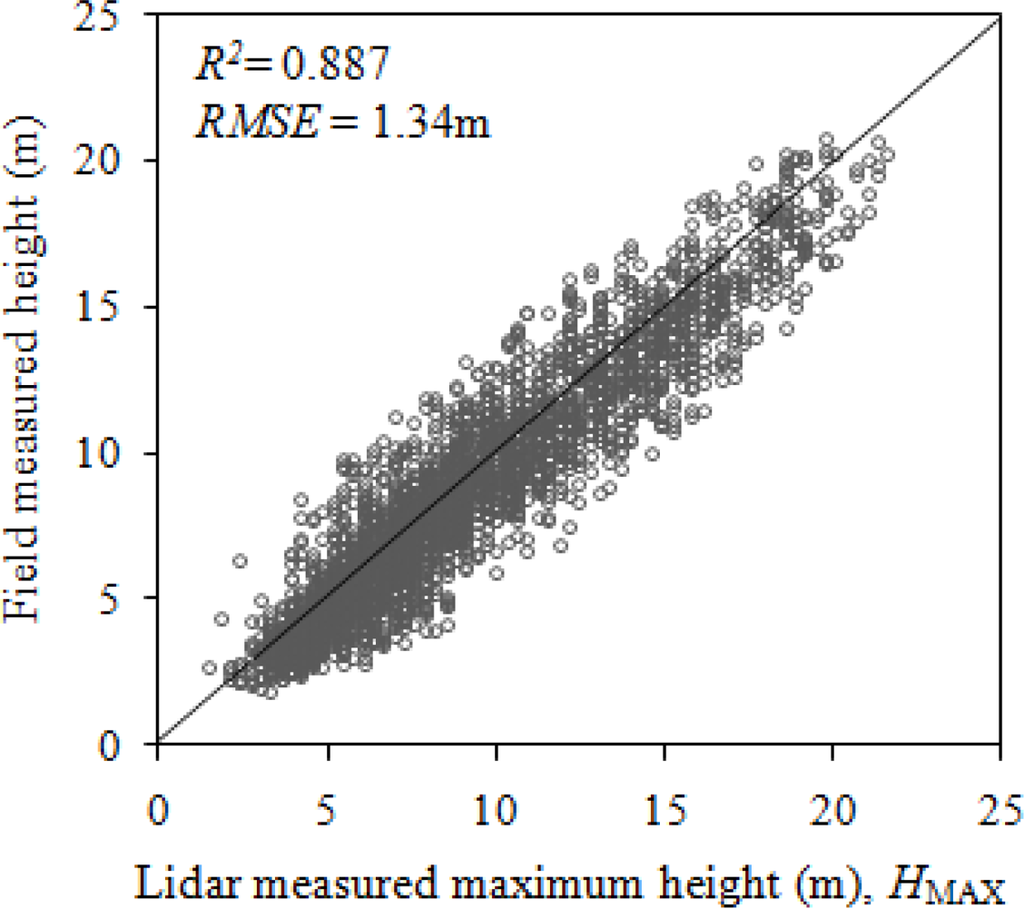
Figure 3.
Relationship between field-measured height and lidar-measured maximum height.
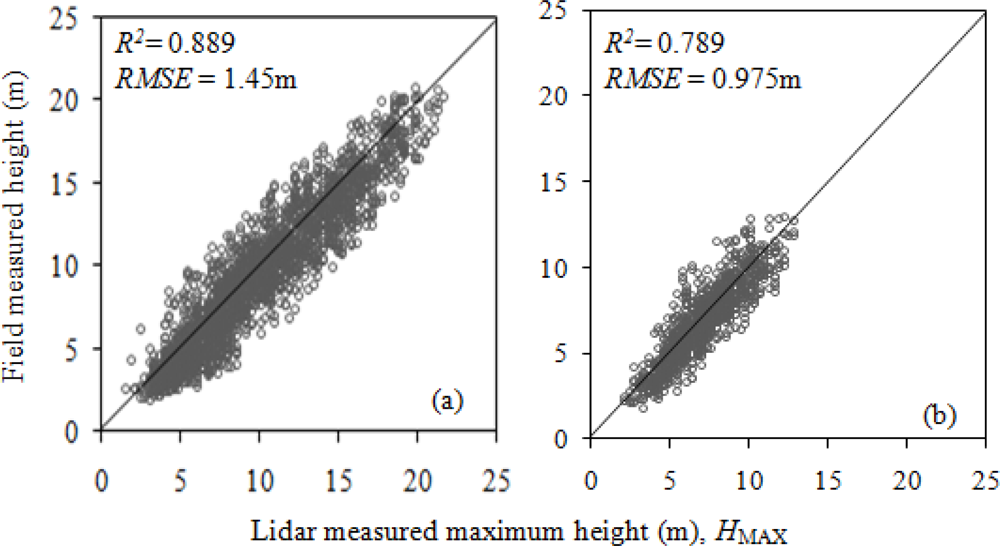
Figure 4.
Relationship between field-measured height and lidar-measured maximum height in (a) broadleaf trees (total 2292 trees) and (b) conifers (total 1058 trees).
The less-pronounced tips of broadleaf trees also contribute to error in field-measured height. The well-defined tips of conifers, on the other hand, make it easier to spot the tip in the field. Two factors are important for achieving good height estimation of individual trees using lidar: (1) correct height filtering and hence accurate estimation of bare-earth surface, and (2) correct delineation of the crown, which reduces error due to false tree tops. Poorer crown boundary delineation can contribute to false tree tops and reduce the R2 considerably [89].
Some species had a better relationship and others had a worse relationship with HMAX (Figure 5). Ulmus parviflora and Acer saccharinum had R2 below 0.7. These species have a rounded crown with no distinct tree top, thus making it difficult to identify the tree top for the lidar as well as for the field measurer.
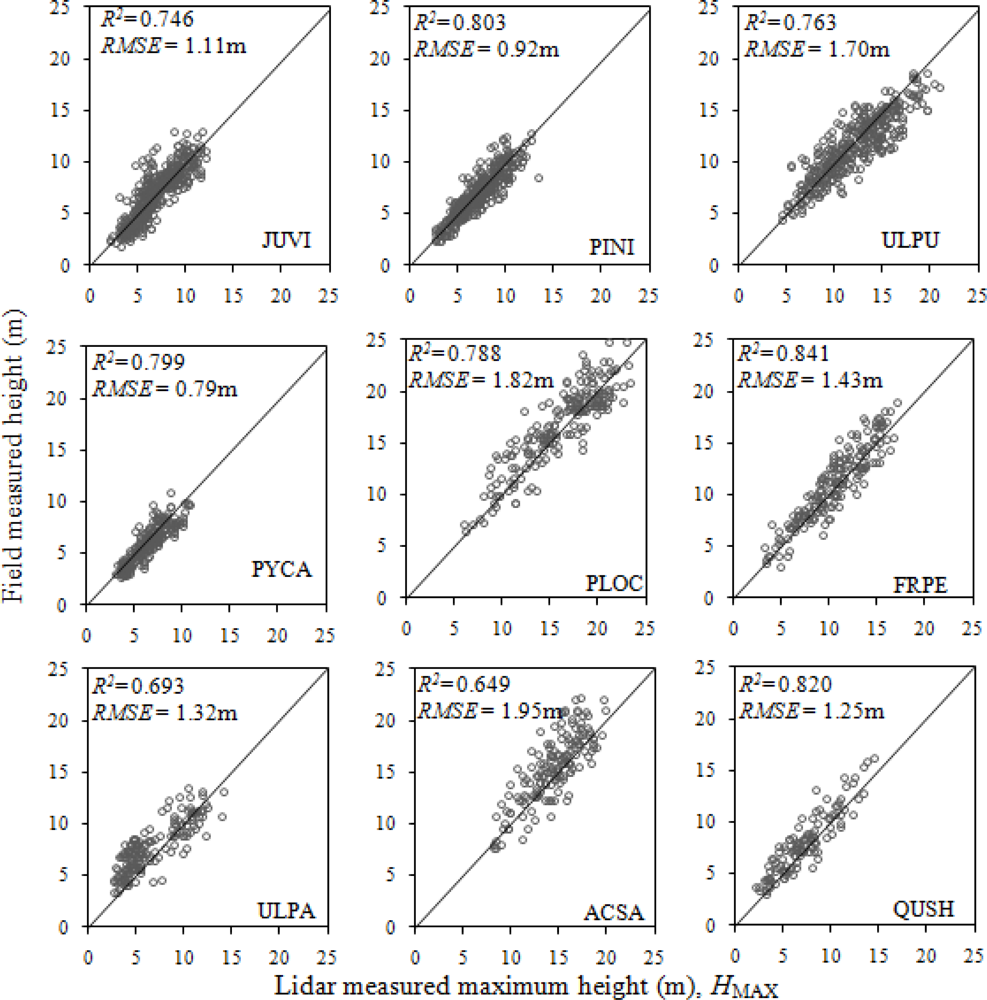
Figure 5.
Relationship between field-measured height and lidar-measured maximum height in major species of the study area. Tree species abbreviations: JUVI = Juniperus virginiana, PINI = Pinus nigra, ULPU = Ulmus pumila, PYCA = Pyrus calleryana, PLOC = Platanus occidentalis, FRPE = Fraxinus pennsylvanica, ULPA = Ulmus parviflora, ACSA = Acer saccharinum, QUSH = Quercus shumardii.
4.2. Diameter at Breast Height
Diameter at breast height (dbh) was estimated with crown-based metrics and height-based metrics separately (Table 8). For both sets, one variable with the best relationship was chosen. Among crown-metrics, crown perimeter, Cp, performed best in all cases, and among height-based metrics different variables performed best in different cases. HMEAN had a good fit with all trees, broadleaf trees, and both conifer species, while for broadleaf species the best variables were HMAX or one of the upper quantiles. Crown metrics had a better R2 value than height-based metrics. The result is similar to that reported by Chen et al. [38] who also found that crown metrics performed better than height metrics to predict basal area and stem volume for individual trees in a deciduous oak woodland in California.

Table 8.
Relationship of diameter at breast height (cm) with crown-size and height metrics.
Broadleaf dbh is better estimated using either crown or height metrics than conifer dbh. If measuring crown size with relatively high accuracy is achievable, crown metrics are better predictors of dbh than height-based metrics. Height-based metrics can also give a robust estimate of dbh for individual broadleaf trees, but are not as good for conifers. Persson et al. [36] and Popescu et al. [48] found both height and crown width significant for predicting dbh for individual trees in forested areas. Estimation of diameter at breast height can be greatly improved through complementary use of terrestrial lidar, as has been demonstrated for urban trees by Omasa et al. [90].
4.3 Crown Radius
A strong correlation (R2 = 0.90) was obtained from the relationship between field measured crown radius and the radius measured on the trees identified with lidar (Figure 6(a)). Field-measured crown radius was the average of the two perpendicular measurements taken in the field. Lidar-based radius was computed by assuming the tree crown as a circle:
.
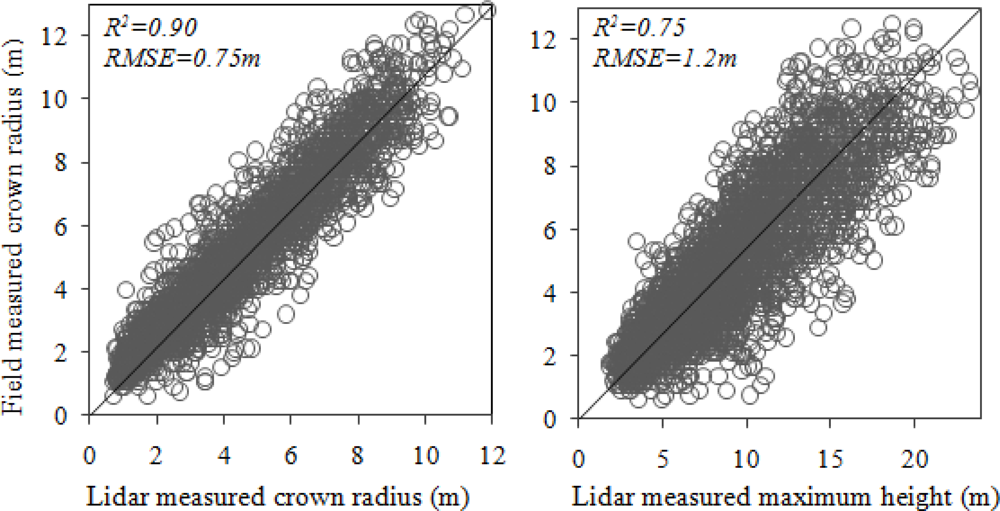
Figure 6.
Relationship of field-measured crown radius (m) with (a) lidar-measured crown-radius (m) and (b) lidar-measured maximum height (m) for all trees.
Because crown radius is often a function of tree height—taller trees have larger crowns and smaller trees have smaller crowns—field-measured crown radius is related to lidar-measured maximum height but has a lower R2 of 0.75 (Figure 6(b)).
An attempt was made to estimate the crown radius using only height-based lidar distribution metrics (Table 9). Lidar height metrics from conifers have a poorer relationship with crown radius compared to those from broadleaf trees. Among broadleaf species only Acer saccharinum has the lowest R2. Among the metrics, HMEAN, HMAX, and the upper quantiles resulted in the best fit with crown-diameter.

Table 9.
Results of regression analysis of crown radius with height-metrics.
4.4. Aboveground Biomass
Aboveground biomass of conifers had the lowest R2 value among broadleaf trees and all trees combined (Table 10). The lower performance of the biomass models for all trees, broadleaf trees, and conifers compared to individual species (Table 11) might have resulted from aggregating the species-wise models to estimate biomass for broader categories. This might have compounded the variation of biomass between species within the category.

Table 10.
Results of regression analysis of aboveground biomass (kg) of individual trees.

Table 11.
Results of regression analysis of aboveground biomass (kg) of individual trees.
Predictors based on Quickbird performed poorly for all trees, broadleaves and conifers (Table 10). While studies have found good stand-level biomass prediction capacity using hyperspectral or multispectral data in forested areas [91–95], studies exploring the relationship between spectral metrics from high-resolution imagery and forest biomass are largely lacking. Instead of using spectral metrics, most studies have used crown-size information from high-resolution imagery to predict forest biomass. Leboeuf et al. [96] used Quickbird-derived tree shadow fraction, which is calculated as the ratio of the area of tree shadows to the ground reference, to predict biomass in black spruce stands in Canada. Gonzalez et al. [97] used Quickbird-derived crown diameter to predict biomass of old-growth forests in California, but found higher uncertainty and lower accuracy than with lidar-derived height. This is due to the poorer relationship between crown diameter and biomass than between lidar-derived height and biomass.
Species-specific relationships had a much higher R2 (from 0.68 to 0.84), Table 11 and Figure 7. Naesset [49] also suggested the use of careful stratification to improve accuracy. The metric crown area (CA) performed well in all the species biomass models, except for Q. schumardii. In Q. schumardii the number of crown returns explained more variance than crown area. Popescu et al. [40] similarly found that lidar-derived crown diameter alone explained 78% of the variance associated with pine biomass.
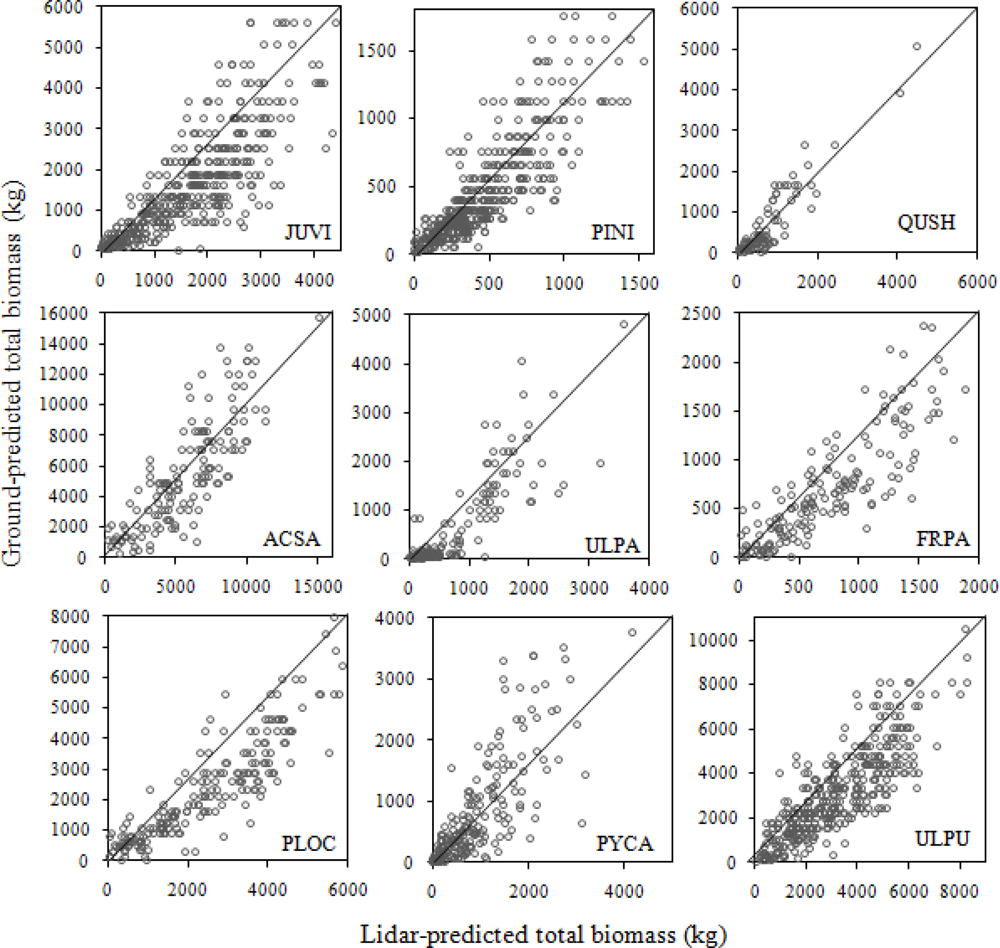
Figure 7.
Relationship between total ground-predicted tree biomass and lidar-predicted biomass of major species of the study area. Tree species abbreviations: JUVI = Juniperus virginiana, PINI = Pinus nigra, ULPU = Ulmus pumila, PYCA = Pyrus calleryana, PLOC = Platanus occidentalis, FRPE = Fraxinus pennsylvanica, ULPA = Ulmus parviflora, ACSA = Acer saccharinum, QUSH = Quercus shumardii.
5. Conclusions
This study is one of the early attempts at estimating biophysical parameters for individual trees in an urban area based on point-based lidar distributional metrics. A high level of accuracy was attained for estimating tree height (R2 = 0.89), dbh (R2 = 0.82), crown diameter (R2 = 0.90) and biomass (R2 = 0.67) using LiDAR based metrics for pooled data of all tree species. Tree height of most species had a good relationship with lidar-measured maximum height, except for species with a round crown and no distinct tree top, which makes it difficult to detect the tree-top for the lidar as well as for the field measurer. The good relationship between field-measured and lidar-measured crown radius indicates that individual tree crown delineation from lidar data was fairly accurate. Species-specific relationships had much higher R2 (0.68 for Juniperus virginiana to 0.84 for Ulmus parviflora) than for general broadleaf (0.63) and conifer (0.45) relationships. Using a general, instead of species-specific, allometric relationship should improve the biomass models for broadleaves and conifers. When estimating the biomass of individual trees during an urban forest inventory, a priori stratification of trees by species affords the use of lidar-based biomass equations developed for the particular species rather than those developed for broader classes. We found that the metric crown area (CA) performed particularly well for most of the species biomass equations. It is imperative that tree crown be delineated accurately, whether manually or using automatic individual tree detection algorithms, to obtain a good estimation of biomass using lidar-based metrics. Though spectral metrics from high-resolution satellite imagery did not perform particularly well in predicting individual tree biomass, future studies can explore other vegetation indices and grey-level texture (such as [98,99]) to improve the prediction capacity of high-resolution imagery. Prediction models from this study, even though developed from trees from a specific urban area, can be applied to other urban areas with similar climate and species composition, and when the lidar data were acquired with mission parameters similar to this study, e.g., density of 8 pulses/m2 and similar footprint size. These kinds of lidar-based prediction models will help in accurate quantification of urban carbon storage at the individual tree level. Future studies should develop models that can predict other biophysical parameters such as leaf area index, stem volume, etc., and management attributes useful for the urban planner such as the pruning level required, potential hazard rating, and age-class of the individual trees. Applicability of the models can be improved by incorporating data from other urban areas, and, if available, using allometric equations based on trees from urban areas rather than forests.
Acknowledgments
This study was funded by grants from NASA (grant number NNS06AA57G) and USDA (NIFA PINEMAP Project). Authors would also thank Jennifer McKee for data collection and Jessica Dorr and the Virginia Tech Conservation Management Institute for providing lidar data.
References
- McPherson, E.G.; Nowak, D.; Heisler, G.; Grimmond, S.; Souch, C.; Grant, R.; Rowntree, R. Quantifying urban forest structure, function, and value: The Chicago Urban Forest Climate Project. Urban Ecosystems 1997, 1, 49–61. [Google Scholar]
- Bolund, P.; Hunhammar, S. Ecosystem services in urban areas. Ecol. Econ 1999, 29, 293–301. [Google Scholar]
- Nowak, D.J.; Crane, D.E. Carbon storage and sequestration by urban trees in the USA. Environ. Pollut 2002, 116, 381–389. [Google Scholar]
- Myeong, S.; Nowak, D.; Duggin, M. A temporal analysis of urban forest carbon storage using remote sensing. Remote Sens. Environ 2006, 101, 277–282. [Google Scholar]
- Pataki, D.E.; Alig, R.J.; Fung, A.S.; Golubiewski, N.E.; Kennedy, C.A.; Mcpherson, E.G.; Nowak, D.J.; Pouyat, R.V.; Lankao, P.R. Urban ecosystems and the North American carbon cycle. Global Change Biol 2006, 12, 2092–2102. [Google Scholar]
- Miller, R.W. Urban Forestry: Planning and Managing Urban Greenspaces; Prentice Hall: Upper Saddle River, NJ, USA, 1996; p. 480. [Google Scholar]
- Duryea, M.L.; Malavasi, M.M. Tree Growth in the Urban Forest; Forestry Report R8-FR; USDA Forest Service, Southern Region: Atlanta, GA, USA, 1995; p. 53. [Google Scholar]
- McHale, M.; Burke, I.; Lefsky, M.; Peper, P.; McPherson, E. Urban forest biomass estimates: Is it important to use allometric relationships developed specifically for urban trees? Urban Ecosystems 2009, 12, 95–113. [Google Scholar]
- Wood, J.P. Tree Inventories and GIS in Urban Forestry. M.Sc. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA. 1999. Available online: http://scholar.lib.vt.edu/theses/available/etd-012499-141520 (accessed on 1 November 2011).
- Boyd, D.S.; Danson, F.M. Satellite remote sensing of forest resources: Three decades of research development. Prog. Phys. Geog 2005, 29, 1–26. [Google Scholar]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens 2006, 27, 1297–1328. [Google Scholar]
- Nelson, R.F.; Kimes, D.S.; Salas, W.A.; Routhier, M. Secondary forest age and tropical forest biomass estimation using thematic mapper imagery. Bioscience 2000, 50, 419–431. [Google Scholar]
- Schlerf, M.; Atzberger, C.; Hill, J. Remote sensing of forest biophysical variables using HyMap imaging spectrometer data. Remote Sens. Environ 2005, 95, 177–194. [Google Scholar]
- Chubey, M.; Franklin, S.; Wulder, M. Object-based analysis of IKONOS-2 imagery for extraction of forest inventory parameters. Photogramm. Eng. Remote Sensing 2006, 72, 383–394. [Google Scholar]
- Wulder, M. Optical remote-sensing techniques for the assessment of forest inventory and biophysical parameters. Prog. Phys. Geog 1998, 22, 449–476. [Google Scholar]
- Lutz, D.; Washington-Allen, R.; Shugart, H. Remote sensing of boreal forest biophysical and inventory parameters: A review. Can. J. Remote Sens 2009, 34, S286–S313. [Google Scholar]
- Dean, T.J.; Cao, Q.V.; Roberts, S.D.; Evans, D.L. Measuring heights to crown base and crown median with LiDAR in a mature, even-aged loblolly pine stand. For. Ecol. Manage 2008, 257, 126–133. [Google Scholar]
- Bortolot, Z.J.; Wynne, R.H. Estimating forest biomass using small footprint LiDAR data: An individual tree-based approach that incorporates training data. ISPRS J. Photogramm 2005, 59, 342–360. [Google Scholar]
- Brandtberg, T.; Warner, T.A.; Landenberger, R.E.; McGraw, J.B. Detection and analysis of individual leaf-off tree crowns in small footprint, high sampling density lidar data from the eastern deciduous forest in North America. Remote Sens. Environ 2003, 85, 290–303. [Google Scholar]
- Hyyppä, H.J.; Hyyppä, J.M. Effects of stand size on the accuracy of remote sensing-based forest inventory. IEEE Trans. Geosci. Remote Sens 2001, 39, 2613–2621. [Google Scholar]
- Popescu, S.C.; Wynne, R.H. Seeing the trees in the forest: Using lidar and multispectral data fusion with local filtering and variable window size for estimating tree height. Photogramm. Eng. Remote Sensing 2004, 70, 589–604. [Google Scholar]
- Todd, K.W.; Csillag, F.; Atkinson, P.M. Three-dimensional mapping of light transmittance and foilage distribution using lidar. Can. J. Remote Sens 2003, 29, 544–555. [Google Scholar]
- Boudreau, J.; Nelson, R.F.; Margolis, H.A.; Beaudoin, A.; Guindon, L.; Kimes, D.S. Regional aboveground forest biomass using airborne and spaceborne LiDAR in Québec. Remote Sens. Environ 2008, 112, 3876–3890. [Google Scholar]
- Nelson, R.; Krabill, W.; Tonelli, J. Estimating forest biomass and volume using airborne laser data. Remote Sens. Environ 1988, 24, 247–267. [Google Scholar]
- Hyyppä, J.; Inkinen, M. Detecting and estimating attributes for single trees using laser scanner. Photogramm. J. Finland 1999, 16, 27–42. [Google Scholar]
- Means, J.E.; Acker, S.A.; Fitt, B.J.; Renslow, M.; Emerson, L.; Hendrix, C.J. Predicting forest stand characteristics with airborne scanning lidar. Photogramm. Eng. Remote Sensing 2000, 66, 1367–1371. [Google Scholar]
- Naesset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ 2002, 80, 88–99. [Google Scholar]
- Naesset, E.; Bjerknes, K.O. Estimating tree heights and number of stems in young forest stands using airborne laser scanner. Remote Sens. Environ 2001, 78, 328–340. [Google Scholar]
- Naesset, E.; Okland, T. Estimating tree height and tree crown properties using airborne scanning laser in a boreal nature reserve. Remote Sens. Environ 2002, 79, 105–115. [Google Scholar]
- Magnussen, S.; Boudewyn, P. Derivations of stand heights from airborne laser scanner data with canopy-based quantile estimators. Can. J. For. Res 1998, 28, 1016–1031. [Google Scholar]
- van Aardt, J.A.N.; Wynne, R.H.; Oderwald, R.G. Forest volume and biomass estimation using small-footprint lidar-distributional parameters on a per-segment basis. For. Sci 2006, 52, 636–649. [Google Scholar]
- Tesfamichael, S.G.; van Aardt, J.A.N.; Ahmed, F. Estimating plot-level tree height and volume of Eucalyptus grandis plantations using small-footprint, discrete return lidar data. Prog. Phys. Geog 2010, 34, 515–540. [Google Scholar]
- Popescu, S.C.; Wynne, R.H. Esimating plot-level forest biophysical parameters using small-footprint airborne lidar measurements. Comput. Electron. Agric 2002, 37, 71–95. [Google Scholar]
- Popescu, S.C.; Wynne, R.H.; Scrivani, J.A. Fusion of small-footprint lidar and multispectral data to estimate plot-level volume and biomass in deciduous and pine forests in Virginia, USA. For. Sci 2004, 50, 551–565. [Google Scholar]
- Bortolot, Z.J. Using tree clusters to derive forest properties from small footprint lidar data. Photogramm. Eng. Remote Sensing 2006, 72, 1379–1388. [Google Scholar]
- Persson, A.; Holmgren, J.; Soderman, U. Detecting and measuring individual trees using an airborne laser scanner. Photogramm. Eng. Remote Sensing 2002, 68, 925–932. [Google Scholar]
- Roberts, S.D.; Dean, T.J.; Evans, D.L.; McCombs, J.W.; Harrington, R.L.; Glass, P.A. Estimating individual tree leaf area in loblolly pine plantations using LiDAR-derived measurements of height and crown dimensions. For. Ecol. Manage 2005, 213, 54–70. [Google Scholar]
- Chen, Q.; Gong, P.; Baldocchi, D.; Tian, Y.Q. Estimating basal area and stem volume for individual trees from lidar data. Photogramm. Eng. Remote Sensing 2007, 73, 1355–1365. [Google Scholar]
- Hyyppä, J.; Kelle, O.; Lehikoinen, M.; Inkinen, M. A segmentation-based method to retrieve stem volume estimates from 3-D tree height models produced by laser scanners. IEEE Trans. Geosci. Remote Sens 2001, 39, 969–975. [Google Scholar]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Measuring individual tree crown diameter with lidar and assessing its influence on estimating forest volume and biomass. Can. J. Remote Sens 2003, 29, 564–577. [Google Scholar]
- Næsset, E.; Gobakken, T. Estimation of above- and below-ground biomass across regions of the boreal forest zone using airborne laser. Remote Sens. Environ 2008, 112, 3079–3090. [Google Scholar]
- Hudak, A.T.; Lefsky, M.A.; Cohen, W.B.; Berterretche, M. Integration of lidar and Landsat ETM+ data for estimating and mapping forest canopy height. Remote Sens. Environ 2002, 82, 397–416. [Google Scholar]
- Holmgren, J.; Persson, A.; Soderman, U. Species identification of individual trees by combining high resolution lidar data with multi-spectral images. Int. J. Remote Sens 2008, 29, 1537–1552. [Google Scholar]
- Dalponte, M.; Bruzzone, L.; Gianelle, D. Fusion of hyperspectral and lidar remote sensing data for classification of complex forest areas. IEEE Trans. Geosci. Remote Sens 2008, 46, 1416–1427. [Google Scholar]
- St-Onge, B.; Hu, Y.; Vega, C. Mapping the height and above-ground biomass of a mixed forest using lidar and stereo Ikonos images. Int. J. Remote Sens 2008, 29, 1277–1294. [Google Scholar]
- van Aardt, J.A.; Wynne, R.H.; Scrivani, J.A. Lidar-based mapping of forest volume and biomass by taxonomic group using structurally homogenous segments. Photogramm. Eng. Remote Sensing 2008, 74, 1033–1044. [Google Scholar]
- Naesset, E.; Gobakken, T. Estimating forest growth using canopy metrics derived from airborne laser scanner data. Remote Sens. Environ 2005, 96, 453–465. [Google Scholar]
- Popescu, S.C. Estimating biomass of individual pine trees using airborne lidar. Biomass Bioenergy 2007, 31, 646–655. [Google Scholar]
- Naesset, E. Practical large-scale forest stand inventory using a small-footprint airborne scanning laser. Scand. J. For. Res 2004, 19, 164–179. [Google Scholar]
- Nelson, R.; Short, A.; Valenti, M. Measuring biomass and carbon in Delaware using an airborne profiling lidar. Scand. J. For. Res 2004, 19, 500–511. [Google Scholar]
- Nelson, R.; Parker, G.; Horn, M. A portable airborne laser system for forest inventory. Photogramm. Eng. Remote Sensing 2003, 69, 267–273. [Google Scholar]
- Nelson, R.F.; Hyde, P.; Johnson, P.; Emessiene, B.; Imhoff, M.L.; Campbell, R.; Edwards, W. Investigating RaDAR-lidar synergy in a North Carolina pine forest. Remote Sens. Environ 2007, 110, 98–108. [Google Scholar]
- Hyde, P.; Nelson, R.; Kimes, D.; Levine, E. Exploring lidar-RaDAR synergy—Predicting aboveground biomass in a southwestern ponderosa pine forest using lidar, SAR and InSAR. Remote Sens. Environ 2007, 106, 28–38. [Google Scholar]
- Hall, S.A.; Burke, I.C.; Box, D.O.; Kaufmann, M.R.; Stoker, J.M. Estimating stand structure using discrete-return lidar: an example from low density, fire prone ponderosa pine forests. For. Ecol. Manage 2005, 208, 189–209. [Google Scholar]
- Banskota, A.; Wynne, R.H.; Johnson, P.; Emessiene, B. Synergistic use of very-high-frequency radar and discrete-return lidar for estimating biomass in temperate hardwood and mixed forests. Ann. Forest Sci 2011, 68, 347–356. [Google Scholar]
- Nelson, R. Modeling forest canopy heights: The effects of canopy shape. Remote Sens. Environ 1997, 60, 327–334. [Google Scholar]
- Jenkins, J.C.; Chojnacky, D.C.; Heath, L.S.; Birdsey, R.A. National-scale biomass estimators for United States tree species. For. Sci 2003, 49, 12–35. [Google Scholar]
- Naesset, E. Estimating timber volume of forest stands using airborne laser scanner data. Remote Sens. Environ 1997, 61, 246–253. [Google Scholar]
- Gary, H. The vertical distribution of needles and branchwood in thinned and unthinned 80-year-old lodgepole pine. Northwest Sci 1978, 52, 303–309. [Google Scholar]
- Peichl, M.; Arain, M.A. Allometry and partitioning of above- and belowground tree biomass in an age-sequence of white pine forests. For. Ecol. Manage 2007, 253, 68–80. [Google Scholar]
- TAFB. Tinker Air Force Base Fact Sheet. 2011. Available online: http://www.tinker.af.mil/library/factsheets/factsheet.asp?id=9404 (accessed on 1 November 2011).
- Otey, J.K. GIS Applications in Urban Tree Inventory; Master Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA; 2007. [Google Scholar]
- Palenichka, R.M.; Zaremba, M.B. Multiscale isotropic matched filtering for individual tree detection in LiDAR images. IEEE Trans. Geosci. Remote Sens 2007, 45, 3944–3956. [Google Scholar]
- Rouse, J.; Haas, R.; Schell, J.; Deering, D.; Harlan, J. Monitoring the Vernal Advancement of Retrogradation of Natural Vegetation; Final Report; NASA/Goddard Space Flight Centre: Greenbelt, MD, USA, 1974. [Google Scholar]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ 1988, 25, 295–309. [Google Scholar]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ 1994, 48, 119–126. [Google Scholar]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ 1991, 35, 161–173. [Google Scholar]
- Avery, T.E.; Burkhart, H.E. Forest Measurements, 5th ed.; McGraw-Hill: Boston, MA, USA, 2002; p. 456. [Google Scholar]
- Pillsbury, N.; Reimer, J.; Thompson, R. Tree Volume Equations for Fifteen Urban Species in California; California Polytechnic State University, Urban Forest Ecosystems Institute: San Louis Obispo, CA, USA, 1995; p. 56. [Google Scholar]
- Snowdon, P.; Eamus, D.; Gibbons, P.; Khanna, P.; Keith, H.; Raison, R.; Kirschbaum, M. Synthesis of Allometrics, Review of Root Biomass, and Design of Future Woody Biomass Sampling Strategies; The Australian Greenhouse Office: Canberra, ACT, Australia, 2001. [Google Scholar]
- Ter-Mikaelian, M.T.; Korzukhin, M.D. Biomass equations for sixty-five North American tree species. For. Ecol. Manage 1997, 97, 1–24. [Google Scholar]
- West, P.W. Tree and Forest Measurement; Springer: Berlin/Heidelberg, Germany, 2004; p. 167. [Google Scholar]
- Norris, M.D.; Blair, J.M.; Johnson, L.C.; McKane, R.B. Assessing changes in biomass, productivity, and C and N stores following Juniperus virginiana forest expansion into tallgrass prairie. Can. J. For. Res 2001, 31, 1940–1946. [Google Scholar]
- Clark, A, III; Phillips, D.R.; Frederick, D.J. Weight, Volume, and Physical Properties of Major Hardwood Species in the Piedmont; Southeastern Forest Experiment Station, North Carolina State University: Raleigh, NC, USA, 1986; p. 88. [Google Scholar]
- Schlaegel, B. Green Ash Volume and Weight Tables; Res. Pap. SO-206.; US Department of Agriculture, Forest Service, Southern Forest Experiment Station: New Orleans, LA, USA, 1984. [Google Scholar]
- Brenneman, B.B.; Frederick, D.J.; Gardner, W.E.; Schoenhofen, L.H.; Marsh, P.L. Biomass of Species and Stands of West Virginia Hardwoods. Proceedings of Central Hardwood Forest Conference II, West LaFayette, Indiana, USA, 14–16 November 1978; pp. 159–178.
- Jenkins, J.; Chojnacky, D.; Heath, L.; Birdsey, R. Comprehensive Database of Diameter-Based Biomass Regressions for North American Tree Species; NE-319; United States Forest Service, Northeastern Research Station: New Town Square, PS, USA, 2004; p. 45. [Google Scholar]
- Johnson, A.; Gerhold, H. Carbon storage by utility-compatible trees. J. Arboricul 2001, 27, 57–68. [Google Scholar]
- Hocking, R.R. Methods and Applications of Linear Models: Regression and the Analysis of Variance, 2nd ed.; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2005; p. 776. [Google Scholar]
- Montgomery, D.; Peck, E. Introduction to Linear Regression Analysis, 4th ed.; Wiley: New York, NY, USA, 2006; p. 640. [Google Scholar]
- Rozeboom, W. Estimation of cross-validated multiple correlation: A clarification. Psychol. Bull 1978, 85, 1348–1351. [Google Scholar]
- Allen, D. The relationship between variable selection and data agumentation and a method for prediction. Technometrics 1974, 16, 125–127. [Google Scholar]
- Kleinbaum, D.; Kupper, L.; Nizam, A.; Muller, K. Applied Regression Analysis and Other Multivariable Methods, 4th ed.; Thompson Higher Education: Belmont, CA, USA, 2007; p. 928. [Google Scholar]
- Hopkinson, C.; Chasmer, L.; Sass, G.; Creed, I.; Sitar, M.; Kalbfleisch, W.; Treitz, P. Vegetation class dependent errors in lidar ground elevation and canopy height estimates in a boreal wetland environment. Can. J. Remote Sens 2005, 31, 191–206. [Google Scholar]
- Hyyppä, J.; Pyysalo, U.; Hyyppä, H.; Samberg, A. Elevation Accuracy of Laser Scanning-Derived Digital Terrain and Target Models in Forest Environment. Proceedings of EARSeL-SIG-Workshop LIDAR, Dresden, Germany, 16–17 June 2000; pp. 14–17.
- Heurich, M.; Persson, A.; Holmgren, J.; Kennel, E. Detecting and Measuring Individual Trees with Laser Scanning in Mixed Mountain Forest of Central Europe Using an Algorithm Developed for Swedish Boreal Forest Conditions. Proceedings of the ISPRS Working Group VIII/2 “Laser-Scanners for Forest and Landscape Assessment”, Freiburg, Germany, 3–6 October 2004; 36, pp. 307–312.
- Falkowski, M.; Smith, A.; Gessler, P.; Hudak, A.; Vierling, L.; Evans, J. The influence of conifer forest canopy cover on the accuracy of two individual tree measurement algorithms using lidar data. Can. J. Remote Sens 2008, 34, S338–S350. [Google Scholar]
- Clark, M.L.; Clark, D.B.; Roberts, D.A. Small-footprint lidar estimation of sub-canopy elevation and tree height in a tropical rain forest landscape. Remote Sens. Environ 2004, 91, 68–89. [Google Scholar]
- Kwak, D.-A.; Lee, W.-K.; Lee, J.-H.; Biging, G.; Gong, P. Detection of individual trees and estimation of tree height using LiDAR data. J. Forest Res.-Jpn 2007, 12, 425–434. [Google Scholar]
- Omasa, K.; Hosoi, F.; Uenishi, T.; Shimizu, Y.; Akiyama, Y. Three-dimensional modeling of an urban park and trees by combined airborne and portable on-ground scanning LIDAR remote sensing. Environ. Model. Assess 2008, 13, 473–481. [Google Scholar]
- Zheng, D.; Rademacher, J.; Chen, J.; Crow, T.; Bresee, M.; Le Moine, J.; Ryu, S.-R. Estimating aboveground biomass using Landsat 7 ETM+ data across a managed landscape in northern Wisconsin, USA. Remote Sens. Environ 2004, 93, 402–411. [Google Scholar]
- Hall, R.J.; Skakun, R.S.; Arsenault, E.J.; Case, B.S. Modeling forest stand structure attributes using Landsat ETM+ data: Application to mapping of aboveground biomass and stand volume. For. Ecol. Manage 2006, 225, 378–390. [Google Scholar]
- Heiskanen, J. Estimating aboveground tree biomass and leaf area index in a mountain birch forest using ASTER satellite data. Int. J. Remote Sens 2006, 27, 1135–1158. [Google Scholar]
- Smith, M.-L.; Ollinger, S.V.; Martin, M.E.; Aber, J.D.; Hallett, R.A.; Goodale, C.L. Direct estimation of aboveground forest productivity through hyperspectral remote sensing of canopy nitrogen. Ecol. Appl 2002, 12, 1286–1302. [Google Scholar]
- Blackard, J.A.; Finco, M.V.; Helmer, E.H.; Holden, G.R.; Hoppus, M.L.; Jacobs, D.M.; Lister, A.J.; Moisen, G.G.; Nelson, M.D.; Riemann, R.; et al. Mapping U.S. forest biomass using nationwide forest inventory data and moderate resolution information. Remote Sens. Environ 2008, 112, 1658–1677. [Google Scholar]
- Leboeuf, A.; Beaudoin, A.; Fournier, R.A.; Guindon, L.; Luther, J.E.; Lambert, M.C. A shadow fraction method for mapping biomass of northern boreal black spruce forests using QuickBird imagery. Remote Sens. Environ 2007, 110, 488–500. [Google Scholar]
- Gonzalez, P.; Asner, G.P.; Battles, J.J.; Lefsky, M.A.; Waring, K.M.; Palace, M. Forest carbon densities and uncertainties from Lidar, QuickBird, and field measurements in California. Remote Sens. Environ 2010, 114, 1561–1575. [Google Scholar]
- Kayitakire, F.; Hamel, C.; Defourny, P. Retrieving forest structure variables based on image texture analysis and IKONOS-2 imagery. Remote Sens. Environ 2006, 102, 390–401. [Google Scholar]
- Ouma, Y.; Tateishi, R. Optimization of second-order grey-level texture in high-resolution imagery for statistical estimation of above-ground biomass. J. Environ. Inform 2006, 8, 70–85. [Google Scholar]