Next Article in Journal
Analyzing Gaps in Hurricane Rain Coverage to Inform Future Satellite Proposals
Next Article in Special Issue
Forest Cover Change Pattern after the Intervention of Community Forestry Management System in the Mid-Hill of Nepal: A Case Study
Previous Article in Journal
Distributed Training and Inference of Deep Learning Models for Multi-Modal Land Cover Classification
Previous Article in Special Issue
Carbon Stocks and Fluxes in Kenyan Forests and Wooded Grasslands Derived from Earth Observation and Model-Data Fusion
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 12
Issue 17
10.3390/rs12172672
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Structural Changes in Boreal Forests Can Be Quantified Using Terrestrial Laser Scanning

by
Tuomas Yrttimaa
1,2,*,
Ville Luoma
2,
Ninni Saarinen
1,2,
Ville Kankare
1,2,
Samuli Junttila
1,2,
Markus Holopainen
2,3,
Juha Hyyppä
3 and
Mikko Vastaranta
1
1
School of Forest Sciences, University of Eastern Finland, 80101 Joensuu, Finland
2
Department of Forest Sciences, University of Helsinki, 00014 Helsinki, Finland
3
Department of Remote Sensing and Photogrammetry, Finnish Geospatial Research Institute, National Land Survey of Finland (NLS), 02431 Masala, Finland
*
Author to whom correspondence should be addressed.
Remote Sens. 2020, 12(17), 2672; https://doi.org/10.3390/rs12172672
Submission received: 6 July 2020 / Revised: 10 August 2020 / Accepted: 17 August 2020 / Published: 19 August 2020
(This article belongs to the Special Issue Feature Paper Special Issue on Forest Remote Sensing)
Browse Figures
Versions Notes

Abstract

:
Terrestrial laser scanning (TLS) has been adopted as a feasible technique to digitize trees and forest stands, providing accurate information on tree and forest structural attributes. However, there is limited understanding on how a variety of forest structural changes can be quantified using TLS in boreal forest conditions. In this study, we assessed the accuracy and feasibility of TLS in quantifying changes in the structure of boreal forests. We collected TLS data and field reference from 37 sample plots in 2014 (T1) and 2019 (T2). Tree stems typically have planar, vertical, and cylindrical characteristics in a point cloud, and thus we applied surface normal filtering, point cloud clustering, and RANSAC-cylinder filtering to identify these geometries and to characterize trees and forest stands at both time points. The results strengthened the existing knowledge that TLS has the capacity to characterize trees and forest stands in space and showed that TLS could characterize structural changes in time in boreal forest conditions. Root-mean-square-errors (RMSEs) in the estimates for changes in the tree attributes were 0.99–1.22 cm for diameter at breast height (Δdbh), 44.14–55.49 cm2 for basal area (Δg), and 1.91–4.85 m for tree height (Δh). In general, tree attributes were estimated more accurately for Scots pine trees, followed by Norway spruce and broadleaved trees. At the forest stand level, an RMSE of 0.60–1.13 cm was recorded for changes in basal area-weighted mean diameter (ΔDg), 0.81–2.26 m for changes in basal area-weighted mean height (ΔHg), 1.40–2.34 m2/ha for changes in mean basal area (ΔG), and 74–193 n/ha for changes in the number of trees per hectare (ΔTPH). The plot-level accuracy was higher in Scots pine-dominated sample plots than in Norway spruce-dominated and mixed-species sample plots. TLS-derived tree and forest structural attributes at time points T1 and T2 differed significantly from each other (p < 0.05). If there was an increase or decrease in dbh, g, h, height of the crown base, crown ratio, Dg, Hg, or G recorded in the field, a similar outcome was achieved by using TLS. Our results provided new information on the feasibility of TLS for the purposes of forest ecosystem growth monitoring.

Graphical Abstract

1. Introduction

Forests change over time and across space due to natural phenomena and anthropogenic processes. Biotic changes, such as forest growth and damage, affect forest structure and tree stems and branches grow annually in width and height. Conifer trees are typically evergreen but leaves of deciduous trees emerge in the spring and fall in the autumn. Forest growth process is also linked to the decomposition process which affects the amount of dead wood [1]. Insect damage, the spread of pathogens, wind damage, and forest fires shape forests at different spatial and temporal scales. Insect damage, that is often combined with the spread of pathogenic fungi, causes defoliation and changes in the bark whereas winds fall trees or cut tree parts [2] and fire burns low vegetation, needle mass, and possibly also reshapes the structure of trees [3,4]. There are also abiotic changes that affect the forest structure. These include land-use changes as well as silvicultural and harvesting operations. In managed forests, trees are often planted, seedlings are tended, and several thinning operations are carried out during the rotation period [5]. Silvicultural practices vary a great deal, but in general, a proportion of trees is typically removed in silvicultural and harvesting operations [5,6]. Spatiotemporal information is needed to improve the understanding of, or quantify, the consequences of these natural phenomena, processes, and human activities with varying temporal and spatial patterns and dimensions.
Close-range sensing technologies, such as terrestrial laser scanning (TLS) provide state-of-the-art tools in characterizing forests. TLS is a powerful close-range sensing method for characterizing forests in three dimensions (3D) [1,7,8,9,10]. Individual trees can be detected from a TLS point cloud by detecting circular shapes (e.g., [11,12]) or clusters of points (e.g., [13,14]), these two representing the most common tree detection methods implemented in forest applications [8]. Then, depending on the algorithm used and the purpose of the processing, architectural structure of a stem [15,16] or a whole tree [17,18] can be reconstructed by using a series of geometrical primitives, preferably circular cylinders [19]. Tree reconstruction requires that points representing a tree are classified based on their origin, in other words, from stem, branches, and foliage. Point cloud classification algorithms are most often based on an assumption that stem points have more planar, vertical, and cylindrical characteristics than points originating from branches and foliage [10,15,17,20]. With careful TLS data collection and pre-processing, a single point in TLS data can reach a millimeter-level accuracy within the data set [21,22] meaning that the reconstructed tree models are geometrically highly accurate [18]. So far, there is a limited number of approaches for classifying points originating from foliage based on geometric features [23,24,25,26]. Use of radiometric features based on laser return intensity have been seen as beneficial in separating foliage and woody material [27,28,29]. After tree architecture is reconstructed for every tree in an area of interest, theoretically all external tree dimensions can be derived from geometrically accurate 3D models for all trees and used further in deriving attributes of interest.
Although it has been demonstrated that TLS technology can be used for detecting structural changes in single trees as well as changes in the canopy structure [30,31,32,33,34,35], there is still a limited understanding on how different kinds of forest structural changes can be quantified using TLS in boreal forest conditions. Srinivasan et al. [30] used TLS data from two time points (2009 and 2012) for modeling tree biomass changes in East Texas. They reported that canopy volume and height change metrics provided the best results for modeling the change in the above-ground biomass (AGB) of 29 loblolly pines (Pinus taeda L.). Kaasalainen et al. [31] collected a time-series of TLS data from one Norway maple (Acer platanoides L.) growing in a city with five observation points during a 4-year time period. They modeled the tree with Quantitative Structure Modelling (QSM, [17,31]) to detect changes in tree branch volume and branch length, caused by growth and mortality. QSMs were used in [32] to investigate annual growth of 21 wild cherry (Prunus avium L.) trees in terms of diameter at breast height (dbh) and height, stem, and branch volume, as well as the fraction of merchantable timber. Sheppard et al. [32] collected TLS data over a 3-year time period so that three QSMs per tree were constructed. Similar to the study by Kaasalainen et al. [31] earlier, the growth of individual branches was detected and quantified as well as volume reductions due to pruning, which was identified in [32]. For the forest change analyses, it is not necessary to reconstruct the whole tree structure. For example, bi-temporal TLS data were used in [33] to develop a voxel-based method for analyzing changes in canopy occupancy through time. The approach can be used at the local neighborhood level for revealing the extent of canopy space-filling, identifying interactions between trees, and analyzing complementary space use. Kunz et al. [34] used TLS data to capture the three-dimensional structure of trees and investigate their temporal dynamics. Bi-temporal TLS data was collected between 2012 and 2016 and QSMs were then used to reconstruct tree stems and branches followed by the generation of 2D and 3D alpha-shapes for deriving additional crown shape and size parameters. With a TLS-based method, they were able to investigate crown complementarity, crown plasticity, and wood volume allocation. Respectively, bi-temporal TLS data (2008 and 2017) was used in [35] to investigate changes in stem forms. Of the 35 investigated trees, which were mainly conifers, changes in stem taper, cylindrical form factor, form quotient, and stem slenderness were analyzed. The changes in the stem taper varied from −34% to 9%, the cylindrical form factor from 1% to 18%, the form quotient from 4% to 35%, and the stem slenderness from −2% to 6%.
The objective of this study was to strengthen the understanding of how TLS can be used to capture boreal forest structure in space and time. Concentrating on the change of only a few attributes with a relatively low number of samples has been the common denominator for all the previous studies related to the use of TLS in quantifying changes in tree attributes. A more comprehensive investigation on the performance of capturing changes in tree and forest structural attributes with a large number of trees and sample plots is needed to assess the feasibility of TLS in monitoring forest structural changes. To fill in the knowledge gap, we used bi-temporal TLS data and field inventory data to cover changes in the structure of 1280 trees and 37 sample plots from varying boreal forest conditions. We hypothesized that TLS has the capacity to accurately estimate tree and forest structural attributes at single time points, and the estimated attributes at the beginning of a monitoring period significantly differ from the respective attributes at the end of the monitoring period. We assessed the performance of change quantification by using the most common tree and forest structural attributes. At tree level, we analyzed changes in dbh (Δdbh), basal area (Δg), tree height (Δh), diameter-height ratio (Δd-h-ratio), height of the crown base (Δhc), and crown ratio (Δcr). At stand (sample plot) level, we analyzed changes in basal area-weighted mean diameter (ΔDg) and -height (i.e., Lorey’s height, ΔHg), mean basal area (ΔG), and number of trees per hectare (ΔTPH). Thus, we used a range of attributes describing changes in horizontal and vertical forest structure.

2. Materials and Methods

2.1. Study Materials

The study materials consisted of a multi-scan TLS data and a field inventory data acquired in 2014 (T1) and 2019 (T2) covering 1280 trees in 37 sample plots. The study site is located in Evo, southern Finland (61°19.6′ N 25°10.8′ E) where 91 sample plots (32 m × 32 m) were initially established in 2014 to cover the structural variation of forests (see e.g., [36]). A TLS data-acquisition campaign was carried out in spring 2014 using a Leica HDS6100 (Leica Geosystems, St. Gallen, Switzerland) and a Faro Focus 3D X330 (Faro Technologies Inc., Lake Mary, FL, USA) phase shift scanners, both operating at 1550 nm wavelength and measuring 508,000 points per second, delivering a hemispherical (310° vertical × 360° horizontal) point cloud with an angular resolution of 0.018° in both vertical and horizontal direction. A multi-scan approach was used to obtain a comprehensive point cloud for each sample plot by merging point clouds from five separate scanning locations. The scan setup consisted of one center scan located at the plot center and four auxiliary scans at quadrant directions (i.e., northeast, southeast, southwest, and northwest) about 11 m away from the plot center. Artificial reference targets were used to register the point clouds together. Trees from each sample plot were located by manually detecting stem-cross sections from horizontal TLS point cloud slices to construct a tree map. The tree maps were verified in the field and completed with the locations of small undergrowth trees that were not visible in the point cloud. A tree-wise field inventory was carried out in the summer of 2014 to acquire reference measurements of the tree attributes for T1. Tree species, dbh, h, and health status (alive/dead) were recorded for all the trees with dbh exceeding 5 cm while hc was measured for Scots pine trees only. Tree species and health status were obtained using visual interpretation. Dbh was measured as a mean of two diameter measurements perpendicular to each other at the height of 1.3 m above the ground using steel calipers. An electronic clinometer was used to measure h and hc. Based on our evaluations, the precision in dbh and tree height measurements in the given forest conditions was approximately 0.3 cm and 0.5 m, respectively [37]. Tree attributes were then aggregated at the plot level to obtain forest structural attributes: Dg (cm) and Hg (m), G (m2/ha), and TPH (n/ha). More detailed description on the TLS data acquisition and field inventory for T1 can be found in [22].
Field inventory and TLS data-acquisition campaigns were repeated for 37 sample plots in autumn 2019 to capture a five-year growth period in between the measurements. The stem maps were updated in the field with missing trees (i.e., trees fallen or harvested during the time period) and in growth of trees (i.e., trees with dbh exceeding the 5 cm threshold during the time period) while dbh and tree height were re-measured for all trees, and height of the crown base for Scots pine trees (Pinus sylvestris L.). TLS data at T2 was collected using a Leica RTC360 3D (Leica Geosystems, St. Gallen, Switzerland) time-of-flight scanner that operates at 1550 nm wavelength and measures 2,000,000 points per second, delivering a hemispherical (300° vertical × 360° horizontal) point cloud with an angular resolution of 0.009° in both vertical and horizontal direction. Similar to T1 TLS data acquisition, a multi-scan approach (i.e., one center scan with four auxiliary scans) was used in the T2 TLS campaign to ensure consistent point cloud quality. The scan setup for T2 was slightly modified from the one used in the T1 campaign based on experience gained in [10] that suggests placing the auxiliary scans approximately at the plot borders to improve point cloud completeness (see Figure 1). Artificial reference targets and a Leica Cyclone 3D Point Cloud Processing Software were used to register the separate point clouds together for each sample plot. Topography was removed from the point clouds by applying a point cloud normalization workflow presented by Ritter et al. [38].
Later on, we found that, due to the slightly different scan setups used in the TLS-campaigns, the overall quality of the point clouds was somewhat poorer in T1 because the auxiliary scans in T1 were located closer to the plot center than in T2 (see Figure 1). Therefore the sample plots were reduced in size, from the rectangular 32 m × 32 m plots (1024.0 m2) to circular sample plots with an 11-m radius (380.1 m2), to achieve more comparable point clouds between time points T1 and T2 (i.e., to ensure that most of the trees were scanned from multiple directions). Thus, the total number of field-measured trees was 1280, of which 270 (21.1%) were Scots pine trees, 649 (50.7%) were Norway spruces (Picea abies (L.) H. Karst.), and 361 (28.2%) were broadleaved trees, mainly birches (Betula sp.) and European aspen (Populus tremula L.). The main tree species was defined for the sample plots based on proportional field-measured G at time point T2 by tree species. A sample plot was classified as a single species-dominated sample plot if any of the tree species accounted for more than 67% of the total basal area. Respectively, a sample plot was classified as a mixed-species sample plot if G of two or more tree species each accounted for more than 30% of the total basal area. This classification resulted in three groups of sample plots as 9 sample plots were classified as Scots pine-dominated, 13 sample plots were classified as Norway spruce-dominated, while 15 sample plots were classified as mixed-species sample plots. The sample plots covered a wide range of forest structural variation (see Table 1).

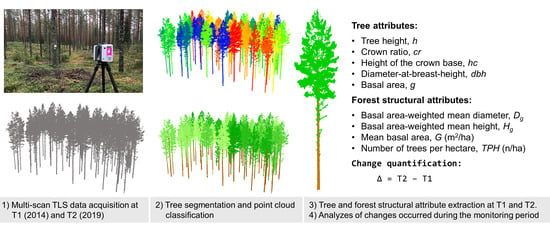
2.2. Deriving Tree and Forest Structural Attributes from TLS Point Clouds

A point cloud processing method presented in [39] was used in this study to measure tree attributes and to estimate forest structural attributes from the multi-scan TLS point clouds for each sample plot and both T1 and T2 (see Figure 1). First, a raster-based canopy segmentation was carried out to partition the normalized point clouds into smaller units using a canopy height model (CHM) at a 20 cm resolution. Variable Window Filter approach [40] was used to identify the local maxima in the CHM, and Marker-Controlled Watershed Segmentation [41] was applied to delineate canopy segments. The point cloud was then split according to the extracted crown segments using point-in-polygon approach. The crown-segmented point cloud was further classified into stem and non-stem points based on a general assumption that stem points had more planar, vertical, and cylindrical characteristics than points representing branches and foliage [10,15]. These characteristics were distinguished by applying surface normal filtering, point cloud clustering, and Random Sample Consensus (RANSAC)-cylinder filtering on horizontal point cloud slices. A more detailed description of the point cloud classification procedure can be found in [39].
Tree attributes, namely dbh, g, h, d-h-ratio, hc, and cr were extracted from the classified point cloud (see Figure 1, Table 2). Dbh and h were measured following the procedure originally presented in [10]. In other words, h was determined as the vertical distance between the highest and lowest points for each tree. Stem taper curve was estimated to determine dbh by measuring diameters through circle fitting at 20-cm vertical intervals to the stem points. The outliers in diameter-height-observations were filtered out by comparing the measured diameters to the mean of three previous (or three closest at the bottom of the stem) diameters. Then a cubic spline curve was fitted to the diameter-height-observations to level unevenness in diameter measurements and to interpolate the missing diameters as suggested in [42]. Dbh was then obtained as the diameter at 1.3 m height from the taper curve. Tree-level g was computed from dbh measurements by considering the stem cross section as a circle (g = π ∗ dbh2/4) and d-h-ratio was computed as a ratio between dbh and h (d-h-ratio = dbh/h). Hc was determined by searching for a height threshold for each tree where an increase in crown horizontal dimensions was recorded. This was done by first binning the non-stem points into horizontal slices with a height of 20 cm, then computing a convex hull around the bin points projected to XY-plane and hc was determined at the height where the convex hull area exceeded a 1.5 m2 threshold and the perimeter-to-area ratio for the convex hull was smaller than 2 (Figure 1c). The threshold values of these parameters were chosen by pre-investigating the characteristics of the crown features with respect to the field-measured hc. Cr was computed as the proportion of the height of a living crown from the tree height (cr = (h − hc)/h). Finally, the forest structural attributes (i.e., Dg, Hg, G, and TPH) were computed by aggregating the tree-level attributes at the plot level (see Table 2). Dg and Hg were computed as a basal area-weighted mean from the TLS-derived dbh and h measurements whereas G was a sum of g and TPH was the total number of trees within a sample plot per unit area.

2.3. Quantifying Changes in Tree and Forest Structural Attributes Using Bi-Temporal TLS Data

Changes in tree and forest structural attributes were quantified by subtracting the TLS-derived T1 attributes from the respective T2 attributes. At tree level, we analyzed changes in dbh (Δdbh), g (Δg), h (Δh), d-h-ratio (Δd-h-ratio), hc (Δhc) and cr (Δcr). At plot level, we analyzed changes in TPH (ΔTPH), G (ΔG), Dg (ΔDg), and Hg (ΔHg).

2.4. Assessing The Performance of The TLS-Based Method in Quantifying Changes in Forest Structure

Performance of the TLS-based method to quantify changes in tree attributes and forest structure was assessed by comparing the TLS-derived tree and forest structural attributes with the field-measured counterparts. For each TLS-derived tree, a corresponding field-measured tree was searched based on its spatial location. Capability of the TLS-based method to detect trees from the point clouds was then assessed by using completeness as an accuracy measure, indicating how large a part of the trees was detected from the point clouds. Accuracy of the TLS point cloud-derived estimates for tree and forest structural attributes at time points T1 and T2 as well as their difference (Δ) was assessed by using bias (mean error) and root-mean-square-error (RMSE) as accuracy measures:
bias   =   ∑ i = 1 n ( X i ^ − X i ) n
RMSE   =   ∑ i = 1 n ( X i ^ − X i ) 2 n
where n is the number of trees or sample plots, X ^ i is the TLS-derived tree attribute or forest structural attribute for tree or plot i, and Xi is the corresponding attribute based on field measurements. Relative RMSE (RMSE%) and bias (bias%) were computed by dividing the absolute RMSE and bias with average value of the respective field-measured attribute. For tree attributes, the accuracy was assessed by tree species (Scots pine, Norway spruce, and broadleaved trees) while for forest structural attributes the accuracy was assessed by main tree species of a sample plot (Scots pine-dominated, Norway spruce-dominated, and mixed-species sample plots). Coefficient of determination (R2) was used to measure the relationship between the TLS-derived and field-measured tree and forest structural attributes at time points T1 and T2 as well as their change. Paired-sample t-tests were used to test whether the TLS-based estimates for tree and forest structural attributes at time point T1 significantly differed from the respective estimates at time point T2.

3. Results

3.1. Performance of Detecting Trees Using Bi-Temporal TLS Data

Out of the total number of 1280 trees that were measured in the field, 795 trees (62.1%) were detected from the point clouds at both time points T1 and T2. The detected trees represented 84.5% of the total basal area of all trees. Tree detection accuracy was highest among Scots pine trees, followed by Norway spruce and broadleaved trees (Table 3). Trees that remained undetected were mainly small in size, while large trees were detected at both time points with high accuracy (Figure 2).

3.2. Performance of Characterizing Trees in Space Using TLS

Strong relationships (R2 = 0.99) between the field-measured and TLS-derived estimates for dbh and g were recorded at both time points (Figure 3a,b,d,e). Dbh was estimated with an RMSE of 1.18 cm (5.7%) and 0.90 cm (4.1%) at T1 and T2, respectively, with no significant (p > 0.05) differences in accuracy between the tree species (Table 4). However, g was estimated more accurately for Norway spruce (RMSE% 6.2–10.6%) than for Scots pine (RMSE% 12.5–13.0%) and broadleaved trees (RMSE% 14.5–16.0%). On average, dbh of Norway spruce were overestimated by 0.26–0.30 cm, while dbh of Scots pine and broadleaved trees were underestimated by 0.43–0.32 cm and 0.03–0.19 cm, respectively. Considering all the trees, slightly lower RMSEs and biases of dbh and g were obtained at T2 than at T1.
Relationship between the field-measured and TLS-derived estimates for h was stronger for Scots pine and Norway spruce (R2 = 0.84–0.92) than for broadleaved trees (R2 = 0.31–0.39; see Figure 3g,h). In general, TLS-derived h was underestimated, and the accuracy of h estimates were improved from T1 to T2 (Table 4). For Scots pine trees, RMSEs of 2.52 m (13.7%) and 2.42 m (12.1%) were recorded at time points T1 and T2, respectively. The estimation accuracy for Norway spruce was slightly lower being 3.99 m (20.1%) for T1 and 3.03 m (14.4%) for T2. For broadleaved trees, the estimation accuracy decreased even more, being 6.26 m (31.7%) at T1 and 6.56 m (30.8%) at T2. Additionally, differences in the accuracy of h estimates led to differences in the accuracy of d-h-ratio estimates between the tree species. R2 of 0.76–0.79 was recorded between the field-measured and TLS-derived d-h-ratio for Scots pine, while the respective values for Norway spruce and broadleaved trees were 0.58–0.73 and 0.43–0.51, respectively (Figure 3j,k).
Hc and cr were estimated for Scots pine trees only. R2 between the field-measured and TLS-derived estimates for hc and cr were 0.78–0.79 and 0.52–0.58, respectively (Figure 3p,q). For hc estimates an RMSE of 2.71 m (25.7%) for T1 and 2.55 m (20.4%) for T2 with an underestimate of 1.36–1.70 m (Table 4). On average, cr was overestimated by 10.3–11.7% with a relative RMSE of 22.5–22.8% (Table 4).

3.3. Performance of Characterizing Tree Attributes in Time Using TLS

It was possible to quantify changes in tree attributes using TLS. Paired sample t-tests showed that the tree attributes estimated at T1 significantly (p < 0.01) differed from the respective attributes estimated at T2 (Table 5). Relationship between the changes in field-measured and TLS-derived tree attributes was stronger for attributes characterizing changes in horizontal tree structure (i.e., Δdbh and Δg) than attributes characterizing changes in vertical tree structure (i.e., Δh, Δhc, and Δcr; Figure 3). In general, the changes in tree attributes were estimated with smaller RMSE for Scots pine than for Norway spruce and broadleaved trees (Table 4). RMSE in Δdbh estimates was 0.99–1.22 cm (83.9–103.5%), and most often Δdbh was overestimated by 0.04–0.17 cm (3.8–15.0%) depending on tree species. Differences in the accuracy of Δg estimates between the tree species were small and not considered statistically significant (p > 0.05). On average, Δh was overestimated by 0.21–0.90 m (13.8–72.3%) with an RMSE of 1.91–4.85 m (122.8–321.5%). In this case, the highest accuracy was recorded for Scots pine, followed by Norway spruce and broadleaved trees. The accuracy of Δd-h-ratio was considerably lower than the accuracy of other tree attributes. Relative errors in Δd-h-ratio were large (RMSE 942.6–4516.2%) due to uncertainty in tree height estimates.
Attributes characterizing changes in crown structure were estimated for Scots pine trees only. R2 of 34% and 35% were recorded between the field-measured and TLS-derived estimates for Δhc and Δcr, respectively (Figure 3o,r). On average, Δhc was overestimated by 0.34 m (20.7%) with an RMSE of 1.97 m (120.6%) which is at the same level to the accuracy of Δh estimates for Scots pine trees (Table 4). Relative errors in Δcr estimates were larger (RMSE% 318.1%) due to uncertainty in h and hc estimates.

3.4. Performance of Characterizing Forest Structural Attributes in Space with TLS

Forest structural attributes were estimated accurately with TLS point clouds from both time points. Strong relationships (R2 > 0.86) between the field-measured and the TLS-derived estimates for Dg, Hg, G, and TPH were recorded for Norway spruce-dominated sample plots (Figure 4). On Scots pine-dominated sample plots, the R2 indicated a stronger relationship between the field-measured and the point cloud-derived estimates for Dg and Hg (R2 > 0.96) than for TPH (R2 = 0.46–0.66) and G (R2 = 0.21–0.34). On mixed-species sample plots, an R2 of 0.93–0.95 was recorded for Dg, 0.50–0.64 for Hg, 0.63–0.72 for G, and 0.44–0.63 for TPH. Considering all the sample plots, the estimation accuracy for Dg and G was at the same level for T1 and T2 while Hg and TPH estimates seemed to be slightly more accurate at T2 (RMSE% 7.9% for Hg and 49.3% for TPH) than at T1 (RMSE% 11.2% for Hg and 58.5% for TPH; Table 6).
Dg was underestimated by 0.15–0.26 cm (0.4–0.7%) on Norway spruce-dominated sample plots while overestimated by 0.08–0.55 cm (0.4–2.4%) on Scots pine-dominated, and by 0.39–0.41 cm (1.6%) on mixed-species sample plots (Table 6). More accurate estimates for Dg were recorded on Norway spruce-dominated and Scots pine-dominated sample plots (RMSE% 2.5–3.4%) than on mixed-species sample plots (RMSE% 8.4–9.6%). Hg was underestimated on all the sample plots by 0.35–2.88 m (1.9–10.7%) except Scots pine-dominated plots at T2 when it was overestimated by 0.20 m (1.0%). Accuracy of Hg estimates was highest on Scots pine-dominated sample plots (relative RMSE 2.9–3.5%) followed by Norway spruce-dominated (RMSE% 3.9–11.6%) and mixed-species sample plots (RMSE% 12.6–13.1%).
G and TPH were underestimated on all the sample plots (Table 6). On Norway spruce-dominated sample plots the underestimation in G estimates was the lowest being 3.24–3.84 m2/ha (8.1–10.2%), followed by Scots pine-dominated and mixed-species sample plots with 5.32–5.56 m2/ha (21.8–23.6%) and 9.79–10.46 m2/ha (29.2–30.2%) of underestimation, respectively. More accurate estimates for G were recorded on Norway spruce-dominated sample plots (RMSE% 10.6–13.5%) followed by Scots pine-dominated sample plots (relative RMSE 31.1–31.6%) and mixed-species sample plots (RMSE% 35.5–35.7%). A similar trend was also visible in the accuracy of TPH estimates. On Norway spruce-dominated sample plots the underestimation of TPH was considerably lower (7.7–14.3%) than on Scots pine-dominated sample plots (26.9–35.0%) and mixed-species sample plots (36.0–43.3%). RMSE in TPH estimates was 65-117 n/ha (10.7–18.5%) on Norway spruce-dominated sample plots, 428-486 n/ha (42.9–50.5%) on Scots pine-dominated sample plots, and 753–914 n/ha (50.6–60.0%) on mixed-species sample plots (Table 6).

3.5. Performance of Characterizing Forest Structural Attributes in Time Using TLS

Changes in forest structural attributes were quantified using TLS. Paired sample t-tests showed that Dg, Hg, and G estimated at T1 significantly (p < 0.000) differed from the respective attributes estimated at T2 (Table 7). In the case of TPH, the differences between T1 and T2 estimates were not considered significant (p > 0.05). Based on field measurements, TPHT1 was significantly larger than TPHT2 on Norway spruce-dominated and mixed-species sample plots due to fallen or harvested trees. On these sample plots, some of the trees that were fallen or harvested were not detected at T1, and thus, change in TPH was not captured. On Scots pine-dominated sample plots, however, the change in TPH was not considered significant and thus, not expected to be captured with TLS. In general, accuracy of characterizing changes in forest structural attributes was at a higher level on Scots pine-dominated sample plots than on Norway spruce-dominated and mixed-species sample plots (Table 6).
The relationship between the field-measured and TLS-derived estimates for ΔDg was similar on Scots pine-dominated and Norway spruce-dominated sample plots (R2 of 0.32 and 0.22, respectively) while being considerably lower on mixed-species sample plots (R2 = 0.01, Figure 4). On average, ΔDg was overestimated by 0.02–0.47 cm (1.4–40.5%, Table 6). Most accurate estimates for ΔDg were obtained on Scots pine-dominated sample plots (RMSE% 52.5%) followed by mixed-species sample plots (RMSE% 67.9%) and Norway spruce-dominated sample plots (RMSE% 86.4%).
In the case of ΔHg, the relationship between the field-measured and the TLS-derived estimates was the strongest on Norway spruce-dominated sample plots (R2 = 0.32) while being considerably lower on Scots pine-dominated and mixed-species sample plots (R2 = 0.05–0.09). On average, ΔHg was overestimated by 0.55 m (35.3%), 2.05 m (165.0%), and 0.98 m (86.6%) with an RMSE of 0.81 m (51.9%), 2.26 m (182.2%), and 1.39 m (122.9%) on Scots pine-dominated, Norway spruce-dominated, and mixed-species sample plots, respectively (Table 6).
R2 indicated a considerably stronger relationship between the field-measured and the TLS-derived estimates for ΔG on Norway spruce-dominated sample plots (R2 = 0.56) than on Scots pine-dominated and mixed-species sample plots (R2 = 0.01–0.04). On Norway spruce-dominated sample plots, ΔG was overestimated by 0.59 m2/ha (26.4%) while on Scots pine-dominated and mixed-species sample plots ΔG was underestimated by 0.23 m2/ha (8.1%) and 0.67 m2/ha (19.3%), respectively (Table 6). The estimation accuracy was the highest on Scots pine-dominated sample plots (RMSE% 48.9%) followed by Norway spruce-dominated and mixed-species sample plots (RMSE% 66.4–68.0%).
Relationship between the field-measured and the TLS-derived estimates for ΔTPH was the strongest on Norway spruce-dominated sample plots (R2 = 0.27) followed by Scots pine-dominated sample plots (R2 = 0.18, Figure 4). On average, ΔTPH was underestimated on all the sample plots by 45–124 n/ha (146.7–366.7%). The highest accuracy of ΔTPH estimates was obtained on Norway spruce-dominated sample plots (RMSE% 245.1%) followed by Scots pine-dominated sample plots (RMSE% 381.5%) and mixed-species sample plots (RMSE% 569.3%).

4. Discussion

The objective of this study was to assess the feasibility of TLS in characterizing boreal forest structure in space and time. We used a bi-temporal TLS dataset covering a five-year growth period in between the data acquisition campaigns in 2014 (T1) and 2019 (T2) and analyzed the accuracy of the TLS-based method to quantify changes in tree and forest structural attributes. The results showed that changes in tree and forest structural attributes were captured using TLS. In general, tree and forest structural attributes estimated at T1 differed significantly (p < 0.01) from the respective estimates at T2 (Table 5 and Table 7). Only in the case of TPH the differences in the TLS-derived estimates at T1 and T2 were not considered statistically significant due to incomplete tree detection. In general, changes in the tree attributes were estimated more accurately for Scots pine trees, followed by Norway spruce and broadleaved trees (Table 4). Similarly, the accuracy of characterizing changes in forest structural attributes was higher on Scots pine-dominated sample plots than on Norway spruce-dominated and mixed-species sample plots (Table 6).
The accuracy of using TLS in estimating tree and forest structural attributes at T1 and T2 was comparable to the previous findings on the performance of TLS in forest characterization. Based on previous studies, it is known that the performance of a TLS-based approach to characterize forest structure is affected by (1) the ability of the method to detect trees, and (2) the accuracy of the method to estimate tree attributes [10,39]. With our method, the g of trees that were detected at T1 and T2 accounted for 84.5% of the basal area of all trees (Table 3). Trees that remained undetected were mainly Norway spruces and broadleaved trees, and small in dbh (Figure 2). Similar performance in tree detection was reported in comparable forest conditions by Yrttimaa et al. [10]. Successful tree detection and characterization requires that a tree must be sufficiently represented by a point cloud. Occlusion decreases the capacity of a point cloud to properly digitize trees or forest stands [43]. Use of a multi-scan approach in TLS data acquisition decreases point cloud occlusion, thus improving the performance of a TLS-based method to characterize forest stands, especially the ones with a complex structure [22,44,45]. On a forest stand, occlusion affects the performance of a TLS-based method on both horizontal and vertical dimensions. Horizontal occlusion causes undetection of trees, as a part of trees remain shaded by other trees and undergrowth vegetation [10,43]. Differences in the tree detection accuracies between the different tree species can be explained by the different forest structures and shapes of dbh distributions. On mixed-species sample plots the vegetation density was higher than on Scots pine-dominated and Norway spruce-dominated sample plots (Table 1), making the horizontal forest structure more complex and occluded. Small trees have less surface visible to the scanner than large trees and thus, are more likely to be completely occluded by other trees (Figure 2). Undetection of trees directly affects the accuracy of G and TPH estimates which are, by definition, computed by summing up individual tree attributes at the sample plot level (see Table 2). In this study, G and TPH were underestimated by 19.1–20.5% and 26.9–35.0%, respectively, with RMSEs of 26.9% and 42.9–50.5%. These results are comparable to the accuracy achieved in similar forest conditions by [10]. In general, attributes characterizing horizontal tree dimensions of forest structure were estimated with high accuracy. In this study, dbh of all trees was estimated with an RMSE of 0.90–1.18 cm (4.1–5.7%) which is similar to results obtained by earlier studies in boreal forest conditions [20,22]. For Dg, the estimation error (RMSE 1.42–1.60 cm/5.2–6.0%) was slightly smaller than in [10] where an RMSE of 3.1 cm (12.3%) was recorded in comparable forest conditions.
Vertical point cloud occlusion causes uncertainty in h estimates as dense canopy layers and overlapping crowns block the visibility from a scanner to treetops [8,46]. Thus, performance of TLS-based approaches to correctly estimate h has been identified as a major bottleneck hindering the use of TLS in practical forest inventory applications [47]. This was confirmed also in this study, as h was underestimated due to limited visibility to treetops. An RMSE of 4.10–4.37 m (19.7–22.5%) in h estimates was recorded for all the trees which is in line with previous findings in comparable forest conditions [22,47]. As expected based on results reported in [10], accuracy of characterizing forest height was improved at the sample plot level where an RMSE of 1.85–2.51 m (7.9–11.2%) was recorded for Hg estimates. The highest accuracy in characterizing vertical forest structure was achieved in Scots pine-dominated sample plots where the canopy structure was favoring the TLS-based method more than in Norway spruce-dominated or mixed-species sample plots. For Scots pine trees, hc was successfully estimated by investigating the outer dimensions of a horizontally binned point cloud consisting of non-stem points (see Figure 1). Accuracy in hc estimates was similar to h estimates of Scots pine trees, providing reliable estimates for cr (Table 4).
The absolute errors in quantifying changes in tree attributes were, in general, at the same level than the errors in characterizing the attributes at T1 and T2 (Table 4). However, the bi-temporal TLS data used in this study covered only five growing seasons, which is a very short time when considering the lifetime of Scots pine or Norway spruce trees normally reaching the age from 80 to 120 years in boreal forests. Thus, changes in tree and forest structural attributes were relatively small, which explains why the errors in quantifying changes in tree attributes were rather large relative to the field-measured changes. In this study, for example, RMSE in dbh estimates (0.90–1.18 cm) was similar to the recorded average increase in dbh (1.16 cm). Short monitoring periods have been still applied in the previous studies related to investigating changes in forest structure using TLS due to the novelty of the method. In this case, it needs to be noted that the effect of measurement errors plays an important role when the changes in the monitored attributes were small. This means that, for example, the recorded changes in dbh and h can be within the expected errors of both TLS-based and traditional measurement methods reported by [8,37]. As Luoma et al. [37] showed earlier, there is some variation also in the caliper and clinometer measurements when the measurements are repeated, which can depend on the different measurement positions (e.g., determining the breast height for dbh measurements) among other subjective factors. Dendrometers, such as a girth band for tree diameter measurement [48], provide probably the most accurate observations for monitoring changes in the dimensions of a living tree. However, dendrometers only measure one attribute at a time (e.g., dbh) and installing girth bands on a large number of trees to only monitor changes in dbh at forest stand level is rather expensive. Thus, data from clinometer and caliper measurements are typically used as a reference for tree attributes. But with their reliability being on a similar level to TLS-derived estimates, especially when measuring tree stem diameters, it needs to be remembered that actually either one of the measurements could be the ground truth, or the true value may be somewhere between the two observations. With longer monitoring periods, changes in tree attributes are expected to be larger and thus, the effect of the measurement errors should decrease, which further improve the reliability of change monitoring. Despite the variation in accuracies, the results of this study allow us to expect that with longer time periods, also the relative accuracies in change monitoring will be improved when the changes in tree attributes to be captured also increases.
There are only a few previous studies where TLS has been used to capture changes in tree attributes. Liang et al. [6] reported that TLS-derived bi-temporal changes accounted for 92 percent of the changed basal area due to harvesting. Sheppard et al. [32] detected changes in the structure and form of wild cherry trees. Kaasalainen et al. [31] and Srinivasan et al. [30] investigated changes in biomass which were either studies in laboratory condition [31] or modeled [30], but not in forest conditions or directly. All the earlier studies only concentrated on a few attributes with a relatively small number of trees, hindering comparisons between this and previous studies. Luoma et al. [35] tested the feasibility of detecting tree growth with TLS on 35 sample trees with a time period of 9 years and made similar conclusions on the abilities of TLS in detecting changes in tree attributes. Whereas all the measurements in this study were TLS-based, Luoma et al. [35] still used field-measured h in their study. Based on our knowledge, this study is the first attempt to investigate changes in tree and forest structural attributes using TLS, which has been performed with such a large number of trees and in varying forest conditions.
The results of this study confirm the feasibility of TLS in characterizing forest structure in space and time. If an increase or decrease in tree and forest attributes was recorded in the field with conventional mensuration tools, a similar outcome was achieved by using bi-temporal TLS data. TPH was the only attribute that could not be characterized in time due to incomplete tree detection at both time points. Changes in TPH were minor, mostly because of a couple of fallen or harvested trees per sample plot during the monitoring period. Thus, it is evident that all trees should be characterized at the beginning and at the end of the monitoring period to reliably estimate ΔTPH. This requires better performance in tree detection which could be achieved with a more complete coverage of TLS data to avoid horizontal point cloud occlusion. However, increasing the number of individual scans used in a multi-scan approach decreases the cost-efficiency of TLS data acquisition. Use of mobile laser scanning (MLS) instead, where a point cloud is collected with a laser scanner mounted on an all-terrain vehicle [49,50] or a backpack [50,51], or with a hand-held laser scanner [52,53], would presumably be a more cost-efficient option to cover entire forest stands. When combined with SLAM (Simultaneous Localization and Mapping)-technology [54], the accuracy of MLS-derived tree attribute estimates is expected to be close to the TLS-derived estimates [51,53]. Another mobile platform for a laser scanner to suit close-range forest monitoring is an unmanned aerial vehicle (UAV) which can be used to collect detailed point clouds from above a forest canopy [55,56,57]. Due to different data acquisition geometries between terrestrial and UAV-borne point clouds, UAV-borne laser scanning is more suitable for characterization of the vertical forest structure whereas TLS or MLS can better capture the horizontal forest structure. An alternative option to combine the benefits of both terrestrial and aerial point cloud-based approaches is to collect the UAV-borne point clouds from inside the canopy [58] or to use a multisensorial approach [59] where photogrammetric UAV point clouds were integrated with TLS data. Use of a combination of bi-temporal terrestrial and aerial point clouds is expected to improve the accuracy of vertical forest characterization in space and time.

5. Conclusions

It is known that TLS is capable of characterizing forest structure in detail in space. Thus far, there has been a limited understanding of how forest structural changes can be quantified in time using TLS in boreal forest conditions. The results of this study confirm the capacity of TLS in providing information on the changes in tree and forest structural attributes. If an increase or decrease in tree and forest attributes was recorded in the field with calipers and clinometers, a similar outcome was achieved by using bi-temporal TLS data. However, incomplete digitization of trees and forest stands due to vertical and horizontal occlusion causes uncertainty in TLS-derived estimates in tree and forest attributes and their changes. Vertical occlusion could be decreased by using a combination of terrestrial and aerial point cloud data. Horizontal occlusion could be decreased with more complete point clouds by applying the MLS technique to preserve cost-efficiency in data acquisition.
In this study, changes in tree and forest structural attributes were small due to a relatively short monitoring period. It is expected that with a longer monitoring time, the changes in tree attributes become more reliably detectable when automated point cloud-based approaches are used in boreal forest conditions.

Author Contributions

Conceptualization, M.V., N.S., V.K., T.Y., and V.L.; methodology, T.Y., V.K., N.S.; formal analysis, T.Y.; investigation, T.Y. and V.L.; resources, M.V., M.H., and J.H.; writing—original draft preparation, T.Y., V.L., S.J., N.S., and M.V.; writing—review and editing, all authors; supervision, N.S. and M.V.; project administration, M.V.; funding acquisition, M.V., J.H., and M.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Academy of Finland, grant numbers 272195, 315079, 307362, 330422.

Acknowledgments

The authors would like to thank Häme University of Applied Sciences for supporting the research activities in Evo.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Yrttimaa, T.; Saarinen, N.; Luoma, V.; Tanhuanpää, T.; Kankare, V.; Liang, X.; Hyyppä, J.; Holopainen, M.; Vastaranta, M. Detecting and characterizing downed dead wood using terrestrial laser scanning. ISPRS J. Photogramm. Remote Sens. 2019, 151, 76–90. [Google Scholar] [CrossRef]
  2. Saarinen, N.; Vastaranta, M.; Honkavaara, E.; Wulder, M.A.; White, J.C.; Litkey, P.; Holopainen, M.; Hyyppä, J. Using multi-source data to map and model the predisposition of forests to wind disturbance. Scand. J. For. Res. 2016, 31, 66–79. [Google Scholar] [CrossRef]
  3. Carvajal-Ramírez, F.; da Silva, J.R.M.; Agüera-Vega, F.; Martínez-Carricondo, P.; Serrano, J.; Moral, F.J. Evaluation of fire severity indices based on pre- and post-fire multispectral imagery sensed from UAV. Remote Sens. 2019, 11, 993. [Google Scholar] [CrossRef] [Green Version]
  4. Gupta, V.; Reinke, K.; Jones, S.; Wallace, L.; Holden, L. Assessing metrics for estimating fire induced change in the forest understorey structure using terrestrial laser scanning. Remote Sens. 2015, 7, 8180–8201. [Google Scholar] [CrossRef] [Green Version]
  5. Holopainen, M.; Vastaranta, M.; Hyyppä, J. Outlook for the next generation’s precision forestry in Finland. Forests 2014, 5, 1682–1694. [Google Scholar] [CrossRef] [Green Version]
  6. Liang, X.; Hyyppä, J.; Kaartinen, H.; Holopainen, M.; Melkas, T. Detecting changes in forest structure over time with bi-temporal terrestrial laser scanning data. ISPRS Int. J. Geo-Inf. 2012, 1, 242–255. [Google Scholar] [CrossRef]
  7. Dassot, M.; Constant, T.; Fournier, M. The use of terrestrial LiDAR technology in forest science: Application fields, benefits and challenges. Ann. For. Sci. 2011, 68, 959–974. [Google Scholar] [CrossRef] [Green Version]
  8. Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
  9. Newnham, G.J.; Armston, J.D.; Calders, K.; Disney, M.I.; Lovell, J.L.; Schaaf, C.B.; Strahler, A.H.; Mark Danson, F. Terrestrial laser scanning for plot-scale forest measurement. Curr. For. Rep. 2015, 1, 239–251. [Google Scholar] [CrossRef] [Green Version]
  10. Yrttimaa, T.; Saarinen, N.; Kankare, V.; Liang, X.; Hyyppä, J.; Holopainen, M.; Vastaranta, M. Investigating the feasibility of multi-scan terrestrial laser scanning to characterize tree communities in southern boreal forests. Remote Sens. 2019, 11, 1423. [Google Scholar] [CrossRef] [Green Version]
  11. Maas, H.-G.; Bienert, A.; Scheller, S.; Keane, E. Automatic forest inventory parameter determination from terrestrial laser scanner data. Int. J. Remote Sens. 2008, 29, 1579–1593. [Google Scholar] [CrossRef]
  12. Aschoff, T.; Thies, M.; Spiecker, H. Describing forest stands using terrestrial laser-scanning. In Proceedings of the 20th ISPRS World Congress, Istanbul, Turkey, 12–23 July 2004; pp. 237–241. [Google Scholar]
  13. Cabo, C.; Ordóñez, C.; López-Sánchez, C.A.; Armesto, J. Automatic dendrometry: Tree detection, tree height and diameter estimation using terrestrial laser scanning. Int. J. Appl. Earth Obs. Geoinf. 2018, 69, 164–174. [Google Scholar] [CrossRef]
  14. Zhang, W.; Wan, P.; Wang, T.; Cai, S.; Chen, Y.; Jin, X.; Yan, G. A novel approach for the detection of standing tree stems from plot-level terrestrial laser scanning data. Remote Sens. 2019, 11, 211. [Google Scholar] [CrossRef] [Green Version]
  15. Liang, X.; Litkey, P.; Hyyppa, J.; Kaartinen, H.; Vastaranta, M.; Holopainen, M. Automatic stem mapping using single-scan terrestrial laser scanning. IEEE Trans. Geosci. Remote Sens. 2012, 50, 661–670. [Google Scholar] [CrossRef]
  16. Heinzel, J.; Huber, M. Detecting tree stems from volumetric TLS data in forest environments with rich understory. Remote Sens. 2016, 9, 9. [Google Scholar] [CrossRef] [Green Version]
  17. Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast automatic precision tree models from terrestrial laser scanner data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef] [Green Version]
  18. Hackenberg, J.; Morhart, C.; Sheppard, J.; Spiecker, H.; Disney, M. Highly accurate tree models derived from terrestrial laser scan data: A method description. Forests 2014, 5, 1069–1105. [Google Scholar] [CrossRef] [Green Version]
  19. Åkerblom, M.; Raumonen, P.; Kaasalainen, M.; Casella, E. Analysis of geometric primitives in quantitative structure models of tree stems. Remote Sens. 2015, 7, 4581–4603. [Google Scholar]
  20. Olofsson, K.; Holmgren, J. Single tree stem profile detection using terrestrial laser scanner data, flatness saliency features and curvature properties. Forests 2016, 7, 207. [Google Scholar] [CrossRef]
  21. Wilkes, P.; Lau, A.; Disney, M.; Calders, K.; Burt, A.; de Tanago, J.G.; Bartholomeus, H.; Brede, B.; Herold, M. Data acquisition considerations for terrestrial laser scanning of forest plots. Remote Sens. Environ. 2017, 196, 140–153. [Google Scholar] [CrossRef]
  22. Liang, X.; Hyyppä, J.; Kaartinen, H.; Lehtomäki, M.; Pyörälä, J.; Pfeifer, N.; Holopainen, M.; Brolly, G.; Francesco, P.; Hackenberg, J.; et al. International benchmarking of terrestrial laser scanning approaches for forest inventories. ISPRS J. Photogramm. Remote Sens. 2018, 144, 137–179. [Google Scholar] [CrossRef]
  23. Moorthy, S.M.K.; Krishna Moorthy, S.M.; Calders, K.; Vicari, M.B.; Verbeeck, H. Improved supervised learning-based approach for leaf and wood classification from LiDAR point clouds of forests. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3057–3070. [Google Scholar] [CrossRef] [Green Version]
  24. Åkerblom, M.; Raumonen, P.; Casella, E.; Disney, M.I.; Danson, F.M.; Gaulton, R.; Schofield, L.A.; Kaasalainen, M. Non-intersecting leaf insertion algorithm for tree structure models. Interface Focus 2018, 8, 20170045. [Google Scholar] [CrossRef] [PubMed]
  25. Vicari, M.B.; Disney, M.; Wilkes, P.; Burt, A.; Calders, K.; Woodgate, W. Leaf and wood classification framework for terrestrial LiDAR point clouds. Methods Ecol. Evol. 2019, 10, 680–694. [Google Scholar] [CrossRef] [Green Version]
  26. Ma, L.; Zheng, G.; Eitel, J.U.H.; Monika Moskal, L.; He, W.; Huang, H. Improved salient feature-based approach for automatically separating photosynthetic and non-photosynthetic components within terrestrial LiDAR point cloud data of forest canopies. IEEE Trans. Geosci. Remote Sens. 2016, 54, 679–696. [Google Scholar] [CrossRef]
  27. Béland, M.; Baldocchi, D.D.; Widlowski, J.-L.; Fournier, R.A.; Verstraete, M.M. On seeing the wood from the leaves and the role of voxel size in determining leaf area distribution of forests with terrestrial LiDAR. Agric. For. Meteorol. 2014, 184, 82–97. [Google Scholar] [CrossRef]
  28. Zhu, X.; Skidmore, A.K.; Darvishzadeh, R.; Olaf Niemann, K.; Liu, J.; Shi, Y.; Wang, T. Foliar and woody materials discriminated using terrestrial LiDAR in a mixed natural forest. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 43–50. [Google Scholar] [CrossRef]
  29. Junttila, S.; Holopainen, M.; Vastaranta, M.; Lyytikäinen-Saarenmaa, P.; Kaartinen, H.; Hyyppä, J.; Hyyppä, H. The potential of dual-wavelength terrestrial LiDAR in early detection of Ips typographus (L.) infestation—Leaf water content as a proxy. Remote Sens. Environ. 2019, 231, 111264. [Google Scholar] [CrossRef]
  30. Srinivasan, S.; Popescu, S.C.; Eriksson, M.; Sheridan, R.D.; Ku, N.-W. Multi-temporal terrestrial laser scanning for modeling tree biomass change. For. Ecol. Manag. 2014, 318, 304–317. [Google Scholar] [CrossRef]
  31. Kaasalainen, S.; Krooks, A.; Liski, J.; Raumonen, P.; Kaartinen, H.; Kaasalainen, M.; Puttonen, E.; Anttila, K.; Mäkipää, R. Change detection of tree biomass with terrestrial laser scanning and quantitative structure modelling. Remote Sens. 2014, 6, 3906–3922. [Google Scholar] [CrossRef] [Green Version]
  32. Sheppard, J.; Morhart, C.; Hackenberg, J.; Spiecker, H. Terrestrial laser scanning as a tool for assessing tree growth. IFOREST 2017, 10, 172–179. [Google Scholar] [CrossRef]
  33. Hess, C.; Härdtle, W.; Kunz, M.; Fichtner, A.; von Oheimb, G. A high-resolution approach for the spatiotemporal analysis of forest canopy space using terrestrial laser scanning data. Ecol. Evol. 2018, 8, 6800–6811. [Google Scholar] [CrossRef] [PubMed]
  34. Kunz, M.; Fichtner, A.; Härdtle, W.; Raumonen, P.; Bruelheide, H.; von Oheimb, G. Neighbour species richness and local structural variability modulate aboveground allocation patterns and crown morphology of individual trees. Ecol. Lett. 2019, 22, 2130–2140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  35. Luoma, V.; Saarinen, N.; Kankare, V.; Tanhuanpää, T.; Kaartinen, H.; Kukko, A.; Holopainen, M.; Hyyppä, J.; Vastaranta, M. Examining changes in stem taper and volume growth with two-date 3D point clouds. Forests 2019, 10, 382. [Google Scholar] [CrossRef] [Green Version]
  36. Vastaranta, M.; Yrttimaa, T.; Saarinen, N.; Yu, X.; Karjalainen, M.; Nurminen, K.; Karila, K.; Kankare, V.; Luoma, V.; Pyörälä, J.; et al. Airborne laser scanning outperforms the alternative 3D techniques in capturing variation in tree height and forest density in southern boreal forests. Baltic For. 2018, 28, 268–277. [Google Scholar]
  37. Luoma, V.; Saarinen, N.; Wulder, M.; White, J.; Vastaranta, M.; Holopainen, M.; Hyyppä, J. Assessing precision in conventional field measurements of individual tree attributes. Forests 2017, 8, 38. [Google Scholar] [CrossRef] [Green Version]
  38. Ritter, T.; Schwarz, M.; Tockner, A.; Leisch, F.; Nothdurft, A. Automatic mapping of forest stands based on three-dimensional point clouds derived from terrestrial laser-scanning. Forests 2017, 8, 265. [Google Scholar] [CrossRef]
  39. Yrttimaa, T.; Saarinen, N.; Kankare, V.; Hynynen, J.; Huuskonen, S.; Holopainen, M.; Hyyppä, J.; Vastaranta, M. Performance of terrestrial laser scanning to characterize managed Scots pine (Pinus sylvestris L.) stands is dependent on forest structural variation. EarthArXiv 2020. [Google Scholar] [CrossRef] [Green Version]
  40. Popescu, S.C.; Wynne, R.H. Seeing the trees in the forest. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef] [Green Version]
  41. Meyer, F.; Beucher, S. Morphological segmentation. J. Visual Commun. Image Represent. 1990, 1, 21–46. [Google Scholar] [CrossRef]
  42. Saarinen, N.; Kankare, V.; Vastaranta, M.; Luoma, V.; Pyörälä, J.; Tanhuanpää, T.; Liang, X.; Kaartinen, H.; Kukko, A.; Jaakkola, A.; et al. Feasibility of terrestrial laser scanning for collecting stem volume information from single trees. ISPRS J. Photogramm. Remote Sens. 2017, 123, 140–158. [Google Scholar] [CrossRef]
  43. Abegg, M.; Kükenbrink, D.; Zell, J.; Schaepman, M.E.; Morsdorf, F. Terrestrial laser scanning for forest inventories—Tree diameter distribution and scanner location impact on occlusion. For. Trees Livelihoods 2017, 8, 184. [Google Scholar] [CrossRef] [Green Version]
  44. Gollob, C.; Ritter, T.; Wassermann, C.; Nothdurft, A. Influence of scanner position and plot size on the accuracy of tree detection and diameter estimation using terrestrial laser scanning on forest inventory plots. Remote Sens. 2019, 11, 1602. [Google Scholar] [CrossRef] [Green Version]
  45. Trochta, J.; Král, K.; Janík, D.; Adam, D. Arrangement of terrestrial laser scanner positions for area-wide stem mapping of natural forests. Can. J. For. Res. 2013, 43, 355–363. [Google Scholar] [CrossRef]
  46. Schneider, F.D.; Kükenbrink, D.; Schaepman, M.E.; Schimel, D.S.; Morsdorf, F. Quantifying 3D structure and occlusion in dense tropical and temperate forests using close-range LiDAR. Agric. For. Meteorol. 2019, 268, 249–257. [Google Scholar] [CrossRef]
  47. Wang, Y.; Lehtomäki, M.; Liang, X.; Pyörälä, J.; Kukko, A.; Jaakkola, A.; Liu, J.; Feng, Z.; Chen, R.; Hyyppä, J. Is field-measured tree height as reliable as believed—A comparison study of tree height estimates from field measurement, airborne laser scanning and terrestrial laser scanning in a boreal forest. ISPRS J. Photogramm. Remote Sens. 2019, 147, 132–145. [Google Scholar] [CrossRef]
  48. Pesonen, E. A new girth band for measuring stem diameter changes. Forestry 2004, 77, 431–439. [Google Scholar] [CrossRef] [Green Version]
  49. Liang, X.; Hyyppa, J.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Yu, X. The use of a mobile laser scanning system for mapping large forest plots. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1504–1508. [Google Scholar] [CrossRef]
  50. Kukko, A.; Kaartinen, H.; Hyyppä, J.; Chen, Y. Multiplatform mobile laser scanning: Usability and performance. Sensors 2012, 12, 11712–11733. [Google Scholar] [CrossRef] [Green Version]
  51. Hyyppä, E.; Kukko, A.; Kaijaluoto, R.; White, J.C.; Wulder, M.A.; Pyörälä, J.; Liang, X.; Yu, X.; Wang, Y.; Kaartinen, H.; et al. Accurate derivation of stem curve and volume using backpack mobile laser scanning. ISPRS J. Photogramm. Remote Sens. 2020, 161, 246–262. [Google Scholar] [CrossRef]
  52. Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest inventory with terrestrial LiDAR: A comparison of static and hand-held mobile laser scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef] [Green Version]
  53. Chen, S.; Liu, H.; Feng, Z.; Shen, C.; Chen, P. Applicability of personal laser scanning in forestry inventory. PLoS ONE 2019, 14, e0211392. [Google Scholar] [CrossRef] [PubMed]
  54. Kukko, A.; Kaijaluoto, R.; Kaartinen, H.; Lehtola, V.V.; Jaakkola, A.; Hyyppä, J. Graph SLAM correction for single scanner MLS forest data under boreal forest canopy. ISPRS J. Photogramm. Remote Sens. 2017, 132, 199–209. [Google Scholar] [CrossRef]
  55. Jaakkola, A.; Hyyppä, J.; Kukko, A.; Yu, X.; Kaartinen, H.; Lehtomäki, M.; Lin, Y. A low-cost multi-sensoral mobile mapping system and its feasibility for tree measurements. ISPRS J. Photogramm. Remote Sens. 2010, 65, 514–522. [Google Scholar] [CrossRef]
  56. Liu, K.; Shen, X.; Cao, L.; Wang, G.; Cao, F. Estimating forest structural attributes using UAV-LiDAR data in Ginkgo plantations. ISPRS J. Photogramm. Remote Sens. 2018, 146, 465–482. [Google Scholar] [CrossRef]
  57. Jaakkola, A.; Hyyppä, J.; Yu, X.; Kukko, A.; Kaartinen, H.; Liang, X.; Hyyppä, H.; Wang, Y. Autonomous collection of forest field reference—The outlook and a first step with UAV laser scanning. Remote Sens. 2017, 9, 785. [Google Scholar] [CrossRef] [Green Version]
  58. Hyyppä, E.; Hyyppä, J.; Hakala, T.; Kukko, A.; Wulder, M.A.; White, J.C.; Pyörälä, J.; Yu, X.; Wang, Y.; Virtanen, J.-P.; et al. Under-canopy UAV laser scanning for accurate forest field measurements. ISPRS J. Photogramm. Remote Sens. 2020, 164, 41–60. [Google Scholar] [CrossRef]
  59. Yrttimaa, T.; Saarinen, N.; Kankare, V.; Viljanen, N.; Hynynen, J.; Huuskonen, S.; Holopainen, M.; Hyyppä, J.; Honkavaara, E.; Vastaranta, M. Multisensorial close-range sensing generates benefits for characterization of managed Scots pine (Pinus sylvestris L.) stands. ISPRS Int. J. Geo-Inf. 2020, 9, 309. [Google Scholar] [CrossRef]
Remotesensing 12 02672 g001 550
Figure 1. Outline of the terrestrial laser scanning (TLS) data processing workflow. (a) One center scan and four auxiliary scans were used to acquire a multi-scan TLS point cloud data in 2014 and 2019. (b) TLS-based canopy height model (CHM) and a Marker-Controlled Watershed Segmentation procedure was applied to normalized TLS point clouds to detect individual trees. Surface normal filtering, point cloud clustering, and Random Sample Consensus (RANSAC)-based cylinder filtering were applied to identify vertical, cylindrical, and planar surfaces to classify TLS point cloud into stem and non-stem points (for more details, see [39]). (c) Then, the classified point cloud was used to extract tree attributes, namely diameter-at-breast-height (dbh) and tree height (h) for all the trees, and height of the crown base (hc) and crown ratio (cr) for Scots pine (Pinus sylvestris L.) trees.
Figure 1. Outline of the terrestrial laser scanning (TLS) data processing workflow. (a) One center scan and four auxiliary scans were used to acquire a multi-scan TLS point cloud data in 2014 and 2019. (b) TLS-based canopy height model (CHM) and a Marker-Controlled Watershed Segmentation procedure was applied to normalized TLS point clouds to detect individual trees. Surface normal filtering, point cloud clustering, and Random Sample Consensus (RANSAC)-based cylinder filtering were applied to identify vertical, cylindrical, and planar surfaces to classify TLS point cloud into stem and non-stem points (for more details, see [39]). (c) Then, the classified point cloud was used to extract tree attributes, namely diameter-at-breast-height (dbh) and tree height (h) for all the trees, and height of the crown base (hc) and crown ratio (cr) for Scots pine (Pinus sylvestris L.) trees.
Remotesensing 12 02672 g001
Remotesensing 12 02672 g002 550
Figure 2. Diameter at breast height (dbh) distributions presenting the relative frequency (f) of trees in 1 cm dbh classes by tree species. Mean values (μ) and standard deviations (σ) based on field (Ref) and terrestrial laser scanning (TLS) measurements are presented as well. The colored bars represent the proportion of trees by dbh classes that were detected from the TLS point clouds at both time points 2014 (T1) and 2019 (T2).
Figure 2. Diameter at breast height (dbh) distributions presenting the relative frequency (f) of trees in 1 cm dbh classes by tree species. Mean values (μ) and standard deviations (σ) based on field (Ref) and terrestrial laser scanning (TLS) measurements are presented as well. The colored bars represent the proportion of trees by dbh classes that were detected from the TLS point clouds at both time points 2014 (T1) and 2019 (T2).
Remotesensing 12 02672 g002
Remotesensing 12 02672 g003 550
Figure 3. Relationship between the field-measured reference measurements and the TLS-derived estimates on tree attributes, such as diameter-at-breast-height (dbh), basal area (g), tree height (h), diameter-height-ratio (d-h-ratio), and crown ratio (cr) by tree species measured in 2014 (T1) and 2019 (T2) as well as their difference (Δdbh, Δg, Δh, Δd-h-ratio, and Δcr). The solid black line represents the 1:1 relationship between the reference and the estimated values. R2p, R2s, and R2b denote coefficient of determination for Scots pine, Norway spruce, and broadleaved trees, respectively.
Figure 3. Relationship between the field-measured reference measurements and the TLS-derived estimates on tree attributes, such as diameter-at-breast-height (dbh), basal area (g), tree height (h), diameter-height-ratio (d-h-ratio), and crown ratio (cr) by tree species measured in 2014 (T1) and 2019 (T2) as well as their difference (Δdbh, Δg, Δh, Δd-h-ratio, and Δcr). The solid black line represents the 1:1 relationship between the reference and the estimated values. R2p, R2s, and R2b denote coefficient of determination for Scots pine, Norway spruce, and broadleaved trees, respectively.
Remotesensing 12 02672 g003
Remotesensing 12 02672 g004 550
Figure 4. Relationship between the field-measured reference measurements and the TLS-derived estimates on forest structural attributes, such as basal area-weighted mean diameter (Dg) and -height (Hg), mean basal area (G), and number of trees per hectare (TPH) by main tree species in 2014 (T1) and 2019 (T2) as well as their difference (ΔDg, ΔHg, ΔG, and ΔTPH). The solid black line represents the 1:1 relationship between the reference and the estimated values. R2p, R2s, and R2b denote coefficient of determination for Scots pine-dominated, Norway spruce-dominated, and mixed-species forest plots, respectively.
Figure 4. Relationship between the field-measured reference measurements and the TLS-derived estimates on forest structural attributes, such as basal area-weighted mean diameter (Dg) and -height (Hg), mean basal area (G), and number of trees per hectare (TPH) by main tree species in 2014 (T1) and 2019 (T2) as well as their difference (ΔDg, ΔHg, ΔG, and ΔTPH). The solid black line represents the 1:1 relationship between the reference and the estimated values. R2p, R2s, and R2b denote coefficient of determination for Scots pine-dominated, Norway spruce-dominated, and mixed-species forest plots, respectively.
Remotesensing 12 02672 g004
Table
Table 1. Variation in tree attributes by tree species and forest structural attributes by main tree species of a sample plot, measured in 2014 (T1) and 2019 (T2). Diameter at breast height (dbh), basal area (g), tree height (h), diameter-height-ratio (d-h-ratio), height of the crown base (hc), and crown ratio (cr) were defined at tree level whereas basal area-weighted mean diameter (Dg) and -height (Hg), mean basal area (G), and number of trees per hectare (TPH) were defined at plot level. Scots pine-dominated plots = basal area of Scots pine (Pinus sylvestris L.) accounts for more than 67% of the total basal area of a plot. Norway spruce-dominated plots = basal area of Norway spruce (Picea abies (L.) H. Karst.) trees account for more than 67% of the total basal area of a plot. Mixed-species plots = basal area of two or more tree species each account for more than 30% of the total basal area of a plot.
Table 1. Variation in tree attributes by tree species and forest structural attributes by main tree species of a sample plot, measured in 2014 (T1) and 2019 (T2). Diameter at breast height (dbh), basal area (g), tree height (h), diameter-height-ratio (d-h-ratio), height of the crown base (hc), and crown ratio (cr) were defined at tree level whereas basal area-weighted mean diameter (Dg) and -height (Hg), mean basal area (G), and number of trees per hectare (TPH) were defined at plot level. Scots pine-dominated plots = basal area of Scots pine (Pinus sylvestris L.) accounts for more than 67% of the total basal area of a plot. Norway spruce-dominated plots = basal area of Norway spruce (Picea abies (L.) H. Karst.) trees account for more than 67% of the total basal area of a plot. Mixed-species plots = basal area of two or more tree species each account for more than 30% of the total basal area of a plot.
Tree/Forest Structural AttributeTree SpeciesMinimum
(T1/T2)		Mean
(T1/T2)		Maximum
(T1/T2)		Standard Deviation
(T1/T2)
Tree Attributesdbh (cm)All trees5.0/5.116.9/17.959.9/64.010.2/10.5
Scots pine5.2/5.120.3/21.359.7/60.110.3/10.6
Norway spruce5.0/5.116.9/18.057.9/61.711.0/11.2
Broadleaved5.1/5.114.9/15.759.9/64.08.1/8.7
g (cm2)All trees20.0/20.0308.0/339.92818.0/3217.0399.1/425.0
Scots pine21.2/20.8407.7/445.52799.2/2836.9468.2/487.1
Norway spruce20.0/20.4318.4/351.72633.0/2989.9416.6/439.0
Broadleaved20.0/20.0225.7/251.82818.0/3217.0291.4/331.7
h (m)All trees2.2/1.916.3/17.436.6/38.47.3/7.5
Scots pine5.0/5.017.8/19.234.5/37.25.5/5.8
Norway spruce2.2/3.515.2/16.436.6/38.48.4/8.5
Broadleaved2.2/1.917.0/17.732.5/35.86.0/6.6
d-h-ratioAll trees0.42/0.411.03/1.024.70/5.000.31/0.33
Scots pine0.57/0.531.10/1.082.24/2.450.29/0.29
Norway spruce0.73/0.651.09/1.082.86/2.150.21/0.19
Broadleaved0.42/0.410.88/0.914.70/5.000.38/0.47
hc (m)Scots pine4.2/6.312.2/13.923.1/24.63.4/3.4
crScots pine0.22/0.190.40/0.370.69/0.590.09/0.08
Forest Structural AttributesDg (cm)All plots13.0/14.327.5/28.842.8/44.09.3/9.3
Scots pine-dominated14.2/15.121.7/22.930.6/31.74.5/4.5
Norway spruce-dominated19.7/21.234.8/36.142.8/44.06.9/6.9
Mixed-species13.0/14.324.8/26.242.8/43.29.7/9.7
Hg (m)All plots12.4/13.722.3/23.631.6/32.44.9/4.9
Scots pine-dominated12.4/13.718.4 /20.023.1/25.33.2/3.4
Norway spruce-dominated18.4/20.326.9/28.231.6/32.43.6/3.7
Mixed-species15.9/17.320.8/21.927.3/27.83.6/3.5
All plots15.3/17.231.6/34.551.5/56.810.5/11.0
G (m2/ha)Scots pine-dominated15.3/17.222.6/25.531.1/34.45.9/6.8
Norway spruce-dominated21.3/23.737.6/39.951.0/53.88.7/8.9
Mixed-species16.2/17.532.4/35.951.5/56.810.6/11.7
TPH (n/ha)All plots368/3681059/10453341/3236706/711
Scots pine-dominated368/368963/9971894/2105495/553
Norway spruce-dominated395/368635/6051289/1289289/301
Mixed-species526/5521522/14883341/3236847/835
Table
Table 2. Description of the attributes used in this study to characterize trees and forest structure in 2014 (T1) and 2019 (T2). A = sample plot area in hectares, n = number of trees within a sample plot.
Table 2. Description of the attributes used in this study to characterize trees and forest structure in 2014 (T1) and 2019 (T2). A = sample plot area in hectares, n = number of trees within a sample plot.
Tree/Forest Structural AttributeAbbreviationDescription/Formula
Tree Attributesdiameter-at-breast-height (cm)dbhtree diameter measured at a 1.3-m height
basal area (cm2)gπ ∗ dbh2/4
tree height (m)hvertical distance between ground and treetop
diameter-height ratiod-h-ratiodbh/h
height of the crown base (m)hcheight of the lowest living branches
crown ratiocr(h − hc)/h
Forest Structural Attributesbasal area-weighted mean diameter (cm)Dg ∑ i = 1 n d b h i * g i / ∑ i = 1 n g i
basal area-weighted mean height (m)Hg ∑ i = 1 n h i * g i / ∑ i = 1 n g i
mean basal area (m2/ha)G ∑ i = 1 n g i / A
number of trees per hectare (n/ha)TPHn/A
Table
Table 3. The number of trees by tree species that were measured in the field (Nref) and detected from the TLS point clouds (NTLS) at the beginning (2014) and at the end of the monitoring period (2019). Completeness indicates how large a part of the detected trees represented the total number and the total basal area of the field measured trees.
Table 3. The number of trees by tree species that were measured in the field (Nref) and detected from the TLS point clouds (NTLS) at the beginning (2014) and at the end of the monitoring period (2019). Completeness indicates how large a part of the detected trees represented the total number and the total basal area of the field measured trees.
Tree SpeciesNrefNTLSCompleteness: Total Stem NumberCompleteness: Total Basal Area
All trees128079562.1%84.5%
Scots pine27022784.1%91.3%
Norway spruce64936656.4%85.7%
Broadleaved36120256.0%73.3%
Table
Table 4. Bias and root-mean-square-error (RMSE) of TLS-derived estimates for tree attributes, namely diameter-at-breast-height (dbh), basal area (g), tree height (h), diameter-height-ratio (d-h-ratio), height of the crown base (hc) and crown ratio (cr) by tree species at time points T1 (2014) and T2 (2019) as well as their change (Δ). Negative bias denotes underestimation.
Table 4. Bias and root-mean-square-error (RMSE) of TLS-derived estimates for tree attributes, namely diameter-at-breast-height (dbh), basal area (g), tree height (h), diameter-height-ratio (d-h-ratio), height of the crown base (hc) and crown ratio (cr) by tree species at time points T1 (2014) and T2 (2019) as well as their change (Δ). Negative bias denotes underestimation.
Tree AttributeTree SpeciesBiasRMSE
T1T2ΔT1T2Δ
dbh (cm)All trees−0.05 (−0.3%)0.04 (0.2%)0.10 (8.3%)1.18 (5.7%)0.90 (4.1%)1.13 (97.4%)
Scots pine−0.43 (−2.0%)−0.32 (−1.4%)0.12 (10.1%)1.11 (5.2%)0.99 (4.5%)0.99 (83.9%)
Norway spruce0.26 (1.2%)0.30 (1.3%)0.04 (3.8%)1.26 (5.7%)0.77 (3.3%)1.22 (103.5%)
Broadleaved−0.19 (−1.1%)−0.03 (−0.15%)0.17 (15.0%)1.11 (6.3%)0.99 (5.27%)1.12 (100.4%)
g (cm2)All trees−7.65 (−1.9%)−3.39 (−0.7%)4.26 (10.2%)49.28 (11.9%)47.59 (10.4%)49.40 (118.4%)
Scots pine−21.47 (−5.1%)−18.48 (−3.9%)2.99 (7.0%)52.82 (12.5%)60.81 (13.0%)44.14 (102.8%)
Norway spruce1.75 (0.4%)7.38 (1.4%)5.64 (12.9%)50.51 (10.6%)32.35 (6.2%)55.49 (126.6%)
Broadleaved−9.16 (−3.1%)−5.96 (−1.8%)3.21 (8.7%)42.42 (14.5%)53.51 (16.3%)42.98 (117.1%)
h (m)All trees−1.33 (−6.9%)−0.74 (−3.6%)0.59 (42.1%)4.37 (22.5%)4.10 (19.7%)3.53 (251.6%)
Scots pine−0.89 (−4.8%)−0.47 (−2.3%)0.43 (27.3%)2.52 (13.7%)2.42 (12.1%)1.91 (122.8%)
Norway spruce−0.51 (−2.6%)0.39 (1.8%)0.90 (72.3%)3.99 (20.1%)3.03 (14.4%)3.43 (274.6%)
Broadleaved−3.31 (−16.8%)−3.11 (−14.6%)0.21 (13.8%)6.26 (31.7%)6.56 (30.8%)4.85 (321.5%)
d-h-ratioAll trees0.10 (9.7%)0.07 (6.3%)−0.04 (226.6%)0.35 (33.6%)0.30 (29.5%)0.33 (2028.6%)
Scots pine0.05 (4.6%)0.03 (2.6%)−0.02 (78.3%)0.28 (24.9%)0.24 (21.6%)0.28 (942.6%)
Norway spruce0.06 (5.3%)−0.01 (0.1%)−0.06 (563.8%)0.26 (23.6%)0.16 (14.8%)0.22 (2123.3%)
Broadleaved0.24 (26.9%)0.23 (26.2%)−0.01 (88.6%)0.53 (59.8%)0.51 (57.7%)0.49 (4516.2%)
hc (m)Scots pine−1.70 (−16.1%)−1.36 (−10.9%)0.34 (20.7%)2.71 (25.7%)2.55 (20.4%)1.97 (120.6%)
crScots pine0.05 (11.7%)0.04 (10.3%)−0.01 (36.2%)0.10 (22.8%)0.09 (22.5%)0.09 (318.1%)
Table
Table 5. The p-values from the paired-sample t-tests indicating the significance of the differences between the TLS-derived estimates of tree attributes, such as diameter-at-breast-height (dbh), basal area (g), tree height (h), diameter-height-ratio (d-h-ratio), and crown ratio (cr) by tree species measured in 2014 (T1) and 2019 (T2).
Table 5. The p-values from the paired-sample t-tests indicating the significance of the differences between the TLS-derived estimates of tree attributes, such as diameter-at-breast-height (dbh), basal area (g), tree height (h), diameter-height-ratio (d-h-ratio), and crown ratio (cr) by tree species measured in 2014 (T1) and 2019 (T2).
Tree Speciesdbhghd-h-Ratiohccr
All trees<0.000<0.000<0.000<0.000<0.000<0.000
Scots pine<0.000<0.000<0.000<0.000<0.000<0.000
Norway spruce<0.000<0.000<0.000<0.000--
Broadleaved tree<0.000<0.000<0.0000.003--
Table
Table 6. Bias and root-mean-square-error (RMSE) of TLS-derived estimates for forest structural attributes, namely basal area-weighted mean diameter (Dg) and -height (Hg), mean basal area (G) and number of trees per hectare (TPH) in 2014 (T1) and 2019 (T2) as well as their change (Δ). Negative bias denotes underestimation.
Table 6. Bias and root-mean-square-error (RMSE) of TLS-derived estimates for forest structural attributes, namely basal area-weighted mean diameter (Dg) and -height (Hg), mean basal area (G) and number of trees per hectare (TPH) in 2014 (T1) and 2019 (T2) as well as their change (Δ). Negative bias denotes underestimation.
Forest Structural AttributeMain Tree SpeciesBiasRMSE
T1T2ΔT1T2Δ
Dg (cm)All plots0.08 (0.3%)0.25 (0.9%)0.17 (13.2%)1.42 (5.2%)1.72 (6.0%)0.93 (72.6%)
Scots pine-dominated0.08 (0.4%)0.55 (2.4%)0.47 (40.5%)0.59 (2.7%)0.77 (3.4%)0.60 (52.5%)
Norway spruce-dominated−0.26 (−0.7%)−0.15 (−0.4%)0.10 (7.8%)0.87 (2.5%)1.06 (2.9%)1.13 (86.4%)
Mixed-species0.39 (1.6%)0.41 (1.6%)0.02 (1.4%)2.09 (8.4%)2.51 (9.6%)0.91 (67.9%)
Hg (m)All plots−1.73 (−7.8%)−0.50 (−2.1%)1.24 (96.3%)2.51 (11.2%)1.85 (7.9%)1.64 (127.8%)
Scots pine-dominated−0.35 (−1.9%)0.20 (1.0%)0.55 (35.3%)0.53 (2.9%)0.70 (3.5%)0.81 (51.9%)
Norway spruce-dominated−2.88 (−10.7%)−0.83 (−2.9%)2.05 (165.0%)3.12 (11.6%)1.09 (3.9%)2.26 (182.2%)
Mixed-species−1.67 (−8.0%)−0.69 (−3.1%)0.98 (86.6%)2.72 (13.1%)2.76 (12.6%)1.39 (122.9%)
G (m2/ha)All plots−6.49 (−20.5%)−6.60 (19.1%)−0.11 (−3.7%)8.52 (26.9%)9.27 (26.9%)1.84 (64.2%)
Scots pine-dominated−5.32 (−23.6%)−5.56 (−21.8%)−0.23 (−8.1%)7.03 (31.1%)8.05 (31.6%)1.40 (48.9%)
Norway spruce-dominated−3.84 (−10.2%)−3.24 (−8.1%)0.59 (26.4%)5.09 (13.5%)4.23 (10.6%)1.48 (66.4%)
Mixed-species−9.79 (−30.2%)−10.46 (−29.2%)−0.67 (−19.3%)11.50 (35.5%)12.82 (35.7%)2.34 (68.0%)
TPH (n/ha)All plots−373 (−35.2%)−292 (−27.9%)−81 (−570%)620 (58.5%)515 (49.3%)143 (1008.7%)
Scots pine-dominated−337 (−35.0%)−268 (−26.9%)−68 (−200.0%)486 (50.5%)428 (42.9%)130 (381.5%)
Norway spruce-dominated−91 (−14.3%)−47 (−7.7%)−45 (−146.7%)117 (18.5%)65 (10.7%)74 (245.1%)
Mixed-species−659 (−43.3%)−536 (−36.0)−124 (−366.7%)914 (60.0%)753 (50.6%)193 (569.3%)
Table
Table 7. The p-values from the paired-sample t-tests indicating the significance of the differences between the TLS-derived estimates on forest structural attributes, such as basal area-weighted mean diameter (Dg) and - height (Hg), mean basal area (G) and trees per hectare (TPH) by main tree species measured in 2014 (T1) and 2019 (T2).
Table 7. The p-values from the paired-sample t-tests indicating the significance of the differences between the TLS-derived estimates on forest structural attributes, such as basal area-weighted mean diameter (Dg) and - height (Hg), mean basal area (G) and trees per hectare (TPH) by main tree species measured in 2014 (T1) and 2019 (T2).
Main Tree speciesDgHgGTPH
All plots<0.000<0.000<0.0000.105
Scots pine-dominated<0.000<0.000<0.0000.014
Norway spruce-dominated<0.000<0.000<0.0000.775
Mixed-species<0.000<0.000<0.0000.984

Share and Cite

MDPI and ACS Style

Yrttimaa, T.; Luoma, V.; Saarinen, N.; Kankare, V.; Junttila, S.; Holopainen, M.; Hyyppä, J.; Vastaranta, M. Structural Changes in Boreal Forests Can Be Quantified Using Terrestrial Laser Scanning. Remote Sens. 2020, 12, 2672. https://doi.org/10.3390/rs12172672

AMA Style

Yrttimaa T, Luoma V, Saarinen N, Kankare V, Junttila S, Holopainen M, Hyyppä J, Vastaranta M. Structural Changes in Boreal Forests Can Be Quantified Using Terrestrial Laser Scanning. Remote Sensing. 2020; 12(17):2672. https://doi.org/10.3390/rs12172672

Chicago/Turabian Style

Yrttimaa, Tuomas, Ville Luoma, Ninni Saarinen, Ville Kankare, Samuli Junttila, Markus Holopainen, Juha Hyyppä, and Mikko Vastaranta. 2020. "Structural Changes in Boreal Forests Can Be Quantified Using Terrestrial Laser Scanning" Remote Sensing 12, no. 17: 2672. https://doi.org/10.3390/rs12172672

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop