Extracting Building Boundaries from High Resolution Optical Images and LiDAR Data by Integrating the Convolutional Neural Network and the Active Contour Model
Abstract
1. Introduction
2. Materials and Methods
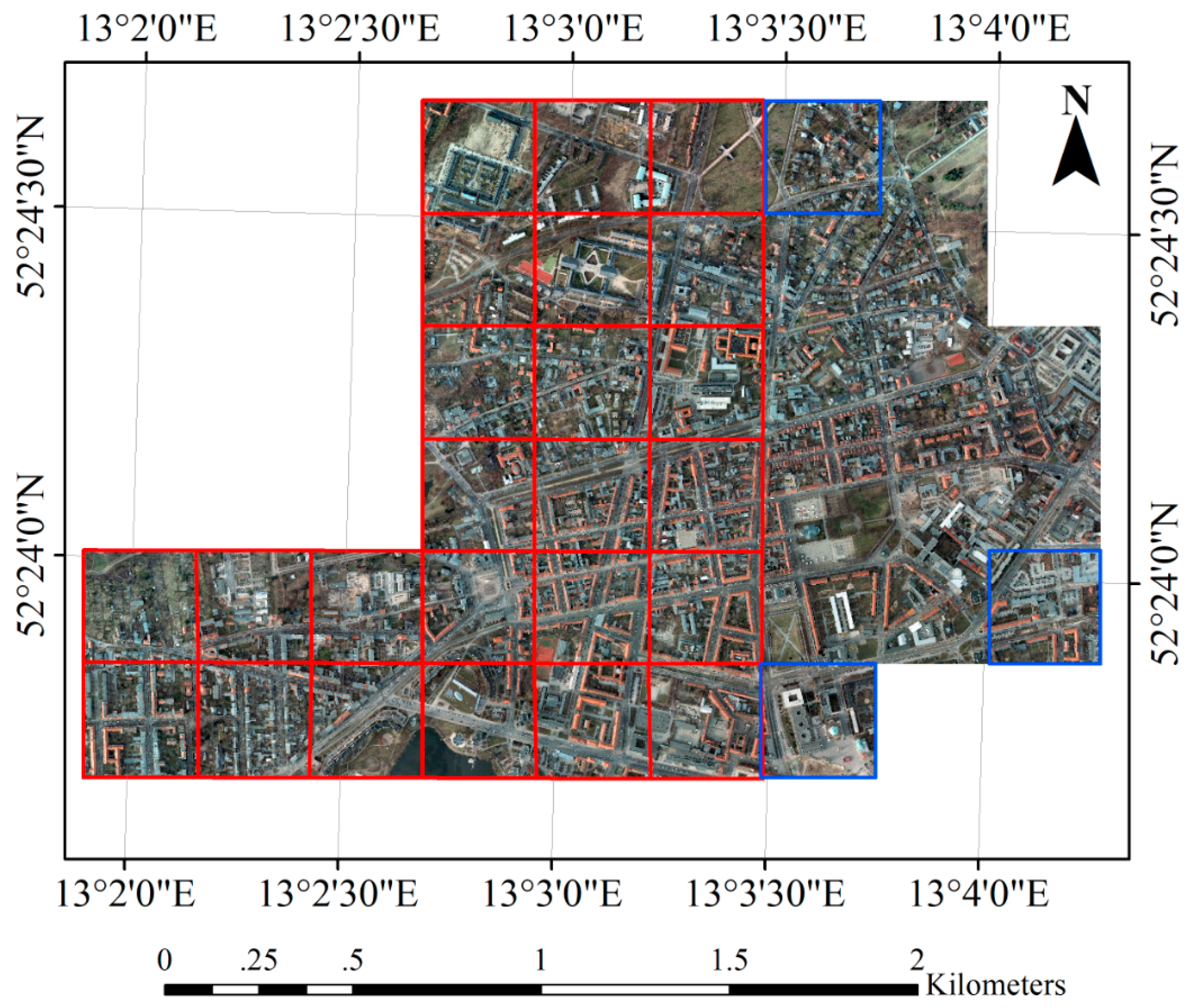
2.1. Study Materials
2.2. Preliminaries
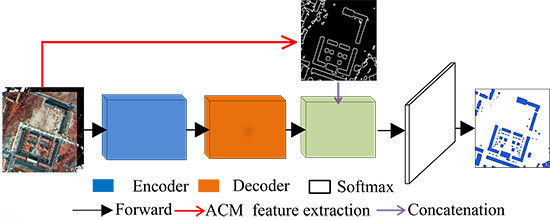
2.3. Building Boundary Extraction Based on CNN and ACM
2.4. Experiment Setup
2.5. Assessment
3. Results
3.1. Building Boundary Extraction Results
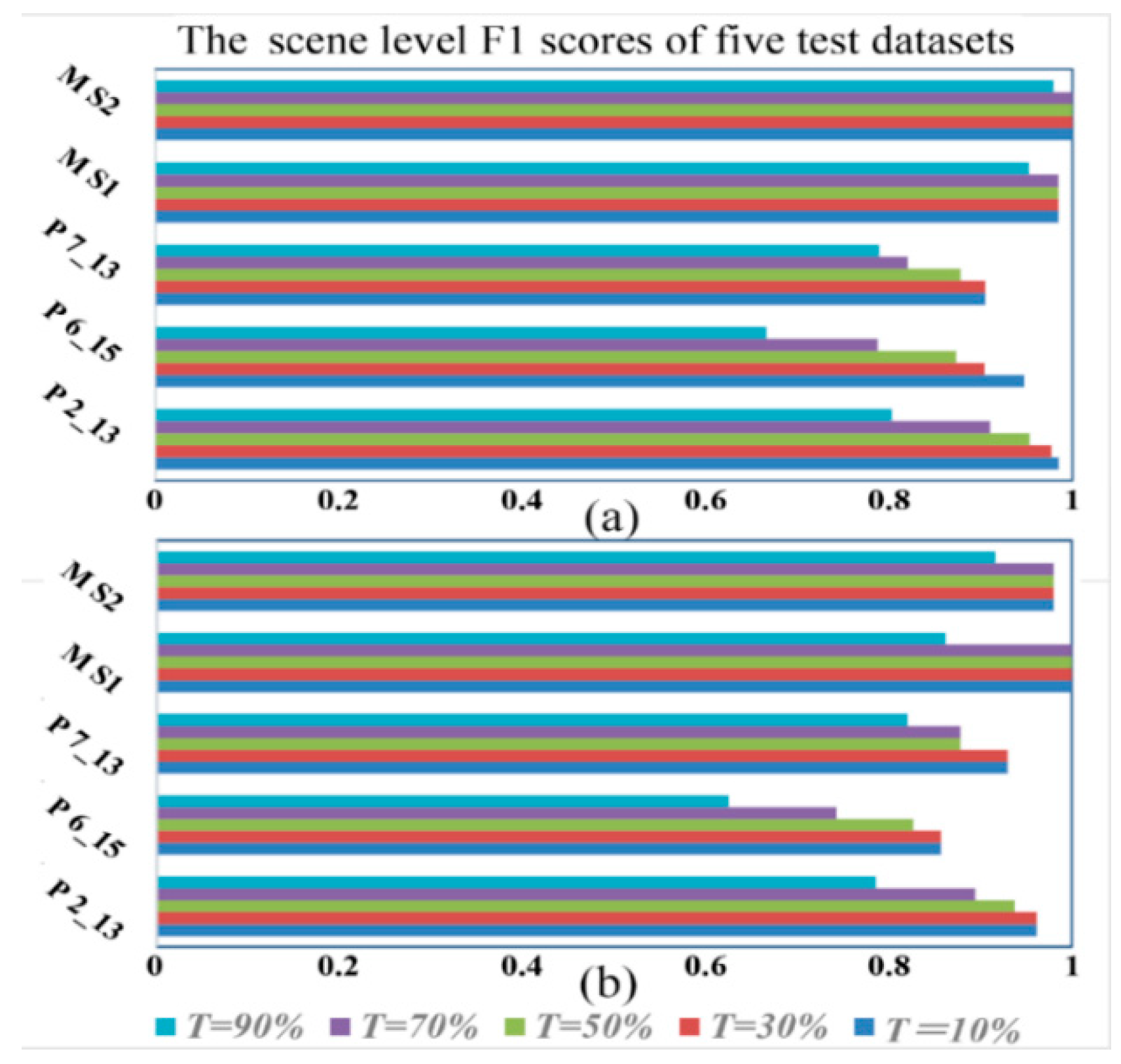
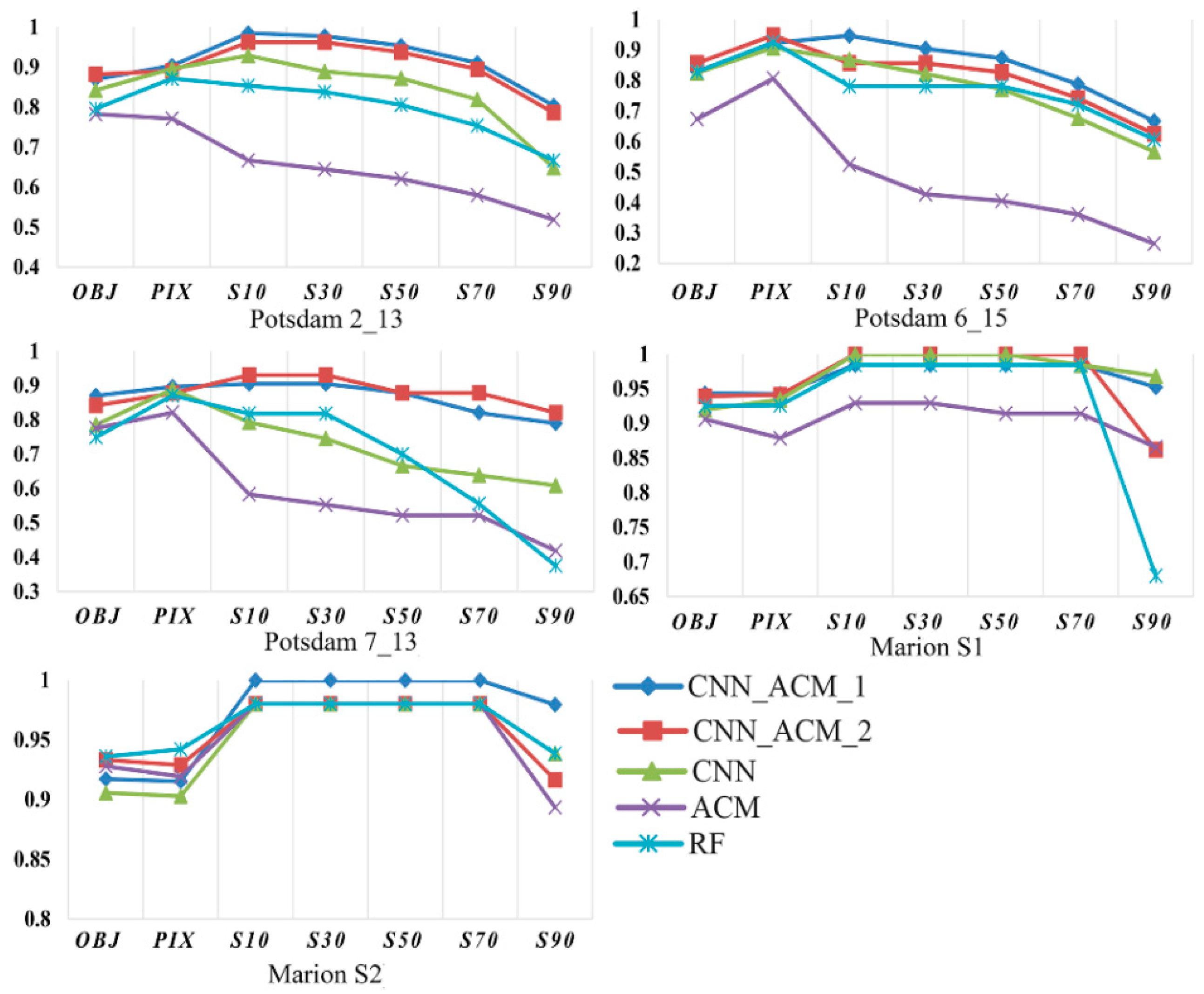
3.2. Performance Assessment
3.3. Comparative Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Scenes | Metrics | Overlapping Threshold | ||||
|---|---|---|---|---|---|---|
| 10% | 30% | 50% | 70% | 90% | ||
| Potsdam 2_13 | Comp | 0.9701 | 0.9552 | 0.9104 | 0.8358 | 0.6716 |
| Corr | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | |
| F1 score | 0.9848 | 0.9771 | 0.9531 | 0.9106 | 0.8036 | |
| Potsdam 6_15 | Comp | 0.9730 | 0.8919 | 0.8378 | 0.7027 | 0.5405 |
| Corr | 0.9231 | 0.9167 | 0.9118 | 0.8966 | 0.8696 | |
| F1 score | 0.9474 | 0.9041 | 0.8732 | 0.7879 | 0.6667 | |
| Potsdam 7_13 | Comp | 0.9048 | 0.9048 | 0.8571 | 0.7619 | 0.7143 |
| Corr | 0.9048 | 0.9048 | 0.9000 | 0.8889 | 0.8824 | |
| F1 score | 0.9048 | 0.9048 | 0.8780 | 0.8205 | 0.7895 | |
| Marion S1 | Comp | 0.9697 | 0.9697 | 0.9697 | 0.9697 | 0.9091 |
| Corr | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | |
| F1 score | 0.9846 | 0.9846 | 0.9846 | 0.9846 | 0.9524 | |
| Marion S2 | Comp | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9600 |
| Corr | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | |
| F1 score | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.9796 | |
| Scenes | Metrics | Overlapping Threshold | ||||
|---|---|---|---|---|---|---|
| 10% | 30% | 50% | 70% | 90% | ||
| Potsdam 2_13 | Comp | 0.9403 | 0.9403 | 0.8955 | 0.8209 | 0.6567 |
| Corr | 0.9844 | 0.9844 | 0.9836 | 0.9821 | 0.9778 | |
| F1 score | 0.9618 | 0.9618 | 0.9375 | 0.8943 | 0.7857 | |
| Potsdam 6_15 | Comp | 0.8919 | 0.8919 | 0.8378 | 0.7027 | 0.5405 |
| Corr | 0.8250 | 0.8250 | 0.8158 | 0.7879 | 0.7407 | |
| F1 score | 0.8571 | 0.8571 | 0.8267 | 0.7429 | 0.6250 | |
| Potsdam 7_13 | Comp | 0.9524 | 0.9524 | 0.8571 | 0.8571 | 0.7619 |
| Corr | 0.9091 | 0.9091 | 0.9000 | 0.9000 | 0.8889 | |
| F1 score | 0.9302 | 0.9302 | 0.8780 | 0.8780 | 0.8205 | |
| Marion S1 | Comp | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.7576 |
| Corr | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | |
| F1 score | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.8621 | |
| Marion S2 | Comp | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.8800 |
| Corr | 0.9615 | 0.9615 | 0.9615 | 0.9615 | 0.9565 | |
| F1 score | 0.9804 | 0.9804 | 0.9804 | 0.9804 | 0.9167 | |
| Scenes | CNN_ACM_1 | CNN_ACM_2 | ||||
|---|---|---|---|---|---|---|
| Mean_Comp | Mean_Corr | Mean_F1 | Mean_Comp | Mean_Corr | Mean_F1 | |
| Potsdam 2_13 | 0.8752 | 0.8949 | 0.8693 | 0.8769 | 0.9086 | 0.8822 |
| Potsdam 6_15 | 0.7827 | 0.9481 | 0.8298 | 0.8278 | 0.9386 | 0.8567 |
| Potsdam 7_13 | 0.9009 | 0.8669 | 0.8701 | 0.8948 | 0.8226 | 0.8415 |
| Marion S1 | 0.9681 | 0.9235 | 0.9435 | 0.9170 | 0.9646 | 0.9396 |
| Marion S2 | 0.9756 | 0.8704 | 0.9173 | 0.9514 | 0.9181 | 0.9333 |
| Scenes | CNN_ACM_1 | CNN_ACM_2 | ||||
|---|---|---|---|---|---|---|
| Comp | Corr | F1 | Comp | Corr | F1 | |
| Potsdam 2_13 | 0.9021 | 0.9054 | 0.9038 | 0.8678 | 0.9140 | 0.8903 |
| Potsdam 6_15 | 0.8866 | 0.9626 | 0.9230 | 0.9369 | 0.9601 | 0.9483 |
| Potsdam 7_13 | 0.9555 | 0.8438 | 0.8962 | 0.9058 | 0.8509 | 0.8775 |
| Marion S1 | 0.9679 | 0.9187 | 0.9427 | 0.9184 | 0.9654 | 0.9413 |
| Marion S2 | 0.9755 | 0.8621 | 0.9153 | 0.9511 | 0.9078 | 0.9290 |
References
- Awrangjeb, M. Using point cloud data to identify, trace, and regularize the outlines of buildings. Int. J. Remote Sens. 2016, 37, 551–579. [Google Scholar] [CrossRef]
- Laefer, D.F.; Hinks, T.; Carr, H.; Truong-Hong, L. New advances in automated urban modelling from airborne laser scanning data. Recent Pat. Eng. 2011, 5, 196–208. [Google Scholar] [CrossRef]
- Awrangjeb, M.; Lu, G.; Fraser, C. Automatic building extraction from LiDAR data covering complex urban scenes. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 25. [Google Scholar] [CrossRef]
- Von Schwerin, J.; Richards-Rissetto, H.; Remondino, F.; Spera, M.G.; Auer, M.; Billen, N.; Loos, L.; Stelson, L.; Reindel, M. Airborne LiDAR acquisition, post-processing and accuracy-checking for a 3D WebGIS of Copan, Honduras. J. Archaeol. Sci. Rep. 2016, 5, 85–104. [Google Scholar] [CrossRef]
- Tomljenovic, I.; Höfle, B.; Tiede, D.; Blaschke, T. Building extraction from airborne laser scanning data: An analysis of the state of the art. Remote Sens. 2015, 7, 3826–3862. [Google Scholar] [CrossRef]
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active contour models. Int. J. Comput. Vis. 1988, 1, 321–331. [Google Scholar] [CrossRef]
- Ahmadi, S.; Zoej, M.V.; Ebadi, H.; Moghaddam, H.A.; Mohammadzadeh, A. Automatic urban building boundary extraction from high resolution aerial images using an innovative model of active contours. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 150–157. [Google Scholar] [CrossRef]
- Chan, T.F.; Vese, L.A. Image Segmentation Using Level Sets and the Piecewise-Constant Mumford-Shah Model; UCLA CAM Report 00-14; Kluwer Academic Publishers: Alphen aan den Rijn, The Netherlands, 2000. [Google Scholar]
- He, L.; Peng, Z.; Everding, B.; Wang, X.; Han, C.Y.; Weiss, K.L.; Wee, W.G. A comparative study of deformable contour methods on medical image segmentation. Image Vis. Comput. 2008, 26, 141–163. [Google Scholar] [CrossRef]
- Kabolizade, M.; Ebadi, H.; Ahmadi, S. An improved snake model for automatic extraction of buildings from urban aerial images and LiDAR data. Comput. Environ. Urban Syst. 2010, 34, 435–441. [Google Scholar] [CrossRef]
- Liasis, G.; Stavrou, S. Building extraction in satellite images using active contours and colour features. Int. J. Remote Sens. 2016, 37, 1127–1153. [Google Scholar] [CrossRef]
- Chan, T.F.; Vese, L.A. Active contours without edges. IEEE Trans. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Kao, C.-Y.; Gore, J.C.; Ding, Z. Minimization of region-scalable fitting energy for image segmentation. IEEE Trans. Image Process. 2008, 17, 1940–1949. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Zhang, K.; Zhang, C.; Chen, S.-C.; Narasimhan, G. Automatic construction of 3-D building model from airborne LiDAR data through 2-D snake algorithm. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3–14. [Google Scholar] [CrossRef]
- Bypina, S.K.; Rajan, K. Semi-automatic extraction of large and moderate buildings from very high-resolution satellite imagery using active contour model. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Milan, Italy, 26–31 July 2015; pp. 1885–1888. [Google Scholar] [CrossRef]
- Dai, Y.; Gong, J.; Li, Y.; Feng, Q. Building segmentation and outline extraction from UAV image-derived point clouds by a line growing algorithm. Int. J. Digit. Earth 2017, 10, 1077–1097. [Google Scholar] [CrossRef]
- Rottensteiner, F.; Sohn, G.; Gerke, M.; Wegner, J.D.; Breitkopf, U.; Jung, J. Results of the ISPRS benchmark on urban object detection and 3D building reconstruction. ISPRS J. Photogramm. Remote Sens. 2014, 93, 256–271. [Google Scholar] [CrossRef]
- Mongus, D.; Lukač, N.; Žalik, B. Ground and building extraction from LiDAR data based on differential morphological profiles and locally fitted surfaces. ISPRS J. Photogramm. Remote Sens. 2014, 93, 145–156. [Google Scholar] [CrossRef]
- Shan, J.; Sampath, A. Building extraction from LiDAR point clouds based on clustering techniques. In Topographic Laser Ranging and Scanning: Principles and Processing; Toth, C.K., Shan, J., Eds.; CRC Press: Boca Raton, FL, USA, 2008; pp. 423–446. [Google Scholar]
- Awrangjeb, M.; Fraser, C.S. Automatic segmentation of raw LiDAR data for extraction of building roofs. Remote Sens. 2014, 6, 3716–3751. [Google Scholar] [CrossRef]
- Wang, R.; Hu, Y.; Wu, H.; Wang, J. Automatic extraction of building boundaries using aerial LiDAR data. J. Appl. Remote Sens. 2016, 10, 016022. [Google Scholar] [CrossRef]
- Fukushima, K.; Miyake, S.; Ito, T. Neocognitron: A neural network model for a mechanism of visual pattern recognition. IEEE Trans. Syst. Man Cybern. 1983, SMC-13, 826–834. [Google Scholar] [CrossRef]
- Lari, Z.; Ebadi, H. Automatic extraction of building features from high resolution satellite images using artificial neural networks. In Proceedings of the ISPRS Conference on Information Extraction from SAR and Optical Data, with Emphasis on Developing Countries, Istanbul, Turkey, 16–18 May 2007. [Google Scholar]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef] [PubMed]
- Turker, M.; Koc-San, D. Building extraction from high-resolution optical spaceborne images using the integration of support vector machine (SVM) classification, Hough transformation and perceptual grouping. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 58–69. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Guo, B.; Huang, X.; Zhang, F.; Sohn, G. Classification of airborne laser scanning data using JointBoost. ISPRS J. Photogramm. Remote Sens. 2015, 100, 71–83. [Google Scholar] [CrossRef]
- Lodha, S.K.; Kreps, E.J.; Helmbold, D.P.; Fitzpatrick, D.N. Aerial LiDAR Data Classification Using Support Vector Machines (SVM). In Proceedings of the 3rd International Symposium on 3D Data Processing, Visualization and Transmission (3DPVT 2006), Chapel Hill, NC, USA, 14–16 June 2006; pp. 567–574. [Google Scholar] [CrossRef]
- Lodha, S.K.; Fitzpatrick, D.M.; Helmbold, D.P. Aerial lidar data classification using AdaBoost. In Proceedings of the Sixth International Conference on 3-D Digital Imaging and Modeling, Montreal, QC, Canada, 21–23 August 2007; pp. 435–442. [Google Scholar] [CrossRef]
- Du, S.; Zhang, F.; Zhang, X. Semantic classification of urban buildings combining VHR image and GIS data: An improved random forest approach. ISPRS J. Photogramm. Remote Sens. 2015, 105, 107–119. [Google Scholar] [CrossRef]
- Niemeyer, J.; Rottensteiner, F.; Soergel, U. Contextual classification of lidar data and building object detection in urban areas. ISPRS J. Photogramm. Remote Sens. 2014, 87, 152–165. [Google Scholar] [CrossRef]
- Vakalopoulou, M.; Karantzalos, K.; Komodakis, N.; Paragios, N. Building detection in very high resolution multispectral data with deep learning features. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Milan, Italy, 26–31 July 2015; pp. 1873–1876. [Google Scholar] [CrossRef]
- Erhan, D.; Szegedy, C.; Toshev, A.; Anguelov, D. Scalable object detection using deep neural networks. arXiv, 2014; arXiv:1312.2249. [Google Scholar]
- Li, Y.; He, B.; Long, T.; Bai, X. Evaluation the performance of fully convolutional networks for building extraction compared with shallow models. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Fort Worth, TX, USA, 23–28 July 2017; pp. 850–853. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Maninis, K.-K.; Pont-Tuset, J.; Arbeláez, P.; Van Gool, L. Convolutional oriented boundaries: From image segmentation to high-level tasks. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 819–833. [Google Scholar] [CrossRef] [PubMed]
- Rupprecht, C.; Huaroc, E.; Baust, M.; Navab, N. Deep active contours. arXiv, 2016; arXiv:1607.05074. [Google Scholar]
- Jing, Y.; An, J.; Liu, Z. A novel edge detection algorithm based on global minimization active contour model for oil slick infrared aerial image. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2005–2013. [Google Scholar] [CrossRef]
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cartogr. Int. J. Geogr. Inf. Geovisual. 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Rutzinger, M.; Rottensteiner, F.; Pfeifer, N. A comparison of evaluation techniques for building extraction from airborne laser scanning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2009, 2, 11–20. [Google Scholar] [CrossRef]






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zhang, X.; Zhao, X.; Xin, Q. Extracting Building Boundaries from High Resolution Optical Images and LiDAR Data by Integrating the Convolutional Neural Network and the Active Contour Model. Remote Sens. 2018, 10, 1459. https://doi.org/10.3390/rs10091459
Sun Y, Zhang X, Zhao X, Xin Q. Extracting Building Boundaries from High Resolution Optical Images and LiDAR Data by Integrating the Convolutional Neural Network and the Active Contour Model. Remote Sensing. 2018; 10(9):1459. https://doi.org/10.3390/rs10091459
Chicago/Turabian StyleSun, Ying, Xinchang Zhang, Xiaoyang Zhao, and Qinchuan Xin. 2018. "Extracting Building Boundaries from High Resolution Optical Images and LiDAR Data by Integrating the Convolutional Neural Network and the Active Contour Model" Remote Sensing 10, no. 9: 1459. https://doi.org/10.3390/rs10091459
APA StyleSun, Y., Zhang, X., Zhao, X., & Xin, Q. (2018). Extracting Building Boundaries from High Resolution Optical Images and LiDAR Data by Integrating the Convolutional Neural Network and the Active Contour Model. Remote Sensing, 10(9), 1459. https://doi.org/10.3390/rs10091459