Estimation of Hedonic Single-Family House Price Function Considering Neighborhood Effect Variables
Abstract
:1. Introduction
2. Hedonic Model with Consideration Given to Neighborhood Effect
2.1. Estimation Model
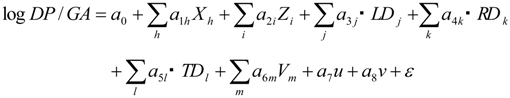
2.2. Data
2.2.1. Single-Family House Price
2.2.2. Data Regarding House Characteristics
2.2.3. Data on Neighborhood Effect Factor
| Symbols | Variables | Contents | Unit |
|---|---|---|---|
| GA | Ground Area/square meters | Ground Area | m2 |
| FS | Floor space/square meters | Floor space | m2 |
| RW | Front Road Widths | Front Road Widths | 10 cm |
| AGE | Number of years since construction | Period between the date when the data is deleted from the magazine and the date of construction of the building. | Years |
| TS | Time to nearest station | Time distance to the nearest station (Time by Walk or Bus) | Minutes |
| BD | Bus dummy | Whether the time distance includes riding time of bus 1 | (0,1) |
| Not including bus time 0 | |||
| TT | Travel Time to central business district | Minimum railway riding time in daytime to seven terminal stations in 2000 | Minutes |
| RT | Market reservation time | Period between the date when the data appear in the magazine for the first time and the date of being deleted. | Weeks |
| SD | South-facing dummy | Windows facing south 1 | (0,1) |
| other directions 0 | |||
| LaD | Land dummy | Transaction is only for land without building 1 | (0,1) |
| otherwise 0 | |||
| LDj (j = 0,…,J) | Location (Ward) dummy | j th administrative district 1 | (0,1) |
| other district 0 | |||
| RDk (k = 0,…,K) | Railway line dummy | k th railway line 1 | (0,1) |
| other railway line 0 | |||
| TDl (l = 0,…,L) | Time dummy (quarterly) | l th quarter 1 | (0,1) |
| other quarter 0 | |||
| FR | Floor Area Ratio | Floor area ratio | % |
| ZD | Zoning dummy | Land use zoning i 1 | (0,1) |
| other land use 0. | |||
| LUn (n = 1,2,3,4) | Land use condition | (1) Average building area, (2) Standard deviation of building area, (3) Building density, and (4) Building density squared | |
| HCo (o = 1,2) | Household Characteristics | (1) Rate of office worker and (2) Average building area per household | |
| EX | Road traffic noise | Road traffic noise | db |
| u, v | Longitude, Latitude | Geographical coordinates |
2.2.4. Statistical Distribution of Single-Family House Prices
| Variables | Average | Standard Deviation | Minimum | Maximum |
|---|---|---|---|---|
| DP: Price of Detached house price (10,000 Yen) | 7211.86 | 4384.60 | 1050.00 | 39,800.00 |
| GA: Ground Area (m2) | 114.99 | 75.07 | 10.11 | 797.35 |
| DP/GA | 68.67 | 24.08 | 12.00 | 392.00 |
| FS: Floor space (m2) | 76.83 | 69.37 | 0.00 | 649.08 |
| RW: Front Road Widths | 4.85 | 2.48 | 2.00 | 50.00 |
| Age: Age of Building(years) | 5.28 | 8.75 | 0.00 | 41.33 |
| TS: Time to the nearest station (minutes) | 9.64 | 4.36 | 0.00 | 36.00 |
| TT: Travel Time to Central Business District (minutes) | 11.45 | 6.08 | 1.00 | 33.00 |
| RT: Reservation Time (week) | 2.39 | 2.53 | 0.00 | 35.00 |
| 01/2000–12/2000 | n = 12,954 |
3. Estimated Results
3.1. Formulation of Hedonic Models
| Independent Variables | Model-1 | Model-2 | Model-3 | |||
|---|---|---|---|---|---|---|
| X:Property Characteristics | Coefficient | p-value | Coefficient | p-value | Coefficient | p-value |
| Constant | 4.7131 | *** | 4.6550 | *** | −53.42 | *** |
| GA: Ground Area | −0.0014 | *** | −0.0014 | *** | −0.0015 | *** |
| FS: Floor space | 0.0008 | *** | 0.0008 | *** | 0.0007 | *** |
| RW: Front Road Widths | 0.0169 | *** | 0.0157 | *** | 0.0143 | *** |
| Age: Age of Building | −0.0115 | *** | −0.0115 | *** | −0.0116 | *** |
| TS: Time to the nearest station | −0.0105 | *** | −0.0099 | *** | −0.0100 | *** |
| BD: Bus Dummy | −0.1773 | *** | −0.1691 | *** | −0.1622 | *** |
| TS × BD | 0.0028 | 0.0024 | 0.0029 | |||
| TT: Travel Time to CBD | −0.0128 | *** | −0.0118 | *** | −0.0100 | *** |
| Z:Other Property Characteristics | Coefficient | Coefficient | Coefficient | |||
| RT: Market Reservation Time | −0.0006 | −0.0008 | −0.0007 | |||
| SD: South Face Dummy | 0.0292 | *** | 0.0285 | *** | 0.0301 | *** |
| LaD: Land Dummy | −0.2824 | *** | −0.2836 | *** | −0.2932 | *** |
| Location (Ward) Dummy LDj (j = 0,…,J) | Yes | Yes | Yes | |||
| Railway/Subway Line Dummy RDk (k = 0,…,K) | Yes | Yes | Yes | |||
| Time Dummy TDl (l = 0,…,L) | Yes | Yes | Yes | |||
| Independent Variables | Model-1 | Model-2 | Model-3 | |||
| V1-2: Neighborhood Effects | Coefficient | Coefficient | Coefficient | |||
| FR: Floor area ratio | − | − | 0.0002 | *** | 0.0003 | *** |
| ZD: Zoning Dummy (Commercial use) | − | − | −0.0056 | −0.0148 | * | |
| V3-8:Neighborhood Effects by GIS | Coefficient | Coefficient | Coefficient | |||
| LU1: Average building area | − | − | − | − | 0.0018 | *** |
| LU2: Standard deviation of building area | − | − | − | − | −0.0001 | *** |
| LU3: BLD: Building Density | − | − | − | − | 0.0001 | *** |
| LU4: BLD2 | − | − | − | − | 0.0000 | *** |
| HC1: Rate of Office worker | − | − | − | − | 0.0058 | *** |
| HC2: Average building area per household | − | − | − | − | 0.0029 | *** |
| EX: Road traffic noise | − | − | − | − | −0.0160 | *** |
| latitude | − | − | − | − | 0.4028 | *** |
| longitude3 | − | − | − | − | 0.0000 | |
| Number of observations = | 12,954 | 12,954 | 12,954 | |||
| Adjusted R-Square = | 0.644 | 0.645 | 0.662 | |||
| AIC = | −3327 | −3372 | −4000 | |||
3.2. Effect of Neighborhood on House Price
3.2.1. Ambient Land-Use Conditions: LU
3.2.2. Household Characteristics: HC
3.2.3. Other Factors
3.3. Omitted Variable Bias
| Estimated Parameters | Model-1 | Model-2 | Test * | Model-2 | Model-3 | Test * |
|---|---|---|---|---|---|---|
| GA: Ground Area | −0.00143 | −0.00139 | −0.00139 | −0.00147 | b | |
| FS: Floor space | 0.00077 | 0.00077 | 0.00077 | 0.00070 | ||
| RW: Front Road Widths | 0.01693 | 0.01575 | 0.01575 | 0.01432 | c | |
| Age: Age of Building | −0.01146 | −0.01148 | −0.01148 | −0.01162 | ||
| TS: Time to the nearest station | −0.01052 | −0.00994 | −0.00994 | −0.01002 | ||
| BD: Bus Dummy | −0.17730 | −0.16906 | −0.16906 | −0.16220 | ||
| TT: Travel Time to CBD | −0.01279 | −0.01177 | b | −0.01177 | −0.01003 | a |
| Neighborhood Effects | No | Yes | Yes | Yes | ||
| Neighborhood Effects by GIS | No | No | No | Yes | ||
| Unobserved Spatial Effects | No | No | No | Yes |
3.3.1. Comparison between Model-1 and Model-2
3.3.2. Comparison between Model-2 and Model-3
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Ekeland, I.; Heckman, J.J.; Nesheim, L. Identification and Estimation of Hedonic Models. J. Polit. Econ. 2004, 112, 60–109. [Google Scholar] [CrossRef]
- Rosen, S. Hedonic Prices and Implicit Markets, Product Differentiation in Pure Competition. J. Polit. Econ. 1974, 82, 34–55. [Google Scholar]
- Kanemoto, Y.; Nakamura, R. A New Approach to the Estimation of Structural Equations in Hedonic Models. J. Urban Econ. 1986, 19, 218–233. [Google Scholar] [CrossRef]
- Asami, Y.; Gao, X.L. Effect of Environmental Factors on Housing Prices: Application of GIS to Urban-Policy Analysis. In GIS-Based Studies in the Humanities and Social Sciences; Okabe, A., Ed.; Taylor & Francis: Boca Raton, FL, USA, 2006; pp. 211–228. [Google Scholar]
- Goodman, A.C.; Thibodeau, T.G. Dwelling Age Heteroskedasticity in Repeat Sales House Price Equations. Real Estate Econ. 1998, 26, 151–171. [Google Scholar]
- Goodman, A.C.; Thibodeau, T.G. Housing market segmentation and hedonic prediction accuracy. J. Hous. Econ. 2003, 12, 181–201. [Google Scholar] [CrossRef]
- Jackson, J. Intraurban Variation in the Price of Housing. J. Urban Econ. 1979, 6, 464–479. [Google Scholar] [CrossRef]
- Shimizu, C.; Nishimura, K.G. Biases in Appraisal Land Price Information: The Case of Japan. J. Prop. Invest. Finance 2006, 26, 150–175. [Google Scholar] [CrossRef]
- Shimizu, C.; Nishimura, K.G. Pricing structure in Tokyo metropolitan land markets and its structural changes: Pre-bubble, bubble, and post-bubble periods. J. Real Estate Finance Econ. 2007, 35, 475–496. [Google Scholar] [CrossRef]
- Diewert, E.; Shimizu, C. Residential Property Price Indexes for Tokyo. Available online: http://www.economics.ubc.ca/files/2014/04/pdf_paper_erwin-diewert-13-7-residential-property.pdf (accessed on 28 April 2014).
- Shimizu, C.; Nishimura, K.G.; Asami, Y. Search and Vacancy Costs in the Tokyo Housing Market: An Attempt to Measure Social Costs of Imperfect Information. Rev. Urban Reg. Dev. Stud. 2004, 16, 210–230. [Google Scholar]
- Shimizu, C.; Nishimura, K.G.; Karato, K. Nonlinearity of Housing Price Structure—The Secondhand Condominium Market in Tokyo Metropolitan Area. Available online: http://www.csis.u-tokyo.ac.jp/dp/86r1.pdf (accessed on 1 May 2010).
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Shimizu, C. Estimation of Hedonic Single-Family House Price Function Considering Neighborhood Effect Variables. Sustainability 2014, 6, 2946-2960. https://doi.org/10.3390/su6052946
Shimizu C. Estimation of Hedonic Single-Family House Price Function Considering Neighborhood Effect Variables. Sustainability. 2014; 6(5):2946-2960. https://doi.org/10.3390/su6052946
Chicago/Turabian StyleShimizu, Chihiro. 2014. "Estimation of Hedonic Single-Family House Price Function Considering Neighborhood Effect Variables" Sustainability 6, no. 5: 2946-2960. https://doi.org/10.3390/su6052946
APA StyleShimizu, C. (2014). Estimation of Hedonic Single-Family House Price Function Considering Neighborhood Effect Variables. Sustainability, 6(5), 2946-2960. https://doi.org/10.3390/su6052946




