Nomenclature
ACR Advanced CANDU Reactor
AFBR Advanced Fast Breeder Reactor
AFBR (Th) Advanced Fast Breeder Reactor with Th blankets
ALWR Advanced Light Water Reactor
BN-K Sodium Cooled Fast Reactor
BR Breeding ratios
FBR Fast Breeder Reactor
FR Fast Reactor
MCDM Multi-Criteria Decision Making
HWR Heavy Water Reactor
NFC Nuclear Fuel Cycle
LWR Light Water Reactor
LWR (Th) Light Water Reactor with 233U oxide fuel
RBMK High Power Channel-type Reactor
VVER Water-Water Energetic Reactor
VVER(m) Modified Water-Water Energetic Reactor
SNF Spent Nuclear Fuel
1. Introduction
As dictated by sustainable development concepts, the future nuclear power system should meet the following basic requirements: to be resource-sufficient and to produce a low amount of wastes in the long run, to be cost effective, to maintain the necessary level of safety and reliability, to ensure the effective resistance to nuclear weapons proliferation [
1,
2].
In this regard, in performing an integrated analysis on the design of the future nuclear power structure, consideration must be given to the full range of system factors and constraints. The final goal of such studies is to find out and study ways of improving safety, competitiveness, environmental acceptability and proliferation resistance of future nuclear power. Only the assessments made taking into account all system factors and constraints will allow making informed decisions about the choice of promising areas of nuclear power development.
There is a growing understanding that the problem of optimizing the structure of nuclear power system is multi-objective. At the same time, the criteria characterizing resource consumption, economy, the risks of unauthorized proliferation and waste management, are conflicting by nature. This means that improving the value of one criterion leads to a decrease in the values of other criteria.
These circumstances bring urgency to the development of multi-objective program systems to solve the problem of optimizing the structure of nuclear power system in multi-objective formulation. Software systems of this kind could provide a basis for decision support systems for multi-objective evaluation of the effectiveness of nuclear power system development scenarios, allowing multi-factorial comparison of its various structures to be made.
2. State-of-the-Art MCDM Techniques and Their Application for Multicriteria Optimization of Nuclear Power Systems
Multi-criteria decision making (MCDM) techniques are a tool aimed at supporting decision makers faced with making numerous and conflicting assessments. MCDM techniques intend to highlight conflicts and find compromises in the decision making process. A large number of multi-criteria techniques have been developed to deal with different kinds of problems (MAVT, AHP, TOPSIS, PROMETHEE, MAUT,
etc) [
3,
4,
5]. At the same time each technique has pros and cons and can be more or less useful depending on the situation. Also, few approaches have been proposed to guide the selection of a technique adapted to a given situation.
The methods for multi-objective optimization problem solving are various. There are several ways to classify these methods, such as classification based on the content and form of supplementary information regarding the decision maker’s preferences. In accordance with this classification, the classes of methods for multi-objective optimization problems solving are the following:
a priori methods;
a posteriori methods;
adaptive methods;
methods based on the preliminary construction of the Pareto set approximation.
The basis of most state-of-the-art multi-criteria decision making methods is the notion of non-dominated solutions set (efficient, Pareto, Pareto-optimal)—that is, the Pareto set. With this expert support, the decision-maker ultimately must choose a solution belonging to the Pareto set. The Pareto set construction is a complicated independent problem; and the information gained about the Pareto boundary form may underlie the interactive multi-criteria decision support systems.
In recent years, the methods based in particular on the preliminary construction of the Pareto set approximation have become increasingly popular in developing decision-making support systems. In this case, the decision-maker chooses a compromise solution on the Pareto front not using formal methods, although the latter may be used, but based on his preferences. The main disadvantage of methods of this type is their high computational complexity which limits their widespread application.
A significant number of methods and algorithms for Pareto set approximate construction are known. The genetic algorithms-based methods belong to a relatively new and highly effective class of such methods.
The Pareto set construction in dynamic systems multi-objective optimization problem requires the repeated simulation of the studied dynamical system for different values of variable parameters. Dynamical systems simulation is a separate problem and a significant amount of software packages were developed to address it.
Let us here consider the multi-objective optimization problem description. Suppose a set of particular M criteria:
![Sustainability 04 00721 i001]()
(1)
Assume that the problem is to minimize each of these criteria in the same feasible region
![Sustainability 04 00721 i002]()
. Here
![Sustainability 04 00721 i003]()
—is the solution space,
![Sustainability 04 00721 i004]()
—is the feasible solution set,
![Sustainability 04 00721 i005]()
—and is n-dimensional arithmetic space.
The set is defined by a constraint set that allows distinguishing an infinite class of feasible solutions. In the case of solving a linear programming problem, this set is defined as follows:
![Sustainability 04 00721 i006]()
(2)
Multi-objective optimization problem (consider the minimization case) can be written as:
![Sustainability 04 00721 i007]()
(3)
Such a notation only implies that minimizing each of the particular criteria is desirable for a decision-maker.
Vector criterion of optimality
![Sustainability 04 00721 i008]()
performs transformation of the feasible solutions set
X in a criteria space set
Y, which is called the feasible set of the criteria,
i.e.,
![Sustainability 04 00721 i009]()
.
Informally, the Pareto set is defined as a set in which the value of any particular optimality criteria can be improved (in the considered case, decreased) only with losing (increasing) in at least one of the other criteria. Thus, any of the solutions belonging to the Pareto set, cannot be improved simultaneously in all the particular optimality criteria [
5].
The formal Pareto set definition is as follows. At first, a preference relation is entered for the set of feasible values of criteria
Y. It is said that the vector
![Sustainability 04 00721 i010]()
is preferred to the vector
![Sustainability 04 00721 i011]()
or the vector
![Sustainability 04 00721 i012]()
dominates the vector
![Sustainability 04 00721 i013]()
and it is written
![Sustainability 04 00721 i014]()
, if among the equalities and inequalities
![Sustainability 04 00721 i015]()
there is at least one strict inequality.
Pareto set in the criteria space
![Sustainability 04 00721 i016]()
is a subset of points
![Sustainability 04 00721 i017]()
, for which there are no more preferred points. The set
![Sustainability 04 00721 i018]()
, corresponding to the set
![Sustainability 04 00721 i019]()
, is called the Pareto set in the solution space.
This approach to solving the problem of optimizing the nuclear power system structure in the multi-objective formulation allows to search for compromises between conflicting system factors determining the nuclear power system development; to evaluate the impact of regional specifics on the whole range of efficient indicators; and, with the use of a calculation tool, to carry out comparative multi-objective analysis of options for nuclear power system development, taking into account the dynamics of development, the structure and the organization features of nuclear fuel cycle (NFC) and the most important system constraints and restrictions.
3. Nuclear Power Systems Multi-Objective Optimization Modules for Energy Planning Software—MESSAGE
MESSAGE software (Model for Energy Supply Strategy Alternatives and their General Environmental Impacts) is a large-scale dynamic system engineering optimization model used for medium-and long-term energy planning, energy policy and energy development scenarios analysis [
6]. The software was originally developed by the International Institute for Applied Systems Analysis. Currently, this software is supported by the IAEA, and is used in the toolbox of the INPRO project. MESSAGE software is a flexible modeling environment that allows the user to formulate a linear programming problem, to find the optimal solution and process the calculation results.
Despite the fact that the MESSAGE allows a multi-objective optimization based on the
reference trajectory method [
6], which is a variation of goal programming approach, this feature is not implemented in due measure. Moreover, this method in its present form does not allow carrying out a representative approximation of the efficient solutions set, a basis for interactive approaches to support the multi-objective decision-making. It should also be noted that the form of data input into the model does not allow to efficiently implement both traditional and state-of-the-art methods of multi-objective optimization and to take into account the uncertainty in the initial data. The latter is necessary to enhance the validity degree of recommendations made on the basis of calculations.
As part of the multi-objective optimization software systems development for multi-objective optimization of nuclear power systems, the following methods have been tested and implemented as computation modules for energy planning software MESSAGE:
methods of effective solutions selection through single criterion optimization (linear direct weighting of criteria and criteria constraints methods);
goal programming method;
reasonable goals method, which is an interactive method of multi-criteria decision-making support.
Let us dwell briefly on the developed software modules.
3.1. Criteria Constraints Method
Reaching the optimal values of several indicators simultaneously is usually impossible. The solution for such difficulties is the implementation of the requirement to support a number of indicators at a level no lower than acceptable, and to direct the selected indicator to its extremal value. By selecting different set of indicators, one can come to duality formulations of optimization problems. They have the same set of optimal solutions for all possible values of limiting levels [
7].
However, in real-world problems the decision-making process subject cannot set numerical values of the limiting levels. As a way out of this situation, it is the required to seek solutions that are unimprovable for any of the criteria without worsening at least one of the other (V. Pareto principle). Just these decisions, which are considering with the multi-criteria decision theory, are of practical interest.
It should be noted that the improvable (dominated, inefficient) points are located within the feasible solution set. It is possible to shift from these points while remaining within the feasible solution set, into other points which are better in at least one criterion and not worse than the given point in other criteria. On the contrary, any improving shifts from the unimprovable point falls outside the boundary of the feasible solution set.
It should be noted that usually there are a lot of unimprovable points. Ultimately, one single point must be chosen either expertly, or formally, by taking some additional hypotheses about the preferences. But these additional hypotheses are not of a general character, in contrast to the original principle of unimprovability proposed by V. Pareto.
In the optimization theory, enough approaches have been developed to find effective solutions. One of them is the criteria constraints method, a universal method which is correct both for problems with convex and non-convex sets of feasibility.
The main idea of this method is based on the fact that all but one criteria values are limited, and the only criterion for selection is extremalized (in this case it is minimized):
![Sustainability 04 00721 i020]()
(4)
The limiting levels are the problem parameters. Setting them at all possible values of the ranges from absolute minimum to absolute maximum of the corresponding figure in the original set of feasibility, it is possible to obtain all the efficient solutions.
3.2. The Goal Programming Method
This set of methods is based on the following heuristic argument: the best vector should be chosen as a vector which is placed in the criteria space closer than all other feasible vectors to some ideal vector, or to a whole set of them. The metric variation for measuring distances in the criteria space leads to a whole family of similar methods which, however, may lead to different results.
Let us briefly describe the principle of the method. Suppose there is a set of M criteria, each of which is desirable to be minimized in the set of possible solutions X. In accordance with the methodology of this approach, it is considered that in the criteria space Rm a nonempty set U is given, which is usually called the set of ideal (the best or utopian) vectors. Typically, this set is unfeasible. In addition, a metric
![Sustainability 04 00721 i021]()
should be set in the criteria space. A solution
![Sustainability 04 00721 i022]()
will be declared optimal if the following equation is realized for it:
![Sustainability 04 00721 i023]()
(5)
which means that the estimate
![Sustainability 04 00721 i024]()
corresponding to the best solution
![Sustainability 04 00721 i025]()
, should be located as close as possible to the set of ideal estimates
![Sustainability 04 00721 i026]()
. Most often, for the solution of applied problems, any metric can be used from the following parametric family:
![Sustainability 04 00721 i027]()
(6)
where
![Sustainability 04 00721 i028]()
Varying the parameter vector аs, the importance of different criteria is taken into account. A greater importance is attached to the parameter vector component which meets the greater value criterion. It should be noted that the use of the above-mentioned parametric family metric does not always lead to Pareto optimal vectors.
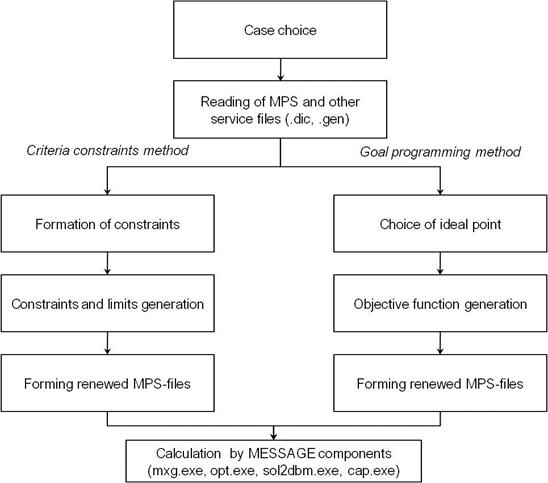
To implement the criteria constraints and the goal programming methods, it is necessary to be able to enter additional information into the model, which represents both limiting levels and the ideal set. MESSAGE generates an MPS file, which is a standardized notation of a linear programming problem, entering the optimization block. To implement the described methods, this file must be corrected. A specially designed module ConCriM allows making necessary changes in order to implement these methods (
Figure 1).
3.3. Module Implementing the Reasonable Goals Method
The reasonable goals method was designed by Dorodnicyn Computing Centre of the Russian Academy of Sciences. The basis of the method is visualization of many possible feasible vectors by imaging it through bi-criterion slices. The use of the method is mainly intended for computationally complex cases of infinite number of possible solutions and vectors [
5].
One of the goal programming method’s weak points lies in the fact that the ideal vector is given without taking into account the real system capabilities. Therefore, the attainable values of figures, even the closest to a given ideal, may prove to be far from it. The given method seeks to overcome this shortcoming. In accordance with this method, a set of practically feasible vectors is accessible for decision-makers in a clear, easy for perception form. One can choose a certain compromise among them.
The program module ParSAM (Pareto Set Approximation Module) for an energy planning software MESSAGE is designed for automation of the approximation and visualization of Pareto set as well as for accounting of uncertainties in system parameters.
With the ParSAM, a user can create a base project set of linear programming problems, which are based on the criteria linear convolution method, and the solution of which conforms to the Pareto efficiency condition. With the created initial data set, the module allows serial calculations, processing the calculation results and presenting them in tabular and graphical form. All the sources, intermediate, and the resulting files are compatible with MESSAGE environment file formats. This allows, if required, making the necessary adjustments through MESSAGE environment.
The basic functionality of the module (
Figure 2):
forming a set of matrices for solving a parametric linear programming problem;
forming a set of files for post-optimization processing of calculation results;
controlling the MESSAGE modules to improve efficiency of the Pareto set approximation;
different ways of weights generation for the Pareto set approximation;
different ways of the Pareto set visualization.
Information on the Pareto set can be used to estimate the marginal rate of substitution, which can effectively support the selection of the most preferred criteria point in multi-objective problems.
Figure 1.
Flow-chart of module implementing the criteria constraints and the goal programming methods.
Figure 1.
Flow-chart of module implementing the criteria constraints and the goal programming methods.
Figure 2.
ParSAM flow-chart.
Figure 2.
ParSAM flow-chart.
3.4. Nuclear Power Systems Modeling Module
MESSAGE software, representing a flexible environment for specification of the energy systems, is not adapted for the description of nuclear power system features. This is due to the fact that the demand for services both at front-end and back-end stages of the NFC is determined by the characteristics of nuclear reactor and its fuel supply. All other system parameters can be calculated for certain values of these variables and a minimum set of additional ones. At the same time, working directly in the MESSAGE environment requires an independent input of these parameters, which makes the work with the model difficult and fallible.
For this reason, a nuclear power systems specification interface was specifically created for energy planning package MESSAGE—NESI (Nuclear Energy System Interface) (
Figure 3). This interface can be used by specialists to facilitate the innovative nuclear power system specification.
The basic functionality of the module:
specification of nuclear power system with regard to possible parameter changes over time;
NFC process chain visualization;
Possibility of integration with neutronics calculation programs;
flexible control function for the MESSAGE’s program components, in order to improve the calculations efficiency.
Currently, a set of basic calculation cases for once-through and closed NFC has also been developed, which allows calculating the NFC material flows and is intended for the modeling of steady-state and developing nuclear power systems.
Figure 3.
NESI module structure.
Figure 3.
NESI module structure.
4. Integrated Approach Based on the System Dynamics and Parameter Space Investigation Methods
In spite of the considerable pool of existing models, approaches and software tools for system studies of the nuclear power system development, active researches are now being done to find new ways of finding solutions for the problems of this class. This is due to a significant increase in the scope of functions and in the range of factors that will determine the future of nuclear power system development. These include such factors as non-proliferation, waste management and safety. Whereas, the existing models of developing nuclear power systems consider mainly the economic aspects.
It should be also noted that the limited application scope of models implies the problem of obtaining the final result, determining the most efficient scenario of its development. So far, no generally accepted algorithms and no methodological approaches have been suggested.
The below described integrated approach allows to partly compensate for these shortcomings. It was developed on the basis of system dynamics and parameter space investigation methods; and allows solving the problems of the nuclear power system structure optimization in the multi-objective formulation.
4.1. System Dynamics Approach for Nuclear Power Systems Development
According to the general methodology of modeling in the system analysis framework, it is necessary to identify the following typical stages: 1) generation of the constraint equations reflecting the actual “physical” limitations; 2) the determination of exogenously defined objective functionals reflecting the concept of efficiency of the relevant object functioning; and 3) if necessary, equations that close the system.
The initial system of constraint equations represents in an aggregated differential form the process of nuclear reactors fueling in a particular region (the capacity increase must be supply by fuel of a given form and amount)
![Sustainability 04 00721 i029]()
(7)
where I = 1,…,n—reactor type number; j = 1,…,m—region number; k = 1,…,l—fuel type number.
The left side of the equation determines the demand for fuel of given form. The demand is composed by the needs to provide new capacities (first component) and to replace burnt-up fuel in the nuclear reactors in operation (second component). The right side of the equation sets an offer for a certain fuel type. It is determined by the existing fuel supply structure of nuclear power system in the relevant region, and by the possibility to import fuel components from other regions. From now on the following conventional signs are used:
![Sustainability 04 00721 i030]()
—initial fuel loading into the reactor,
![Sustainability 04 00721 i031]()
—the annual refueling of reactor. The functional dependence of the equation parameters on time takes into account possible technology updating.
Let us introduce the following notation: N(t),Nc(t),Nd(t)—are respectively installed capacity of reactors in year t, the total capacity of reactors put into operation by the year t, and the total decommission of reactors by the year t. These values are related by:
![Sustainability 04 00721 i032]()
(8)
where [·]—the integer part.
Taking this fact into account is necessary for correct modeling of the real need for the introduction of new nuclear reactor capacity, caused not only by increasing demand for nuclear power, but also by decommission of worn-out reactors.
Structural and organizational features of the NFC can be taken into account as additional equations and constraints. In particular, the following conditions can be considered: the nuclear materials supply from other regions and other types of reactors; delays on various stages and capacities of NFC facilities; property changes in fuel materials and possible technological modifications of the NFC facilities in the nuclear power system deployment.
Incoming and outgoing flows can be defined in two ways. Firstly, additional equations can be introduced for linking the definable variables and ultimately closing the initial fuel balance system. In general, the model will appear as a set of differential equations with retarded argument.
Secondly, if the objective functional is set, a part of the flow can be defined by solving the corresponding optimal control problem, whereas the others are solved by the closing system of equations. Various constraints on the variables’ acceptable region of models or functionals calculated with their help, allows taking into account the system constraints directly. Thus, the calculations will not lead into a non-physical solution region.
Thirdly, this simulation method can be effectively integrated with the described below method described below of the parameter space investigation that allows solving the nuclear power system structure optimization problem in the multi-objective formulation.
4.2. The Parameter Space Investigation Method
The parameter space investigation method was suggested by I.M. Sobol and R.B. Statnikov, who demonstrated its wide opportunities in solving engineering optimization and optimal control problems [
8,
9]. The method is intended to solve multi-objective nonlinear programming problems and is based on the idea of random search, where so-called low-discrepancy sequences are used as the random numbers.
The parameter space investigation method consists of three phases:
formation of test tables—that is, a set of calculated values of the criteria for a given set of testing points that satisfy a given system of equations and system of constraints;
selection of criteria constraints and choice of solutions to satisfy them;
checking the solvability of the problem and formation of an effective solutions set.
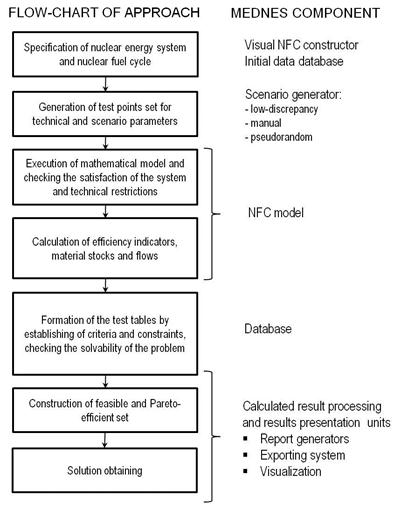
Figure 4 shows the flow-chart and related software components that implement an integrated approach based on the system dynamics and parameter space investigation methods.
Figure 4.
Flow-chart and related software components of the integrated approach.
Figure 4.
Flow-chart and related software components of the integrated approach.
The developed methodology allows taking into account nonlinear constraints and nonlinear functionals on model variables, to approximate the Pareto set in the case of multi-objective problems. The internal mechanism of alternatives selection helps identify the most effective directions; and the dynamic character of the model assists in evaluation of the transition to the asymptotic scenarios.
4.3. MEDNES Software
The described integrated approach is implemented as a MEDNES software system (Multi-objective Evaluator of Developing Nuclear Energy Systems). MEDNES is designed to solve multi-objective problems, e.g., structure optimization, parameters identification, control, etc. MEDNES is intended for construction of the feasible solutions set during interactive dialogues between expert and computer. MEDNES is applicable for analyzing the dependence of criteria on the parameters; on the criteria and constraints correction.
The number of variable parameters depends on sample points generator used. Different sample point generators can be used. Currently, implemented are the generators of Holton, Sobol and Faure low-discrepancy sequences [
10]. The standard pseudorandom number generators and uniform sequences can also be used.
The expert chooses the most preferred solution on a basis of feasible set and Pareto set analysis. MEDNES includes the following analysis tools:
test tables;
feasible and Pareto-optimal solutions table;
tables of vectors not satisfying functional constraints;
“criteria-parameters” and “criteria-criteria” plots reflecting the criteria sensitivity to parameters and criteria dependence on the criteria.
Because the multi-objective problems with high parameter vector dimensionality require a lot of computer time, the possibility is provided to run MEDNES in parallel mode.
6. Results of Multicriteria Optimization Studies of Nuclear Power Structures
A number of studies on multi-objective evaluation of the nuclear power system structures’ effectiveness, both at national and global levels, were carried out with the use of the developed tools, enabling finding harmonized development strategies and reasonable compromises between the conflicting system factors [
12,
13,
14].
6.1. Multi-Objective Comparative Analysis of the Structures of the Developing Global Nuclear Power System
The method of criteria constraints implemented in a software module ConCriM was used to optimize the structure of the global nuclear power taking into account regional restrictions and presence of fast reactors in a closed U-Pu-Th fuel cycle in its structure. As indicators, which are restricted and determine finally the choice of a solution from a set of effective solutions, fraction of fast and heavy water reactors, natural uranium reserves, the accumulated amount of spent nuclear fuel and plutonium were selected.
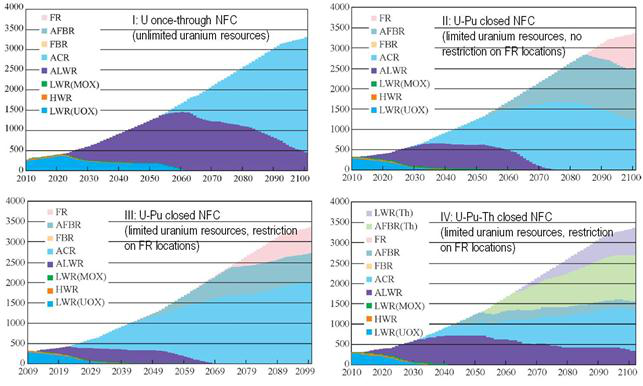
In the framework of MESSAGE following options of global nuclear power with closed NFC were considered (
Figure 5):
(1) U-Pu closed NFC with LWR, HWR and their advanced prototypes as well as fast breeder and burner reactors;
(2) U-Pu-Th closed NFC with fast breeders with Th blankets and Pu cores.
Figure 5.
U-Pu-Th closed NFC.
Figure 5.
U-Pu-Th closed NFC.
The latter case corresponds to so-called mixed NFC with the fuel exchange between the uranium thermal and fast reactors with plutonium cores and thorium blankets. In such a fuel cycle of fast reactors, keeping plutonium fuel in the core, to produce 233U in its thorium blankets to start-up and recharge uranium thermal reactors, which, in turn, working in uranium fuel from a mixture of 233 and 238 uranium isotopes, accumulating plutonium to start-up new fast reactors.
The step-by-step setting of restrictions, reflecting the system requirements to nuclear power (such as total amount of natural uranium, spent nuclear fuel, the locations of fast reactors) have defined the following structure based on the solution of optimization problem on the criterion of minimizing the total discounted costs (
Figure 6):
once-through uranium NFC with no restrictions on uranium resources (I);
closed U-Pu NFC with and without restrictions on the locations of fast reactors and the limitations on the amount of available natural uranium (II, III);
closed U-Pu-Th NFC with restrictions on the location of fast reactors and the amount of available natural uranium (IV).
Figure 6.
Structures of developing nuclear power, GWe·yr.
Figure 6.
Structures of developing nuclear power, GWe·yr.
The study results have proven that it is difficult, or even impossible with certain reactor technologies, to meet the set of constraints that reflect the system requirements for a nuclear power system, taking into account the regional restrictions, for unlimited time. In respect to this type of system constraints, the nuclear power system structure becomes extremely sensitive to the reactor technology types and loses its ability to adapt to changing external conditions, while meeting the set of conflicting system constraints at the same time. In such a system, each technology plays an important role. If one of them is lost, there will be no optimal solution for a given set of constraints. In this study a compromise could be found in transition to U-Pu-Th NFC.
At the same time, the system must remain flexible enough to adapt to changing external conditions, while meeting a set of system constraints. To balance the conflicting factors in such a system, it seems appropriate to implement specialized multifunction innovative reactor systems, whose tasks must be determined depending on the particular stage of development.
6.2. Multi-Objective Analysis of Comparative Structures of Russian Nuclear Power with Fast Reactors with Different Breeding Ratios
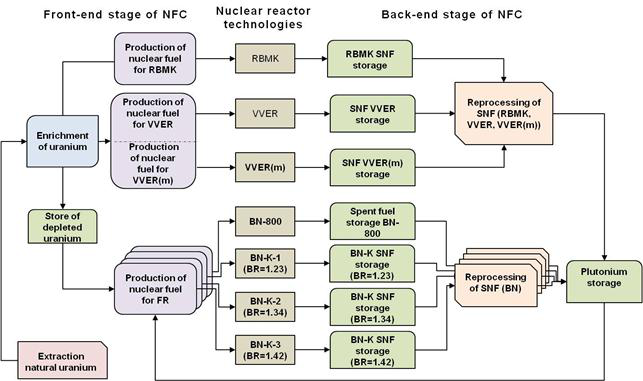
Using the reasonable goals method, the studies on Russian nuclear power with fast reactors with different breeding parameters were carried out to establish a compromise development strategy on a set of conflicting criteria (
Figure 7).
Figure 7.
NFC model of Russian nuclear power.
Figure 7.
NFC model of Russian nuclear power.
The ParSAM module was used to perform a multi-objective optimization of Russian nuclear power structure on the criteria of minimizing total discounted costs, total consumption of natural uranium, total amount of spent nuclear fuel and capacities of “sensitive” NFC technologies. For this set of criteria, a set of effective solutions was built demonstrating the upper productive limits of a given reactor technologies mix, and allowing choosing a compromise strategy of Russian nuclear power development on the set of criteria mentioned above.
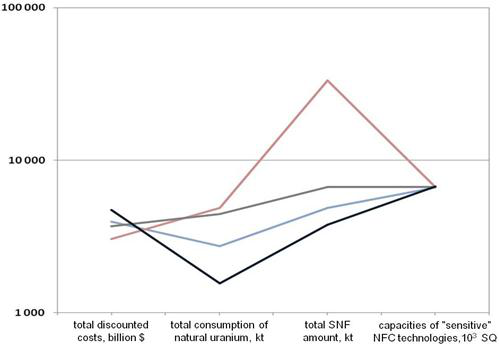
For example,
Figure 8 shows the so called alternative profiles of the four non-dominated solutions demonstrating the changes in integral indicator values for the last year’s forecasting for four possible nuclear power structures. As can be seen from
Figure 8, the improvement of an indicator is achieved by the deterioration of another, which corresponds to the condition of Pareto optimality.
The estimates performed showed the principal opportunity to solve the problem of finding a perspective nuclear power structure compromised from a set of indicators. It should be noted that a more diverse structure of nuclear power formed based on different reactor types allows getting closer to the desirable compromise goal. This approach, in contrast to the method of criteria restrictions, provides an opportunity to directly assess trade-offs between conflicting indicators.
The results show that different structures of developing nuclear power systems based on considered NFC are comparable by the indicators: “total amount of fissile materials in NFC” and “potential productivity of fissionable materials”. It should be noted that the improvement of one indicator is achieved by the worsening of another. This suggests that it is impossible to make definitive judgments about the prospect of a nuclear power structure and the NFC type from the non-proliferation viewpoint based on material flow assessment, without a detailed analysis of the proliferation scenarios and specification of acting national and international systems of nuclear security and nonproliferation regime management.
Figure 8.
Profiles for four various nuclear power structures
Figure 8.
Profiles for four various nuclear power structures
The values of levelized cost for the entire development program calculated taking into account the uncertainty in unit costs for goods and services of NFC and reactors investment costs, in accordance with data collected from set international sources [
15,
16] for two different scenario assumptions, are presented in Table 1. The uncertainty assessment of levelized cost was performed by using the GRS method implemented in the ParSAM module.
Table 1.
Levelized cost.
| The structure of nuclear power | Levelized cost, cents (kW·h) |
|---|
| Uranium resources are not limited, two-component structure of nuclear power | 1.66 ± 0.185 |
| Uranium resources are limited (1.2 million tons), two-component structure of nuclear power | 1.76 ± 0.143 |
The quantitative analysis performed shows that the considered scenarios are statistically indistinguishable (90% confidence intervals of uncertainty of the levelized cost for various scenarios overlap). This suggests that it is impossible to make definitive judgments about the prospects of one or other structure on economic indicators, taking into account the existing uncertainties in the unit cost data.
7. Conclusions
The prospects of nuclear power to meet future energy needs are vast. However, a unified view of an optimal nuclear power structure is extremely difficult to achieve. The problem of optimization of a nuclear power structure is multi-objective. The criteria characterizing resources consumption, economy, proliferation and waste management risks are conflicting in nature. Lack of common methodologies for decision-making in multi-objective optimization problems complicates the procedure of formulating a coordinated vision of a preeminent nuclear power structure.
To make reasonable decisions on the future structure of nuclear power, it is necessary to allow discourse of unbiased experts, free of preferences on the specific modeling assumptions, and able to organize systematic research taking all possible options of nuclear power development into account.
The developed software enables solving such optimization problems in multi-objective formulation. This allows searching for compromises between the conflicting system factors that determine the nuclear power system development; to evaluate the impact of regional development differences on the whole range of efficiency indicators; and, with the use of a unified calculation tool, to carry out comparative multi-criteria analysis of alternatives for nuclear power system development, taking into account development dynamics, the structure and the organization of NFC and the most important system constraints and restrictions.
 (1)
(1) . Here
. Here  —is the solution space,
—is the solution space,  —is the feasible solution set,
—is the feasible solution set,  —and is n-dimensional arithmetic space.
—and is n-dimensional arithmetic space. (2)
(2) (3)
(3) performs transformation of the feasible solutions set X in a criteria space set Y, which is called the feasible set of the criteria, i.e.,
performs transformation of the feasible solutions set X in a criteria space set Y, which is called the feasible set of the criteria, i.e.,  .
. is preferred to the vector
is preferred to the vector  or the vector
or the vector  dominates the vector
dominates the vector  and it is written
and it is written  , if among the equalities and inequalities
, if among the equalities and inequalities  there is at least one strict inequality.
there is at least one strict inequality. is a subset of points
is a subset of points  , for which there are no more preferred points. The set
, for which there are no more preferred points. The set  , corresponding to the set
, corresponding to the set  , is called the Pareto set in the solution space.
, is called the Pareto set in the solution space. (4)
(4) should be set in the criteria space. A solution
should be set in the criteria space. A solution  will be declared optimal if the following equation is realized for it:
will be declared optimal if the following equation is realized for it: (5)
(5) corresponding to the best solution
corresponding to the best solution  , should be located as close as possible to the set of ideal estimates
, should be located as close as possible to the set of ideal estimates  . Most often, for the solution of applied problems, any metric can be used from the following parametric family:
. Most often, for the solution of applied problems, any metric can be used from the following parametric family: (6)
(6)


 (7)
(7) —initial fuel loading into the reactor,
—initial fuel loading into the reactor,  —the annual refueling of reactor. The functional dependence of the equation parameters on time takes into account possible technology updating.
—the annual refueling of reactor. The functional dependence of the equation parameters on time takes into account possible technology updating. (8)
(8)