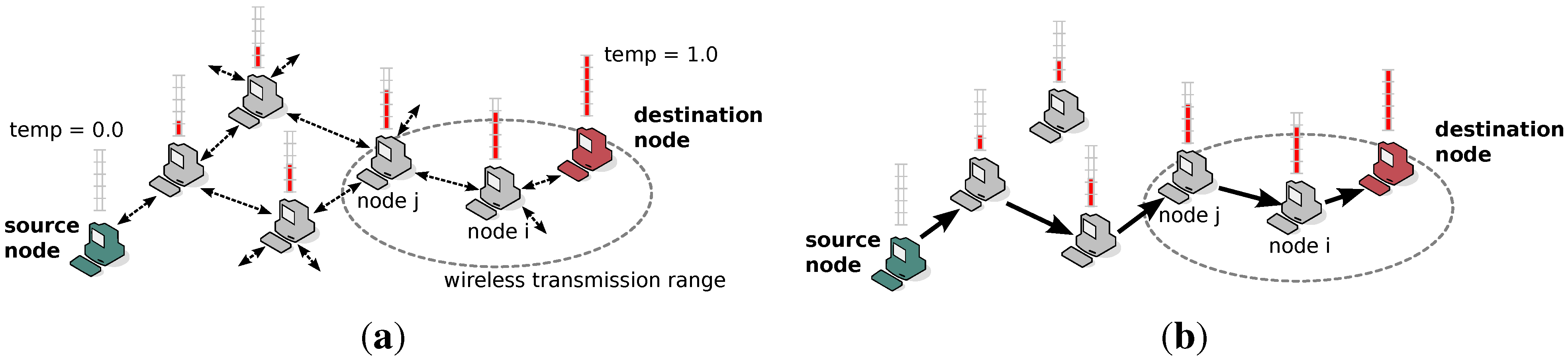
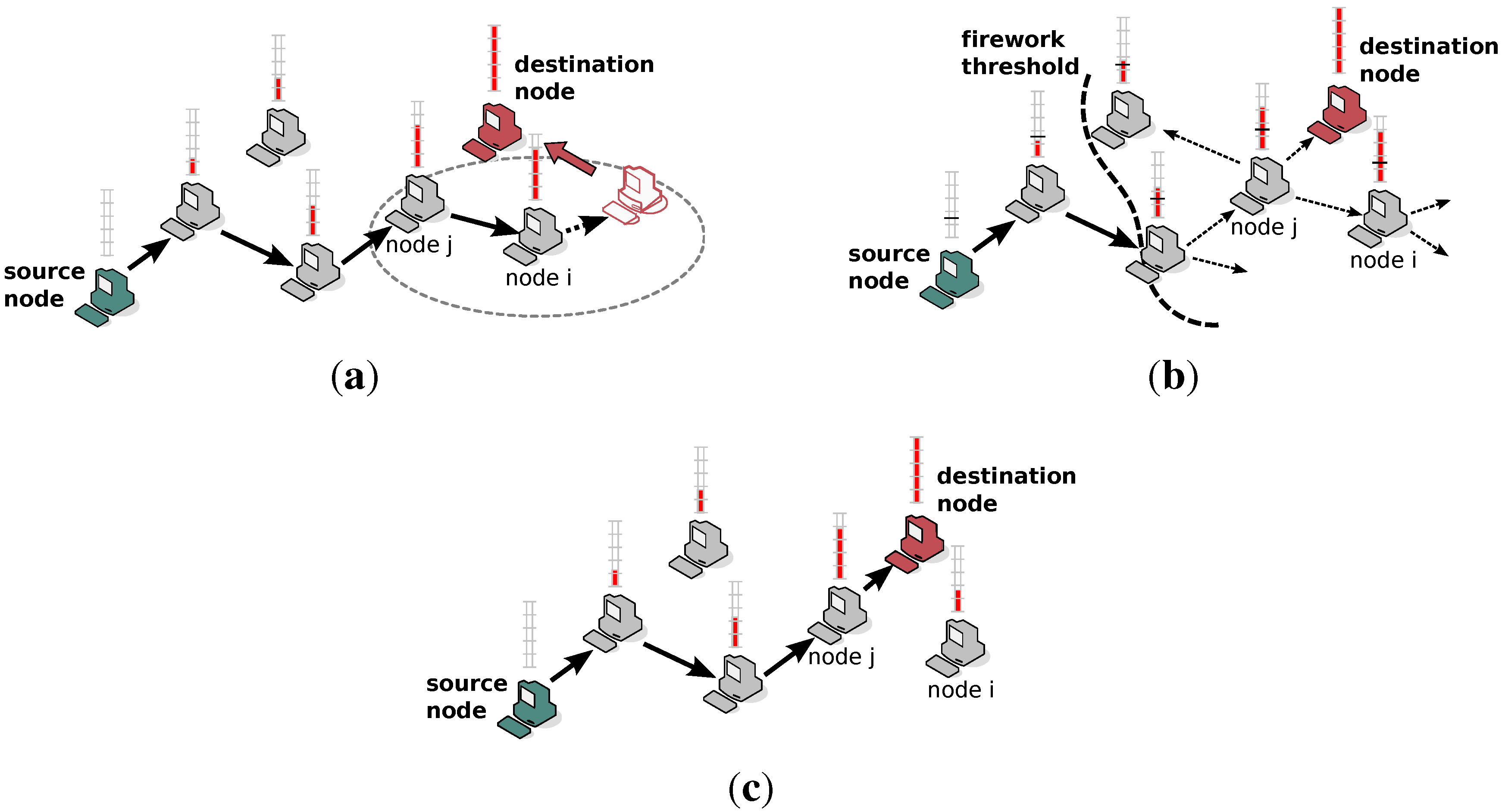
In this section, we evaluate our proposed method by a simulation program developed in C using the random walk (RWK) mobility model for
N nodes. In our mobility model, nodes are distributed in a uniformly random manner at initial setup and move in one randomly selected direction for a certain fixed time (0.1 s). In addition, we introduced a bouncing rule when nodes encounter the area boundary. The time until the convergence of the potential is considered as the transient phase, after which simulation results start to be monitored. Unlike in [
2], evaluations are performed to study the detailed behavior of our proposed method, and hence, parameter values are used that cover a wide range from optimistic to pessimistic scenarios. Basic simulation parameters are listed in
Table 1, where default values are shown in bold. Each presented result is obtained as the average of 1000 simulation runs, so we omit showing confidence intervals. If not mentioned otherwise, the default number of nodes is 4000, the mobile speed is 100 m/s, the firework hop limit is set to 5 hops, the firework temperature threshold is 0.5 and the simulation time is 100 s. Note that the high vehicular speed only represents the relative difference between the traveled distance of a node and the transmission range, and we assumed a rather large value of 100 m/s in this paper in order to cause sufficiently large changes in connectivity, although it may appear unrealistic to actually occur in reality. Moreover, from the viewpoint of simplicity, an ideal wireless transmission channel is assumed in our simulation, and therefore, the success or failure of packet transmissions depends on the wireless range and the mutual distance of nodes. The bandwidth of the wireless channel is set at 2 Mbps, representing the practical bandwidth of WiFi.
4.1. Effects of Wireless Coverage
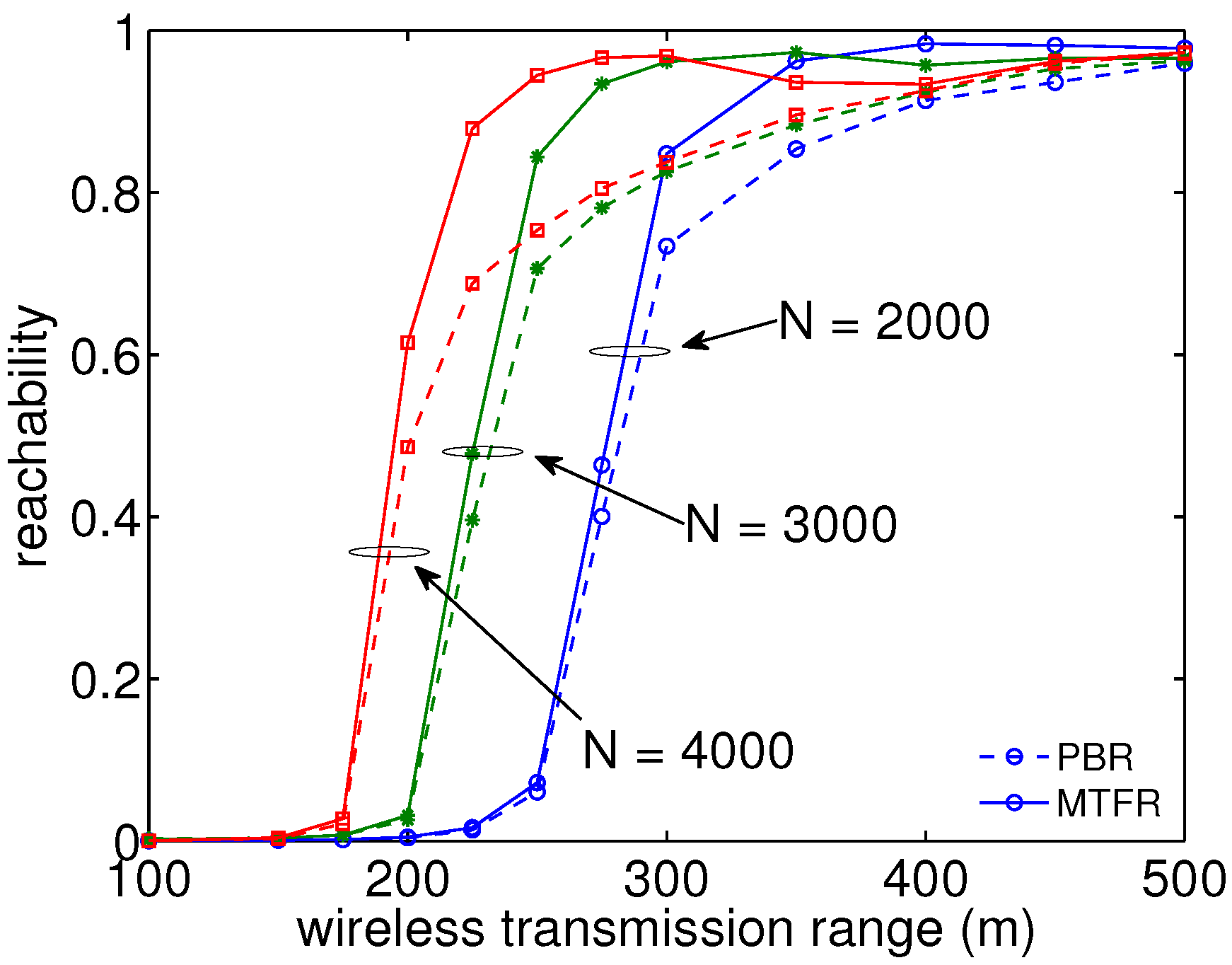
First, we investigate the basic tendency of the firework effect on the influence of packet reachability over the number of nodes and the wireless transmission range for both MTFR and conventional potential-based routing (PBR). In this paper, reachability probability is defined as the ratio of the number of packets successfully reaching the destination over the number of all transmitted packets. From
Figure 3, we can conclude that packet reachability improves with a growing number of nodes and with transmission range. This is because increasing both values results in a wider wireless coverage area. MTFR is able to restore reachability almost completely to that of the theoretically maximum possible without mobility. The wireless transmission range affects the node density with an exponent of two, which produces a stronger relationship with reachability. Therefore, steeply increasing curves are observed.
Figure 3.
Reachability increases in an S-shape manner with growing transmission range and number of nodes. PBR, potential-based routing.
Figure 3.
Reachability increases in an S-shape manner with growing transmission range and number of nodes. PBR, potential-based routing.
It was also observed that there are some unrecoverable conditions in certain densely populated cases, like 4000 nodes and over 400 m wireless ranges. This is because the increase of possible links with more neighbors has the side effect of increasing the hop count between the source node and the destination node. The wider the transmission range becomes, the more links one node has, which eliminates the firework effect by the hop number limit. In conclusion, there is an optimal point against the number of nodes and wireless transmission range on the reachability improvement under some specific conditions. Here, the firework improvement effect represents the difference between results obtained with and without firework.
In addition,
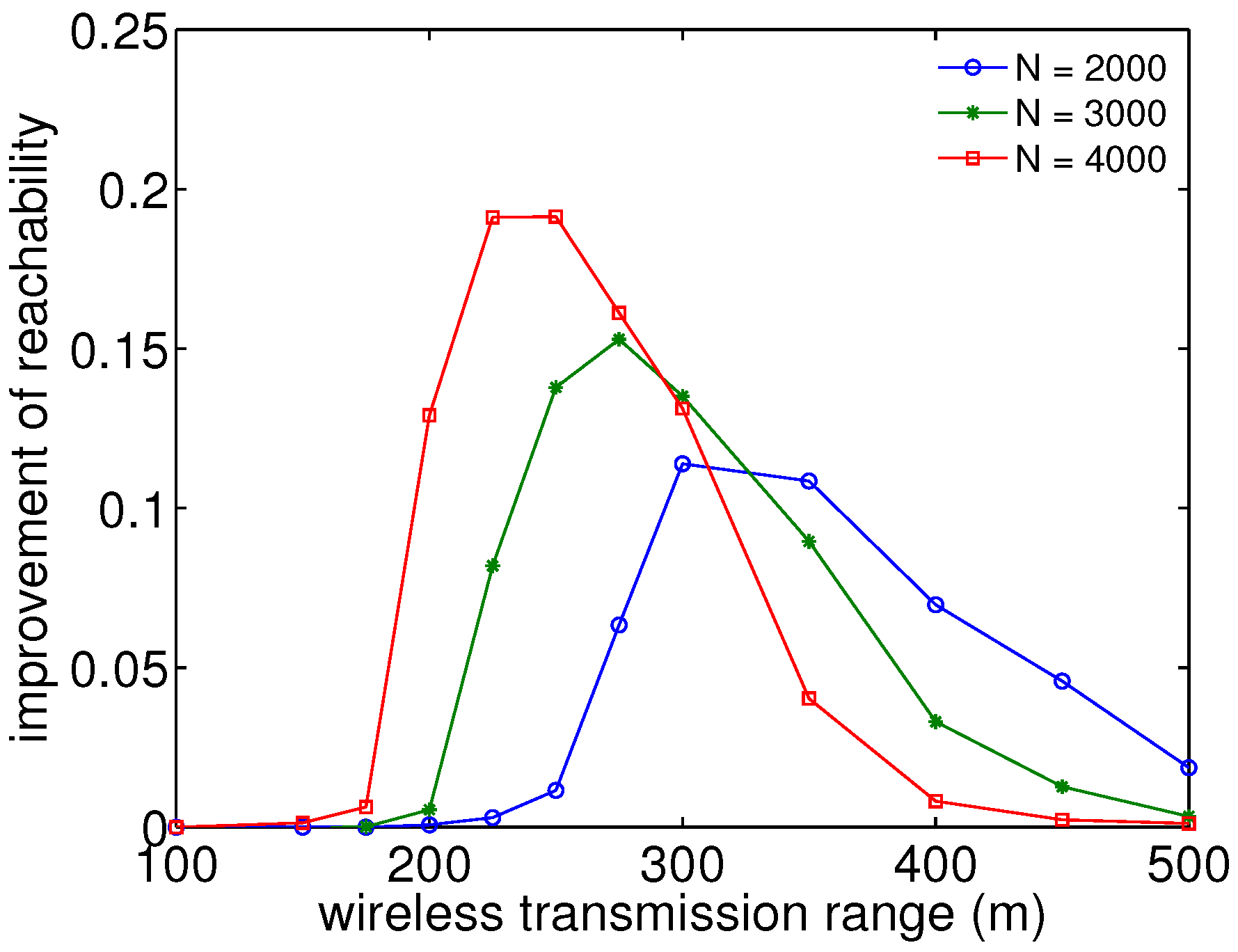
Figure 4 shows the simulation results of reachability improvement by firework with different numbers of nodes under RWK at the speed of 100 m/s and with different wireless ranges for packet transmission. Here, reachability improvement is defined as the difference in reachability between the methods with firework and without firework and for which absolute values can be found in
Figure 3. In smaller and larger wireless transmission ranges, reachability improvement is almost zero, due to the lack of connectivity and no room for improvement, respectively. On the other hand, in middle ranges, there is a peak for each curve in which the wireless range is increasing as the number of nodes decreases. In addition, the maximum value slightly decreases as the number of nodes decreases, and therefore, as mentioned above, the wireless range has a larger effect on producing full reachability than the number of nodes.
In [
2], we also investigated the effects of vehicular speed, the node mobility model, the temperature update interval and transmission delays against the traffic overhead. Those results are left out for the sake of brevity, and the reader is referred to [
2] for further details.
Figure 4.
Reachability improvement analysis as the difference between results with and without firework shows the largest improvements for intermediate transmission ranges.
Figure 4.
Reachability improvement analysis as the difference between results with and without firework shows the largest improvements for intermediate transmission ranges.
4.2. Evaluation of Transmission Delay
Figure 5 shows the simulation results of end-to-end transmission delays per packet transmission generated with different numbers of nodes under RWK at the speed of 100 m/s and with different ranges for packet transmission. Here, end-to-end delay corresponds to the average time period for completing a packet transmission from the source node to the destination node, which is equivalent to the number of hops under the condition that each hop-by-hop transmission time is equal. In smaller wireless ranges, transmission delays are observed as almost zero in all conditions, due to the lack of reachability, and in addition, in larger wireless ranges, delays converge to around 15–20 hops in all conditions, due to almost full reachability. In middle wireless ranges, we can recognize some additional transmission delays, due to the firework procedure. However, even in the worst conditions, delays are in total less than 40 hops in
Figure 5. In addition, it turned out that delay differences between results with and without firework were limited to at most eight hops in all cases. This fact indicates that our MTFR is feasible enough for real communication scenarios. As a result, MTFR produces better reachability at the expense of a small additional transmission delay from the overall viewpoint.
In addition,
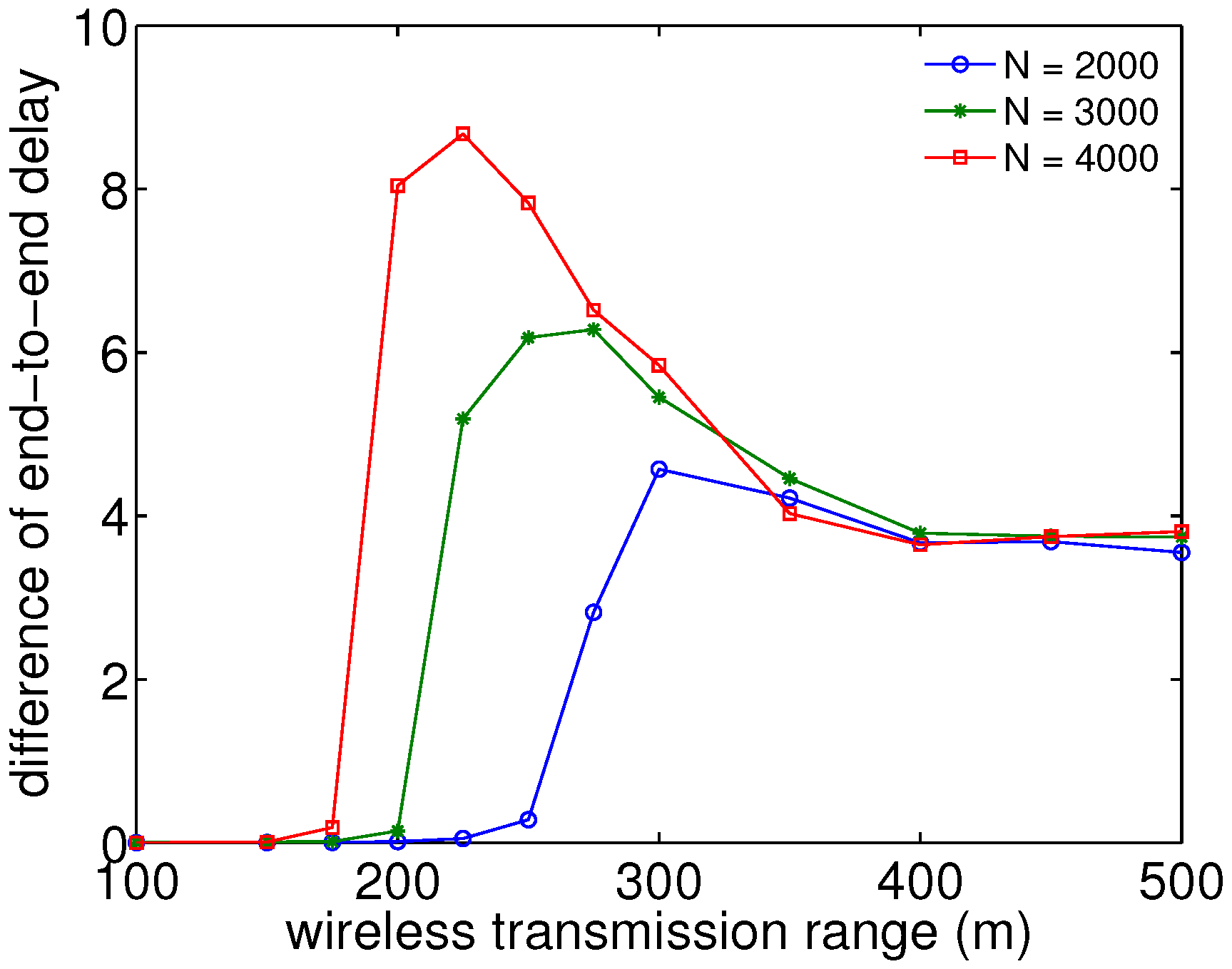
Figure 6 shows the simulation results of the end-to-end delay increase per packet transmission generated with different numbers of nodes under RWK at the speed of 100 m/s and with different ranges for packet transmission. Here, the difference of end-to-end delay is the discrepancy in delay between with firework and without firework for the absolute values shown in
Figure 5. In smaller and middle wireless transmission ranges, the tendency of maximum delay increase shows similar results as those of reachability. However, in larger wireless transmission ranges, degradation is saturated at the level of about 4 hops. This is because the temperature gradient sustains the basic principal communication route on one side, but it does not allow shortcut routes on the other side. The sufficient number of nodes with a sufficient wireless transmission range redundantly increases the average number of links that each node has. This produces a higher probability of equal cost links than in the situations with a smaller density of wireless coverage, and hence, a random selection feature is taken into account for path selection. In addition, our firework mechanism emphasizes this randomness more. Hence, it produces a certain fixed delay.
Figure 5.
Transmission delays (hop count) show clear differences between with and without firework for larger wireless transmission ranges.
Figure 5.
Transmission delays (hop count) show clear differences between with and without firework for larger wireless transmission ranges.
Figure 6.
The difference of end-to-end delay per packet transmission shows saturation for larger wireless transmission ranges, due to the effects of randomness.
Figure 6.
The difference of end-to-end delay per packet transmission shows saturation for larger wireless transmission ranges, due to the effects of randomness.
4.3. Evaluation of Traffic Overhead
In addition, we analyze the tendency from the viewpoint of traffic overhead accompanied by the firework procedure.
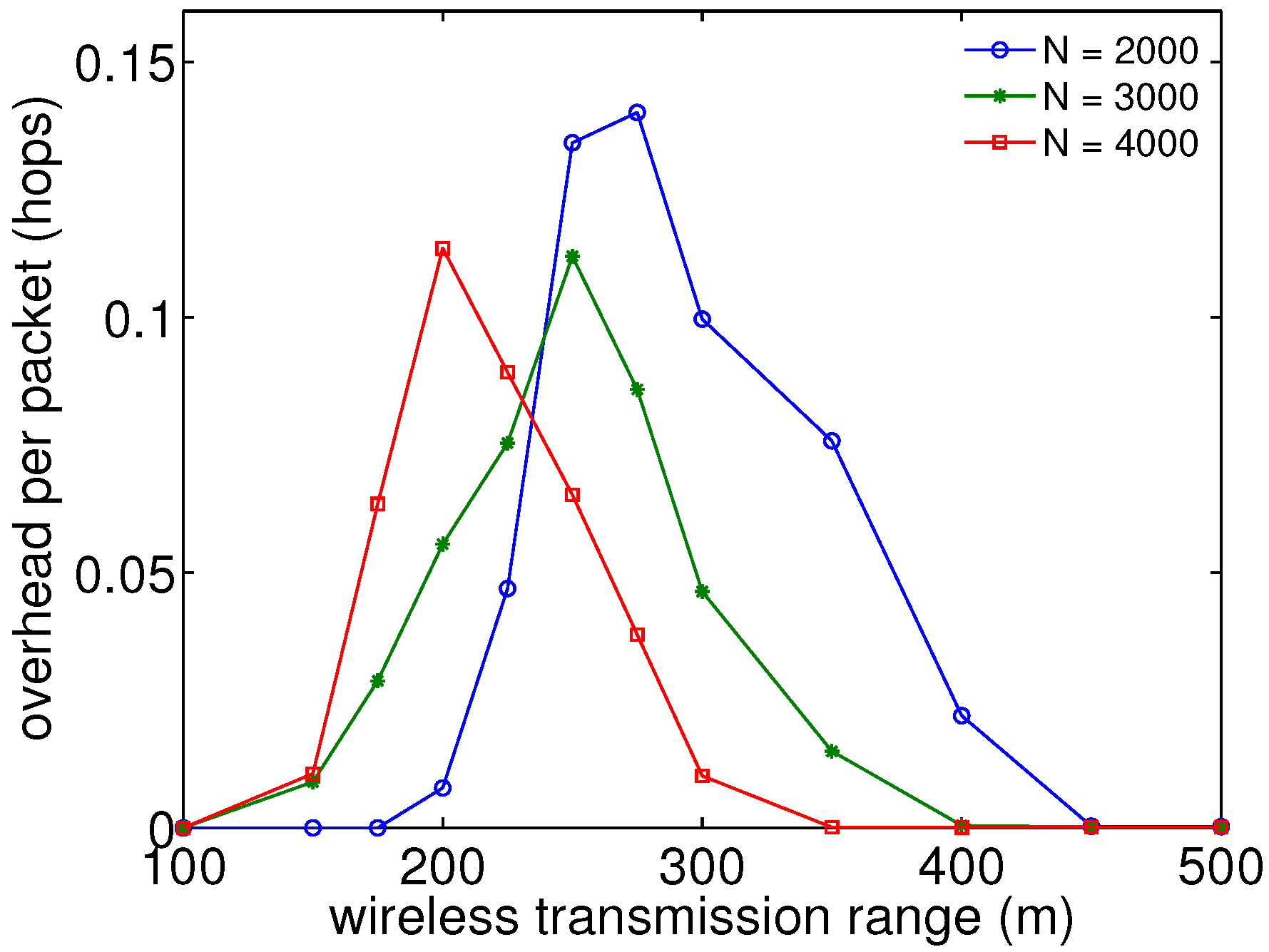
Figure 7 shows the simulation results of additional traffic overhead by firework with different numbers of nodes under RWK at the speed of 100 m/s and with different wireless ranges for packet transmission. Here, traffic overhead is defined as the total number of hops traveled by transmitted packets, including replicated packets, which is substituted by the total number of hops under the condition that the size of all transmitted and replicated packets is equal. In
Figure 7, traffic overhead is normalized by the number of nodes and the total amount of transmitted packets.
The normalized traffic overhead without firework is almost zero, which can be used as a criteria to evaluate our method. From
Figure 7, in higher wireless transmission ranges, such as more than 350 m, it is shown that there is not much difference between without and with firework. On the other hand, in the middle wireless transmission ranges from 200 m to 350 m, additional traffic overhead by firework is observed, but remains less than 0.2 hops. In addition, in lower wireless transmission ranges, such as less than 200 m, there is no difference between without and with firework, due to poor reachability in both cases. Even though firework routing requires in the medium range cases additional traffic overhead, reachability recovery has more importance over overhead increases for the future network infrastructure, since it allows a connection to the destination compared to the case without firework. Moreover, here, in our simulation, we use a fixed firework threshold (0.5 ), and the higher the firework threshold we utilize, the less additional traffic overhead produced. We can also easily embed some additional intelligence to reduce the overhead by avoiding unwanted replicated packets, for example by not broadcasting packets to nodes that have a low expectation of recovery, due to their temperature or vehicular motion. As a consequence, the above results can be seen as the worst case scenario and indicate that firework inevitably produces an increase of traffic overhead to some extent, but the benefits of higher connectivity with MTFR outweigh this drawback to make it feasible enough for an actual system implementation.
Figure 7.
Traffic overhead analysis shows differences between with and without firework for intermediate wireless transmission ranges.
Figure 7.
Traffic overhead analysis shows differences between with and without firework for intermediate wireless transmission ranges.
In addition,
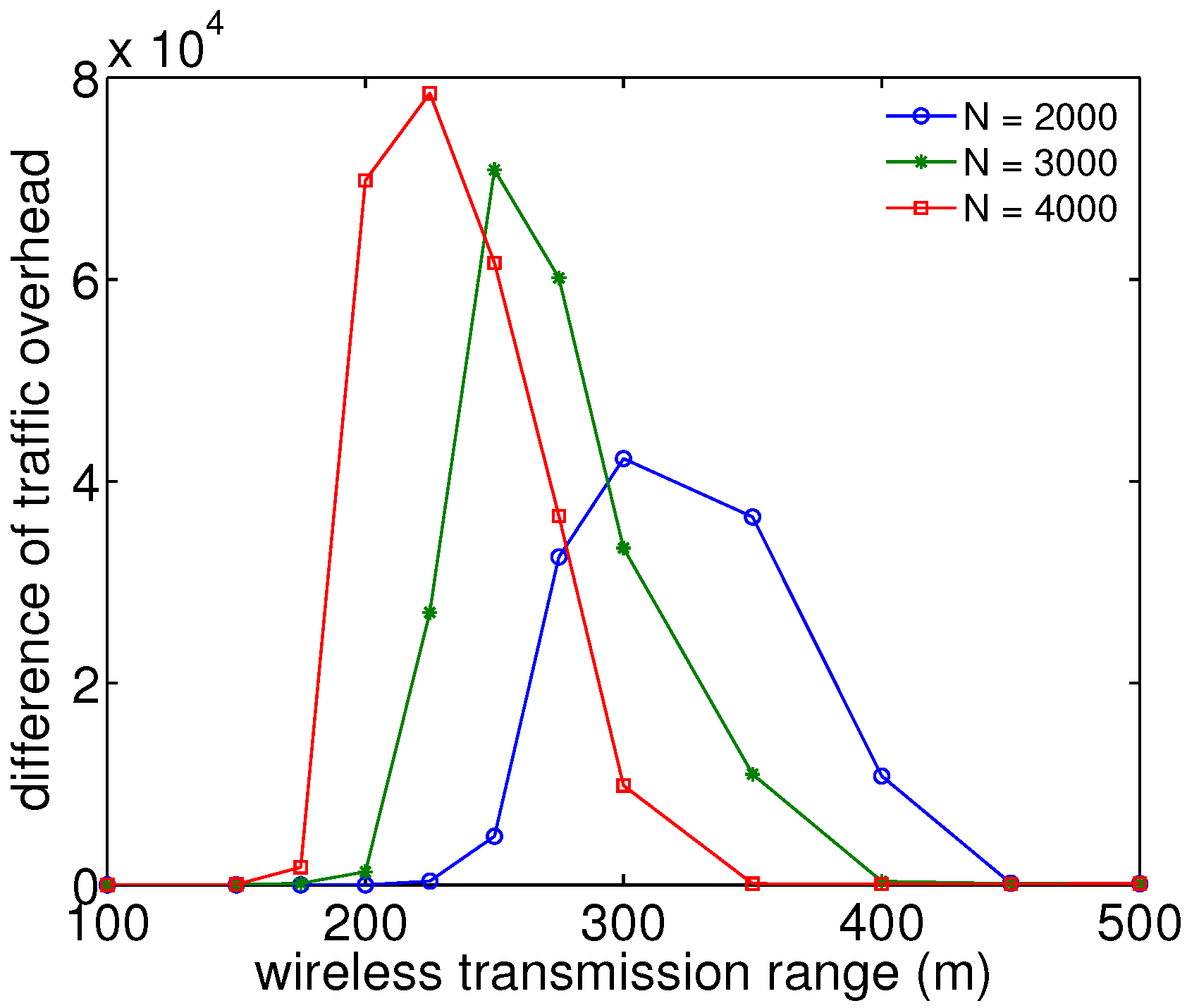
Figure 8 shows the simulation results of an additional traffic overhead increase by firework with different numbers of nodes under RWK at the speed of 100 m/s and with different wireless ranges for packet transmission. Here, traffic overhead is expressed as the average number of traversed hops by a packet transmission from the source node to the destination node. The difference of traffic overhead is the discrepancy in traffic overhead between the results with firework and without firework. In addition, absolute values for the traffic overhead with and without firework are given in
Figure 8. As the number of nodes increases, the difference of traffic overhead increases, though the overhead per packet in
Figure 7 remains almost constant irrespective of the number of nodes. In smaller and larger wireless transmission ranges, the overhead increase is almost zero for the same reason as in the reachability improvement analysis of
Section 4.1. The wireless range for each maximum overhead peak shifts similarly from a small range to a large range.
Figure 8.
Traffic overhead degradation analysis shows that the peak of overhead difference between with and without firework shifts as the number of nodes decreases.
Figure 8.
Traffic overhead degradation analysis shows that the peak of overhead difference between with and without firework shifts as the number of nodes decreases.
4.4. Firework Parameter Study
Finally, we analyze parameter influences by the firework method.
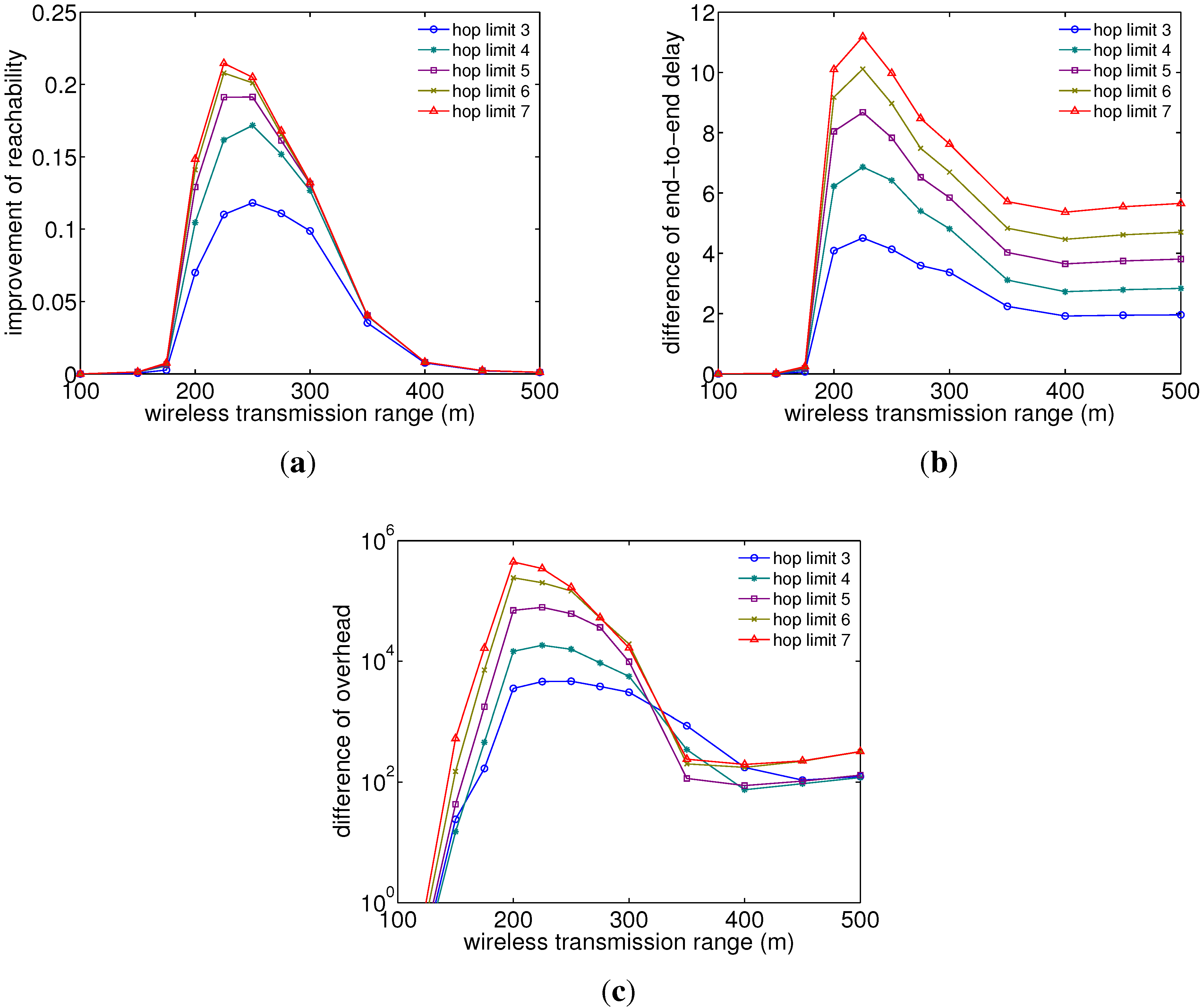
Figure 9 and
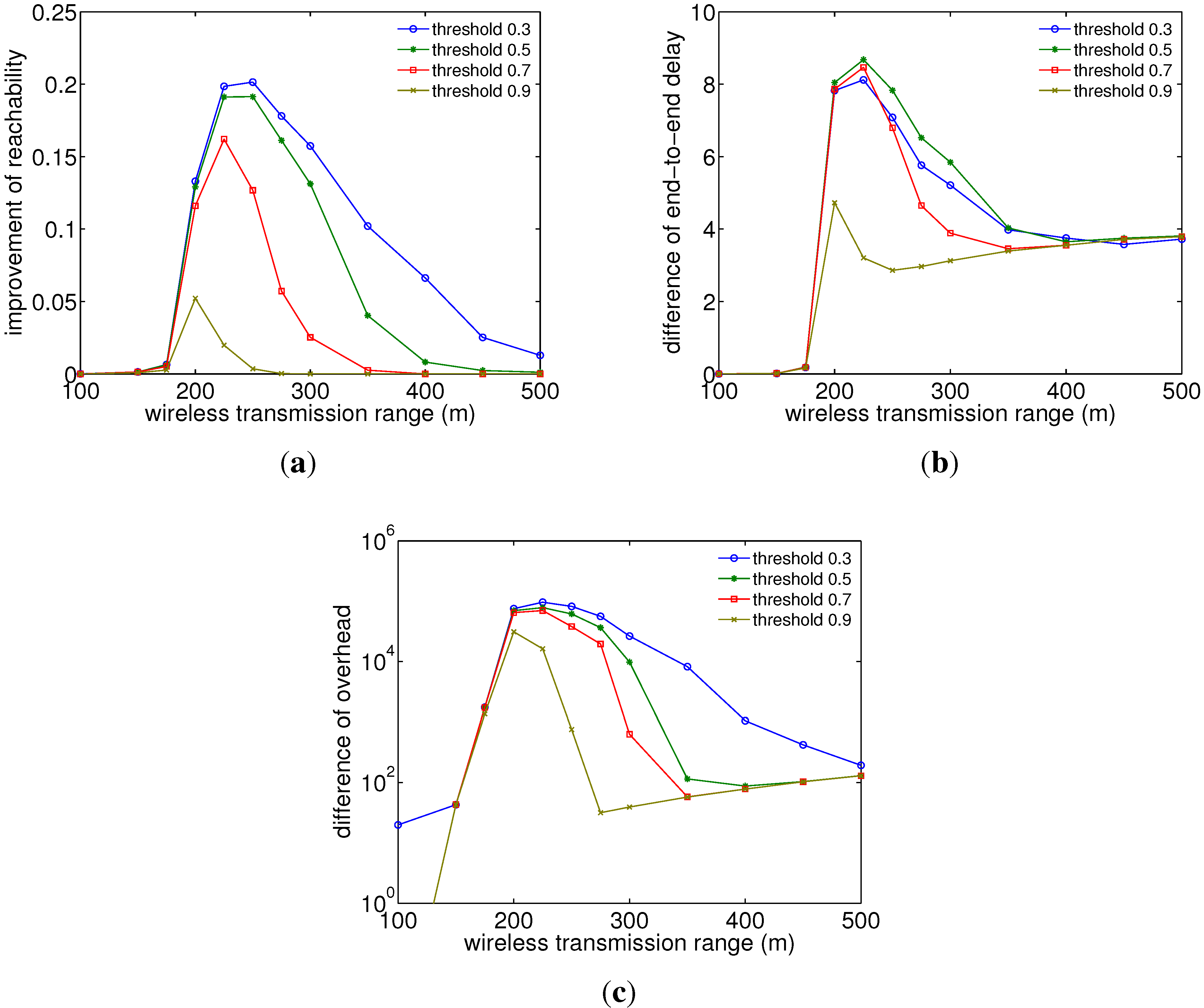
Figure 10 show the simulation results of the improvement of reachability, the difference of delay and the difference of overhead by firework routing with different firework hop limits and firework threshold values, respectively, which are simulated for 4000 nodes under RWK at the speed of 100 m/s and with different wireless ranges for packet transmission. Here, the firework hop limit is defined as the maximum number of hops for packets to be replicated and transferred to neighboring nodes by intermediate nodes. In other words, the intermediate nodes replicate and transfer packets with a hop count up to the firework hop limit and stop broadcasting packets beyond the firework hop limit. In addition, the firework threshold is defined as the minimum temperature value at which intermediate nodes replicate and transfer packets received from neighboring nodes. Hence, intermediate nodes with the temperature of a firework threshold value or larger replicate and transfer intercepted packets, while, on the other hand, nodes with a smaller temperature than firework threshold do not replicate them and operate the same way as conventional potential-based routing.
From
Figure 9(a), a firework hop limit of five hops appears to achieve high reachability, while trying to maintain a low delay (
Figure 9(b)) and overhead (
Figure 9(c)) to some extent. It is observed that the best hop limit value depends on current conditions, such as node density. Increasing the hop limit too much does not yield much improvement in reachability, but increases delay and especially overhead. An interesting observation can be further made in
Figure 9(c). Although it would be expected that an increased firework hop limit would lead to more overhead, for transmission ranges between 300–400 m, the overhead actually drops below that of a hop limit of three. The reason for this is that with a large wireless transmission range and hop limit, there is a large overlap of neighboring nodes, and since each node only participates once in each broadcast process beyond the firework threshold, the overhead for large ranges becomes less after the first hop of the broadcast.
Figure 9.
Evaluation of the hop limit versus the transmission range shows that even a hop limit threshold = 3 yields a fair improvement, while a hop limit of five appears to produce sufficient reachability (). (a) Reachability difference; (b) delay difference; (c) overhead difference.
Figure 9.
Evaluation of the hop limit versus the transmission range shows that even a hop limit threshold = 3 yields a fair improvement, while a hop limit of five appears to produce sufficient reachability (). (a) Reachability difference; (b) delay difference; (c) overhead difference.
In addition, from
Figure 10, it is shown that the firework threshold value should be selected in a more precise manner than the hop limit value. For example, the firework thresholds between 0.5 and 0.7 might be the best parameters in the case of wireless transmission ranges 250 m, 300–350 m and 400 m or above, respectively. A firework threshold between 0.5 and 0.7 produces overall better reachability improvement, much closer to the best performance at a firework threshold of 0.3, while at the same time having a smaller traffic overhead. However, the threshold of 0.5 has a slightly higher delay difference than the other values, and all thresholds converge for large ranges to the same values. Note that a firework threshold of zero means that we have a pure broadcasting mechanism, while a threshold of one is the same as conventional potential-based routing.
Figure 10.
Reachability improvement versus firework threshold shows that a firework threshold of 0.5 reveals a good tradeoff between reachability improvement and delay/overhead (). (a) Reachability difference; (b) delay difference; (c) overhead difference.
Figure 10.
Reachability improvement versus firework threshold shows that a firework threshold of 0.5 reveals a good tradeoff between reachability improvement and delay/overhead (). (a) Reachability difference; (b) delay difference; (c) overhead difference.
4.5. Theoretical Discussion
From the results, we saw that there is a fundamental relationship between the number of nodes, the wireless transmission range and reachability. In this subsection, we will briefly discuss some results on random geometric graphs [
13,
14] that provide theoretical insights into this relationship. Random geometric graphs have become a useful theoretical tool for modeling connectivity in static networks [
15] or dynamic networks [
16], i.e., where nodes move with a random walk, and they are defined as follows.
Let N nodes be placed at independent and identically distributed random positions in the unit torus . We define the random geometric graph over this set of N nodes and the set of edges connecting each pair of nodes, and , if , where r is a positive real-valued number and denotes the Euclidean distance in the torus. This definition resembles our static network configuration in a MANET for nodes having the wireless transmission range, r.
It was shown that for such a random geometric graph, a critical radius,
exists for which connectivity occurs with high probability as
. By rescaling
from the unit torus to our modeled area side
, we obtain the scaled radius,
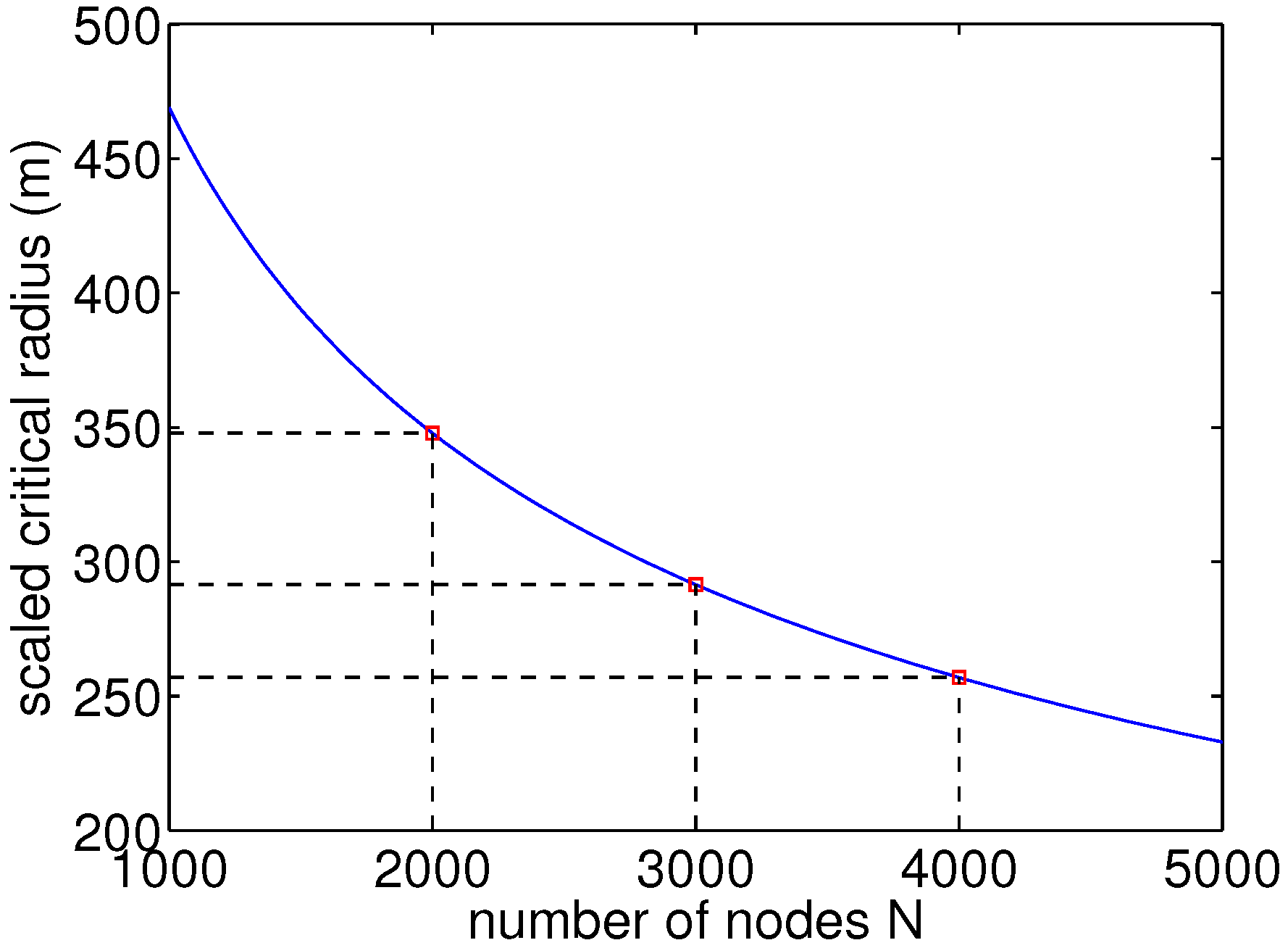
, which we can compare with our simulated results (
Figure 11). For the considered number of nodes in this paper of
, 3000 and 4000, we obtain numerical values of
, 291.46 m and 256.91 m, respectively. It should be noted that these values can only be roughly compared, since the theoretical values only consider static nodes, while our simulation includes an RWK mobility model. However, they show that for our considered number of nodes, the critical transmission ranges lie around 250–350 m, as we could also see from the simulation results.
Figure 11.
Scaled critical radius for the investigated number of nodes, N, in this study.
Figure 11.
Scaled critical radius for the investigated number of nodes, N, in this study.
Furthermore, Diaz
et al. [
16] investigated the analytical properties of random geometric graphs with mobility. Similar to our simulations, each node performs a random walk with a speed,
s. The expected length of the connectivity period is derived in [
16] as:
where
. By rescaling
from the unit torus to our real-world values as
, we obtain
Figure 12, where
is plotted over
r. We limited the y-axis to 100, which is the length of our simulation time, and can see that the radius for which
reaches 100 matches quite well to the ranges in which we have a reachability probability of nearly one, as shown in
Figure 3.
Figure 12.
Scaled connection lengths for different numbers of nodes N within 100 s simulation time.
Figure 12.
Scaled connection lengths for different numbers of nodes N within 100 s simulation time.