The Flux of Phenolic Compounds through Silicone Membranes

Abstract

Phenols as a class of molecules have been reported to exhibit higher log maximum fluxes through human stratum corneum, SC, from water, log J_MHAQ, than other classes of molecules. This suggests that their corresponding log maximum fluxes through silicone from water, log J_MPAQ, may be useful to extend the existing n = 63 log J_MPAQ database to include more log J_MPAQ values greater than 0.0. The log J_MPAQ values for n = 7 phenols predicted to give log J_MPAQ values greater than 0.0 based on their log J_MHAQ values have been experimentally determined. These n = 7 new log J_MPAQ values have been added to the existing n = 63 log J_MPAQ database to give a new n = 70 database and the n = 7 literature log J_MHAQ values have been added to the existing n = 48 log J_MHAQ database (matched to the n = 63 log J_MPAQ database) to give a new n = 55 database. The addition of the n = 7 phenols improved the correlations of these flux databases when fitted to the Roberts-Sloan equation, RS, as well as the correlation between the matched experimental (Exp.) log J_MPAQ with the Exp. log J_MHAQ.

1. Introduction

The rate-limiting barrier to diffusion of molecules through human skin is the stratum corneum, SC. The SC is comprised of highly dense, polar, proteinous corneocytes embedded in a lipid matrix. The lipid matrix in turn is comprised of multiple lipid bilayers containing mostly ceramides, fatty acids and cholesterol [1,2,3]. A tortuous pathway through this lipid matrix and around the corneocytes is generally considered to be the route followed by molecules diffusing through the SC. Since the route of molecules diffusing through the SC is lipid-like, the lipid solubility of molecules diffusing through the SC is an important physiochemical determinant of the efficiency of the diffusion process. Similarly, any surrogate for the SC must present with substantially lipid-like properties. Since silicone membranes present with highly lipid-like properties, it has been suggested that silicone membranes could be a surrogate for skin in diffusion cell studies and that those results could be used to predict diffusion through human skin [4,5]. Also, from a theoretical basis it can be assumed that, if the diffusion of unit mass per unit area per unit time, flux, through silicone membranes can be accurately modeled by an equation (Roberts–Sloan, RS, [6]) that accurately models maximum flux through human skin [7] exists, a linear relationship exists between the maximum flux of molecules through silicone membranes from water, log J_MPAQ, and their maximum flux through human skin in vitro from water, log J_MHAQ [5]. Thus experimental (Exp.) log J_MPAQ could be used to predict Exp. log J_MHAQ.

The flux data for molecules from which the Roberts–Sloan, RS, equation was derived is based on the application of saturated solutions (suspensions of molecules in a solvent) to the membrane being used to give maximum flux, J_M. Thus all the molecules are presented to the membrane at their maximum thermodynamic activity in that solvent [6,7,8]. Since the molecules are presented to the membrane at their maximum thermodynamic activity, at equilibrium the molecules are also at their maximum thermodynamic activity in the membrane [8,9], i.e., at their solubility limit or saturated solubility in the first few layers of the membrane, S_M1. Thus, J_M depends only on the solubility of the molecules in the first layers of the membrane, and unless the solvent changes the solubility limit of the membrane, the solvent/vehicle has no effect on J_M. The form of the RS equation for predicting J_M derives from an expansion of Fick’s law, Equation 1, so that the dependent variables are molecular weight, MW, solubility in a lipid, S_LIPID, and solubility in water, S_AQ. S_M1 can then be estimated from the product of the partition coefficient between the vehicle (water in this case, AQ) and a surrogate lipid for the membrane (octanol in this case, S_OCT), (K_OCT:AQ)^y∙constant, and the solubility in the vehicle, S_AQ: (K_OCT:AQ)^y∙constant∙S_AQ. Expansion of that product into solubilities and taking the logs gives: log S_M1 = y log S_OCT − y log S_AQ + log S_AQ + log constant = y log S_OCT + (1 − y) log S_AQ + log constant.

J = D/L (C_M1 - C_Mn ): J_M = D/L (S_M1 - C_Mn)

(1)

where D is the diffusion coefficient of the molecule in the membrane, L is the thickness of the membrane, C_M1 is the concentration of the molecule in the first few layers of the membrane and C_Mn is the concentration in the last few layers of the membrane which is assumed to approach zero. A linear relationship must exist between log D + log S_M1 of molecules in a silicone membrane and log D + log S_M1 of molecules in human skin in order for a linear relationship between log J_MPAQ and log J_MHAQ to exist.

One problem with determining if the linear relationship between log J_MPAQ and log J_MHAQ exists is that there are only about n = 63 molecules for which log J_MPAQ (output) and the necessary corresponding physicochemical properties (log S_AQ and log S_OCT, input) literature values exist which can be fitted to RS [5]. Of those n = 63, only 18 molecules exhibit high output values; log J_MPAQ values greater than 0.0. Simple phenols present an opportunity to extend the existing n = 63 log J_MPAQ database to include more log J_MPAQ values greater than 0.0. The log J_MHAQ values for n = 18 phenols and their corresponding physicochemical properties that are necessary to determine their fit to RS were published by Roberts, et al. in 1977 [10]. The fit of the n = 18 phenols to RS in the fit of the n = 62 edited Flynn database to RS was published in 2007 [7]. In the edited Flynn database only n = 16 of the n = 62 molecules exhibited log J_MHAQ values greater than 0.0 and of those n = 16, n = 11 were from among the n = 18 phenol subset [10]. Thus, phenols as a subset represent molecules that exhibit physicochemical properties (input) that give higher flux (output) than other types of molecules give.

At present, only n = 6 of the n = 18 simple phenol subset from Roberts, et al. [10] have been included in the n = 63 log J_MPAQ database and only n = 2 exhibit log J_MPAQ greater than 0.0. In order to improve the correlation of the n = 63 log J_MPAQ database with a matched n = 48 log J_MHAQ database, the number of log J_MPAQ and log J_MHAQ greater than 0.0 in each database should be increased. Hence, n = 7 additional phenols have been selected from the n = 18 subset which exhibit physicochemical properties (input) for which RS predicts high log J_MPAQ values (output). In addition, the n = 7 phenols exhibit an average log J_MHAQ value significantly greater than that of the n = 48 log J_MHAQ database: means ± 95% confidence intervals of 0.04 ± 0.42 log units and −1.06 ± 0.31 log units, respectively. Given the increased range and total number of entries resulting from the addition of these n = 7 compounds to the n = 48 log J_MHAQ database and the n = 63 log J_MPAQ database, the fit of these databases to the RS should improve, and correlation of the log J_MPAQ with log J_MHAQ values matched in these databases should also improve.

Further, since the addition of the n = 7 new entries to the new n = 63 log J_MPAQ database, each potentially exhibiting higher log J_MPAQ values than the average of the initial n = 63 log J_MPAQ values, will change the relative distribution of flux values in the database, it is imperative to determine if other models would then fit the database better than they did before the addition of the n = 7 new entries. Thus, we will also determine the fit of the new databases to the Kasting–Smith–Cooper (KSC) model [11] and to the Magnusson–Anissimov–Cross–Roberts (MACR) model [12] and compare these fits to the fit of RS to the new databases.

2. Materials and Methods

The phenolic compounds used are listed in Table 1. These compounds were obtained from Aldrich and their solubility values were acquired or approximated from literature sources. The phenols were all solids except for 3-methylphenol.

The measurement of maximum flux through silicone was performed according to a literature procedure [13] at 32 °C, except that the silicone membrane was in contact with the receptor for only 24 h to condition them. The receptor was a 7.1 pH phosphate buffer.

The donor suspensions were prepared by stirring approximately 0.5 g (1 g in the case of 3-methylphenol) of the compounds in 10 mL of water for 24 h. For all compounds, this surpassed the aqueous solubility by a factor of at least 20, which ensured saturation and excess solid/oil present in the donor phase. After the membranes were conditioned, the receptor phases were changed and the donor suspensions (first application, 1 mL) were applied; n = 3. The donor cells were sealed by Parafilm. Samples were taken from the receptor every 2–3 h after application. Following sample collection, the receptor phases were changed to ensure sink conditions, and the donor suspensions were either changed or had more solid/oil added to the existing suspension, depending upon the visible extent of depletion. After 4–5 sampling intervals, the donor suspensions were removed with methanol and the receptors were changed. The membranes were leached with methanol in the donor phase for 48–72 h with samples taken and receptor phases changed every 12–24 h to remove any residual phenol in the membrane.

To ensure that flux data was not altered by possible membrane damage, a standard solute/solvent was applied and its flux determined. A donor suspension was prepared from 400 mg of theophylline suspended with stirring in 6 mL of propylene glycol (PG) for 24 h. This suspension (second application, 0.50 mL) was applied to all the silicone membranes after they were leached with methanol (see above). Samples were taken from the receptor every 24 h after application for at least 72 h so that at least 3 samples were obtained. Following sample collection, the receptor phases were changed and the donor suspensions were changed every other sampling interval. After 3–5 sampling intervals, the diffusion cells were disassembled and the membranes were placed in a methanol bath for maintenance leaching.

The flux values of the first and second application were determined by UV absorption. The wavelengths (λ_ε) and molar absorptivities (ε) used for the phenolic compounds are listed in Table 1. The log flux of theophylline through silicone from PG, log J_MPPG, for each membrane was found to be within the standard deviation of the literature value of −2.68 ± 0.12 log units [13].

Nonlinear regression was performed by SPSS 20.0 (Rel. 20.0.0). The compounds were fitted to the Roberts–Sloan equation for maximum flux, log J_MAQ:

log J_MAQ = x + y log S_OCT + (1 − y) log S_AQ − z MW

(2)

to the KSC Equation:

log J_MAQ = x + y log S_OCT − z MW

(3)

and to the MACR Equation:

log J_MAQ = x − z MW

(4)

3. Results and Discussion

The results are displayed in Table 1. All but 4-chloro-3,5-dimethylphenol exhibited a log J_MPAQ greater than 0.0, and even it was very close. As a subset the n = 7 simple phenols had an average log J_MPAQ significantly greater than the average log J_MPAQ of the n = 63 log J_MPAQ database: means ± 95% confidence intervals 1.03 ± 0.45 log units and −0.42 ± 0.29 log units, respectively. The average log J_MPAQ in the n = 70 log J_MPAQ database has not significantly increased, but is no longer significantly less than 0.0: mean ± 95% confidence interval −0.27 ± 0.29. Unfortunately, the addition of the n = 7 phenols did not significantly increase the average log J_MHAQ of the n = 55 log J_MHAQ database relative to the n = 48 log J_MHAQ database: means ± 95% confidence intervals, −0.918 ± 0.29 log units and −1.058 ± 0.31 log units, respectively.

Table 1. The relevant measured or literature physicochemical properties for the n = 7 phenolic compounds used in this study.

Cmpd. a	MW	Log SAQ b,d	Log KOCT:AQ b	Log SOCT b,d	λε c	ε c,e	Log JMPAQ c,f	Log JMHAQ b,f
1	143	1.55	3.10	4.65	283	1241	1.01	0.29
2	157	0.28	3.39	3.67	285	1041	−0.027	−0.95
3	122	1.61	2.35	3.96	277	1668	1.37	0.17
4	108	2.29	1.95	4.24	276	1614	1.62	0.53
5	163	1.49	3.08	4.57	285	1791	1.16	0.27
6	197	0.66	3.69	4.35	312	4518	0.49	−0.57
7	108	2.36	1.96	4.32	271	1468	1.61	0.54

^a Substituted phenols. 1, 4-chloro-3-methyl; 2, 4-chloro-3,5-dimethyl; 3, 3,4-dimethyl; 4, 4-methyl; 5, 2,4-dichloro; 6, 2,4,6-trichloro; 7, 3-methyl; ^b From Roberts et al. 1977 [10] and Majumdar et al. 2007 [7]; ^c Measured directly. ^d Solubility in water (S_AQ) or octanol (S_OCT) in μmole cm⁻³; ^e Molar absorptivity coefficient in L mole⁻¹ cm⁻¹; ^f Maximum flux through silicone (J_MPAQ) or human stratum corneum (J_MHAQ) from water in μmole cm⁻² h⁻¹.

Table 1. The relevant measured or literature physicochemical properties for the n = 7 phenolic compounds used in this study.

Cmpd. a	MW	Log SAQ b,d	Log KOCT:AQ b	Log SOCT b,d	λε c	ε c,e	Log JMPAQ c,f	Log JMHAQ b,f
1	143	1.55	3.10	4.65	283	1241	1.01	0.29
2	157	0.28	3.39	3.67	285	1041	−0.027	−0.95
3	122	1.61	2.35	3.96	277	1668	1.37	0.17
4	108	2.29	1.95	4.24	276	1614	1.62	0.53
5	163	1.49	3.08	4.57	285	1791	1.16	0.27
6	197	0.66	3.69	4.35	312	4518	0.49	−0.57
7	108	2.36	1.96	4.32	271	1468	1.61	0.54

^a Substituted phenols. 1, 4-chloro-3-methyl; 2, 4-chloro-3,5-dimethyl; 3, 3,4-dimethyl; 4, 4-methyl; 5, 2,4-dichloro; 6, 2,4,6-trichloro; 7, 3-methyl; ^b From Roberts et al. 1977 [10] and Majumdar et al. 2007 [7]; ^c Measured directly. ^d Solubility in water (S_AQ) or octanol (S_OCT) in μmole cm⁻³; ^e Molar absorptivity coefficient in L mole⁻¹ cm⁻¹; ^f Maximum flux through silicone (J_MPAQ) or human stratum corneum (J_MHAQ) from water in μmole cm⁻² h⁻¹.

The addition of these n = 7 phenols to the n = 63 log J_MPAQ database and the n = 48 log J_MHAQ database improved the fit of these databases to the RS as expected. The fit of the new n = 70 log J_MPAQ database gave an r² of 0.907, an average absolute residual log J_MPAQ (Δlog J_MPAQ) of 0.300 log units and the coefficients x = −1.606, y = 0.695 and z = 0.00490 were all significant (p < 0.05):

log J_MPAQ = −1.606 + 0.695 log S_OCT + 0.305 log S_AQ − 0.00490 MW

(5)

The fit of the n = 70 log J_MPAQ database is an improvement over the n = 63 log J_MPAQ database, which had r² = 0.896 and Δlog J_MPAQ = 0.310 log units, but had similar coefficient values: x = −1.607, y = 0.701, z = 0.00492. The fit of the new n = 55 log J_MHAQ database gave an r² of 0.883, an average absolute residual log J_MHAQ (Δlog J_MHAQ) of 0.282 log units and the coefficients x = −3.005 and y = 0.654 were significant (p < 0.05), but the coefficient z = 0.00112 was not significant (p = 0.25):

log J_MHAQ = −3.005 + 0.645 log S_OCT + 0.346 log S_AQ − 0.00112 MW

(6)

The lack of statistical significance for the z coefficient indicates a need to further extend the n = 55 log J_MHAQ database, since the significance of MW to maximum flux is well-established [12]. The fit of the n = 55 log J_MHAQ database to the RS is an improvement over the n = 48 log J_MHAQ database, which had r² = 0.867 and Δlog J_MHAQ = 0.331 log units and the coefficients x = −2.763, y = 0.635 and z = 0.00207. The x and y coefficients for the new log J_MHAQ database are substantially closer to those coefficients determined for the n = 62 edited Flynn log J_MHAQ database: x = −3.008, y = 0.732, z = 0.0048. Relevant results are displayed in Table 2 and Figure 1, Figure 2. Figure 1 shows a plot of experimental (Exp.) log J_MPAQ versus log J_MPAQ calculated (Calc.) from the coefficients for the fit of the n = 70 database to RS, and Figure 2 shows a plot of Exp. log J_MHAQ versus log J_MHAQ Calc. from the coefficients for the fit of the n = 55 database to RS.

Table 2. The calculated (Calc.), predicted (Pred.), and experimental (Exp.) maximum flux values through silicone from water (log J_MPAQ) and through human stratum corneum from water (log J_MHAQ) for the n = 7 phenolic compounds.

Cmpd. a	Exp. log JMPAQ b	Pred. n = 63 log JMPAQ b,c	Calc. n = 70 log JMPAQ b,d	Exp. log JMHAQ b	Pred. n = 48 log JMHAQ b,e	Calc. n = 55 log JMHAQ b,f
1	1.01	1.41	1.40	0.29	0.46	0.41
2	−0.027	0.28	0.26	−0.95	−0.66	−0.68
3	1.37	1.05	1.04	0.17	0.087	0.0053
4	1.62	1.52	1.51	0.53	0.54	0.44
5	1.16	1.24	1.23	0.27	0.35	0.32
6	0.49	0.67	0.65	−0.57	−0.17	−0.15
7	1.61	1.60	1.59	0.54	0.62	0.52
Δlog JMAQ g		0.200	0.195		0.159	0.162

^a Substituted phenols. 1, 4-chloro-3-methyl; 2, 4-chloro-3,5-dimethyl; 3, 3,4-dimethyl; 4, 4-methyl; 5, 2,4-dichloro; 6, 2,4,6-trichloro; 7, 3-methyl; ^b Given in units μmole cm⁻² h⁻¹; ^c Using RS coefficients x = −1.607, y = 0.701, z = 0.00492 [6]; ^d Using RS coefficients x = −1.606, y = 0.695, z = 0.00490; ^e Using RS coefficients x = −2.763, y = 0.635 and z = 0.00207 [6]; ^f Using RS coefficients x = −3.005, y = 0.654, z = 0.00112; ^g Average absolute residual log J_MPAQ or log J_MHAQ for the n = 7 phenols.

Table 2. The calculated (Calc.), predicted (Pred.), and experimental (Exp.) maximum flux values through silicone from water (log J_MPAQ) and through human stratum corneum from water (log J_MHAQ) for the n = 7 phenolic compounds.

Cmpd. a	Exp. log JMPAQ b	Pred. n = 63 log JMPAQ b,c	Calc. n = 70 log JMPAQ b,d	Exp. log JMHAQ b	Pred. n = 48 log JMHAQ b,e	Calc. n = 55 log JMHAQ b,f
1	1.01	1.41	1.40	0.29	0.46	0.41
2	−0.027	0.28	0.26	−0.95	−0.66	−0.68
3	1.37	1.05	1.04	0.17	0.087	0.0053
4	1.62	1.52	1.51	0.53	0.54	0.44
5	1.16	1.24	1.23	0.27	0.35	0.32
6	0.49	0.67	0.65	−0.57	−0.17	−0.15
7	1.61	1.60	1.59	0.54	0.62	0.52
Δlog JMAQ g		0.200	0.195		0.159	0.162

^a Substituted phenols. 1, 4-chloro-3-methyl; 2, 4-chloro-3,5-dimethyl; 3, 3,4-dimethyl; 4, 4-methyl; 5, 2,4-dichloro; 6, 2,4,6-trichloro; 7, 3-methyl; ^b Given in units μmole cm⁻² h⁻¹; ^c Using RS coefficients x = −1.607, y = 0.701, z = 0.00492 [6]; ^d Using RS coefficients x = −1.606, y = 0.695, z = 0.00490; ^e Using RS coefficients x = −2.763, y = 0.635 and z = 0.00207 [6]; ^f Using RS coefficients x = −3.005, y = 0.654, z = 0.00112; ^g Average absolute residual log J_MPAQ or log J_MHAQ for the n = 7 phenols.

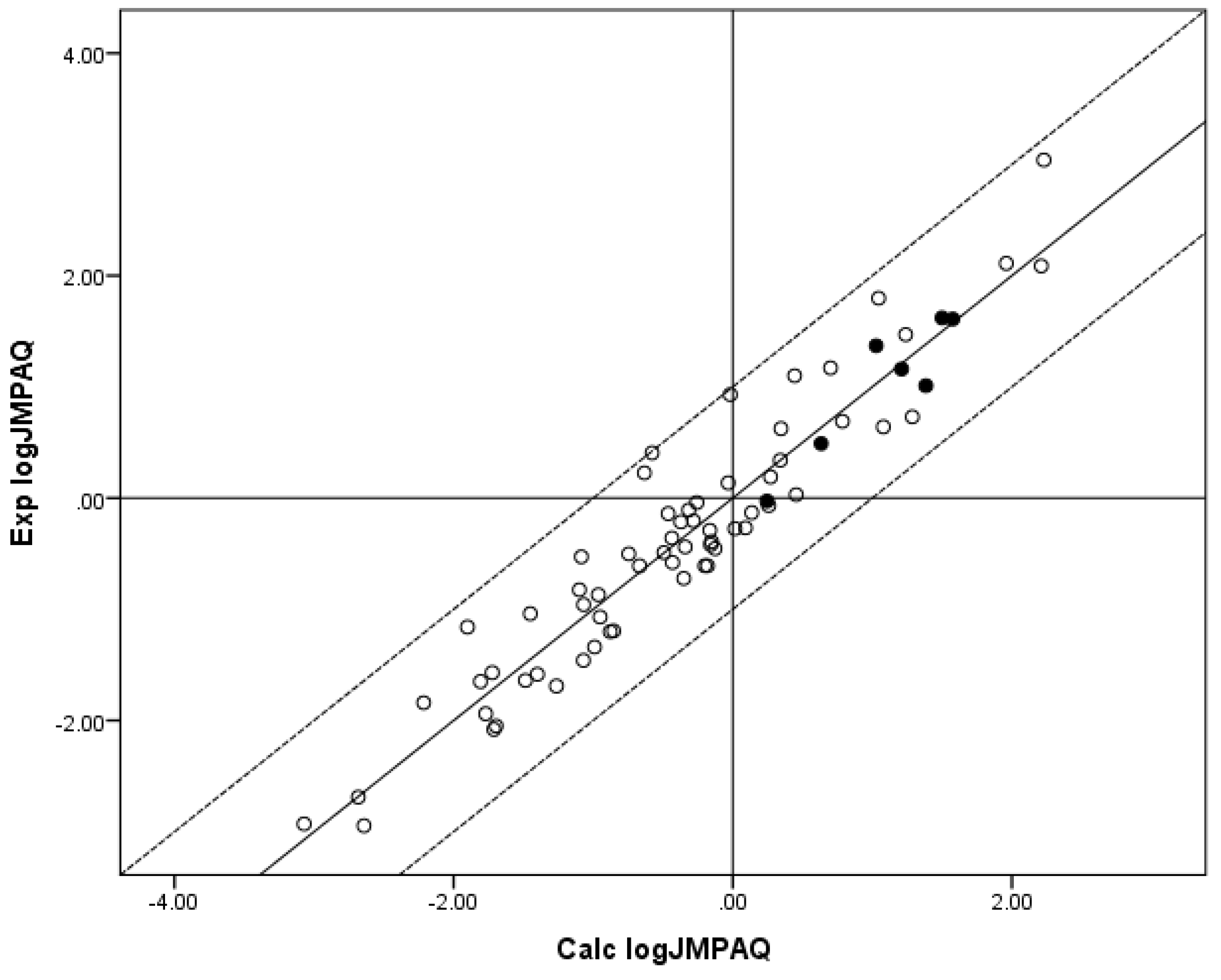
Figure 1. The correlation of the calculated (Calc.) log J_MPAQ from the fit of n = 70 to RS with the experimental (Exp.) log J_MPAQ. The dashed lines represent the boundaries for residual log J_MPAQ greater than 1.0, the solid line indicates points where the Calc. log J_MPAQ is equivalent to the Exp. log J_MPAQ. The filled circles indicate the n = 7 phenols. The Calc. log J_MPAQ values were determined with Equation 5: log J_MPAQ = −1.606 + 0.695 log S_OCT + 0.305 log S_AQ − 0.00490MW. r² = 0.907, average absolute residual log J_MPAQ = 0.300.

Figure 1. The correlation of the calculated (Calc.) log J_MPAQ from the fit of n = 70 to RS with the experimental (Exp.) log J_MPAQ. The dashed lines represent the boundaries for residual log J_MPAQ greater than 1.0, the solid line indicates points where the Calc. log J_MPAQ is equivalent to the Exp. log J_MPAQ. The filled circles indicate the n = 7 phenols. The Calc. log J_MPAQ values were determined with Equation 5: log J_MPAQ = −1.606 + 0.695 log S_OCT + 0.305 log S_AQ − 0.00490MW. r² = 0.907, average absolute residual log J_MPAQ = 0.300.

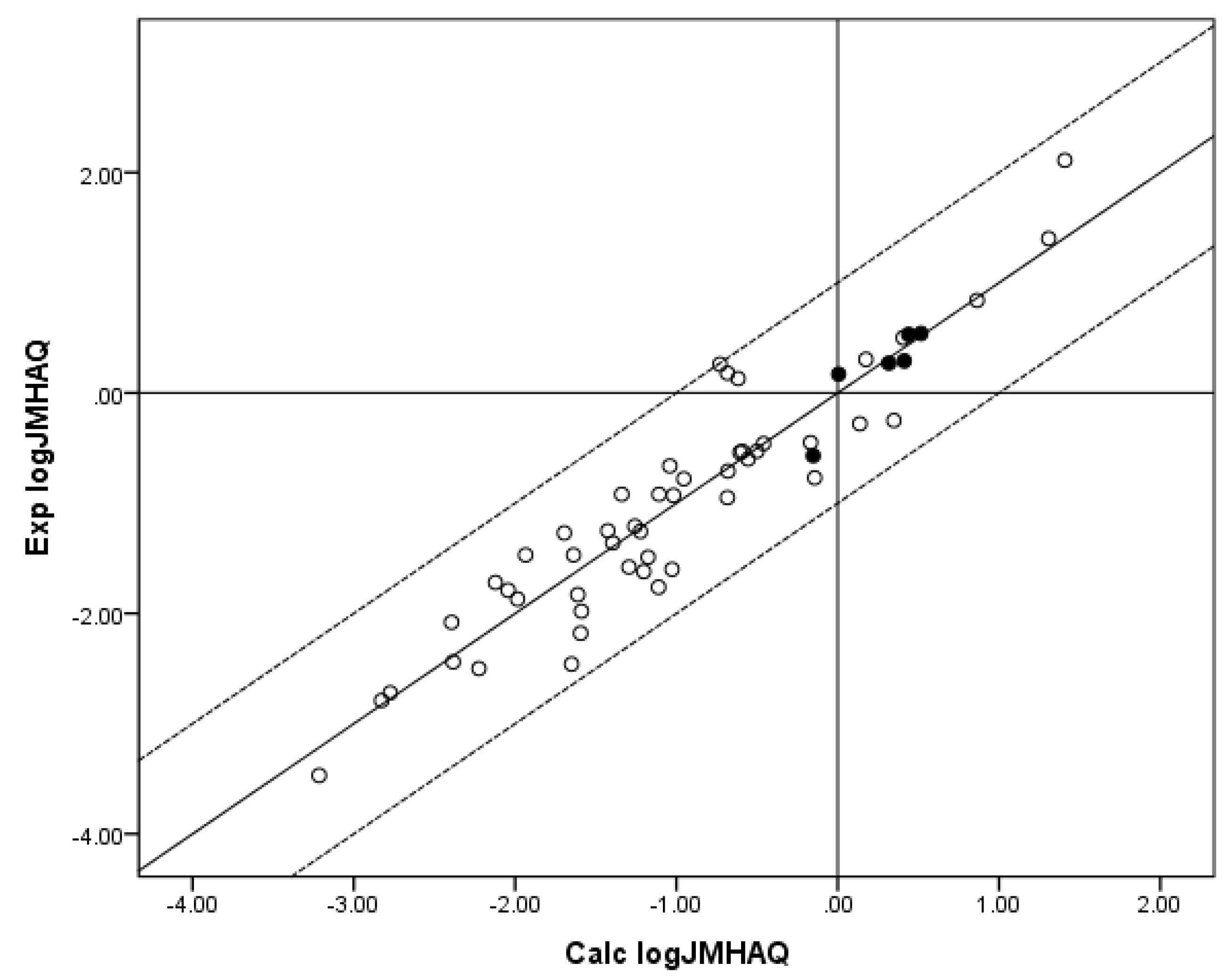
Figure 2. The correlation of the calculated (Calc.) log J_MHAQ from the fit of n = 55 to RS with the experimental (Exp.) log J_MHAQ. The dashed lines represent the boundaries for residual Exp. log J_MHAQ greater than 1.0, and the solid line indicates points where the Calc. log J_MHAQ is equivalent to the Exp. log J_MHAQ. The filled circles indicate the n = 7 phenols. The Calc. log J_MHAQ values were determined with Equation 6: log J_MHAQ = −3.005 + 0.654 log S_OCT + 0.346 log S_AQ − 0.00112 MW, r² = 0.883, average absolute residual log J_MHAQ = 0.282.

Figure 2. The correlation of the calculated (Calc.) log J_MHAQ from the fit of n = 55 to RS with the experimental (Exp.) log J_MHAQ. The dashed lines represent the boundaries for residual Exp. log J_MHAQ greater than 1.0, and the solid line indicates points where the Calc. log J_MHAQ is equivalent to the Exp. log J_MHAQ. The filled circles indicate the n = 7 phenols. The Calc. log J_MHAQ values were determined with Equation 6: log J_MHAQ = −3.005 + 0.654 log S_OCT + 0.346 log S_AQ − 0.00112 MW, r² = 0.883, average absolute residual log J_MHAQ = 0.282.

Plots of the individual independent variables, log S_OCT, log S_AQ and MW, against log J_MPAQ (n = 70) and against log J_MHAQ (n = 55) gave the following r² values: (a) log J_MPAQ versus log S_OCT, r² = 0.677; versus log S_AQ, r² = 0.554; versus MW, r² = 0.541; (b) log J_MHAQ versus log S_OCT, r² = 0.603; versus log S_AQ, r² = 0.526; versus MW, r² = 0.520. All regression equations had statistically significant (p < 0.05) slope and intercept estimates. In each case, the best regression of the individual independent variables against flux values was by log S_OCT. It is worth noting that the n = 7 phenol subset gives the following r² values and significance profiles when the individual independent variables log S_OCT and log S_AQ are plotted against log J_MPAQ and log J_MHAQ: (a) log J_MPAQ versus log S_OCT, r² = 0.180, without a statistically significant slope (p = 0.34) or intercept (p = 0.51); versus log S_AQ, r² = 0.949, with a statistically significant slope (p < 0.05), but without a statistically significant intercept (p = 0.50); (b) log J_MHAQ versus log S_OCT, r² = 0.335, without a statistically significant slope (p = 0.17) or intercept (p = 0.18); versus log S_AQ, r² = 0.933, with statistically significant (p < 0.05) slope and intercept. The improved dependence of maximum flux from water on the aqueous solubility of highly water-soluble compounds is demonstrated here as a property of both silicone and human stratum corneum, and will be a topic of future investigations. When two individual independent variables, log S_OCT and MW, from the n = 70 log J_MPAQ database were fitted to the KSC equation (Equation 3) the following x, y and z coefficients to the parameters were obtained along with r² and Δlog J_MPAQ values: x = −0.923, y = 0.794, z = 0.0089, r² = 0.797 and Δlog J_MPAQ = 0.431. All but the y coefficient (p = 0.069) were statistically significant (p < 0.05):

log J_MPAQ = −0.923 + 0.794 log S_OCT − 0.0089 MW

(7)

Figure 3 shows a plot of Exp. log J_MPAQ versus log J_MPAQ values calculated from the coefficients for the fit of the n = 70 database to Equation 7. Although the r² was substantially improved by including MW with log S_OCT as independent variables in the regression against flux, the r² was poorer than the r² for the fit of all three independent variables to the Roberts–Sloan Equation (Equation 5). Similarly, when two individual independent variables, log S_OCT and MW, from the n = 55 log J_MHAQ database were fit to the KSC equation (Equation 8) the following x, y and z coefficients to the parameters were obtained along with r² and the Δlog J_MHAQ values: x = −1.252, y = 0.602, z = 0.0080, r² = 0.723 and Δlog J_MHAQ = 0.441. The estimates for the coefficients were all statistically significant (p < 0.05):

log J_MHAQ = −1.252 + 0.602 log S_OCT − 0.0080 MW

(8)

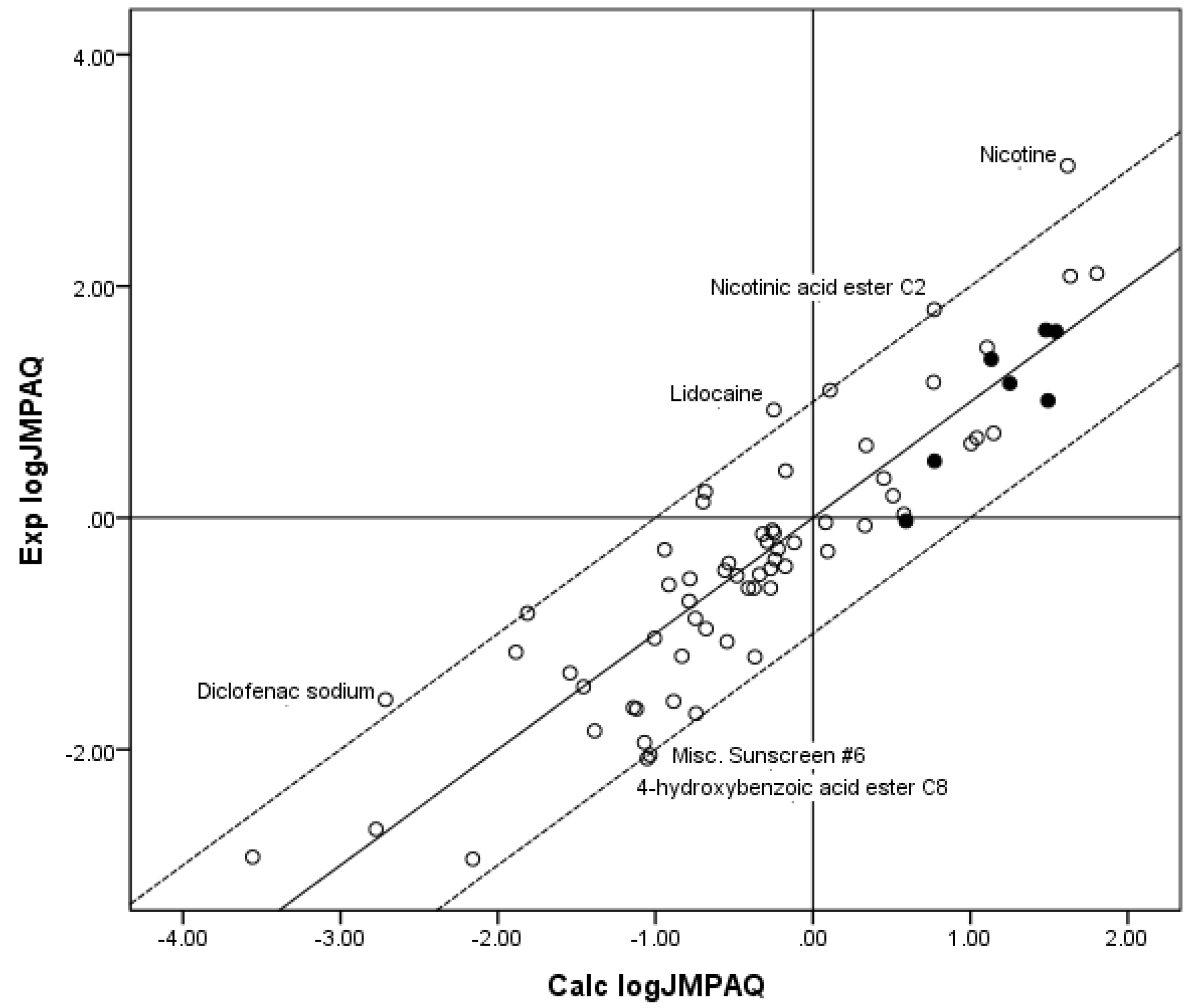
Figure 3. The correlation of the calculated (Calc.) log J_MPAQ from the fit of n = 70 to KSC with the experimental (Exp.) log J_MPAQ. The dashed lines represent the boundaries for residual Exp. log J_MPAQ greater than 1.0, the solid line indicates points where the Calc. log J_MPAQ is equivalent to the Exp. log J_MPAQ. The filled circles indicate the n = 7 phenols. The Calc. log J_MPAQ values were determined with Equation 7: log J_MPAQ = −0.923 + 0.794 log S_OCT − 0.0089 MW, r² = 0.797, average absolute residual log J_MPAQ = 0.431.

Figure 3. The correlation of the calculated (Calc.) log J_MPAQ from the fit of n = 70 to KSC with the experimental (Exp.) log J_MPAQ. The dashed lines represent the boundaries for residual Exp. log J_MPAQ greater than 1.0, the solid line indicates points where the Calc. log J_MPAQ is equivalent to the Exp. log J_MPAQ. The filled circles indicate the n = 7 phenols. The Calc. log J_MPAQ values were determined with Equation 7: log J_MPAQ = −0.923 + 0.794 log S_OCT − 0.0089 MW, r² = 0.797, average absolute residual log J_MPAQ = 0.431.

Figure 4 shows a plot of Exp. log J_MHAQ versus log J_MHAQ values calculated from the coefficients for the fit of the n = 55 database to Equation 8. Again, although a substantial improvement in r² was obtained by including MW with log S_OCT as independent variables in the regression against flux, the r² was poorer than the r² for the fit of all three independent variables to the RS equation (Equation 6). The fit of both databases to the MACR equation (Equation 4), which is the remaining model used to predict maximum flux, is simply the regression of MW against log J_MPAQ or log J_MHAQ shown above to give a somewhat poorer fit than regression of the two individual independent variables, log S_OCT or log S_AQ, against log J_MPAQ or log J_MHAQ. Finally, it should be noted the popular Potts–Guy Equation [14] was not included as a model because its output is permeability coefficient which is not clinically relevant.

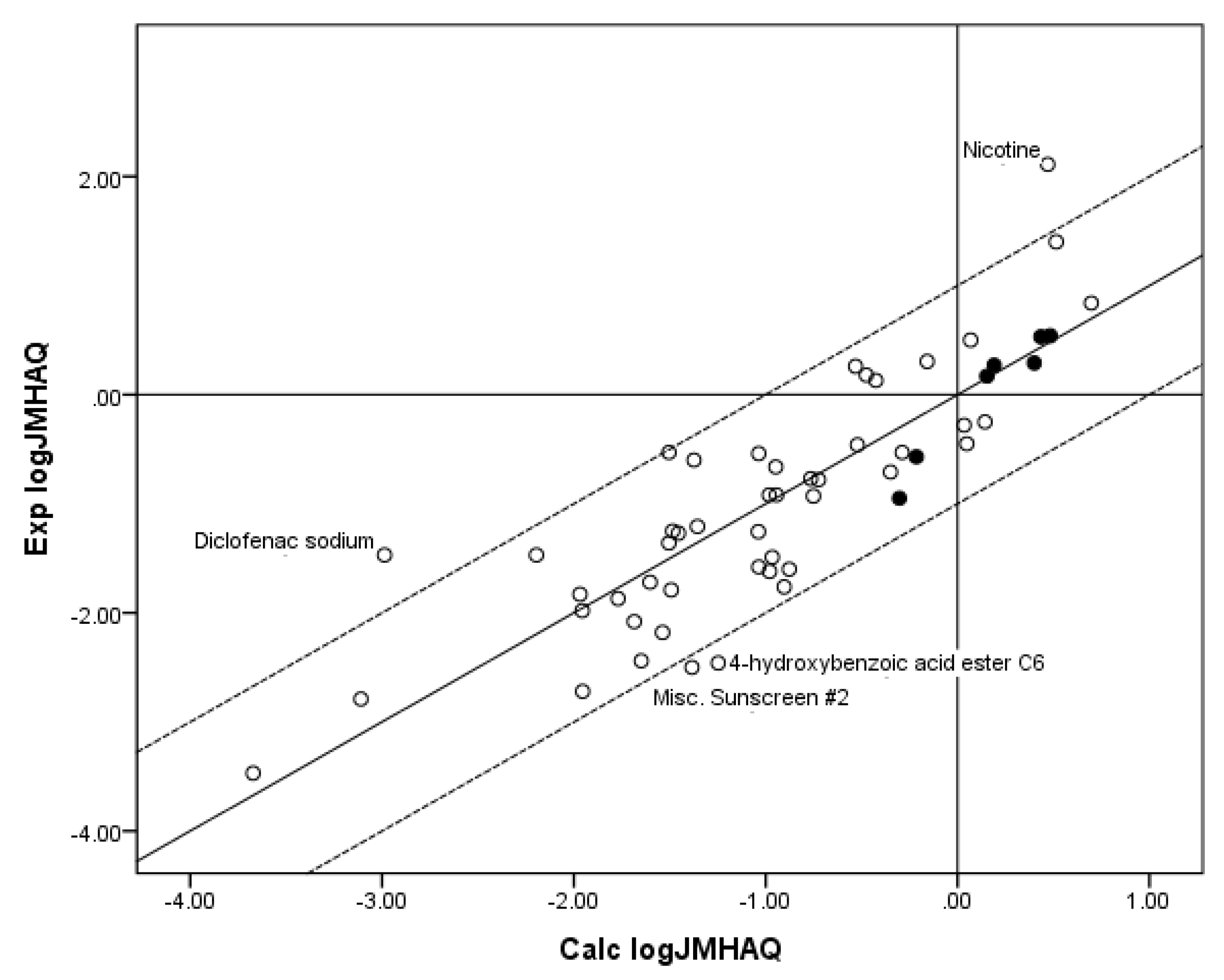
Figure 4. The correlation of the calculated (Calc.) log J_MHAQ from the fit of n = 55 to KSC with the experimental (Exp.) log J_MHAQ. The dashed lines represent the boundaries for residual Exp. log J_MHAQ greater than 1.0, and the solid line indicates points where the Calc. log J_MHAQ is equivalent to the Exp. log J_MHAQ. The filled circles indicate the n = 7 phenols. The Calc. log J_MHAQ values were determined with Equation 8: log J_MHAQ = −1.252 + 0.602 log S_OCT − 0.0080 MW, r² = 0.723, average absolute residual log J_MHAQ = 0.441.

Figure 4. The correlation of the calculated (Calc.) log J_MHAQ from the fit of n = 55 to KSC with the experimental (Exp.) log J_MHAQ. The dashed lines represent the boundaries for residual Exp. log J_MHAQ greater than 1.0, and the solid line indicates points where the Calc. log J_MHAQ is equivalent to the Exp. log J_MHAQ. The filled circles indicate the n = 7 phenols. The Calc. log J_MHAQ values were determined with Equation 8: log J_MHAQ = −1.252 + 0.602 log S_OCT − 0.0080 MW, r² = 0.723, average absolute residual log J_MHAQ = 0.441.

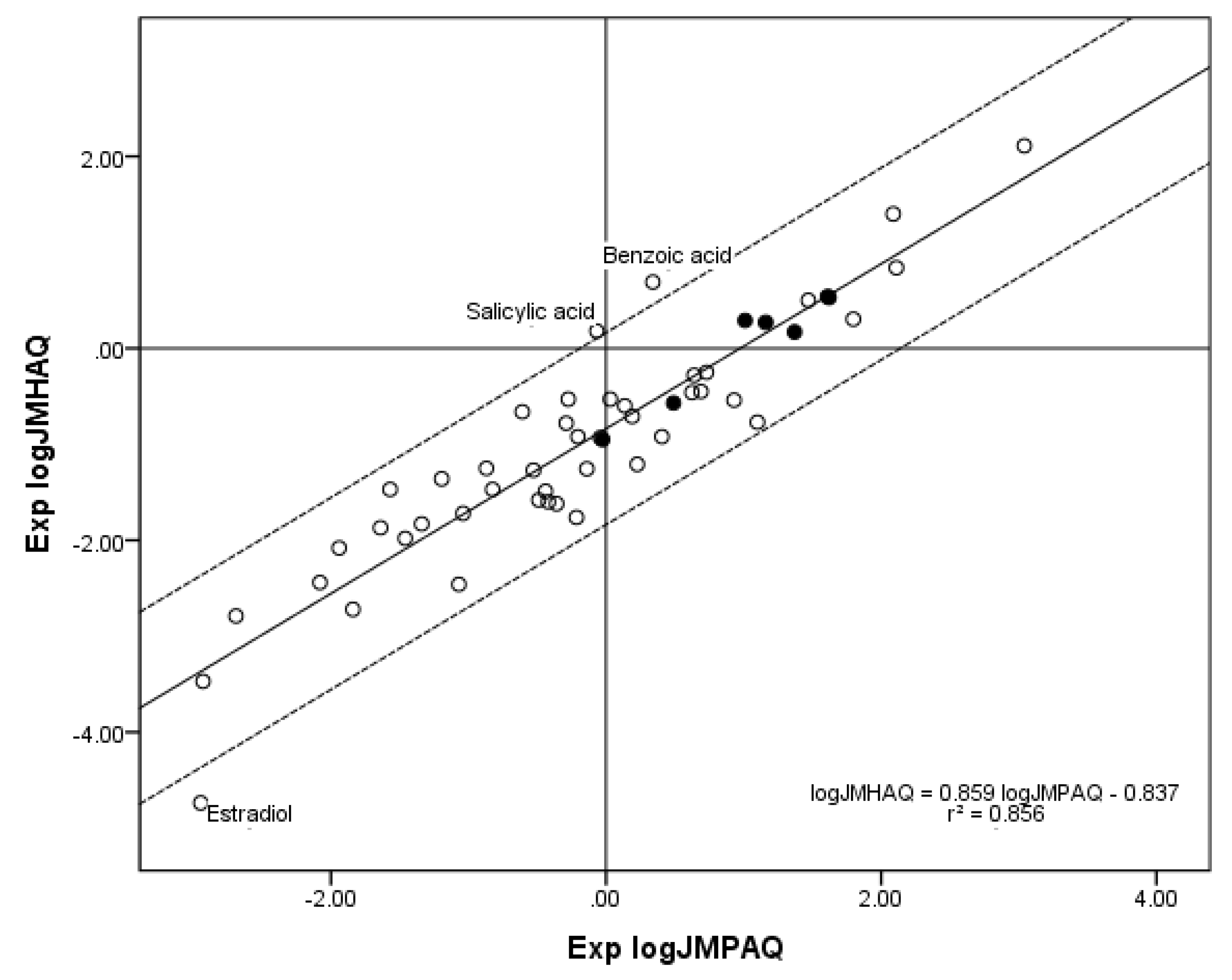
The new n = 52 database of compounds contributing to both the n = 70 log J_MPAQ database and the n = 55 log J_MHAQ database also gives a higher correlation between Exp. log J_MPAQ and Exp. log J_MHAQ than the previous n = 45 database. A linear regression yielded the expression Exp. log J_MHAQ = 0.859 Exp. log J_MPAQ − 0.837, r² = 0.856, which is an improvement over r² = 0.838 for the n = 45 database. Figure 5 shows the plot of Exp. log J_MPAQ versus Exp. log J_MHAQ for n = 52.

Figure 5. The correlation of the n = 52 log J_MHAQ with log J_MPAQ database. The dashed lines represent the boundaries for residual Exp. log J_MHAQ greater than 1.0, and the solid line is the regression equation. The filled circles indicate the n = 7 phenols. The regression information is in the figure.

Figure 5. The correlation of the n = 52 log J_MHAQ with log J_MPAQ database. The dashed lines represent the boundaries for residual Exp. log J_MHAQ greater than 1.0, and the solid line is the regression equation. The filled circles indicate the n = 7 phenols. The regression information is in the figure.

4. Conclusions

The addition of the n = 7 phenols improved all aspects of the log J_MPAQ database with regards to comparison with the matched log J_MHAQ database. Along with strengthening the validity of the assertion that silicone membranes are good surrogates for human stratum corneum, these improvements demonstrate that this surrogate nature holds for a wider range of log J_MPAQ and log J_MHAQ values than had been previously reported.