On the Kung-Traub Conjecture for Iterative Methods for Solving Quadratic Equations

Abstract

Kung-Traub’s conjecture states that an optimal iterative method based on d function evaluations for finding a simple zero of a nonlinear function could achieve a maximum convergence order of $2^{d-1}$. During the last years, many attempts have been made to prove this conjecture or develop optimal methods which satisfy the conjecture. We understand from the conjecture that the maximum order reached by a method with three function evaluations is four, even for quadratic functions. In this paper, we show that the conjecture fails for quadratic functions. In fact, we can find a 2-point method with three function evaluations reaching fifth order convergence. We also develop 2-point 3rd to 8th order methods with one function and two first derivative evaluations using weight functions. Furthermore, we show that with the same number of function evaluations we can develop higher order 2-point methods of order $r+2$, where r is a positive integer, $\ge 1$. We also show that we can develop a higher order method with the same number of function evaluations if we know the asymptotic error constant of the previous method. We prove the local convergence of these methods which we term as Babajee’s Quadratic Iterative Methods and we extend these methods to systems involving quadratic equations. We test our methods with some numerical experiments including an application to Chandrasekhar’s integral equation arising in radiative heat transfer theory.

1. Introduction

The problem of finding a simple zero of a nonlinear equation $f(x)=0,$ is an often discussed problem in many applications of science and technology. The most commonly used method is the Newton-Raphson method (simply called as Newton’s method). Many higher order variants of Newton’s method have been developed and rediscovered in the last 15 years. Recently, the order of convergence of many variants of Newton’s method has been improved using the same number of functional evaluations by means of weight functions (see [1,2,3,4,5,6] and the references therein). The aim of such research is to develop optimal methods which satisfy Kung-Traub’s conjecture. In this paper, we develop 2-point methods with 1 function and 2 first derivative evaluations for solving quadratic equations and study Kung-Traub’s conjecture for these methods. We extend these methods to systems of quadratic equations and conduct some numerical experiments to test the efficiencies of the methods.

2. Developments of the Methods

Let $x^{(k+1)}=\psi (x^{(k)})$ define an Iterative Function (I.F.).

Definition 1. 

[7] If the sequence $\left\{x^{(k)}\right\}$ tends to a limit $x^{*}$ in such a way that

$$\underset{n\to \infty }{lim}\frac{x^{(k+1)}-x^{*}}{{(x^{(k)}-x^{*})}^p}=C$$

for $p\ge 1$, then the order of convergence of the sequence is said to be p, and C is known as the asymptotic error constant. If $p=1$, $p=2$ or $p=3$, the convergence is said to be linear, quadratic or cubic, respectively.

Let $e^{(k)}=x^{(k)}-x^{*}$, then the relation

$$e^{(k+1)}=C{(e^{(k)})}^p+O\left({(e^{(k)})}^{p+1}\right)=O\left({(e^{(k)})}^p\right)$$

(1)

is called the error equation. The value of p is called the order of convergence of the method.

Definition 2. 

[8] The Efficiency Index is given by

$$EI=p^{\frac{1}{d}}$$

(2)

where d is the total number of new function evaluations (the values of f and its derivatives) per iteration.

Let $x^{(k+1)}$ be determined by new information at $x^{(k)},{\varphi }_1(x^{(k)}),...,{\varphi }_{\mathrm{i}}(x^{(k)}),\mathrm{i}\ge 1$

No old information is reused. Thus,

$$x^{(k+1)}=\psi (x^{(k)},{\varphi }_1(x^{(k)}),...,{\varphi }_{\mathrm{i}}(x^{(k)}))$$

(3)

Then ψ is called a multipoint I.F without memory. Kung-Traub’s Conjecture [9]

Let ψ be an I.F. without memory with d evaluations. Then

$$p(\psi )\le p_{Opt}=2^{d-1}$$

(4)

where $p_{opt}$ is the maximum order.

The second order Newton I.F. (2^ndNR) is given by

$${\psi }_{2^{nd}NR}(x)=x-u(x),u(x)=\frac{f(x)}{f^{\prime }(x)}$$

(5)

The 2^ndNR I.F. is a 1-point I.F. with 2 functions evaluations and it satisfies the Kung-Traub conjecture with $d=2$. Thus, $E{I}_{2^{nd}NR}=1.414$. The 2-point fourth order Jarratt I.F. (4thJM) [10] is given by

$${\psi }_{4^{th}JM}(x)=x-u(x)\left(\frac{3\tau +1}{6\tau -2}\right)\tau =\frac{f^{\prime }\left[{\displaystyle x-\frac{2}{3}u(x)}\right]}{f^{\prime }(x)}$$

(6)

The 4thJM I.F. with 3 function evaluations satisfies the Kung-Traub conjecture with $d=3$.

According to Kung-Traub’s conjecture, it is not possible to obtain an I.F. with three function evaluations reaching an order greater than four. We show that this conjecture fails for quadratic functions.

We consider the quadratic function $f(x)={\kappa }_2{x}^2+{\kappa }_{1}x+{\kappa }_0$, where ${\kappa }_2\ne 0,{\kappa }_1,{\kappa }_0$ are constants. Consider the following I.F. for quadratic function:

$${\psi }_{{(r+2)}^{th}BQIM}(x)=x-u(x)H(\tau ,r)$$

(7)

where

$$H(\tau ,r)=1+\sum _{i=1}^r{a}_i{(\tau -1)}^i$$

where $a_i$’s are constants.

The error equation of the I.F. defined by Equation (7) for $r=6$ is given by

$$\begin{array}{cc}& \psi (x)-x^{*}=\left(\left(\frac{4}{3}{a}_1+1\right)c_2\right){(e^{(k)})}^2+\left(\left(-\frac{16}{3}{a}_1-\frac{16}{9}{a}_2-2\right){c_2}^2\right){(e^{(k)})}^3\hfill \\ & +\left(\left(\frac{52}{3}{a}_1+\frac{112}{9}{a}_2+\frac{64}{27}{a}_3+4\right){c_2}^3\right){(e^{(k)})}^4\hfill \\ & +\left(\left(-\frac{152}{3}{a}_1-\frac{176}{3}{a}_2-\frac{640}{27}{a}_3-\frac{256}{81}{a}_4-8\right){c_2}^4\right){(e^{(k)})}^5\hfill \\ & +\left(\left(\frac{3968}{27}{a}_3+\frac{688}{3}{a}_2+\frac{416}{3}{a}_1+\frac{3328}{81}{a}_4+16+\frac{1024}{243}{a}_5\right){c_2}^5\right){(e^{(k)})}^6\hfill \\ & +\left(\left(-\frac{1088}{3}{a}_1-800a_2-\frac{19456}{27}{a}_3-\frac{16384}{243}{a}_5-\frac{25600}{81}{a}_4-32-\frac{4096}{729}{a}_6\right){c_2}^6\right){(e^{(k)})}^7\hfill \\ & +\left(\left(64+\frac{2752}{3}{a}_1+\frac{7744}{3}{a}_2+\frac{82496}{27}{a}_3+\frac{151040}{81}{a}_4+\frac{50176}{81}{a}_5+\frac{77824}{729}{a}_6\right){c_2}^7\right){(e^{(k)})}^8+....\hfill \end{array}$$

where ${\displaystyle c_2=\frac{f^{″}(x^{*})}{f^{\prime }(x^{*})},f^{\prime }(x^{*})\ne 0}$.

Eliminating the terms in ${(e^{(k)})}^j$, $j=2,3,4,5,6,7$ we obtain a system of 6 linear equations with 6 unknowns:

$$\mathbf{A}\mathbf{X}=\mathbf{B}$$

where

$$\mathbf{A}=\left(\begin{array}{cccccc}\frac{4}{3}& 0& 0& 0& 0& 0\\ -\frac{16}{3}& -\frac{16}{9}& 0& 0& 0& 0\\ \frac{52}{3}& \frac{112}{9}& \frac{64}{27}& 0& 0& 0\\ -\frac{152}{3}& -\frac{176}{3}& -\frac{640}{27}& -\frac{256}{81}& 0& 0\\ \frac{416}{3}& \frac{688}{3}& \frac{3968}{27}& \frac{3328}{81}& \frac{1024}{243}& 0\\ -\frac{1088}{3}& -800& -\frac{19456}{27}& -\frac{25600}{81}& -\frac{16384}{243}& -\frac{4096}{729}\end{array}\right)$$

$$\mathbf{X}=\left(\begin{array}{c}{a}_1\\ a_2\\ a_3\\ a_4\\ a_5\\ a_6\end{array}\right),\mathbf{B}=\left(\begin{array}{c}-1\\ 2\\ -4\\ 8\\ -16\\ 32\end{array}\right)$$

whose solutions are given by

$$\mathbf{X}=\left(\begin{array}{c}{a}_1\\ a_2\\ a_3\\ a_4\\ a_5\\ a_6\end{array}\right)={\mathbf{A}}^{-1}\mathbf{B}=\left(\begin{array}{c}-\frac{3}{4}\\ \frac{9}{8}\\ -\frac{135}{64}\\ \frac{567}{128}\\ -\frac{5103}{512}\\ \frac{24057}{1024}\end{array}\right)$$

We note that $\mathbf{A}$ is a lower triangular matrix and the solutions are easily obtained once the first solution is obtained from the first equation.

In this way, we obtain a family of higher order I.F.s which we term as higher order 2-point Babajee’s Quadratic Iterative Methods for solving quadratic equations ($(r+2)$thBQIM).

The first six members of $(r+2)$thBQIM’s family in Equation (7) with their error equation are

• $r=1$: 2-point 3rdBQIM I.F.

  $$H(\tau ,1)=1-\frac{3}{4}(\tau -1)$$

  $${\psi }_{3^{th}BQIM}(x)-x^{*}=\left(2{c_2}^2\right){(e^{(k)})}^3+O\left({(e^{(k)})}^4\right)$$
• $r=2$: 2-point 4thBQIM I.F.

  $$H(\tau ,2)=1-\frac{3}{4}(\tau -1)+\frac{9}{8}{(\tau -1)}^2$$

  $${\psi }_{4^{th}BQIM}(x)-x^{*}=\left(5{c_2}^3\right){(e^{(k)})}^4+O\left({(e^{(k)})}^5\right)$$
• $r=3$: 2-point 5thBQIM I.F.

  $$H(\tau ,3)=1-\frac{3}{4}(\tau -1)+\frac{9}{8}{(\tau -1)}^2-\frac{135}{64}{(\tau -1)}^3$$

  $${\psi }_{5^{th}BQIM}(x)-x^{*}=\left(14{c_2}^4\right){(e^{(k)})}^5+O\left({(e^{(k)})}^6\right)$$
• $r=4$: 2-point 6thBQIM I.F.

  $$H(\tau ,4)=1-\frac{3}{4}(\tau -1)+\frac{9}{8}{(\tau -1)}^2-\frac{135}{64}{(\tau -1)}^3+\frac{567}{128}{(\tau -1)}^4$$

  $${\psi }_{6^{th}BQIM}(x)-x^{*}=\left(42{c_2}^5\right){(e^{(k)})}^6+O\left({(e^{(k)})}^7\right)$$
• $r=5$: 2-point 7thBQIM I.F.

  $$H(\tau ,5)=1-\frac{3}{4}(\tau -1)+\frac{9}{8}{(\tau -1)}^2-\frac{135}{64}{(\tau -1)}^3+\frac{567}{128}{(\tau -1)}^4-\frac{5103}{512}{(\tau -1)}^5$$

  $${\psi }_{7^{th}BQIM}(x)-x^{*}=\left(132{c_2}^6\right){(e^{(k)})}^7+O\left({(e^{(k)})}^8\right)$$
• $r=6$: 2-point 8thBQIM I.F.

  $$H(\tau ,6)=1-\frac{3}{4}(\tau -1)+\frac{9}{8}{(\tau -1)}^2-\frac{135}{64}{(\tau -1)}^3+\frac{567}{128}{(\tau -1)}^4-\frac{5103}{512}{(\tau -1)}^5+\frac{24057}{1024}{(\tau -1)}^6$$

  $${\psi }_{8^{th}BQIM}(x)-x^{*}=\left(429{c_2}^7\right){(e^{(k)})}^8+O\left({(e^{(k)})}^9\right)$$

We note that the maximum order reached by optimal methods with four function evaluations is eight. We have obtained an eighth order 2-point method with only three function evaluations for solving quadratic equations. This implies that the Kung-Traub conjecture fails for quadratic equations.

3. Convergence Analysis

Theorem 3. 

Let a sufficiently smooth function $f:D\subset \mathbb{R}\to \mathbb{R}$ has a simple root $x^{*}$ in the open interval D. Then the six members of 2-point$(r+2)$thBQIM’s family in Equation (7) ($r=1,2,3,4,5,6$) are of local 3rd to 8th order convergence, respectively.

Proof. 

We will prove the 3rd order convergence of the 2-point 3rdBQIM I.F. and 8th order convergence of the 2-point 8thBQIM I.F.

The proofs for the 2-point 4th to 7th order I.F.s follow on similar lines.

It is easy to see that for a quadratic function,

$$f(x)=f^{\prime }(x^{*})\left[e^{(k)}+c_2{(e^{(k)})}^2\right]$$

and

$$f^{\prime }(x)=f^{\prime }(x^{*})\left[1+2c_2{e}^{(k)}\right]$$

By Taylor expansion and using computer algebra software as Maple

$$\begin{array}{cc}\hfill u(x)& =e^{(k)}-c_2{(e^{(k)})}^2+2{c_2}^2{(e^{(k)})}^3-4{c_2}^3{(e^{(k)})}^4+8{c_2}^4{(e^{(k)})}^5-16{c_2}^5{(e^{(k)})}^6\hfill \\ & +32{c_2}^6{(e^{(k)})}^7-64{c_2}^7{(e^{(k)})}^8+128{c_2}^8{(e^{(k)})}^9+...\hfill \end{array}$$

(8)

so that

$$\begin{array}{cc}\hfill \tau & =1-\frac{4}{3}{c}_2{e}^{(k)}+4{c_2}^2{(e^{(k)})}^2-\frac{32}{3}{c_2}^3{(e^{(k)})}^3+\frac{80}{3}{c_2}^4{(e^{(k)})}^4-64{c_2}^5{(e^{(k)})}^5+\frac{448}{3}{c_2}^6{(e^{(k)})}^6\hfill \\ & -\frac{1024}{3}{c_2}^7{(e^{(k)})}^7+768{c_2}^8{(e^{(k)})}^8+...\hfill \end{array}$$

(9)

Now,

$$\begin{array}{cc}\hfill H(\tau ,1)& =1+c_2{e}^{(k)}-3{c_2}^2{(e^{(k)})}^2+8{c_2}^3{(e^{(k)})}^3+...\hfill \end{array}$$

(10)

Using Equations (8) and (10), we have

$$u(x)H(\tau ,1)=e^{(k)}-2{c_2}^2{(e^{(k)})}^3+O\left({(e^{(k)})}^4\right)$$

which leads to the error equation for the 2-point 3rdBQIM I.F.

Similarly,

$$\begin{array}{cc}\hfill H(\tau ,6)& =1+c_2{e}^{(k)}-{c_2}^2{(e^{(k)})}^2+{c_2}^3{(e^{(k)})}^3-{c_2}^4{(e^{(k)})}^4+{c_2}^5{(e^{(k)})}^5-{c_2}^6{(e^{(k)})}^6-428{c_2}^7{(e^{(k)})}^7+...\hfill \end{array}$$

(11)

Using Equations (8) and (11), we have

$$u(x)H(\tau ,6)=e^{(k)}-429{c_2}^7{(e^{(k)})}^8+O\left({(e^{(k)})}^9\right)$$

which leads to the error equation for the 2-point 8thBQIM I.F.

☐

We next prove the local convergence of the 2-point $(r+2)$thBQIM’s family for any r.

Theorem 4. 

Let a sufficiently smooth function $f:D\subset \mathbb{R}\to \mathbb{R}$ has a simple root $x^{*}$ in the open interval D. Then the members of 2-point$(r+2)$thBQIM’s family in Equation (7) are of local $(r+2)$th order convergence.

Proof. 

We prove this result by induction.

The case $r=1$ corresponds to the 3rdBQIM I.F.

Assume the 2-point $(r+2)$thBQIM family has order of convergence of $(r+2)$. Then it satisfies the error equation

$${\psi }_{{(r+2)}^{th}BQIM}(x)-x^{*}=C_r{c_2}^{r+1}{(e^{(k)})}^{r+2}+O\left({(e^{(k)})}^{r+3}\right)$$

(12)

where $C_r$ is the asymptotic error constant.

Assume that Equation (12) holds for $r=m$.

Now from Equation (9), we have

$$\tau -1=-\frac{4}{3}{c}_2{e}^{(k)}\left(1-3c_2{e}^{(k)}+8{c_2}^2{(e^{(k)})}^2+...\right)$$

so that

$$\begin{array}{ccc}\hfill {(\tau -1)}^{m+1}& =& {\left(-\frac{4}{3}\right)}^{m+1}{c_2}^{m+1}{(e^{(k)})}^{m+1}{\left(1-3c_2{e}^{(k)}+8{c_2}^2{(e^{(k)})}^2+...\right)}^{m+1}\hfill \\ & =& {\left(-\frac{4}{3}\right)}^{m+1}{c_2}^{m+1}{(e^{(k)})}^{m+1}\left(1+O\left(e^{(k)}\right)\right)\hfill \end{array}$$

(13)

For the case $r=m+1$,

$$\begin{array}{cc}& {\psi }_{{(m+3)}^{th}BQIM}(x)-x^{*}\hfill \\ & =x-u(x)H(\tau ,m+1)-x^{*}\hfill \\ & =x-u(x)H(\tau ,m)-x^{*}-a_{m+1}u(x){(\tau -1)}^{m+1}\hfill \\ & ={\psi }_{{(m+2)}^{th}BQIM}(x)-x^{*}-a_{m+1}u(x){(\tau -1)}^{m+1}\hfill \\ & =C_m{c_2}^{m+1}{(e^{(k)})}^{m+2}-a_{m+1}{\left(-\frac{4}{3}\right)}^{m+1}{c_2}^{m+1}{(e^{(k)})}^{m+2}+O\left({(e^{(k)})}^{m+3}\right)\text{using Equations (8), (12) and (13)}\hfill \\ & =\left(C_m-a_{m+1}{\left(-\frac{4}{3}\right)}^{m+1}\right){c_2}^{m+1}{(e^{(k)})}^{m+2}+O\left({(e^{(k)})}^{m+3}\right)\hfill \end{array}$$

which shows that the 2-point $(m+3)$thBQIM family has $(m+3)$th order of convergence if we choose

$$a_{m+1}=C_m{\left(-\frac{3}{4}\right)}^{m+1}$$

(14)

☐

From Equation (14), we can obtain higher order I.F. if we know the asymptotic error constant of the previous I.F.

For example, for the 2-point 3rdBQIM I.F., $C_1=2$ and from Equation (14),

$${\displaystyle a_2=C_1{\left(-\frac{3}{4}\right)}^2=\frac{9}{8}}$$

and we can obtain the 4thBQIM I.F.

Similarly, for the 2-point 8thBQIM I.F., ${\displaystyle C_6=429}$ and from Equation (14),

$${\displaystyle a_7=C_6{\left(-\frac{3}{4}\right)}^7=-\frac{938223}{16384}}$$

and we can obtain the 2-point 9thBQIM I.F. with

$$\begin{array}{cc}\hfill H(\tau ,7)& =1-\frac{3}{4}(\tau -1)+\frac{9}{8}{(\tau -1)}^2-\frac{135}{64}{(\tau -1)}^3+\frac{567}{128}{(\tau -1)}^4-\frac{5103}{512}{(\tau -1)}^5\hfill \\ & +\frac{24057}{1024}{(\tau -1)}^6-\frac{938223}{16384}{(\tau -1)}^7\hfill \end{array}$$

From Theorem 4, we conclude that we can have a family of order $r+2$, $r=1,2,...$ with only 3 function evaluations.

The Efficiency Index of the 2-point $(r+2)$thBQIM family is given by

$$EI={(r+2)}^{\frac{1}{3}},r\ge 1$$

(15)

In the following section, we extend our methods to systems of equations.

4. Extension to Systems of Equations

Consider the system of nonlinear equations $\mathbf{f}(\mathbf{x})=\mathbf{0},$ where $\mathbf{f}(\mathbf{x})={(f_1(\mathbf{x}),f_2(\mathbf{x}),...,f_n(\mathbf{x}))}^T$, $\mathbf{x}={(x_1,x_2,...,x_n)}^T$, $f_i:{\mathbb{R}}^n\to \mathbb{R},\forall i=1,2,\dots ,n$ defined as

$$f_i(\mathbf{x})=b_i+\sum _{l=1}^n\sum _{m=1}^n{b}_{l,m}{x}_l{x}_m,b_i,b_{l,m},i,l,m=1,..n,\text{are}\text{constants}.$$

and $\mathbf{f}:\mathbf{D}\subset {\mathbb{R}}^n\to {\mathbb{R}}^n$ is a smooth map and $\mathbf{D}$ is an open and convex set, where we assume that ${\mathbf{x}}^{*}={(x_1^{*},x_2^{*},...,x_n^{*})}^T$ is a zero of the system and ${\mathbf{x}}^{(0)}={\left(x_1^{(0)},x_2^{(0)},...,x_n^{(0)}\right)}^T$ is an initial guess sufficiently close to ${\mathbf{x}}^{*}$.

We define the 2-point $(r+2)$thBQIM’s family for systems of quadratic equations as:

$${\psi }_{{(r+2)}^{th}BQIM}(\mathbf{x})=\mathbf{x}-\mathbf{H}(\tau (\mathbf{x}),r)\mathbf{u}(\mathbf{x})$$

(16)

where

$$\begin{array}{cc}\hfill \mathbf{u}(\mathbf{x})& ={\mathbf{f}}^{\prime }{(\mathbf{x})}^{-1}\mathbf{f}(\mathbf{x})\hfill \\ \hfill \mathbf{y}(\mathbf{x})& =\mathbf{x}-\frac{2}{3}\mathbf{u}(\mathbf{x})\hfill \\ \hfill \tau (\mathbf{x})& ={\mathbf{f}}^{\prime }{(\mathbf{x})}^{-1}{\mathbf{f}}^{\prime }\left(\mathbf{y}(\mathbf{x})\right)\hfill \\ \hfill \mathbf{H}(\tau (\mathbf{x}),r)& =\mathbf{I}+\sum _{i=1}^r{a}_i{(\tau (\mathbf{x})-\mathbf{I})}^i,\mathbf{I}\text{is}\text{the}\text{identity}\text{matrix.}\hfill \end{array}$$

Let us define

$${\mathbf{c}}_2=\frac{1}{2}{\left[{\mathbf{f}}^{\prime }({\mathbf{x}}^{*})\right]}^{-1}{\mathbf{f}}^{(2)}({\mathbf{x}}^{*}),{\mathbf{e}}^{(k)}={\mathbf{x}}^{(k)}-{\mathbf{x}}^{*}$$

Using the notations in [11], it is noted that ${\mathbf{c}}_2{\mathbf{e}}^{(k)}\in \mathcal{L}({\mathbb{R}}^n)$.

The error at the $(k+1)$th iteration is ${\mathbf{e}}^{(k+1)}=\mathbf{L}{({\mathbf{e}}^{(k)})}^p+O\left({({\mathbf{e}}^{(k)})}^{p+1}\right)$, where $\mathbf{L}$ is a p-linear function $\mathbf{L}\in \mathcal{L}({\mathbb{R}}^n\times \cdots \times {\mathbb{R}}^n,{\mathbb{R}}^n)$, is called the error equation and p is the order of convergence.

Observe that ${({\mathbf{e}}^{(k)})}^p$ is $({\mathbf{e}}^{(k)},{\mathbf{e}}^{(k)},\cdots ,{\mathbf{e}}^{(k)})$.

The first six members of $(r+2)$thBQIM’s family in Equation (16) with their error equation are

• $r=1$: 2-point 3rdBQIM I.F.

  $$H(\tau (\mathbf{x}),1)=\mathbf{I}-\frac{3}{4}(\tau (\mathbf{x})-\mathbf{I})$$

  $${\psi }_{3^{th}BQIM}(\mathbf{x})-{\mathbf{x}}^{*}=\left(2{{\mathbf{c}}_2}^2\right){({\mathbf{e}}^{(k)})}^3+O\left({({\mathbf{e}}^{(k)})}^4\right)$$
• $r=2$: 2-point 4thBQIM I.F.

  $$H(\tau (\mathbf{x}),2)=\mathbf{I}-\frac{3}{4}(\tau (\mathbf{x})-\mathbf{I})+\frac{9}{8}{(\tau (\mathbf{x})-\mathbf{I})}^2$$

  $${\psi }_{4^{th}BQIM}(\mathbf{x})-{\mathbf{x}}^{*}=\left(5{{\mathbf{c}}_2}^3\right){({\mathbf{e}}^{(k)})}^4+O\left({({\mathbf{e}}^{(k)})}^5\right)$$
• $r=3$: 2-point 5thBQIM I.F.

  $$H(\tau (\mathbf{x}),3)=\mathbf{I}-\frac{3}{4}(\tau (\mathbf{x})-\mathbf{I})+\frac{9}{8}{(\tau (\mathbf{x})-\mathbf{I})}^2-\frac{135}{64}{(\tau (\mathbf{x})-\mathbf{I})}^3$$

  $${\psi }_{5^{th}BQIM}(\mathbf{x})-{\mathbf{x}}^{*}=\left(14{{\mathbf{c}}_2}^4\right){({\mathbf{e}}^{(k)})}^5+O\left({({\mathbf{e}}^{(k)})}^6\right)$$
• $r=4$: 2-point 6thBQIM I.F.

  $$H(\tau (\mathbf{x}),4)=\mathbf{I}-\frac{3}{4}(\tau (\mathbf{x})-\mathbf{I})+\frac{9}{8}{(\tau (\mathbf{x})-\mathbf{I})}^2-\frac{135}{64}{(\tau (\mathbf{x})-\mathbf{I})}^3+\frac{567}{128}{(\tau (\mathbf{x})-\mathbf{I})}^4$$

  $${\psi }_{6^{th}BQIM}(\mathbf{x})-{\mathbf{x}}^{*}=\left(42{{\mathbf{c}}_2}^5\right){({\mathbf{e}}^{(k)})}^6+O\left({({\mathbf{e}}^{(k)})}^7\right)$$
• $r=5$: 2-point 7thBQIM I.F.

  $$H(\tau (\mathbf{x}),5)=\mathbf{I}-\frac{3}{4}(\tau (\mathbf{x})-\mathbf{I})+\frac{9}{8}{(\tau (\mathbf{x})-\mathbf{I})}^2-\frac{135}{64}{(\tau (\mathbf{x})-\mathbf{I})}^3+\frac{567}{128}{(\tau (\mathbf{x})-\mathbf{I})}^4-\frac{5103}{512}{(\tau (\mathbf{x})-\mathbf{I})}^5$$

  $${\psi }_{7^{th}BQIM}(\mathbf{x})-{\mathbf{x}}^{*}=\left(132{{\mathbf{c}}_2}^6\right){({\mathbf{e}}^{(k)})}^7+O\left({({\mathbf{e}}^{(k)})}^8\right)$$
• $r=6$: 2-point 8thBQIM I.F.

  $$\begin{array}{cc}\hfill \mathbf{H}(\tau (\mathbf{x}),6)& =\mathbf{I}-\frac{3}{4}(\tau (\mathbf{x})-\mathbf{I})+\frac{9}{8}{(\tau (\mathbf{x})-\mathbf{I})}^2-\frac{135}{64}{(\tau (\mathbf{x})-\mathbf{I})}^3+\frac{567}{128}{(\tau (\mathbf{x})-\mathbf{I})}^4\hfill \\ & -\frac{5103}{512}{(\tau (\mathbf{x})-\mathbf{I})}^5+\frac{24057}{1024}{(\tau (\mathbf{x})-\mathbf{I})}^6\hfill \end{array}$$

  $${\psi }_{8^{th}BQIM}(\mathbf{x})-{\mathbf{x}}^{*}=\left(429{{\mathbf{c}}_2}^7\right){({\mathbf{e}}^{(k)})}^8+O\left({({\mathbf{e}}^{(k)})}^9\right)$$

4.1. Convergence Analysis

Theorem 5. 

Let $\mathbf{f}:\mathbf{D}\subseteq {\mathbb{R}}^n⟶{\mathbb{R}}^n$ be twice Frechet differentiable at each point of an open convex neighborhood $\mathbf{D}$ of ${\mathbf{x}}^{*}\in {\mathbb{R}}^n$, that is a solution of the quadratic system $\mathbf{f}(\mathbf{x})=\mathbf{0}$. Let us suppose that ${\mathbf{f}}^{\prime }(\mathbf{x})$ is continuous and nonsingular in ${\mathbf{x}}^{*}$, and ${\mathbf{x}}^{(0)}$ is close enough to ${\mathbf{x}}^{*}$. Then the sequence ${\left\{{\mathbf{x}}^{(k)}\right\}}_{k\ge 0}$ obtained using the iterative expressions Equation (16), $r=1,2,...,6$ converge to ${\mathbf{x}}^{*}$ with order 3 to 8, respectively.

Proof. 

We will prove for the case $r=6$. The other cases follow along similar lines. Since $\mathbf{f}$ is a quadratic function of several variables, we have

$$\mathbf{f}({\mathbf{x}}^{(k)})={\mathbf{f}}^{\prime }({\mathbf{x}}^{*})\left[{\mathbf{e}}^{(k)}+{\mathbf{c}}_2{({\mathbf{e}}^{(k)})}^2\right]$$

(17)

and

$${\mathbf{f}}^{\prime }({\mathbf{x}}^{(k)})={\mathbf{f}}^{\prime }({\mathbf{x}}^{*})\left[\mathbf{I}+2{\mathbf{c}}_2{\mathbf{e}}^{(k)}\right]$$

(18)

$$\begin{array}{cc}\hfill {\mathbf{f}}^{\prime }{({\mathbf{x}}^{(k)})}^{-1}& =[\mathbf{I}-2{\mathbf{c}}_2{\mathbf{e}}^{(k)}+4{{\mathbf{c}}_2}^2{({\mathbf{e}}^{(k)})}^2-8{{\mathbf{c}}_2}^3{({\mathbf{e}}^{(k)})}^3+16{{\mathbf{c}}_2}^4{({\mathbf{e}}^{(k)})}^4-32{{\mathbf{c}}_2}^5{({\mathbf{e}}^{(k)})}^5\hfill \\ & +64{{\mathbf{c}}_2}^6{({\mathbf{e}}^{(k)})}^6-128{{\mathbf{c}}_2}^7{({\mathbf{e}}^{(k)})}^7+256{{\mathbf{c}}_2}^8{({\mathbf{e}}^{(k)})}^8...]{\left[{\mathbf{f}}^{\prime }({\mathbf{x}}^{*})\right]}^{-1}\hfill \end{array}$$

(19)

Using Equations (17) and (19), we have

$$\begin{array}{cc}\hfill \mathbf{u}({\mathbf{x}}^{(k)})& ={\mathbf{e}}^{(k)}-{\mathbf{c}}_2{({\mathbf{e}}^{(k)})}^2+2{{\mathbf{c}}_2}^2{({\mathbf{e}}^{(k)})}^3-4{{\mathbf{c}}_2}^3{({\mathbf{e}}^{(k)})}^4+8{{\mathbf{c}}_2}^4{({\mathbf{e}}^{(k)})}^5-16{{\mathbf{c}}_2}^5{({\mathbf{e}}^{(k)})}^6\hfill \\ & +32{{\mathbf{c}}_2}^6{({\mathbf{e}}^{(k)})}^7-64{{\mathbf{c}}_2}^7{({\mathbf{e}}^{(k)})}^8+...\hfill \end{array}$$

(20)

and the expression for $\mathbf{y}({\mathbf{x}}^{(k)})$ is given by

$$\begin{array}{cc}\hfill \mathbf{y}({\mathbf{x}}^{(k)})& ={\mathbf{x}}^{*}+\frac{1}{3}{\mathbf{e}}^{(k)}+\frac{2}{3}{\mathbf{c}}_2{({\mathbf{e}}^{(k)})}^2-\frac{4}{3}{{\mathbf{c}}_2}^2{({\mathbf{e}}^{(k)})}^3+\frac{8}{3}{{\mathbf{c}}_2}^3{({\mathbf{e}}^{(k)})}^4-\frac{16}{3}{{\mathbf{c}}_2}^4{({\mathbf{e}}^{(k)})}^5+\frac{32}{3}{{\mathbf{c}}_2}^5{({\mathbf{e}}^{(k)})}^6\hfill \\ & -\frac{64}{3}{{\mathbf{c}}_2}^6{({\mathbf{e}}^{(k)})}^7+\frac{128}{3}{{\mathbf{c}}_2}^7{({\mathbf{e}}^{(k)})}^8+....\hfill \end{array}$$

The Taylor expansion of Jacobian matrix ${\mathbf{f}}^{\prime }(\mathbf{y}({\mathbf{x}}^{(k)}))$ is then given by

$$\begin{array}{cc}\hfill {\mathbf{f}}^{\prime }(\mathbf{y}({\mathbf{x}}^{(k)}))& ={\mathbf{f}}^{\prime }({\mathbf{x}}^{*})\left[\mathbf{I}+2{\mathbf{c}}_2(\mathbf{y}({\mathbf{x}}^{(k)})-{\mathbf{x}}^{*})\right]\hfill \\ & ={\mathbf{f}}^{\prime }({\mathbf{x}}^{*})[\mathbf{I}+\frac{2}{3}{\mathbf{c}}_2({\mathbf{e}}^{(k)})+\frac{4}{3}{{\mathbf{c}}_2}^2{({\mathbf{e}}^{(k)})}^2-\frac{8}{3}{{\mathbf{c}}_2}^3{({\mathbf{e}}^{(k)})}^3+\frac{16}{3}{{\mathbf{c}}_2}^4{({\mathbf{e}}^{(k)})}^4-\frac{32}{3}{{\mathbf{c}}_2}^5{({\mathbf{e}}^{(k)})}^5\hfill \\ & +\frac{64}{3}{{\mathbf{c}}_2}^6{({\mathbf{e}}^{(k)})}^6-\frac{128}{3}{{\mathbf{c}}_2}^7{({\mathbf{e}}^{(k)})}^7+\frac{256}{3}{{\mathbf{c}}_2}^8{({\mathbf{e}}^{(k)})}^8+....]\hfill \end{array}$$

Therefore, using Equation (19), we obtain

$$\begin{array}{cc}\hfill \tau ({\mathbf{x}}^{(k)})& ={\left[{\mathbf{f}}^{\prime }({\mathbf{x}}^{(k)})\right]}^{-1}{\mathbf{f}}^{\prime }(\mathbf{y}({\mathbf{x}}^{(k)}))\hfill \\ & =\mathbf{I}-\frac{4}{3}{\mathbf{c}}_2({\mathbf{e}}^{(k)})+4{{\mathbf{c}}_2}^2{({\mathbf{e}}^{(k)})}^2-\frac{32}{3}{{\mathbf{c}}_2}^3{({\mathbf{e}}^{(k)})}^3+\frac{80}{3}{{\mathbf{c}}_2}^4{({\mathbf{e}}^{(k)})}^4-64{{\mathbf{c}}_2}^5{({\mathbf{e}}^{(k)})}^5\hfill \\ & +\frac{448}{3}{{\mathbf{c}}_2}^6{({\mathbf{e}}^{(k)})}^6-\frac{1024}{3}{{\mathbf{c}}_2}^7{({\mathbf{e}}^{(k)})}^7+768{{\mathbf{c}}_2}^8{({\mathbf{e}}^{(k)})}^8+....\hfill \end{array}$$

so that

$$\begin{array}{cc}\hfill \mathbf{H}(\tau (\mathbf{x}),6)& =\mathbf{I}+{\mathbf{c}}_2({\mathbf{e}}^{(k)})-{{\mathbf{c}}_2}^2{({\mathbf{e}}^{(k)})}^2+{{\mathbf{c}}_2}^3{({\mathbf{e}}^{(k)})}^3-{{\mathbf{c}}_2}^4{({\mathbf{e}}^{(k)})}^4+{{\mathbf{c}}_2}^5{({\mathbf{e}}^{(k)})}^5\hfill \\ & -{{\mathbf{c}}_2}^6{({\mathbf{e}}^{(k)})}^6-428{{\mathbf{c}}_2}^7{({\mathbf{e}}^{(k)})}^7+.....\hfill \end{array}$$

(21)

Using Equations (20) and (21), we have, after simplifications,

$$\mathbf{H}(\tau (\mathbf{x}),6)\mathbf{u}({\mathbf{x}}^{(k)})={\mathbf{e}}^{(k)}-429{{\mathbf{c}}_2}^7{({\mathbf{e}}^{(k)})}^8+...$$

and, thus,

$$\begin{array}{cc}\hfill \mathbf{x}-\mathbf{H}(\tau (\mathbf{x}),6)\mathbf{u}({\mathbf{x}}^{(k)})& ={\mathbf{x}}^{*}+{\mathbf{e}}^{(k)}-({\mathbf{e}}^{(k)}-429{{\mathbf{c}}_2}^7{({\mathbf{e}}^{(k)})}^8+...)\hfill \\ & ={\mathbf{x}}^{*}+429{{\mathbf{c}}_2}^7{({\mathbf{e}}^{(k)})}^8+...\hfill \end{array}$$

☐

Theorem 6. 

Let $\mathbf{f}:\mathbf{D}\subseteq {\mathbb{R}}^n⟶{\mathbb{R}}^n$ be twice Frechet differentiable at each point of an open convex neighborhood $\mathbf{D}$ of ${\mathbf{x}}^{*}\in {\mathbb{R}}^n$, that is a solution of the quadratic system $\mathbf{f}(\mathbf{x})=\mathbf{0}$. Let us suppose that ${\mathbf{f}}^{\prime }(\mathbf{x})$ is continuous and nonsingular in ${\mathbf{x}}^{*}$, and ${\mathbf{x}}^{(0)}$ is close enough to ${\mathbf{x}}^{*}$. Then the sequence ${\left\{{\mathbf{x}}^{(k)}\right\}}_{k\ge 0}$ obtained using the iterative expressions Equation (16), $r=1,2,...$ converges to ${\mathbf{x}}^{*}$ with order $r+2$ with the error equation

$${\psi }_{{(r+2)}^{th}BQIM}(\mathbf{x})-{\mathbf{x}}^{*}=C_r{{\mathbf{c}}_2}^{r+1}{({\mathbf{e}}^{(k)})}^{r+2}+...$$

(22)

The proof is by induction and follows along similar lines.

Similarly as in the case of scalar equations, we can obtain higher order I.F. for systems if we know the asymptotic error constant of the previous I.F. using

$$a_{r+1}=C_r{\left(-\frac{3}{4}\right)}^{r+1},r=1,2,...$$

5. Numerical Experiments

5.1. Scalar Equation

We consider the Test problem 1 (TP1) of finding the positive zero of the quadratic function $f(x)=x^2-2$ to compare the efficiency of the proposed methods. Numerical computations have been carried out in the MATLAB software rounding to 1000 significant digits. Depending on the precision of the computer, we use the stopping criteria for the iterative process $|x^{(k+1)}-x^{(k)}|<ϵ$ where $ϵ={10}^{-50}$. Let N be the number of iterations required for convergence. For simplicity, we denote $Xe-Y=X\times {10}^{-Y}$.

The computational order of convergence is given by

$$\rho =\frac{ln|(x^{(N)}-x^{(N-1)}/(x^{(N-1)}-x^{(N-2)})|}{ln|(x^{(N-1)}-x^{(N-2)})/(x^{(N-2)}-x^{(N-3)})|}$$

We choose $x^{(0)}=1$. The results in Table 1 show that, as the order of the $(r+2)$thBQIM I.F. (r = 1,2,3,4,5,6), the methods converge in less iterations. The computational order of convergence agree with the theoretical order of convergence confirming that Kung-Traub’s conjecture fails for quadratic functions.

Table 1. Results of the quadratic function $f(x)=x^2-2$ for the 3rdBQIM, 4thBQIM, 5thBQIM, 6thBQIM, 7thBQIM and 8thBQIM I.F.s.

Error	3$\mathit{rd}$$\mathit{BQIM}$	4$\mathit{th}$$\mathit{BQIM}$	5$\mathit{th}$$\mathit{BQIM}$	6$\mathit{th}$$\mathit{BQIM}$	7$\mathit{th}$$\mathit{BQIM}$	8$\mathit{th}$$\mathit{BQIM}$
$|x_1-x_0|$	5.6e−1	5.8e−1	5.8e−1	5.8e−1	5.9e−1	5.9e−1
$|x_2-x_1|$	2.3e−2	7.7e−3	2.8e−3	1.1e−3	4.3e-4	1.8e−4
$|x_3-x_2|$	3.0e−6	7.5e−10	3.6e−14	3.5e−19	6.9e−25	2.9e−31
$|x_4-x_3|$	7.0e−18	6.9e−38	1.3e−68	4.0e−112	1.8e−170	1.3e−245
$|x_5-x_4|$	8.7e−53	4.9e−150	-	-	-	-
$|x_6-x_5|$	-	-	-	-	-	-
ρ	3	4	5	6	7	8

Table 1. Results of the quadratic function $f(x)=x^2-2$ for the 3rdBQIM, 4thBQIM, 5thBQIM, 6thBQIM, 7thBQIM and 8thBQIM I.F.s.

Error	3$\mathit{rd}$$\mathit{BQIM}$	4$\mathit{th}$$\mathit{BQIM}$	5$\mathit{th}$$\mathit{BQIM}$	6$\mathit{th}$$\mathit{BQIM}$	7$\mathit{th}$$\mathit{BQIM}$	8$\mathit{th}$$\mathit{BQIM}$
$|x_1-x_0|$	5.6e−1	5.8e−1	5.8e−1	5.8e−1	5.9e−1	5.9e−1
$|x_2-x_1|$	2.3e−2	7.7e−3	2.8e−3	1.1e−3	4.3e-4	1.8e−4
$|x_3-x_2|$	3.0e−6	7.5e−10	3.6e−14	3.5e−19	6.9e−25	2.9e−31
$|x_4-x_3|$	7.0e−18	6.9e−38	1.3e−68	4.0e−112	1.8e−170	1.3e−245
$|x_5-x_4|$	8.7e−53	4.9e−150	-	-	-	-
$|x_6-x_5|$	-	-	-	-	-	-
ρ	3	4	5	6	7	8

5.2. Dynamic Behaviour in the Complex Plane

Consider our Test problem 2 (TP2) based on the quadratic function $f(z)=z^2-1$ where z is a complex number. We let $z_1^{*}=-1$ and $z_2^{*}=1$ which are the roots of unity for $f(z)=z^2-1$. We study the dynamic behaviour of higher order $(r+2)$thBQIM I.F.s ($r=1,2,3,4,5,6$). We take a square $\mathbb{R}\times \mathbb{R}=[-2,2]\times [-2,2]$ of $256\times 256$ points and we apply our iterative methods starting in every $z^{(0)}$ in the square. If the sequence generated by the iterative method attempts a zero $z_j^{*}$ of the polynomial with a tolerance $|f(z^{(k)})|<1e-4$ and a maximum of 100 iterations, we decide that $z^{(0)}$ is in the basin of attraction of this zero.

If the iterative method starting in $z^{(0)}$ reaches a zero in N iterations ($N\le 100$), then we mark this point $z^{(0)}$ with a blue color if $|z^{(N)}-z_1^{*}|<1e-4$ or green color if $|z^{(N)}-z_2^{*}|<1e-4$. If $N>100,$ we conclude that the starting point has diverged and we assign a dark blue color. Let $N_D$ be number of diverging points and we count the number of starting points which converge in 1, 2, 3, 4, 5 or above 5 iterations.

Table 2 shows that all 6 methods are globally convergent and as the order of the method increases, the number of starting points converging to a root in 1 or 2 iterations increases. This is the advantage of higher order methods.

Table 2. Results of the quadratic function $f(z)=z^2-1$ for the 3rdBQIM, 4thBQIM, 5thBQIM, 6thBQIM, 7thBQIM and 8thBQIM I.F.s.

I.F.	$N=1$	$N=2$	$N=3$	$N=4$	$N=5$	$N>5$	$N_D$
3rdBQIM	56	6536	28,736	16,240	5428	8540	0
4thBQIM	232	16,908	27,532	7780	3700	9564	0
5thBQIM	528	23,348	23,196	5928	3340	9196	0
6thBQIM	928	27,880	19,680	5272	3072	8704	0
7thBQIM	1392	31,304	16,736	4856	2864	8394	0
8thBQIM	1892	33,924	14,220	4564	2788	8184	0

Table 2. Results of the quadratic function $f(z)=z^2-1$ for the 3rdBQIM, 4thBQIM, 5thBQIM, 6thBQIM, 7thBQIM and 8thBQIM I.F.s.

I.F.	$N=1$	$N=2$	$N=3$	$N=4$	$N=5$	$N>5$	$N_D$
3rdBQIM	56	6536	28,736	16,240	5428	8540	0
4thBQIM	232	16,908	27,532	7780	3700	9564	0
5thBQIM	528	23,348	23,196	5928	3340	9196	0
6thBQIM	928	27,880	19,680	5272	3072	8704	0
7thBQIM	1392	31,304	16,736	4856	2864	8394	0
8thBQIM	1892	33,924	14,220	4564	2788	8184	0

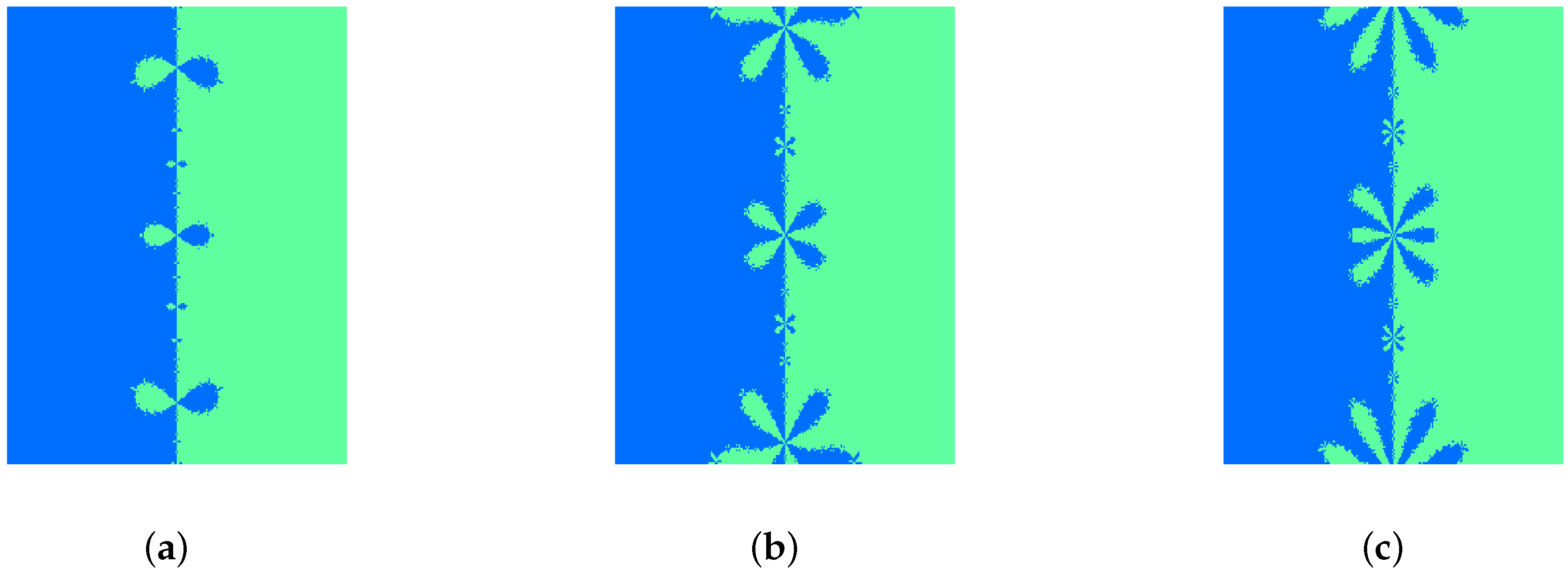
Figure 1. Polynomiographs of 3rdBQIM, 4thBQIM and 5thBQIM I.F.s. for $f(z)=z^2-1$. (a) 3rdBQIM; (b) 4thBQIM; (c) 5thBQIM.

Figure 1. Polynomiographs of 3rdBQIM, 4thBQIM and 5thBQIM I.F.s. for $f(z)=z^2-1$. (a) 3rdBQIM; (b) 4thBQIM; (c) 5thBQIM.

Bahman Kalantari coined the term “polynomiography” to be the art and science of visualization in the approximation of roots of polynomial using I.F. [12]. Figure 1 and Figure 2 show the polynomiography of the six methods. It can be observed as the order of the method increases, the methods behave more chaotically (the size of the “petals” become larger).

Figure 2. Polynomiographs of 6thBQIM, 7thBQIM and 8thBQIM I.F.s. for $f(z)=z^2-1$. (a) 6thBQIM; (b) 7thBQIM; (c) 8thBQIM.

Figure 2. Polynomiographs of 6thBQIM, 7thBQIM and 8thBQIM I.F.s. for $f(z)=z^2-1$. (a) 6thBQIM; (b) 7thBQIM; (c) 8thBQIM.

5.3. Systems of Quadratic Equations

For our numerical experiments in this section, the approximate solutions are calculated correct to 1000 digits by using variable precision arithmetic in MATLAB. We use the following stopping criterion for the numerical scheme:

$$\parallel {\mathbf{x}}^{(k+1)}-{\mathbf{x}}^{(k)}{\parallel }_2<1e-50$$

(23)

For a system of equations, we used the approximated computational order of convergence $p_c$ given by (see [13])

$$p_c\approx \frac{log(\parallel {\mathbf{x}}^{(k+1)}-{\mathbf{x}}^{(k)}{\parallel }_2/\parallel {\mathbf{x}}^{(k)}-{\mathbf{x}}^{(k-1)}{\parallel }_2)}{log(\parallel {\mathbf{x}}^{(k)}-{\mathbf{x}}^{(k-1)}{\parallel }_2/\parallel {\mathbf{x}}^{(k-1)}-{\mathbf{x}}^{(k-2)}{\parallel }_2)}$$

(24)

We consider the Test Problem 3 (TP3) which is a system of 2 equations:

$$\begin{array}{c}{x}_1^2+x_2^2-7=0\hfill \\ x_1-x_2+1=0\hfill \end{array}$$

(25)

Using the substitution method, Equation (25) reduces to the quadratic equation $x_2^2-x_2-3=0$ whose positive root is given by ${\displaystyle x_2^{*}=\frac{1+\sqrt{13}}{2}=2.302775638..}$ Therefore ${\displaystyle x_1^{*}=x_2^{*}-1=\frac{\sqrt{13}}{2}=1.302775638..}$

We use ${\mathbf{x}}^{(0)}={(1,2)}^T$ as starting vector and apply our Equation (16), $r=1,2,...,6$ to calculate the approximate solutions of Equation (25).

Table 3. Results of the TP3 for the 3rdBQIM, 4thBQIM, 5thBQIM, 6thBQIM, 7thBQIM and 8thBQIM I.F.s.

Error	3$\mathit{rd}$$\mathit{BQIM}$	4$\mathit{th}$$\mathit{BQIM}$	5$\mathit{th}$$\mathit{BQIM}$	6$\mathit{th}$$\mathit{BQIM}$	7$\mathit{th}$$\mathit{BQIM}$	8$\mathit{th}$$\mathit{BQIM}$
$\parallel {\mathbf{x}}^{(1)}-{\mathbf{x}}^{(0)}{\parallel }_2$	4.2e−1	4.3e−1	4.3e−1	4.3e−1	4.3e−1	4.3e−1
$\parallel {\mathbf{x}}^{(2)}-{\mathbf{x}}^{(1)}{\parallel }_2$	9.2e−3	2.5e−3	7.6e−4	2.5e−4	8.6e−5	3.1e−5
$\parallel {\mathbf{x}}^{(3)}-{\mathbf{x}}^{(2)}{\parallel }_2$	6.0e−8	1.4e−12	5.1e−18	2.9e−24	2.7e−31	4.0e−39
$\parallel {\mathbf{x}}^{(4)}-{\mathbf{x}}^{(3)}{\parallel }_2$	1.6e−23	1.5e−49	7.5e−89	7.4e−144	7.0e−217	3.0e−310
$\parallel {\mathbf{x}}^{(5)}-{\mathbf{x}}^{(4)}{\parallel }_2$	3.4e−70	1.9e−197	-	-	-	-
$p_c$	3	4	5	6	7	8

Table 3. Results of the TP3 for the 3rdBQIM, 4thBQIM, 5thBQIM, 6thBQIM, 7thBQIM and 8thBQIM I.F.s.

Error	3$\mathit{rd}$$\mathit{BQIM}$	4$\mathit{th}$$\mathit{BQIM}$	5$\mathit{th}$$\mathit{BQIM}$	6$\mathit{th}$$\mathit{BQIM}$	7$\mathit{th}$$\mathit{BQIM}$	8$\mathit{th}$$\mathit{BQIM}$
$\parallel {\mathbf{x}}^{(1)}-{\mathbf{x}}^{(0)}{\parallel }_2$	4.2e−1	4.3e−1	4.3e−1	4.3e−1	4.3e−1	4.3e−1
$\parallel {\mathbf{x}}^{(2)}-{\mathbf{x}}^{(1)}{\parallel }_2$	9.2e−3	2.5e−3	7.6e−4	2.5e−4	8.6e−5	3.1e−5
$\parallel {\mathbf{x}}^{(3)}-{\mathbf{x}}^{(2)}{\parallel }_2$	6.0e−8	1.4e−12	5.1e−18	2.9e−24	2.7e−31	4.0e−39
$\parallel {\mathbf{x}}^{(4)}-{\mathbf{x}}^{(3)}{\parallel }_2$	1.6e−23	1.5e−49	7.5e−89	7.4e−144	7.0e−217	3.0e−310
$\parallel {\mathbf{x}}^{(5)}-{\mathbf{x}}^{(4)}{\parallel }_2$	3.4e−70	1.9e−197	-	-	-	-
$p_c$	3	4	5	6	7	8

Table 3 shows that as the order of the methods increase the methods converge in less iterations (4 iterations) and with a smaller error. Similarly, as in the case for scalar equations, the computational order of convergence for this system of 2 equations agree with the theoretical one.

We next consider the Test Problem 4 (TP4) [14]

$$\begin{array}{c}{x}_1^2+x_2^2-1=0\hfill \\ x_1^2-x_2^2-0.5=0\hfill \end{array}$$

(26)

Using the elimination method, Equation (26) reduces to the simple quadratic equation $2x_2^2-1.5=0$ whose positive root is given by ${\displaystyle x_2^{*}=\frac{\sqrt{3}}{2}=0.866025403..}$ and therefore ${\displaystyle x_1^{*}=\frac{1}{2}}$.

Using ${\mathbf{x}}^{(0)}={(2,3)}^T$ as starting vector far from the root, we apply our methods (16), $r=1,2,...,6$ to find the numerical solutions of Equation (26).

Table 4. Results of TP4 for the 3rdBQIM, 4thBQIM, 5thBQIM, 6thBQIM, 7thBQIM and 8thBQIM I.F.s.

Error	3$\mathit{rd}$$\mathit{BQIM}$	4$\mathit{th}$$\mathit{BQIM}$	5$\mathit{th}$$\mathit{BQIM}$	6$\mathit{th}$$\mathit{BQIM}$	7$\mathit{th}$$\mathit{BQIM}$	8$\mathit{th}$$\mathit{BQIM}$
$\parallel {\mathbf{x}}^{(1)}-{\mathbf{x}}^{(0)}{\parallel }_2$	2.0e0	2.2e0	2.3e0	2.4e0	2.4e0	2.5e0
$\parallel {\mathbf{x}}^{(2)}-{\mathbf{x}}^{(1)}{\parallel }_2$	5.3e−1	3.8e−1	2.8e−1	2.2e−1	1.7e−1	1.4e−1
$\parallel {\mathbf{x}}^{(3)}-{\mathbf{x}}^{(2)}{\parallel }_2$	3.5e−2	5.0e−3	6.3e−4	6.8e−5	6.2e−6	4.5e−7
$\parallel {\mathbf{x}}^{(4)}-{\mathbf{x}}^{(3)}{\parallel }_2$	3.1e−5	1.5e−9	9.2e−16	3.5e−24	4.1e−35	6.9e−49
$\parallel {\mathbf{x}}^{(5)}-{\mathbf{x}}^{(4)}{\parallel }_2$	5.2e−14	2.3e−35	9.0e−75	8.3e−140	2.5e−239	0
$\parallel {\mathbf{x}}^{(6)}-{\mathbf{x}}^{(5)}{\parallel }_2$	2.7e−40	1.3e−138	-	-	-	-
$\parallel {\mathbf{x}}^{(7)}-{\mathbf{x}}^{(6)}{\parallel }_2$	4.2e−119	-	-	-	-	-
$p_c$	3.00	4.00	4.98	6.00	7.00	7.63

Table 4. Results of TP4 for the 3rdBQIM, 4thBQIM, 5thBQIM, 6thBQIM, 7thBQIM and 8thBQIM I.F.s.

Error	3$\mathit{rd}$$\mathit{BQIM}$	4$\mathit{th}$$\mathit{BQIM}$	5$\mathit{th}$$\mathit{BQIM}$	6$\mathit{th}$$\mathit{BQIM}$	7$\mathit{th}$$\mathit{BQIM}$	8$\mathit{th}$$\mathit{BQIM}$
$\parallel {\mathbf{x}}^{(1)}-{\mathbf{x}}^{(0)}{\parallel }_2$	2.0e0	2.2e0	2.3e0	2.4e0	2.4e0	2.5e0
$\parallel {\mathbf{x}}^{(2)}-{\mathbf{x}}^{(1)}{\parallel }_2$	5.3e−1	3.8e−1	2.8e−1	2.2e−1	1.7e−1	1.4e−1
$\parallel {\mathbf{x}}^{(3)}-{\mathbf{x}}^{(2)}{\parallel }_2$	3.5e−2	5.0e−3	6.3e−4	6.8e−5	6.2e−6	4.5e−7
$\parallel {\mathbf{x}}^{(4)}-{\mathbf{x}}^{(3)}{\parallel }_2$	3.1e−5	1.5e−9	9.2e−16	3.5e−24	4.1e−35	6.9e−49
$\parallel {\mathbf{x}}^{(5)}-{\mathbf{x}}^{(4)}{\parallel }_2$	5.2e−14	2.3e−35	9.0e−75	8.3e−140	2.5e−239	0
$\parallel {\mathbf{x}}^{(6)}-{\mathbf{x}}^{(5)}{\parallel }_2$	2.7e−40	1.3e−138	-	-	-	-
$\parallel {\mathbf{x}}^{(7)}-{\mathbf{x}}^{(6)}{\parallel }_2$	4.2e−119	-	-	-	-	-
$p_c$	3.00	4.00	4.98	6.00	7.00	7.63

In Table 4, with the starting vector distant from the root, we observe that the methods take more iterations to converge. As from the third iteration, the iterate of the methods are close to the root and they converge to the root at their respective rate of convergence.

We next consider the Test Problem 5 (TP5) which is a system of 4 equations [15].

$$\begin{array}{c}{x}_2{x}_3+x_4(x_2+x_3)=0\hfill \\ x_1{x}_3+x_4(x_1+x_3)=0\hfill \\ x_1{x}_2+x_4(x_1+x_2)=0\hfill \\ x_1{x}_2+x_1{x}_3+x_2{x}_3=1\hfill \end{array}$$

(27)

Using the substitution method, Equation (27) reduces to the simple quadratic equation $3x_1^2-1=0$ whose positive root is given by ${\displaystyle x_1^{*}=\frac{1}{\sqrt{3}}=0.577350269..}$ Therefore ${\displaystyle x_2^{*}=x_3^{*}=x_1^{*}=\frac{1}{\sqrt{3}}=0.577350269..}$ and ${\displaystyle x_4^{*}=-\frac{x_1^{*}}{2}=-\frac{1}{2\sqrt{3}}=-0.288675134..}$

Using ${\mathbf{x}}^{(0)}={(0.5,0.5,0.5,-0.25)}^T$ as starting vector, we apply our Equation (16), $r=1,2,...,6$ to find the numerical solutions of Equation (27).

In Table 5, we deduce that similar observations on computational order of convergence can be made for this system of four equations.

Table 5. Results of TP5 for the 3rdBQIM, 4thBQIM, 5thBQIM, 6thBQIM, 7thBQIM and 8thBQIM I.F.s.

Error	3$\mathit{rd}$$\mathit{BQIM}$	4$\mathit{th}$$\mathit{BQIM}$	5$\mathit{th}$$\mathit{BQIM}$	6$\mathit{th}$$\mathit{BQIM}$	7$\mathit{th}$$\mathit{BQIM}$	8$\mathit{th}$$\mathit{BQIM}$
$\parallel {\mathbf{x}}^{(1)}-{\mathbf{x}}^{(0)}{\parallel }_2$	1.4e−1	1.4e−1	1.4e−1	1.4e−1	1.4e−1	1.4e−1
$\parallel {\mathbf{x}}^{(2)}-{\mathbf{x}}^{(1)}{\parallel }_2$	1.7e−3	3.5e−4	8.1e−5	2.0e−5	5.2e−6	1.4e−6
$\parallel {\mathbf{x}}^{(3)}-{\mathbf{x}}^{(2)}{\parallel }_2$	2.4e−9	8.6e−15	2.6e−21	7.1e−29	1.7e−37	3.9e−47
$\parallel {\mathbf{x}}^{(4)}-{\mathbf{x}}^{(3)}{\parallel }_2$	6.5e−27	3.1e−57	9.7e−104	1.4e−169	7.9e−258	0
$\parallel {\mathbf{x}}^{(5)}-{\mathbf{x}}^{(4)}{\parallel }_2$	1.3e−79	-	-	-	-	-
$p_c$	3	4	5	6	7	8.1

Table 5. Results of TP5 for the 3rdBQIM, 4thBQIM, 5thBQIM, 6thBQIM, 7thBQIM and 8thBQIM I.F.s.

Error	3$\mathit{rd}$$\mathit{BQIM}$	4$\mathit{th}$$\mathit{BQIM}$	5$\mathit{th}$$\mathit{BQIM}$	6$\mathit{th}$$\mathit{BQIM}$	7$\mathit{th}$$\mathit{BQIM}$	8$\mathit{th}$$\mathit{BQIM}$
$\parallel {\mathbf{x}}^{(1)}-{\mathbf{x}}^{(0)}{\parallel }_2$	1.4e−1	1.4e−1	1.4e−1	1.4e−1	1.4e−1	1.4e−1
$\parallel {\mathbf{x}}^{(2)}-{\mathbf{x}}^{(1)}{\parallel }_2$	1.7e−3	3.5e−4	8.1e−5	2.0e−5	5.2e−6	1.4e−6
$\parallel {\mathbf{x}}^{(3)}-{\mathbf{x}}^{(2)}{\parallel }_2$	2.4e−9	8.6e−15	2.6e−21	7.1e−29	1.7e−37	3.9e−47
$\parallel {\mathbf{x}}^{(4)}-{\mathbf{x}}^{(3)}{\parallel }_2$	6.5e−27	3.1e−57	9.7e−104	1.4e−169	7.9e−258	0
$\parallel {\mathbf{x}}^{(5)}-{\mathbf{x}}^{(4)}{\parallel }_2$	1.3e−79	-	-	-	-	-
$p_c$	3	4	5	6	7	8.1

5.4. Application

As an application, we consider the quadratic integral equation of the type:

$$x(s)=g(s)+\lambda x(s){\int }_0^{1}K(s,t)x(t)dt$$

(28)

Equation (28) appears in [16] and is known as Chandrasekhar’s integral equation. It arises from the study of the radiative transfer theory, the transport of neutrons and the kinetic theory of the gases. It is studied in [17] and, under certain conditions for the kernel, in [18,19].

We define the kernel $K(s,t)$ as a continuous function in $s,t\in [0,1]$ such that $0<K(s,t)<1$ and $K(s,t)+K(t,s)=1$. Moreover, we assume that $g(s)\in C[0,1]$ is a given function and λ is a real constant. The solution of Equation (28) is equivalent to solving the equation $F(x)=0$, where $F:C[0,1]\to C[0,1]$ and

$$F(x)(s)=x(s)-g(s)-\lambda x(s){\int }_0^{1}K(s,t)x(t)dt,x\in C[0,1],s\in [0,1]$$

We choose $g(s)=1$ and ${\displaystyle K(s,t)=\frac{s}{s+t}}$ so that we are required to solve the following equation:

$$F(x)(s)=x(s)-1-\lambda x(s){\int }_0^1\frac{s}{s+t}x(t)dt,x\in C[0,1],s\in [0,1]$$

(29)

If we discretize the integral given in Equation (29) using the Mid-point Integration Rule with n grid points

$${\int }_0^1\frac{s}{s+t}x(t)dt=\frac{1}{n}\sum _{j=1}^n\frac{t_j}{t_i+t_j}{x}_j,x_j=x(t_j),t_j=(j-0.5)h,h=\frac{1}{n},1\le j\le n$$

we obtain the resulting system of non-linear equations:

$$f_i(\mathbf{x})=x_i-\lambda \frac{x_i}{n}\sum _{j=1}^n\frac{t_j}{t_i+t_j}{x}_j,1\le i\le n$$

(30)

The λ are equally spaced with $\Delta \lambda =0.01$ in the interval $\lambda \in (0,0.5)$. We choose $n=100$ and ${(1,1,.....,1)}^T$ as the starting vector. In this case, for each λ, we let $M_{\lambda }$ be the minimum number of iterations for which the infinity norm between the successive approximations $\parallel {\mathbf{x}}^{(k+1)}-{\mathbf{x}}^{(k)}{\parallel }_{\infty }<1e-13$, where the approximation ${\mathbf{x}}^{(k)}$ is calculated correct to 16 digits (double precision in MATLAB). Let $\overline{M_{\lambda }}$ be the mean of iteration number for the 49 λ’s.

All methods converge for all 49 values of λ. The results are given in Table 6 which shows that all methods converge in less than five iterations. It is the 8thBQIM I.F. which has the greatest number of λ converging in two or three iterations and the smallest mean iteration number. We also observe that there is a small difference in the mean iteration number between the 7thBQIM and 8thBQIM I.F.s. Developing 9th or higher order I.F.s would not be necessary for this application.

Table 6. Results of the Chandrasekhar’s integral equation for the 3rdBQIM, 4thBQIM, 5thBQIM, 6thBQIM, 7thBQIM and 8thBQIM I.F.s.

Method	$M=2$	$M=3$	$M=4$	$M=5$	$M>5$	$\overline{M_{\lambda }}$
3rdBQIM	0	21	23	5	0	3.67
4thBQIM	1	34	13	1	0	3.29
5thBQIM	3	38	8	0	0	3.10
6thBQIM	3	40	6	0	0	3.06
7thBQIM	3	41	5	0	0	3.04
8thBQIM	3	42	4	0	0	3.02

Table 6. Results of the Chandrasekhar’s integral equation for the 3rdBQIM, 4thBQIM, 5thBQIM, 6thBQIM, 7thBQIM and 8thBQIM I.F.s.

Method	$M=2$	$M=3$	$M=4$	$M=5$	$M>5$	$\overline{M_{\lambda }}$
3rdBQIM	0	21	23	5	0	3.67
4thBQIM	1	34	13	1	0	3.29
5thBQIM	3	38	8	0	0	3.10
6thBQIM	3	40	6	0	0	3.06
7thBQIM	3	41	5	0	0	3.04
8thBQIM	3	42	4	0	0	3.02

6. Conclusions and Future Work

In this work, we have shown that Kung-Traub’s conjecture fails for quadratic functions, that is, we can obtain iterative methods for solving quadratic equations with three functions evaluations reaching order of convergence greater than four. Furthermore, using weight functions, we showed that it is possible to develop methods with three function evaluations of any order. These methods are extended to systems involving quadratic equations. We have developed 3rd to 8th order methods and applied them in some numerical experiments including an application to Chandrasekhar’s integral equation. The dynamic behaviour of the methods were also studied. This research will open the door to new avenues. For example, for solving quadratic equations numerically, we can improve the order of fourth order method with two function and one first derivative evaluations (Ostrowski’s method [8]) or fourth order derivative-free method with three function evaluations (higher order Steffensen’s method (see [20])). The question we now pose: Is it possible to develop fifth order methods with three function evaluations for solving cubic or higher order polynomials? This is for future considerations.