Numerical Properties of Different Root-Finding Algorithms Obtained for Approximating Continuous Newton’s Method

Abstract

This paper is dedicated to the study of continuous Newton’s method, which is a generic differential equation whose associated flow tends to the zeros of a given polynomial. Firstly, we analyze some numerical features related to the root-finding methods obtained after applying different numerical methods for solving initial value problems. The relationship between the step size and the order of convergence is particularly considered. We have analyzed both the cases of a constant and non-constant step size in the procedure of integration. We show that working with a non-constant step, the well-known Chebyshev-Halley family of iterative methods for solving nonlinear scalar equations is obtained.

1. Introduction

We can find the origins of continuous Newton’s method in the seminal paper of Neuberger [1]. Actually, it appears in the study of the basins of attraction related with the relaxed Newton’s method for solving a complex equation $p\left(z\right)=0$

$$z_{n+1}=z_n-h\frac{p\left(z_n\right)}{p^{\prime }\left(z_n\right)},n\ge 0,h\in \mathbb{C}$$

(1)

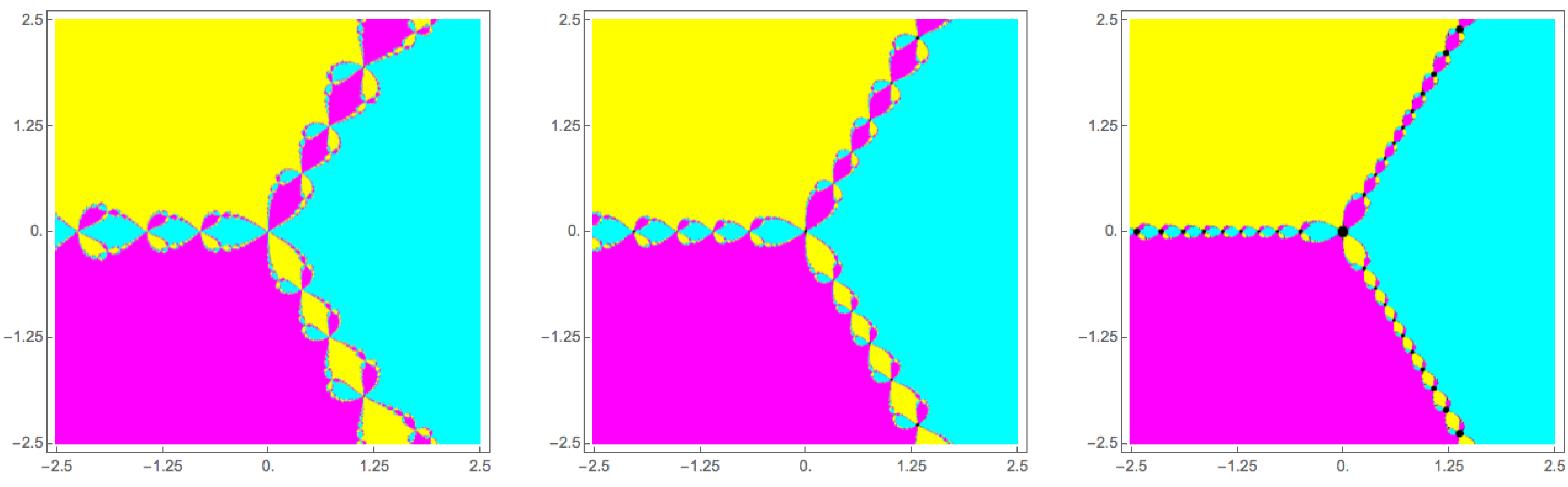
It is well known, since the works of Cayley and Schröder at the end of the 19th century, and Fatou and Julia in the early 20th century, that the basins of attraction of Newton’s method (obtained for $h=1$ in Equation (1)) have an intricate fractal structure. Neuberger, as well other authors ([2,3]), has realized that this fractal structure shrinks away when $h\to 0$, as we can appreciate in Figure 1.

Figure 1. Basins of attraction of the relaxed Newton’s method given in Equation (1) applied to the polynomial $p\left(z\right)=z^3-1$ for $h=1$, $h=2/3$ and $h=1/3$, respectively.

Figure 1. Basins of attraction of the relaxed Newton’s method given in Equation (1) applied to the polynomial $p\left(z\right)=z^3-1$ for $h=1$, $h=2/3$ and $h=1/3$, respectively.

We can identify iterative method Equation (1) as an Euler approximation of the differential equation

$$z\left(0\right)=z_0,z^{\prime }\left(t\right)=-\frac{p\left(z\right(t\left)\right)}{p^{\prime }\left(z\left(t\right)\right)}$$

(2)

with step size h.

Initial value problem Equation (2), or its improved version of finding a function $z:[0,\infty )\to \mathbb{C}$ such that

$$\begin{array}{c}\hfill z\left(0\right)=z_0,p{\left(z\right)}^{\prime }\left(t\right)=-p\left(z\left(t\right)\right)\end{array}$$

(3)

for a given z₀ ∈ $\mathbb{C}$, where p is a non-constant complex polynomial is known as continuous Newton’s method. We refer to [1] for the theoretical basis of continuous Newton’s method. In particular, it is shown that solutions $z\left(t\right)$ of Equation (2) (or Equation (3)) flow to a zero of p while keeping the argument of $p\left(z\right(t\left)\right)$ constant at $arg\left(p\left(z_0\right)\right)$.

For instance, as it was pointed out by Jacobsen et al. [3], if $p\left(z\right)=z^3-1$ in Equation (2), the explicit solution is

$$z\left(t\right)=\sqrt[3]{(z_0^3-1)e^{-t}+1}$$

The choice of the appropriate branch of the cube root, defined by the rays $\theta =\pi /3$, $\theta =\pi$ and $\theta =-\pi /3$, determines the ternary division of the complex plane that can be seen in the three graphics of Figure 1. According to these authors, the fractal boundaries in the basins of attraction of the roots can be originated by numerical errors inherent to the discretization of initial value problem Equation (2).

This work is two fold. In Section 2, we consider other different strategies (not only Euler’s method) for solving initial value problem Equation (2). The efficiency of the iterative processes obtained in this way is analyzed.

2. Numerical Algorithms Applied to Continuous Newton’s Method

In [3] the dynamical properties of six numerical methods for solving differential equations are considered when they are applied to continuous Newton’s method Equation (2). In particular, they compare the basins of attraction of these methods applied to Equation (2) for $p\left(z\right)=z^3-1$. They estimate the corresponding fractal dimension using a box-counting algorithm. The main conclusion is that higher-order algorithms are not necessarily related with basin boundaries with smaller fractal dimension.

In this section we are concerned with some numerical properties of root-finding methods derived from the application of numerical methods for solving differential equations

$$\left\{\begin{array}{ccc}\hfill \frac{dz}{dt}& =& f(t,z(t\left)\right)\hfill \\ \hfill z\left(t_0\right)& =& z_0\hfill \end{array}\right.$$

(4)

as continuous Newton’s method Equation (2). So, as it has been done in [3], we use $y_n$ for the approximations of $z\left(t_n\right)$, where $t_{n+1}=t_n+h$ and h for the step size. The six methods considered by Jacobsen et al. in [3] are:

• Euler’s method:

  $$y_{n+1}=y_n+hf(t_n,y_n)$$

  (5)
• Refined Euler’s method:

  $$\left\{\begin{array}{ccc}\hfill y^{*}& =& y_n+h/2f(t_n,y_n)\hfill \\ \hfill y_{n+1}& =& y_n+hf(t_n+h/2,y^{*})\hfill \end{array}\right.$$

  (6)
• Heun’s method:

  $$\left\{\begin{array}{ccc}\hfill y^{*}& =& y_n+hf(t_n,y_n)\hfill \\ \hfill y_{n+1}& =& y_n+h/2\left(f(t_n,y_n)+f(t_n+h,y^{*})\right)\hfill \end{array}\right.$$

  (7)
• Runge-Kutta method of order 2:

  $$\left\{\begin{array}{ccc}\hfill y^{*}& =& y_n+2h/3f(t_n,y_n)\hfill \\ \hfill y_{n+1}& =& y_n+h/4\left(f(t_n,y_n)+3f(t_n+2h/3,y^{*})\right)\hfill \end{array}\right.$$

  (8)
• Runge-Kutta method of order 4:

  $$\left\{\begin{array}{ccc}\hfill k_1& =& hf(t_n,y_n)\hfill \\ \hfill k_2& =& hf(t_n+h/2,y_n+k_1/2)\hfill \\ \hfill k_3& =& hf(t_n+h/2,y_n+k_2/2)\hfill \\ \hfill k_4& =& hf(t_n+h,y_n+k_3)\hfill \\ \hfill y_{n+1}& =& y_n+1/6\left(k_1+2k_2+2k_3+k_4\right)\hfill \end{array}\right.$$

  (9)
• Adams-Bashforth method of order 2:

  $$\left\{\begin{array}{ccc}\hfill y^{*}& =& y_0+2h/3f(t_n,y_0)\hfill \\ \hfill y_1& =& y_0+h/4\left(f(t_n,y_0)+3f(t_n+2h/3,y^{*})\right)\hfill \\ \hfill y_{n+1}& =& y_n+y_n+h\left(3/2f(t_n,y_n)-1/2f(t_{n-1},y_{n-1})\right)\hfill \end{array}\right.$$

  (10)

Note that, in the case of continuous Newton’s method, the function $f(t,z(t\left)\right)$ that appears in differential equation Equation (4) is

$$f(t,z\left(t\right))=-\frac{p\left(z\right(t\left)\right)}{p^{\prime }\left(z\left(t\right)\right)}$$

So, the application of Euler’s method Equation (5) gives rise to the root-finding algorithm

$$z_{n+1}=F_1\left(z_n\right)=z_n-h\frac{p\left(z_n\right)}{p^{\prime }\left(z_n\right)},n\ge 0$$

(11)

that is the wel-known relaxed Newton’s method. Note that the role of the step size h in the methods for solving differential equations is moved to a relaxing parameter in Equation (12). As it was stated in [3] and we have previously mentioned, h has a clear influence in the dynamical properties of an iterative method. We analyze now the influence of h in the numerical properties of an iterative method. Let $F_1$ be the iteration map related to the relaxed Newton’s method Equation (12) and let $z^{*}$ be a simple root of $p\left(z\right)=0$. It is a straightforward calculation to show that

$$F_1\left(z^{*}\right)=z^{*},F_1^{\prime }\left(z^{*}\right)=1-h$$

So, we have that method Equation (12) is consistent (the roots of p are attracting fixed points of the iteration map $F_1$) only for $h\in (0,2)$. In addition, we obtain iterative methods with just linear convergence, except for the case $h=1$, that is the classical Newton’s method with quadratic convergence.

Now, we see what happens with the refined Euler’s method defined in Equation (6). The corresponding root-finding algorithm can be written as

$$z_{n+1}=F_2\left(z_n\right)=z_n-h\frac{p\left({\omega }_2\left(z_n\right)\right)}{p^{\prime }\left({\omega }_2\left(z_n\right)\right)},n\ge 0,{\omega }_2\left(z\right)=z-\frac{h}{2}\frac{p\left(z\right)}{p^{\prime }\left(z\right)}$$

(12)

If $z^{*}$ is a simple root of $p\left(z\right)=0$, we have ${\omega }^{\prime }\left(z\right)=1-h(1-L_p\left(z\right))/2$, where

$$L_p\left(z\right)=p\left(z\right)p^{″}\left(z\right)/p^{\prime }{\left(z\right)}^2$$

(13)

Therefore, $\omega \left(z^{*}\right)=z^{*}$, ${\omega }^{\prime }\left(z^{*}\right)=1-h/2$ and then

$$F_2\left(z^{*}\right)=z^{*},F_2^{\prime }\left(z^{*}\right)=\frac{1+{(1-h)}^2}{2}$$

As a consequence, iterative method Equation (12) is consistent only for $h\in (0,2)$. All the methods deduced in this case have linear convergence (the lower value for the asymptotic constant error is obtained for $h=1$). This fact together with a number of function evaluations equals to four, makes this method uninteresting from an efficiency point of view.

Something similar happens with Heun’s method given in Equation (7) and Runge-Kutta method of second order given in Equation (8). They have different iteration maps, respectively $z_{n+1}=F_3\left(z_n\right)$ and $z_{n+1}=F_4\left(z_n\right)$, where

$$F_3\left(z\right)=z-\frac{h}{2}\left(\frac{p\left({\omega }_3\left(z\right)\right)}{p^{\prime }\left({\omega }_3\left(z\right)\right)}+\frac{p\left(z\right)}{p^{\prime }\left(z\right)}\right)n\ge 0,{\omega }_3\left(z\right)=z-h\frac{p\left(z\right)}{p^{\prime }\left(z\right)}$$

$$F_4\left(z\right)=z-\frac{h}{4}\left(\frac{p\left({\omega }_4\left(z\right)\right)}{p^{\prime }\left({\omega }_4\left(z\right)\right)}+\frac{p\left(z\right)}{p^{\prime }\left(z\right)}\right),n\ge 0,{\omega }_4\left(z\right)=z-\frac{2h}{3}\frac{p\left(z\right)}{p^{\prime }\left(z\right)}$$

In both cases, we have

$$F_j\left(z^{*}\right)=z^{*},F_j^{\prime }\left(z^{*}\right)=\frac{1+{(1-h)}^2}{2},j=3,4$$

for a simple root $z^{*}$ of $p\left(z\right)=0$. So, as in the case of the refined Euler’s method, only linear convergence is achieved for $h\in (0,2)$ and then these two methods are inefficient from a numerical perspective.

The study of the Runge-Kutta method of order fourth defined in Equation (9) applied to Equation (4) leads us to the iteration scheme $z_{n+1}=F_5\left(z_n\right)$, where

$$F_5\left(z\right)=z-\frac{h}{6}\left(\frac{p\left(z\right)}{p^{\prime }\left(z\right)}+2\frac{p(z+k_1\left(z\right)/2)}{p^{\prime }(z+k_1\left(z\right)/2)}+2\frac{p(z+k_2\left(z\right)/2)}{p^{\prime }(z+k_2\left(z\right)/2)}+\frac{p(z+k_3\left(z\right))}{p^{\prime }(z+k_3\left(z\right))}\right)$$

and

$$k_1\left(z\right)=-h\frac{p\left(z\right)}{p^{\prime }\left(z\right)},k_2\left(z\right)=-h\frac{p(z+k_1\left(z\right)/2)}{p^{\prime }(z+k_1\left(z\right)/2)},k_3\left(z\right)=-h\frac{p(z+k_2\left(z\right)/2)}{p^{\prime }(z+k_2\left(z\right)/2)}$$

Note that, for a simple root $z^{*}$, we have $k_1\left(z^{*}\right)=0$, $k_1^{\prime }\left(z^{*}\right)=-h$, $k_2\left(z^{*}\right)=0$, $k_2^{\prime }\left(z^{*}\right)=-h(1-h/2)$, $k_3\left(z^{*}\right)=0$, $k_3^{\prime }\left(z^{*}\right)=-h(1-h/2+h^2/4)$ and then

$$F_5\left(z^{*}\right)=z^{*},F_5^{\prime }\left(z^{*}\right)=\frac{h^4-4h^3+12h^2-24h+24}{24}$$

There are no real values of h such that $F_5^{\prime }\left(z^{*}\right)=0$, then only linear convergence can be attained. In addition, we obtain consistent methods, that is $z^{*}$ is an attracting fixed point of $F_5$ if $\left|F_5^{\prime }\left(z^{*}\right)\right|<1$. These inequalities happens for $h\in (0,2.7853)$ where $2.7853$ is, approximately, the only real root of the polynomial $-24+12h-4h^2+h^3$. The optimum value for h, for which the asymptotic error constant has the lowest value, is $h^{*}=1.5961$. In this case $F_5^{\prime }(1.5961)=0.2704$.

The analysis of the Adams-Bahforth second order method given in Equation (10) leads us to the following two-step multipoint method:

$$z_{n+1}=z_n-\frac{h}{2}\left(3\frac{p\left(z_n\right)}{p^{\prime }\left(z_n\right)}-\frac{p\left(z_{n-1}\right)}{p^{\prime }\left(z_{n-1}\right)}\right),n\ge 1$$

(14)

To study the local order of convergence related to Equation (14), we consider a simple root $z^{*}$ of $p\left(z\right)=0$ and the error in the n-th step $e_n=z_n-z^{*}$. Then,

$${\displaystyle e_{n+1}=e_n-\frac{h}{2}(3u(z^{*}+e_n)-u(z^{*}+e_{n-1}))\approx \left({\displaystyle 1-\frac{3h}{2}}\right)e_n+\frac{h}{2}{e}_{n-1}}$$

where the terms of order higher than two in the error have been neglected. This approached formula for the errors generates a linear recurrence of second order, whose characteristic equation is

$${\lambda }^2-\left({\displaystyle 1-\frac{3h}{2}}\right)\lambda -\frac{h}{2}$$

Consequently, the method Equation (14) is consistent if the two roots of the previous equation,

$${\lambda }_{-}=\frac{1}{4}\left(-3h+2-\sqrt{9h^2-4h+4}\right),{\lambda }_{+}=\frac{1}{4}\left(-3h+2+\sqrt{9h^2-4h+4}\right)$$

have module less than one. Note that ${\lambda }_{+}<1$ for all $h>0$ but ${\lambda }_{-}\le -1$ for $h\ge 1$. So, the consistency condition is satisfied only if $h\in (0,1)$. In this case, ${\lambda }_{+}\in (1/3,1)$ and ${\lambda }_{-}\in (-1,0)$. Taking into account that ${\lambda }_{+}$ is a decreasing function for $h>0$ and $-{\lambda }_{-}$ is an increasing function for $h>0$, we can then obtain the best convergence rate when ${\lambda }_{+}=-{\lambda }_{-}$, that is, for $h=2/3$.

In Table 1 we show, in brief, the numerical information that we have deduced for methods Equations (5)–(9) considered by Jacobsen et al. in [3]. In fact, for each method, we show the asymptotic error constant (A.E.C.), the interval of values of h for which consistent methods are obtained (I.C.) and the optimal value for h regarding the order of convergence, $h^{*}$. In addition, the Adams-Basforth method given in Equation (10) is consistent for $h\in (0,2)$ with $h^{*}=2/3$. As a conclusion, we can say that, despite the order of the numerical methods for solving differential equations and the size of the step h, the root-finding algorithms derived from their application to continuous Newton’s method Equation (2) have only a linear order of convergence, with the exception of Euler’s method with $h=1$, where the convergence is quadratic. In this sense, we conclude that the numerical efficiency of these methods is poor. However, the study of the aforementioned methods can be interesting from other points of view, that reveals other topological or dynamical aspects as, for instance, the impact of the stepsize on the fractal dimension of the boundaries of the basins of attraction for the associated roots.

Table 1. Some numerical properties of the root-finding methods obtained after applying methods Equations (5)–(9) to continuous Newton’s method Equation (2).

Method	A.E.C.	I.C.	${\mathit{h}}^{\mathbf{*}}$
Euler Equation (5)	$1-h$	$(0,2)$	1
Refined Euler Equation (6)	$(1+{(1-h)}^2)/2$	$(0,2)$	1
Heun Equation (7)	$(1+{(1-h)}^2)/2$	$(0,2)$	1
Runge-Kutta 2 Equation (8)	$(1+{(1-h)}^2)/2$	$(0,2)$	1
Runge-Kutta 4 Equation (9)	$(h^4-4h^3+12h^2-24h+24)/24$	$(0,2.7853)$	$1.5961$

Table 1. Some numerical properties of the root-finding methods obtained after applying methods Equations (5)–(9) to continuous Newton’s method Equation (2).

Method	A.E.C.	I.C.	${\mathit{h}}^{\mathbf{*}}$
Euler Equation (5)	$1-h$	$(0,2)$	1
Refined Euler Equation (6)	$(1+{(1-h)}^2)/2$	$(0,2)$	1
Heun Equation (7)	$(1+{(1-h)}^2)/2$	$(0,2)$	1
Runge-Kutta 2 Equation (8)	$(1+{(1-h)}^2)/2$	$(0,2)$	1
Runge-Kutta 4 Equation (9)	$(h^4-4h^3+12h^2-24h+24)/24$	$(0,2.7853)$	$1.5961$

3. Numerical Algorithms with Non-Constant Step Size

As we can see, the application of the numerical algorithms considered in [3] to the continuous Newton’s method Equation (2) generates iterative root finding methods that does not present a high numerical efficiency. The situation does not improve if we consider higher order numerical methods for the initial value problem Equation (2). In fact, if we consider the second order Taylor’s method

$$z_{n+1}=z_n+hf(t_n,z_n)+\frac{h^2}{2}\left(\frac{\partial f}{\partial t}(t_n,z_n)+\frac{\partial f}{\partial z}(t_n,z_n)\right)f(t_n,z_n)$$

we obtain the following iterative method

$$z_{n+1}=F_6\left(z_n\right)=z_n-h\frac{p\left(z_n\right)}{p^{\prime }\left(z_n\right)}+\frac{h^2}{2}(1-L_p\left(z_n\right))\frac{p\left(z_n\right)}{p^{\prime }\left(z_n\right)}$$

where $L_p\left(z\right)$ has been defined in Equation (13). But, once again,

$$F_6\left(z^{*}\right)=z^{*},F_6^{\prime }\left(z^{*}\right)=\frac{1+{(1-h)}^2}{2}$$

so that the convergence of the method is just linear although the number of functional evaluations have been increased.

To avoid these difficulties, we can consider iterative methods with a non-constant step size. For instance, instead of considering method Equation (12) derived from Euler’s method, we consider methods where the step h is substituted by a non-constant function $H\left(z_n\right)$:

$$z_{n+1}=F\left(z_n\right)=z_n-H\left(z_n\right)\frac{p\left(z_n\right)}{p^{\prime }\left(z_n\right)},n\ge 1$$

(15)

As in the previous section, if we consider a simple root $z^{*}$ of $p\left(z\right)=0$, we have $F\left(z^{*}\right)=z^{*}$. In addition,

$$\begin{array}{cc}\hfill F^{\prime }\left(z^{*}\right)=0& \mathrm{if}H\left(z^{*}\right)=1\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill F^{″}\left(z^{*}\right)=0& \mathrm{if}{H}^{\prime }\left(z^{*}\right)=L_p^{\prime }\left(z^{*}\right)/2\hfill \end{array}$$

(17)

So, if we consider a function H that satisfies conditions Equations (16) and (17), we can obtain iterative methods with at least cubic convergence. One choice (not the only one) for function H that fulfills Equations (16) and (17) is

$$H\left(z\right)=1+\frac{1}{2}{L}_p\left(z\right)$$

that leads us to the well-known Chebyshev’s method ([4,5]):

$$z_{n+1}=F_7\left(z_n\right)=z_n-\left(1+\frac{1}{2}{L}_p\left(z_n\right)\right)\frac{p\left(z_n\right)}{p^{\prime }\left(z_n\right)}$$

(18)

Even more, if we choose

$$H\left(z\right)=1+\frac{L_p\left(z\right)}{2(1-\alpha L_p\left(z\right))}$$

we deduce the well-known Chebyshev-Halley family of methods ([4,5]):

$$z_{n+1}=F_{\alpha }\left(z_n\right)=z_n-\left(1+\frac{L_p\left(z_n\right)}{2(1-\alpha L_p\left(z_n\right))}\right)\frac{p\left(z_n\right)}{p^{\prime }\left(z_n\right)},\alpha \in \mathbb{C}$$

(19)

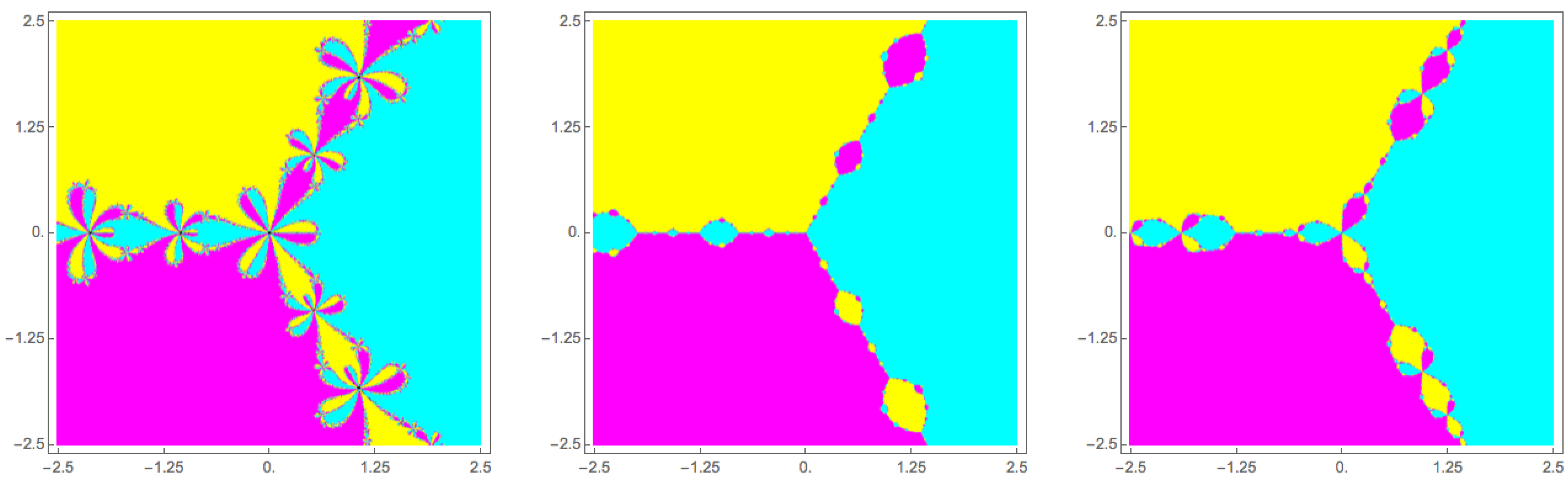
Note that Chebyshev’s iterative method defined in Equation (18) is one of the methods defined in Equation (19), actually for $\alpha =0$. Other methods belonging to this family are Halley’s method ($\alpha =1/2$) or super-Halley’s method ($\alpha =1$). The dynamical behavior of methods in the family Equation (19) have been studied in detail in the work of Cordero et al. [6]. The structure and dynamical properties of the basins of attraction of the roots of a given function changes depending on the choice of the iterative method considered for solving the equation. As a visual sample we show in Figure 2 the basins of attraction of three methods in family Equation (19) when they applied to the polynomial $p\left(z\right)=z^3-1$.

Figure 2. Basins of attraction of the Chebyshev, Halley and super-Halley methods ($\alpha =0$, $\alpha =1/2$ and $\alpha =1$, respectively, in Equation (19)) applied to the polynomial $p\left(z\right)=z^3-1$.

Figure 2. Basins of attraction of the Chebyshev, Halley and super-Halley methods ($\alpha =0$, $\alpha =1/2$ and $\alpha =1$, respectively, in Equation (19)) applied to the polynomial $p\left(z\right)=z^3-1$.

We can generalize family Equation (19) to obtain the general form of methods with cubic convergence given by Gander in [7]. In fact, the iteration given by

$$z_{n+1}=z_n-H\left(L_p\left(z_n\right)\right)\frac{p\left(z_n\right)}{p^{\prime }\left(z_n\right)}$$

where H is a function satisfying $H\left(0\right)=1$, $H^{\prime }\left(0\right)=1/2$ and $H^{″}\left(0\right)<\infty$, has cubic convergence to simple roots of p. The task of extending in this way Gander’s result to a higher order of convergence seems to be difficult. An approach for the quadratic case was given by Romero et al. in [8].

4. Conclusions

We have made a numerical incursion in some properties of the root-finding methods obtained when different numerical procedures have been applied to the initial value problem known as continuous Newton’s method. In particular, we have shown that, for a constant step size, the deduced iterative root-finding methods have a poor efficiency behavior. However, if we consider numerical methods with non-constant step size, a plethora of root-finding methods can be constructed. In this work we are only concerned with the famous Chebyshev-Halley family of methods, but many other iterative methods can be built up in this way. We must take into account that just Euler’s method with non-constant step size has been considered in this work.