On Some Improved Harmonic Mean Newton-Like Methods for Solving Systems of Nonlinear Equations
Abstract
:1. Introduction
2. Development of the Methods
3. Convergence Analysis
4. Numerical Examples
4.1. Test Problems
| Methods | TP1 | TP2 | TP3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| M | M | M | |||||||
| Equation (1) | 7 | 4.6e−114 | 2.00 | 9 | 1.7e−107 | 2.00 | 8 | 3.9e−145 | 2.02 |
| Equation (2) | 5 | 1.4e−174 | 2.99 | 6 | 4.5e−139 | 3.00 | 5 | 2.9e−291 | 4.10 |
| Equation (3) | 4 | 4.6e−114 | 4.02 | 5 | 1.7e−107 | 4.00 | 5 | 2.9e−291 | 4.11 |
| Equation (4) | 4 | 7.1−108 | 3.99 | 6 | 0 | 3.99 | 5 | 8.8e−257 | 4.03 |
| Equation (6) | 4 | 1.4e−105 | 3.99 | 6 | 0 | 4.00 | 5 | 5.5e−247 | 4.12 |
| Equation (5) | 4 | 0 | 5.91 | 5 | 0 | 5.98 | 4 | 4.6e−199 | 6.12 |
| Equation (7) | 4 | 0 | 5.90 | 5 | 0 | 5.98 | 4 | 6.1e−194 | 6.13 |
| Equation (7) | 4 | 0 | 7.90 | 4 | 1.9e−133 | 7.99 | 4 | 0 | 8.64 |
| Equation (7) | 3 | 1.1e−154 | 9.90 | 4 | 2.2e−248 | 9.99 | 4 | 0 | 10.76 |
| Methods | TP1 | TP2 | TP3 |
|---|---|---|---|
| 1.161405 | 1.734549 | 1.758380 | |
| 0.950678 | 2.445676 | 1.969176 | |
| 0.808851 | 1.569021 | 1.452089 | |
| 1.052950 | 2.649530 | 2.571427 | |
| 1.001148 | 2.170088 | 2.456138 | |
| 1.132364 | 2.117847 | 2.405149 | |
| 0.944062 | 2.137319 | 2.528262 | |
| 0.986300 | 2.328460 | 2.071641 | |
| 1.029707 | 2.482167 | 2.213744 |
4.2. 1-D Bratu Problem

| Method | ||||||
|---|---|---|---|---|---|---|
| 0 | 12 | 114 | 143 | 81 | 4.92 | |
| 0 | 140 | 206 | 2 | 2 | 3.62 | |
| 4 | 237 | 100 | 8 | 1 | 3.33 | |
| 4 | 234 | 103 | 7 | 2 | 3.35 | |
| 3 | 213 | 124 | 8 | 2 | 3.42 | |
| 35 | 281 | 32 | 1 | 1 | 3.00 |
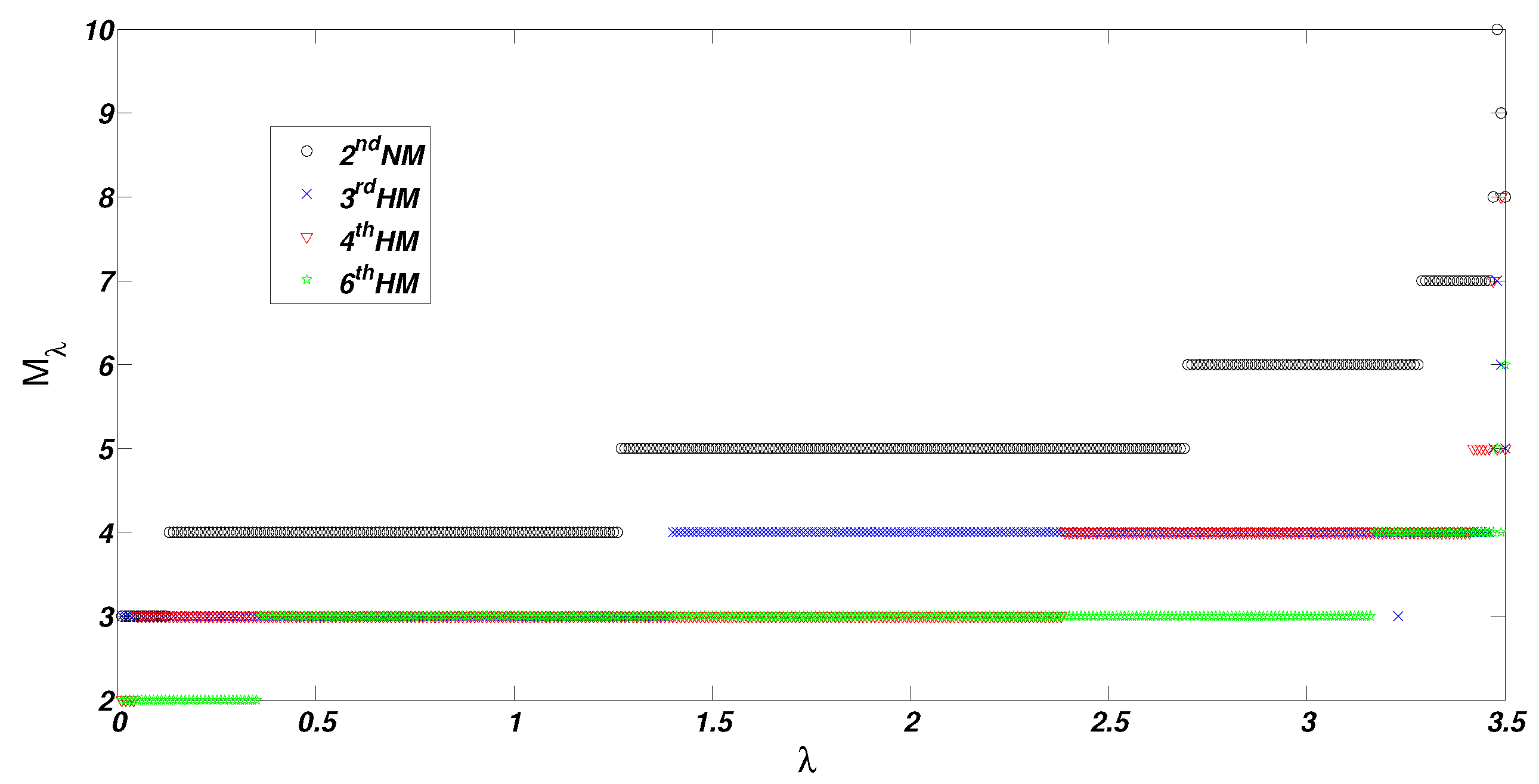
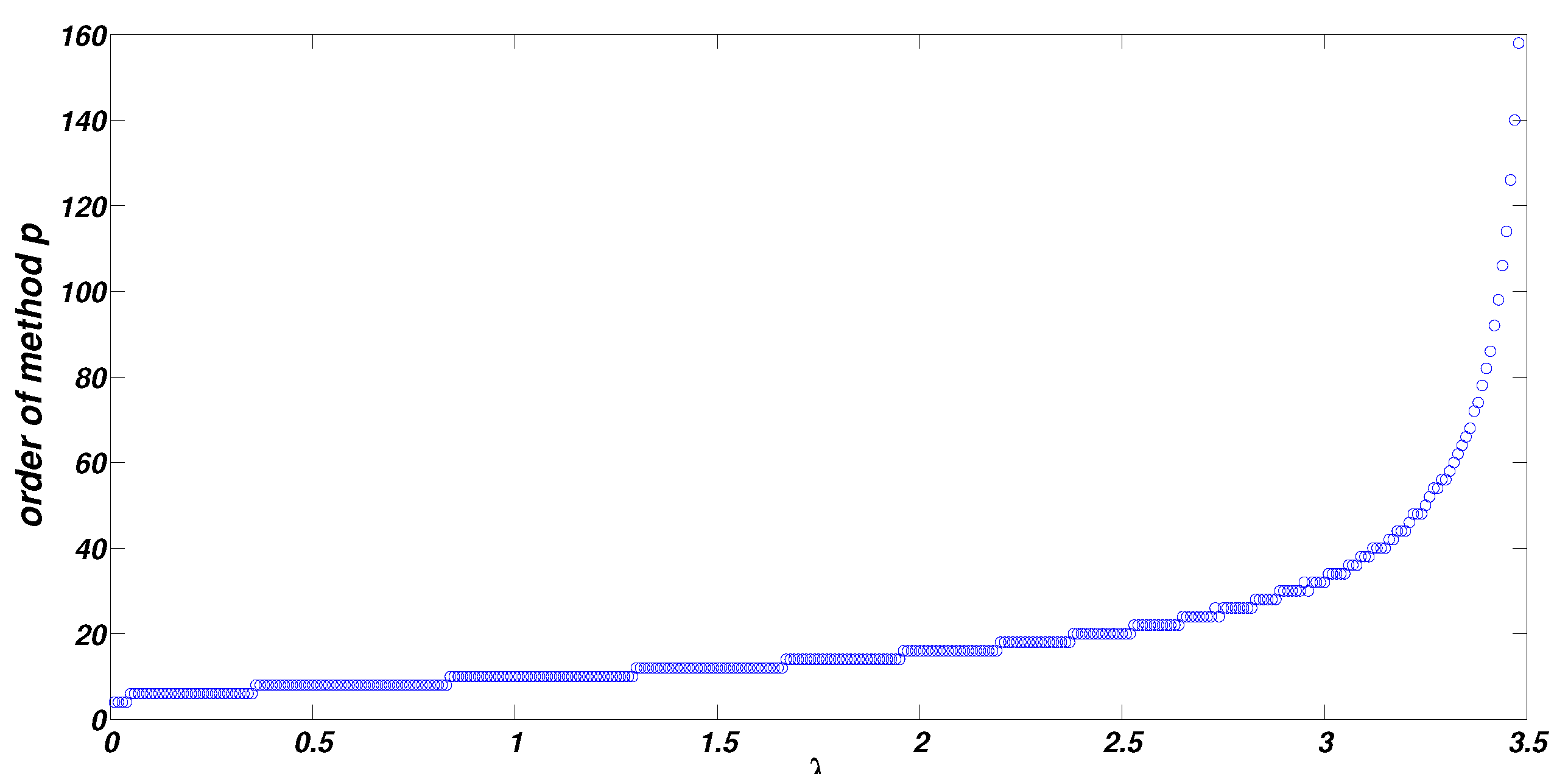
5. Conclusion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ostrowski, A.M. Solutions of Equations and System of Equations; Academic Press: New York, NY, USA, 1960. [Google Scholar]
- Homeier, H.H.H. On Newton-type methods with cubic convergence. Comp. Appl. Math. 2005, 176, 425–432. [Google Scholar] [CrossRef]
- Babajee, D.K.R. Analysis of Higher Order Variants of Newton’s Method and Their Applications to Differential and Integral Equations and in Ocean Acidification. Ph.D. Thesis, University of Mauritius, Moka, Mauritius, October 2010. [Google Scholar]
- Noor, M.A.; Waseem, M. Some iterative methods for solving a system of nonlinear equations. Comput. Math. Appl. 2009, 57, 101–106. [Google Scholar] [CrossRef]
- Sharma, J.R.; Guha, R.K.; Sharma, R. An efficient fourth order weighted-Newton method for systems of nonlinear equations. Numer. Algor. 2013, 62, 307–323. [Google Scholar] [CrossRef]
- Cordero, A.; Hueso, J.L.; Martinez, E.; Torregrosa, J.R. Increasing the convergence order of an iterative method for nonlinear systems. Appl. Math. Lett. 2012, 25, 2369–2374. [Google Scholar] [CrossRef]
- Babajee, D.K.R. On a two-parameter Chebyshev-Halley-like family of optimal two-point fourth order methods free from second derivatives. Afr. Mat. 2015, 26, 689–697. [Google Scholar] [CrossRef]
- Buckmire, R. Investigations of nonstandard Mickens-type finite-difference schemes for singular boundary value problems in cylindrical or spherical coordinates. Num. Meth. P. Diff. Eqns. 2003, 19, 380–398. [Google Scholar] [CrossRef]
- Babajee, D.K.R.; Kalyanasundaram, M.; Jayakumar, J. A family of higher order multi-point iterative methods based on power mean for solving nonlinear equations. Afr. Mat. 2015. [Google Scholar] [CrossRef]
- Cordero, A.; Hueso, J.L.; Martinez, E.; Torregrosa, J.R. A modified Newton-Jarratt’s composition. Numer. Algor. 2010, 55, 87–99. [Google Scholar] [CrossRef]
- Ortega, J.M.; Rheinbolt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Cordero, A.; Torregrosa, J.R. Variants of Newton’s method using fifth-order quadrature formulas. Appl. Math. Comp. 2007, 190, 686–698. [Google Scholar] [CrossRef]
- Frontini, M.; Sormani, E. Third-order methods from Quadrature Formulae for solving systems of nonlinear equations. Appl. Math. Comp. 2004, 140, 771–782. [Google Scholar] [CrossRef]
- Odejide, S.A.; Aregbesola, Y.A.S. A note on two dimensional Bratu problem. Kragujevac J. Math. 2006, 29, 49–56. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Babajee, D.K.R.; Madhu, K.; Jayaraman, J. On Some Improved Harmonic Mean Newton-Like Methods for Solving Systems of Nonlinear Equations. Algorithms 2015, 8, 895-909. https://doi.org/10.3390/a8040895
Babajee DKR, Madhu K, Jayaraman J. On Some Improved Harmonic Mean Newton-Like Methods for Solving Systems of Nonlinear Equations. Algorithms. 2015; 8(4):895-909. https://doi.org/10.3390/a8040895
Chicago/Turabian StyleBabajee, Diyashvir Kreetee Rajiv, Kalyanasundaram Madhu, and Jayakumar Jayaraman. 2015. "On Some Improved Harmonic Mean Newton-Like Methods for Solving Systems of Nonlinear Equations" Algorithms 8, no. 4: 895-909. https://doi.org/10.3390/a8040895






