Computing the Eccentricity Distribution of Large Graphs
Abstract
:1. Introduction
2. Preliminaries
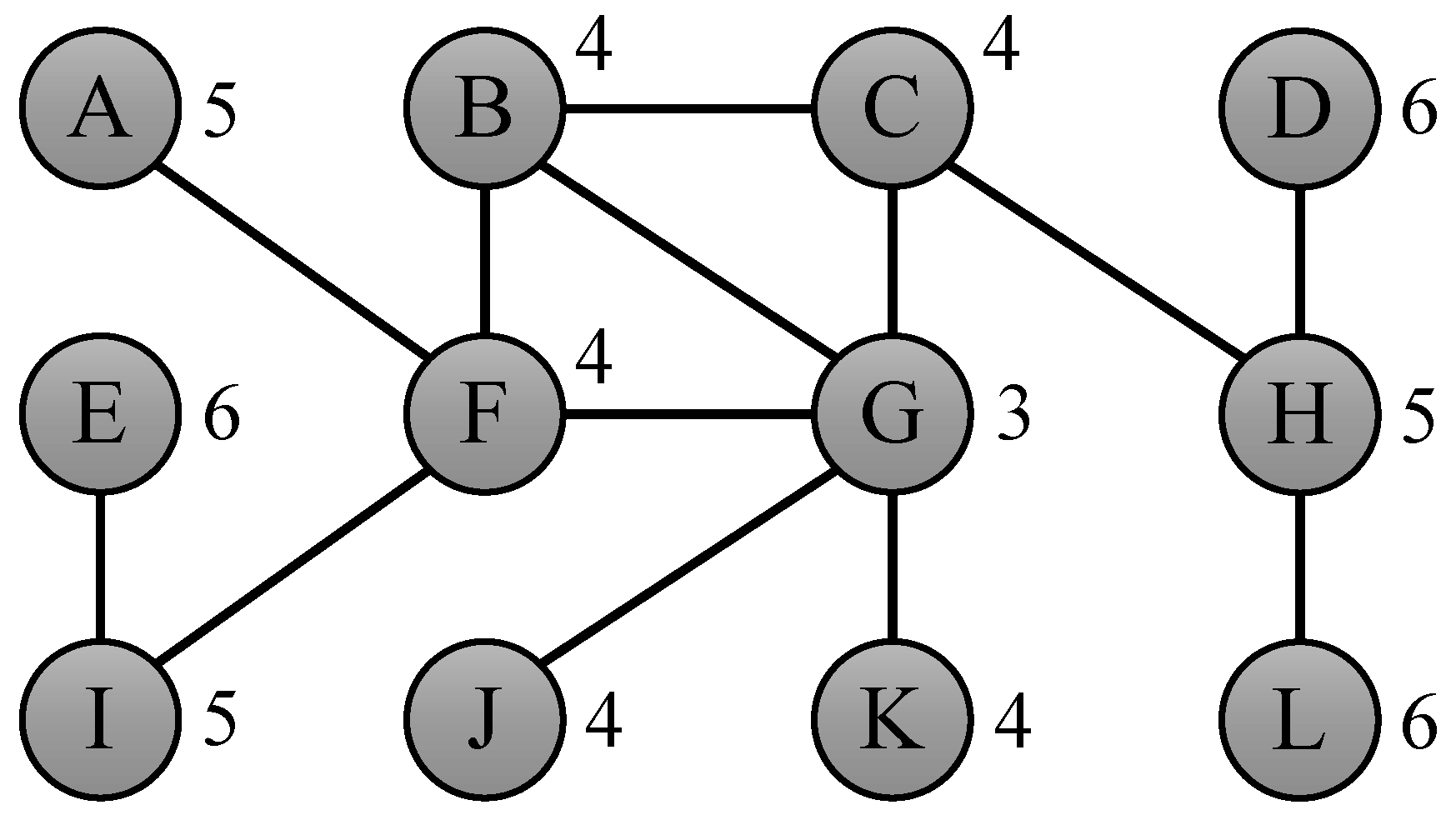
| Algorithm 1 NaiveEccentricities |
1: Input: Graph G(V, E) 2: Output: Vector ε, containing ε(v) for all v ∈ V 3: for v ∈ V do 4: ε[v] ← ECCENTRICITY(v) // O(m) 5: end for 6: return ε |
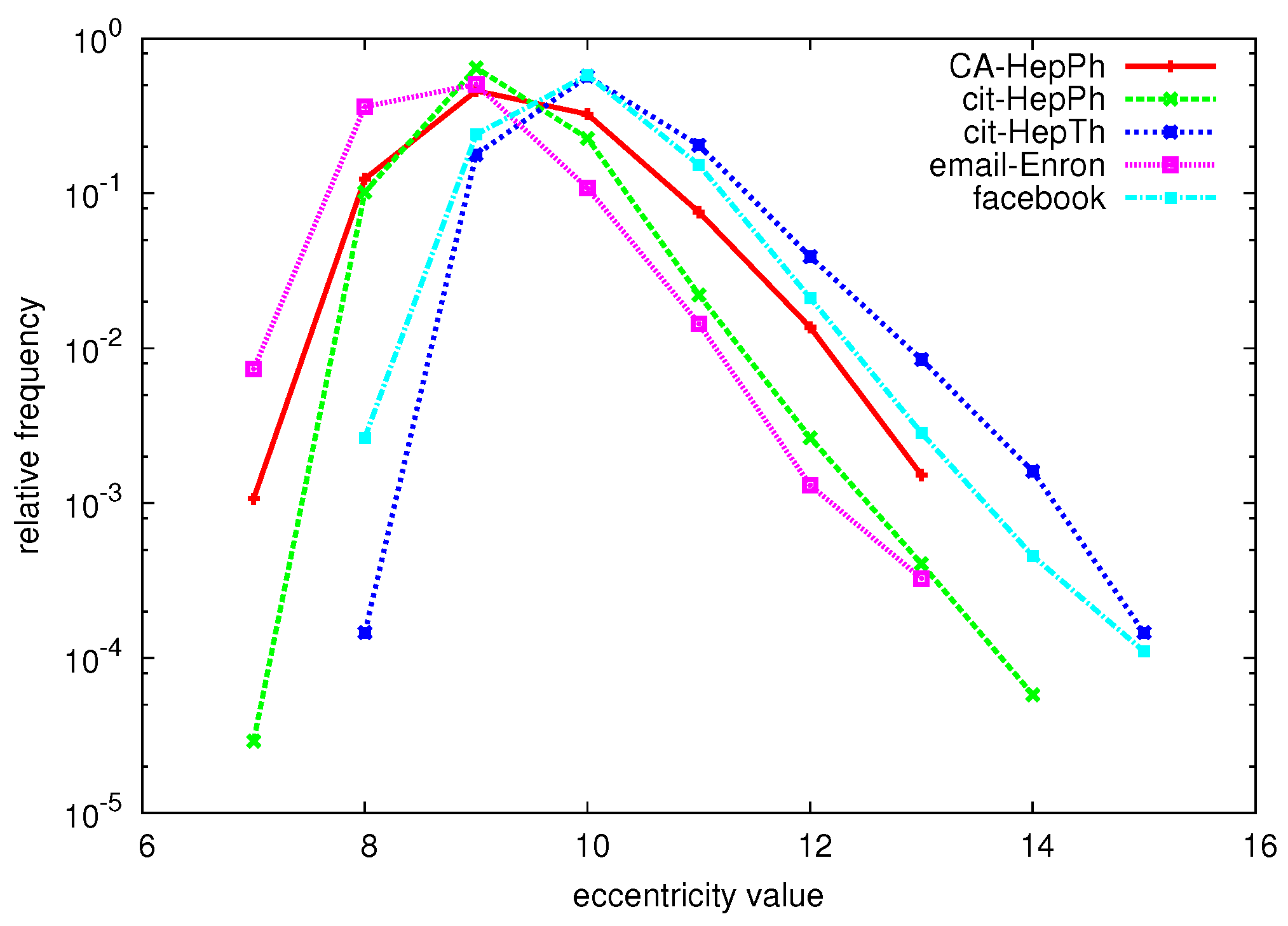
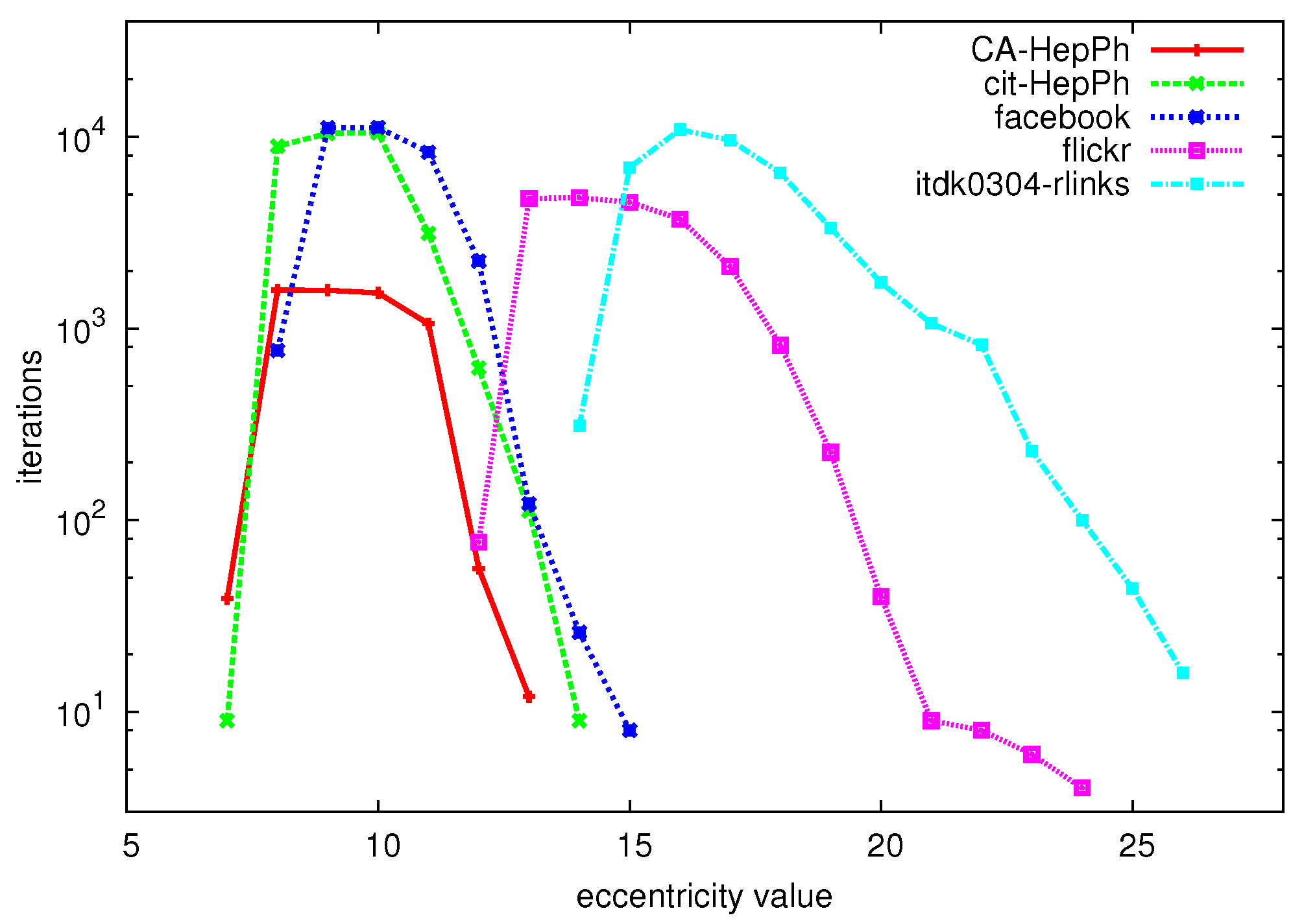
- The (relative) eccentricity distribution as a whole.
- Finding the extreme values of the eccentricity distribution, i.e., the radius and diameter, as well as derived measures such as the center and periphery of the graph.
3. Related Work
4. Exact Algorithm
- Reduce the size of the graph as a whole to speed up one eccentricity computation.
- Reduce the number of eccentricity computations.
4.1. Eccentricity Bounds
| Algorithm 2 BoundingEccentricities |
1: Input: Graph G(V, E) 2: Output: Vector ε, containing ε(v) for all v ∈ V 3: W ← V 4: for w ∈ W do 5: ε[w] ← 0 εL[w] ← −∞ εU[w] ← +∞ 6: end for 7: while W ≠ Ø do 8: v ← SelectFrom(W) 9: ε[v] ← Eccentricities(v) 10: for w ∈ W do 11: εL[w] ← max(εL[w], max(ε[v] − d(v,w), d(v,w))) 12: εU[w] ← min(εU[w], ε[v] + d(v,w)) 13: if (εL[w] = εU[w]) then 14: ε[w] ← εL[w] 15: W ← W − {w} 16: end if 17: end for 18: end while 19: return ε |
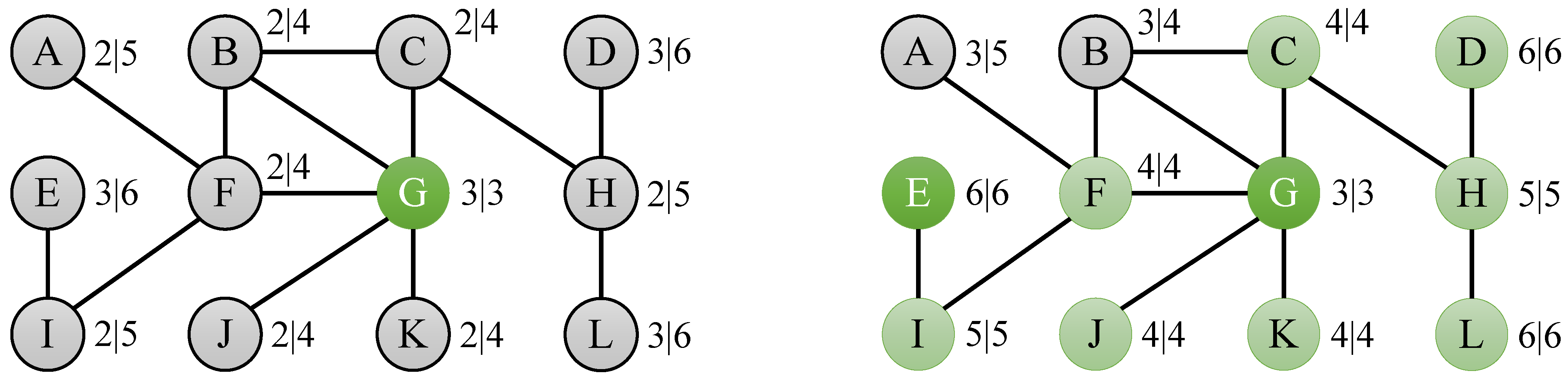
4.2. Pruning
5. Sampling
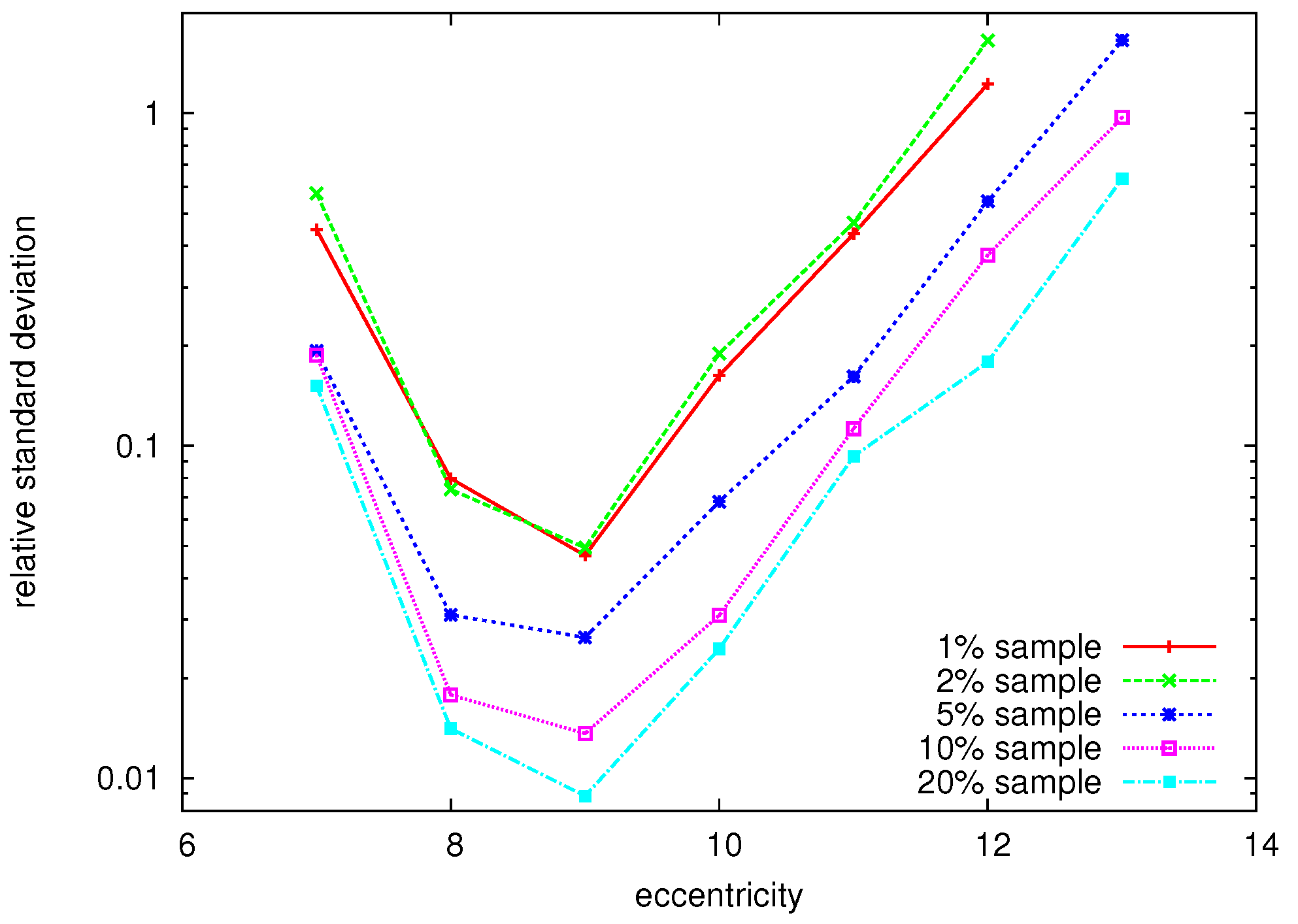
5.1. Random Node Selection
| ε(v) | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| f(ε(v)) | 24 | 12 210 | 17 051 | 3 647 | 485 | 44 | 11 |
5.2. Hybrid Algorithm
| Algorithm 3 HybridEccentricities |
1: Input: Graph G(V, E) and sampling rate q 2: Output: Vector f, containing the eccentricity distribution of G, initialized to 0 3: ε′ ← BoundingEccentricitiesLR(G, ℓ, r) 4: Z ← Ø 5: for v ∈ V do 6: if ε′[v] ≠ 0 and (ε′[v] ≤ ℓ or ε′[v] ≥ r) then 7: f[ε′[v]] ← f[ε′[v]] + 1 8: else 9: Z ← Z∪{v} 10: end if 11: end for 12: for i ← 1 to n·q do 13: v ← RandomFrom(Z) 14: ε[v] ← Eccentricities(v) 15: f[ε[v]] ← f[ε[v]] + (1/q) 16: Z ← Z − {v} 17: end for 19: return f |
5.3. Neighborhood Approximation
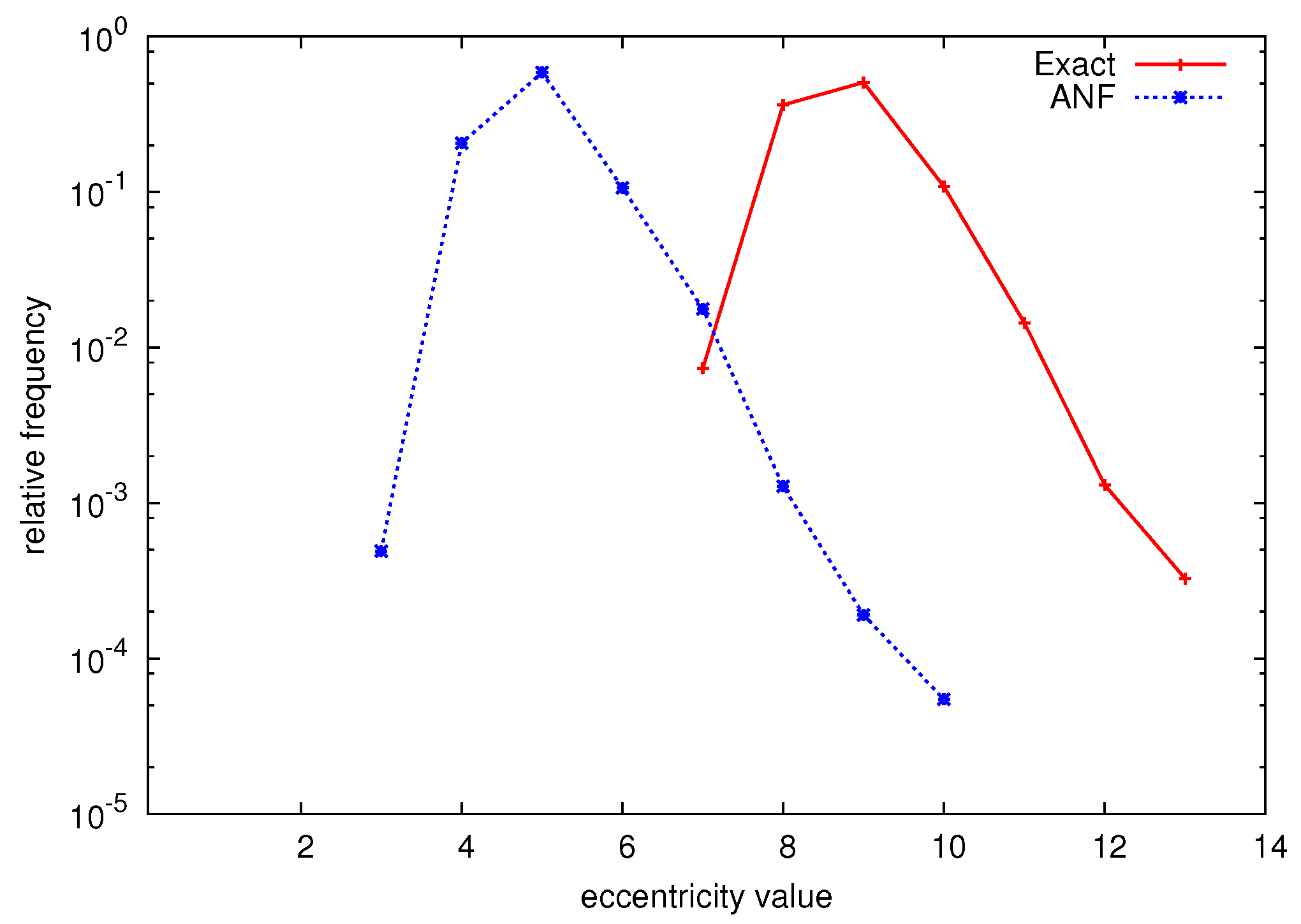
6. Experiments
6.1. Datasets
| Dataset | Type | Source | Nodes | Edges | |||||
|---|---|---|---|---|---|---|---|---|---|
| YEAST | protein | [24] | 1 846 | 4 406 | 13.28 | 11 | 19 | 48 | 4 |
| CA-HEPTH | collab. | [25] | 8 638 | 49 612 | 12.53 | 10 | 18 | 74 | 4 |
| CA-HEPPH | collab. | [25] | 11 204 | 235 238 | 9.40 | 7 | 13 | 12 | 17 |
| DIP20090126 | protein | [26] | 19 928 | 82 406 | 22.01 | 15 | 30 | 1 | 2 |
| CA-CONDMAT | collab. | [13] | 21 363 | 182 572 | 10.58 | 8 | 15 | 6 | 11 |
| CIT-HEPTH | citation | [13] | 27 400 | 704 042 | 10.14 | 8 | 15 | 4 | 4 |
| ENRON | commun. | [22] | 33 696 | 361 622 | 8.77 | 7 | 13 | 248 | 11 |
| CIT-HEPPH | citation | [13] | 34 401 | 841 568 | 9.18 | 7 | 14 | 1 | 2 |
| SLASHDOT | commun. | [27] | 51 083 | 243 780 | 11.66 | 9 | 17 | 7 | 3 |
| P2P-GNUTELLA | peer-to-peer | [25] | 62 561 | 295 756 | 8.94 | 7 | 11 | 55 | 118 |
| social | [28] | 63 392 | 1 633 772 | 9.96 | 8 | 15 | 168 | 7 | |
| EPINIONS | social | [29] | 75 877 | 811 478 | 9.74 | 8 | 15 | 614 | 6 |
| SOC-SLASHDOT | social | [30] | 82 168 | 1 008 460 | 8.91 | 7 | 13 | 484 | 3 |
| ITDK0304-RLINKS | router | [26] | 190 914 | 1 215 220 | 17.09 | 14 | 26 | 155 | 7 |
| WEB-STANFORD | webgraph | [30] | 255 265 | 3 883 852 | 106.49 | 82 | 164 | 1 | 3 |
| WEB-NOTREDAME | webgraph | [31] | 325 729 | 2 180 216 | 27.76 | 23 | 46 | 12 | 172 |
| DBLP20080824 | collab. | [26] | 511 163 | 3 742 140 | 14.79 | 12 | 22 | 72 | 9 |
| EU-2005 | webgraph | [26] | 862 664 | 37 467 426 | 14.03 | 11 | 21 | 3 | 4 |
| FLICKR | social | [28] | 1 624 992 | 30 953 670 | 15.03 | 12 | 24 | 17 | 3 |
| AS-SKITTER | router | [13] | 1 694 616 | 22 188 418 | 21.22 | 16 | 31 | 5 | 2 |
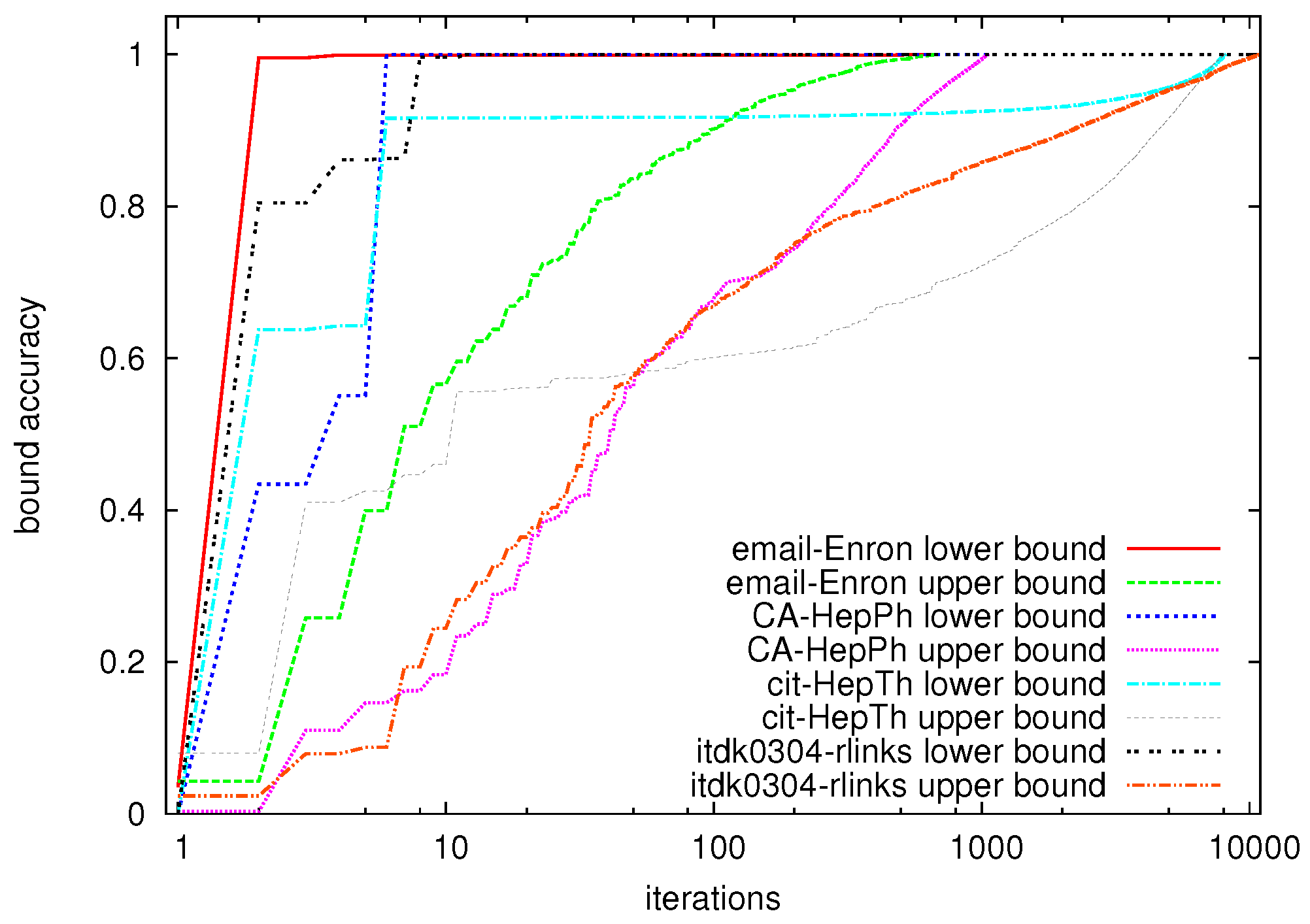
6.2. Exact Algorithm
| Dataset | Nodes | Exact algorithm | Hybrid algorithm | |||||
|---|---|---|---|---|---|---|---|---|
| Pruned | Iterations | Speedup | Exact | Sampling | Total | Speedup | ||
| YEAST | 1 846 | 399 | 213 | 8.7 | 104 | 483 | 587 | 3.1 |
| CA-HEPTH | 8 638 | 351 | 1 055 | 8.2 | 150 | 350 | 500 | 17.3 |
| CA-HEPPH | 11 204 | 282 | 1 588 | 7.1 | 57 | 264 | 321 | 34.9 |
| DIP20090126 | 19 928 | 3 032 | 224 | 89.0 | 8 | 1321 | 1 329 | 15.0 |
| CA-CONDMAT | 21 363 | 353 | 3 339 | 6.4 | 73 | 388 | 461 | 46.3 |
| CIT-HEPTH | 27 400 | 140 | 8 104 | 3.4 | 57 | 444 | 501 | 54.7 |
| ENRON | 33 696 | 8 715 | 678 | 49.7 | 536 | 145 | 681 | 49.5 |
| CIT-HEPPH | 34 401 | 150 | 10 498 | 3.3 | 37 | 271 | 308 | 112 |
| SLASHDOT | 51 083 | 19,255 | 31 | 1648 | 24 | 180 | 204 | 250 |
| P2P-GNUTELLA | 62 561 | 16 413 | 21 109 | 3.0 | 8 575 | 177 | 8 752 | 7.1 |
| 63 392 | 1 075 | 11 185 | 5.7 | 780 | 168 | 948 | 66.9 | |
| EPINIONS | 75 877 | 20 779 | 4302 | 17.6 | 1 308 | 75 | 1 383 | 54.9 |
| SOC-SLASHDOT | 82 168 | 14 848 | 1460 | 56.3 | 990 | 156 | 1 146 | 71.7 |
| ITDK0304-RLINKS | 190 914 | 16 434 | 10 830 | 17.6 | 312 | 960 | 1 272 | 150 |
| WEB-STANFORD | 255 265 | 10 350 | 9 | 28 363 | 8 | 1 198 | 1 206 | 212 |
| WEB-NOTREDAME | 325 729 | 141,178 | 143 | 2277 | 94 | 1 381 | 1 475 | 4528 |
| DBLP20080824 | 511 163 | 22 579 | 42 273 | 12.1 | 150 | 355 | 505 | 1012 |
| EU-2005 | 862 664 | 26 507 | 59 751 | 14.4 | 71 | 1 630 | 1 701 | 507 |
| FLICKR | 1 624 992 | 553 242 | 4 810 | 338 | 200 | 1 618 | 1 818 | 932 |
| AS-SKITTER | 1 694 616 | 114 803 | 42 996 | 39.4 | 14 | 308 | 322 | 5502 |
6.3. Hybrid Algorithm
7. Conclusions
Acknowledgments
References
- Sala, A.; Cao, L.; Wilson, C.; Zablit, R.; Zheng, H.; Zhao, B. Measurement-Calibrated Graph Models for Social Network Experiments. In Proceedings of the 19th ACM International Conference on the World Wide Web (WWW), Raleigh, NC, USA, 26–30 April 2010; pp. 861–870.
- Magoni, D.; Pansiot, J. Analysis of the autonomous system network topology. ACM SIGCOMM Comput. Commun. Rev. 2001, 31, 26–37. [Google Scholar] [CrossRef]
- Magoni, D.; Pansiot, J. Analysis and Comparison of Internet Topology Generators. In Proceedings of the 2nd International Conference on Networking Technologies, Services, and Protocols; Performance of Computer and Communication Networks; and Mobile and Wireless Communications, Pisa, Italy, 19–24 May 2002; pp. 364–375.
- Pavlopoulos, G.; Secrier, M.; Moschopoulos, C.; Soldatos, T.; Kossida, S.; Aerts, J.; Schneider, R.; Bagos, P. Using graph theory to analyze biological networks. BioData Min. 2011, 4, article 10. [Google Scholar] [CrossRef] [PubMed]
- Magnien, C.; Latapy, M.; Habib, M. Fast computation of empirically tight bounds for the diameter of massive graphs. J. Exp. Algorithm. 2009, 13, article 10. [Google Scholar] [CrossRef]
- Takes, F.W.; Kosters, W.A. Determining the Diameter of Small World Networks. In Proceedings of the 20th ACM International Conference on Information and Knowledge Management (CIKM), Glasgow, UK, 24–28 October 2011; pp. 1191–1196.
- Crescenzi, P.; Grossi, R.; Habib, M.; Lanzi, L.; Marino, A. On computing the diameter of real-world undirected graphs. Theor. Comput. Sci. 2012, in press. [Google Scholar] [CrossRef]
- Borgatti, S.P.; Everett, M.G. A graph-theoretic perspective on centrality. Soc. Netw. 2006, 28, 466–484. [Google Scholar] [CrossRef]
- Brandes, U. A faster algorithm for betweenness centrality. J. Math. Sociol. 2001, 25, 163–177. [Google Scholar] [CrossRef]
- Lesniak, L. Eccentric sequences in graphs. Period. Math. Hung. 1975, 6, 287–293. [Google Scholar] [CrossRef]
- Hage, P.; Harary, F. Eccentricity and centrality in networks. Soc. Netw. 1995, 17, 57–63. [Google Scholar] [CrossRef]
- Kang, U.; Tsourakakis, C.; Appel, A.; Faloutsos, C.; Leskovec, J. Hadi: Mining radii of large graphs. ACM Trans. Knowl. Discov. Data (TKDD) 2011, 5, article 8. [Google Scholar] [CrossRef]
- Leskovec, J.; Kleinberg, J.; Faloutsos, C. Graph evolution: Densification and shrinking diameters. ACM Trans. Knowl. Discov. Data (TKDD) 2007, 1, article 2. [Google Scholar] [CrossRef]
- Palmer, C.; Gibbons, P.; Faloutsos, C. ANF: A Fast and Scalable Tool for Data Mining in Massive Graphs. In Proceedings of the 8th ACM International Conference on Knowledge Discovery and Data Mining (KDD), Edmonton, Canada, 23–26 July 2002; pp. 81–90.
- Buckley, F.; Harary, F. Distance in Graphs; Addison-Wesley: Boston, MA, USA, 1990. [Google Scholar]
- Yuster, R.; Zwick, U. Answering Distance Queries in Directed Graphs Using Fast Matrix Multiplication. In Proceedings of the 46th IEEE Symposium on Foundations of Computer Science (FOCS), Pittsburgh, PA, USA, 23–25 October 2005; pp. 389–396.
- Kleinberg, J. The Small-World Phenomenon: An Algorithm Perspective. In Proceedings of the 32nd ACM symposium on Theory of Computing, Portland, OR, USA, 21–23 May 2000; pp. 163–170.
- Faloutsos, M.; Faloutsos, P.; Faloutsos, C. On power-law relationships of the internet topology. ACM SIGCOMM Comput. Commun. Rev. 1999, 29, 251–262. [Google Scholar] [CrossRef]
- Leskovec, J.; Faloutsos, C. Sampling from Large Graphs. In Proceedings of the 12th ACM International Conference on Knowledge Discovery and Data Mining (KDD), Philadelphia, PA, USA, 20–23 August 2006; pp. 631–636.
- Eppstein, D.; Wang, J. Fast Approximation of Centrality. In Proceedings of the 12th ACM-SIAM Symposium on Discrete Algorithms (SODA), Washington, DC, USA, 7–9 January 2001; pp. 228–229.
- Crescenzi, P.; Grossi, R.; Lanzi, L.; Marino, A. A Comparison of Three Algorithms for Approximating the Distance Distribution in Real-World Graphs. In Proceedings of the Theory and Practice of Algorithms in (Computer) Systems (TAPAS), LNCS 6595, Rome, Italy, 18–20 April 2011; pp. 92–103.
- Klimt, B.; Yang, Y. The Enron Corpus: A New Dataset for Email Classification Research. In Proceedings of the 15th European Conference on Machine Learning (ECML), LNCS 3201, Pisa, Italy, 20–24 September 2004; pp. 217–226.
- Boldi, P.; Rosa, M.; Vigna, S. HyperANF: Approximating the Neighbourhood Function of very Large Graphs on a Budget. In Proceedings of the 20th ACM International Conference on the World Wide Web (WWW), Hyderabad, India, 16–20 April 2011; pp. 625–634.
- Jeong, H.; Mason, S.; Barabási, A.; Oltvai, Z. Lethality and centrality in protein networks. Nature 2001, 411, 41–42. [Google Scholar] [CrossRef] [PubMed]
- Leskovec, J.; Kleinberg, J.; Faloutsos, C. Graph evolution: Densification and shrinking diameters. ACM Trans. Knowl. Discov. Data 2007, 1, article 2. [Google Scholar] [CrossRef]
- Sommer, C. Graphs. Available online: http://www.sommer.jp/graphs (accessed on 1 September 2012).
- Gómez, V.; Kaltenbrunner, A.; López, V. Statistical Analysis of the Social Network and Discussion Threads in Slashdot. In Proceedings of the 17th International Conference on the World Wide Web (WWW), Beijng, China, 21–25 April 2008; pp. 645–654.
- Mislove, A.; Marcon, M.; Gummadi, K.; Druschel, P.; Bhattacharjee, B. Measurement and Analysis of Online Social Networks. In Proceedings of the 7th ACM Conference on Internet Measurement, San Diego, CA, USA, 24–26 October 2007; pp. 29–42.
- Richardson, M.; Agrawal, R.; Domingos, P. Trust Management for the Semantic Web. In Proceedings of the 2nd International Semantic Web Conference (ISWC), LNCS 2870, Sanibel Island, FL, USA, 20–23 October 2003; pp. 351–368.
- Leskovec, J.; Lang, K.; Dasgupta, A.; Mahoney, M. Community structure in large networks: Natural cluster sizes and the absence of large well-defined clusters. Int. Math. 2009, 6, 29–123. [Google Scholar] [CrossRef]
- Barabási, A.; Albert, R.; Jeong, H. Scale-free characteristics of random networks: The topology of the world-wide web. Phys. Stat. Mech. Appl. 2000, 281, 69–77. [Google Scholar] [CrossRef]
- Magoni, D.; Pansiot, J. Internet Topology Modeler Based on Map Sampling. In Proceedings of the 7th International Symposium on Computers and Communications (ISCC), Taormina, Italy, 1–4 July 2002; pp. 1021–1027.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Takes, F.W.; Kosters, W.A. Computing the Eccentricity Distribution of Large Graphs. Algorithms 2013, 6, 100-118. https://doi.org/10.3390/a6010100
Takes FW, Kosters WA. Computing the Eccentricity Distribution of Large Graphs. Algorithms. 2013; 6(1):100-118. https://doi.org/10.3390/a6010100
Chicago/Turabian StyleTakes, Frank W., and Walter A. Kosters. 2013. "Computing the Eccentricity Distribution of Large Graphs" Algorithms 6, no. 1: 100-118. https://doi.org/10.3390/a6010100
APA StyleTakes, F. W., & Kosters, W. A. (2013). Computing the Eccentricity Distribution of Large Graphs. Algorithms, 6(1), 100-118. https://doi.org/10.3390/a6010100




