1. Introduction
In many emerging applications one needs to process a continuous stream of data in real time. Sensor networks [
1], network monitoring [
2], and real-time analysis of financial data [
3,
4] are examples of such applications. Monitoring queries is a particular class of queries in the context of data streams. Previous work in this area deals with monitoring simple aggregates [
2], or term frequency occurrence in a set of distributed streams [
5].
A general framework for efficient local algorithms monitoring
l2 norm of the data average of large networks of computers, wireless sensors, or mobile devices was introduced in [
6], and further developed in [
7]. The current contribution is motivated by results recently reported in [
8,
9] with focus on a special case of the general model considered in [
7]. This special case can be briefly described as follows:
Let
![Algorithms 05 00379 i002]()
be a set of data streams collected at
n nodes. Let v
1(
t),...,v
n(
t) be
d dimensional real time varying vectors derived from the streams. For a function
![Algorithms 05 00379 i004]()
we would like to confirm the inequality
while minimizing communication between the nodes. Monitoring inequality (1), or monitoring geometric location of the mean is a problem that can be addressed using a variety of different mathematical tools. A specific choice of a monitoring tool is up to the user. We note that the problem as stated above does not specify any particular tool, l2, or any other norm that is required to address it.
The problem was recently addressed in [
10], where the approach proposed imposes equal constraints on each node. In addition to previously used
l2 norm (see, e.g., [
6,
7,
8,
9,
11]) the paper provides theoretical framework for using a wide variety of convex functions, and, as an illustration, runs numerical experiments using
l2,
l1 and
l∞ norms. In all numerical experiments reported in [
10] an application of the same algorithm with
l1 norm generates superior results. This paper extends results in [
10] in a machine learning direction—a constraint imposed on each node depends on the stream history at the node.
As a simple illustration of the problem considered in the paper we focus on two scalar functions v1(t) and v2(t), and the identity function f (i.e., f(x) = x).We would like to guarantee the inequality
while keeping the nodes silent as much as possible. A possible strategy is to verify the initial inequality
![Algorithms 05 00379 i012]()
and to keep both nodes silent while
The first time
t1 when one of the functions, say
v1(
t), crosses the boundary of the local constraint,
i.e.,
![Algorithms 05 00379 i015]()
the nodes communicate, the mean
v(
t1) is computed, the local constraint
δ is updated and made available to the nodes, and nodes are kept silent as long as the inequalities hold.
The main contributions of this paper are listed next. We demonstrate that:
1. This approach works for a non-linear monitoring function f.
2. The results depend on the choice of a norm, and the numerical results reported show that l2 is probably not the best norm when one aims to minimize communication between nodes. In addition to the numerical results presented we also provide a simple illustrative example that highlights this point (see Remark 4.2).
3. Selection of node dependent local constraints may decrease communication between the nodes.
4. The approach suggested in [
10] and adopted in this paper paves the way to achieve further communication savings by clustering nodes, and monitoring cluster coordinators. Although this research direction is beyond the scope of this paper we address it briefly in
Section 6.
In the next section we provide a text mining related example that leads to a non-linear threshold function f.
2. Text Mining Application
Let T be a finite text collection (for example a collection of mail or news items). We denote the size of the set T by |T|. We will be concerned with two subsets of T:
1. R–the set of “relevant" texts (text not labeled as spam),
2. F–the set of texts that contain a “feature" (word or term for example).
We denote complements of the sets by
![Algorithms 05 00379 i020]()
respectably (
i.e.,
![Algorithms 05 00379 i021]()
), and consider the relative size of the four sets
![Algorithms 05 00379 i022]()
as follows:
Note that
The function
f is defined on the simplex (
i.e.,
![Algorithms 05 00379 i025]()
,
![Algorithms 05 00379 i026]()
), and given by
where
![Algorithms 05 00379 i028]()
throughout the paper. We next relate empirical version of information gain Equation (3) and the information gain (see e.g., [
12]).
Let Y and X be random variable with know distributions
Entropy of Y is defined by
Entropy of
Y conditional on
X =
x denoted by
![Algorithms 05 00379 i035]()
is defined by
Conditional entropy
![Algorithms 05 00379 i037]()
and information gain
![Algorithms 05 00379 i038]()
are given by
Information gain is symmetric, indeed
Due to convexity of
![Algorithms 05 00379 i041]()
, information gain is non-negative
It is easy to see that Equation (3) provides information gain for the “feature".
As an example, we consider
n agents installed on
n different servers and a stream of texts arriving at the servers. Let
![Algorithms 05 00379 i044]()
be the last
w texts received at the
![Algorithms 05 00379 i046]()
server, with
![Algorithms 05 00379 i047]()
. Note that
i.e., entries of the global contingency table
![Algorithms 05 00379 i049]()
are the average of the local contingency tables
![Algorithms 05 00379 i050]()
.
For the given “feature" and a predefined positive threshold r we would like to verify the inequality
while minimizing communication between the servers. Note that Equation (3) is a nonlinear function. The case of a nonlinear monitoring function is different from that of linear one (in fact [
8] calls the nonlinear monitoring function case “fundamentally different"). In the next section we demonstrate the difference, and describe an efficient way to handle the nonlinear case.
3. Non-Linear Threshold Function: An Example
We start with a slight modification of a simple one dimensional example presented in [
8].
Example 3.1Let ![Algorithms 05 00379 i053]() , and
, and ![Algorithms 05 00379 i054]() ,
, ![Algorithms 05 00379 i055]() are scalar values stored at two distinct nodes. Note that if
are scalar values stored at two distinct nodes. Note that if ![Algorithms 05 00379 i056]() , and
, and ![Algorithms 05 00379 i057]() , then
, then If ![Algorithms 05 00379 i060]() , and
, and ![Algorithms 05 00379 i061]() , then
, then Finally, when ![Algorithms 05 00379 i064]() , and
, and ![Algorithms 05 00379 i061]() one has
one has The simple illustrative example leads the authors of [
8] to conclude that it is impossible to determine from the values of
f at the nodes whether its value at the average is above the threshold or not. The remedy proposed is to consider the vectors
![Algorithms 05 00379 i066]()
and to monitor the values of
f on the convex hull conv
![Algorithms 05 00379 i067]()
instead of the value of
f at the average Equation (1). This strategy leads to sufficient conditions for Equation (1), and may be conservative.
The monitoring techniques for values of
f on conv
![Algorithms 05 00379 i067]()
without communication between the nodes are based on the following two observations:
1.
Convexity property. The mean v(
t) is given by
![Algorithms 05 00379 i069]()
,
i.e., the mean v(
t) is in the convex hull of
![Algorithms 05 00379 i070]()
, and
![Algorithms 05 00379 i071]()
is available to node
j without much communication with other nodes.
2. If
![Algorithms 05 00379 i073]()
is an
l2 ball of radius
![Algorithms 05 00379 i074]()
centered at
![Algorithms 05 00379 i075]()
, then
can be monitored by node
j with no communication with other nodes, Equation (8) allows to split monitoring of conv
![Algorithms 05 00379 i078]()
into
n independent tasks executed by the
n nodes separately and without communication.
While the inclusion Equation (8) holds when
![Algorithms 05 00379 i081]()
is substituted by
![Algorithms 05 00379 i082]()
with
![Algorithms 05 00379 i083]()
as we show later (see Remark 4.3) the inclusion fails when, for example,
![Algorithms 05 00379 i084]()
(for experimental results obtained with different norms see
Section 5).
In this paper we propose an alternative strategy that will be briefly explained next using Example 3.1,
![Algorithms 05 00379 i053]()
, and assignment provided by Equation (7). Let
δ be a positive number. Consider two intervals of radius
δ centered at
![Algorithms 05 00379 i064]()
and
![Algorithms 05 00379 i061]()
,
i.e., we are interested in the intervals
If
![Algorithms 05 00379 i086]()
,
![Algorithms 05 00379 i087]()
, and
δ is small, then the average
![Algorithms 05 00379 i088]()
is not far from
![Algorithms 05 00379 i089]()
, and
![Algorithms 05 00379 i090]()
is not far from 7 (hence positive). In fact the sum of the intervals is the interval
![Algorithms 05 00379 i092]()
, and
The “zero" points
![Algorithms 05 00379 i094]()
of
f are -3 and 3, and as soon as
δ is large enough so that the interval
![Algorithms 05 00379 i097]()
“hits" a point where
f vanishes, communication between the nodes is required in order to verify Equation (1). In this particular example as long as
![Algorithms 05 00379 i098]()
, and, therefore,
no communication is required between the nodes.
The condition presented above is a sufficient condition that guarantees Equation (1). As any sufficient condition is, this condition can be conservative. In fact when the distance is provided by the
l2 norm, this sufficient condition is more conservative than the one provided by “ball monitoring" Equation (9) suggested in [
8]. On the other hand, since only a scalar
δ should be communicated to each node, the value of the updated mean
![Algorithms 05 00379 i102]()
should not be transmitted (hence communication savings are possible), and there is no need to compute the distance from the center of each ball
![Algorithms 05 00379 i103]()
,
![Algorithms 05 00379 i104]()
,
![Algorithms 05 00379 i105]()
to the zero set
![Algorithms 05 00379 i094]()
. For detailed comparison of results we refer the reader to [
10].
We conclude the section by remarking that when inequality Equation (1) is reversed the same technique can be used to monitor the reversed inequality while minimizing communication between the nodes. We provide additional details in
Section 5. In the next section we extend the above “monitoring with no communication" argument to the general vector setting. The approach suggested in the next section is motivated by an earlier research on robust stability of control systems (see e.g., [
13]).
4. Convex Minimization Problem
In this section we state the monitoring problem as a convex minimization problem. For an appropriate analysis background we refer the interested reader to the classical monograph [
14]. For the relevant convex analysis material see [
15].
Consider the following optimization problem:
Problem 4.1For a function ![Algorithms 05 00379 i106]() concave with respect to the first d variables
concave with respect to the first d variables ![Algorithms 05 00379 i108]() and convex with respect to the last nd variables
and convex with respect to the last nd variables ![Algorithms 05 00379 i110]() , solve
, solve A solution for Problem 4.1 with appropriately selected
![Algorithms 05 00379 i112]()
concludes the section.
The connection between Problem 4.1, and the monitoring problem is explained next. Let
B be a
![Algorithms 05 00379 i114]()
matrix made of
n blocks, where each block is the
![Algorithms 05 00379 i115]()
identity matrix multiplied by
![Algorithms 05 00379 i116]()
, so that for a set of
n vectors
![Algorithms 05 00379 i117]()
in
![Algorithms 05 00379 i118]()
one has
Assume that inequality Equation (1) holds for the vector w,
i.e.,
![Algorithms 05 00379 i120]()
. We are looking for a vector x “nearest" to w so that
![Algorithms 05 00379 i121]()
,
i.e.,
![Algorithms 05 00379 i122]()
for some
![Algorithms 05 00379 i123]()
(where
![Algorithms 05 00379 i094]()
is the zero set of
f,
i.e.,
![Algorithms 05 00379 i124]()
). We now fix z
![Algorithms 05 00379 i125]()
and denote the distance from w to the set
![Algorithms 05 00379 i126]()
. Note that for each y inside the ball of radius
![Algorithms 05 00379 i127]()
centered at w, one has
![Algorithms 05 00379 i128]()
. If y belongs to a ball of radius
![Algorithms 05 00379 i129]()
centered at w, then the inequality
![Algorithms 05 00379 i130]()
holds true.
Let
![Algorithms 05 00379 i001]()
be a “norm" on
![Algorithms 05 00379 i131]()
(specific functions
F we run the numerical experiments with will be described later). The nearest “bad" vector problem described above is the following.
Problem 4.2For ![Algorithms 05 00379 i125]() identify
identify We note that Equation (13) is equivalent to
![Algorithms 05 00379 i135]()
The function
is concave (actually linear) in
λ, and convex in x. Hence (see e.g., [
15])
The right hand side of the above equality can be conveniently written as follows
The conjugate
![Algorithms 05 00379 i140]()
of a function
![Algorithms 05 00379 i141]()
is defined by
![Algorithms 05 00379 i142]()
(see e.g., [
15]). We note that
hence to compute
one has to deal with
For many functions
g the conjugate
![Algorithms 05 00379 i147]()
can be easily computed. Next we list conjugate functions for the most popular norms
1.
![Algorithms 05 00379 i148]()
2.
![Algorithms 05 00379 i149]()
3.
![Algorithms 05 00379 i150]()
We note that some of the functions
F we consider in this paper are different from
lP norms (see
Table 1 for the list of the functions). We first select
![Algorithms 05 00379 i153]()
, and show below that in this case
Note that with the choice
![Algorithms 05 00379 i155]()
the problem
![Algorithms 05 00379 i156]()
becomes
Since
![Algorithms 05 00379 i158]()
the problem reduces to
The solution to this maximization problem is
![Algorithms 05 00379 i160]()
. Analogously, when
one has
![Algorithms 05 00379 i162]()
Assuming
![Algorithms 05 00379 i163]()
one has to look at
Hence
and
![Algorithms 05 00379 i166]()
. Finally the value for
![Algorithms 05 00379 i167]()
is given by
![Algorithms 05 00379 i168]()
. When
![Algorithms 05 00379 i169]()
one has
![Algorithms 05 00379 i170]()
. For clarity sake we collect the above results in
Table 1.
Table 1.
norm–ball radius correspondence for three different norms and fixed
![Algorithms 05 00379 i171]()
.
In the algorithm described below the norm is denoted just by
![Algorithms 05 00379 i175]()
(numerical experiments presented in
Section 5 are conducted with all three norms). The monitoring algorithm we propose is the following.
Algorithm 4.1Threshold monitoring algorithm.
1. Set ![Algorithms 05 00379 i176]() .
. 2. Until end of stream.
3. Set ![Algorithms 05 00379 i177]() ,
, ![Algorithms 05 00379 i104]() (
(i.e.
, remember “initial" values for the vectors). 4. Set ![Algorithms 05 00379 i178]() (for definition of w see Equation (12)).
(for definition of w see Equation (12)). 5. Set ![Algorithms 05 00379 i180]() .
. 6. If ![Algorithms 05 00379 i181]() for each
for each ![Algorithms 05 00379 i104]()
go to step 5
else
go to step 3
In what follows, we assume that transmission of a double precision real number amounts to broadcasting one message. The message computation is based on the assumption that all nodes are updated by a new text simultaneously. When mean update is required, a coordinator (root) requests and receives messages from the nodes.
We next count a number of messages that should be broadcast per one iteration if the local constraint
δ is violated at least at one node. We shall denote the set of all nodes by N, the set of nodes complying with the constraint by
![Algorithms 05 00379 i182]()
, and the set of nodes violating the constraint by
![Algorithms 05 00379 i183]()
(so that
![Algorithms 05 00379 i184]()
). The cardinality of the sets is denoted by
![Algorithms 05 00379 i185]()
respectively, so that
![Algorithms 05 00379 i186]()
. Assuming
![Algorithms 05 00379 i187]()
one has the following:
1.
![Algorithms 05 00379 i188]()
nodes violators transmit their scalar ID and new coordinates to the root (
![Algorithms 05 00379 i189]()
messages).
2. the root sends scalar requests for new coordinates to the complying
![Algorithms 05 00379 i190]()
nodes (
![Algorithms 05 00379 i191]()
messages).
3. the
![Algorithms 05 00379 i191]()
complying nodes transmit new coordinates to the root (
![Algorithms 05 00379 i193]()
messages).
4. root updates itself, computes new distance
δ to the surface, and sends
δ to each node (
![Algorithms 05 00379 i194]()
messages).
This leads to total of
We conclude the section with three remarks. The first one compares conservatism of Algorithm 4.1 and the one suggested in [
8]. The second one again compares the ball cover suggested in [
8] and application of Algorithm 4.1 with
l1 norm. The last one shows by an example that Equation (8) fails when
![Algorithms 05 00379 i081]()
is substituted by
![Algorithms 05 00379 i196]()
. Significance of this negative result becomes clear in
Section 5.
Remark 4.1 Let ![Algorithms 05 00379 i197]() ,and
,and ![Algorithms 05 00379 i198]() . If the Step 6 inequality holds for each node, then each point of the ball centered at
. If the Step 6 inequality holds for each node, then each point of the ball centered at ![Algorithms 05 00379 i199]() with radius
with radius ![Algorithms 05 00379 i200]() is contained in the l2 ball of radius δ centered at
is contained in the l2 ball of radius δ centered at v
(see Figure 2). Hence the sufficient condition offered by Algorithm 4.1 is more conservative than the one suggested in [
8]
.
Figure 2.
conservative cover by a single l2 ball.
Figure 2.
conservative cover by a single l2 ball.
Algorithm 4.1 can be executed with a variety of different norms, and, as we show next, l2 might not be the best one when communication between the nodes should be minimized.
Remark 4.2 Let ![Algorithms 05 00379 i202]()
,
thedistance is given by the l1 norm, and the aim is to monitor the inequality ![Algorithms 05 00379 i204]() . Let
. Let On the other hand the l1 distance from ![Algorithms 05 00379 i216]() to the set
to the set ![Algorithms 05 00379 i217]() is 1, and since
is 1, and since Algorithm 4.1 requires no communication between nodes at time t1. In this particular case the sufficient condition offered by Algorithm 4.1 is less conservative than the one suggested in [
8]
.
Figure 3.
l2 ball cover requires communication.
Figure 3.
l2 ball cover requires communication.
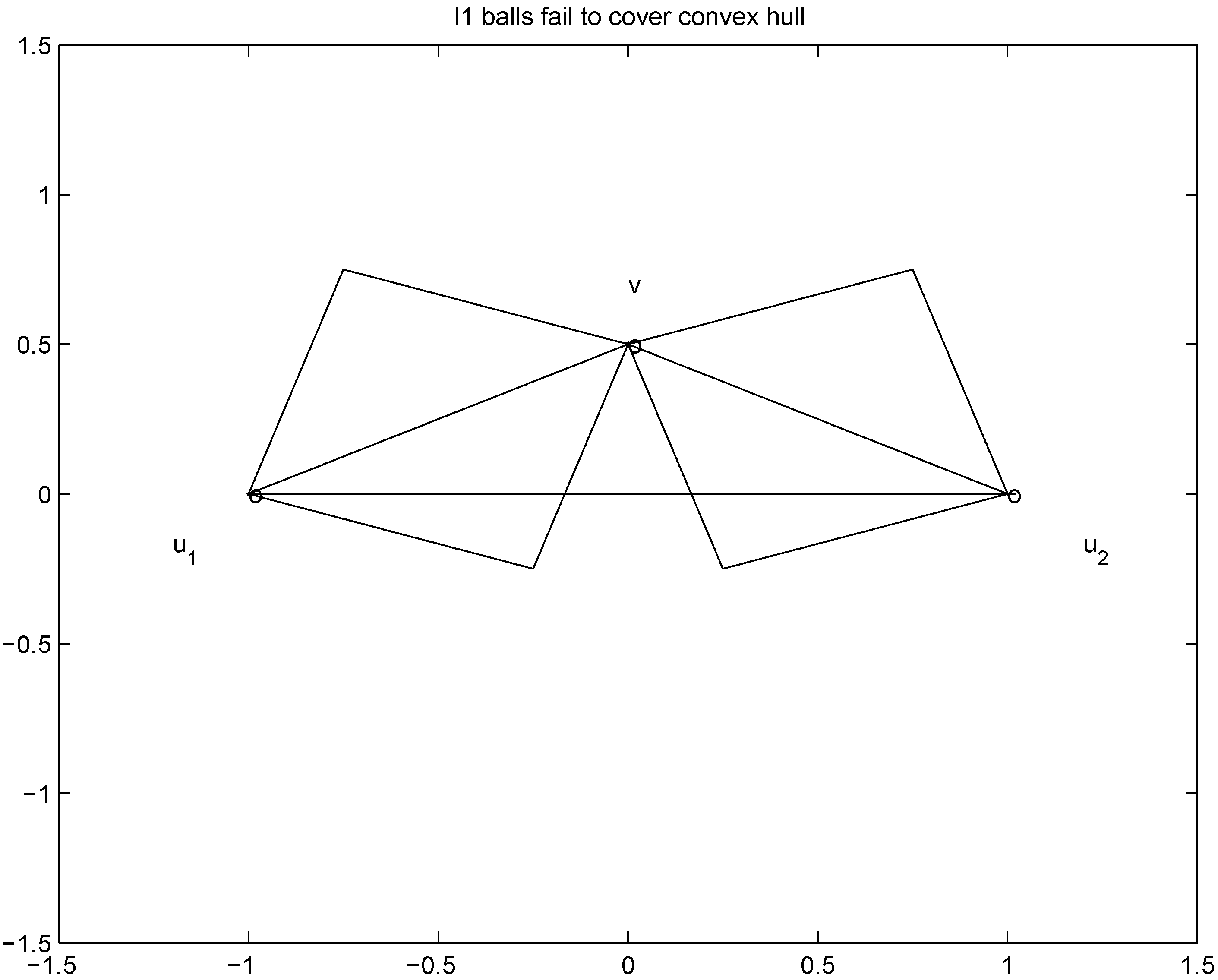
Remark 4.3It is easy to see that inclusion Equation (8) fails when ![Algorithms 05 00379 i220]() is an l1 ball of radius
is an l1 ball of radius ![Algorithms 05 00379 i221]() centered at
centered at ![Algorithms 05 00379 i222]() . Indeed, when, for example,
. Indeed, when, for example, In the next section we apply Algorithm 4.1 to a real life data and report number of required mean computations.
Figure 4.
failed cover by l1 balls.
Figure 4.
failed cover by l1 balls.
5. Experimental Results
We apply Algorithm 4.1 to data streams generated from the Reuters Corpus RCV1–V2. The data is available from [
16] and consists of 781,265 tokenized documents with DID (document ID) ranging from 2651 to 810596.
The methodology described below attempts to follow that presented in [
8]. We simulate
n streams by arranging the feature vectors in ascending order with respect to DID, and selecting feature vectors for the stream in the round robin fashion.
In the Reuters Corpus RCV1–V2 each document is labeled as belonging to one or more categories. We label a vector as “relevant" if it belongs to the “CORPORATE/INDUSTRIAL" (“CCAT") category, and “spam" otherwise. Following [
9] we focus on three features: “bosnia", “ipo", and “febru". Each experiment was performed with 10 nodes, where each node holds a sliding window containing the last 6700 documents it received.
First we use 67,000 documents to generate initial sliding windows. The remaining 714,265 documents are used to generate data streams, hence the selected feature information gain is computed 714,265 times. Based on all the documents contained in the sliding window at each one of the 714,266 time instances, we compute and graph 714,266 information gain values for the feature “bosnia" (see
Figure 5).
For the experiments described below the threshold value
r is predefined, and the goal is to monitor the inequality
![Algorithms 05 00379 i226]()
while minimizing communication between the nodes. From now on we shall assume simultaneous arrival of a new text at each node.
Figure 5.
information gain values for the feature “bosnia”.
Figure 5.
information gain values for the feature “bosnia”.
As new texts arrive, the local constraint (
i.e., inequalities
![Algorithms 05 00379 i227]()
) at each node is verified. If at least one node violates the local constraint, the average
![Algorithms 05 00379 i228]()
is updated. Our numerical experiment with the feature “bosnia", the
l2 norm, and the threshold
![Algorithms 05 00379 i229]()
(reported in [
8] as the threshold for feature “bosnia" incurring the highest communication cost) shows overall 4006 computation of the mean vector. An application of Equation (14) yields 240,360 messages. We repeat this experiment with
l∞, and
l1 norms. The results obtained and collected in
Table 2 show that the smallest number of the mean updates is required for the
l1 norm.
Table 2.
number of mean computations, messages, and crossings per norm for feature “bosnia" with threshold
![Algorithms 05 00379 i229]()
.
Table 2.
number of mean computations, messages, and crossings per norm for feature “bosnia" with threshold ![Algorithms 05 00379 i229]() .
.
| Distance | Mean Comps | Messages | LL | LG | GL | GG |
|---|
| l2 | 4006 | 240,360 | 959 | 2 | 2 | 3043 |
| l∞ | 3801 | 228,060 | 913 | 2 | 2 | 2884 |
| l1 | 3053 | 183,180 | 805 | 2 | 2 | 2244 |
Throughout the iterations the mean
![Algorithms 05 00379 i231]()
goes through a sequence of updates, and the values
![Algorithms 05 00379 i232]()
may be larger than, equal to, or less than the threshold
r. We monitor the case
![Algorithms 05 00379 i233]()
the same way as that of
![Algorithms 05 00379 i234]()
. In addition to the number of mean computations, we collect statistics concerning “crossings" (or lack of thereof),
i.e., number of instances when the location of the mean v and its update
![Algorithms 05 00379 i235]()
relative to the surface
![Algorithms 05 00379 i236]()
are either identical or different. Specifically over the monitoring period we denote by:
1. “LL" the number of instances when
![Algorithms 05 00379 i237]()
and
![Algorithms 05 00379 i238]()
,
2. “LG" the number of instances when
![Algorithms 05 00379 i237]()
and
![Algorithms 05 00379 i239]()
,
3. “GL" the number of instances when
![Algorithms 05 00379 i240]()
and
![Algorithms 05 00379 i238]()
,
4. “GG" the number of instances when
![Algorithms 05 00379 i240]()
and
![Algorithms 05 00379 i239]()
.
The number of “crossings" is reported in the last four columns of
Table 2.
Note that variation of vectors
![Algorithms 05 00379 i003]()
does not have to be uniform. Taking on account distribution of signals at each node may lead to additional communication savings. We illustrate this statement by a simple example involving just two nodes. If, for example, there is a reason to believe that
then the number of node violations may be reduced by imposing node dependent constraints
so that the faster varying signal at the second node enjoys larger “freedom" of change, while the inequality
holds true. Assignments of “weighted" local constraints requires information provided by Equation (15). With no additional assumptions about signal distribution, this information is not available. Unlike [
11] we refrain from making assumptions regarding possible underlying data distributions, instead we estimate the weights as follows:
Broadcasts of weights cause increase of total number of messages per iteration to
With inequalities in Step 6 of Algorithm 4.1 substituted by
![Algorithms 05 00379 i254]()
the number of mean computations is reported in
Table 3.
It is of interest to compare results presented in
Table 3 with those reported, for example, in [
9]. The comparison, however, is not an easy task. While [
9] reports the threshold
![Algorithms 05 00379 i229]()
as the threshold value that incurred the highest communication cost, the paper leaves the concept of “communication cost" undefined (we define transmission of a double precision real number as a single “message"). In addition [
9] provides a graph of “Messages
vs. Threshold" only. It appears that the maximal value of “bosnia Messages
vs. Threshold" graph is somewhere between 100,000 and 200,000.
Table 3.
number of mean computations, messages, and crossings per norm for feature “bosnia" with threshold
![Algorithms 05 00379 i229]()
, and stream dependent local constraint
![Algorithms 05 00379 i255]()
.
Table 3.
number of mean computations, messages, and crossings per norm for feature “bosnia" with threshold ![Algorithms 05 00379 i229]() , and stream dependent local constraint
, and stream dependent local constraint ![Algorithms 05 00379 i255]() .
.
| Distance | Mean Comps | Messages | LL | LG | GL | GG |
|---|
| l2 | 2388 | 191,040 | 726 | 2 | 2 | 1658 |
| l∞ | 2217 | 177,360 | 658 | 2 | 2 | 1555 |
| l1 | 1846 | 147,680 | 611 | 2 | 2 | 1231 |
We repeat the experiments with “ipo" and “febru" and report the results in
Table 4 and
Table 5 respectively. The results obtained with stream dependent local constraints is a significant improvement over those presented in [
10]. Consistent with the results in [
10]
l1 norm comes up as the norm that requires smallest number of mean updates in all reported experiments.
Table 4.
number of mean computations, messages, and crossings per norm for feature “febru" with threshold
![Algorithms 05 00379 i229]()
, and stream dependent local constraint
![Algorithms 05 00379 i255]()
.
Table 4.
number of mean computations, messages, and crossings per norm for feature “febru" with threshold ![Algorithms 05 00379 i229]() , and stream dependent local constraint
, and stream dependent local constraint ![Algorithms 05 00379 i255]() .
.
| Distance | Mean Comps | Messages |
|---|
| l2 | 1491 | 119,280 |
| l∞ | 1388 | 111,040 |
| l1 | 1304 | 104,320 |
Table 5.
number of mean computations, messages, and crossings per norm for feature “ipo" with threshold
![Algorithms 05 00379 i229]()
, and stream dependent local constraint
![Algorithms 05 00379 i255]()
.
Table 5.
number of mean computations, messages, and crossings per norm for feature “ipo" with threshold ![Algorithms 05 00379 i229]() , and stream dependent local constraint
, and stream dependent local constraint ![Algorithms 05 00379 i255]() .
.
| Distance | Mean Comps | Messages |
|---|
| l2 | 7656 | 612,480 |
| l∞ | 7377 | 590,160 |
| l1 | 6309 | 504,720 |
6. Future Research Directions
In what follows we briefly outline a number of immediate research directions we plan to pursue.
The local constraints introduced in this paper depend on history of a data stream at each node, and variations
![Algorithms 05 00379 i256]()
over time contribute uniformly to local constraints. Attaching more weight to recent changes than to older ones may contribute to further improvement of monitoring process.
Table 6 (borrowed from [
10]) shows that in about 75% of instances (3034 out of 4006) the mean
![Algorithms 05 00379 i257]()
is updated because of a single node violation. This observation naturally leads to the idea of clustering nodes, and independent monitoring of the node clusters equipped with a coordinator. The monitoring will become a two step procedure. At the first step node violations are checked in each node separately. If a node violates its local constraint, the corresponding cluster computes updated cluster coordinator. At the second step, violations of local constraints by coordinators are checked, and if at least one violation is detected the root is updated.
Table 6 indicates that in most of the instances only one coordinator will be effected, and, since communication within cluster requires less messages, the two step procedure briefly described above has a potential to bring additional savings.
Table 6.
number of nodes simultaneously violating local constraints. for feature “bosnia" with threshold
![Algorithms 05 00379 i229]()
, and
l2 norm
Table 6.
number of nodes simultaneously violating local constraints. for feature “bosnia" with threshold ![Algorithms 05 00379 i229]() , and l2 norm
, and l2 norm
| nodes | violations |
|---|
| 1 | 3034 |
| 2 | 620 |
| 3 | 162 |
| 4 | 70 |
| 5 | 38 |
| 6 | 26 |
| 7 | 34 |
| 8 | 17 |
| 9 | 5 |
| 10 | 0 |
We note that a standard clustering problem is often described as “…finding and describing cohesive or homogeneous chunks in data, the clusters" (see e.g., [
17]). The monitoring data streams problem requires to assign to the same cluster
i nodes
![Algorithms 05 00379 i259]()
so that the total change within cluster
![Algorithms 05 00379 i260]()
is minimized,
i.e., nodes with
different variations
![Algorithms 05 00379 i261]()
that cancel out each other as much as possible should be assigned to the same cluster. Hence, unlike classical clustering procedures, one needs to combine “dissimilar" nodes together. This is a challenging new type of a difficult clustering problem.
Realistically, verification of inequality
![Algorithms 05 00379 i262]()
should be conducted with an error margin (
i.e., the inequality
![Algorithms 05 00379 i263]()
should be investigated, see [
9]). A possible effect of an error margin on the required communication load is another direction of future research.
 be a set of data streams collected at n nodes. Let v1(t),...,vn(t) be d dimensional real time varying vectors derived from the streams. For a function
be a set of data streams collected at n nodes. Let v1(t),...,vn(t) be d dimensional real time varying vectors derived from the streams. For a function  we would like to confirm the inequality
we would like to confirm the inequality 

 and to keep both nodes silent while
and to keep both nodes silent while
 the nodes communicate, the mean v(t1) is computed, the local constraint δ is updated and made available to the nodes, and nodes are kept silent as long as the inequalities hold.
the nodes communicate, the mean v(t1) is computed, the local constraint δ is updated and made available to the nodes, and nodes are kept silent as long as the inequalities hold.
 respectably (i.e.,
respectably (i.e.,  ), and consider the relative size of the four sets
), and consider the relative size of the four sets  as follows:
as follows:

 ,
,  ), and given by
), and given by 
 throughout the paper. We next relate empirical version of information gain Equation (3) and the information gain (see e.g., [12]).
throughout the paper. We next relate empirical version of information gain Equation (3) and the information gain (see e.g., [12]).

 is defined by
is defined by 
 and information gain
and information gain  are given by
are given by 

 , information gain is non-negative
, information gain is non-negative 
 be the last w texts received at the
be the last w texts received at the  server, with
server, with  . Note that
. Note that 
 are the average of the local contingency tables
are the average of the local contingency tables  .
.
 , and
, and  ,
,  are scalar values stored at two distinct nodes. Note that if
are scalar values stored at two distinct nodes. Note that if  , and
, and  , then
, then

 , and
, and  , then
, then 

 , and
, and  one has
one has 
 and to monitor the values of f on the convex hull conv
and to monitor the values of f on the convex hull conv  instead of the value of f at the average Equation (1). This strategy leads to sufficient conditions for Equation (1), and may be conservative.
instead of the value of f at the average Equation (1). This strategy leads to sufficient conditions for Equation (1), and may be conservative. without communication between the nodes are based on the following two observations:
without communication between the nodes are based on the following two observations: , i.e., the mean v(t) is in the convex hull of
, and
is available to node j without much communication with other nodes.
is an l2 ball of radius
centered at
, then


 into n independent tasks executed by the n nodes separately and without communication.
into n independent tasks executed by the n nodes separately and without communication.
 is substituted by
is substituted by  with
with  as we show later (see Remark 4.3) the inclusion fails when, for example,
as we show later (see Remark 4.3) the inclusion fails when, for example,  (for experimental results obtained with different norms see Section 5).
(for experimental results obtained with different norms see Section 5). , and assignment provided by Equation (7). Let δ be a positive number. Consider two intervals of radius δ centered at
, and assignment provided by Equation (7). Let δ be a positive number. Consider two intervals of radius δ centered at  and
and  , i.e., we are interested in the intervals
, i.e., we are interested in the intervals 
 ,
,  , and δ is small, then the average
, and δ is small, then the average  is not far from
is not far from  , and
, and  is not far from 7 (hence positive). In fact the sum of the intervals is the interval
is not far from 7 (hence positive). In fact the sum of the intervals is the interval  , and
, and 
 of f are -3 and 3, and as soon as δ is large enough so that the interval
of f are -3 and 3, and as soon as δ is large enough so that the interval  “hits" a point where f vanishes, communication between the nodes is required in order to verify Equation (1). In this particular example as long as
“hits" a point where f vanishes, communication between the nodes is required in order to verify Equation (1). In this particular example as long as  , and, therefore,
, and, therefore, 
 should not be transmitted (hence communication savings are possible), and there is no need to compute the distance from the center of each ball
should not be transmitted (hence communication savings are possible), and there is no need to compute the distance from the center of each ball  ,
,  ,
,  to the zero set
to the zero set  . For detailed comparison of results we refer the reader to [10].
. For detailed comparison of results we refer the reader to [10]. concave with respect to the first d variables
concave with respect to the first d variables  and convex with respect to the last nd variables
and convex with respect to the last nd variables  , solve
, solve 
 concludes the section.
concludes the section. matrix made of n blocks, where each block is the
matrix made of n blocks, where each block is the  identity matrix multiplied by
identity matrix multiplied by  , so that for a set of n vectors
, so that for a set of n vectors  in
in  one has
one has 
 . We are looking for a vector x “nearest" to w so that
. We are looking for a vector x “nearest" to w so that  , i.e.,
, i.e.,  for some
for some  (where
(where  is the zero set of f, i.e.,
is the zero set of f, i.e.,  ). We now fix z
). We now fix z  and denote the distance from w to the set
and denote the distance from w to the set  . Note that for each y inside the ball of radius
. Note that for each y inside the ball of radius  centered at w, one has
centered at w, one has  . If y belongs to a ball of radius
. If y belongs to a ball of radius  centered at w, then the inequality
centered at w, then the inequality  holds true.
holds true. be a “norm" on
be a “norm" on  (specific functions F we run the numerical experiments with will be described later). The nearest “bad" vector problem described above is the following.
(specific functions F we run the numerical experiments with will be described later). The nearest “bad" vector problem described above is the following. identify
identify
 The function
The function 





 can be easily computed. Next we list conjugate functions for the most popular norms
can be easily computed. Next we list conjugate functions for the most popular norms



 , and show below that in this case
, and show below that in this case 
 the problem
the problem  becomes
becomes 
 the problem reduces to
the problem reduces to 
 . Analogously, when
. Analogously, when 
 Assuming
Assuming  one has to look at
one has to look at 

 . Finally the value for
. Finally the value for  is given by
is given by  . When
. When  one has
one has  . For clarity sake we collect the above results in Table 1.
. For clarity sake we collect the above results in Table 1.


 (numerical experiments presented in Section 5 are conducted with all three norms). The monitoring algorithm we propose is the following.
(numerical experiments presented in Section 5 are conducted with all three norms). The monitoring algorithm we propose is the following..
,
(i.e., remember “initial" values for the vectors).
(for definition of w see Equation (12)).
.
for each
go to step 5elsego to step 3 , and the set of nodes violating the constraint by
, and the set of nodes violating the constraint by  (so that
(so that  ). The cardinality of the sets is denoted by
). The cardinality of the sets is denoted by  respectively, so that
respectively, so that  . Assuming
. Assuming  one has the following:
one has the following:nodes violators transmit their scalar ID and new coordinates to the root (
messages).
nodes (
messages).
complying nodes transmit new coordinates to the root (
messages).
messages).

 is substituted by
is substituted by  . Significance of this negative result becomes clear in Section 5.
. Significance of this negative result becomes clear in Section 5. ,and
,and  . If the Step 6 inequality holds for each node, then each point of the ball centered at
. If the Step 6 inequality holds for each node, then each point of the ball centered at  with radius
with radius  is contained in the l2 ball of radius δ centered at v (see Figure 2). Hence the sufficient condition offered by Algorithm 4.1 is more conservative than the one suggested in [8].
is contained in the l2 ball of radius δ centered at v (see Figure 2). Hence the sufficient condition offered by Algorithm 4.1 is more conservative than the one suggested in [8]. 
 ,
,
 . Let
. Let 
 with
with  , and
, and  with
with  . At the same time
. At the same time 
 . It is easy to see that the l2 ball of radius
. It is easy to see that the l2 ball of radius  centered at
centered at  intersects the l1 ball of radius 1 centered at
intersects the l1 ball of radius 1 centered at  (see Figure 3). Hence the algorithm suggested in [8] requires nodes to communicate at time t1.
(see Figure 3). Hence the algorithm suggested in [8] requires nodes to communicate at time t1. to the set
to the set  is 1, and since
is 1, and since 

 is an l1 ball of radius
is an l1 ball of radius  centered at
centered at  . Indeed, when, for example,
. Indeed, when, for example, 

 while minimizing communication between the nodes. From now on we shall assume simultaneous arrival of a new text at each node.
while minimizing communication between the nodes. From now on we shall assume simultaneous arrival of a new text at each node.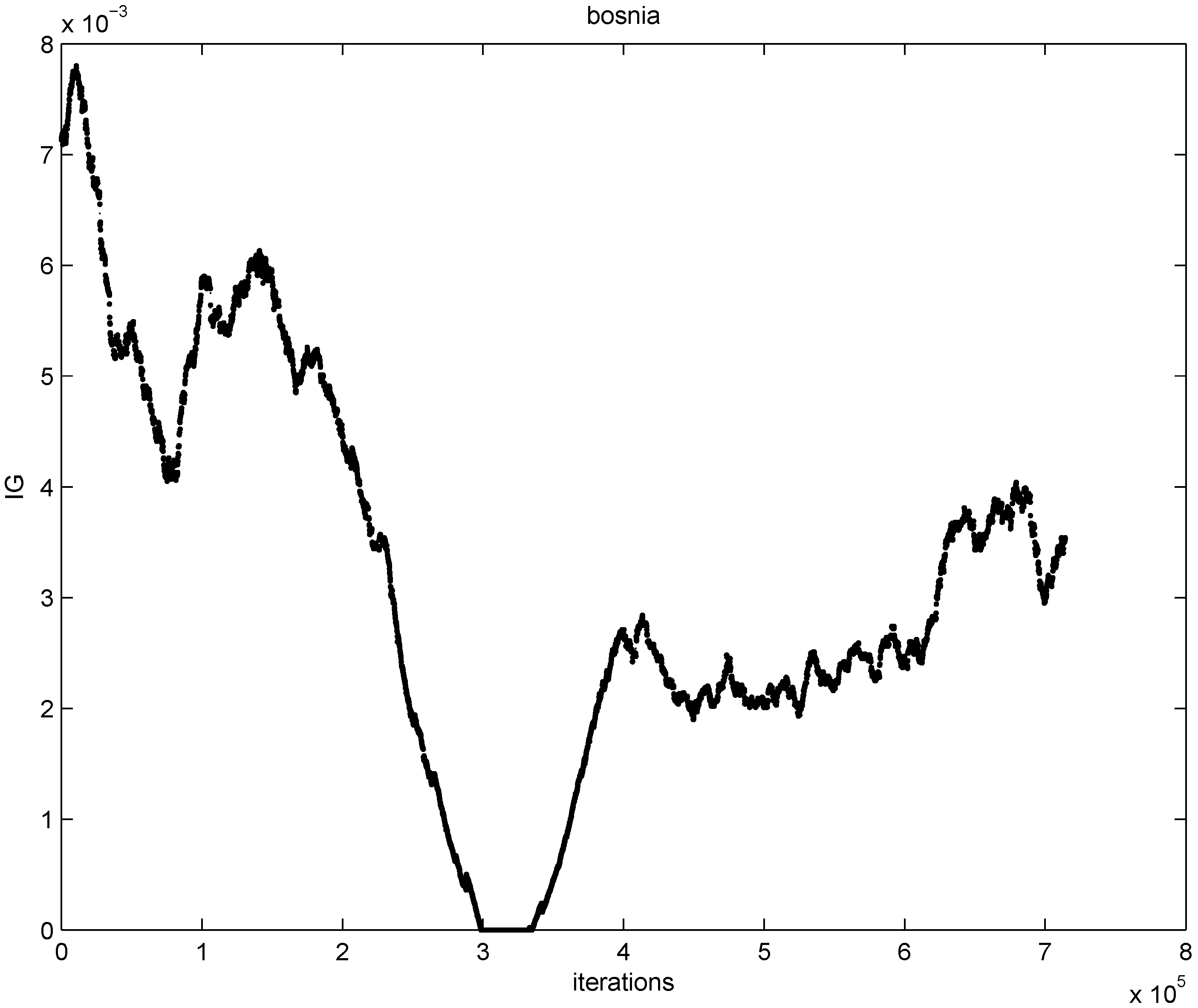
 ) at each node is verified. If at least one node violates the local constraint, the average
) at each node is verified. If at least one node violates the local constraint, the average  is updated. Our numerical experiment with the feature “bosnia", the l2 norm, and the threshold
is updated. Our numerical experiment with the feature “bosnia", the l2 norm, and the threshold  (reported in [8] as the threshold for feature “bosnia" incurring the highest communication cost) shows overall 4006 computation of the mean vector. An application of Equation (14) yields 240,360 messages. We repeat this experiment with l∞, and l1 norms. The results obtained and collected in Table 2 show that the smallest number of the mean updates is required for the l1 norm.
(reported in [8] as the threshold for feature “bosnia" incurring the highest communication cost) shows overall 4006 computation of the mean vector. An application of Equation (14) yields 240,360 messages. We repeat this experiment with l∞, and l1 norms. The results obtained and collected in Table 2 show that the smallest number of the mean updates is required for the l1 norm.  .
.
 goes through a sequence of updates, and the values
goes through a sequence of updates, and the values  may be larger than, equal to, or less than the threshold r. We monitor the case
may be larger than, equal to, or less than the threshold r. We monitor the case  the same way as that of
the same way as that of  . In addition to the number of mean computations, we collect statistics concerning “crossings" (or lack of thereof), i.e., number of instances when the location of the mean v and its update
. In addition to the number of mean computations, we collect statistics concerning “crossings" (or lack of thereof), i.e., number of instances when the location of the mean v and its update  relative to the surface
relative to the surface  are either identical or different. Specifically over the monitoring period we denote by:
are either identical or different. Specifically over the monitoring period we denote by:and
,
and
,
and
,
and
.
 does not have to be uniform. Taking on account distribution of signals at each node may lead to additional communication savings. We illustrate this statement by a simple example involving just two nodes. If, for example, there is a reason to believe that
does not have to be uniform. Taking on account distribution of signals at each node may lead to additional communication savings. We illustrate this statement by a simple example involving just two nodes. If, for example, there is a reason to believe that 


each node computes
If at timea local constraint is violated, then, in addition to
messages (see Equation (14)), each node j broadcasts
to the root, the root computes
, and transmits the updated weights
back to node j.
 the number of mean computations is reported in Table 3.
the number of mean computations is reported in Table 3. as the threshold value that incurred the highest communication cost, the paper leaves the concept of “communication cost" undefined (we define transmission of a double precision real number as a single “message"). In addition [9] provides a graph of “Messages vs. Threshold" only. It appears that the maximal value of “bosnia Messages vs. Threshold" graph is somewhere between 100,000 and 200,000.
as the threshold value that incurred the highest communication cost, the paper leaves the concept of “communication cost" undefined (we define transmission of a double precision real number as a single “message"). In addition [9] provides a graph of “Messages vs. Threshold" only. It appears that the maximal value of “bosnia Messages vs. Threshold" graph is somewhere between 100,000 and 200,000. , and stream dependent local constraint
, and stream dependent local constraint  .
.
 , and stream dependent local constraint
, and stream dependent local constraint  .
.
 , and stream dependent local constraint
, and stream dependent local constraint  .
.
 over time contribute uniformly to local constraints. Attaching more weight to recent changes than to older ones may contribute to further improvement of monitoring process.
over time contribute uniformly to local constraints. Attaching more weight to recent changes than to older ones may contribute to further improvement of monitoring process. is updated because of a single node violation. This observation naturally leads to the idea of clustering nodes, and independent monitoring of the node clusters equipped with a coordinator. The monitoring will become a two step procedure. At the first step node violations are checked in each node separately. If a node violates its local constraint, the corresponding cluster computes updated cluster coordinator. At the second step, violations of local constraints by coordinators are checked, and if at least one violation is detected the root is updated. Table 6 indicates that in most of the instances only one coordinator will be effected, and, since communication within cluster requires less messages, the two step procedure briefly described above has a potential to bring additional savings.
is updated because of a single node violation. This observation naturally leads to the idea of clustering nodes, and independent monitoring of the node clusters equipped with a coordinator. The monitoring will become a two step procedure. At the first step node violations are checked in each node separately. If a node violates its local constraint, the corresponding cluster computes updated cluster coordinator. At the second step, violations of local constraints by coordinators are checked, and if at least one violation is detected the root is updated. Table 6 indicates that in most of the instances only one coordinator will be effected, and, since communication within cluster requires less messages, the two step procedure briefly described above has a potential to bring additional savings. , and l2 norm
, and l2 norm
 so that the total change within cluster
so that the total change within cluster  is minimized, i.e., nodes with different variations
is minimized, i.e., nodes with different variations  that cancel out each other as much as possible should be assigned to the same cluster. Hence, unlike classical clustering procedures, one needs to combine “dissimilar" nodes together. This is a challenging new type of a difficult clustering problem.
that cancel out each other as much as possible should be assigned to the same cluster. Hence, unlike classical clustering procedures, one needs to combine “dissimilar" nodes together. This is a challenging new type of a difficult clustering problem. should be conducted with an error margin (i.e., the inequality
should be conducted with an error margin (i.e., the inequality  should be investigated, see [9]). A possible effect of an error margin on the required communication load is another direction of future research.
should be investigated, see [9]). A possible effect of an error margin on the required communication load is another direction of future research. 




































