Application of Genetic Control with Adaptive Scaling Scheme to Signal Acquisition in Global Navigation Satellite System Receiver
Abstract
:1. Introduction
2. Problem Formulation
2.1. Signal Model

 . The variables fd, θ and τ denote the Doppler frequency, carrier phase, and code delay, respectively. The noise components w(tk) are referred to as white Gaussian noise distribution, in which the power spectrum density is N0/2. The N0 stands for single sideband power spectrum density of noise. G(·) is the filtered code sequence expressed by C/A-code, P-code or binary offset carrier (BOC) signal [12,21,22].
. The variables fd, θ and τ denote the Doppler frequency, carrier phase, and code delay, respectively. The noise components w(tk) are referred to as white Gaussian noise distribution, in which the power spectrum density is N0/2. The N0 stands for single sideband power spectrum density of noise. G(·) is the filtered code sequence expressed by C/A-code, P-code or binary offset carrier (BOC) signal [12,21,22]. 2.2. Correlation and Detection Process

 is an unfiltered local replica. The in-phase Ik and quadrature-phase Qk are squared respectively and then summed altogether. The result is accumulated after K non-coherent integration time. The correlation output is shown as follows:
is an unfiltered local replica. The in-phase Ik and quadrature-phase Qk are squared respectively and then summed altogether. The result is accumulated after K non-coherent integration time. The correlation output is shown as follows:


 and code delay
and code delay  can be obtained. The constant threshold v = vσ2ln(PFA-1) is often selected in order to achieve a certain probability of false alarm in noise alone by employing the well-known Neyman–Pearson criterion [26].
can be obtained. The constant threshold v = vσ2ln(PFA-1) is often selected in order to achieve a certain probability of false alarm in noise alone by employing the well-known Neyman–Pearson criterion [26]. 3. Methodology
3.1. Signal Acquisition with Genetic Control
Step 1. Doppler frequency and code delay encoding

Step 2. Fitness function determination

Step 3. Initial population size selection

Step 4. Selection and reproduction

Step 5. Crossover


Step 6. Mutation
 (1→0), shown as follows:
(1→0), shown as follows:
3.2. GC with Adaptive Scaling Scheme

 . When the Qmax(p) exceeds the noise floor, GC method initiates two procedures. The first procedure is that when Qmax(p) exceeds the set detection threshold v (depicted in Section 2), it indicates that the desired signal has been acquired and the GC process terminates. The second procedure is when the Qmax(p) is between the detection threshold and the initial detection threshold. In such case, the adaptive scaling scheme begins to control the number of initial population. The initial detection margin is set at 1.4Q and the definition of Q is the same as that in Equation 7. The only difference is that Q is the fitness value acquired under the scenario of no desired signal. Meanwhile, the scaler also controls and adjusts the search space of Doppler frequency and code delay, which is depicted in the following:
. When the Qmax(p) exceeds the noise floor, GC method initiates two procedures. The first procedure is that when Qmax(p) exceeds the set detection threshold v (depicted in Section 2), it indicates that the desired signal has been acquired and the GC process terminates. The second procedure is when the Qmax(p) is between the detection threshold and the initial detection threshold. In such case, the adaptive scaling scheme begins to control the number of initial population. The initial detection margin is set at 1.4Q and the definition of Q is the same as that in Equation 7. The only difference is that Q is the fitness value acquired under the scenario of no desired signal. Meanwhile, the scaler also controls and adjusts the search space of Doppler frequency and code delay, which is depicted in the following: 





3.3. Termination Criterion

4. Simulation Results and Performance Analysis
4.1. Performance Criterion

4.2. Simulation Parameters Setup


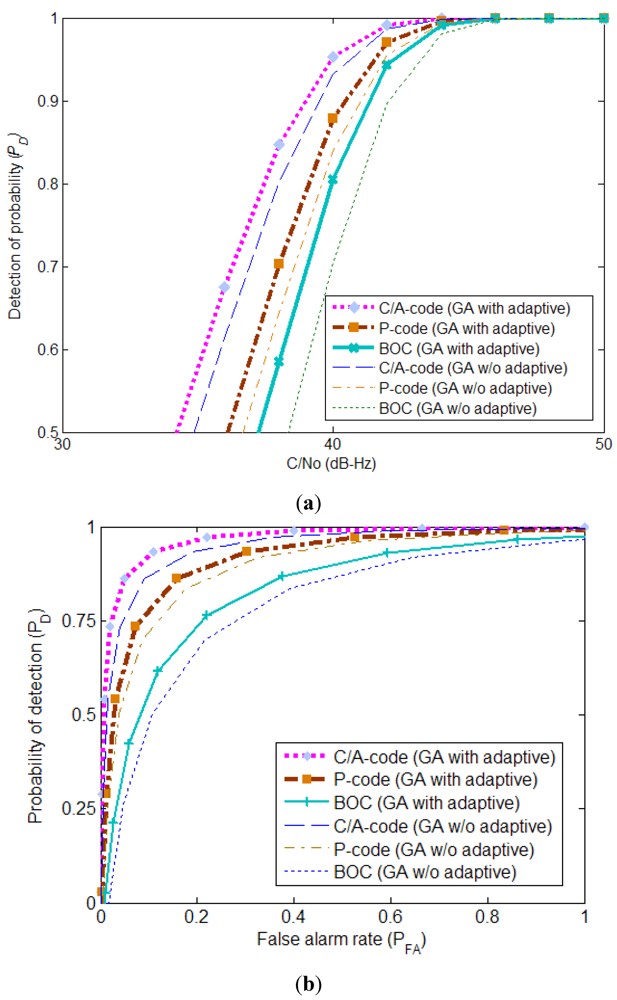
4.3. Simulation Results

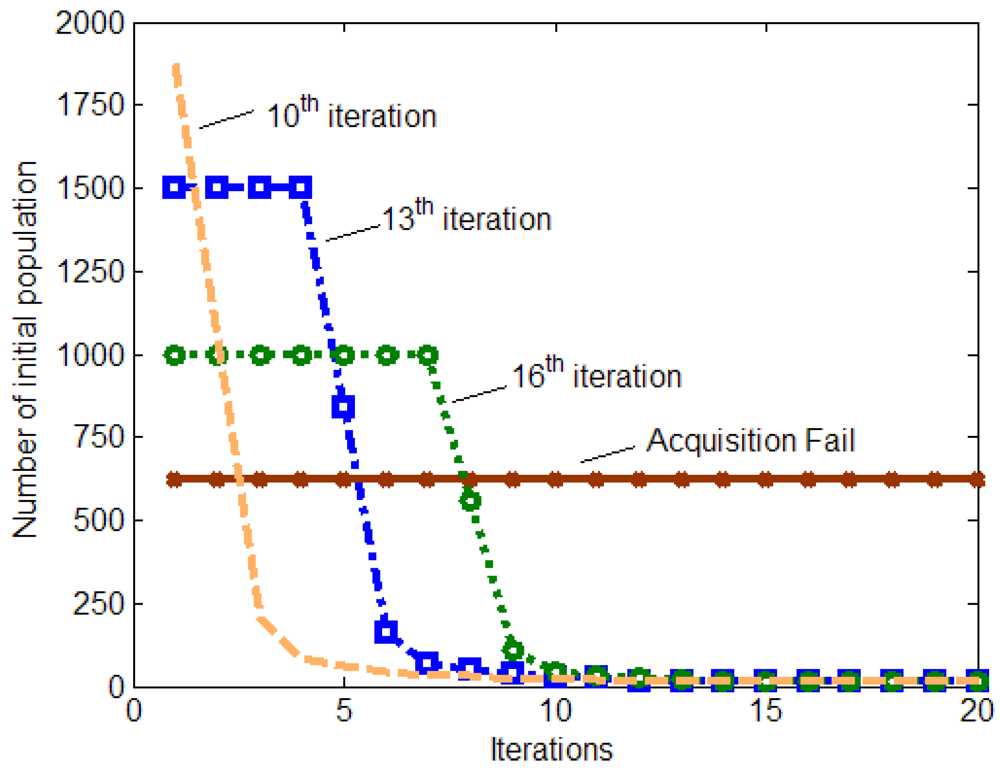
| Method | Traditional (Serial search) (Fixed search space bound) | Parallel code delay [28] (Fixed code/Doppler search space bound) | Parallel frequency [28] (Fixed code/Doppler search space bound) | Parallel code delay [12] (Adaptive logiccontrol method) | Parallel code delay (GC with adaptive scaling scheme) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Type | C/A-code | P-code/BOC | C/A code | P-code/BOC | C/A-code | P-code/BOC | C/A-code | P-code/BOC | C/A-code | P-code/BOC |
| Execute time | 1505.2 | 2202.3/1704.3 | 720.5 | 1392.3/983,2 | 901.2 | 1793.8/1103.6 | 700.4 | 1226.1/960.4 | 650.4 | 1783.2/850.9 |
| Repetitions (Without Pull-in) | 401 (50 Hz step size) | 401 (50 Hz step size) | 401 (50 Hz step size) | 401 (50 Hz step size) | 1 ms code chip length | 0.5 s/4 ms code chip length | 34 (10~1 KHz) | 140/78 (10~280 Hz) | 39 | 145/96 |
| Parameter Precision | Poor (Count on number of bins) | Poor (Count on number of bins) | Fair (Count on number of bins) | Fair (Count on number of bins) | Fair | Poor | High | Fair | High | Fair |
| Complexity | Low | Fair | Fair (Count onFFT size) | High (Count on FFT size) | Fair (Count onFFT size) | High (Count on FFT size) | Fair | High | Fair | High (Count on number of population) |
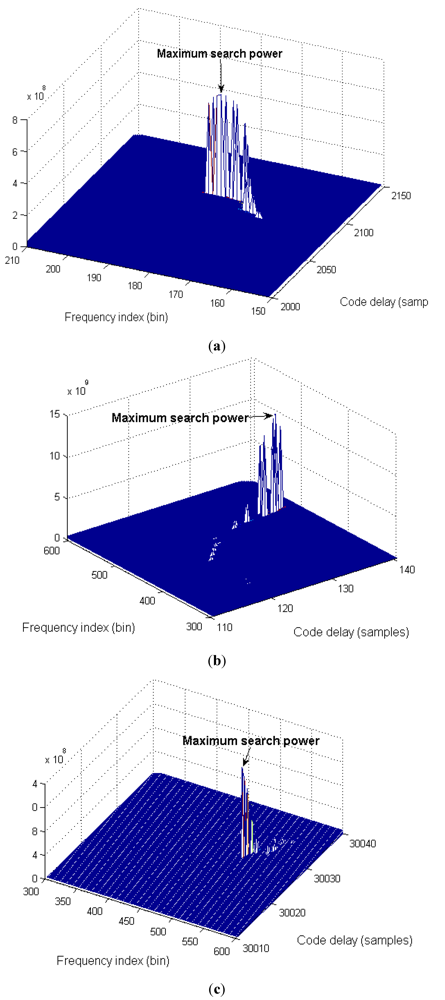
4.4. Experimental Results
| PRN | Traditional (Serial search) method (frequency search step size: 50 Hz) | GC with adaptive scaling scheme | GC w/o adaptive scaling scheme | ||||||
|---|---|---|---|---|---|---|---|---|---|
 |  (samples) (samples) | PSNR |  |  (samples) (samples) | PSNR (Iterations) |  |  (samples) (samples) | PSNR (Iterations) | |
| 11 | 2050 | 12728 | 21.1701 | 2014 | 12731 | 21.2801(15) | 2021 | 12724 | 21.2709(17) |
| 8 | 2250 | 550 | 18.7897 | 2275 | 553 | 18.8675(29) | 2268 | 548 | 18.8602(57) |
| 27 | 2000 | 4363 | 21.2701 | 2020 | 4360 | 21.2784(15) | 2010 | 4365 | 21.2712(25) |
| 25 | 1350 | 9790 | 21.0104 | 1370 | 9787 | 21.0341(14) | 1364 | 9782 | 21.0292(25) |
| 28 | 6600 | 12400 | 21.5693 | 6610 | 12403 | 21.5718(14) | 6614 | 12407 | 21.5782(34) |
| 19 | 6050 | 10911 | 21.5326 | 6069 | 10912 | 21.5332(14) | 6049 | 10911 | 21.5301(26) |
| 20 | 2450 | 15905 | 19.1023 | 2441 | 15907 | 19.1238(17) | 2438 | 15906 | 19.1211(25) |
| 17 | 5350 | 4016 | 23.7094 | 5380 | 4014 | 23.7832(11) | 5383 | 4016 | 23.7621(13) |
| 4 | 2900 | 3105 | 18.7036 | 2884 | 3103 | 18.7432 (30) | 2890 | 3106 | 18.7419(60) |

| Signal type | GPS C/A PRN-8 | ||
|---|---|---|---|
| Method | Traditional(Serial search) | GC with adaptive scaling scheme | GC w/o adaptive scaling scheme (Fixed code/Doppler search space bound) |
Code delay
 (chip) (chip) | 34.43 chip | 553 samples | 548 samples |
| (550 samples) | |||
Frequency shift
 (Hz) (Hz) | 2250 Hz | 2275 Hz | 2268 Hz |
| Repetitions | 6563568 (401 × 16368) | 16048 | 84000 |
| (50 Hz step size) | (29 iterations) | (25 iterations) × 1500 | |
| Post-correlation SNR (dB) | 18.7897 | 18.8675 | 18.8602 |
| Execution Time (sec) | 1817.24 | 806 | 705 |
5. Conclusions
Acknowledgements
References
- Parkinson, B.W.; Spilker, J.J. Global Positioning System: Theory and Applications; American Institute of Aeronautics and Astronautics: Washington, DC, USA, 1996; Volume 1. [Google Scholar]
- Braasch, M.S.; van Dierendonck, A.J. GPS receiver architectures and measurements. Proc. IEEE 1999, 87, 48–64. [Google Scholar] [CrossRef]
- Van Nee, D.J.R.; Coenen, A.J.R.M. New fast GPS code-acquisition technique using FFT. Electron. Lett. 1991, 27, 158–160. [Google Scholar] [CrossRef]
- Namgoong, W.; Meng, T.H. Minimizing power consumption in direct sequence spread spectrum correlators by resampling IF samples-part I: Performance analysis. IEEE Trans. Circuits Syst. II 2001, 48, 450–459. [Google Scholar] [CrossRef]
- Starzyk, J.; Zhu, Z. Averaging Correlation for C/A Code Acquisition and Tracking in Frequency Domain. In Proceeding of the IEEE Midwest Symposium on Circuits and Systems, Dayton, OH, USA, 14-17 August 2001; 2, pp. 905–908.
- Pang, J.; van Graas, F.; Starzyk, J.; Zhu, Z. Fast direct GPS P-code acquisition. GPS Solut. 2003, 7, 168–175. [Google Scholar] [CrossRef]
- Akopian, D. Fast FFT based GPS satellite acquisition methods. IEE Proc Radar Sonar Navig. 2005, 152, 277–286. [Google Scholar] [CrossRef]
- Wilde, W.D.E.; Sleewaegen, J.M.; Simsky, A.; Vandewiele, C.; Peeters, E.; Grauwen, J.; Boon, F. New Fast Signal Acquisition Unit for GPS/Galileo Receivers. In Proceeding of the ENC GNSS, Manchester, UK, 8-10 May 2006; pp. 1–11.
- Brown, A.; May, M.; Tanju, B. Benefits of software GPS receivers for enhanced signal processing. GPS Solut. 2000, 4, 56–66. [Google Scholar] [CrossRef]
- Sagiraju, P.K.; Raju, G.V.S.; Akopian, D. Fast acquisition implementation for high sensitivity global positioning systems receivers based on joint and reduced space search. IET Radar Sonar Navi. 2008, 2, 376–387. [Google Scholar]
- Jan, S.S.; Lin, Y.C. A new multi-C/A code acquisition method for GPS. GPS Solut. 2009, 13, 293–303. [Google Scholar] [CrossRef]
- Chang, C.L. Using fuzzy logic controller with adaptive detection scheme for fast acquisition of satellite navigation signals. J. Chin. Inst. Eng. 2010, 33, 367–378. [Google Scholar]
- Bagley, J.D. The Behavior of Adaptive Systems Which Employ Genetic and Correlative Algorithms. Ph.D. Dissertation, University of Michigan, Ann Arbor, MI, USA, 1967. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Dugan, N.; Erkoç, Ş. Genetic algorithms in application to the geometry optimization of nanoparticles. Algorithms 2009, 2, 410–428. [Google Scholar] [CrossRef]
- De Jong, K.A. An Analysis of the Behavior of a Class of Genetic Adaptive Systems. Ph.D. Dissertation, University of Michigan, Ann Arbor, MI, USA, 1975. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Fogel, D.B. An introduction to simulated evolutionary optimization. IEEE Trans. Neural. Netw. 1994, 5, 3–14. [Google Scholar] [CrossRef]
- Cilla, R.; Patricio, M.A.; García, J.; Berlanga, A.; Molina, J.M. Recognizing human activities from sensors using hidden Markov models constructed by feature selection techniques. Algorithms 2009, 2, 282–300. [Google Scholar] [CrossRef]
- Chang, C.L.; Shou, H.N.; Juang, J.C. Application of Innovation-Based Genetic Control Scheme to Signal Acquisition for Global Navigation Satellite Systems. In Proceedings of theICROS-SICE International Joint Conference, Fukuoka, Japan, 18-21 August 2009; pp. 3569–3574.
- Rockwell International Corporation, Interface Control Document ICD-GPS-200; Rockwell International Corporation: Downey, CA, USA, 1991; pp. 9–86.
- European Space Agency. Galileo Open Service Signal-In-Space Interface Control Document (OS SIS ICD). September 2010. Available online: http://ec.europa.eu/enterprise/policies/satnav/galileo/open-service/index_en.htm (accessed on 16 February 2012).
- Zigangirov, K.S. Theory of Code Division Multiple Access Communication; IEEE Press, Wiley: New York, NY, USA, 2004. [Google Scholar]
- Torrieri, D. Principles of Spread-Spectrum Communication Systems; Springer: New York, NY, USA, 2004. [Google Scholar]
- Barket, M. Signal Detection and Estimation, 2nd ed; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Dillard, G.M. Mean-level detection of nonfluctuating signals. IEEE Trans. Aerosp. Electron. Syst. 1974, AES-10, 795–799. [Google Scholar] [CrossRef]
- Davis, L. Handbook of Genetic Algorithms; Van Nostrand Reinhold: New York, NY, USA, 1991. [Google Scholar]
- Borre, K.; Akos, D.M.; Bertelsen, N.; Rinder, P.; Jensen, S.H. A Software-Defined GPS and Galileo Receiver: A Signal-Frequency Approach; Birkhauser Boston: New York, NY, USA, 2007. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chang, C.-L.; Shou, H.-N. Application of Genetic Control with Adaptive Scaling Scheme to Signal Acquisition in Global Navigation Satellite System Receiver. Algorithms 2012, 5, 56-75. https://doi.org/10.3390/a5010056
Chang C-L, Shou H-N. Application of Genetic Control with Adaptive Scaling Scheme to Signal Acquisition in Global Navigation Satellite System Receiver. Algorithms. 2012; 5(1):56-75. https://doi.org/10.3390/a5010056
Chicago/Turabian StyleChang, Chung-Liang, and Ho-Nien Shou. 2012. "Application of Genetic Control with Adaptive Scaling Scheme to Signal Acquisition in Global Navigation Satellite System Receiver" Algorithms 5, no. 1: 56-75. https://doi.org/10.3390/a5010056
APA StyleChang, C.-L., & Shou, H.-N. (2012). Application of Genetic Control with Adaptive Scaling Scheme to Signal Acquisition in Global Navigation Satellite System Receiver. Algorithms, 5(1), 56-75. https://doi.org/10.3390/a5010056






