Segment LLL Reduction of Lattice Bases Using Modular Arithmetic
Abstract
:1. Introduction
1.1. Definitions of Reduced Lattice Bases
- D1.
- A basis is called size-reduced if The notion of a size reduced basis goes back to Hermite [12].
- D2.
- A basis is called (δ,η)-reduced if for , , , . For and it is called 2-reduced because the above inequality becomes . A basis is called δ-LLL reduced if it is size-reduced and δ-reduced. It is simply called LLL reduced if it is size-reduced and 2-reduced. The LLL reduced basis was introduced by Lenstra, Lenstra, and Lovász [7].
- D3.
- A basis is called semi-reduced if it is size-reduced and satisfies weaker conditions for .
- D4.
- A basis is called Korkine-Zolotarev basis if it is size-reduced and if for where is the orthogonal projection of L on the orthogonal complement of .
- D5.
- A basis is called Block KZ reduced basis if it is size-reduced and if the projections of all -blocks on the orthogonal complement of for are Korkine-Zolotarev reduced.
- D6.
- A basis is called k-segment LLL reduced if the following conditions hold.
- C1.
- It is size-reduced.
- C2.
- for , , i.e., vectors within each segment of the basis are δ-reduced, and
- C3.
- Letting , two successive segments of the basis are connected by the following two conditions.
- C3.1.
- for.
- C3.2.
- for.
1.2. Discussion on Various Reduced Bases
| Algorithm | Lower Bounds on | Upper Bounds on | Arithmetic Steps | Precision |
|---|---|---|---|---|
| LLL reduced [7] | ||||
| LLL reduced [13] | ||||
| Modular LLL [14] | ||||
| Semi-reduced [8] | ||||
| Kannan [9] | ||||
| Block KZ [10,15] 1 | ||||
| Segment LLL [11] | ||||
| Mod-Seg LLL | ||||
| Mod-Seg LLL FMM | ||||
| Nguyen and Stehle [16] | fl | |||
| Schnorr [17] SLL | fl |
1.3. Paper Contribution and Organization
2. Methods for LLL-Reduced Lattice Bases
2.1. The LLL Basis Reduction Algorithm
Size Reduction of B
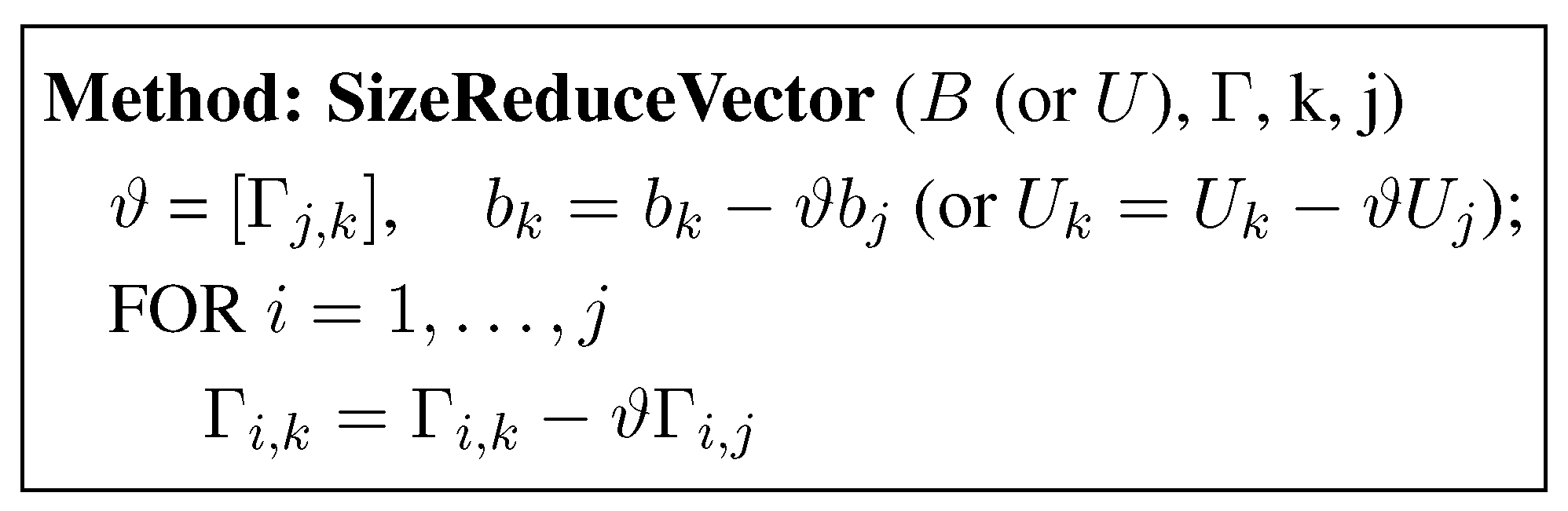

Swap of Two Adjacent Rows of B


3. Storjohann’s Improvements
3.1. The LLL-Reduction with Fraction Free Computations

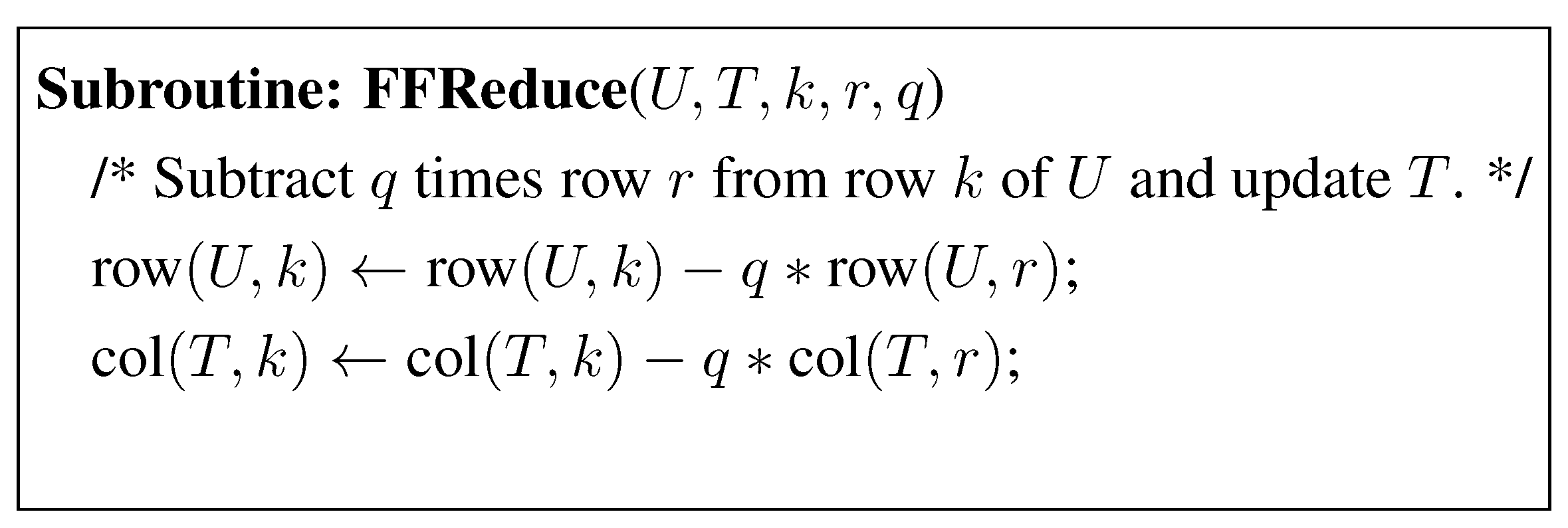
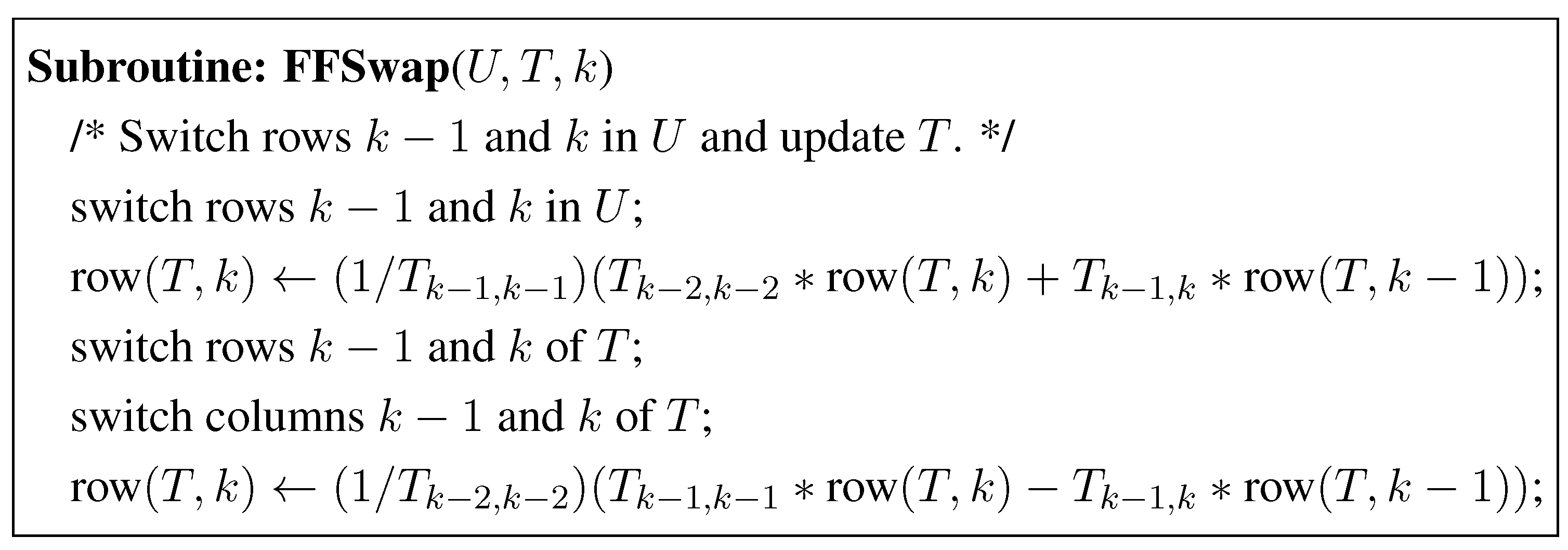
3.2. The Modified LLL Algorithm with Modular Arithmetic


4. The Segment LLL Reduction of Lattice Bases


5. The Modular Segment LLL Reduction with Modular Arithmetic
5.1. Algorithm and Its Complexity



5.2. Correctness of the ModSegmentLLL Algorithm
Updating E
5.3. The Modular Segment LLL using Fast Matrix Multiplication
6. Concluding Remarks
Acknowledgement
References
- Cassels, J.W.S. An Introduction to the Geometry of Numbers; Springer-Verlag: Berlin, Germany, 1971. [Google Scholar]
- Dwork, C. Lattices and their application to cryptography. Availible online: http://www.dim.uchile.cl/m̃kiwi/topicos/00/dwork-lattice-lectures.ps (accessed on 15 June 2010).
- Lenstra, H.W. Integer programming with a fixed number of variables. Math. Operat. Res. 1983, 8, 538–548. [Google Scholar] [CrossRef]
- Ajtai, M. The shortest vector problem in L2 is NP-hard for randomized reductions. In Proceedings of the 30th ACM Symposium on Theory of Computing, Dallas, TX, USA, May 1998; pp. 10–19.
- Micciancio, D. The shortest vector in a lattice is hard to approximate to within some constant. SIAM J. Comput. 2001, 30, 2008–2035. [Google Scholar] [CrossRef]
- van Emde Boas, P. Another NP-complete partition problem and the complexity of computing short vectors in lattices; Technical report MI-UvA-81-04; University of Amsterdam: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Lenstra, A.K.; Lenstra, H.W.; Lovász, L. Factoring polynomials with rational coefficients. Math. Ann. 1982, 261, 515–534. [Google Scholar] [CrossRef]
- Schönhage, A. Factorization of univariate integer polynomials by diophantine approximation and improved lattice basis reduction algorithm. In Proceedings of 11th Colloquium Automata, Languages and Programming; Springer-Verlag: Antwerpen, Belgium, 1984; LNCS 172, pp. 436–447. [Google Scholar]
- Kannan, R. Improved algorithms for integer programming and related lattice problems. In Proceedings of the 15th Annual ACM Symposium On Theory of Computing, Boston, MA, USA, May 1983; pp. 193–206.
- Schnorr, C.P. A hierarchy of polynomial time lattice basis reduction algorithms. Theor. Comput. Sci. 1987, 53, 201–224. [Google Scholar] [CrossRef]
- Koy, H.; Schnorr, C.P. Segment LLL-reduction with floating point orthogonalization. LNCS 2001, 2146, 81–96. [Google Scholar]
- Hermite, C. Second letter to Jacobi. Crelle J. 1850, 40, 279–290. [Google Scholar] [CrossRef]
- Schnorr, C.P. A more efficient algorithm for lattice basis reduction. J. Algorithms 1988, 9, 47–62. [Google Scholar] [CrossRef]
- Storjohann, A. Faster Algorithms for Integer Lattice Basis Reduction; Technical Report 249; Swiss Federal Institute of Technology: Zurich, Switzerland, 1996. [Google Scholar]
- Schnorr, C.P. Block Korkin-Zolotarev Bases and Suceessive Minima; Technical Report 92-063; University of California at Berkley: Berkley, CA, USA, 1992. [Google Scholar]
- Nguyen, P.Q.; Stehlé, D. Floating-point LLL revisited. LCNS 2005, 3494, 215–233. [Google Scholar]
- Schnorr, C.P. Fast LLL-type lattice reduction. Inf. Comput. 2006, 204, 1–25. [Google Scholar] [CrossRef]
- Kaib, M.; Ritter, H. Block Reduction for Arbitrary Norms. Availible online: http://www.mi.informatik.uni-frankfurt.de/research/papers.html (accessed on 15 June 2010).
- Lovász, L.; Scarf, H. The generalized basis reduction algorithm. Math. Operat. Res. 1992, 17, 754–764. [Google Scholar] [CrossRef]
- Koy, H.; Schnorr, C.P. Segment LLL-reduction of lattice bases. LNCS 2001, 2146, 67–80. [Google Scholar]
- Geddes, K.O.; Czapor, S.R.; Labahn, G. Algorithms for Computer Algebra; Kluwer: Boston, MA, USA, 1992. [Google Scholar]
- Coppersmith, D.; Winograd, S. Matrix multiplication via arithmetic progressions. J. Symbol. Comput. 1990, 9, 251–280. [Google Scholar] [CrossRef]
- Stehlé, D. Floating-point LLL: Theoretical and practical aspects. In The LLL Algorithm; Springer-verlag: New York, NY, USA, 2009; Chapter 5. [Google Scholar]
- Schönhage, A.; Strassen, V. Schnelle Multiplikation grosser Zahlen. Computing 1971, 7, 281–292. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.
Share and Cite
Mehrotra, S.; Li, Z. Segment LLL Reduction of Lattice Bases Using Modular Arithmetic. Algorithms 2010, 3, 224-243. https://doi.org/10.3390/a3030224
Mehrotra S, Li Z. Segment LLL Reduction of Lattice Bases Using Modular Arithmetic. Algorithms. 2010; 3(3):224-243. https://doi.org/10.3390/a3030224
Chicago/Turabian StyleMehrotra, Sanjay, and Zhifeng Li. 2010. "Segment LLL Reduction of Lattice Bases Using Modular Arithmetic" Algorithms 3, no. 3: 224-243. https://doi.org/10.3390/a3030224




