Mechanical and Electronic Properties of XC6 and XC12
Abstract
:1. Introduction
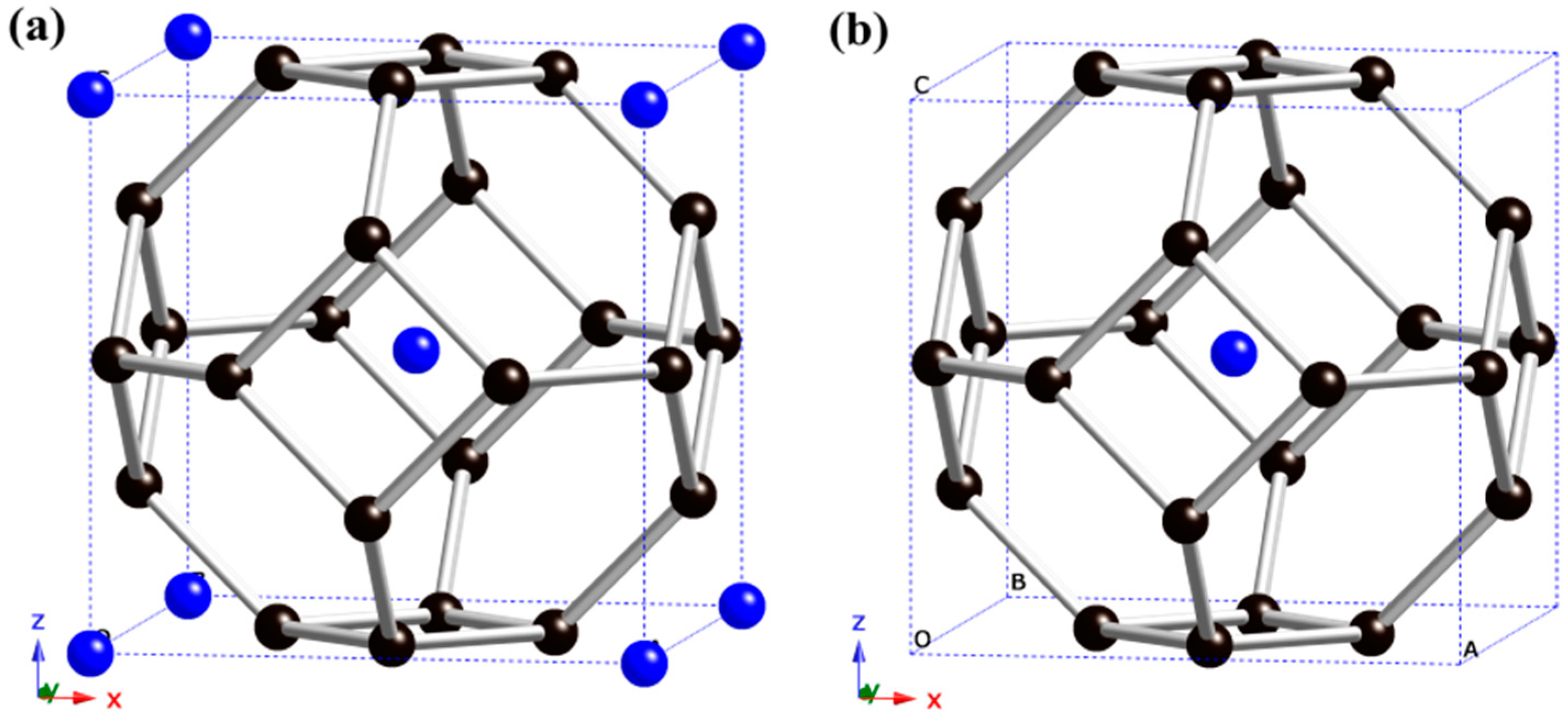
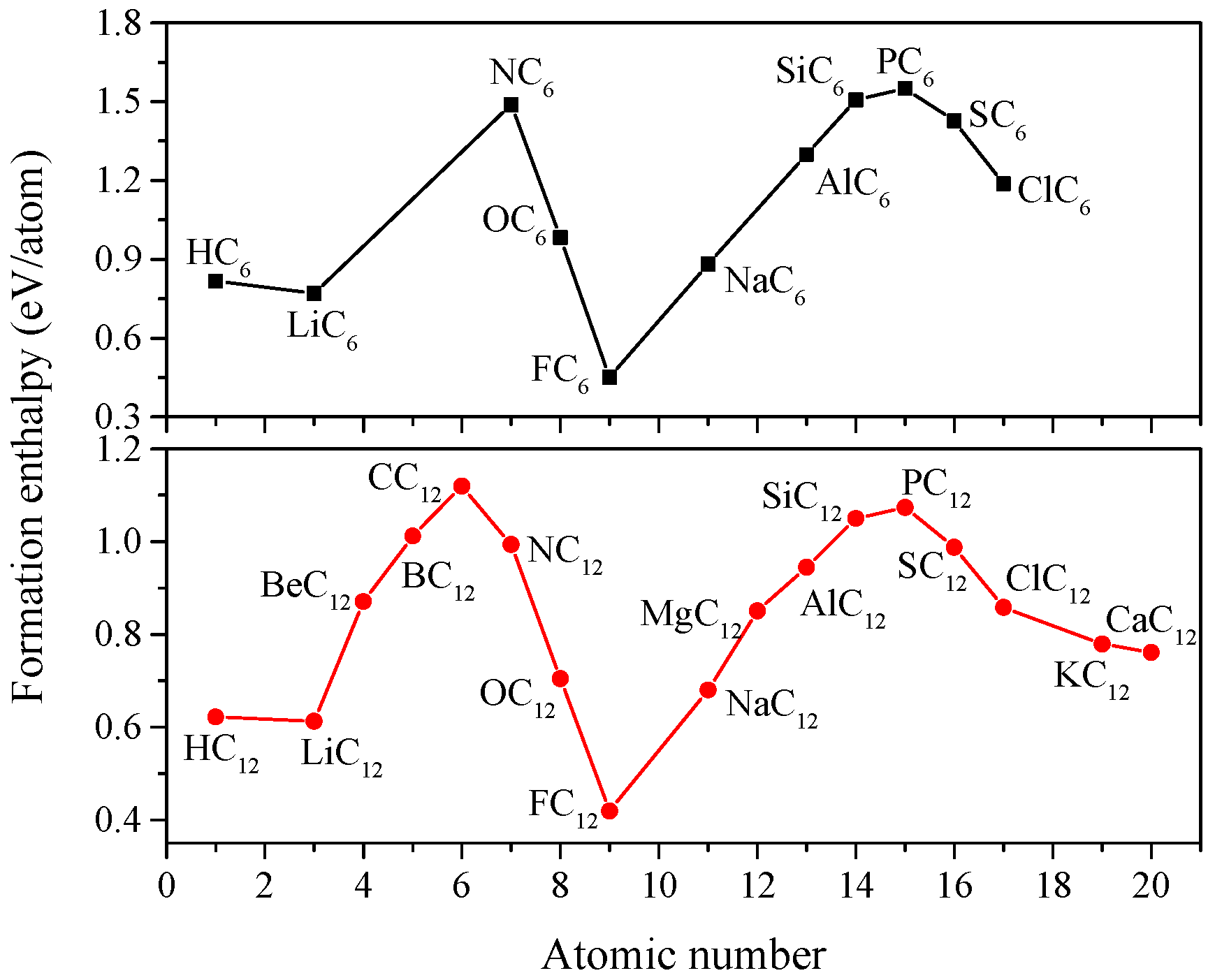
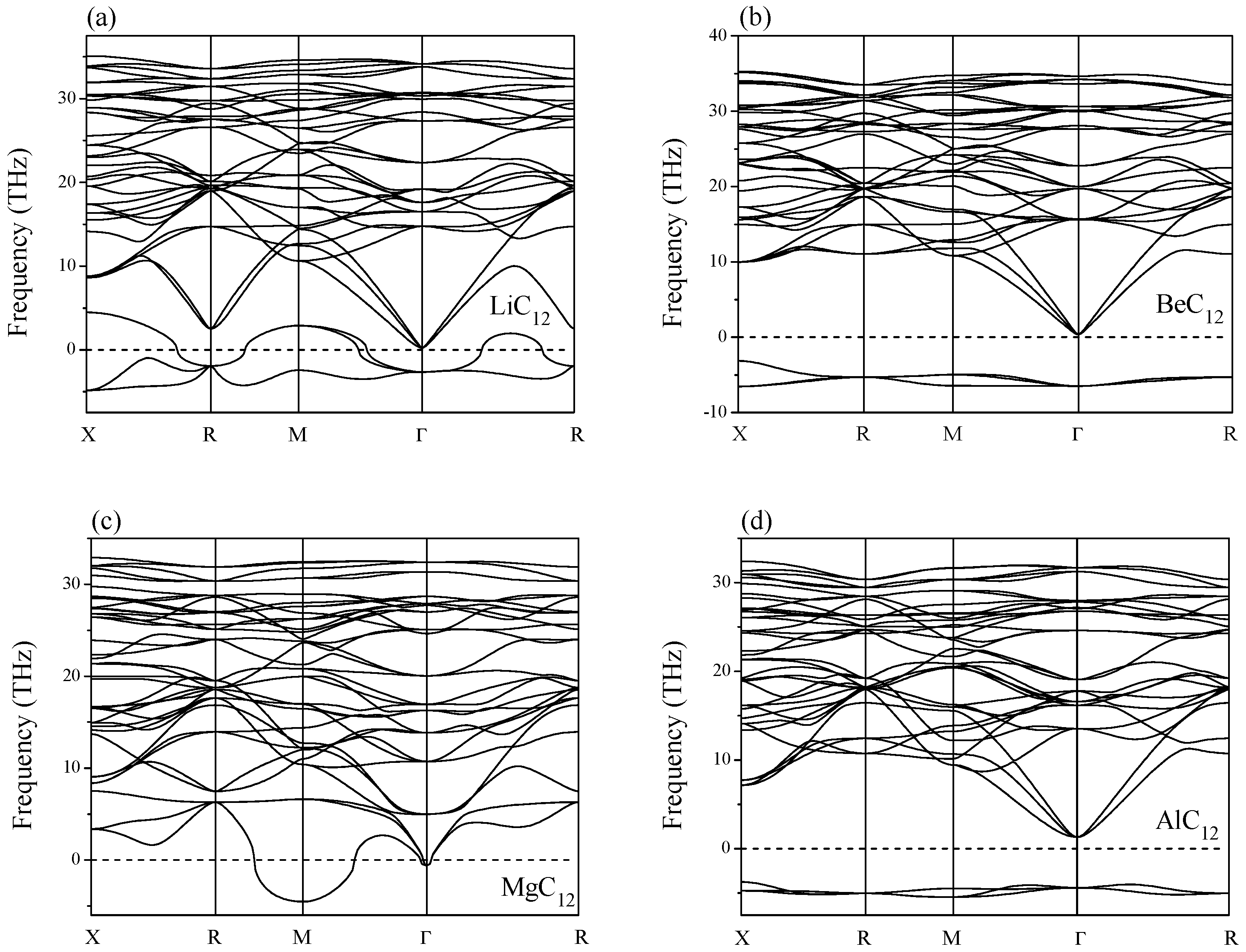
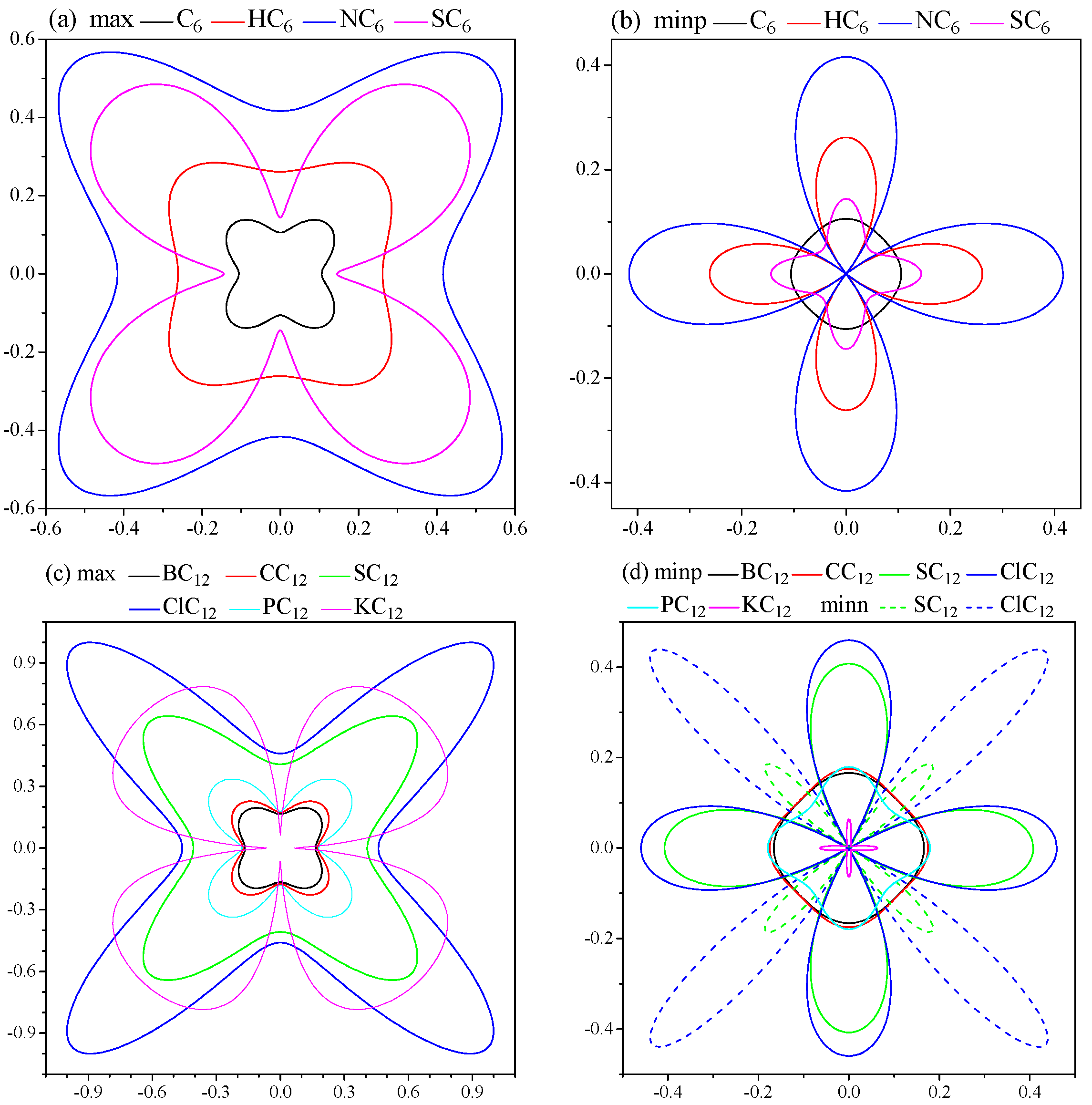
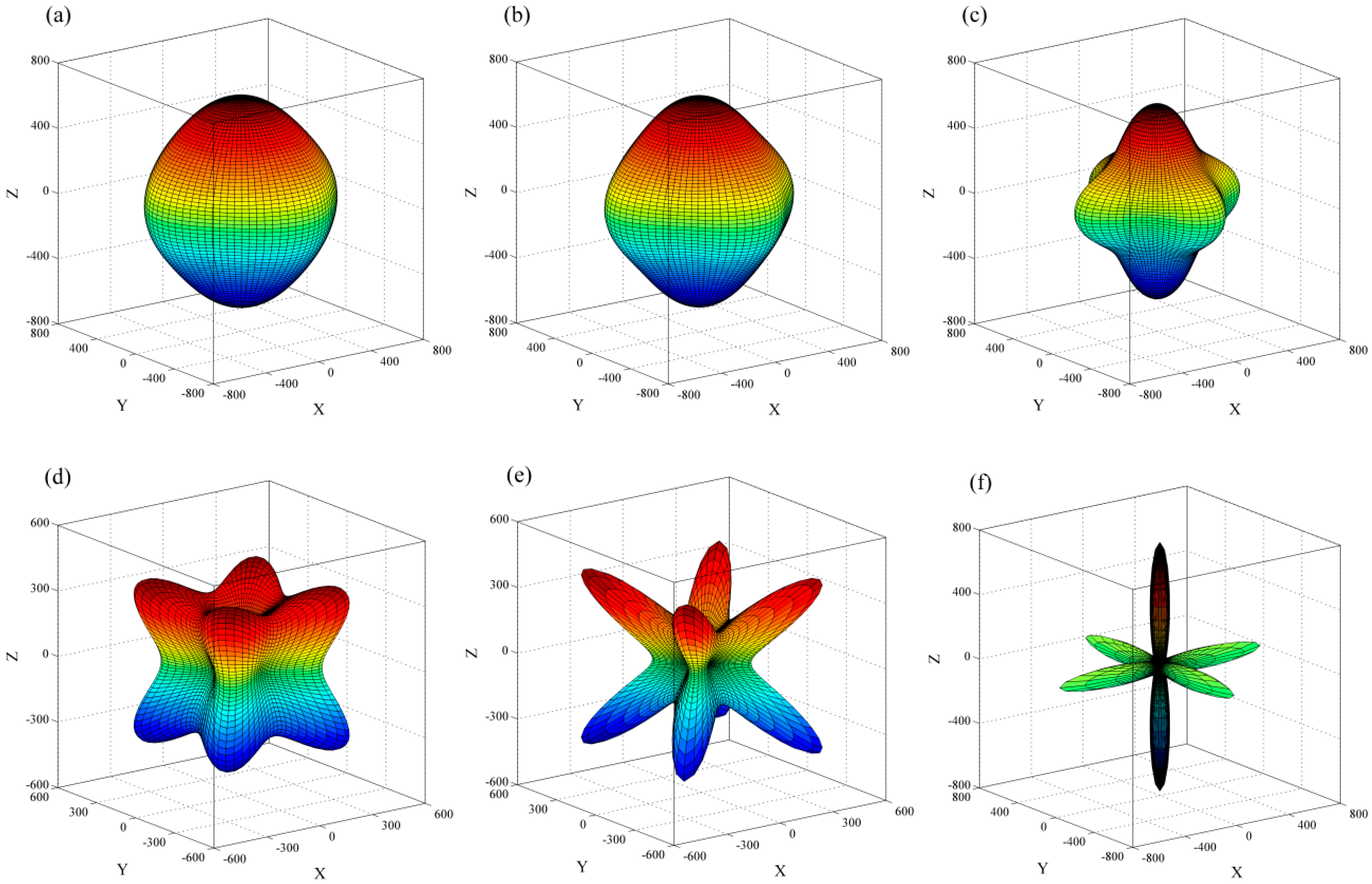
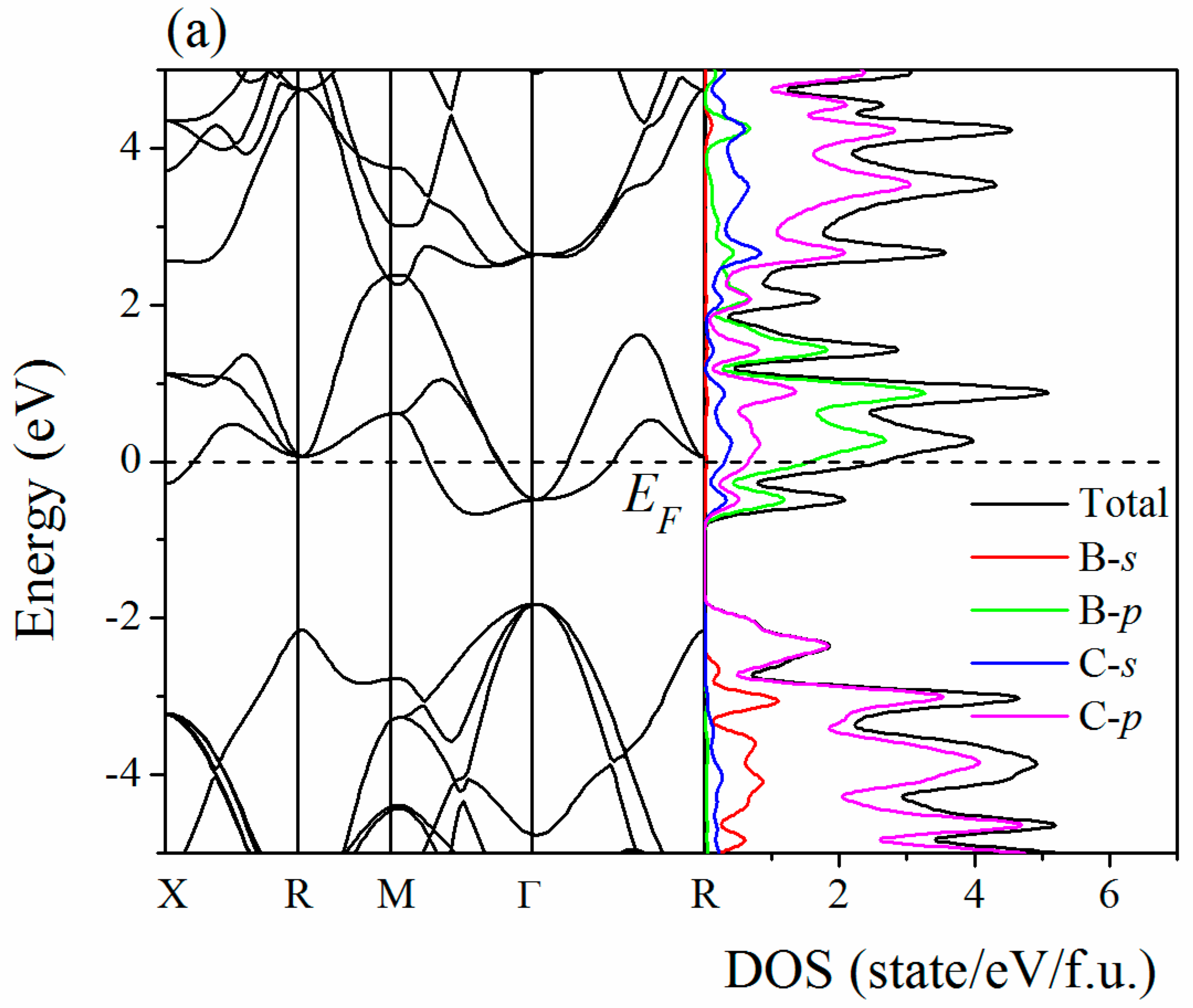
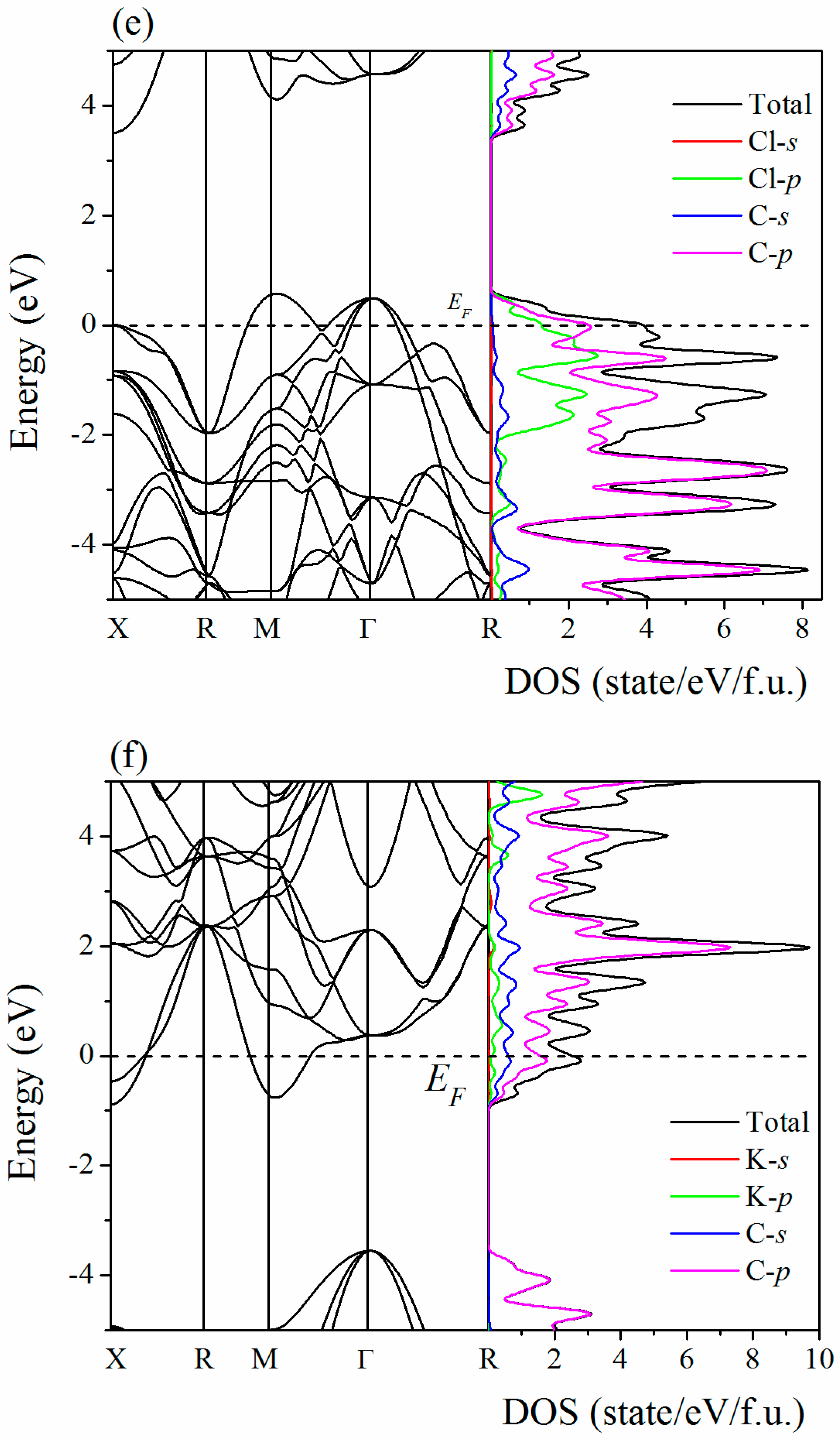
2. Results and Discussion
- for [100],
- for [110],
- for [111],
3. Computational Methods
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pan, B.; Xiao, J.; Li, J.; Liu, P.; Wang, C.; Yang, G. Carbyne with finite length: The one-dimensional sp carbon. Sci. Adv. 2015, 1. [Google Scholar] [CrossRef] [PubMed]
- Boulfelfel, S.E.; Oganov, A.R.; Leoni, S. Understanding the nature of “superhard graphite”. Sci. Rep. 2012, 2, 471. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Zhang, M.; Yan, H.; Lin, Z.; Zhu, X. Structural, electronic and mechanical properties of Imma-carbon. EPL 2014, 107, 27007. [Google Scholar] [CrossRef]
- Falcao, E.H.L.; Wudl, F. Carbon allotropes: Beyond graphite and diamond. J. Chem. Technol. Biotechnol. 2007, 82, 524–531. [Google Scholar] [CrossRef]
- Liu, H.; Li, Q.; Zhu, L.; Ma, Y. Superhard and superconductive polymorphs of diamond-like BC3. Phys. Lett. A 2011, 375, 771–774. [Google Scholar] [CrossRef]
- Li, Q.; Wang, H.; Tian, Y.; Xia, Y.; Cui, T.; He, J.; Ma, Y.; Zou, G. Superhard and superconducting structures of BC5. J. Appl. Phys. 2010, 108, 023507. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, Z.; Wang, Q.; Wang, L.M.; Xu, B.; He, J.; Tian, Y. Prediction of a superconductive superhard material: Diamond-like BC7. J. Appl. Phys. 2011, 110, 013501. [Google Scholar] [CrossRef]
- Liu, H.; Li, Q.; Zhu, L.; Ma, Y. Superhard polymorphs of diamond-like BC7. Solid State Commun. 2011, 151, 716–719. [Google Scholar] [CrossRef]
- Wang, D.Y.; Yan, Q.; Wang, B.; Wang, Y.X.; Yang, J.; Yang, G. Predicted boron-carbide compounds: A first-principles study. J. Chem. Phys. 2014, 140, 224704. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B.; Zhang, M.; Chang, S. Mechanical properties and atomic explanation of plastic deformation for diamond-like BC2. Materials 2016, 9, 514. [Google Scholar] [CrossRef]
- Naguib, M.; Mochalin, V.N.; Barsoum, M.W.; Gogotsi, Y. 25th anniversary article: MXenes: A new family of two-dimensional materials. Adv. Mater. 2014, 26, 992–1005. [Google Scholar] [PubMed]
- Ribeiro, F.J.; Tangney, P.; Louie, S.G.; Cohen, M.L. Hypothetical hard structures of carbon with cubic symmetry. Phys. Rev. B 2006, 74. [Google Scholar] [CrossRef]
- Lu, S.; Liu, H.; Naumov, I.I.; Meng, S.; Li, Y.; Tse, J.S.; Yang, B.; Hemley, R.J. Superconductivity in dense carbon-based materials. Phys. Rev. B 2016, 93. [Google Scholar] [CrossRef]
- Fan, Q.; Wei, Q.; Chai, C.; Yan, H.; Zhang, M.; Lin, Z.; Zhang, Z.; Zhang, J.; Zhang, D. Structural, mechanical, and electronic properties of P3m1-BCN. J. Phys. Chem. Solids 2015, 79, 89–96. [Google Scholar] [CrossRef]
- Wu, Z.; Zhao, E.; Xiang, H.; Hao, X.; Liu, X.; Meng, J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 2007, 76, 054115. [Google Scholar] [CrossRef]
- Voigt, W. Lehrburch der Kristallphysik; Teubner: Leipzig, Germany, 1928. [Google Scholar]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. J. Appl. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hill, R. The Elastic behaviour of a crystalline aggregate. Phys. Soc. Lond. Sect. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Wei, Q.; Zhang, M.; Guo, L.; Yan, H.; Zhu, X.; Lin, Z.; Guo, P. Ab initio studies of novel carbon nitride phase C2N2(CH2). Chem. Phys. 2013, 415, 36–43. [Google Scholar] [CrossRef]
- Wei, Q.; Zhang, Q.; Zhang, M. Crystal structures and mechanical properties of Ca2C at high pressure. Materials 2016, 9, 570. [Google Scholar] [CrossRef]
- Pugh, S.F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Universal elastic anisotropy index. Phys. Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef] [PubMed]
- Zener, C. Elasticity and Anelasticity of Metals; University of Chicago: Chicago, IL, USA, 1948. [Google Scholar]
- Ravindran, P.; Fast, L.; Korzhavyi, P.A.; Johansson, B.; Wills, J.; Eriksson, O. Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi2. J. Appl. Phys. 1998, 84, 4891–4904. [Google Scholar] [CrossRef]
- Marmiera, A.; Lethbridge, Z.A.D.; Walton, R.I.; Smith, C.W.; Parker, S.C.; Evans, K.E. ElAM: A computer program for the analysis and representation of anisotropic elastic properties. Comput. Phys. Commun. 2010, 181, 2102–2115. [Google Scholar] [CrossRef]
- Zhang, Q.; Wei, Q.; Yan, H.; Fan, Q.; Zhu, X.; Zhang, J.; Zhang, D. Mechanical and electronic properties of P42/mnm silicon carbides. Z. Naturforsch. A 2016, 71, 387–396. [Google Scholar] [CrossRef]
- Baughman, R.H.; Shacklette, J.M.; Zakhidov, A.A.; Stafström, S. Negative Poisson’s ratios as a common feature of cubic metals. Nature 1998, 392, 362–365. [Google Scholar] [CrossRef]
- Wei, Q.; Zhang, M.; Yan, H.; Li, R.; Zhu, X.; Lin, Z.; Yao, R. A new superhard phase of C3N2 polymorphs. Z. Naturforsch. A 2015, 70, 1001. [Google Scholar] [CrossRef]
- Brugger, K. Determination of third-order elastic coefficients in crystals. J. Appl. Phys. 1965, 36, 768. [Google Scholar] [CrossRef]
- Sun, L.; Gao, Y.; Xiao, B.; Li, Y.; Wang, G. Anisotropic elastic and thermal properties of titanium borides by first-principles calculations. J. Alloys Compd. 2013, 579, 457–467. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Pfrommer, B.G.; Côté, M.; Louie, S.G.; Cohen, M.L. Relaxation of crystals with the quasi-newton method. J. Comput. Phys. 1997, 131, 233–240. [Google Scholar] [CrossRef]



| Materials | a | C11 | C12 | C44 | Mechanical Stability | B | G | E | ν | B/G |
|---|---|---|---|---|---|---|---|---|---|---|
| Diamond | 3.566 a | 1053 a | 120 a | 563 a | 431 a | 522 a | 1116 a | 0.07 a | ||
| C6 | 4.375 | 803 | 95 | 307 | stable | 331 | 325 | 735 | 0.13 | 1.018 |
| 4.34 b | 352 b | |||||||||
| HC6 | 4.390 | 607 | 215 | 344 | stable | 346 | 275 | 652 | 0.186 | 1.258 |
| LiC6 | 4.491 | 634 | 118 | −78 | unstable | |||||
| NC6 | 4.446 | 414 | 295 | 162 | stable | 335 | 108 | 293 | 0.354 | 3.102 |
| OC6 | 4.434 | 196 | 407 | 216 | unstable | |||||
| FC6 | 4.427 | 269 | 370 | 335 | unstable | |||||
| NaC6 | 4.566 | 659 | 91 | −548 | unstable | |||||
| AlC6 | 4.618 | 497 | 162 | −59 | unstable | |||||
| SiC6 | 4.614 | 527 | 165 | −66 | unstable | |||||
| PC6 | 4.605 | 542 | 179 | −132 | unstable | |||||
| SC6 | 4.608 | 683 | 115 | 90 | stable | 305 | 146 | 378 | 0.294 | 2.089 |
| ClC6 | 4.613 | 92 | 374 | 104 | unstable | |||||
| HC12 | 4.383 | 103 | 461 | 336 | unstable | |||||
| LiC12 | 4.444 | 695 | 108 | 32 | stable | 304 | 93 | 253 | 0.361 | 3.269 |
| BeC12 | 4.451 | 743 | 98 | 289 | stable | 313 | 302 | 686 | 0.135 | 1.036 |
| BC12 | 4.439 | 684 | 136 | 233 | stable | 319 | 248 | 591 | 0.191 | 1.286 |
| CC12 | 4.376 | 689 | 146 | 214 | stable | 327 | 235 | 569 | 0.21 | 1.391 |
| NC12 | 4.415 | 275 | 361 | 278 | unstable | |||||
| OC12 | 4.404 | −661 | 830 | 526 | unstable | |||||
| FC12 | 4.401 | −33 | 529 | 476 | unstable | |||||
| NaC12 | 4.476 | 741 | 77 | −9 | unstable | |||||
| MgC12 | 4.508 | 667 | 108 | 31 | stable | 294 | 89 | 240 | 0.363 | 3.303 |
| AlC12 | 4.513 | 645 | 123 | 56 | stable | 297 | 110 | 294 | 0.335 | 2.700 |
| SiC12 | 4.511 | 559 | 170 | −25 | unstable | |||||
| PC12 | 4.504 | 645 | 141 | 144 | stable | 309 | 181 | 454 | 0.255 | 1.707 |
| SC12 | 4.502 | 397 | 273 | 251 | stable | 314 | 144 | 375 | 0.301 | 2.181 |
| ClC12 | 4.503 | 349 | 297 | 295 | stable | 314 | 123 | 326 | 0.326 | 2.553 |
| KC12 | 4.512 | 779 | 53 | 18 | stable | 295 | 93 | 252 | 0.357 | 3.172 |
| CaC12 | 4.543 | 734 | 58 | −2166 | unstable |
| Parameter | C6 | HC6 | NC6 | SC6 | BC12 | CC12 | PC12 | SC12 | ClC12 | KC12 |
|---|---|---|---|---|---|---|---|---|---|---|
| AU | 0.024 | 0.398 | 1.30 | 1.77 | 0.032 | 0.068 | 0.3814 | 2.752 | 11.084 | 21.252 |
| A | 0.8672 | 1.755 | 2.723 | 0.317 | 0.851 | 0.788 | 0.572 | 4.048 | 11.346 | 0.0496 |
| AG (%) | 0.243 | 3.752 | 11.567 | 15.016 | 0.315 | 0.678 | 3.714 | 21.596 | 53.098 | 68.612 |
| Parameters | Diamond | C6 | HC6 | NC6 | SC6 | BC12 | CC12 | PC12 | SC12 | ClC12 | KC12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρ | 3.517 | 2.857 | 2.869 | 3.252 | 3.535 | 2.941 | 2.992 | 3.182 | 3.206 | 3.265 | 3.313 | |
| [100] | vl | 17,303 | 16,765 | 14,546 | 11,283 | 13,900 | 15,251 | 15,175 | 14,237 | 11,128 | 10,339 | 2331 |
| [010]vt1 | 12,652 | 10,366 | 10,950 | 7058 | 5046 | 8901 | 8457 | 6727 | 8848 | 9505 | 2331 | |
| [001]vt2 | 12,652 | 10,366 | 10,950 | 7058 | 5046 | 8901 | 8457 | 6727 | 8848 | 9505 | 2331 | |
| [110] | vl | 18,079 | 16,267 | 16,222 | 12,603 | 11,762 | 14,786 | 14,528 | 12,991 | 13,520 | 13,758 | 11,446 |
| vt1 | 11,517 | 11,131 | 8265 | 4277 | 8963 | 9652 | 9526 | 8899 | 4398 | 2822 | 10,467 | |
| [001]vt2 | 12,652 | 10,366 | 10,950 | 7058 | 5046 | 8901 | 8457 | 6727 | 8848 | 9505 | 2331 | |
| [111] | vl | 18,330 | 16,098 | 16,744 | 13,013 | 10,956 | 14,628 | 14,306 | 12,548 | 14,228 | 14,722 | 9813 |
| vt1,2 | 11,907 | 10,882 | 9247 | 5367 | 7877 | 9409 | 9184 | 8239 | 6244 | 5952 | 8652 | |
| vl | 17,901 | 16,356 | 15,761 | 12,136 | 11,889 | 14,851 | 14,629 | 13,151 | 12,563 | 12,100 | 11,246 | |
| vt | 12,183 | 10,666 | 9791 | 5763 | 6427 | 9183 | 8863 | 7542 | 6702 | 6138 | 5298 | |
| vm | 13,282 | 11,692 | 10,792 | 6483 | 7173 | 10,128 | 9795 | 8378 | 7487 | 6880 | 5963 | |
| ΘD | 2219 | 1823 | 1766 | 1047 | 1118 | 1598 | 1551 | 1303 | 1165 | 1069 | 926 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Q.; Zhang, Q.; Zhang, M. Mechanical and Electronic Properties of XC6 and XC12. Materials 2016, 9, 726. https://doi.org/10.3390/ma9090726
Wei Q, Zhang Q, Zhang M. Mechanical and Electronic Properties of XC6 and XC12. Materials. 2016; 9(9):726. https://doi.org/10.3390/ma9090726
Chicago/Turabian StyleWei, Qun, Quan Zhang, and Meiguang Zhang. 2016. "Mechanical and Electronic Properties of XC6 and XC12" Materials 9, no. 9: 726. https://doi.org/10.3390/ma9090726
APA StyleWei, Q., Zhang, Q., & Zhang, M. (2016). Mechanical and Electronic Properties of XC6 and XC12. Materials, 9(9), 726. https://doi.org/10.3390/ma9090726






