A New Superhard Phase and Physical Properties of ZrB3 from First-Principles Calculations
Abstract
:1. Introduction
2. Computational Methods
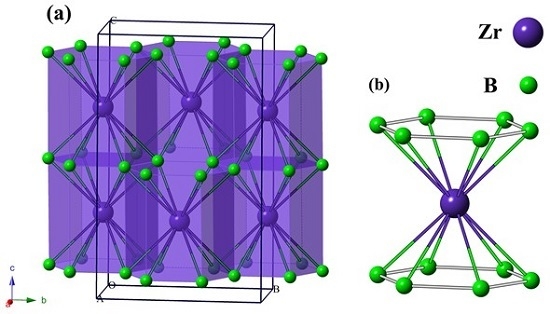
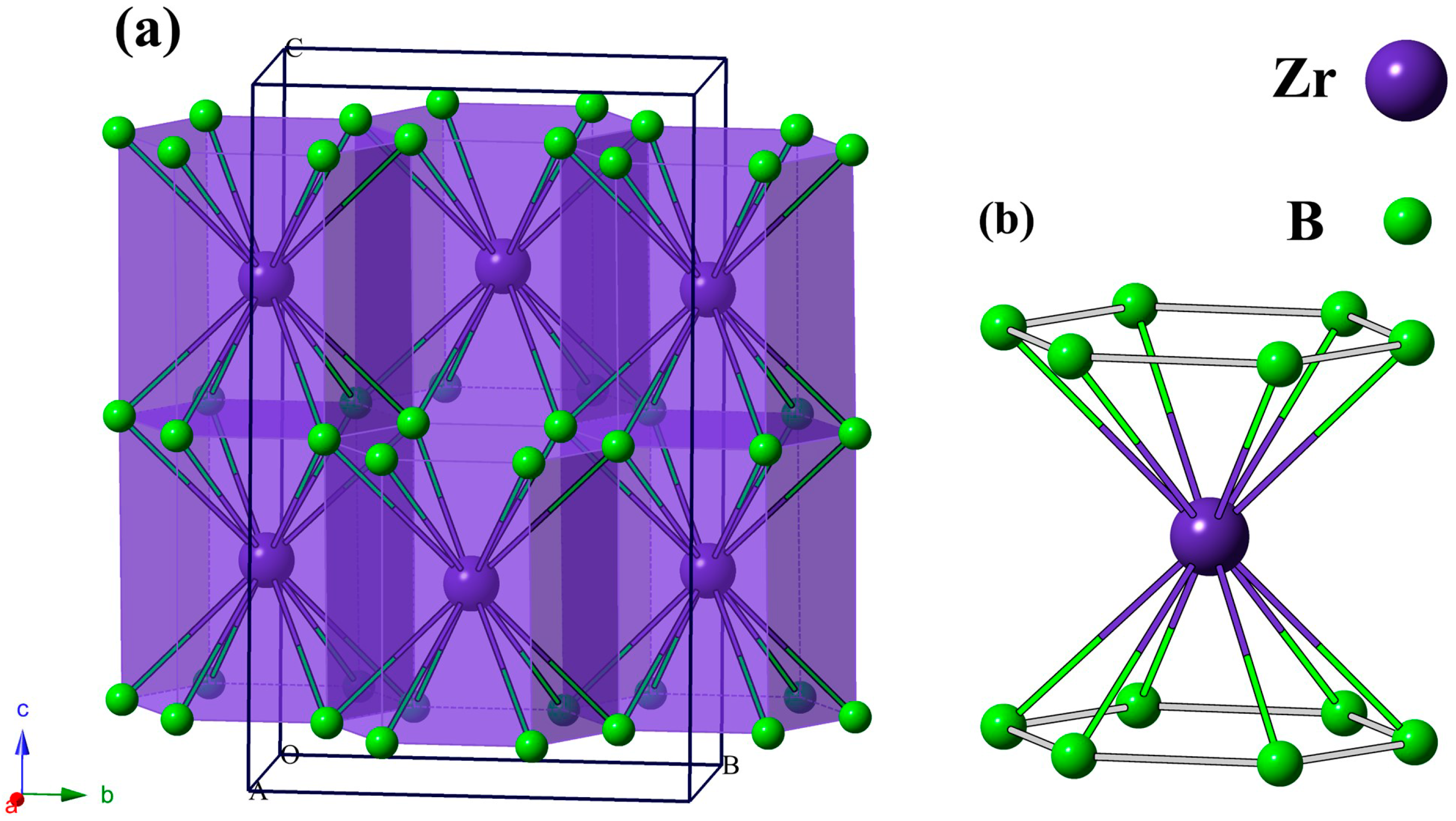
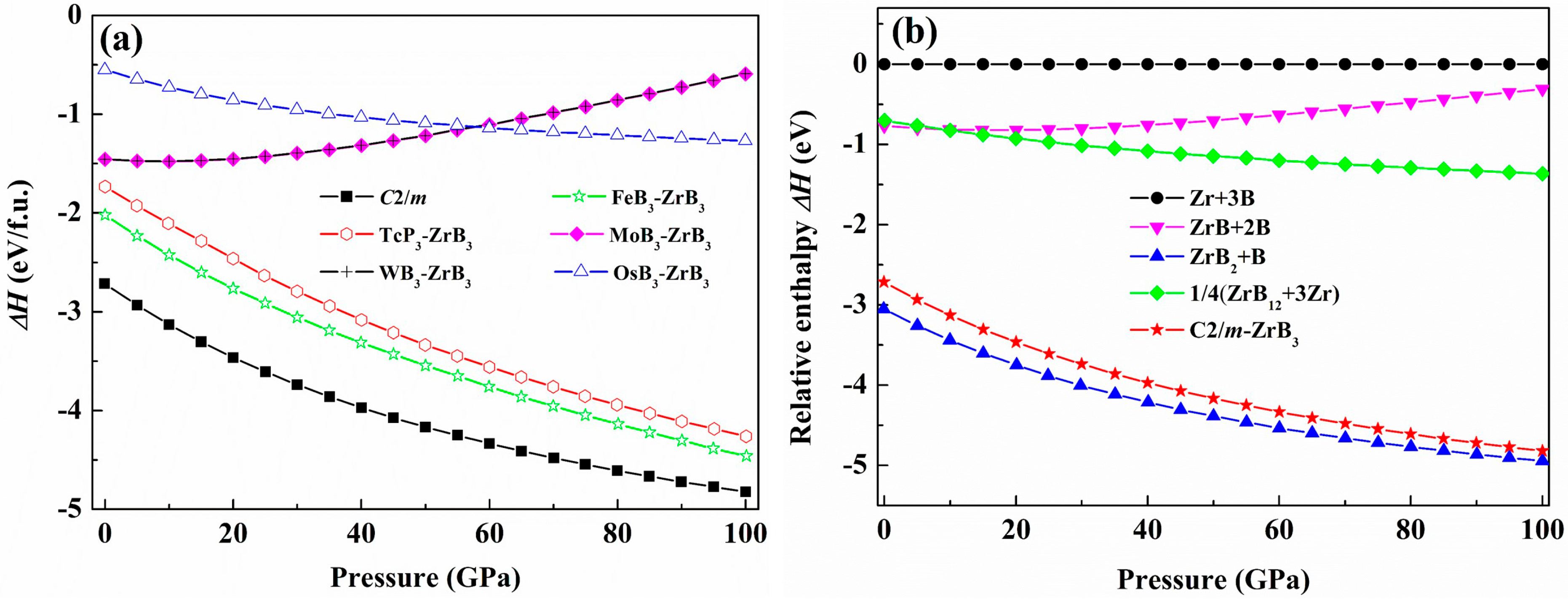
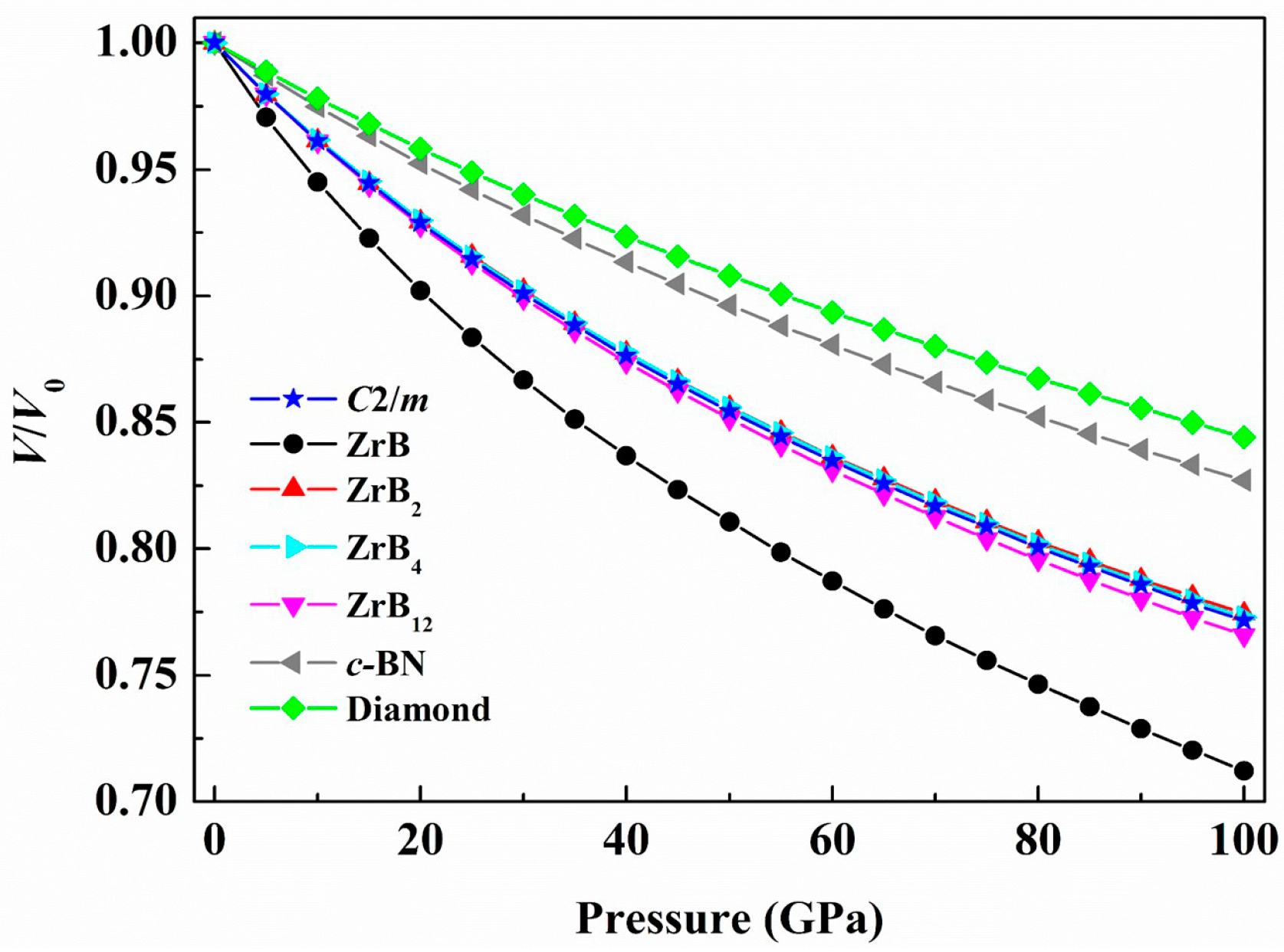
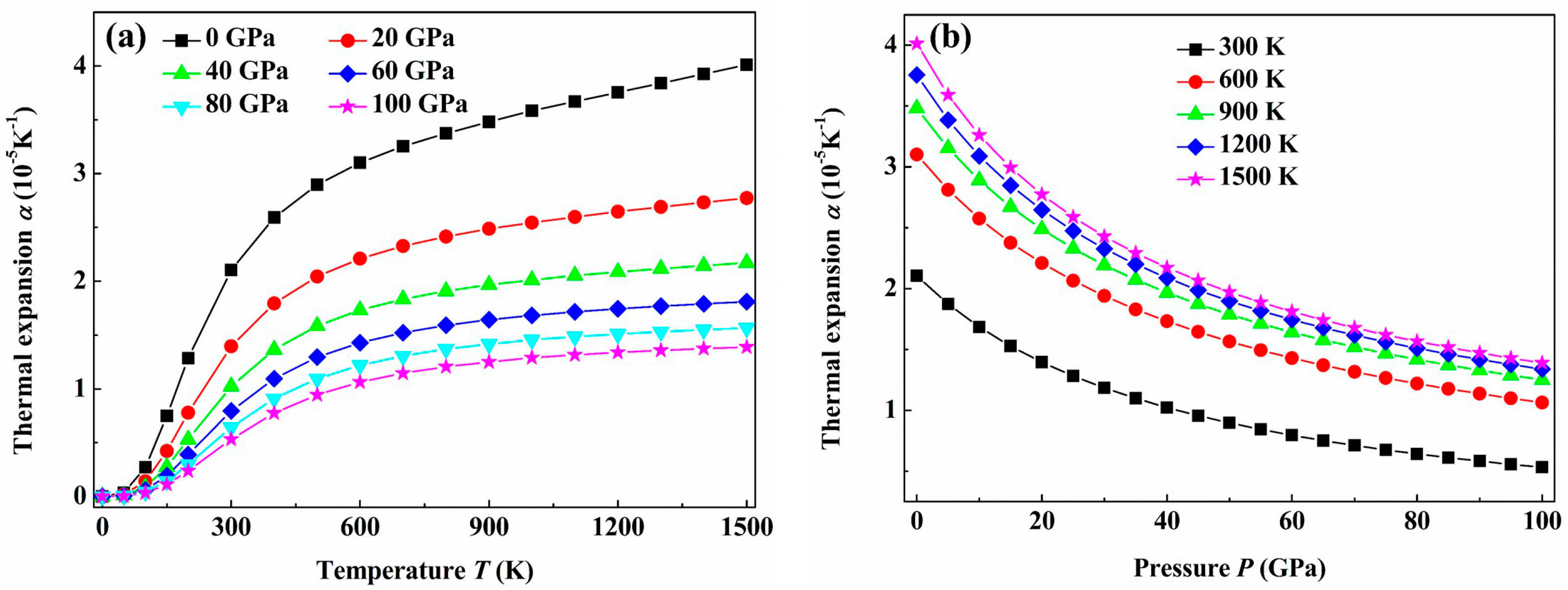
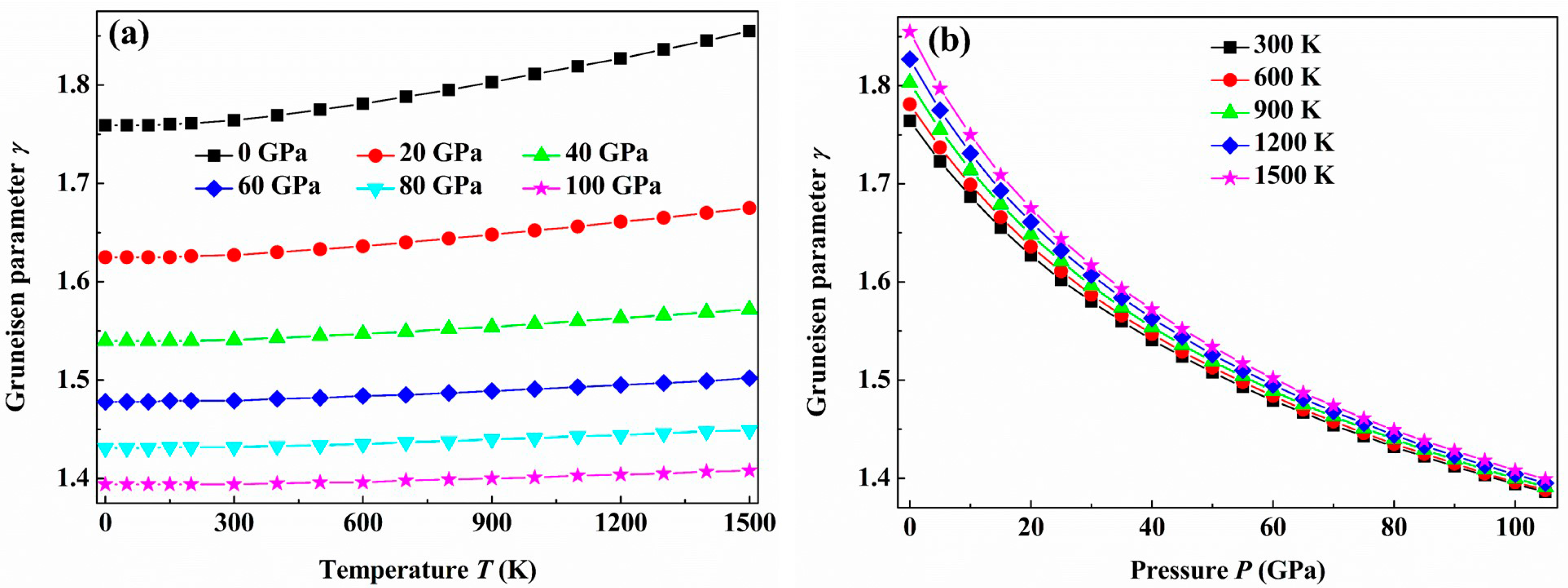
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Occelli, F.; Farber, D.L.; Toullec, R.L. Properties of diamond under hydrostatic pressures up to 140 GPa. Nat. Mater. 2003, 2, 151–154. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Sun, H.; Chen, C.F. Structural deformation, strength and instability of cubic BN compared to diamond: A first-principles study. Phys. Rev. B 2006, 73, 144115. [Google Scholar] [CrossRef]
- He, D.W.; Zhao, Y.S.; Daemen, L.; Qian, J.; Shen, T.D.; Zerda, T.W. Boron suboxide: As hard as cubic boron nitride. Appl. Phys. Lett. 2002, 81, 643–645. [Google Scholar] [CrossRef]
- Chung, H.Y.; Weinberger, M.B.; Levine, J.B.; Kavner, A.; Yang, J.M.; Tolbert, S.H.; Kaner, R.B. Synthesis of ultra-incompressible superhard rhenium diboride at ambient pressure. Science 2007, 316, 436–439. [Google Scholar] [CrossRef] [PubMed]
- Cumberland, R.W.; Weinberger, M.B.; Gilman, J.J.; Clark, S.M.; Tolbert, S.H.; Kaner, R.B. Osmium diboride, an ultra-incompressible, hard material. J. Am. Chem. Soc. 2005, 127, 7264–7265. [Google Scholar] [CrossRef] [PubMed]
- Gu, Q.F.; Krauss, G.; Steurer, W. Transition metal borides: Superhard versus ultra-incompressible. Adv. Mater. 2008, 20, 3620–3626. [Google Scholar] [CrossRef]
- Zhang, R.F.; Legut, D.; Lin, Z.J.; Zhao, Y.S.; Mao, H.K.; Veprek, S. Stability and strength of transition-metal tetraborides and triborides. Phys. Rev. Lett. 2012, 108, 255502. [Google Scholar] [CrossRef] [PubMed]
- Gou, H.Y.; Li, Z.P.; Niu, H.; Gao, F.M.; Zhang, J.W.; Rodney, C.E.; Lian, J. Unusual rigidity and ideal strength of CrB4 and MnB4. Appl. Phys. Lett. 2012, 100, 111907. [Google Scholar] [CrossRef]
- Glaser, F.W.; Post, B. Phase diagram zirconium–boron. Trans. AIME 1953, 197, 1117–1118. [Google Scholar]
- Nowotny, H.; Rudy, E.; Benesovsky, F. Untersuchungen in den systemen: Zirkonium-bor-kohlenstoff und zirkonium-bor-stickstoff. Mh. Chem. 1960, 91, 963–974. (In Germany) [Google Scholar] [CrossRef]
- Portnoi, K.I.; Romashov, V.M.; Burobina, L.N. Constitution diagram of the system zirconium-boron. Sov. Powder Metall. Met. Ceram. 1970, 9, 577–580. [Google Scholar] [CrossRef]
- Tokunaga, T.; Terashima, K.; Ohtani, H.; Hasebe, M. Thermodynamic analysis of the phase equilibria in the Fe-Zr-B system. Mater. Trans. 2008, 49, 2534–2540. [Google Scholar] [CrossRef]
- Opeka, M.M.; Talmy, I.G.; Wuchina, E.J.; Zaykoski, J.A.; Causey, S.J. Mechanical, thermal, and oxidation properties of refractory hafnium and zirconium compounds. J. Eur. Ceram. Soc. 1999, 19, 2405–2414. [Google Scholar] [CrossRef]
- Wang, Y.G.; Liu, W.; Cheng, L.F.; Zhang, L.T. Preparation and properties of 2D C/ZrB2-SiC ultra high temperature ceramic. Mater. Sci. Eng. A 2009, 524, 129–133. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Gadalla, A.M. Synthesis and analysis of ZrB2-based composites. Mater. Manuf. Process. 1996, 11, 575–587. [Google Scholar] [CrossRef]
- Martinez, M.; Rodriguez, D. Characterisation and high temperature mechanical properties of zirconium boride-based materials. J. Eur. Ceram. Soc. 2002, 22, 2543–2549. [Google Scholar] [CrossRef]
- Li, H.; Zhang, L.T.; Zeng, Q.F.; Wang, J.J.; Cheng, L.F.; Ren, H.T.; Guan, K. Crystal structure and elastic properties of ZrB compared with ZrB2: A first-principles study. Comput. Mater. Sci. 2010, 49, 814–819. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, W.; Chen, X.; Liu, H.Y.; Ding, Z.H.; Ma, Y.M.; Wang, X.D.; Cao, Q.P.; Jiang, J.Z. Crystal structures, stability, electronic and elastic properties of 4d and 5d transition metal monoborides: First-principles calculations. J. Alloys Compd. 2012, 538, 115–124. [Google Scholar] [CrossRef]
- Huang, B.; Duan, Y.H.; Hu, W.C.; Sun, Y.; Chen, S. Structural, anisotropic elastic and thermal properties of MB (M = Ti, Zr and Hf) monoborides. Ceram. Int. 2015, 41, 6831–6843. [Google Scholar] [CrossRef]
- Okamoto, N.L.; Kusakari, M.; Tanaka, K.; Inui, H.; Yamaguchi, M.; Otani, S. Temperature dependence of thermal expansion and elastic constants of single crystals of ZrB2 and the suitability of ZrB2 as a substrate for GaN film. J. Appl. Phys. 2003, 93, 88–93. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.H.; Luo, X.G.; Han, J.C.; Li, J.P.; Han, W.B. Electronic structure, elasticity and hardness of diborides of zirconium and hafnium: First principles calculations. Comput. Mater. Sci. 2008, 44, 411–421. [Google Scholar] [CrossRef]
- Zhang, X.H.; Luo, X.G.; Li, J.P.; Han, J.C.; Han, W.B.; Hong, C.Q. Structure and bonding features of ZrB2 (0001) surface. Comput. Mater. Sci. 2009, 46, 1–6. [Google Scholar] [CrossRef]
- Okamoto, N.L.; Kusakari, M.; Tanaka, K.; Inui, H.; Otani, S. Anisotropic elastic constants and thermal expansivities in monocrystal CrB2, TiB2, and ZrB2. Acta Mater. 2010, 58, 76–84. [Google Scholar] [CrossRef] [Green Version]
- Jäger, B.; Paluch, S.; Żogal, O.J.; Wolf, W.; Herzig, P.; Filippov, V.B.; Shitsevalova, N.; Paderno, Y. Characterization of the electronic properties of YB12, ZrB12, and LuB12 using 11B NMR and first-principles calculations. J. Phys. Condens. Matter 2006, 18, 2525–2535. [Google Scholar] [CrossRef]
- Korozlu, N.; Colakoglu, K.; Deligoz, E.; Aydin, S. The elastic and mechanical properties of MB12 (M = Zr, Hf, Y, Lu) as a function of pressure. J. Alloys Compd. 2013, 546, 157–164. [Google Scholar] [CrossRef]
- Ai, B.C.; Luo, X.G.; Yu, J.J.; Miao, W.B.; Hu, P. Theoretical elastic stiffness and thermodynamic properties of zirconium dodecaboride from first principles calculation. Comput. Mater. Sci. 2014, 82, 37–44. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Qin, J.Q.; Sun, X.W.; Xue, Y.N.; Ma, M.Z.; Liu, R.P. First-principles structural design of superhard material of ZrB4. Phys. Chem. Chem. Phys. 2013, 15, 20894–20899. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.Q.; Peng, Y.S.; Hu, M.; Li, C.M.; Luo, Y.T. Elasticity, hardness, and thermal properties of ZrBn (n = 1, 2, 12). Ceram. Int. 2016, 42, 6624–6631. [Google Scholar] [CrossRef]
- Wang, Y.C.; Lv, J.; Zhu, L.; Ma, Y.M. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 2010, 82, 094116. [Google Scholar] [CrossRef]
- Wang, Y.C.; Lv, J.; Zhu, L.; Ma, Y.M. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 2012, 183, 2063–2070. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Y.C.; Lv, J.; Li, Q.; Zhang, L.J.; Ma, Y.M. CALYPSO structure prediction method and its wide application. Comput. Mater. Sci. 2016, 112, 406–415. [Google Scholar] [CrossRef]
- Ma, Y.M.; Wang, Y.C.; Lv, J.; Zhu, L. CALYPSO (Crystal Structure AnaLYsis by Particle Swarm Optimization). Available online: http://www.calypso.cn (accessed on 18 August 2016).
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Togo, A.; Oba, F.; Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 2008, 78, 134106. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Chen, X.Q.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
- Blanco, M.A.; Francisco, E.; Luaña, V. GIBBS: Isothermal-isobaric thermodynamics of solids from energy curves using a quasi-harmonic Debye model. Comput. Phys. Commun. 2004, 158, 57–72. [Google Scholar] [CrossRef]
- Fahrenholtz, G.W.; Hilmas, G.E. Refractory diborides of zirconium and hafnium. J. Am. Ceram. Soc. 2007, 90, 1347–1364. [Google Scholar] [CrossRef]
- Wiley, D.E.; Manning, W.R.; Hunter, O. Elastic properties of polycrystalline TiB2, ZrB2 and HfB2 from room temperature to 1300 K. J. Less Common Met. 1969, 18, 149–157. [Google Scholar] [CrossRef]
- Grechnev, G.E.; Baranovskiy, A.E.; Fil, V.D.; Ignatova, T.V.; Kolobov, I.G.; Logosha, A.V.; Shitsevalova, N.Y.; Filippov, V.B.; Eriksson, O. Electronic structure and bulk properties of MB6 and MB12 borides. Low. Temp. Phys. 2008, 34, 921. [Google Scholar] [CrossRef]
- Kim, K.H.; Shim, K.B. The effect of lanthanum on the fabrication of ZrB2–ZrC composites by spark plasma sintering. Mater. Charact. 2003, 50, 31–37. [Google Scholar] [CrossRef]
- Wang, Y.C.; Yao, T.K.; Wang, L.M.; Yao, J.L.; Li, H.; Zhang, J.W.; Gou, H.Y. Structural and relative stabilities, electronic properties and possible reactive routing of osmium and ruthenium borides from first-principles calculations. Dalton Trans. 2013, 42, 7041–7050. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.G.; Wang, H.; Wang, H.B.; Cui, T.; Ma, Y.M. Structural modifications and mechanical properties of molybdenum borides from first principles. J. Phys. Chem. C 2010, 114, 6722–6725. [Google Scholar] [CrossRef]
- Liang, Y.C.; Yuan, X.; Zhang, W.Q. Thermodynamic identification of tungsten borides. Phys. Rev. B 2011, 83, 220102. [Google Scholar] [CrossRef]
- Ji, Z.W.; Hu, C.H.; Wang, D.H.; Zhong, Y.; Yang, J.; Zhang, W.Q.; Zhou, H.Y. Mechanical properties and chemical bonding of the Os–B system: A first-principles study. Acta Mater. 2012, 60, 4208–4217. [Google Scholar] [CrossRef]
- Pugh, S.F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Ravindran, P.; Fast, L.; Korzhavyi, P.A.; Johansson, B.; Wills, J.; Eriksson, O. Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi2. J. Appl. Phys. 1998, 84, 4891–4904. [Google Scholar] [CrossRef]
- Anderson, O.L. A simplified method for calculating the Debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]
- Hao, X.F.; Xu, Y.H.; Wu, Z.J.; Zhou, D.F.; Liu, X.J.; Meng, J. Elastic anisotropy of OsB2 and RuB2 from first-principles study. J. Alloys Compd. 2008, 453, 413–417. [Google Scholar] [CrossRef]
- Li, Y.L.; Zeng, Z. New potential super-incompressible phase of ReN2. Chem. Phys. Lett. 2009, 474, 93–96. [Google Scholar] [CrossRef]
- Li, Y.L.; Zeng, Z. Structural, elastic and electronic properties of ReO2. Chin. Phys. Lett. 2008, 25, 4086–4089. [Google Scholar] [CrossRef]
- Hao, X.F.; Xu, Y.H.; Wu, Z.J.; Zhou, D.F.; Liu, X.J.; Cao, X.Q.; Meng, J. Low-compressibility and hard materials ReB2 and WB2: Prediction from first-principles study. Phys. Rev. B 2006, 74, 224112. [Google Scholar] [CrossRef]
- Sung, C.M.; Sung, M. Carbon nitride and other speculative superhard materials. Mater. Chem. Phys. 1996, 43, 1–18. [Google Scholar] [CrossRef]
- Xu, J.H.; Freeman, A.J. Phase stability and electronic structure of ScA13 and ZrA13 and of Sc-stabilized cubic ZrA13 precipitates. Phys. Rev. B 1990, 41, 12553–12561. [Google Scholar] [CrossRef]
- Grechnev, G.E.; Ushakova, N.V.; Kervalishvili, P.D.; Kvachantiradze, G.G.; Kharebov, K.S. Electron structure of diborides of 3d metals. Low Temp. Phys. 1997, 23, 217–219. [Google Scholar] [CrossRef]
- Vajeeston, P.; Ravindran, P.; Ravi, C.; Asokamani, R. Electronic structure, bonding, and ground-state properties of AlB2-type transition-metal diborides. Phys. Rev. B 2001, 63, 045115. [Google Scholar] [CrossRef]
- Imai, Y.; Mukaida, M.; Tsunoda, T. Comparison of density of states of transition metal disilicides and their related compounds systematically calculated by a first-principle pseudopotential method using plane-wave basis. Intermetallics 2000, 8, 381–390. [Google Scholar] [CrossRef]
- Huang, L.F.; Lu, X.Z.; Tennessen, E.; Rondinelli, J.M. An efficient ab-initio quasiharmonic approach for the thermodynamics of solids. Comput. Mater. Sci. 2016, 120, 84–93. [Google Scholar] [CrossRef]
- Yan, H.Y.; Zhang, M.G.; Huang, D.H.; Wei, Q. First-principles study of elastic and thermodynamic properties of orthorhombic OsB4 under high pressure. Solid State Sci. 2013, 18, 17–23. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Qin, J.Q.; Ning, J.L.; Sun, X.W.; Li, X.T.; Ma, M.Z.; Liu, R.P. First principle study of elastic and thermodynamic properties of FeB4 under high pressure. J. Appl. Phys. 2013, 114, 183517. [Google Scholar] [CrossRef]
- Zhao, Y.R.; Zhang, G.T.; Yan, H.Y.; Bai, T.T.; Zheng, B.B.; Yuan, Y.Q. First-principles investigations of the structure and physical properties for new TcN crystal structure. Mol. Phys. 2016, 114, 1–8. [Google Scholar] [CrossRef]


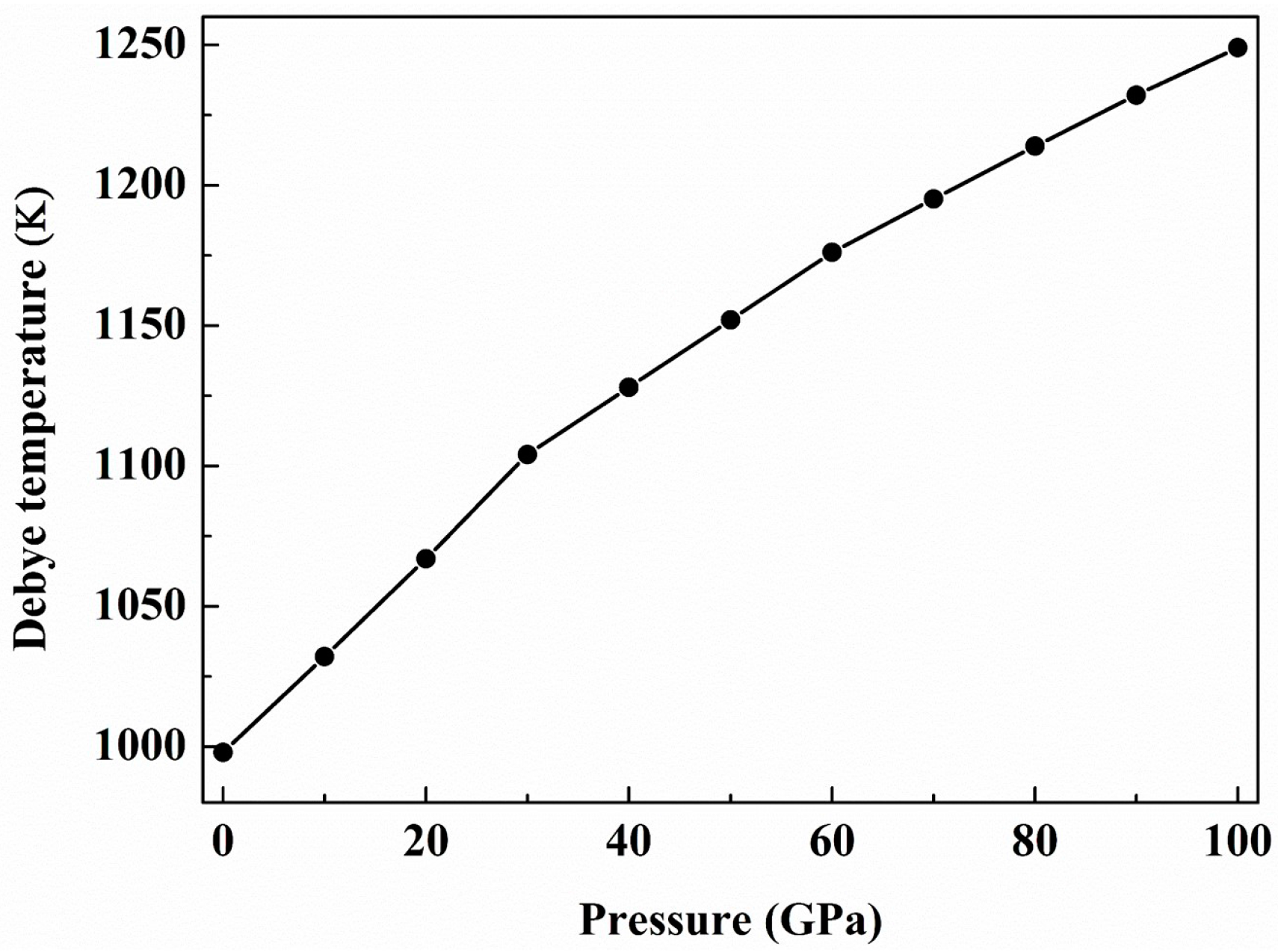
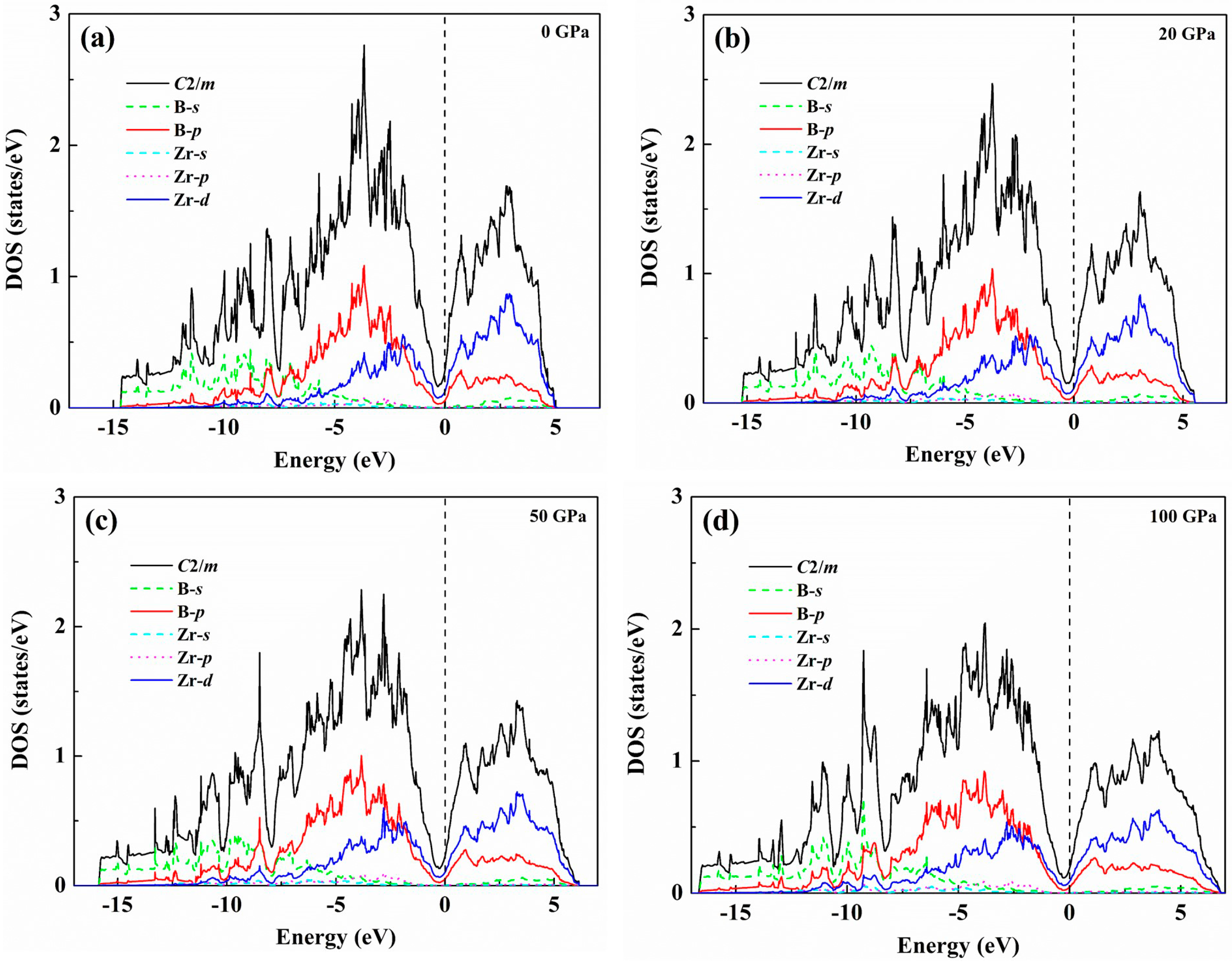
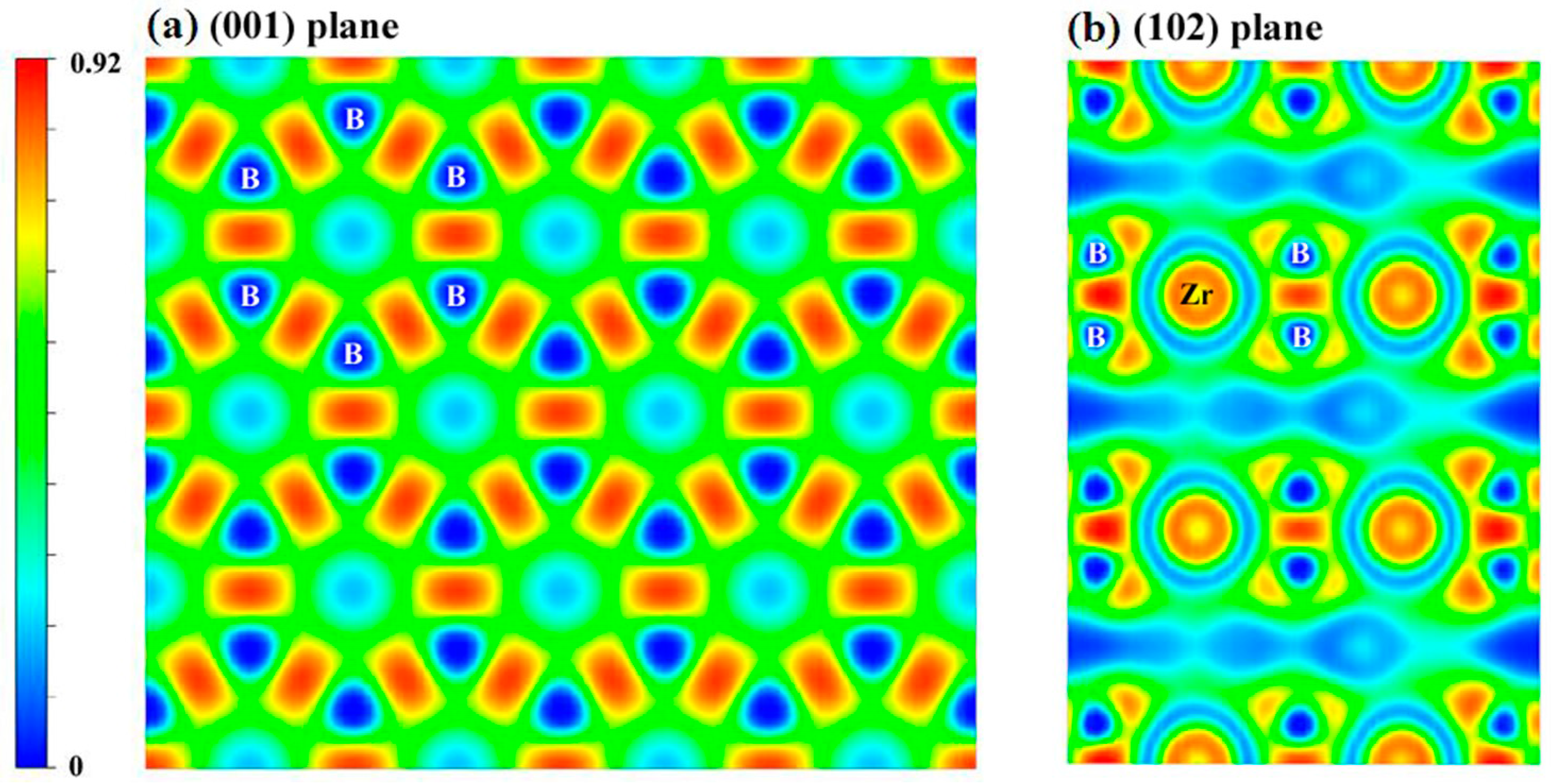
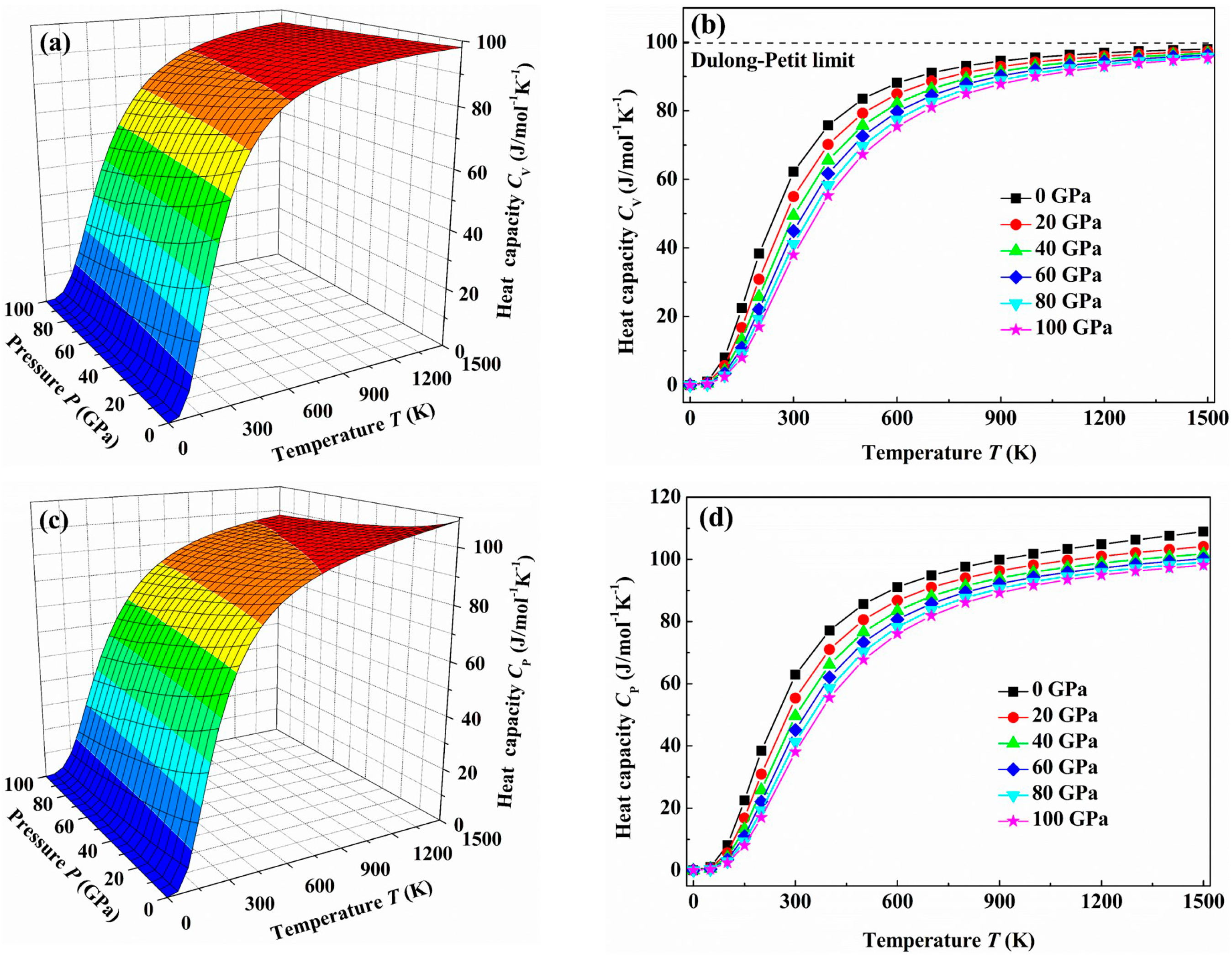
| Structure | Work | C11 | C22 | C33 | C44 | C55 | C66 | C12 | C13 | C23 | B | B0 | G | E | G/B | ν | ΘD | Hv |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C2/m-ZrB3 | this work | 576 | 564 | 466 | 207 | 244 | 250 | 45 | 115 | 109 | 238 | 237 | 227 | 517 | 0.95 | 0.14 | 998 | 42.2 |
| Fm-3m-ZrB | this work | 363 | - | - | 60 | - | - | 60 | - | - | 161 | 160 | 88 | 223 | 0.55 | 0.27 | 529 | 10.5 |
| theory [17] | 282 | - | - | 111 | - | - | 100 | - | - | 161 | - | 103 | 254 | - | 0.24 | - | - | |
| theory [18] | 350 | - | - | 43 | - | - | 70 | - | - | 163 | - | 71 | 186 | - | 0.31 | - | 5.5 | |
| theory [19] | 353 | - | - | 51 | - | - | 64 | - | - | 160 | - | 78 | 202 | - | 0.29 | - | 11.8 | |
| theory [28] | 274 | - | - | 42 | - | - | 51 | - | - | 125 | - | 63 | 162 | 0.50 | 0.28 | 450 | 7.9 | |
| experiment [41] | - | - | - | - | - | - | - | - | - | 148 | - | - | 244 | - | 0.23 | - | - | |
| P6/mmm-ZrB2 | this work | 565 | - | 432 | 252 | - | 255 | 54 | 121 | - | 239 | 238 | 233 | 527 | 0.98 | 0.13 | 930 | 44.1 |
| theory [17] | 504 | - | 427 | 241 | - | - | 91 | 112 | - | 229 | - | 211 | 484 | - | 0.15 | - | - | |
| theory [21] | 551 | - | 436 | 252 | - | - | 65 | 121 | - | 239 | - | 229 | 520 | - | 0.14 | 921 | - | |
| theory [28] | 502 | - | 374 | 225 | - | 229 | 43 | 85 | - | 199 | - | 211 | 468 | 1.06 | 0.11 | 884 | 43.5 | |
| experiment [20] | 581 | - | 445 | 240 | - | 261 | 55 | 121 | - | 245 | - | 243 | 554 | - | - | - | - | |
| experiment [42] | - | - | - | - | - | - | - | - | - | 220 | - | 225 | 502 | - | 0.11 | 910 | ||
| Amm2-ZrB4 | theory [27] | 554 | 576 | 454 | 223 | 243 | 254 | 50 | 122 | 113 | 241 | - | 229 | 522 | 0.95 | 0.14 a | - | 42.6 |
| Fm-3m-ZrB12 | this work | 412 | - | - | 251 | - | - | 144 | - | - | 233 | 233 | 195 | 458 | 0.84 | 0.17 | 933 | 32.5 |
| theory [26] | 413 | - | - | 244 | - | - | 141 | - | - | 232 | - | 193 | 453 | 0.83 | 0.174 | 1206 | - | |
| theory [28] | 420 | - | - | 249 | - | - | 123 | - | - | 222 | - | 202 | 466 | 0.91 | 0.15 | 1231 | 35.4 | |
| experiment [43] | 443 | - | - | 265 | - | - | 129 | - | - | 234 | - | - | - | - | 0.23 | 1260 | - | |
| experiment [44] | - | - | - | - | - | - | - | - | - | - | - | - | - | 1260 | - | |||
| Pnma-RuB3 | theory [45] | 497 | 462 | 471 | 224 | 219 | 187 | 111 | 229 | - | 267 | 185 | 451 | 0.69 | 0.219 | - | 26.3 | |
| R-3m-MoB3 | theory [46] | 602 | - | 420 | 247 | - | - | 106 | 166 | - | 276 | 277 | 222 | 526 | 0.80 | 0.18 | - | 31.8 |
| P63/mmc-WB3 | theory [47] | 656 | - | 479 | 277 | - | - | - | - | - | 291 | - | 252 | 588 | - | 0.168 | - | 42 |
| P-6m2-OsB3 | theory [48] | 525 | - | 751 | 186 | - | - | 125 | 221 | - | 317 | - | 195 | 485 | 0.62 | 0.245 | 36.9 | |
| P21/m-OsB3 | theory [45] | 674 | 525 | 584 | 135 | 291 | 128 | 97 | 247 | - | 303 | - | 186 | 463 | 0.61 | 0.245 | 25.1 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Bai, T.; Zhao, Y.; Hu, Y. A New Superhard Phase and Physical Properties of ZrB3 from First-Principles Calculations. Materials 2016, 9, 703. https://doi.org/10.3390/ma9080703
Zhang G, Bai T, Zhao Y, Hu Y. A New Superhard Phase and Physical Properties of ZrB3 from First-Principles Calculations. Materials. 2016; 9(8):703. https://doi.org/10.3390/ma9080703
Chicago/Turabian StyleZhang, Gangtai, Tingting Bai, Yaru Zhao, and Yanfei Hu. 2016. "A New Superhard Phase and Physical Properties of ZrB3 from First-Principles Calculations" Materials 9, no. 8: 703. https://doi.org/10.3390/ma9080703
APA StyleZhang, G., Bai, T., Zhao, Y., & Hu, Y. (2016). A New Superhard Phase and Physical Properties of ZrB3 from First-Principles Calculations. Materials, 9(8), 703. https://doi.org/10.3390/ma9080703