Acoustic Emission of Deformation Twinning in Magnesium
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Mechanical and Nondestructive Evaluation Setup
2.2. Sample Preparation
3. Results and Discussion
3.1. Single Crystal Compression
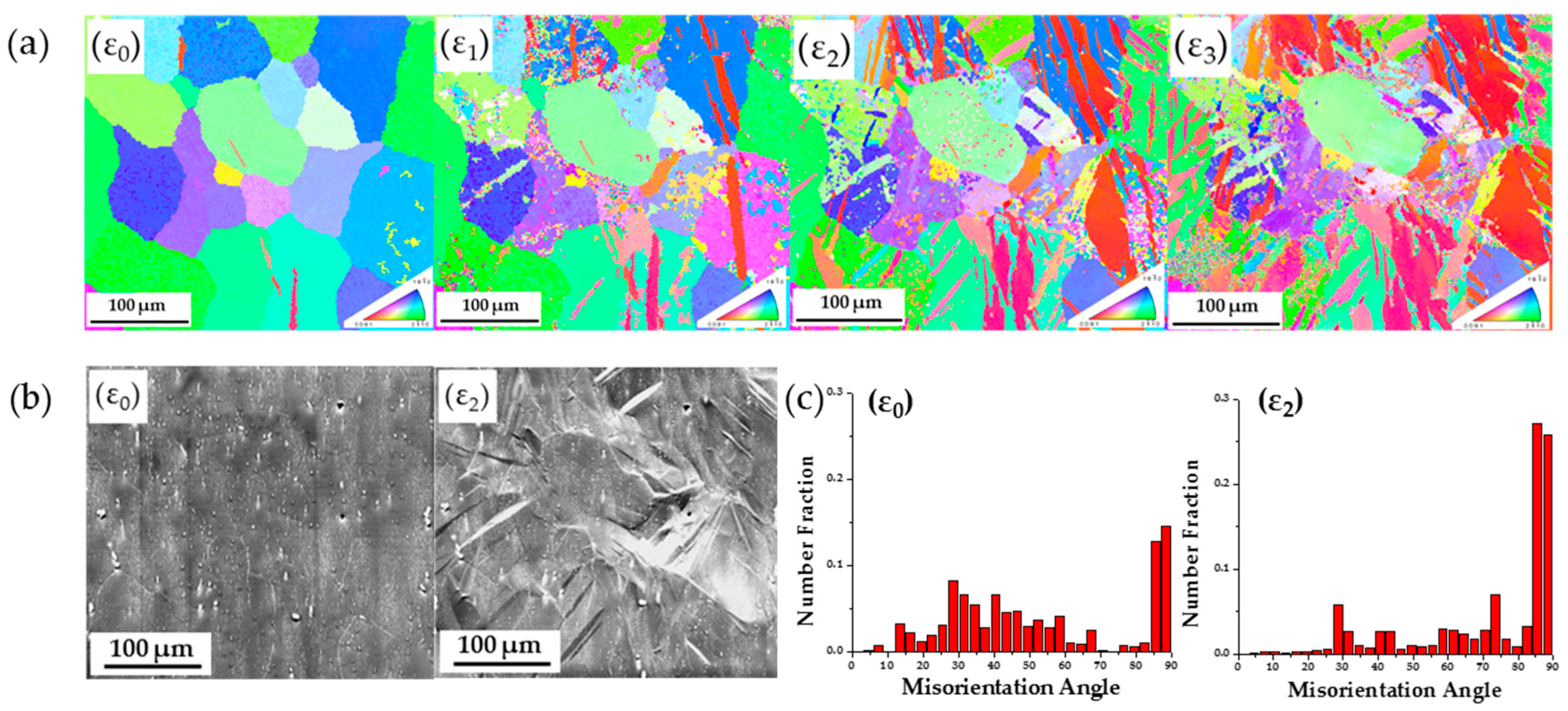
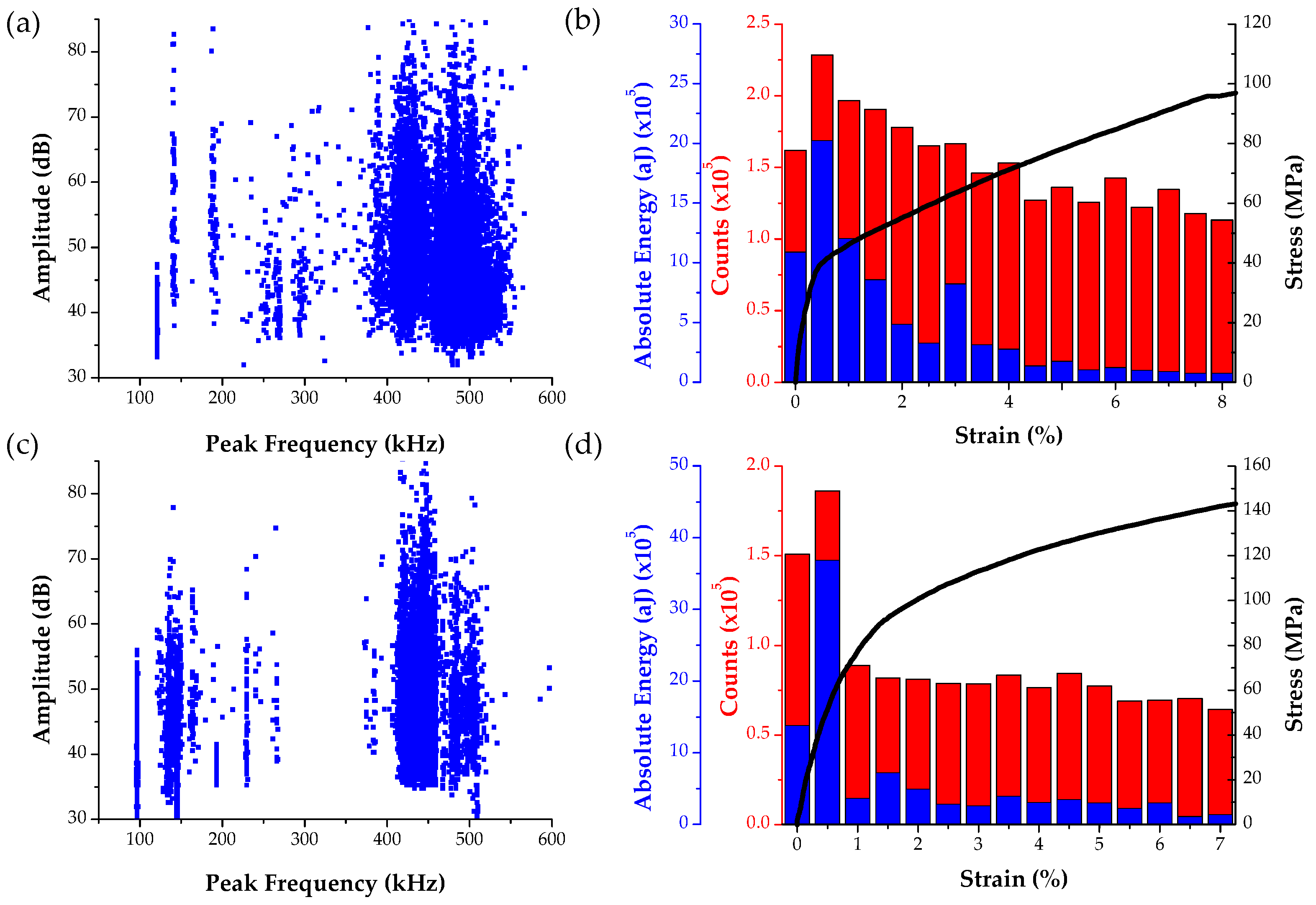
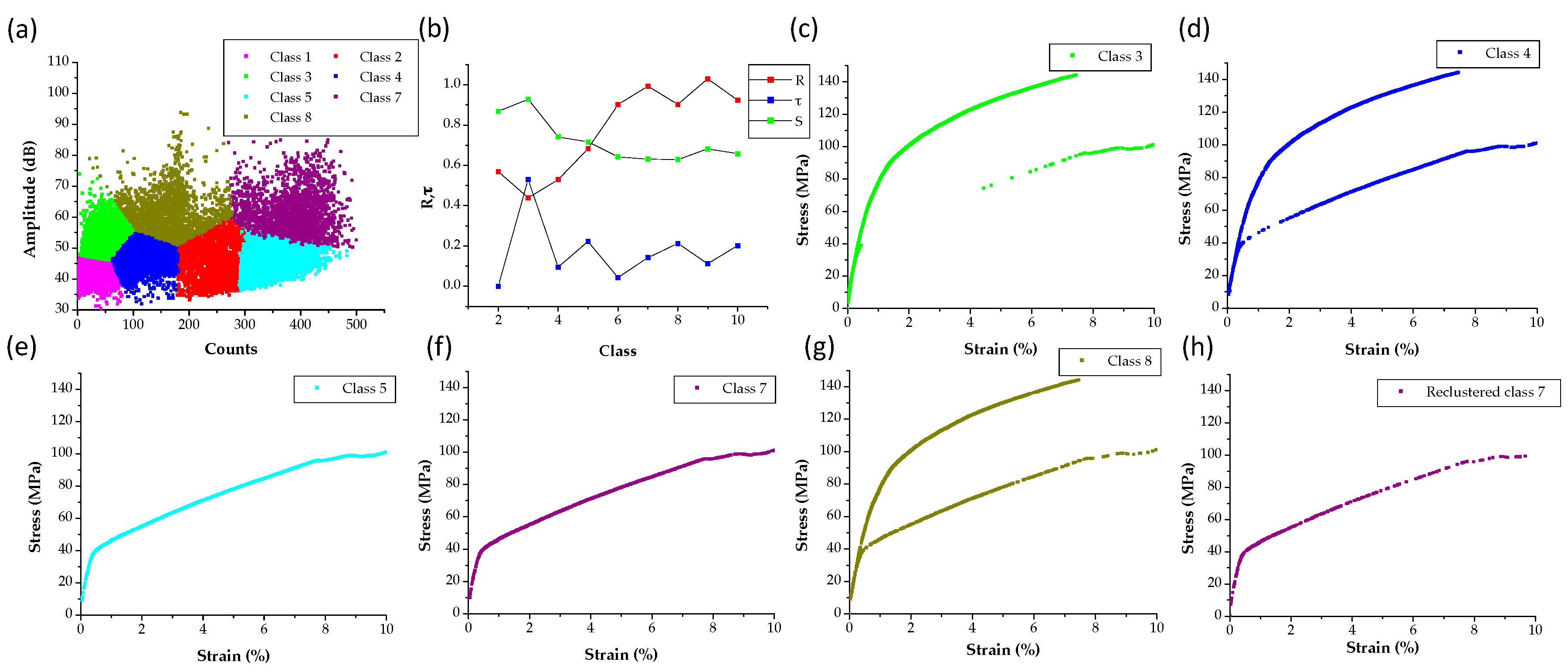
3.2. AZ31 Tensile Tests Inside the SEM
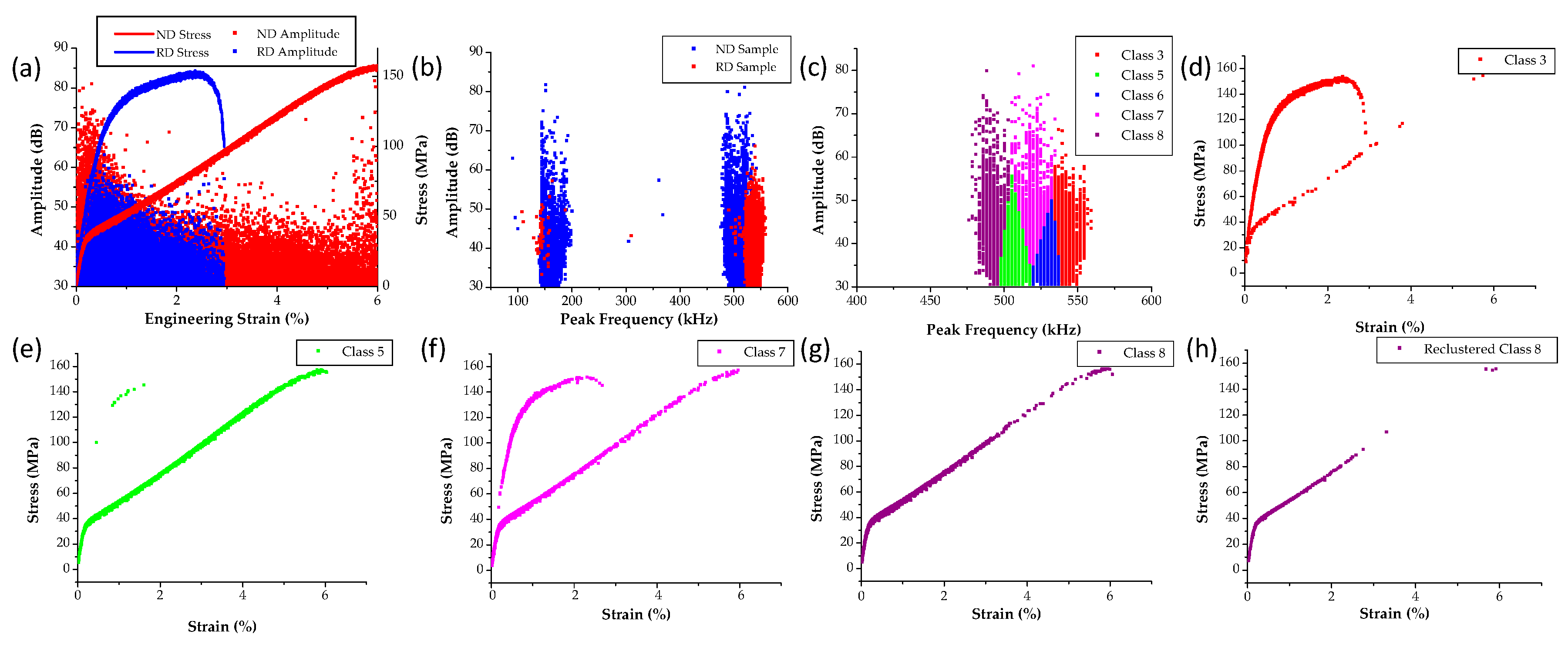
3.3. AZ 31 Tensile Tests Using the MTS
3.4. Summary of AE Signals by Twinning in Magnesium
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hull, D. Introduction to Dislocations; Pergamon Press Ltd.: Oxford, UK, 1965. [Google Scholar]
- Yoo, M.H. Slip, twinning, and fracture in hexagonal close-packed metals. Metall. Trans. A 1981, 12A, 409–418. [Google Scholar]
- Kalidindi, S.; Salem, A.; Doherty, R.D. Role of deformation twinning on strain hardening in cubic and hexagonal polycrystalline metals. Adv. Eng. Mater. 2003, 5, 229–232. [Google Scholar] [CrossRef]
- Ando, D.; Koike, J.; Sutou, Y. Relationship between deformation twinning and surface step formation in AZ31 magnesium alloys. Acta Mater. 2010, 58, 4316–4324. [Google Scholar] [CrossRef]
- Knezevic, M.; Levinson, A.; Harris, R.; Mishra, R.K.; Doherty, R.D.; Kalidindi, S.R. Deformation twinning in AZ31: Influence on strain hardening and texture evolution. Acta Mater. 2010, 58, 6230–6242. [Google Scholar] [CrossRef]
- Matsuzuki, M.; Horibe, M. Analysis of fatigue damage process in magnesium alloy AZ31. Mater. Sci. Eng. A 2009, 504, 169–174. [Google Scholar] [CrossRef]
- Wu, L.; Agnew, S.R.; Ren, Y.; Brown, D.W.; Clausen, B.; Stoica, G.M.; Wenk, H.R.; Liaw, P.K. The effects of texture and extension twinning on the low-cycle fatigue behavior of a rolled magnesium alloy AZ31B. Mater. Sci. Eng. A 2010, 527, 7057–7067. [Google Scholar] [CrossRef]
- Wu, L.; Agnew, S.; Brown, D.; Stoica, G.; Clausen, B.; Jain, A.; Fielden, D.; Liaw, P. Internal stress relaxation and load redistribution during the twinning–detwinning-dominated cyclic deformation of a wrought magnesium alloy, ZK60A. Acta Mater. 2008, 56, 3699–3707. [Google Scholar] [CrossRef]
- Barnett, M.R.; Keshavarz, Z.; Beer, A.G.; Ma, X. Non-Schmid behaviour during secondary twinning in a polycrystalline magnesium alloy. Acta Mater. 2008, 56, 5–15. [Google Scholar] [CrossRef]
- Molodov, K.D.; Al-Samman, T.; Molodov, D.A.; Gottstein, G. Mechanisms of exceptional ductility of magnesium single crystal during deformation at room temperature: Multiple twinning and dynamic recrystallization. Acta Mater. 2014, 76, 314–330. [Google Scholar] [CrossRef]
- El Kadiri, H.; Kapil, J.; Oppedal, A.L.; Hector, L.G.; Agnew, S.R.; Cherkaoui, M.; Vogel, S.C. The effect of twin–twin interactions on the nucleation and propagation {10–12} of twinning in magnesium. Acta Mater. 2013, 61, 3549–3563. [Google Scholar] [CrossRef]
- Beyerlein, I.J.; Wang, J.; Barnett, M.R.; Tome, C.N. Double twinning mechanisms in magnesium alloys via dissociation of lattice dislocations. Proc. R. Soc. A 2012, 468, 1496–1520. [Google Scholar] [CrossRef]
- Lou, X.; Li, M.; Boger, R.; Agnew, S.; Wagoner, R. Hardening evolution of AZ31B Mg sheet. Int. J. Plast. 2007, 23, 44–86. [Google Scholar] [CrossRef]
- Barnett, M.R. Twinning and the ductility of magnesium alloys PartI: “Tension” twins. Mater. Sci. Eng. A 2007, 464, 1–7. [Google Scholar] [CrossRef]
- Kleiner, S.; Uggowitzer, P.J. Mechanical anisotropy of extruded Mg–6% Al–1% Zn alloy. Mater. Sci. Eng. A 2004, 379, 258–263. [Google Scholar] [CrossRef]
- Yi, S.B.; Davies, C.H.J.; Brokmeier, H.G.; Bolmaro, R.E.; Kainer, K.U.; Homeyer, J. Deformation and texture evolution in AZ31 magnesium alloy during uniaxial loading. Acta Mater. 2006, 54, 549–562. [Google Scholar] [CrossRef]
- El Kadiri, H.; Baird, J.C.; Kapil, J.; Oppedal, A.L.; Cherkaoui, M.; Vogel, S.C. Flow asymmetry and nucleation stresses of twinning and non-basal slip in magnesium. Int. J. Plast. 2013, 44, 111–120. [Google Scholar] [CrossRef]
- Oppedal, A.; Kadiri, H.E.; Tomé, C.; Vogel, S.C.; Horstemeyer, M. Anisotropy in hexagonal close-packed structures: Improvements to crystal plasticity approaches applied to magnesium alloy. Philos. Mag. 2013, 93, 4311–4330. [Google Scholar] [CrossRef]
- Bian, M.Z.; Shin, K.S. {10–12} twinning behavior in magnesium single crystal. Met. Mater. Int. 2013, 19, 999–1004. [Google Scholar] [CrossRef]
- Al-Samman, T.; Molodov, K.D.; Molodov, D.A.; Gottstein, G.; Suwas, S. Softening and dynamic recrystallization in magnesium single crystals during c-axis compression. Acta Mater. 2012, 60, 537–545. [Google Scholar] [CrossRef]
- Molodov, K.D.; Al-Samman, T.; Molodov, D.A.; Gottstein, G. On the role of anomalous twinning in the plasticity of magnesium. Acta Mater. 2016, 103, 711–723. [Google Scholar] [CrossRef]
- Shin, J.H.; Kim, S.H.; Ha, T.K.; Oh, K.H.; Choi, I.S.; Han, H.N. Nanoindentation study for deformation twinning of magnesium single crystal. Scr. Mater. 2013, 68, 483–486. [Google Scholar] [CrossRef]
- Byer, C.M.; Li, B.; Cao, B.; Ramesh, K.T. Microcompression of single-crystal magnesium. Scr. Mater. 2010, 62, 536–539. [Google Scholar] [CrossRef]
- Molodov, K.D.; Al-Samman, T.; Molodov, D.A. On the diversity of the plastic response of magnesium in plane strain compression. Mater. Sci. Eng. A 2016, 651, 63–68. [Google Scholar] [CrossRef]
- Prasad, K.E.; Ramesh, K.T. In-situ observations and quantification of twin boundary mobility in polycrystalline magnesium. Mater. Sci. Eng. A 2014, 617, 121–126. [Google Scholar] [CrossRef]
- Kostopoulos, V.; Loutas, T.H.; Kontsos, A.; Sotiriadis, G.; Pappas, Y.Z. On the identification of the failure mechanisms in oxide/oxide composites using acoustic emission. NDT E Int. 2003, 36, 571–580. [Google Scholar] [CrossRef]
- Pappas, Y.Z.; Kontsos, A.; Loutas, T.H.; Kostopoulos, V. On the characterization of continuous fibres fracture by quantifying acoustic emission and acousto-ultrasonics waveforms. NDT E Int. 2004, 37, 389–401. [Google Scholar] [CrossRef]
- Kontsos, A.; Loutas, T.; Kostopoulos, V.; Hazeli, K.; Anasori, B.; Barsoum, M.W. Nanocrystalline Mg-MAX composites: Mechanical behavior characterization via acoustic emission monitoring. Acta Mater. 2011, 59, 5716–5727. [Google Scholar] [CrossRef]
- Miguel, M.-C.; Vespignani, A.; Zapperi, S.; Weiss, J.; Grasso, J.-R. Intermittent dislocation flow in viscoplastic deformation. Nature 2001, 410, 667–671. [Google Scholar] [CrossRef] [PubMed]
- Vinogradov, A.; Hashimoto, S.; Miura, S. Effect of grain boundary on acoustic emission during plastic deformation of copper-aluminum bicrystals. Acta Mater. 1996, 44, 2883–2890. [Google Scholar] [CrossRef]
- Koslowski, M.; LeSar, R.; Thomson, R. Avalanches and scaling in plastic deformation. Phys. Rev. Lett. 2004, 93, 125502. [Google Scholar] [CrossRef] [PubMed]
- Ioka, I.; Yoda, S. Acoustic emission for polycrystalline graphite under compressive loading. Carbon 1990, 28, 489–495. [Google Scholar] [CrossRef]
- Chung, J.-B.; Kannatey-Asibu, E. Acoustic emission from plastic deformation of a pure single crystal. J. Appl. Phys. 1992, 72, 1812–1820. [Google Scholar] [CrossRef]
- Lamark, T.T.; Chmelı́k, F.; Estrin, Y.; Lukáč, P. Cyclic deformation of a magnesium alloy investigated by the acoustic emission technique. J. Alloys Compd. 2004, 378, 202–206. [Google Scholar] [CrossRef]
- Richeton, T.; Dobron, P.; Chmelik, F.; Weiss, J.; Louchet, F. On the critical character of plasticity in metallic single crystals. Mater. Sci. Eng. A 2006, 424, 190–195. [Google Scholar] [CrossRef]
- Máthis, K.; Čapek, J.; Zdražilová, Z.; Trojanová, Z. Investigation of tension–compression asymmetry of magnesium by use of the acoustic emission technique. Mater. Sci. Eng. A 2011, 528, 5904–5907. [Google Scholar] [CrossRef]
- Moorthy, V.; Jayakumar, T.; Raj, B. Acoustic Emission Teqcnique For Detecting Micro and Micro yeilding in solution annealed AISI Type 316 austenetic stainless steel. Int. J. Pres. Ves. Piping 1995, 64, 161–168. [Google Scholar] [CrossRef]
- Van Bohemen, S.M.C.; Sietsma, J.; Hermans, M.J.M.; Richardson, I.M. Kinetics of the martensitic transformation in low-alloy steel studied by means of acoustic emission. Acta Mater. 2003, 51, 4183–4196. [Google Scholar] [CrossRef]
- Vinogradov, A.; Merson, D.L.; Patlan, V.; Hashimoto, S. Effect of solid solution hardening and stacking fault energy on plastic flow and acoustic emission in Cu-Ge alloys. Mater. Sci. Eng. A 2003, 341, 57–73. [Google Scholar] [CrossRef]
- Lu, Y.; Charghouri, M.; Taheri, F. Effect of texture on acoustic emission produced by slip and twinning in AZ31B magnesium alloy-part II: Clustering and neural network analysis. Nondestruct. Test. Eval. 2008, 23, 211–228. [Google Scholar] [CrossRef]
- Bohlen, J.; Chmelı́k, F.; Dobroň, P.; Letzig, D.; Lukáč, P.; Kainer, K.U. Acoustic emission during tensile testing of magnesium AZ alloys. J. Alloys Compd. 2004, 378, 214–219. [Google Scholar] [CrossRef]
- Meza-García, E.; Dobroň, P.; Bohlen, J.; Letzig, D.; Chmelík, F.; Lukáč, P.; Kainer, K.U. Deformation mechanisms in an AZ31 cast magnesium alloy as investigated by the acoustic emission technique. Mater. Sci. Eng. A 2007, 462, 297–301. [Google Scholar] [CrossRef]
- Muránsky, O.; Barnett, M.R.; Carr, D.G.; Vogel, S.C.; Oliver, E.C. Investigation of deformation twinning in a fine-grained and coarse-grained ZM20 Mg alloy: Combined in situ neutron diffraction and acoustic emission. Acta Mater. 2010, 58, 1503–1517. [Google Scholar] [CrossRef]
- Bohlen, J.; Dobron, P.; Meza, G.E.; Chmelík, F.; Lukáč, P.; Letzig, D.; Kainer, K.U. The Effect of Grain Size on the Deformation Behaviour of Magnesium Alloys Investigated by the Acoustic Emission Technique. Adv. Eng. Mater. 2006, 8, 422–427. [Google Scholar] [CrossRef]
- Bohlen, J.; Dobroň, P.; Swiostek, J.; Letzig, D.; Chmelík, F.; Lukáč, P.; Kainer, K.U. On the influence of the grain size and solute content on the AE response of magnesium alloys tested in tension and compression. Mater. Sci. Eng. A 2007, 462, 302–306. [Google Scholar] [CrossRef]
- Vinogradov, A.; Orlov, D.; Danyuk, A.; Estrin, Y. Effect of grain size on the mechanisms of plastic deformation in wrought Mg–Zn–Zr alloy revealed by acoustic emission measurements. Acta Mater. 2013, 61, 2044–2056. [Google Scholar] [CrossRef]
- Drozdenko, D.; Bohlen, J.; Chmelík, F.; Lukáč, P.; Dobroň, P. Acoustic emission study on the activity of slip and twin mechanisms during compression testing of magnesium single crystals. Mater. Sci. Eng. A 2016, 650, 20–27. [Google Scholar] [CrossRef]
- Čapek, J.; Máthis, K.; Clausen, B.; Stráská, J.; Beran, P.; Lukáš, P. Study of the loading mode dependence of the twinning in random textured cast magnesium by acoustic emission and neutron diffraction methods. Mater. Sci. Eng. A 2014, 602, 25–32. [Google Scholar] [CrossRef]
- Drozdenko, D.; Bohlen, J.; Yi, S.; Minárik, P.; Chmelík, F.; Dobroň, P. Investigating a twinning–detwinning process in wrought Mg alloys by the acoustic emission technique. Acta Mater. 2016, 110, 103–113. [Google Scholar] [CrossRef]
- Hazeli, K.; Askari, H.; Cuadra, J.; Streller, F.; Carpick, R.W.; Zbib, H.M.; Kontsos, A. Microstructure-sensitive investigation of magnesium alloy fatigue. Int. J. Plast. 2015, 68, 55–76. [Google Scholar] [CrossRef]
- Kawai, S.; Yoshida, Y.; Asano, H.; Miura, S.; Kobayashi, M.; Shibano, J.-I. Acoustic emission response of magnesium alloy during cyclic and creep tests. Mater. Sci. Eng. A 2016, 668, 120–124. [Google Scholar] [CrossRef]
- Chang, H. Identification of damage mode in AZ31 magnesium alloy under tension using acoustic emission. Trans. Nonferr. Metal. Soc. 2015, 25, 1840–1846. [Google Scholar] [CrossRef]
- Vinogradov, A.; Orlov, D.; Danyuk, A.; Estrin, Y. Deformation mechanisms underlying tension–compression asymmetry in magnesium alloy ZK60 revealed by acoustic emission monitoring. Mater. Sci. Eng. A 2015, 621, 243–251. [Google Scholar] [CrossRef]
- Vinogradov, A.; Lazarev, A.; Linderov, M.; Weidner, A.; Biermann, H. Kinetics of deformation processes in high-alloyed cast transformation-induced plasticity/twinning-induced plasticity steels determined by acoustic emission and scanning electron microscopy: Influence of austenite stability on deformation mechanisms. Acta Mater. 2013, 61, 2434–2449. [Google Scholar] [CrossRef]
- Linderov, M.; Segel, C.; Weidner, A.; Biermann, H.; Vinogradov, A. Deformation mechanisms in austenitic TRIP/TWIP steels at room and elevated temperature investigated by acoustic emission and scanning electron microscopy. Mater. Sci. Eng. A 2014, 597, 183–193. [Google Scholar] [CrossRef]
- Hazeli, K.; Cuadra, J.; Streller, F.; Barr, C.M.; Taheri, M.L.; Carpick, R.W.; Kontsos, A. Three-dimensional effects of twinning in magnesium alloys. Scr. Mater. 2015, 100, 9–12. [Google Scholar] [CrossRef]
- Hazeli, K.; Cuadra, J.; Vanniamparambil, P.A.; Kontsos, A. In situ identification of twin-related bands near yielding in a magnesium alloy. Scr. Mater. 2013, 68, 83–86. [Google Scholar] [CrossRef]
- Hazeli, K.; Sadeghi, A.; Pekguleryuz, M.; Kontsos, A. The effect of Strontium in Plasticity of Magnesium alloys. Mater. Sci. Eng. A 2013, 578, 383–393. [Google Scholar] [CrossRef]
- Wisner, B.; Cabal, M.; Vanniamparambil, P.A.; Hochhalter, J.; Leser, W.P.; Kontsos, A. In Situ Microscopic Investigation to Validate Acoustic Emission Monitoring. Exp. Mech. 2015, 55, 1705–1715. [Google Scholar] [CrossRef]
- Vanniamparambil, P.A.; Guclu, U.; Kontsos, A. Identification of Crack Initiation in Aluminum Alloys using Acoustic Emission. Exp. Mech. 2015, 55, 837–850. [Google Scholar] [CrossRef]
- Yu, Q.; Jiang, Y.; Wang, J. Cyclic deformation and fatigue damage in single-crystal magnesium under fully reversed strain-controlled tension–compression in the [10–10] direction. Scr. Mater. 2015, 96, 41–44. [Google Scholar] [CrossRef]
- Baxevanakis, K.P.; Cabal, M.; Kontsos, A. The Role of Shear Bands in Mechanical Behavior of Magnesium Alloys. Int. J. Soids Struct. 2016. under review. [Google Scholar]
- Aydıner, C.C.; Telemez, M.A. Multiscale deformation heterogeneity in twinning magnesium investigated with in situ image correlation. Int. J. Plast. 2014, 56, 203–218. [Google Scholar] [CrossRef]
- Barnett, M.R.; Nave, M.D.; Ghaderi, A. Yield point elongation due to twinning in a magnesium alloy. Acta Mater. 2012, 60, 1433–1443. [Google Scholar] [CrossRef]
- Li, Y.; Enoki, M. Twinning behavior of pure magnesium quantitatively investigated by acoustic emission. Mater. Sci. Eng. A 2012, 536, 8–13. [Google Scholar] [CrossRef]
- Máthis, K.; Chmelík, F.; Janeček, M.; Hadzima, B.; Trojanová, Z.; Lukáč, P. Investigating deformation processes in AM60 magnesium alloy using the acoustic emission technique. Acta Mater. 2006, 54, 5361–5366. [Google Scholar] [CrossRef]
- Tou, J.T. A Dynamic Optimal Cluster-seeking Technique. Int. J. Comput. Int. Sci. 1979, 8, 541–547. [Google Scholar] [CrossRef]
- Cabal, M. Microstructurally-driven investigation of strain localization in wrought magnesium alloys. In Mechanical Engineering & Mechanics; Drexel University: Philadelphia, PA, USA, 2015. [Google Scholar]



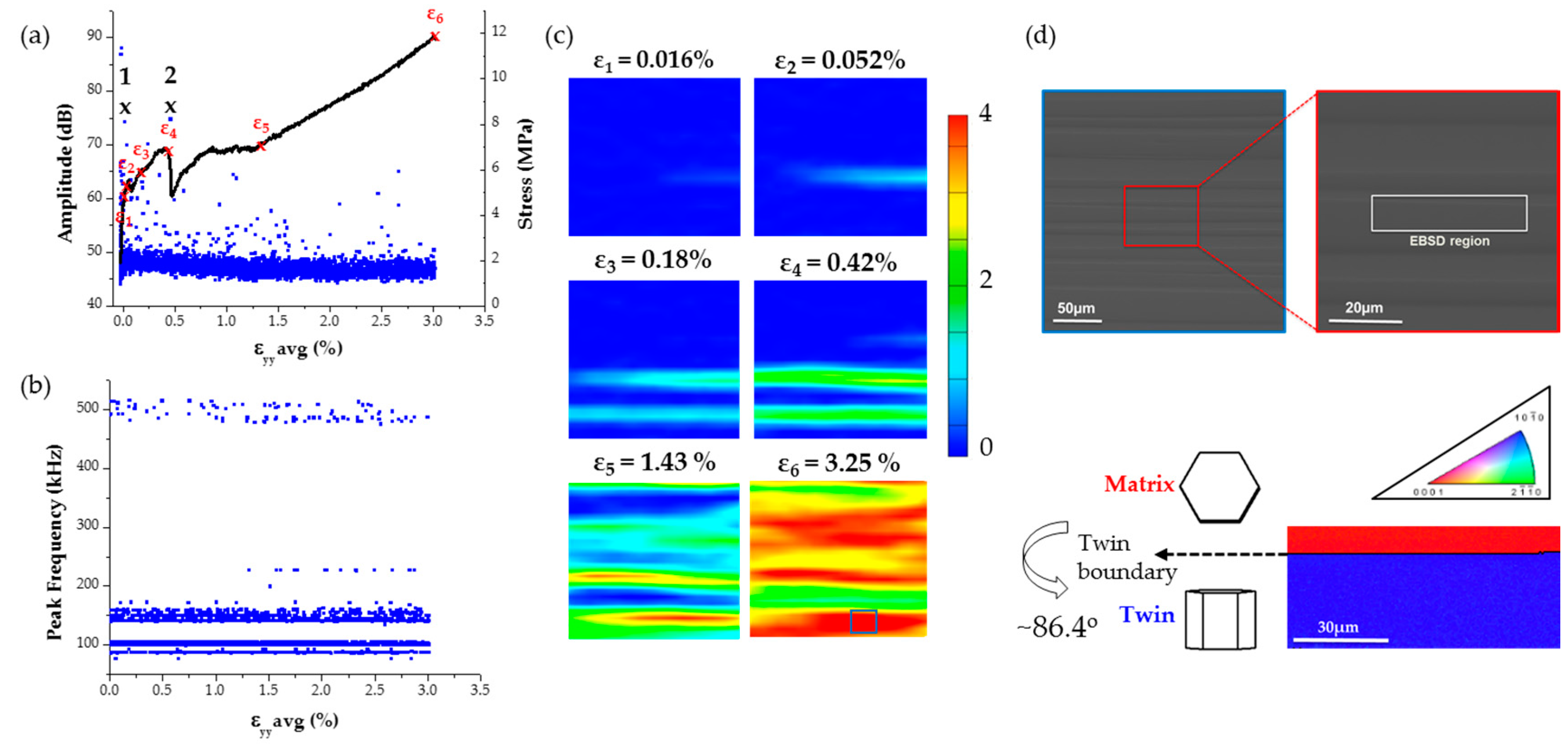
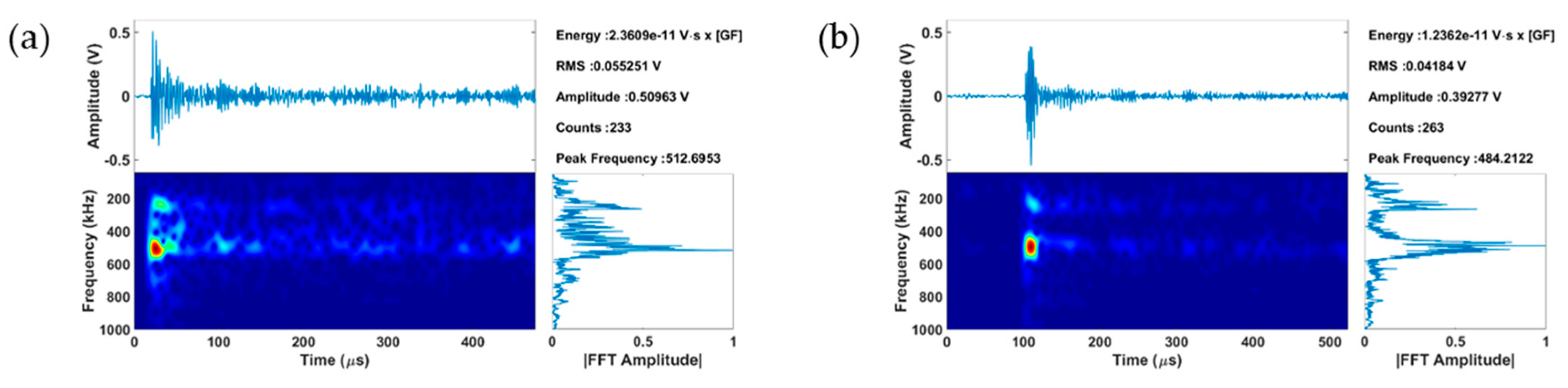
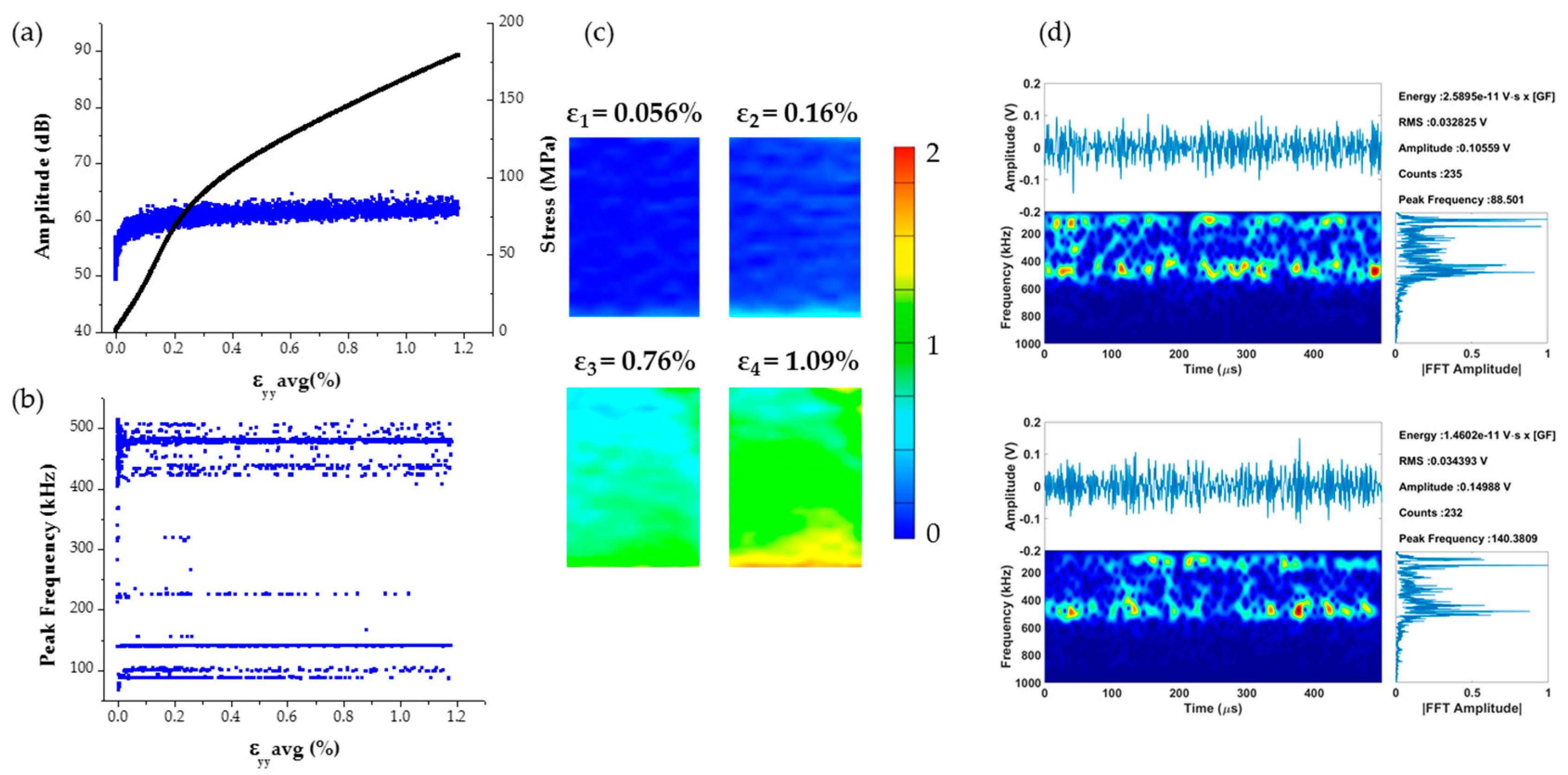



| AE Features of Twinning | Single Crystal Twin 1 | Single Crystal Twin 2 | SEM AZ31 Twin Clustering (388 hits) | MTS AZ31 Twin Clustering (410 hits) |
|---|---|---|---|---|
| Amplitude (dB) | 74 | 75 | 69 ± 6 | 60 ± 8 |
| Rise Angle | 0.721 | 0.724 | 0.92 ± 0.41 | 0.51 ± 0.45 |
| Decay Angle | 0.838 | 0.913 | 0.89 ± 0.38 | 0.46 ± 0.42 |
| Peak Frequency (kHz) | 513 | 484 | 465 ± 37 | 507 ± 14 |
| Frequency Centroid (kHz) | 471 | 500 | 502 ± 70 | 520 ± 68 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mo, C.; Wisner, B.; Cabal, M.; Hazeli, K.; Ramesh, K.T.; El Kadiri, H.; Al-Samman, T.; Molodov, K.D.; Molodov, D.A.; Kontsos, A. Acoustic Emission of Deformation Twinning in Magnesium. Materials 2016, 9, 662. https://doi.org/10.3390/ma9080662
Mo C, Wisner B, Cabal M, Hazeli K, Ramesh KT, El Kadiri H, Al-Samman T, Molodov KD, Molodov DA, Kontsos A. Acoustic Emission of Deformation Twinning in Magnesium. Materials. 2016; 9(8):662. https://doi.org/10.3390/ma9080662
Chicago/Turabian StyleMo, Chengyang, Brian Wisner, Mike Cabal, Kavan Hazeli, K. T. Ramesh, Haitham El Kadiri, Talal Al-Samman, Konstantin D. Molodov, Dmitri A. Molodov, and Antonios Kontsos. 2016. "Acoustic Emission of Deformation Twinning in Magnesium" Materials 9, no. 8: 662. https://doi.org/10.3390/ma9080662
APA StyleMo, C., Wisner, B., Cabal, M., Hazeli, K., Ramesh, K. T., El Kadiri, H., Al-Samman, T., Molodov, K. D., Molodov, D. A., & Kontsos, A. (2016). Acoustic Emission of Deformation Twinning in Magnesium. Materials, 9(8), 662. https://doi.org/10.3390/ma9080662










