A Critical Evaluation of the Influence of the Dark Exchange Current on the Performance of Dye-Sensitized Solar Cells
Abstract
:1. Introduction
2. Theoretical Background
2.1. Determination of J0 from Steady State Measurements
2.2. Determination of J0 from Small Perturbation Techniques
3. Experimental Section
Elaboration and Characterization of Dye-Sensitized Solar Cells
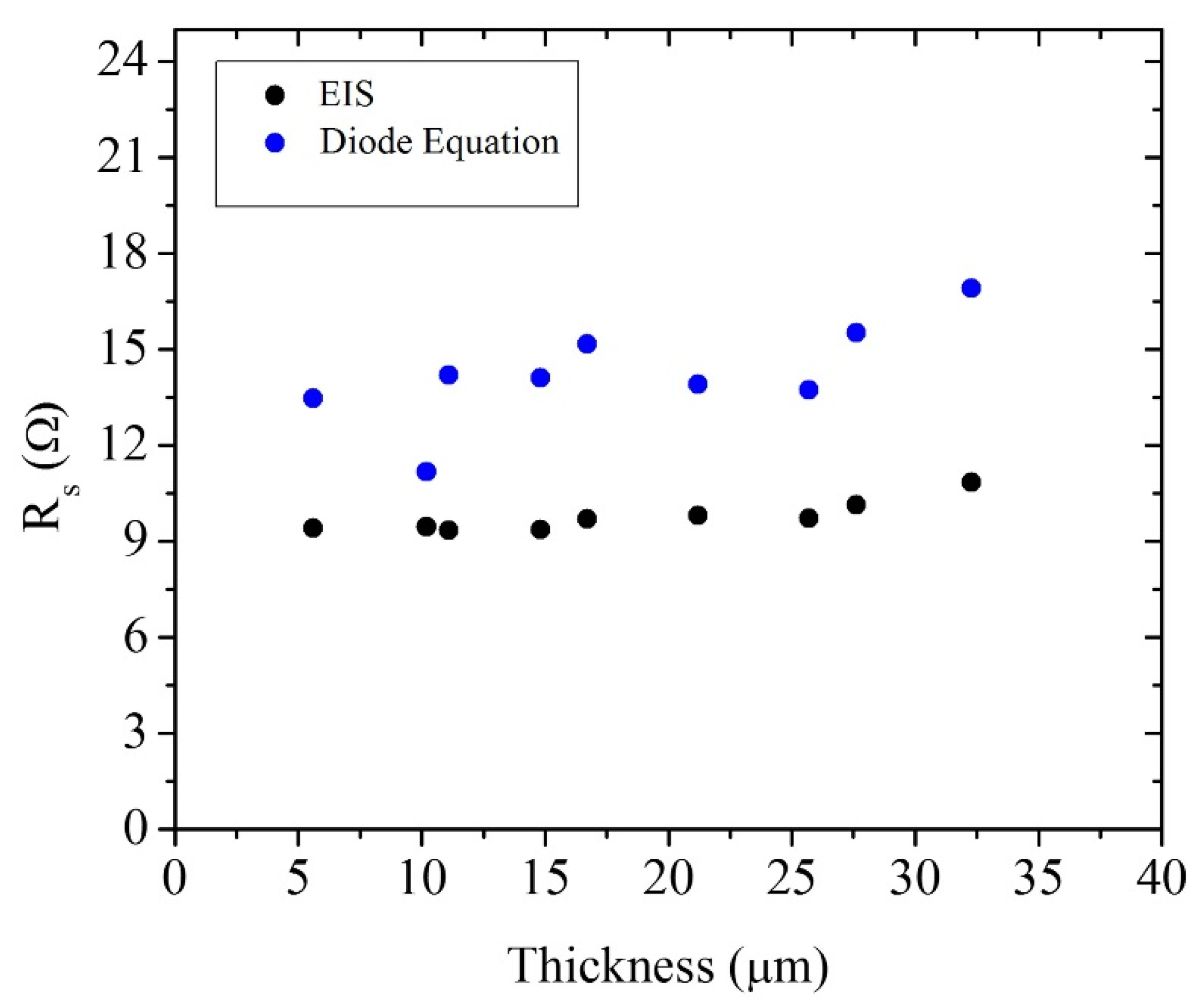
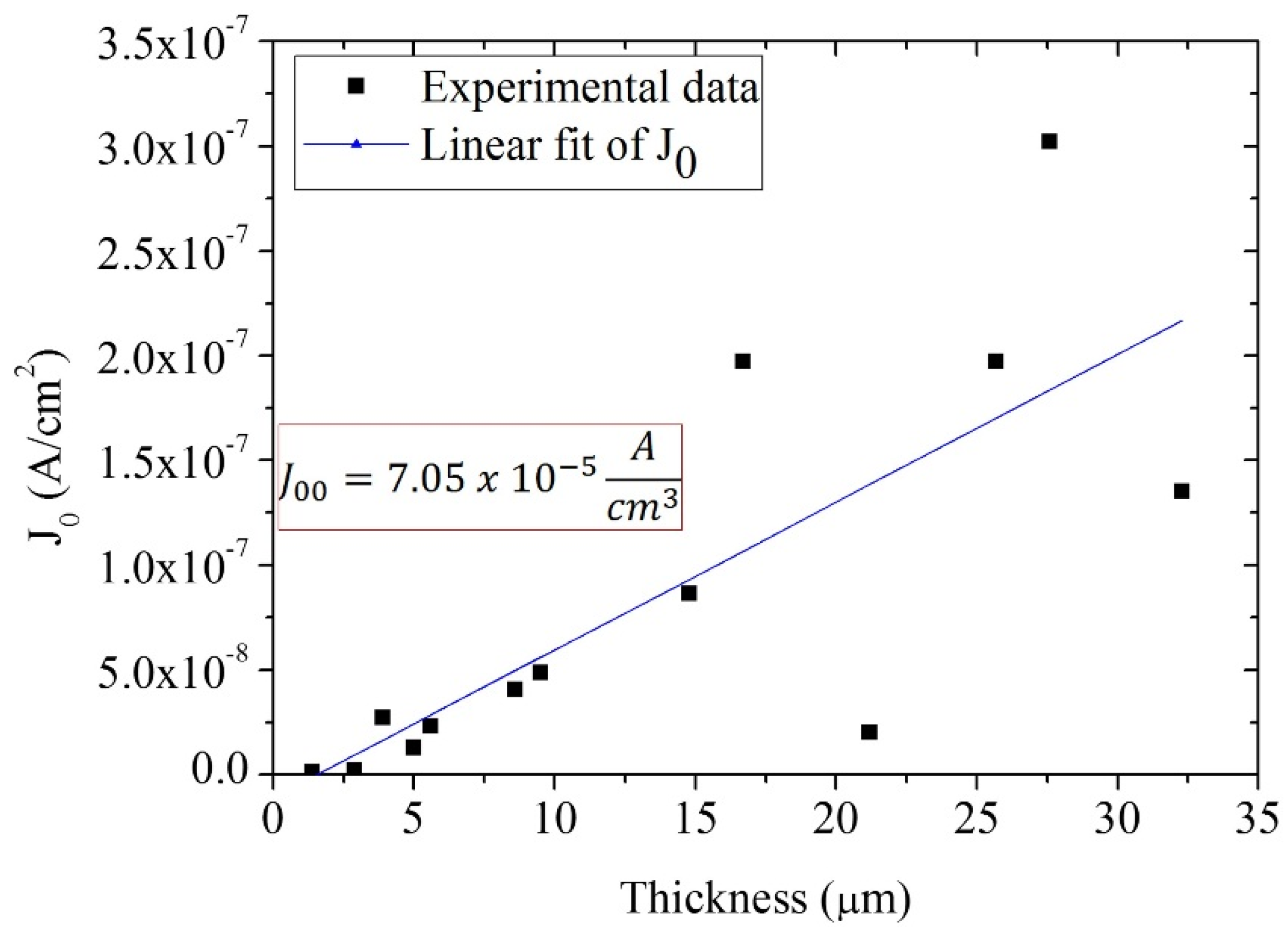
4. Results and Discussion
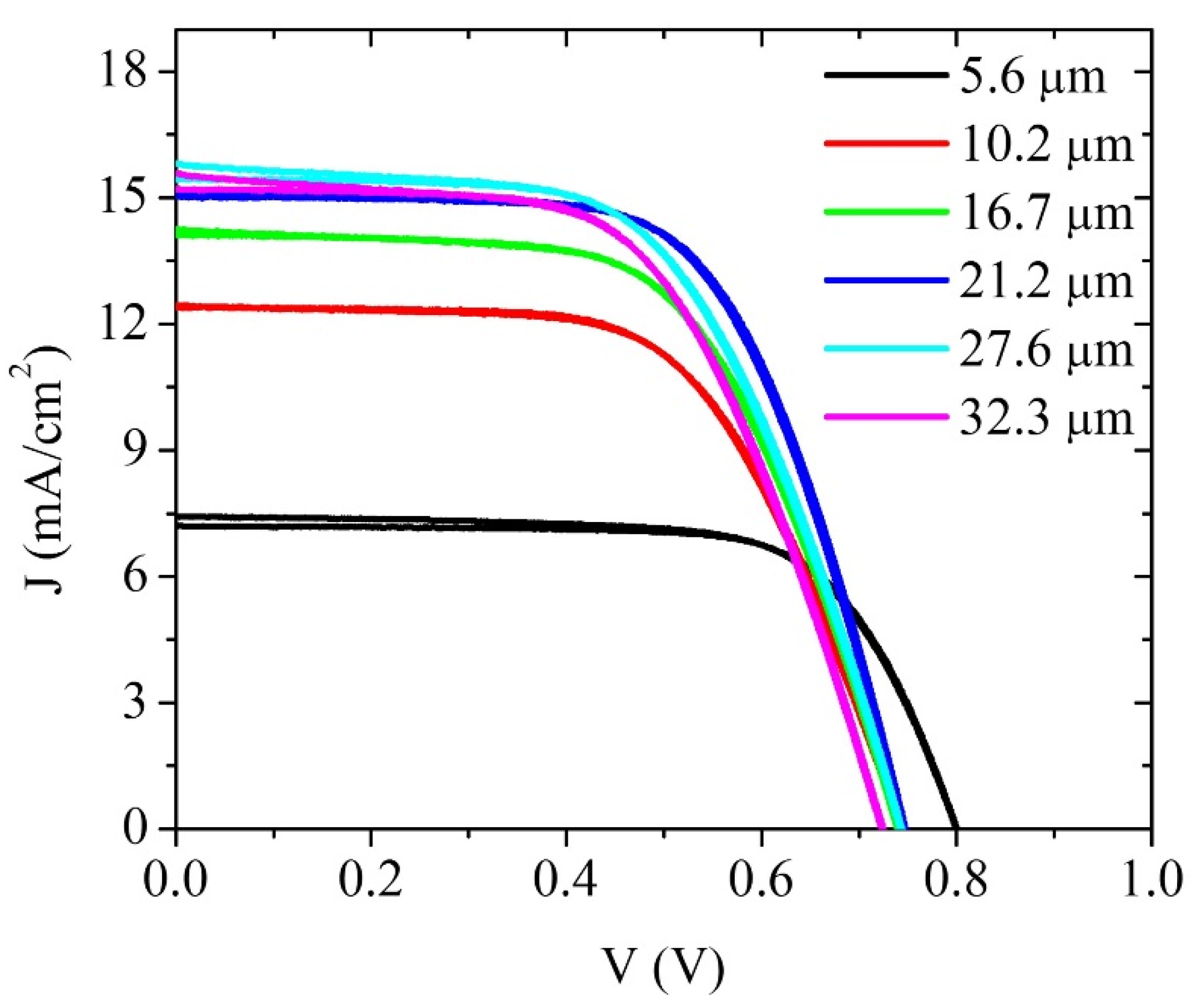
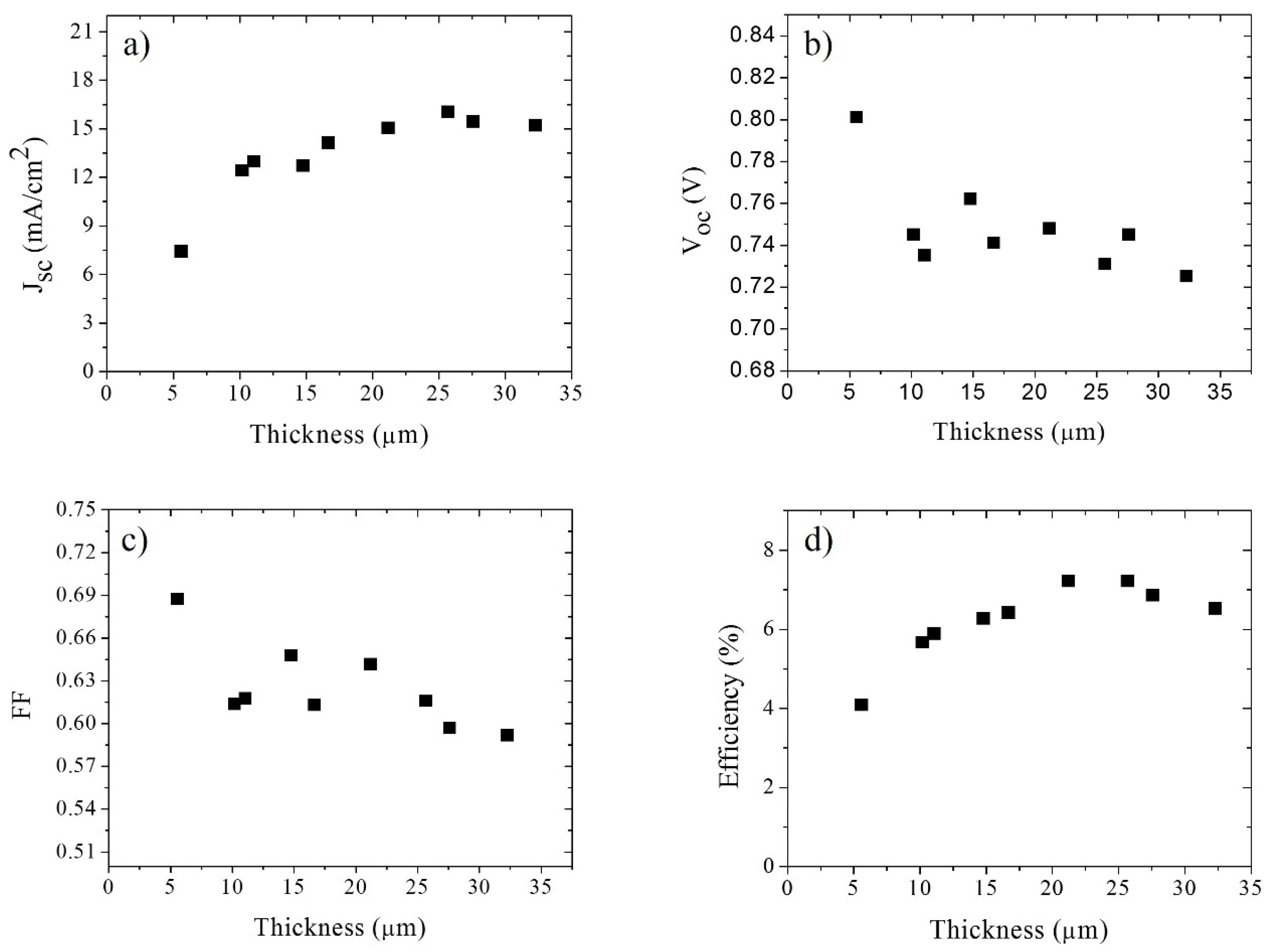

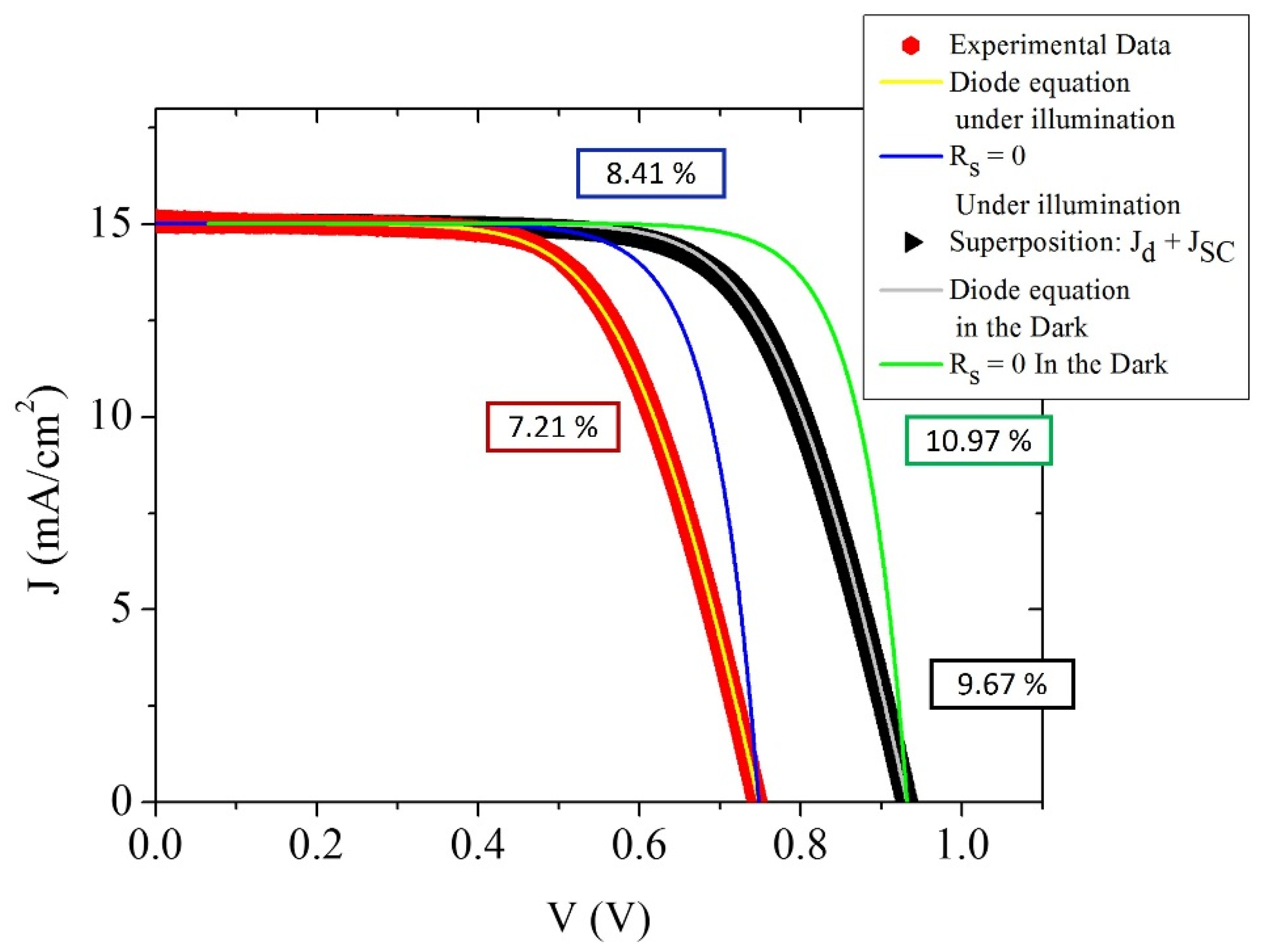
| 21.2 μm Solar Cell Data | Cell under Illumination | Cell under Illumination; Rs = 0 Ω | Superposition Approximation | Superposition Approximation; Rs = 0 Ω |
|---|---|---|---|---|
| J0 (A/cm2) | 2.01 × 10−8 | 2.01 × 10−8 | 7.2 × 10−10 | 7.2 × 10−10 |
| J00 (A/cm3) | 9.47 × 10−6 | 9.47 × 10−6 | 3.4 × 10−7 | 3.4 × 10−7 |
| Rs (Ω) | 13.90 | 0 | 13.90 | 0 |
| β | 0.47 | 0.47 | 0.47 | 0.47 |
| Efficiency (%) | 7.21 | 8.41 | 9.67 | 10.97 |
| 21.2 μm Solar Cell Data | Diode Equation under Illumination | Diode Equation with Superposition Approximation | IMVS and IMPS | EIS under Illumination | EIS in the Dark |
|---|---|---|---|---|---|
| J0 (A/cm2) | 2.01 × 10−8 | 6.75 × 10−11 | 1.17 × 10−8 | 2.44 × 10−9 | 9.44 × 10−11 |
| J00 (A/cm3) | 9.47 × 10−6 | 3.19 × 10−8 | 5.51 × 10−6 | 1.15 × 10−6 | 4.45 × 10−8 |
| Rs (Ω) | 13.90 | 15.45 | – | 9.80 | 9.75 |
| β | 0.47 | 0.53 | 0.79 | 0.82 | 0.55 |
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Reddy, K.G.; Deepak, T.G.; Anjusree, G.S.; Thomas, S.; Vadukumpully, S.; Subramanian, K.R.V.; Nair, S.V.; Nair, A.S. On global energy scenario, dye-sensitized solar cells and the promise of nanotechnology. Phys. Chem. Chem. Phys. 2014, 16, 6838–6858. [Google Scholar] [CrossRef] [PubMed]
- Litzov, I.; Brabec, C.J. Development of efficient and stable inverted bulk heterojunction (BHJ) solar cells using different metal oxide interfaces. Materials 2013, 6, 5796–5820. [Google Scholar] [CrossRef]
- Oprea, C.I.; Panait, P.; Cimpoesu, F.; Ferbinteanu, M.; Gîrţu, M.A. Density functional theory (DFT) study of coumarin-based dyes adsorbed on TiO2 nanoclusters—Applications to dye-sensitized solar cells. Materials 2013, 6, 2372–2392. [Google Scholar] [CrossRef]
- Yang, J.; Bark, C.; Kim, K.; Choi, H. Characteristics of the dye-sensitized solar cells using TiO2 nanotubes treated with TiCl4. Materials 2014, 7, 3522–3532. [Google Scholar] [CrossRef]
- Hardin, B.E.; Snaith, H.J.; McGehee, M.D. The renaissance of dye-sensitized solar cells. Nat. Photon. 2012, 6, 162–169. [Google Scholar] [CrossRef]
- Nazeeruddin, M.K.; Baranoff, E.; Grätzel, M. Dye-sensitized solar cells: A brief overview. Sol. Energy 2011, 85, 1172–1178. [Google Scholar] [CrossRef]
- Bella, F. Polymer electrolytes and perovskites: Lights and shadows in photovoltaic devices. Electrochimica Acta 2015, 175, 151–161. [Google Scholar] [CrossRef]
- Gonzalez-Pedro, V.; Juarez-Perez, E.J.; Arsyad, W.-S.; Barea, E.M.; Fabregat-Santiago, F.; Mora-Sero, I.; Bisquert, J. General working principles of CH3NH3PbX3 perovskite solar cells. Nano Lett. 2014, 14, 888–893. [Google Scholar] [CrossRef] [PubMed]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef] [PubMed]
- Bi, D.; Boschloo, G.; Hagfeldt, A. High-efficient solid-state perovskite solar cell without lithium salt in the hole transport material. Nano 2014, 9, 1440001. [Google Scholar] [CrossRef]
- Yella, A.; Lee, H.-W.; Tsao, H.N.; Yi, C.; Chandiran, A.K.; Nazeeruddin, M.K.; Diau, E.W.-G.; Yeh, C.-Y.; Zakeeruddin, S.M.; Grätzel, M. Porphyrin-sensitized solar cells with cobalt (ii/iii)–based redox electrolyte exceed 12 percent efficiency. Science 2011, 334, 629–634. [Google Scholar] [CrossRef] [PubMed]
- Nusbaumer, H.; Moser, J.-E.; Zakeeruddin, S.M.; Nazeeruddin, M.K.; Grätzel, M. CoII(dbbip)22+ complex rivals tri-iodide/iodide redox mediator in dye-sensitized photovoltaic cells. J. Phys. Chem. B 2001, 105, 10461–10464. [Google Scholar] [CrossRef]
- Feldt, S.M.; Gibson, E.A.; Gabrielsson, E.; Sun, L.; Boschloo, G.; Hagfeldt, A. Design of organic dyes and cobalt polypyridine redox mediators for high-efficiency dye-sensitized solar cells. J. Am. Chem. Soc. 2010, 132, 16714–16724. [Google Scholar] [CrossRef] [PubMed]
- Hao, Y.; Tian, H.; Cong, J.; Yang, W.; Bora, I.; Sun, L.; Boschloo, G.; Hagfeldt, A. Triphenylamine groups improve blocking behavior of phenoxazine dyes in cobalt-electrolyte-based dye-sensitized solar cells. Chem. Phys. Chem. 2014, 15, 3476–3483. [Google Scholar] [CrossRef] [PubMed]
- Peng, M.; Zou, D. Flexible fiber/wire-shaped solar cells in progress: Properties, materials, and designs. J. Mater. Chem. A 2015, 3, 20435–20458. [Google Scholar] [CrossRef]
- Cid, J.-J.; Yum, J.-H.; Jang, S.-R.; Nazeeruddin, M.K.; Martínez-Ferrero, E.; Palomares, E.; Ko, J.; Grätzel, M.; Torres, T. Molecular cosensitization for efficient panchromatic dye-sensitized solar cells. Angew. Chem. Int. Ed. 2007, 119, 8510–8514. [Google Scholar] [CrossRef]
- Hattori, S.; Wada, Y.; Yanagida, S.; Fukuzumi, S. Blue copper model complexes with distorted tetragonal geometry acting as effective electron-transfer mediators in dye-sensitized solar cells. J. Am. Chem. Soc. 2005, 127, 9648–9654. [Google Scholar] [CrossRef] [PubMed]
- Freitag, M.; Daniel, Q.; Pazoki, M.; Sveinbjornsson, K.; Zhang, J.; Sun, L.; Hagfeldt, A.; Boschloo, G. High-efficiency dye-sensitized solar cells with molecular copper phenanthroline as solid hole conductor. Energy Environ. Sci. 2015, 8, 2634–2637. [Google Scholar] [CrossRef]
- Bai, Y.; Yu, Q.; Cai, N.; Wang, Y.; Zhang, M.; Wang, P. High-efficiency organic dye-sensitized mesoscopic solar cells with a copper redox shuttle. Chem. Commun. 2011, 47, 4376–4378. [Google Scholar] [CrossRef] [PubMed]
- Escalante, R.; García-Rodríguez, R.; Heredia-Cervera, B.E.; Aguilar-Frutis, M.A.; Gómez-Ortíz, N.; Villanueva-Cab, J.; Oskam, G. Influence of TiO2 film thickness on the performance of dye-sensitized solar cells: Relation between optimum film thickness and electron diffusion length. Energy Environ. Focus 2013, 2, 280–286. [Google Scholar] [CrossRef]
- Hsu, C.-P.; Lee, K.-M.; Huang, J.T.-W.; Lin, C.-Y.; Lee, C.-H.; Wang, L.-P.; Tsai, S.-Y.; Ho, K.-C. EIS analysis on low temperature fabrication of TiO2 porous films for dye-sensitized solar cells. Electrochimica Acta 2008, 53, 7514–7522. [Google Scholar] [CrossRef]
- Huang, C.-Y.; Hsu, Y.-C.; Chen, J.-G.; Suryanarayanan, V.; Lee, K.-M.; Ho, K.-C. The effects of hydrothermal temperature and thickness of TiO2 film on the performance of a dye-sensitized solar cell. Sol. Energy Mater. Sol. Cells 2006, 90, 2391–2397. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, W.; Liu, H.; Wang, R.; Chen, Y.; Wang, Z. Effects of TiO2 film thickness on photovoltaic properties of dye-sensitized solar cell and its enhanced performance by graphene combination. Mater. Res. Bull. 2014, 49, 126–131. [Google Scholar] [CrossRef]
- Kao, M.C.; Chen, H.Z.; Young, S.L.; Kung, C.Y.; Lin, C.C. The effects of the thickness of TiO2 films on the performance of dye-sensitized solar cells. Thin Solid Films 2009, 517, 5096–5099. [Google Scholar] [CrossRef]
- Shin, I.; Seo, H.; Son, M.-K.; Kim, J.-K.; Prabakar, K.; Kim, H.-J. Analysis of TiO2 thickness effect on characteristic of a dye-sensitized solar cell by using electrochemical impedance spectroscopy. Curr. Appl. Phys. 2010, 10, S422–S424. [Google Scholar] [CrossRef]
- Park, K.-H.; Kim, T.-Y.; Kim, J.-H.; Kim, H.J.; Hong, C.K.; Lee, J.-W. Adsorption and electrochemical properties of photoelectrodes depending on TiO2 film thickness for dye-sensitized solar cells. J. Electroanal. Chem. 2013, 708, 39–45. [Google Scholar] [CrossRef]
- Wang, Z.-S.; Kawauchi, H.; Kashima, T.; Arakawa, H. Significant influence of TiO2 photoelectrode morphology on the energy conversion efficiency of N719 dye-sensitized solar cell. Coord. Chem. Rev. 2004, 248, 1381–1389. [Google Scholar] [CrossRef]
- Zhu, K.; Jang, S.-R.; Frank, A.J. Impact of high charge-collection efficiencies and dark energy-loss processes on transport, recombination, and photovoltaic properties of dye-sensitized solar cells. J. Phys. Chem. Lett. 2011, 2, 1070–1076. [Google Scholar] [CrossRef]
- Ito, S.; Liska, P.; Comte, P.; Charvet, R.; Pechy, P.; Bach, U.; Schmidt-Mende, L.; Zakeeruddin, S.M.; Kay, A.; Nazeeruddin, M.K.; et al. Control of dark current in photoelectrochemical (TiO2/I−–I3−) and dye-sensitized solar cells. Chem. Commun. 2005, 4351–4353. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Dong, X. Coupled analysis of steady-state and dynamic characteristics of dye-sensitized solar cells for determination of conduction band movement and recombination parameters. Phys. Chem. Chem. Phys. 2013, 15, 299–306. [Google Scholar] [CrossRef] [PubMed]
- Fabregat-Santiago, F.; Garcia-Belmonte, G.; Mora-Sero, I.; Bisquert, J. Characterization of nanostructured hybrid and organic solar cells by impedance spectroscopy. Phys. Chem. Chem. Phys. 2011, 13, 9083–9118. [Google Scholar] [CrossRef] [PubMed]
- Nelson, J. The Physics of Solar Cells; Imperial College Press: London, UK, 2007; p. 363. [Google Scholar]
- Anta, J.A.; Idigoras, J.; Guillen, E.; Villanueva-Cab, J.; Mandujano-Ramirez, H.J.; Oskam, G.; Pelleja, L.; Palomares, E. A continuity equation for the simulation of the current-voltage curve and the time-dependent properties of dye-sensitized solar cells. Phys. Chem. Chem. Phys. 2012, 14, 10285–10299. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Vazquez, J.P.; Oskam, G.; Anta, J.A. Origin of nonlinear recombination in dye-sensitized solar cells: Interplay between charge transport and charge transfer. J. Phys. Chem. C 2012, 116, 22687–22697. [Google Scholar] [CrossRef]
- Bisquert, J.; Fabregat-Santiago, F.; Mora-Seró, I.; Garcia-Belmonte, G.; Giménez, S. Electron lifetime in dye-sensitized solar cells: Theory and interpretation of measurements. J. Phys. Chem. C 2009, 113, 17278–17290. [Google Scholar] [CrossRef]
- Frank, J.A.; Kopidakis, N.; Lagemaat, J. Electrons in nanostructured TiO2 solar cells: Transport, recombination and photovoltaic properties. Coord. Chem. Rev. 2004, 248, 1165–1179. [Google Scholar] [CrossRef]
- Bisquert, J.; Mora-Seró, I. Simulation of steady-state characteristics of dye-sensitized solar cells and the interpretation of the diffusion length. J. Phys. Chem. Lett. 2010, 1, 450–456. [Google Scholar] [CrossRef]
- Hegedus, S.S.; Shafarman, W.N. Thin-film solar cells: Device measurements and analysis. Prog. Photovolt. Res. Appl. 2004, 12, 155–176. [Google Scholar] [CrossRef]
- Barnes, P.R.F.; Anderson, A.Y.; Juozapavicius, M.; Liu, L.; Li, X.; Palomares, E.; Forneli, A.; O’Regan, B.C. Factors controlling charge recombination under dark and light conditions in dye sensitised solar cells. Phys. Chem. Chem. Phys. 2011, 13, 3547–3558. [Google Scholar] [CrossRef] [PubMed]
- Zhu, K.; Kopidakis, N.; Neale, N.R.; van de Lagemaat, J.; Frank, A.J. Influence of surface area on charge transport and recombination in dye-sensitized TiO2 solar cells. J. Phys. Chem. B 2006, 110, 25174–25180. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Jennings, J.R.; Wang, Q. Determination of sensitizer regeneration efficiency in dye-sensitized solar cells. ACS Nano 2013, 7, 8233–8242. [Google Scholar] [CrossRef] [PubMed]
- Jennings, J.R.; Liu, Y.; Wang, Q. Efficiency limitations in dye-sensitized solar cells caused by inefficient sensitizer regeneration. J. Phys. Chem. C 2011, 115, 15109–15120. [Google Scholar] [CrossRef]
- Halme, J.; Vahermaa, P.; Miettunen, K.; Lund, P. Device physics of dye solar cells. Adv. Mater. 2010, 22, E210–E234. [Google Scholar] [CrossRef] [PubMed]
- Jennings, J.R.; Liu, Y.; Safari-Alamuti, F.; Wang, Q. Dependence of dye-sensitized solar cell impedance on photoelectrode thickness. J. Phys. Chem. C 2011, 116, 1556–1562. [Google Scholar] [CrossRef]
- Guldin, S.; Docampo, P.; Stefik, M.; Kamita, G.; Wiesner, U.; Snaith, H.J.; Steiner, U. Layer-by-layer formation of block-copolymer-derived TiO2 for solid-state dye-sensitized solar cells. Small 2012, 8, 432–440. [Google Scholar] [CrossRef] [PubMed]
- Barnes, P.R.F.; Anderson, A.Y.; Durrant, J.R.; O’Regan, B.C. Simulation and measurement of complete dye sensitised solar cells: Including the influence of trapping, electrolyte, oxidised dyes and light intensity on steady state and transient device behaviour. Phys. Chem. Chem. Phys. 2011, 13, 5798–5816. [Google Scholar] [CrossRef] [PubMed]
- Fabregat-Santiago, F.; Bisquert, J.; Garcia-Belmonte, G.; Boschloo, G.; Hagfeldt, A. Influence of electrolyte in transport and recombination in dye-sensitized solar cells studied by impedance spectroscopy. Sol. Energ. Mater. Sol. Cells 2005, 87, 117–131. [Google Scholar] [CrossRef]
- Gonzalez-Vazquez, J.P.; Morales-Flórez, V.; Anta, J.A. How important is working with an ordered electrode to improve the charge collection efficiency in nanostructured solar cells? J. Phys. Chem. Lett. 2012, 3, 386–393. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Rodríguez, R.; Villanueva-Cab, J.; Anta, J.A.; Oskam, G. A Critical Evaluation of the Influence of the Dark Exchange Current on the Performance of Dye-Sensitized Solar Cells. Materials 2016, 9, 33. https://doi.org/10.3390/ma9010033
García-Rodríguez R, Villanueva-Cab J, Anta JA, Oskam G. A Critical Evaluation of the Influence of the Dark Exchange Current on the Performance of Dye-Sensitized Solar Cells. Materials. 2016; 9(1):33. https://doi.org/10.3390/ma9010033
Chicago/Turabian StyleGarcía-Rodríguez, Rodrigo, Julio Villanueva-Cab, Juan A. Anta, and Gerko Oskam. 2016. "A Critical Evaluation of the Influence of the Dark Exchange Current on the Performance of Dye-Sensitized Solar Cells" Materials 9, no. 1: 33. https://doi.org/10.3390/ma9010033





