Holographic Spectroscopy: Wavelength-Dependent Analysis of Photosensitive Materials by Means of Holographic Techniques
Abstract
:1. Introduction
2. Recording a Test Hologram and the Properties of Its Permittivity
2.1. Recording of a Test Hologram
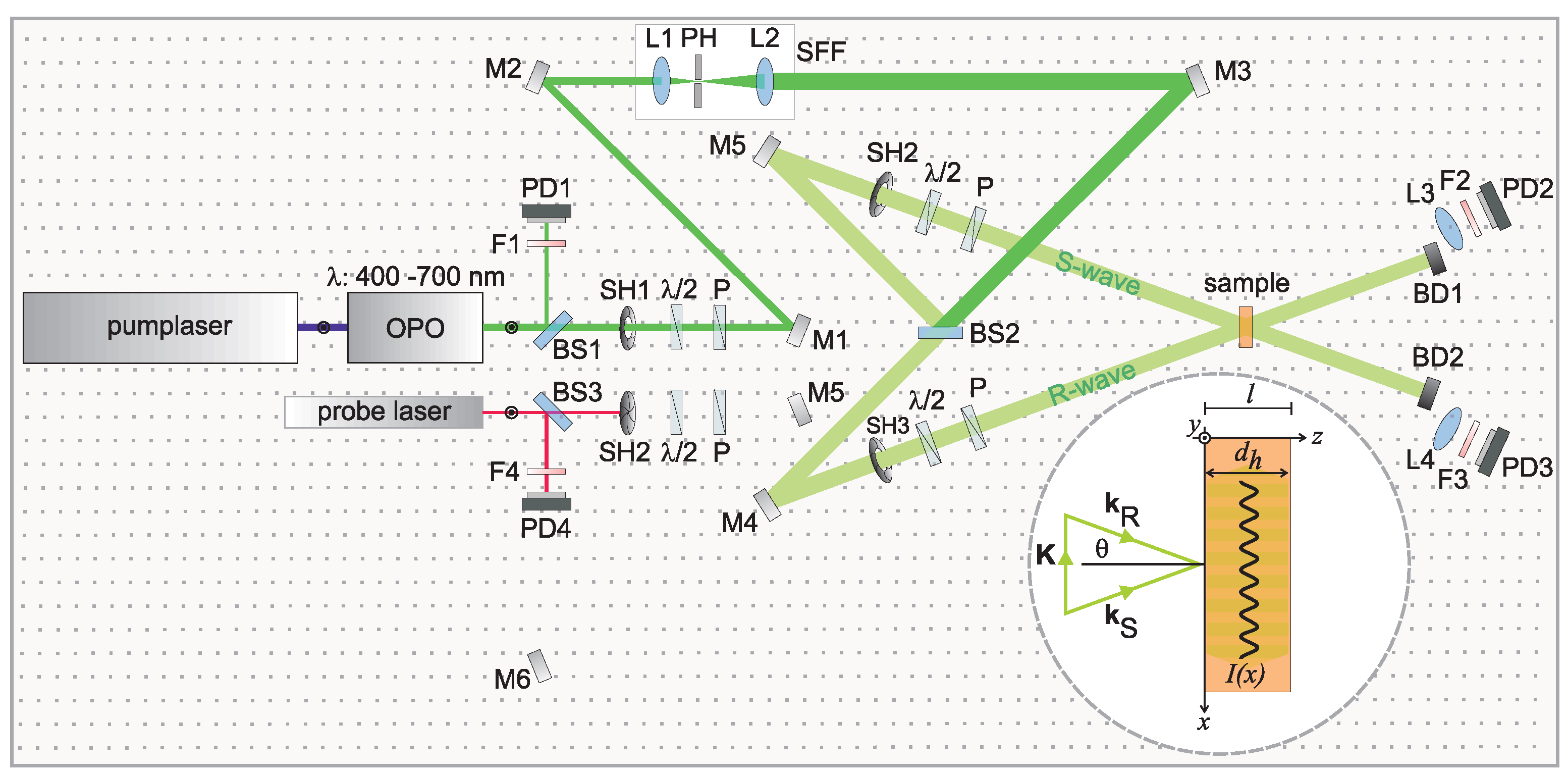
2.2. Properties of the Permittivity of the Test Hologram
| Characteristic of the optical setup | Simplification for the theoretical analysis |
|---|---|
| hologram recording is performed with equal wavelengths of R- and S-waves degenerate wave-mixing) | , i.e., |
| hologram recording is performed by the superposition of planar wave fronts | sinusoidal permittivity modulation * |
| R- and S-waves feature flat-top intensity profile | the electric field amplitudes are constant within the beam paths and the beam is assumed to have infinite diameter |
| hologram recording is performed with equal directions of the electric field vectors of R- and S-wave and with equal intensities | , i.e., the modulation depth becomes unity (), |
| hologram recording is homogeneously over the entire volume, i.e., exponential decrease of the grating parameters in z-direction is excluded (cf. [9]) ** | permittivity modulation is not z-dependent |
| wave vector of the hologram is directed perpendicularly to the samples’ normal | permittivity modulation is aligned parallel to x-axis (unslanted hologram) |
3. Dispersion of First Order Diffracted Waves
3.1. Signal Wave Reconstruction
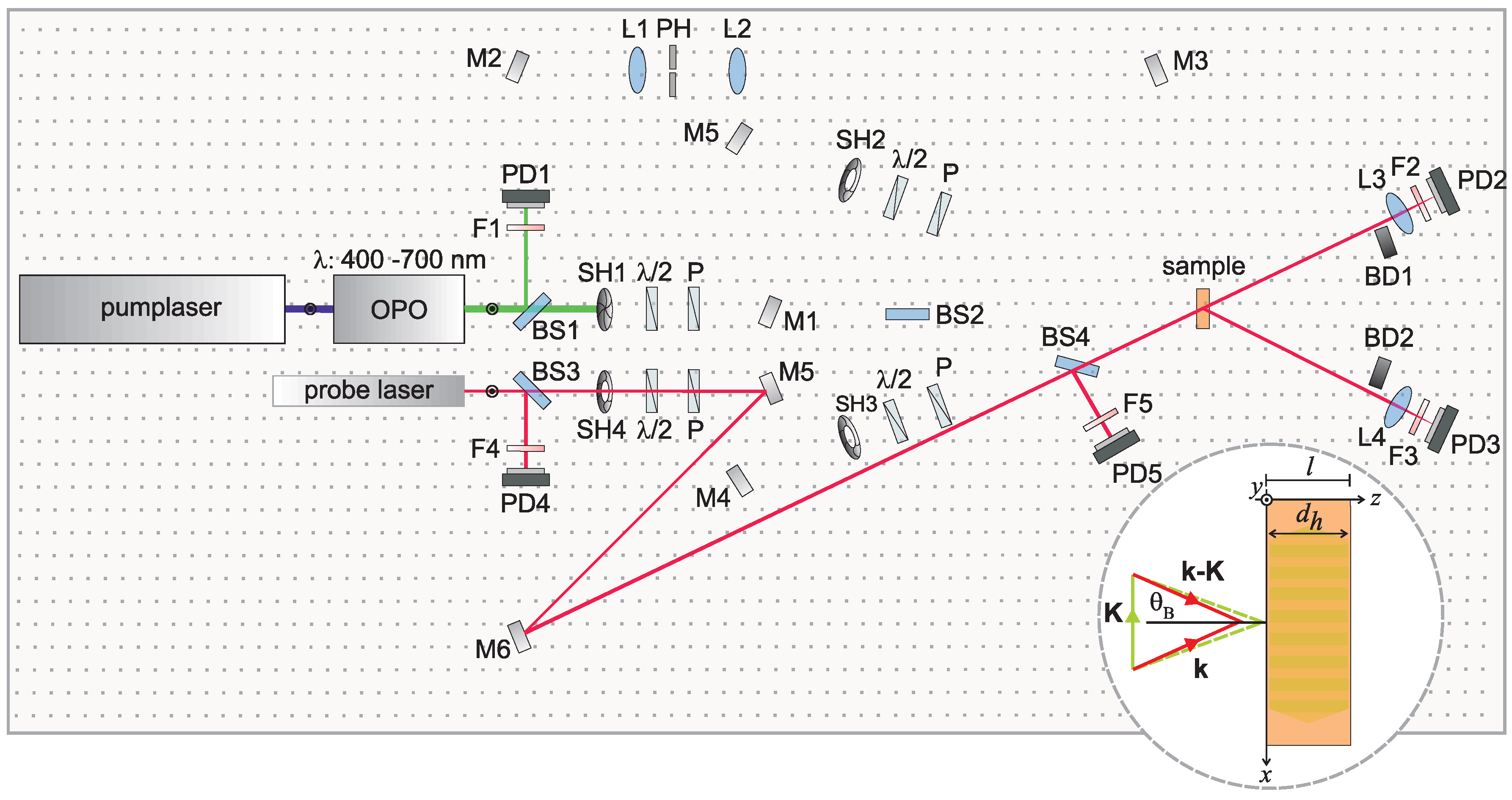
3.2. Coupled-Wave Theory
3.3. Diffraction Efficiency of Out-of-Phase Mixed Gratings
3.4. Pure Refractive Index and Absorption Gratings
3.5. In-Bragg Cases
3.6. Transmission Efficiency
4. Examples
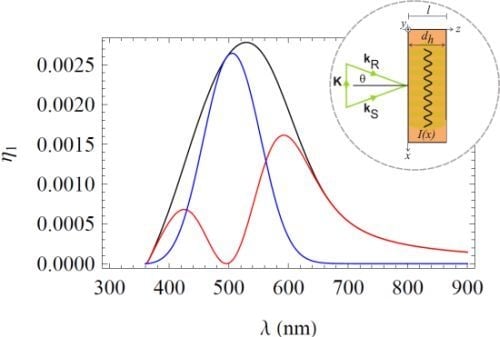
4.1. Spectroscopic in-Bragg Analysis of the Diffraction Efficiency
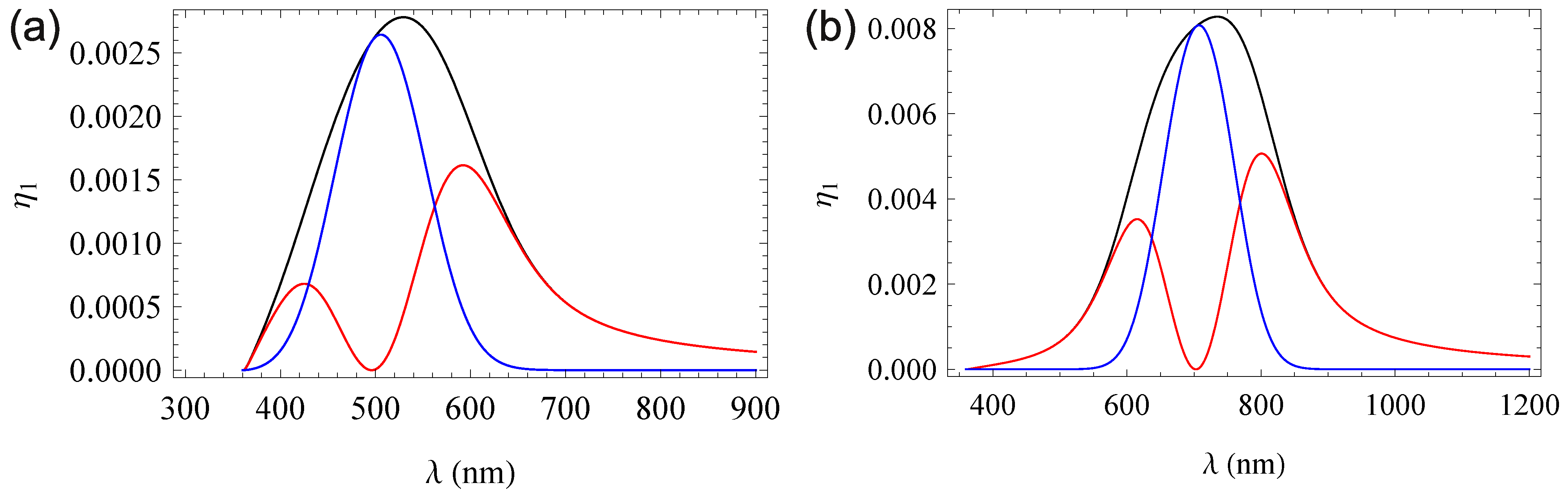
4.2. Effects of Phase Shifts in Mixed Gratings
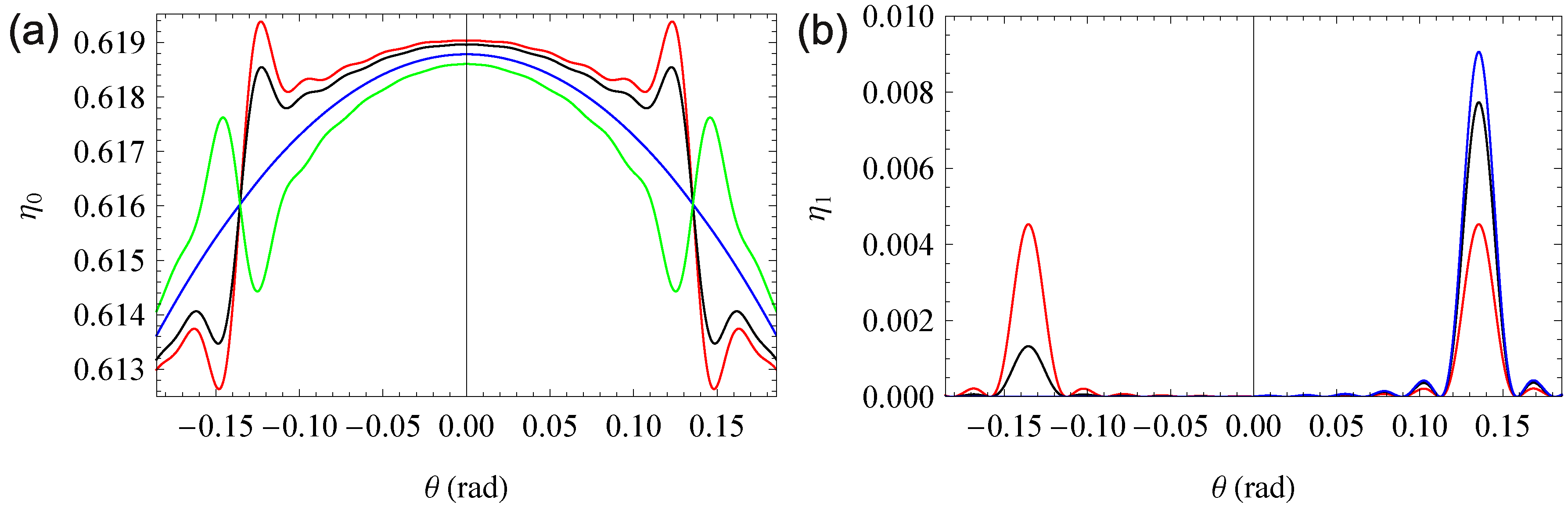
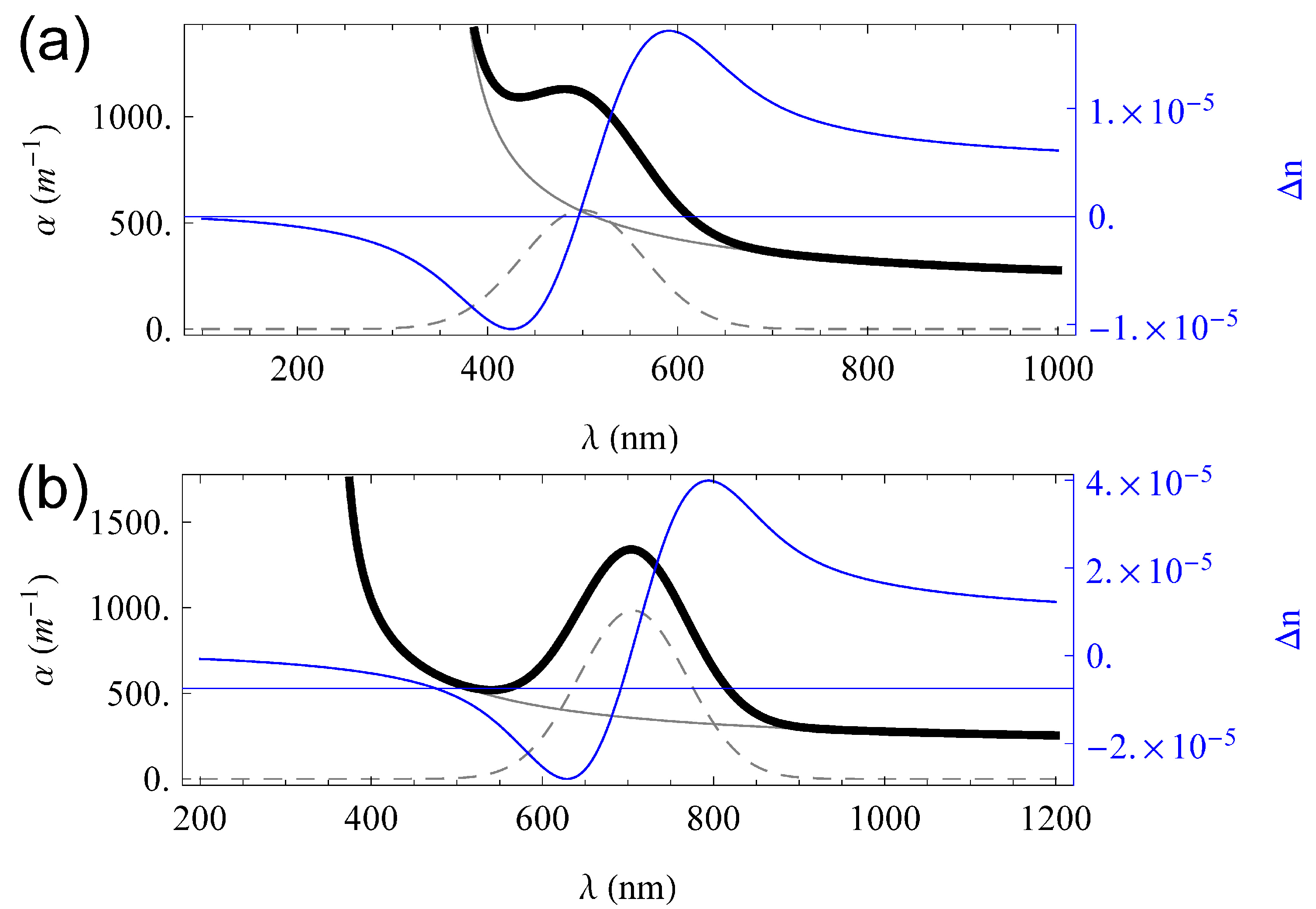
5. Quantitative Analysis of the Borrmann Effect
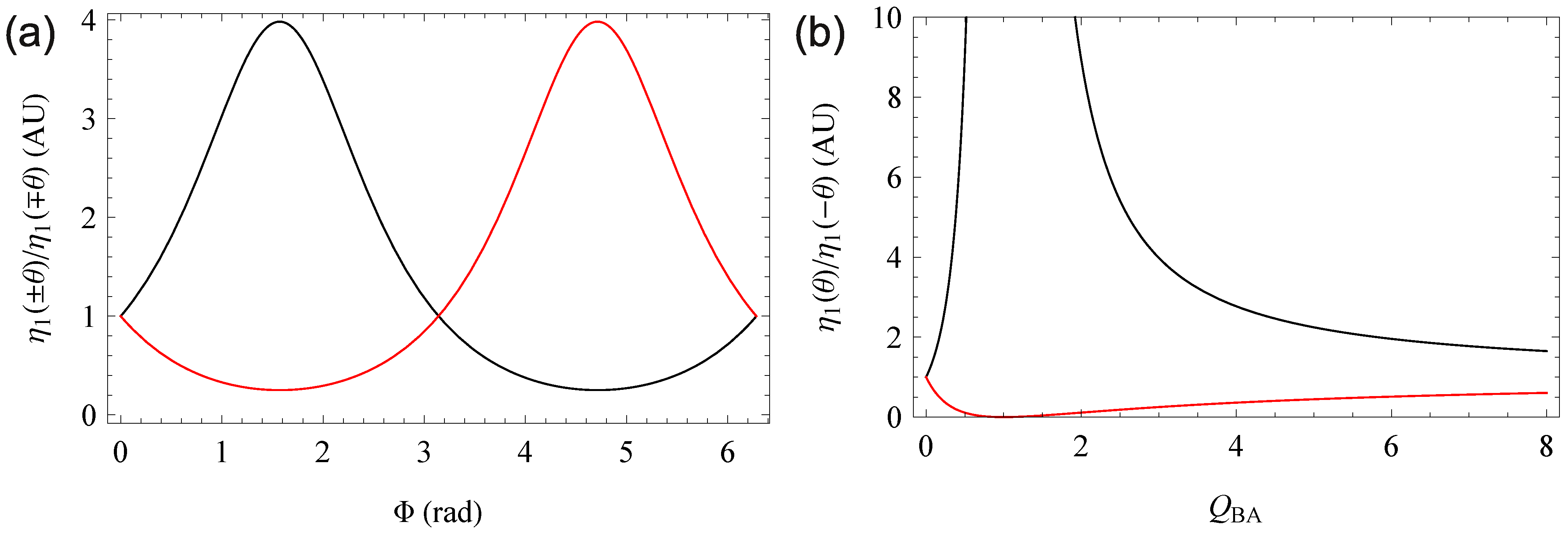
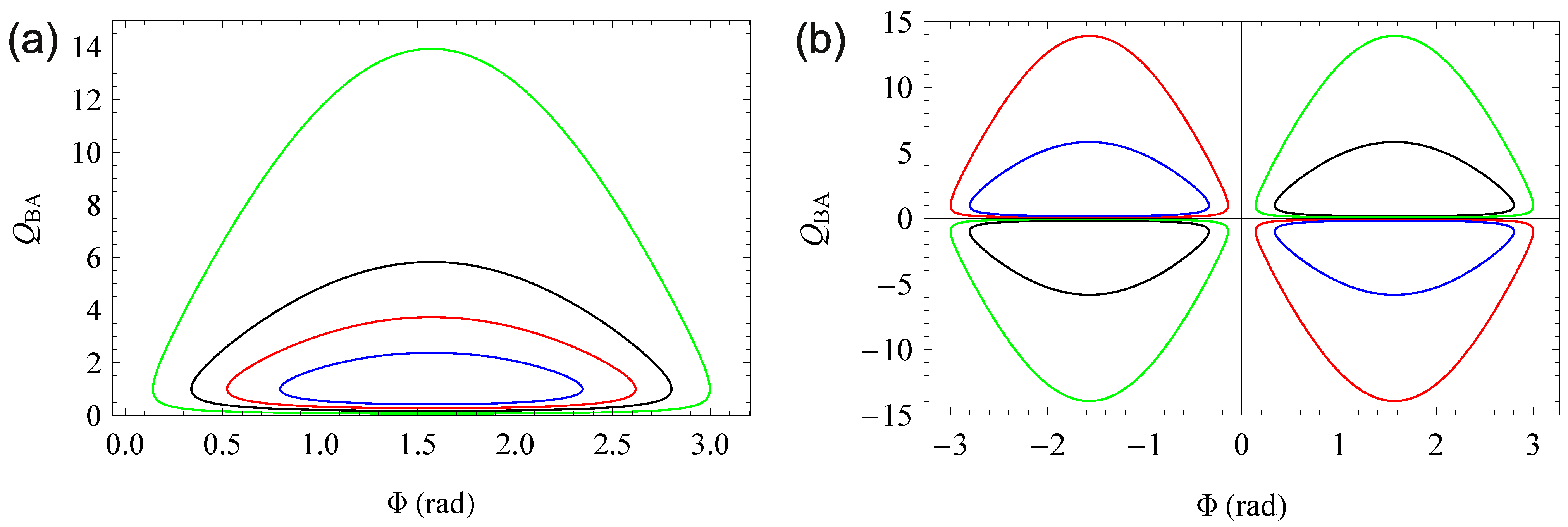
6. Conclusions
Nomenclature of Material Properties
| ϵ(x, λ) | Complex permittivity |
Mean real permittivity | |
Mean imaginary permittivity | |
Amplitude of real permittivity grating | |
Amplitude of imaginary permittivity grating | |
| ΦB | Phase offset of real permittivity grating compared with interference pattern at z = 0 |
| ΦA | Phase offset of imaginary permittivity grating compared with interference pattern at z = 0 |
| Φ | ΦA − ΦB (for diffraction experiments with no interference pattern at z = 0) |
| n(x, λ) | Complex refractive index |
| α0(λ) | Mean absorption coefficient |
| n(x, λ) | Real refractive index |
| n0(λ) | Mean real refractive index |
| n1(λ) | Amplitude of real refractive index grating |
| Φn | Phase offset of real refractive index grating |
| κ0(λ) | Mean absorption index |
| κ1(λ) | Amplitude of grating |
| Φκ | Phase offset of absorption index grating |
| K | Grating vector in material |
Nomenclature of LightWave Properties
| R(z)/S(z) | Electric field amplitude of reference/signal beam inside material |
| R0/S0 | Intial electric field amplitude of reference/signal beam inside material |
| eR(z)/eS(z) | Polarisation unit vector of reference/signal beam |
| ΦDiff | Phase difference between reference and signal beam inside the material |
| k | Wave vector of reference beam inside material |
| Φ0 | Phase shift of interference pattern between reference/signal beam |
| m | Modulation depth of interference pattern |
| I/IR/IS | Intensity of interference pattern/reference beam/signal beam |
| η0/η1 | Transmission efficiency/diffraction efficiency |
Acknowledgements
References
- Gabor, D. A new microscopic principle. Nature 1948, 161, 777–778. [Google Scholar] [CrossRef] [PubMed]
- Imlau, M.; Fally, M.; Coufal, H.; Burr, G.; Sincerbox, G. Holography and Optical Storage. In Springer Handbook of Lasers and Optics; Träger, F., Ed.; Springer: New York, NY, USA, 2007; pp. 1205–1249. [Google Scholar]
- Moser, C.; Havermeyer, F. Method and Apparatus for Large Spectral Coverage Measurement of Volume Holographic Gratings. U.S. Patent 8,049,885, 1 November 2011. [Google Scholar]
- Moser, C.; Havermeyer, F. Measurement of Volume Holographic Gratings. U.S. Patent 8,139,212, 20 March 2012. [Google Scholar]
- Imlau, M.; Brüning, H.; Schoke, B.; Hardt, R.; Conradi, D.; Merschjann, C. Hologram recording via spatial density modulation of NbLi4+/5+ antisites in lithium niobate. Opt. Express 2011, 19, 15322–15338. [Google Scholar] [CrossRef] [PubMed]
- Dieckmann, V.; Eicke, S.; Springfeld, K.; Imlau, M. Transition metal compounds towards holography. Materials 2012, 5, 1155–1175. [Google Scholar] [CrossRef]
- Guibelalde, E. Coupled wave analysis for out-of-phase mixed thick hologram gratings. Opt. Quantum Electron. 1984, 16, 173–178. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K. Rigorous coupled-wave analysis of planar-grating diffraction. J. Opt. Soc. Am. 1981, 71, 811–818. [Google Scholar] [CrossRef]
- Uchida, N. Calculation of diffraction efficiency in hologram gratings attenuated along the direction perpendicular to the grating vector. J. Opt. Soc. Am. 1973, 63, 280–287. [Google Scholar] [CrossRef]
- Kukhtarev, N.V.; Markov, V.B.; Odulov, S.G.; Soskin, M.S.; Vinetskii, V.L. Holographic storage in electrooptic crystals. I. steady state. Ferroelectrics 1978, 22, 949–960. [Google Scholar] [CrossRef]
- Kukhtarev, N.V.; Markov, V.B.; Odulov, S.G.; Soskin, M.S.; Vinetskii, V.L. Holographic storage in electrooptic crystals. II. Beam coupling—Light amplification. Ferroelectrics 1978, 22, 961–964. [Google Scholar] [CrossRef]
- Russell, P. Optical volume holography. Phys. Rep. 1981, 71, 209–312. [Google Scholar] [CrossRef]
- Strait, J.; Reed, J.D.; Kukhtarev, N.V. Orientational dependence of photorefractive two-beam coupling in InP:Fe. Opt. Lett. 1990, 15, 209–211. [Google Scholar] [CrossRef] [PubMed]
- Sturman, B.I.; Webb, D.J.; Kowarschik, R.; Shamonina, E.; Ringhofer, K.H. Exact solution of the Bragg-diffraction problem in sillenites. J. Opt. Soc. Am. B 1994, 11, 1813–1819. [Google Scholar] [CrossRef]
- Sheridan, J.T. Generalization of the boundary diffraction method for volume gratings. J. Opt. Soc. Am. A 1994, 11, 649–656. [Google Scholar] [CrossRef]
- Michael, R.; Gleeson, J.G.; John, T.S. Optimisation of photopolymers for holographic applications using the non-local photo-polymerization driven diffusion model. Opt. Express 2011, 19, 22423–22436. [Google Scholar]
- Kogelnik, H. Coupled wave theory for thick hologram gratings. Bell Syst. Tech. J. 1969, 48, 2909–2947. [Google Scholar] [CrossRef]
- Montemezzani, G.; Zgonik, M. Light diffraction at mixed phase and absorption gratings in anisotropic media for arbitrary geometries. Phys. Rev. E 1997, 55, 1035–1047. [Google Scholar] [CrossRef]
- Sturman, B.I.; Podivilov, E.V.; Ringhofer, K.H.; Shamonina, E.; Kamenov, V.P.; Nippolainen, E.; Prokofiev, V.V.; Kamshilin, A.A. Theory of photorefractive vectorial wave coupling in cubic crystals. Phys. Rev. E 1999, 60, 3332–3352. [Google Scholar] [CrossRef]
- Fally, M.; Ellabban, M.; Drevensek-Olenik, I. Out-of-phase mixed holographic gratings: A quantative analysis. Opt. Express 2008, 16, 6528–6536. [Google Scholar] [CrossRef] [PubMed]
- Haarer, D.; Spiess, H.W. Spektroskopie Amorpher und Kristalliner Festkörper; Springer DE: Heidelberg, Germany, 1995. [Google Scholar]
- Shafer, D. Gaussian to Flat-Top intensity distributing lens. Opt. Laser Technol. 1982, 14, 159–160. [Google Scholar] [CrossRef]
- Au, L.B.; Solymar, L. Space-charge field in photorefractive materials at large modulation. Opt. Lett. 1988, 13, 660–662. [Google Scholar] [CrossRef] [PubMed]
- Ellen, O.; Frederick, V.; Lambertus, H. Higher-order analysis of the photorefractive effect for large modulation depths. J. Opt. Soc. Am. A 1986, 3, 181–187. [Google Scholar]
- Träger, F. Springer Handbook of Lasers and Optics, 2nd ed.; Springer: Heidelberg, Germany, 2012. [Google Scholar]
- Sheridan, J. A comparison of diffraction theories for off-bragg replay. J. Mod. Opt. 1992, 39, 1709–1718. [Google Scholar] [CrossRef]
- Solymar, L.; Cooke, D.J. Volume Holography and Volume Gratings; Academic Press Inc: Waltham, MA, USA, 1982. [Google Scholar]
- Syms, R.R.A. Practical Volume Holography; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Hartwig, U.; Peithmann, K.; Sturman, B.; Buse, K. Strong permanent reversible diffraction gratings in copper-doped lithium niobate crystals caused by a zero-electric-field photorefractive effect. Appl. Phys. B 2004, 80, 227–230. [Google Scholar] [CrossRef]
- Gaylord, T.K.; Moharam, M.G. Planar dielectric grating diffraction theories. Appl. Phys. B Lasers Opt. 1982, 28, 1–14. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K. Rigorous coupled-wave analysis of grating diffraction—E-mode polarization and losses. J. Opt. Soc. Am. 1983, 73, 451–455. [Google Scholar] [CrossRef]
- Moharam, M.G.; Grann, E.B.; Pommet, D.A.; Gaylord, T.K. Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings. J. Opt. Soc. Am. A 1995, 12, 1068–1076. [Google Scholar] [CrossRef]
- Gallego, S.; Cristian, N.; Estepa, L.A.; Ortuño, M.; Márquez, A.; Francés, J.; Pascual, I.; Beléndez, A. Volume holograms in photopolymers: Comparison between analytical and rigorous theories. Materials 2012, 5, 1373–1388. [Google Scholar] [CrossRef]
- Fally, M.; Klepp, J.; Tomita, Y. An experimental study on the validity of diffraction theories for off-Bragg replay of volume holographic gratings. Appl. Phys. B Lasers Opt. 2012, 108, 89–96. [Google Scholar] [CrossRef]
- Dittrich, P.; Koziarska-Glinka, B.; Montemezzani, G.; Günter, P.; Takekawa, S.; Kitamura, K.; Furukawa, Y. Deep-ultraviolet interband photorefraction in lithium tantalate. J. Opt. Soc. Am. B 2004, 21, 632–639. [Google Scholar] [CrossRef]
- Krätzig, E.; Buse, K. Two-Step processes and IR recording in photorefractive crystals. In Infrared Holography for Optical Communications; Springer: Berlin/Heidelberg, Germany, 2003; Volume 86, pp. 23–40. [Google Scholar]
- Schirmer, O.F.; Imlau, M.; Merschjann, C.; Schoke, B. Electron small polarons and bipolarons in LiNbO3. J. Phys. Condens. Matter 2009, 21, 123201:1–123201:29. [Google Scholar] [CrossRef] [PubMed]
- Schirmer, O.; Thiemann, O.; Wöhlecke, M. Defects in LiNbO3—I. Experimental aspects. J. Phys. Chem. Solids 1991, 52, 185–200. [Google Scholar] [CrossRef]
- Günter, P.; Huignard, J.P. Photorefractive Materials and Their Applications 1: Basic Effects; Springer: Berlin, Germany, 2006. [Google Scholar]
- Brüning, H.; Dieckmann, V.; Schoke, B.; Voit, K.; Imlau, M.; Corradi, G.; Merschjann, C. Small-polaron based holograms in LiNbO3 in the visible spectrum. Opt. Express 2012, 20, 13326–13336. [Google Scholar] [CrossRef] [PubMed]
- Neipp, C.; Pascual, I.; Beléndez, A. Experimental evidence of mixed gratings with a phase difference between the phase and amplitude grating in volume holograms. Opt. Express 2002, 10, 1374–1383. [Google Scholar] [CrossRef] [PubMed]
- Kahmann, F. Separate and simultaneous investigation of absorption gratings and refractive-index gratings by beam-coupling analysis. J. Opt. Soc. Am. A 1993, 10, 1562–1569. [Google Scholar] [CrossRef]
- Fally, M. Separate and simultaneous investigation of absorption gratings and refractive-index gratings by beam-coupling analysis: Comment. J. Opt. Soc. Am. A 2006, 23, 2662–2663. [Google Scholar] [CrossRef]
- Carretero, L.; Madrigal, R.F.; Fimia, A.; Blaya, S.; Beléndez, A. Study of angular responses of mixed amplitude–phase holographic gratings: Shifted Borrmann effect. Opt. Lett. 2001, 26, 786–788. [Google Scholar] [CrossRef] [PubMed]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Voit, K.-M.; Imlau, M. Holographic Spectroscopy: Wavelength-Dependent Analysis of Photosensitive Materials by Means of Holographic Techniques. Materials 2013, 6, 334-358. https://doi.org/10.3390/ma6010334
Voit K-M, Imlau M. Holographic Spectroscopy: Wavelength-Dependent Analysis of Photosensitive Materials by Means of Holographic Techniques. Materials. 2013; 6(1):334-358. https://doi.org/10.3390/ma6010334
Chicago/Turabian StyleVoit, Kay-Michael, and Mirco Imlau. 2013. "Holographic Spectroscopy: Wavelength-Dependent Analysis of Photosensitive Materials by Means of Holographic Techniques" Materials 6, no. 1: 334-358. https://doi.org/10.3390/ma6010334