Description of Residual Stress and Strain Fields in FGM Hollow Disc Subject to External Pressure
Abstract
:1. Introduction
2. Statement of the Problem
3. Purely Elastic Solution
4. Elastic/Plastic Stress Solution
5. Elastic/Plastic Strain Solution
6. Unloading
7. Illustrative Example
8. Discussion
9. Conclusions
- A remarkable feature of the strain solution is that the equations in (18), which are derived from the associated flow rule written in terms of plastic strain rates, can be immediately integrated with respect to the time to result in the equations in terms of plastic strains (Equation (20)). This significantly facilitates the solution.
- Another remarkable feature of the strain solution is that all strain components are proportional to k introduced in (9). Therefore, simple scaling of any strain solution provides the strain solution for similar discs of material with the same other properties and geometry, but any value of k.
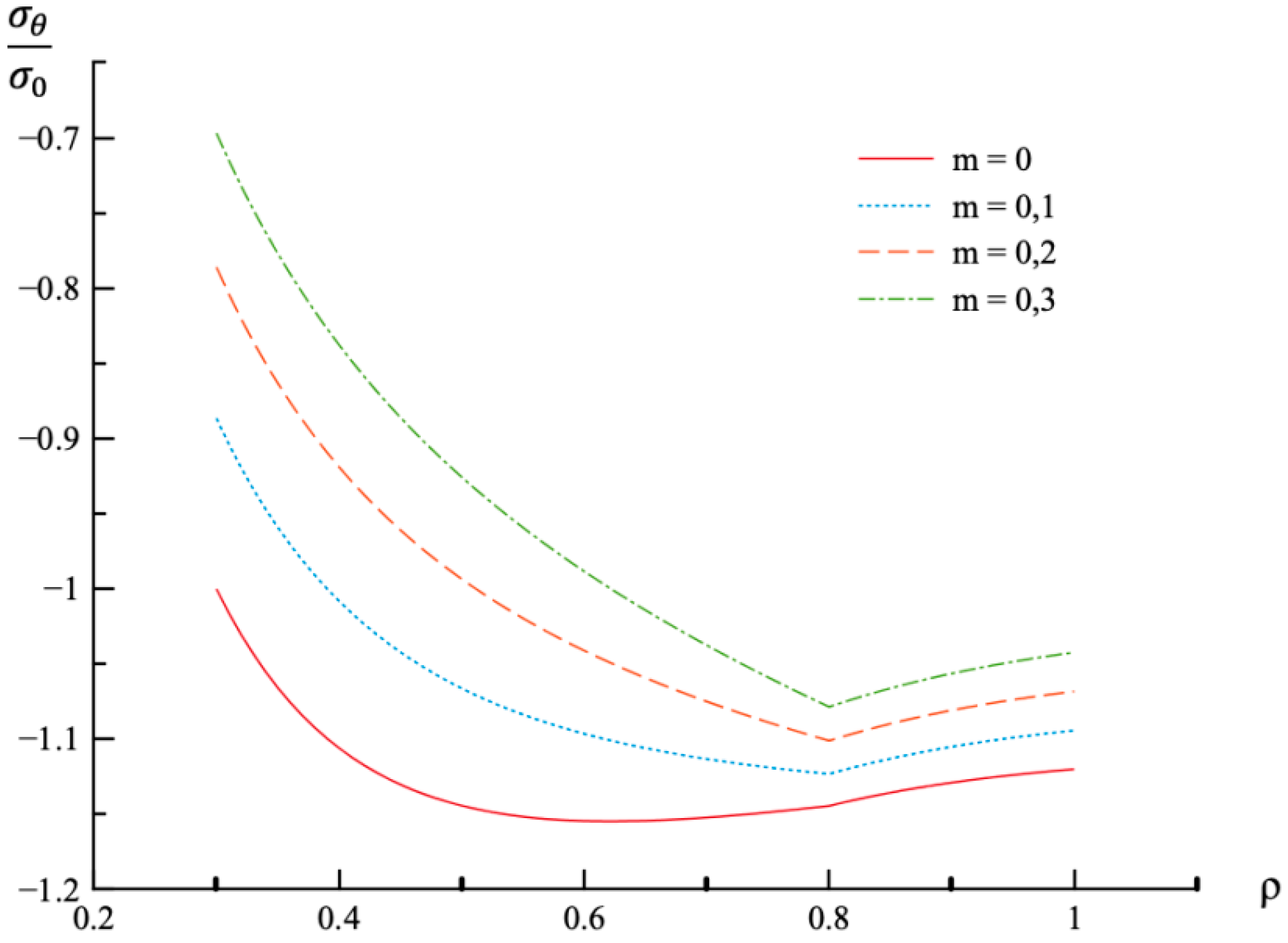
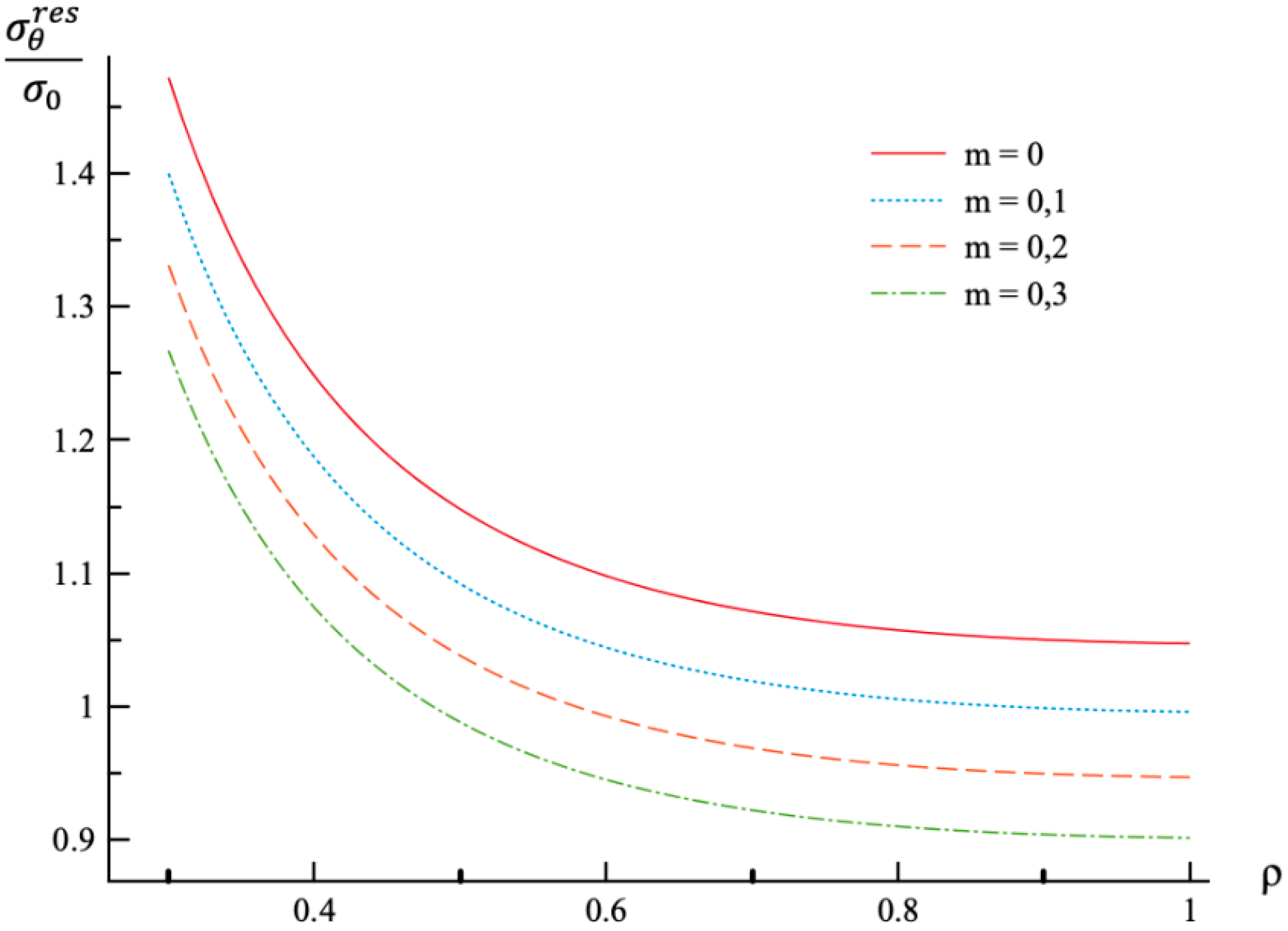
- In the case of the stress solution, the effect of m-value involved in (31) is most significant on the distribution of the circumferential stress and the residual circumferential stress.
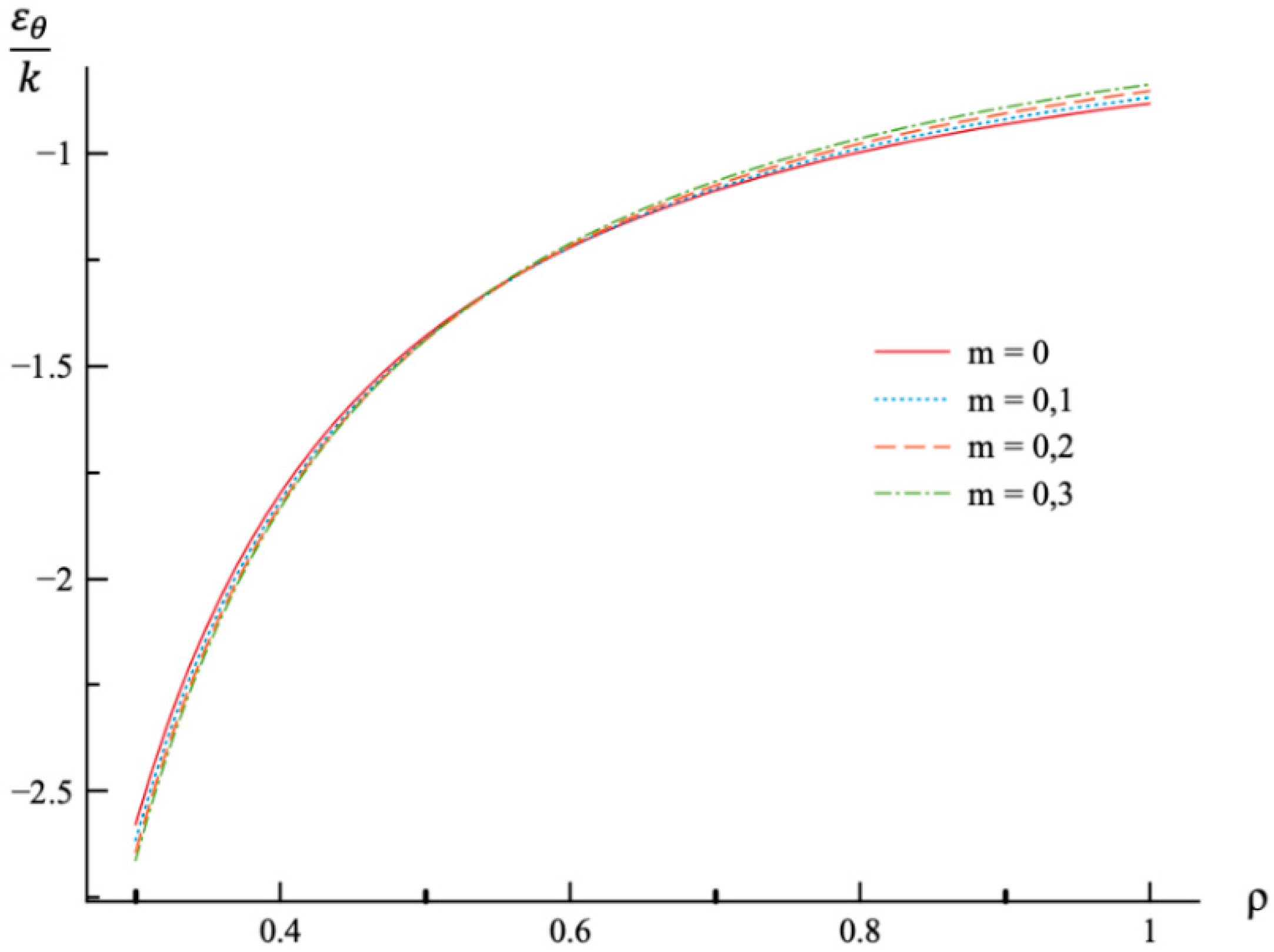
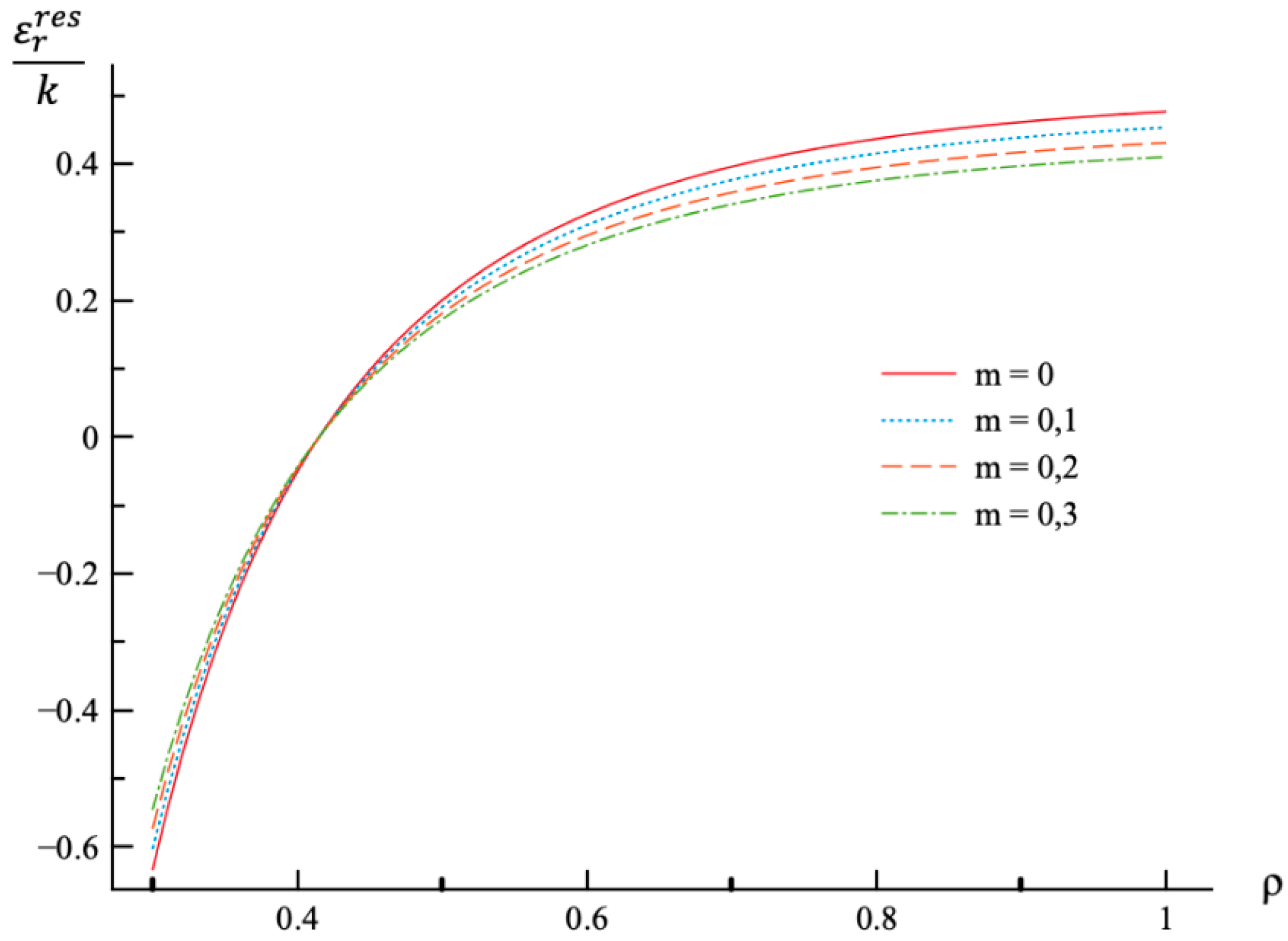
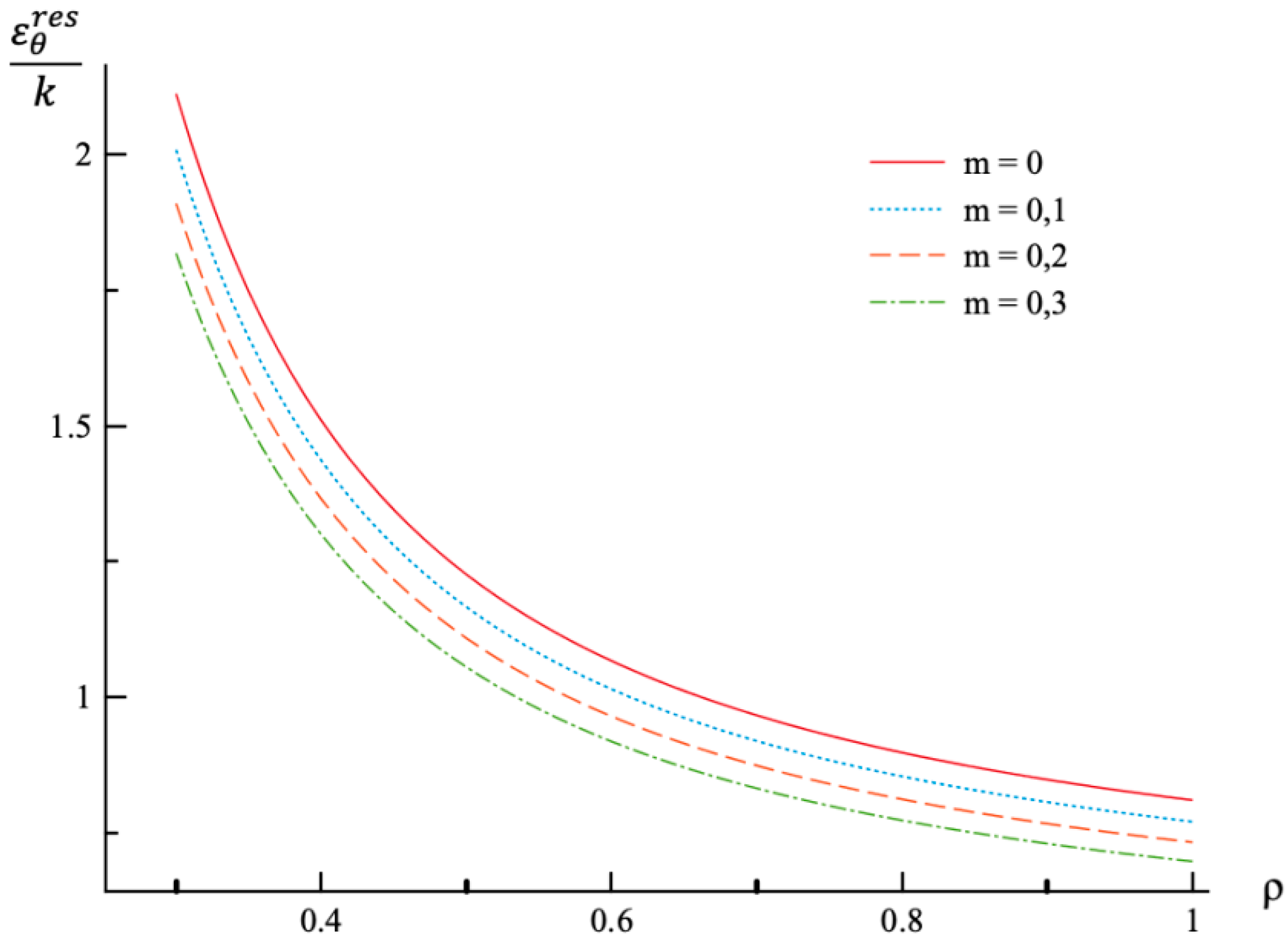
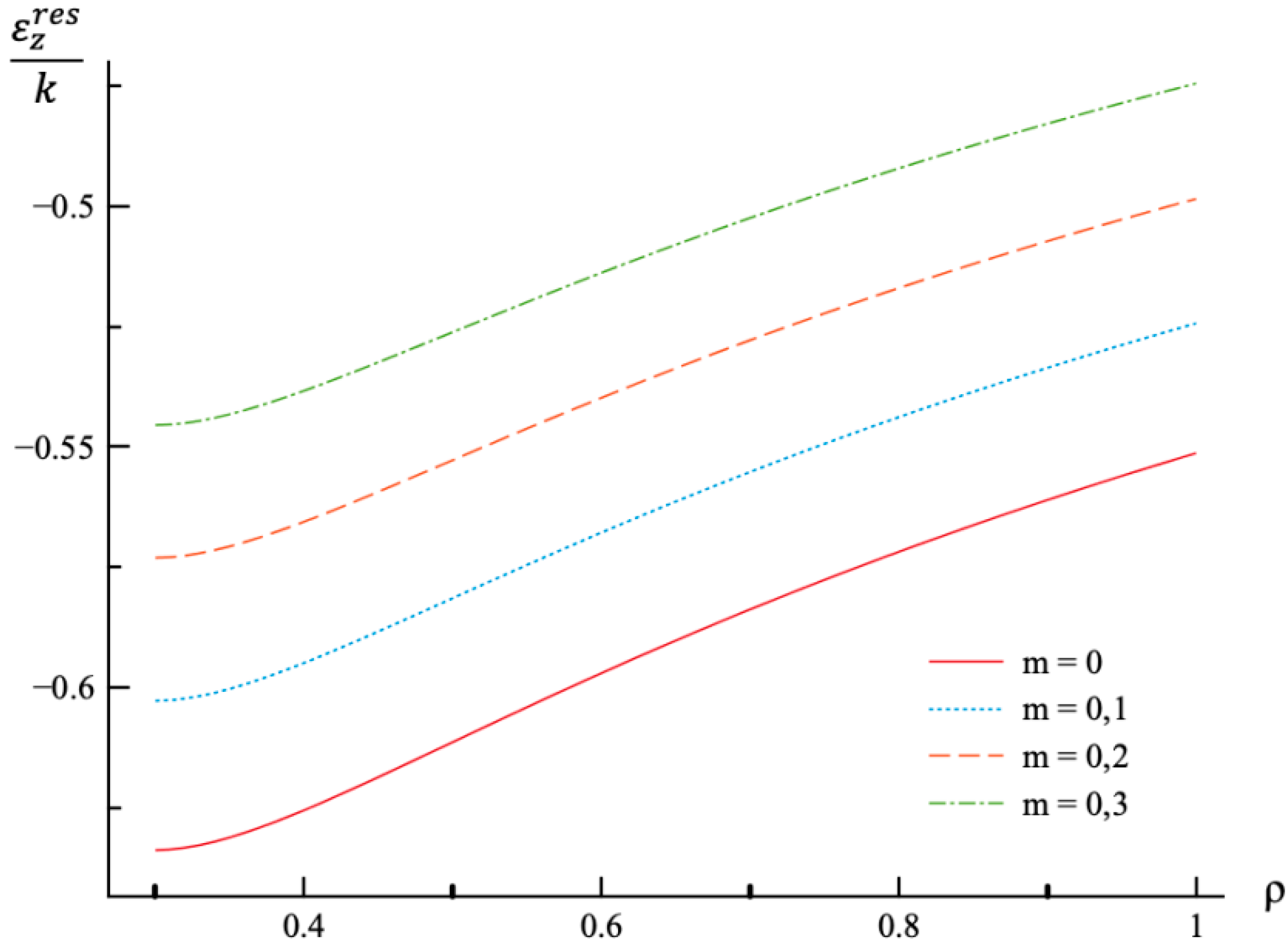
- In the case of the strain solution, the effect of m-value is most significant on the distribution of the axial strain and the residual axial strain.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Horgan, C.O.; Chan, A.M. The Pressurized Hollow Cylinder or Disk Problem for Functionally Graded Isotropic Linearly Elastic Materials. J. Elast. 1999, 55, 43–59. [Google Scholar] [CrossRef]
- You, L.H.; Wang, J.X.; Tang, B.P. Deformations and stresses in annular disks made of functionally graded materials subjected to internal and/or external pressure. Meccanica 2009, 44, 283–292. [Google Scholar] [CrossRef]
- Tutuncu, N. Stresses in thick-walled FGM cylinders with exponentially-varying properties. Eng. Struct. 2007, 29, 2032–2035. [Google Scholar] [CrossRef]
- Gönczi, D.; Ecsedi, I. Thermoelastic Analysis of Functionally Graded Hollow Circular Disc. Arch. Mech. Eng. 2015, 62, 5–18. [Google Scholar] [CrossRef] [Green Version]
- Yeo, W.H.; Purbolaksono, J.; Aliabadi, M.H.; Ramesh, S.; Liew, H.L. Exact solution for stresses/displacements in a multilayered hollow cylinder under thermo-mechanical loading. Int. J. Press. Vessels Pip. 2017, 151, 45–53. [Google Scholar] [CrossRef]
- Shabana, Y.M.; Elsawaf, A.; Khalaf, H.; Khalil, Y. Stresses minimization in functionally graded cylinders using particle swarm optimization technique. Int. J. Press. Vessels Pip. 2017, 154, 1–10. [Google Scholar] [CrossRef]
- Haghpanah Jahromi, B.; Farrahi, G.H.; Maleki, M.; Nayeb-Hashemi, H.; Vaziri, A. Residual stresses in autofrettaged vessel made of functionally graded material. Eng. Struct. 2009, 31, 2930–2935. [Google Scholar] [CrossRef]
- Eraslan, A.N.; Akis, T. Plane strain analytical solutions for a functionally graded elastic–plastic pressurized tube. Int. J. Press. Vessels Pip. 2006, 83, 635–644. [Google Scholar] [CrossRef]
- Yildirim, V. Numerical/analytical solutions to the elastic response of arbitrarily functionally graded polar orthotropic rotating discs. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 320. [Google Scholar] [CrossRef]
- Jalali, M.H.; Shahriari, B. Elastic Stress Analysis of Rotating Functionally Graded Annular Disk of Variable Thickness Using Finite Difference Method. Math. Probl. Eng. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Hosseini Kordkheili, S.A.; Naghdabadi, R. Thermoelastic analysis of a functionally graded rotating disk. Compos. Struct. 2007, 79, 508–516. [Google Scholar] [CrossRef]
- Hassani, A.; Hojjati, M.H.; Farrahi, G.; Alashti, R.A. Semi-exact elastic solutions for thermo-mechanical analysis of functionally graded rotating disks. Compos. Struct. 2011, 93, 3239–3251. [Google Scholar] [CrossRef]
- Dai, T.; Dai, H.-L. Thermo-elastic analysis of a functionally graded rotating hollow circular disk with variable thickness and angular speed. Appl. Math. Model. 2016, 40, 7689–7707. [Google Scholar] [CrossRef]
- Allam, M.N.M.; Tantawy, R.; Zenkour, A.M. Thermoelastic stresses in functionally graded rotating annular disks with variable thickness. J. Theor. Appl. Mech. 2018, 56, 1029–1041. [Google Scholar] [CrossRef]
- Leu, S.-Y.; Chien, L.-C. Thermoelastic analysis of functionally graded rotating disks with variable thickness involving non-uniform heat source. J. Therm. Stress. 2015, 38, 415–426. [Google Scholar] [CrossRef]
- Allam, M.N.M.; Tantawy, R.; Yousof, A.; Zenkour, A.M. Elastic and Viscoelastic Stresses of Nonlinear Rotating Functionally Graded Solid and Annular Disks with Gradually Varying Thickness. Arch. Mech. Eng. 2017, 64, 423–440. [Google Scholar] [CrossRef] [Green Version]
- Sondhi, L.; Sanyal, S.; Saha, K.; Bhowmick, S. Limit Elastic Speeds of Functionally Graded Annular Disks. FME Trans. 2018, 46, 603–611. [Google Scholar]
- Zheng, Y.; Bahaloo, H.; Mousanezhad, D.; Vaziri, A.; Nayeb-Hashemi, H. Displacement and Stress Fields in a Functionally Graded Fiber-Reinforced Rotating Disk with Nonuniform Thickness and Variable Angular Velocity. J. Eng. Mater. Technol. 2017, 139, 1–10. [Google Scholar] [CrossRef]
- Khorsand, M.; Tang, Y. Design functionally graded rotating disks under thermoelastic loads: Weight optimization. Int. J. Press. Vessels Pip. 2018, 161, 33–40. [Google Scholar] [CrossRef]
- Nejad, M.Z.; Rastgoo, A.; Hadi, A. Exact elasto-plastic analysis of rotating disks made of functionally graded materials. Int. J. Eng. Sci. 2014, 85, 47–57. [Google Scholar] [CrossRef]
- Nejad, M.Z.; Fatehi, P. Exact elasto-plastic analysis of rotating thick-walled cylindrical pressure vessels made of functionally graded materials. Int. J. Eng. Sci. 2015, 86, 26–43. [Google Scholar] [CrossRef]
- Hassani, A.; Hojjati, M.H.; Farrahi, G.H.; Alashti, R.A. Semi-exact solution for thermo-mechanical analysis of functionally graded elastic-strain hardening rotating disks. Commun. Nonlinear Sci. Numer. Simulat. 2012, 17, 3747–3762. [Google Scholar] [CrossRef]
- Haghpanah Jahromi, B.; Nayeb-Hashemi, H.; Vaziri, A. Elasto-Plastic Stresses in a Functionally Graded Rotating Disk. J. Eng. Mater. Technol. 2012, 134, 1–11. [Google Scholar]
- Mahdavi, E.; Ghasemi, A.; Alashti, R.A. Elastic–plastic analysis of functionally graded rotating disks with variable thickness and temperature-dependent material properties under mechanical loading and unloading. Aerosp. Sci. Technol. 2016, 59, 57–68. [Google Scholar] [CrossRef]
- Kalali, A.T.; Hadidi-Moud, S.; Hassani, B. Elasto-Plastic Stress Analysis in Rotating Disks and Pressure Vessels Made of Functionally Graded Materials. Latin Am. J. Solids Struct. 2016, 13, 819–834. [Google Scholar] [CrossRef] [Green Version]
- Pirumov, A.; Alexandrov, S.; Jeng, Y.-R. Enlargement of a Circular Hole in a Disc of Plastically Compressible Material. Acta Mech. 2013, 224, 2965–2976. [Google Scholar] [CrossRef]
- Çallıoglu, H.; Sayer, M.; Demir, E. Elastic–plastic stress analysis of rotating functionally graded discs. Thin-Walled Struct. 2015, 94, 38–44. [Google Scholar] [CrossRef]
- Zheng, Y.; Bahaloo, H.; Mousanezhad, D.; Mahdi, E.; Vaziri, A.; Nayeb-Hashemi, H. Stress analysis in functionally graded rotating disks with non-uniform thickness and variable angular velocity. Int. J. Mech. Sci. 2016, 116, 283–293. [Google Scholar] [CrossRef]
- Chakrabarty, J. Theory of Plasticity; McGraw-Hill Book Company: New York, NY, USA, 1987. [Google Scholar]
- Rees, D.W.A. Basic Engineering Plasticity; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Alexandrov, S. Elastic/Plastic Discs under Plane Stress Conditions; Springer: Berlin, Germany, 2015. [Google Scholar]
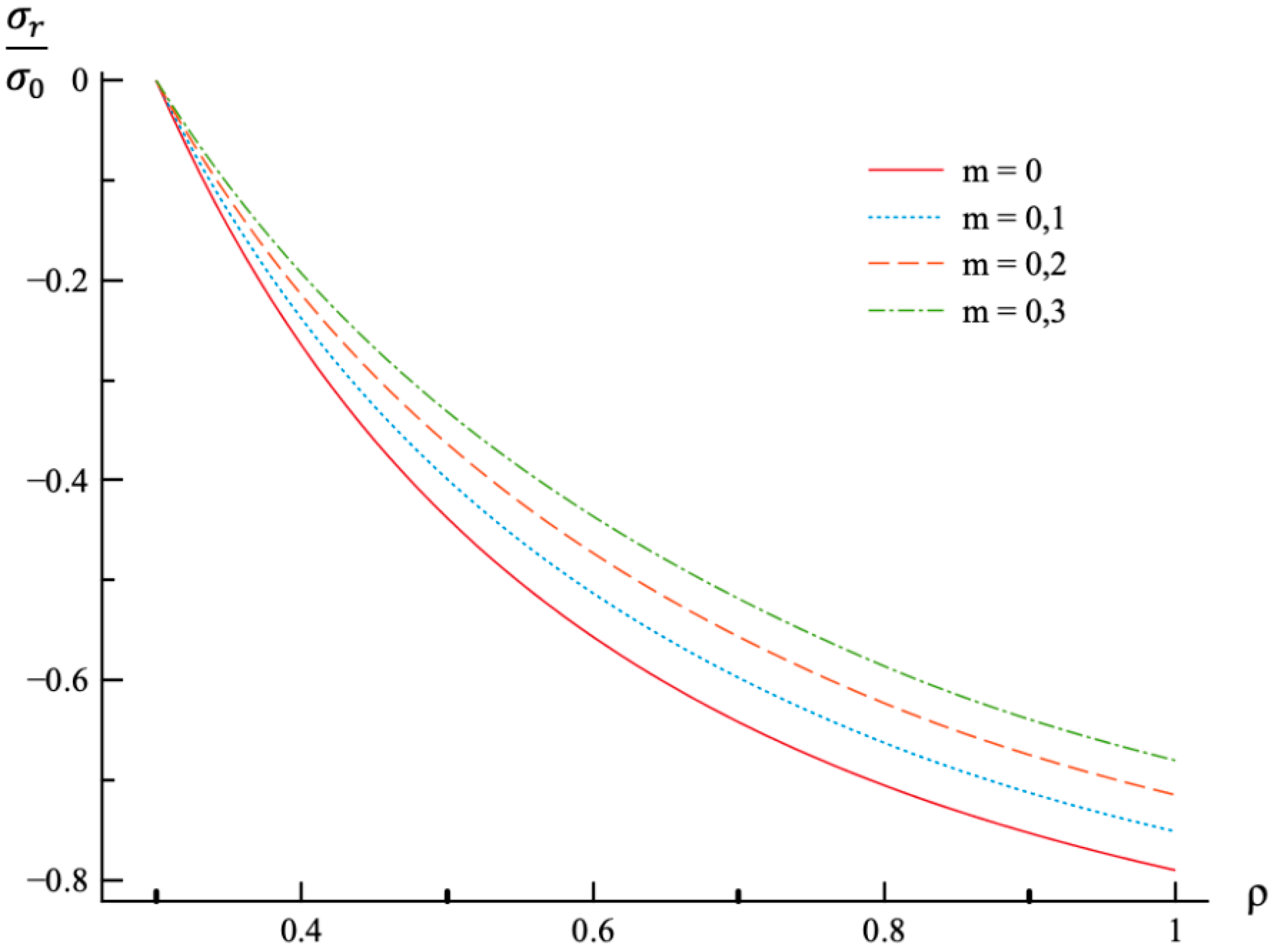


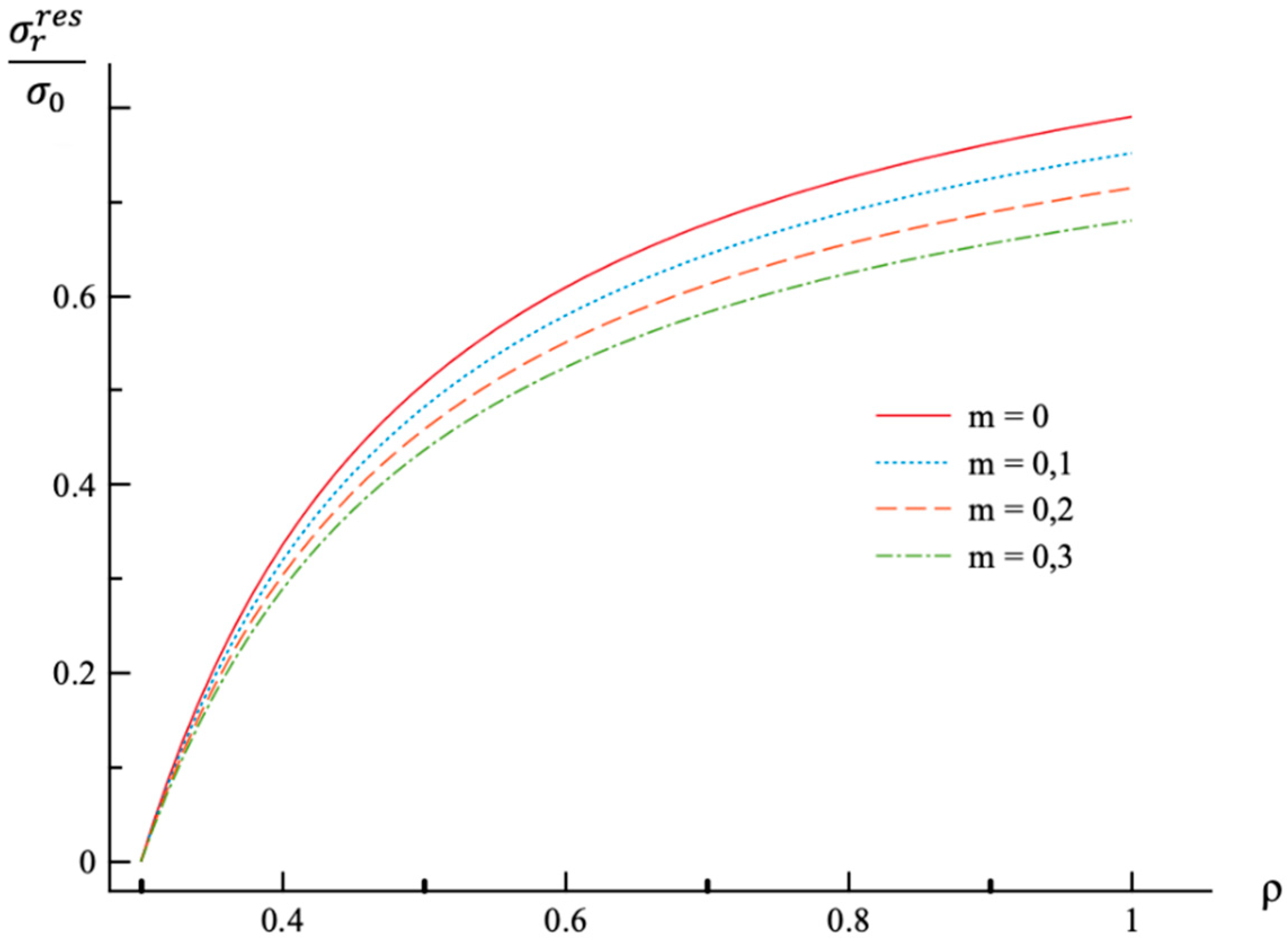
| 0 | 0.79 |
| 0.1 | 0.75 |
| 0.2 | 0.71 |
| 0.3 | 0.68 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strashnov, S.; Alexandrov, S.; Lang, L. Description of Residual Stress and Strain Fields in FGM Hollow Disc Subject to External Pressure. Materials 2019, 12, 440. https://doi.org/10.3390/ma12030440
Strashnov S, Alexandrov S, Lang L. Description of Residual Stress and Strain Fields in FGM Hollow Disc Subject to External Pressure. Materials. 2019; 12(3):440. https://doi.org/10.3390/ma12030440
Chicago/Turabian StyleStrashnov, Stanislav, Sergei Alexandrov, and Lihui Lang. 2019. "Description of Residual Stress and Strain Fields in FGM Hollow Disc Subject to External Pressure" Materials 12, no. 3: 440. https://doi.org/10.3390/ma12030440







