Nonlinear Stability Analysis of Eccentrically Stiffened Functionally Graded Truncated Conical Sandwich Shells with Porosity
Abstract
:1. Introduction
2. Model Configurations and Elastic Foundations
- ,
- is the core layer thickness,
- , denote stringers and rings thickness respectively,
- is the porosity coefficient of the core layer,
- k, k2, and k3 are the shell, stringers, and rings volume fraction indexes respectively.
- and denote shell, metal, ceramic, ring, and stringer respectively.
- denotes stiffeners in general, stiffeners are stringers and rings.
- are Young’s moduli of ceramic and metal.
- and are the Young moduli of shell, stringer, and ring of materials respectively.
3. Theoretical Formulations
4. Prebuckling State Analysis
5. Nonlinear Stability Formulations
6. Buckling and Post-Buckling Analysis
7. Numerical Results and Discussion
7.1. Verification Study
7.2. The PSTC on Pasternak Elastic Foundations
7.2.1. Effect of Porosity Coefficients and Thickness of Core Layer
7.2.2. Effect of Semi-Vertex Angle α
7.2.3. Effect of Geometrical Ratios
7.2.4. Effects of Volume Fraction Index
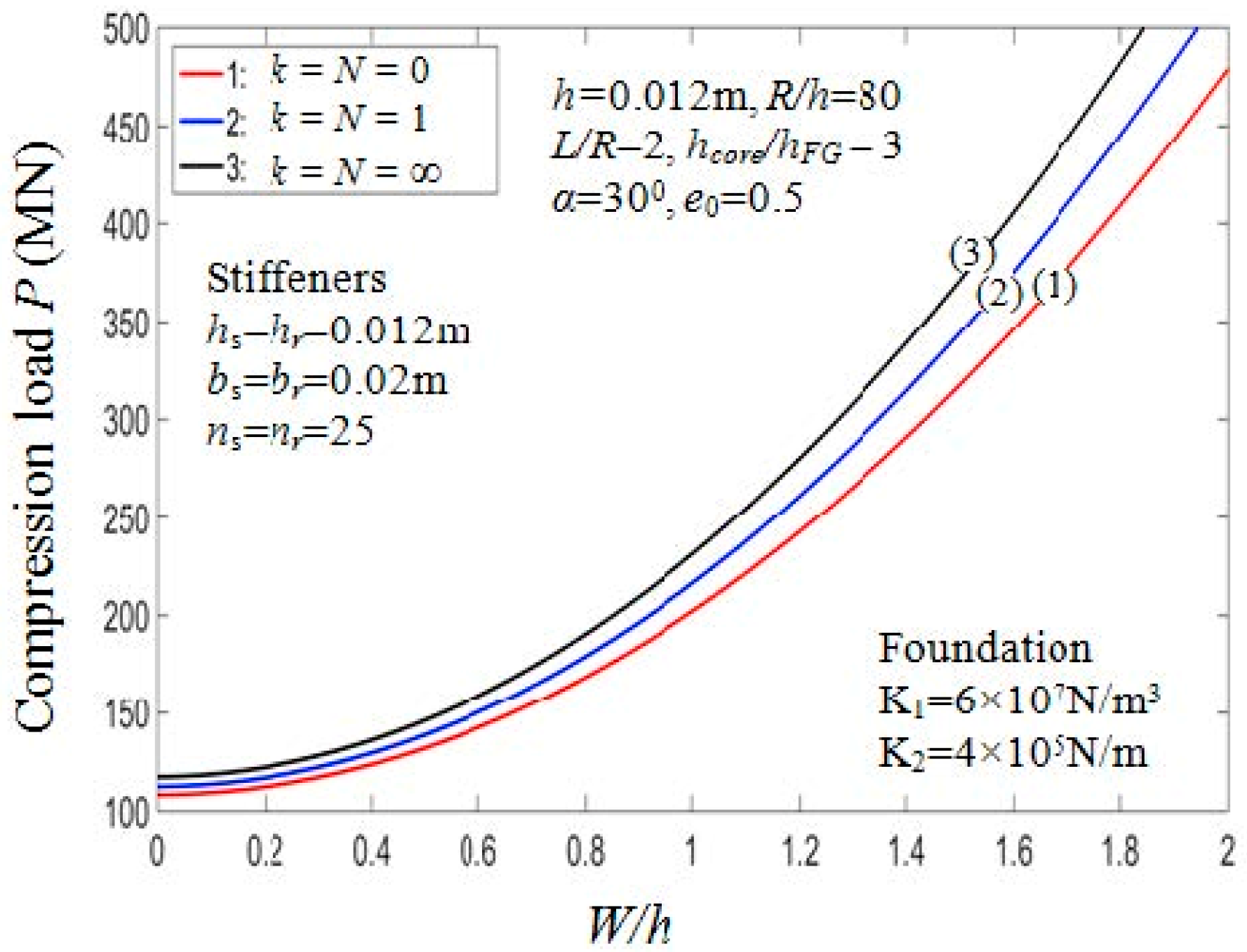
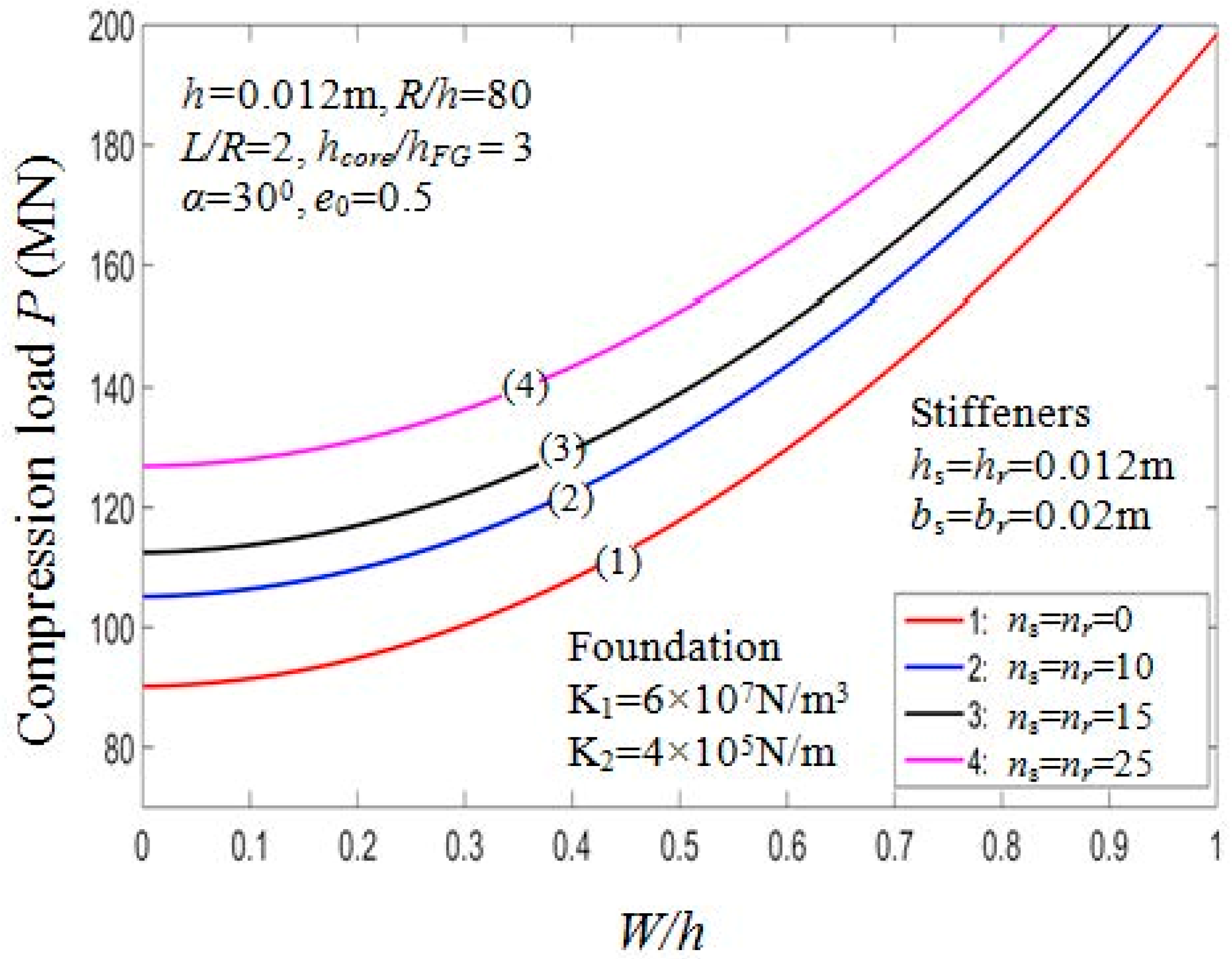
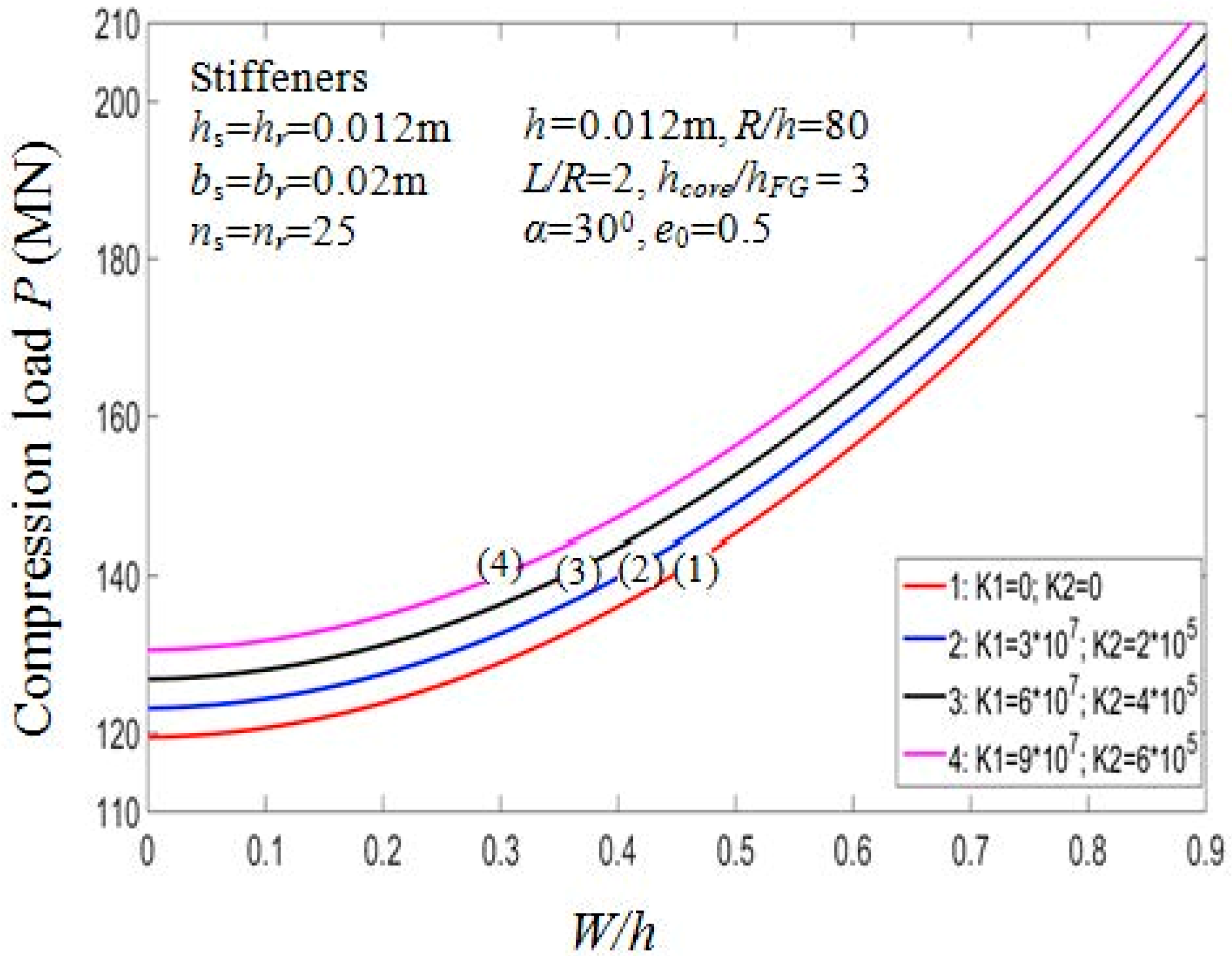
7.2.5. Effect of Stiffeners and Foundation
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Huang, H.; Han, Q. Nonlinear elastic buckling and postbuckling of axially compressed functionally graded cylindrical shells. Int. J. Mech. Sci. 2009, 51, 500–507. [Google Scholar] [CrossRef]
- Naj, R.; Boroujerdy, M.S.; Eslami, M. Thermal and mechanical instability of functionally graded truncated conical shells. Thin-Walled Struct. 2008, 46, 65–78. [Google Scholar]
- Sofiyev, A. Influences of shear stresses on the dynamic instability of exponentially graded sandwich cylindrical shells. Compos. Part B Eng. 2015, 77, 349–362. [Google Scholar]
- Sofiyev, A.; Kuruoglu, N. Non-linear buckling of an FGM truncated conical shell surrounded by an elastic medium. Int. J. Press. Vessels Pip. 2013, 107, 38–49. [Google Scholar]
- Sofiyev, A. Buckling analysis of freely-supported functionally graded truncated conical shells under external pressures. Compos. Struct. 2015, 132, 746–758. [Google Scholar] [CrossRef]
- Sofiyev, A.; Kuruoglu, N. On the solution of the buckling problem of functionally graded truncated conical shells with mixed boundary conditions. Compos. Struct. 2015, 123, 282–291. [Google Scholar]
- Sofiyev, A.H.; Avcar, M. The stability of cylindrical shells containing an FGM layer subjected to axial load on the Pasternak foundation. Engineering 2010, 2, 228–236. [Google Scholar] [CrossRef]
- Sofiyev, A. Influence of the initial imperfection on the non-linear buckling response of FGM truncated conical shells. Int. J. Mech. Sci. 2011, 53, 753–761. [Google Scholar] [CrossRef]
- Sofiyev, A. The buckling of FGM truncated conical shells subjected to combined axial tension and hydrostatic pressure. Compos. Struct. 2010, 92, 488–498. [Google Scholar]
- Sofiyev, A. Non-linear buckling behavior of FGM truncated conical shells subjected to axial load. Int. J. Non-Linear Mech. 2011, 46, 711–719. [Google Scholar]
- Duc, N.D.; Thang, P.T. Nonlinear response of imperfect eccentrically stiffened ceramic–metal–ceramic FGM thin circular cylindrical shells surrounded on elastic foundations and subjected to axial compression. Compos. Struct. 2014, 110, 200–206. [Google Scholar] [CrossRef]
- Duc, N.D.; Thang, P.T. Nonlinear buckling of imperfect eccentrically stiffened metal–ceramic–metal S-FGM thin circular cylindrical shells with temperature-dependent properties in thermal environments. Int. J. Mech. Sci. 2014, 81, 17–25. [Google Scholar] [CrossRef]
- Duc, N.D.; Van Tung, H. Nonlinear analysis of stability for functionally graded cylindrical panels under axial compression. Comput. Mater. Sci. 2010, 49, S313–S316. [Google Scholar] [CrossRef]
- Duc, N.D.; Thang, P.T.; Dao, N.T.; Tac, H.V. Nonlinear buckling of higher deformable S-FGM thick circular cylindrical shells with metal–ceramic–metal layers surrounded on elastic foundations in thermal environment. Compos. Struct. 2015, 121, 134–141. [Google Scholar] [CrossRef]
- Duc, N.D.; Cong, P.H.; Anh, V.M.; Quang, V.D.; Tran, P.; Tuan, N.D.; Thinh, N.H. Mechanical and thermal stability of eccentrically stiffened functionally graded conical shell panels resting on elastic foundations and in thermal environment. Compos. Struct. 2015, 132, 597–609. [Google Scholar] [CrossRef]
- Duc, N.D.; Quan, T.Q. Nonlinear response of imperfect eccentrically stiffened FGM cylindrical panels on elastic foundation subjected to mechanical loads. Eur. J. Mech. A Solids 2014, 46, 60–71. [Google Scholar] [CrossRef]
- Duc, N.D.; Tuan, N.D.; Quan, T.Q.; Quyen, N.V.; Anh, T.V. Nonlinear mechanical, thermal and thermo-mechanical postbuckling of imperfect eccentrically stiffened thin FGM cylindrical panels on elastic foundations. Thin-Walled Struct. 2015, 96, 155–168. [Google Scholar] [CrossRef]
- Phuong, N.T.; Bich, D.H. Buckling analysis of eccentrically stiffened functionally graded circular cylindrical thin shells under mechanical load. VNU J. Sci. Math. Phys. 2013, 29, 55–72. [Google Scholar]
- Ninh, D.G.; Bich, D.H. Nonlinear torsional buckling and post-buckling of eccentrically stiffened ceramic functionally graded material metal layer cylindrical shell surrounded by elastic foundation subjected to thermo-mechanical load. J. Sandw. Struct. Mater. 2016, 18, 712–738. [Google Scholar] [CrossRef]
- Bich, D.H.; van Dung, D.; Nam, V.H. Nonlinear dynamical analysis of eccentrically stiffened functionally graded cylindrical panels. Compos. Struct. 2012, 94, 2465–2473. [Google Scholar] [CrossRef]
- Dung, D.V.; Hoa, L.K.; Thuyet, B.T.; Nga, N.T. Buckling analysis of functionally graded material (FGM) sandwich truncated conical shells reinforced by FGM stiffeners filled inside by elastic foundations. Appl. Math. Mech. 2016, 37, 879–902. [Google Scholar] [CrossRef]
- Van Dung, D.; Nga, N.T. Instability of eccentrically stiffened functionally graded truncated conical shells under mechanical loads. Compos. Struct. 2013, 106, 104–113. [Google Scholar] [CrossRef]
- Van Dung, D.; Chan, D.Q. Analytical investigation on mechanical buckling of FGM truncated conical shells reinforced by orthogonal stiffeners based on FSDT. Compos. Struct. 2017, 159, 827–841. [Google Scholar] [CrossRef]
- Van Dung, D.; Hoai, B.T.T. Postbuckling nonlinear analysis of FGM truncated conical shells reinforced by orthogonal stiffeners resting on elastic foundations. Acta Mech. 2017, 228, 1457–1479. [Google Scholar] [CrossRef]
- Magnucki, K.; Stasiewicz, P. Elastic buckling of a porous beam. J. Theor. Appl. Mech. 2004, 42, 859–868. [Google Scholar]
- Magnucka-Blandzi, E. Mathematical Modeling of a Rectangular Sandwich Plate with a Non-Homogeneous Core. AIP Conf. Proc. 2007, 936. [Google Scholar] [CrossRef]
- Magnucka-Blandzi, E. Mathematical modelling of a rectangular sandwich plate with a metal foam core. J. Theor. Appl. Mech. 2011, 49, 439–455. [Google Scholar]
- Magnucka-Blandzi, E. Axi-symmetrical deflection and buckling of circular porous-cellular plate. Thin-Walled Struct. 2008, 46, 333–337. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Elastic buckling and static bending of shear deformable functionally graded porous beam. Compos. Struct. 2015, 133, 54–61. [Google Scholar] [CrossRef] [Green Version]
- Kitipornchai, S.; Chen, D.; Yang, J. Free vibration and elastic buckling of functionally graded porous beams reinforced by graphene platelets. Mater. Des. 2017, 116, 656–665. [Google Scholar] [CrossRef]
- Jabbari, M.; Mojahedin, A.; Khorshidvand, A.R.; Eslami, M.R. Buckling analysis of a functionally graded thin circular plate made of saturated porous materials. J. Eng. Mech. 2013, 140, 287–295. [Google Scholar] [CrossRef]
- Mojahedin, A.; Jabbari, M.; Khorshidvand, A.R.; Eslami, M.R. Buckling analysis of functionally graded circular plates made of saturated porous materials based on higher order shear deformation theory. Thin-Walled Struct. 2016, 99, 83–90. [Google Scholar] [CrossRef]
- Barretta, R.; Faghidian, S.A.; Luciano, R.; Medaglia, C.M.; Penna, R. Free vibrations of FG elastic Timoshenko nano-beams by strain gradient and stress-driven nonlocal models. Compos. Part B Eng. 2018, 154, 20–32. [Google Scholar] [CrossRef]
- Mahmoudpour, E.; Hosseini-Hashemi, S.; Faghidian, S. Nonlinear vibration analysis of FG nano-beams resting on elastic foundation in thermal environment using stress-driven nonlocal integral model. Appl. Math. Model. 2018, 57, 302–315. [Google Scholar] [CrossRef]
- Tang, H.; Li, L.; Hu, Y. Coupling effect of thickness and shear deformation on size-dependent bending of micro/nano-scale porous beams. Appl. Math. Model. 2018, 66, 527–547. [Google Scholar] [CrossRef]
- Barretta, R.; Luciano, R.; de Sciarra, F.M. Stress-driven nonlocal integral model for Timoshenko elastic nano-beams. Eur. J. Mech. A Solids 2018, 72, 275–286. [Google Scholar] [CrossRef]
- Mathew, T.V.; Natarajan, S.; Martínez-Pañeda, E. Size effects in elastic-plastic functionally graded materials. Compos. Struct. 2018, 204, 43–51. [Google Scholar] [CrossRef]
- Martínez-Pañeda, E.; Niordson, C.F. On fracture in finite strain gradient plasticity. Int. J. Plast. 2016, 80, 154–167. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Pañeda, E.; Niordson, C.F.; Bardella, L. A finite element framework for distortion gradient plasticity with applications to bending of thin foils. Int. J. Solids Struct. 2016, 96, 288–299. [Google Scholar] [CrossRef] [Green Version]
- Sofiyev, A. The buckling of FGM truncated conical shells subjected to axial compressive load and resting on Winkler–Pasternak foundations. Int. J. Press. Vessels Pip. 2010, 87, 753–761. [Google Scholar] [CrossRef]
- Brush, D.O.; Almroth, B.O. Buckling of Bars, Plates, and Shells; McGraw-Hill: New York, NY, USA, 1975; Volume 6. [Google Scholar]
- Baruch, M.; Harari, O.; Singer, J. Low buckling loads of axially compressed conical shells. J. Appl. Mech. 1970, 37, 384–392. [Google Scholar] [CrossRef]
- Deniz, A. Non-linear stability analysis of truncated conical shell with functionally graded composite coatings in the finite deflection. Compos. Part B Eng. 2013, 51, 318–326. [Google Scholar] [CrossRef]

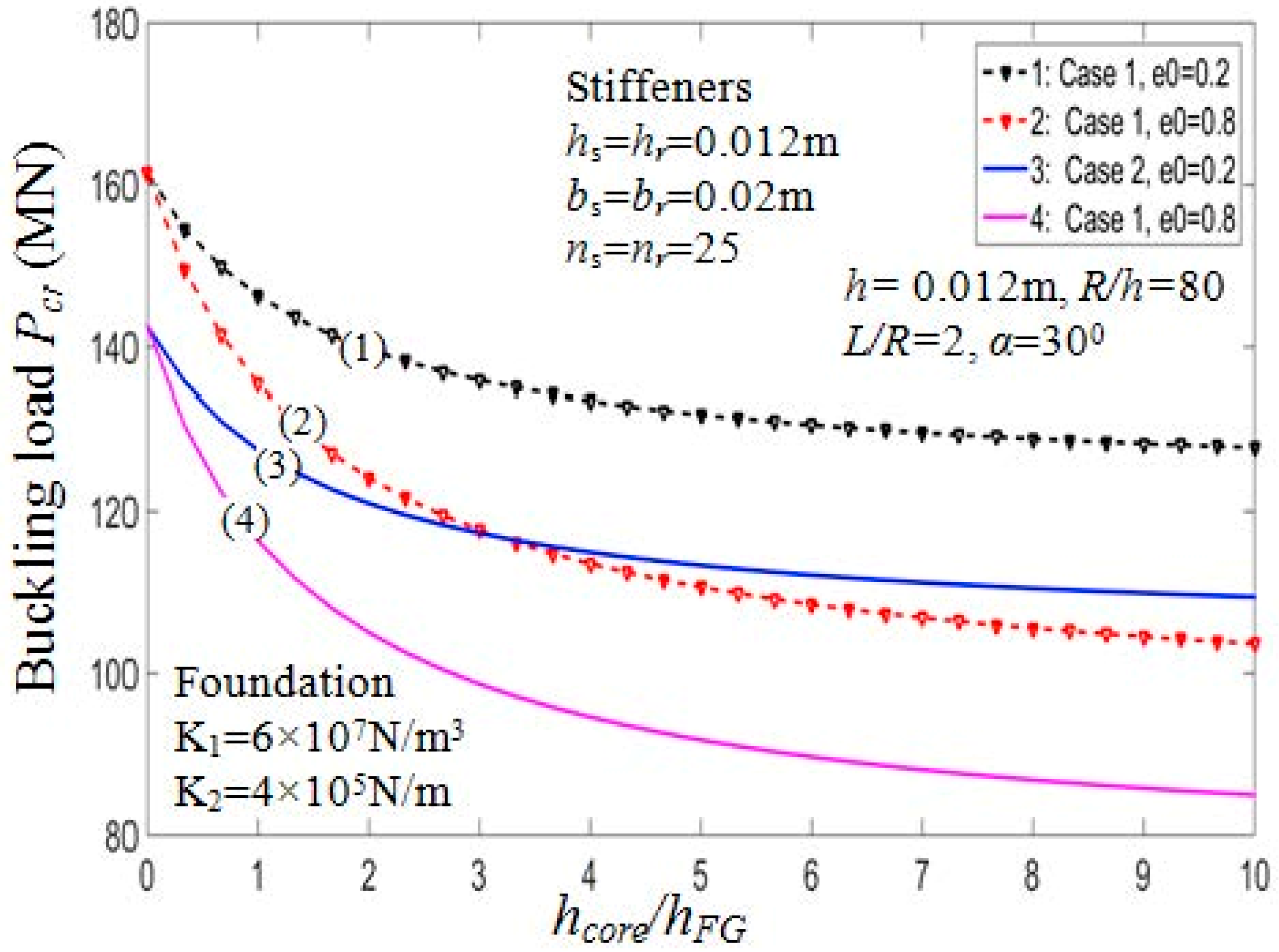

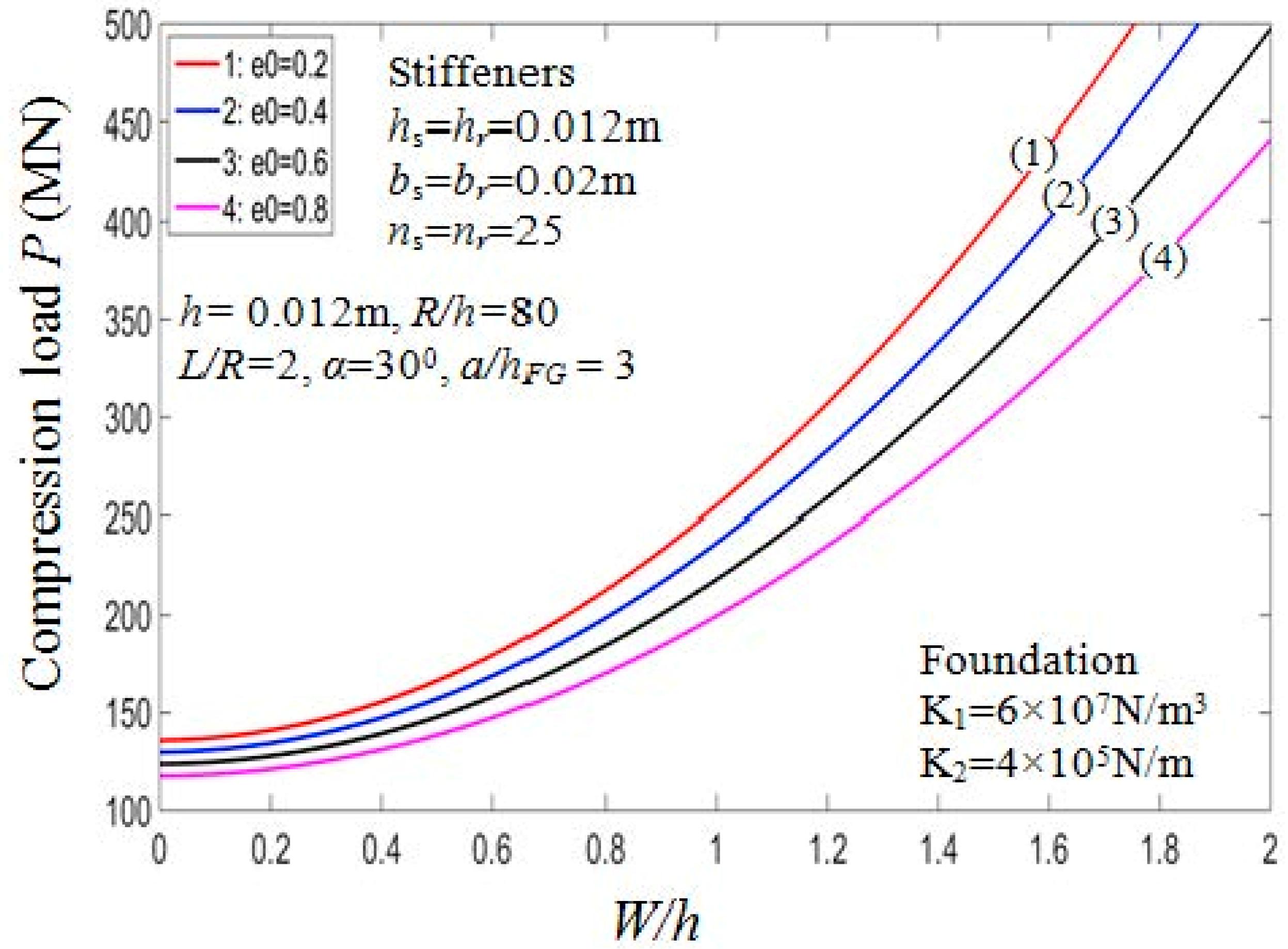
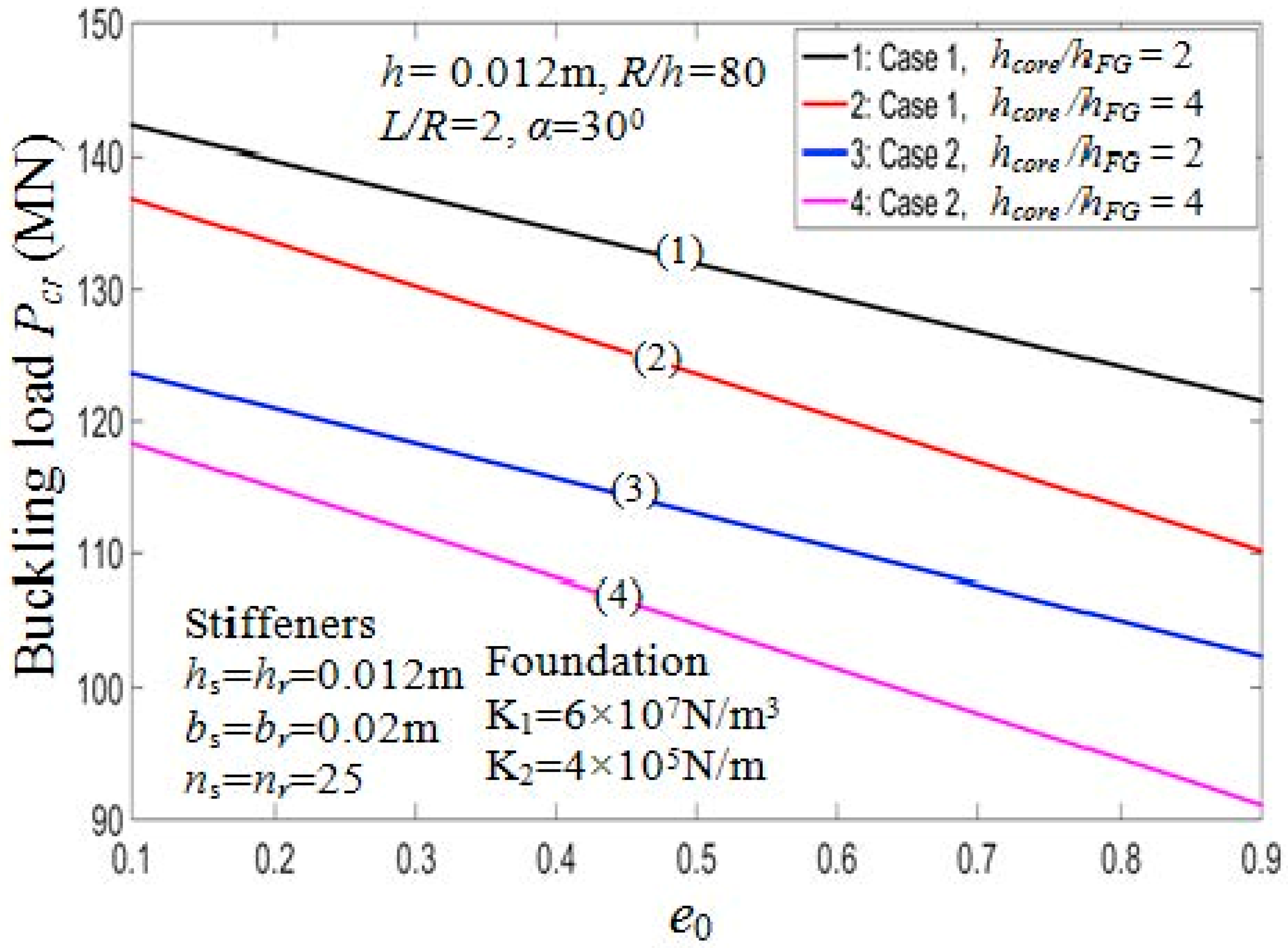
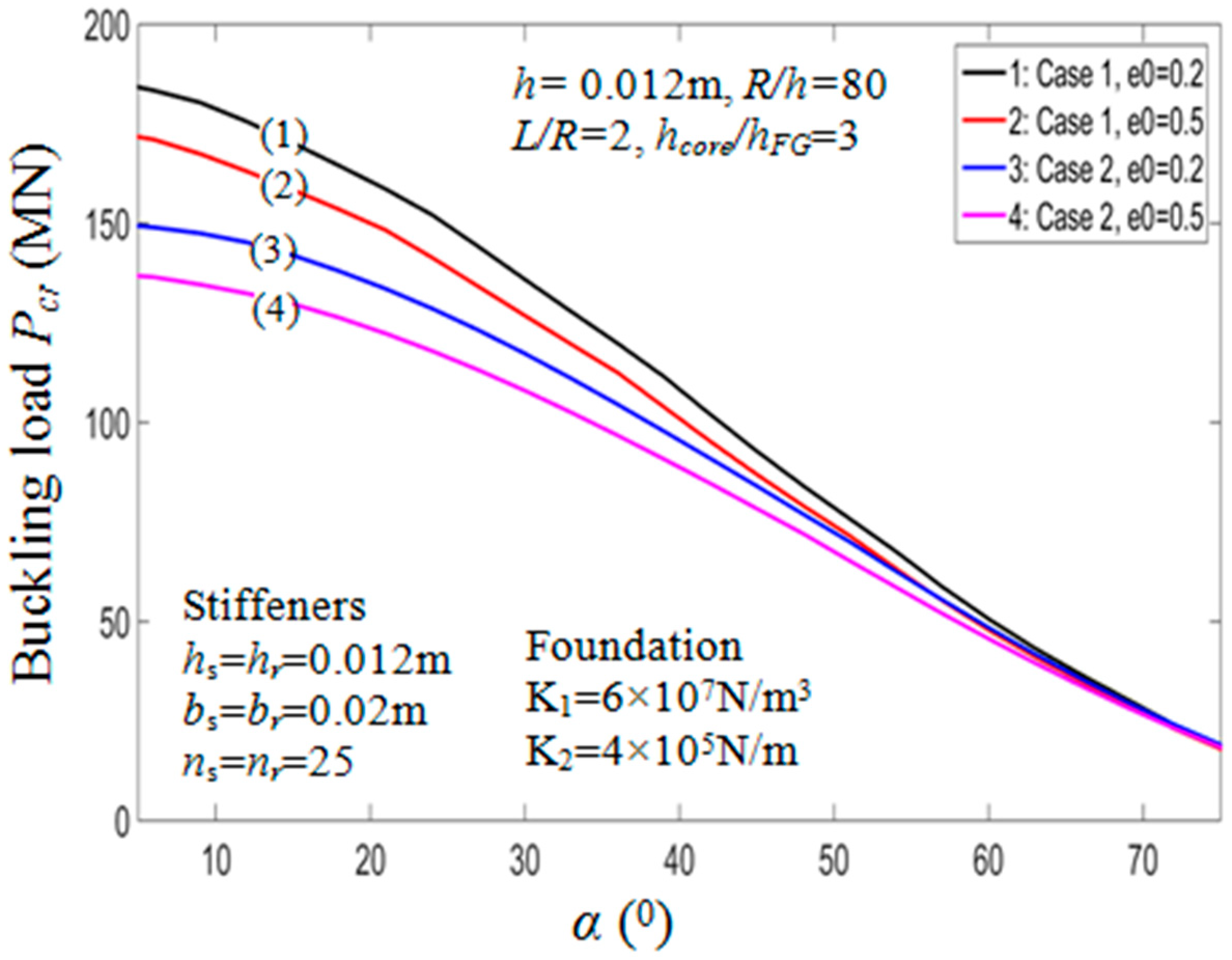
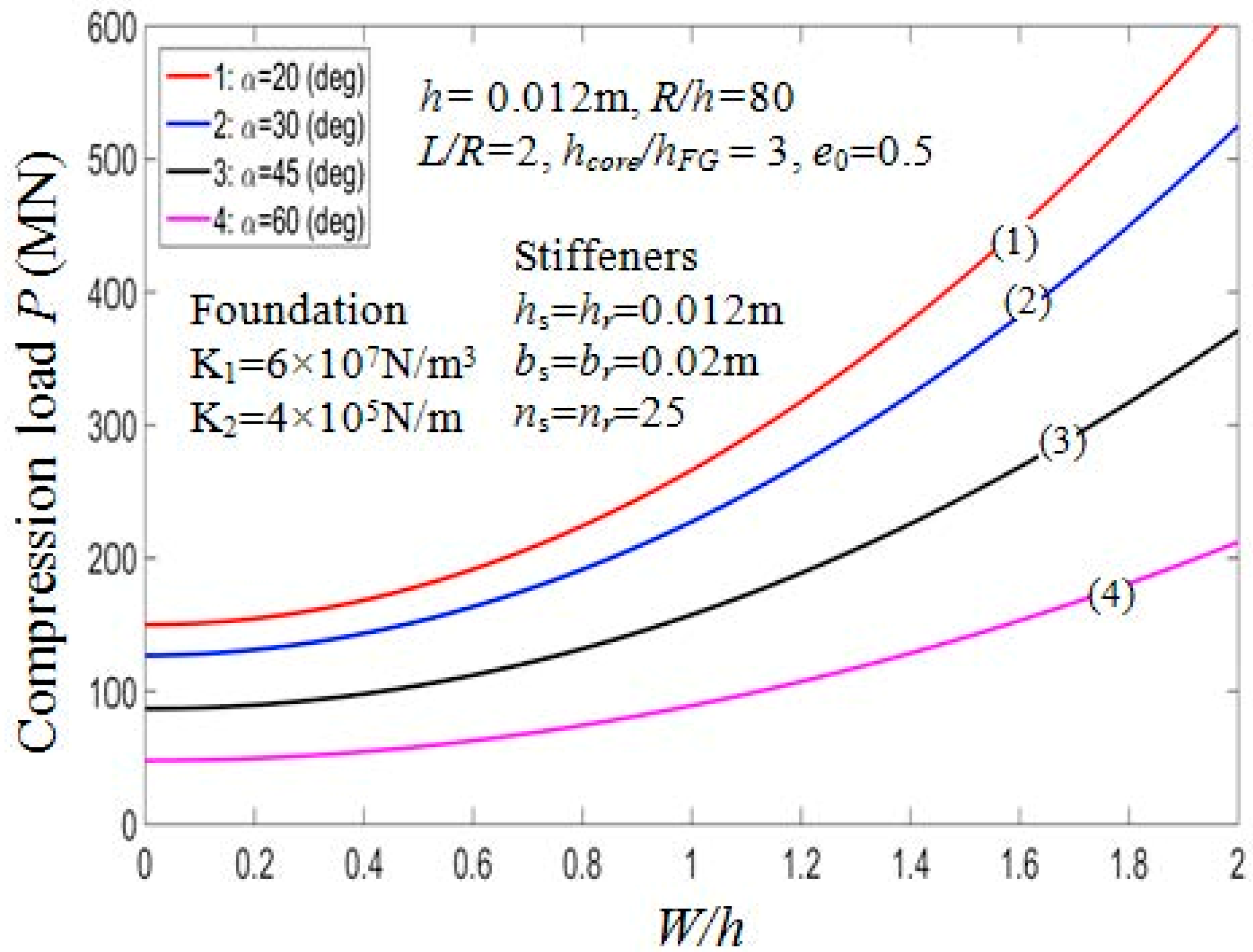
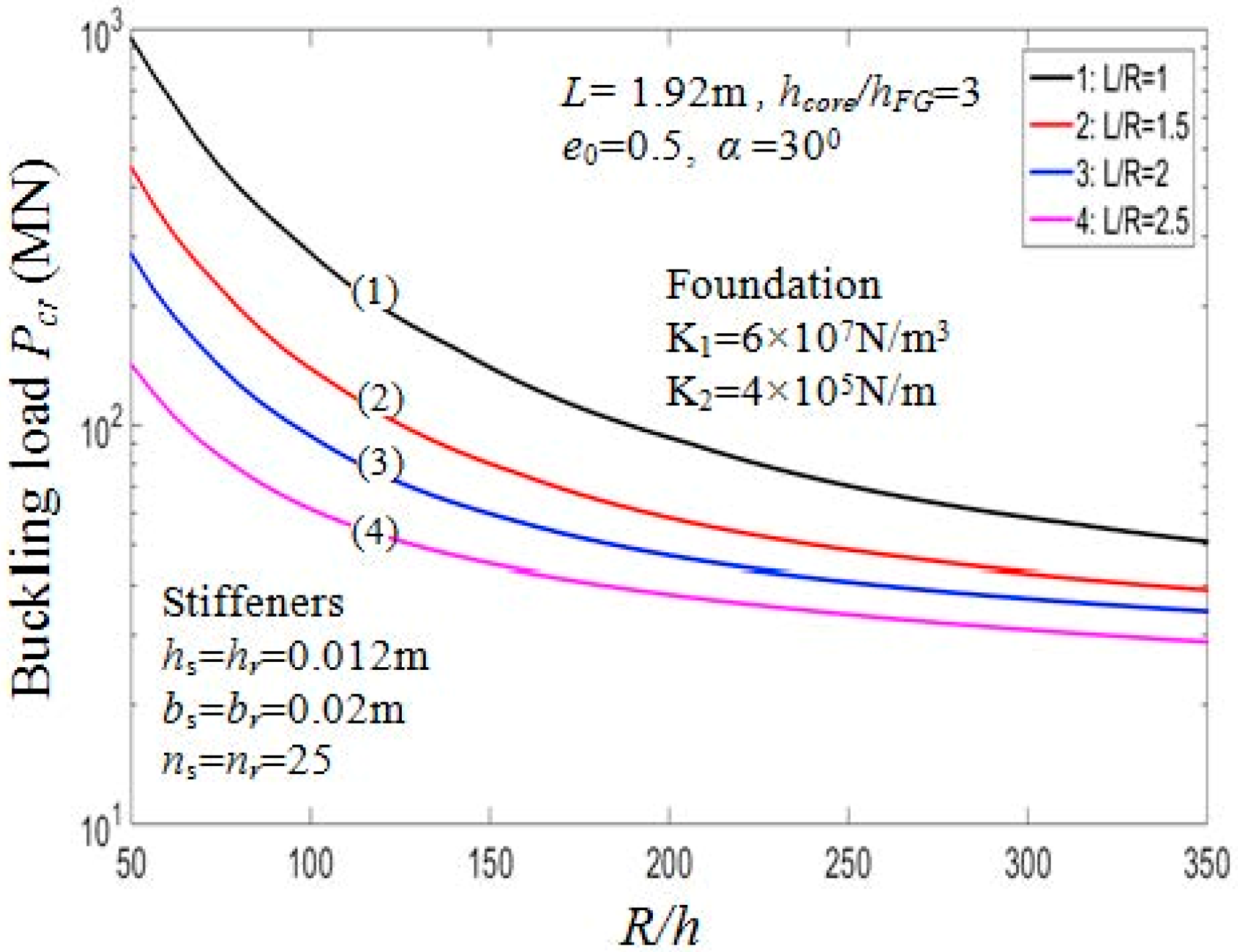
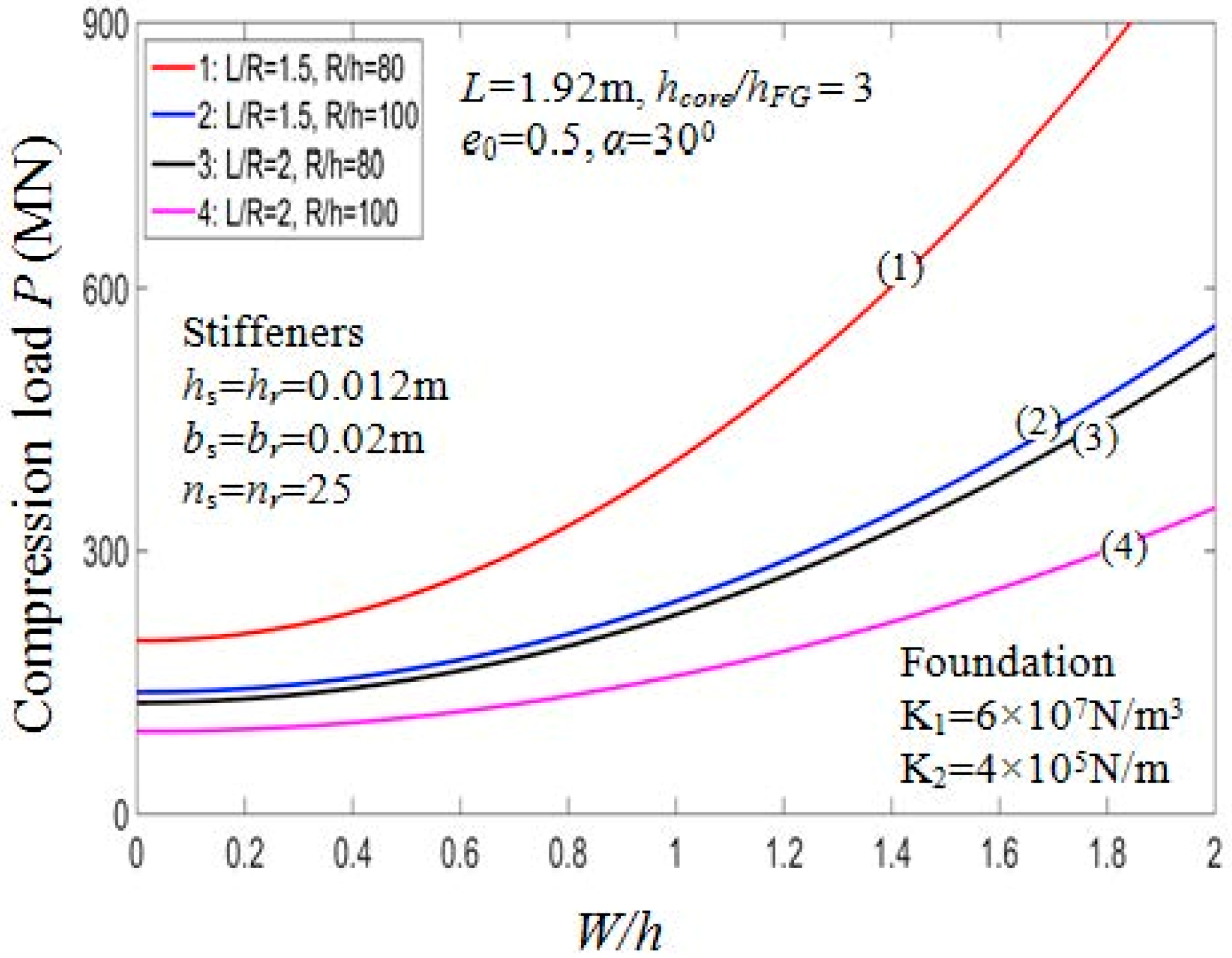
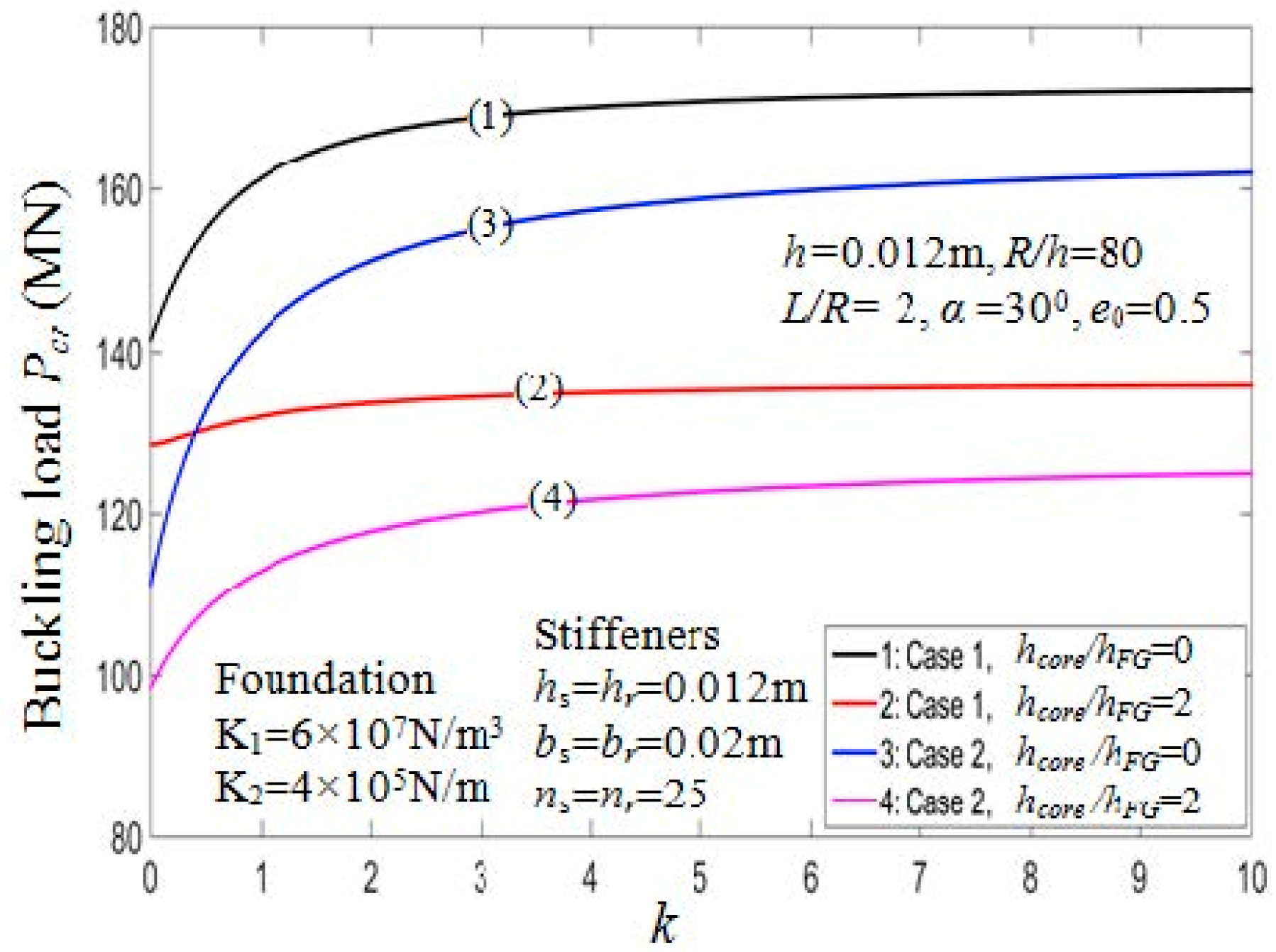
| Model | (m) | (°) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| M1 | 0.2; 0.5 | 100 | 0.01 | 1 to 80 | - | - | - | - | - |
| M2 | 2 | 150 | 0.05 | 30 | 0 to 5 | 0.02 | 0.03 | 50 | 30 |
| M3 | 2 | 150 | 0.01 | 45 | 0 to 8 | - | - | - | - |
| M4 | 2 | 80 | 0.012 | 30 | 3 | 0.02 | 0.012 | 35 | 25 |
| L/R = 0.2 | L/R = 0.5 | |||||
|---|---|---|---|---|---|---|
| Naj et al. [2] | Baruch et al. [42] | Present | Naj et al. [2] | Baruch et al. [42] | Present | |
| 1° | 1.005 (7) | 1.005 (7) | 1.0002 (1,12) a | 1.0017 (8) | 1.002 (8) | 1.0001 (2,17) |
| 5° | 1.006 (7) | 1.006 (7) | 1.0001 (1,12) | 1.001 (8) | 1.002 (8) | 1.0002 (2,17) |
| 10° | 1.007 (7) | 1.007 (7) | 1.0002 (1,12) | 1.000 (8) | 1.002 (8) | 1.0005 (2,17) |
| 30° | 1.0171 (5) | 1.017 (5) | 1.0017 (1,7) | 0.987 (7) | 1.001 (7) | 1.0023 (2,15) |
| 60° | 1.148 (0) | 1.144 (0) | 1.1299 (1,1) | 1.045 (7) | 1.044 (7) | 1.0150 (1,14) |
| 80° | 2.492 (0) | 2.477 (0) | 2.5091 (1,1) | 1.004 (5) | 1.015 (5) | 1.0266 (1,4) |
| Case 1 (Outside Stiffeners) | Case 2 (Inside Stiffeners) | |||
|---|---|---|---|---|
| hcore/hFG | Dung et al. [21] | Present | Dung et al. [21] | Present |
| 0 | 19.46667 (8,18) | 19.4667 (8,18) a | 19.14549 (7,21) | 19.1455 (7,21) |
| 0.5 | 16.12768 (8,16) | 16.1277 (8,16) | 15.79773 (6,22) | 15.7977 (6,22) |
| 1 | 14.09267 (8,16) | 14.0927 (8,16) | 13.76594 (6,22) | 13.7659 (6,22) |
| 2 | 11.74586 (8,15) | 11.7459 (8,15) | 11.42875 (6,22) | 11.4288 (6,22) |
| 3 | 10.43697 (8,16) | 10.4370 (8,16) | 10.12653 (6,22) | 10.1265 (6,22) |
| 4 | 9.60325 (8,16) | 9.6033 (8,16) | 9.29804 (6,22) | 9.2980 (6,22) |
| 5 | 9.02635 (8,16) | 9.0264 (8,16) | 8.72504 (6,22) | 8.7250 (6,22) |
| k = 1 | k = 2 | k = 5 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Deniz [43] | Present | Error | Deniz [43] | Present | Error | Deniz [43] | Present | Error | |
| hcore/hFG = 0 | 1.244 | 1.2914 (6,22) a | 3.7% | 1.314 | 1.3605 (6.22) | 3.4% | 1.390 | 1.4392 (6,22) | 3.4% |
| hcore/hFG = 2 | 1.190 | 1.1459 (6,22) | −3.8% | 1.246 | 1.2021 (6,22) | −3.7% | 1.297 | 1.2649 (6,22) | −3.8% |
| hcore/hFG = 4 | 1.135 | 1.0915 (6,22) | −3.8% | 1.178 | 1.1321 (6,22) | −3.5% | 1.217 | 1.1713 (6,22) | −3.9% |
| hcore/hFG = 6 | 1.105 | 1.0654 (6,23) | −3.6% | 1.139 | 1.1086 (6,22) | −2.7% | 1.171 | 1.1307 (6,22) | −3.6% |
| hcore/hFG = 8 | 1.085 | 1.0502 (6,23) | −3.2% | 1.113 | 1.0887 (6,22) | −2.2% | 1.140 | 1.0968 (6,22) | −3.9% |
| Pcr (MN) | Case 1: Outside Stiffener | Case 2: Inside Stiffener | ||||
|---|---|---|---|---|---|---|
| hcore/hFG = 0 | 161.4554 (7,1) | 161.4554 (7,1) | 161.4554 (7,1) | 142.5447 (5,16) | 142.5447 (5,16) | 142.5447 (5,16) |
| hcore/hFG = 0.5 | 152.0344 (7,1) | 148.6324 (7,1) | 145.2239 (7,1) | 133.1968 (5,15) | 129.6503 (5,15) | 126.1000 (5,18) |
| hcore/hFG = 1 | 146.3406 (7,1) | 140.9428 (7,1) | 135.5258 (7,1) | 127.5050 (5,15) | 121.9165 (5,15) | 116.3167 (5,15) |
| hcore/hFG = 2 | 139.6989 (7,1) | 131.9538 (7,1) | 124.1623 (7,1) | 120.9373 (5,15) | 112.9854 (5,15) | 105.0065 (5,15) |
| hcore/hFG = 3 | 135.9469 (7,1) | 126.8605 (7,1) | 117.7094 (7,1) | 117.3071 (5,15) | 108.0130 (5,15) | 98.6459 (5,15) |
| hcore/hFG = 4 | 133.5555 (7,1) | 123.5999 (7,1) | 113.5562 (7,1) | 114.9159 (5,15) | 104.7698 (5,15) | 94.5725 (5,15) |
| hcore/hFG = 5 | 131.8897 (7,1) | 121.3272 (7,1) | 110.6618 (7,1) | 113.2905 (5,15) | 102.5464 (5,15) | 91.7425 (5,15) |
| hcore/hFG = 10 | 127.8946 (7,1) | 115.8633 (7,1) | 103.6858 (7,1) | 109.4029 (5,15) | 97.2183 (5,15) | 84.9488 (5,15) |
| hcore/hFG = 20 | 125.4750 (7,1) | 112.5450 (7,1) | 99.4363 (7,1) | 107.0552 (5,15) | 93.9934 (5,15) | 80.8281 (5,15) |
| (MN) | Case 1: Outside Stiffener | Case 2: Inside Stiffener | ||
|---|---|---|---|---|
| α = 5° | 184.2470 (9,1) | 171.8857 (9,1) | 149.3844 (6,14) | 136.8875 (6,14) |
| α = 10° | 178.8700 (8,5) | 166.0860 (8,3) | 146.9110 (6,14) | 133.9463 (5,14) |
| α = 20° | 160.5859 (8,1) | 150.1258 (8,1) | 135.1141 (5,15) | 123.7183 (5,15) |
| α = 30° | 135.9469 (7,1) | 126.8605 (7,1) | 117.3071 (5,15) | 108.0130 (5,15) |
| α = 45° | 92.8172 (6,1) | 86.9674 (6,1) | 84.0426 (5,14) | 78.3735 (5,14) |
| α = 60° | 50.6289 (5,1) | 47.8436 (5,1) | 48.4738 (4,13) | 45.6781 (4,12) |
| α = 70° | 28.1649 (4,1) | 26.8487 (4,1) | 27.7523 (4,10) | 26.5536 (4,9) |
| α = 80° | 11.2994 (4,1) | 10.9997 (4,1) | 11.6098 (4,1) | 11.3076 (4,2) |
| (MN) | R/h = 60 | R/h = 80 | R/h = 100 | R/h = 200 | R/h = 300 |
|---|---|---|---|---|---|
| Case 1: Outside stiffeners | |||||
| L/R = 1 | 684.7950 (3,9) | 398.8262 (4,1) | 272.3611 (5,1) | 93.1743 (6,1) | 58.5103 (7,1) |
| L/R = 1.5 | 320.8777 (5,1) | 197.8373 (6,1) | 139.0107 (6,1) | 58.4647 (8,1) | 42.7500 (9,1) |
| L/R = 2 | 197.9920 (6,1) | 126.8605 (7,1) | 94.1463 (8,1) | 47.0167 (9,1) | 37.0240 (9,7) |
| L/R = 3 | 109.9757 (8,1) | 77.4973 (8,6) | 61.4766 (9,1) | 37.9004 (9,10) | 30.9346 (8,13) |
| Case 2: Inside stiffeners | |||||
| L/R = 1 | 648.9722 (3,11) | 379.1878 (3,14) | 255.0781 (4,14) | 82.7254 (5,20) | 50.4788 (6,23) |
| L/R = 1.5 | 297.5119 (4,12) | 177.0668 (4,15) | 122.2705 (5,16) | 47.5955 (6,20) | 33.5999 (7,21) |
| L/R = 2 | 175.2790 (4,14) | 108.0130 (5,15) | 77.5981 (5,16) | 35.7277 (6,18) | 26.9945 (7,19) |
| L/R = 3 | 89.9204 (5,14) | 60.0620 (6,15) | 46.3523 (6,15) | 26.2785 (7,16) | 21.2033 (7,16) |
| (MN) | Case 1: Outside Stiffener (k2 = k3 = 1/k) | Case 2: Inside Stiffener (k2 = k3 = k) | ||
|---|---|---|---|---|
| k = 0 | 135.4442 (7,1) | 126.2111 (7,1) | 105.4436 (5,16) | 96.2521 (5,15) |
| k = 1 | 135.9469 (7,1) | 126.8605 (7,1) | 117.3071 (5,15) | 108.0130 (5,15) |
| k = 5 | 137.5855 (7,1) | 128.5525 (7,1) | 125.4939 (5,15) | 116.1792 (5,15) |
| k = 10 | 137.9374 (7,1) | 128.9140 (7,1) | 127.4802 (5,15) | 118.1596 (5,15) |
| k = ∞ | 138.3158 (7,1) | 129.3029 (7,1) | 130.0065 (5,15) | 120.6781 (5,15) |
| (MN) | ||||
|---|---|---|---|---|
| Case 1: Conical Shell Reinforced by Outside Stiffener | ||||
| ns = 0, nr = 0 | 81.8418 (5,16) | 86.4019 (7,4) | 90.1237 (7,4) | 93.8390 (7,3) |
| ns = 50, nr = 0 | 96.7739 (2,16) | 110.7194 (4,17) | 118.5695 (5,14) | 124.6769 (5,14) |
| ns = 0, nr = 50 | 111.2085 (8,1) | 114.4478 (8,1) | 117.6871 (8,1) | 120.9264 (8,1) |
| ns = 25, nr = 25 | 119.4573 (7,1) | 123.1589 (7,1) | 126.8605 (7,1) | 130.5622 (7,1) |
| ns = 50, nr = 50 | 153.6013 (6,9) | 157.5907 (7,1) | 161.2924 (7,1) | 164.9940 (7,1) |
| Case 2: Conical Shell Reinforced by Inside Stiffener | ||||
| ns = 0, nr = 0 | 81.8418 (5,16) | 86.4019 (7,4) | 90.1237 (7,4) | 93.8390 (7,3) |
| ns = 50, nr = 0 | 85.6480 (2,16) | 101.4708 (3,17) | 111.2717 (4,17) | 120.2202 (4,17) |
| ns = 0, nr = 50 | 84.7967 (6,15) | 89.6205 (6,15) | 94.4443 (6,15) | 99.2681 (6,15) |
| ns = 25, nr = 25 | 94.3881 (4,15) | 101.8290 (5,15) | 108.0130 (5,15) | 114.1970 (5,15) |
| ns = 50, nr = 50 | 103.4412 (4,14) | 112.0060 (4,14) | 120.2306 (5,15) | 126.4147 (5,15) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thai, D.-K.; Tu, T.M.; Hoa, L.K.; Hung, D.X.; Linh, N.N. Nonlinear Stability Analysis of Eccentrically Stiffened Functionally Graded Truncated Conical Sandwich Shells with Porosity. Materials 2018, 11, 2200. https://doi.org/10.3390/ma11112200
Thai D-K, Tu TM, Hoa LK, Hung DX, Linh NN. Nonlinear Stability Analysis of Eccentrically Stiffened Functionally Graded Truncated Conical Sandwich Shells with Porosity. Materials. 2018; 11(11):2200. https://doi.org/10.3390/ma11112200
Chicago/Turabian StyleThai, Duc-Kien, Tran Minh Tu, Le Kha Hoa, Dang Xuan Hung, and Nguyen Ngọc Linh. 2018. "Nonlinear Stability Analysis of Eccentrically Stiffened Functionally Graded Truncated Conical Sandwich Shells with Porosity" Materials 11, no. 11: 2200. https://doi.org/10.3390/ma11112200





