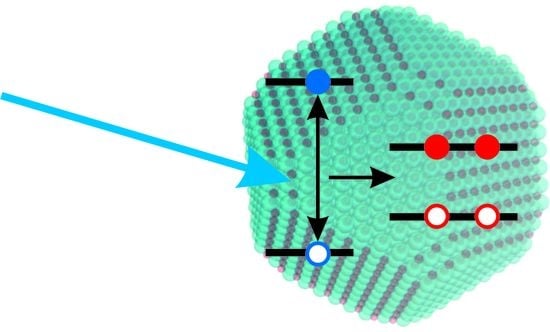
Carrier Multiplication Mechanisms and Competing Processes in Colloidal Semiconductor Nanostructures
Abstract
:1. Introduction
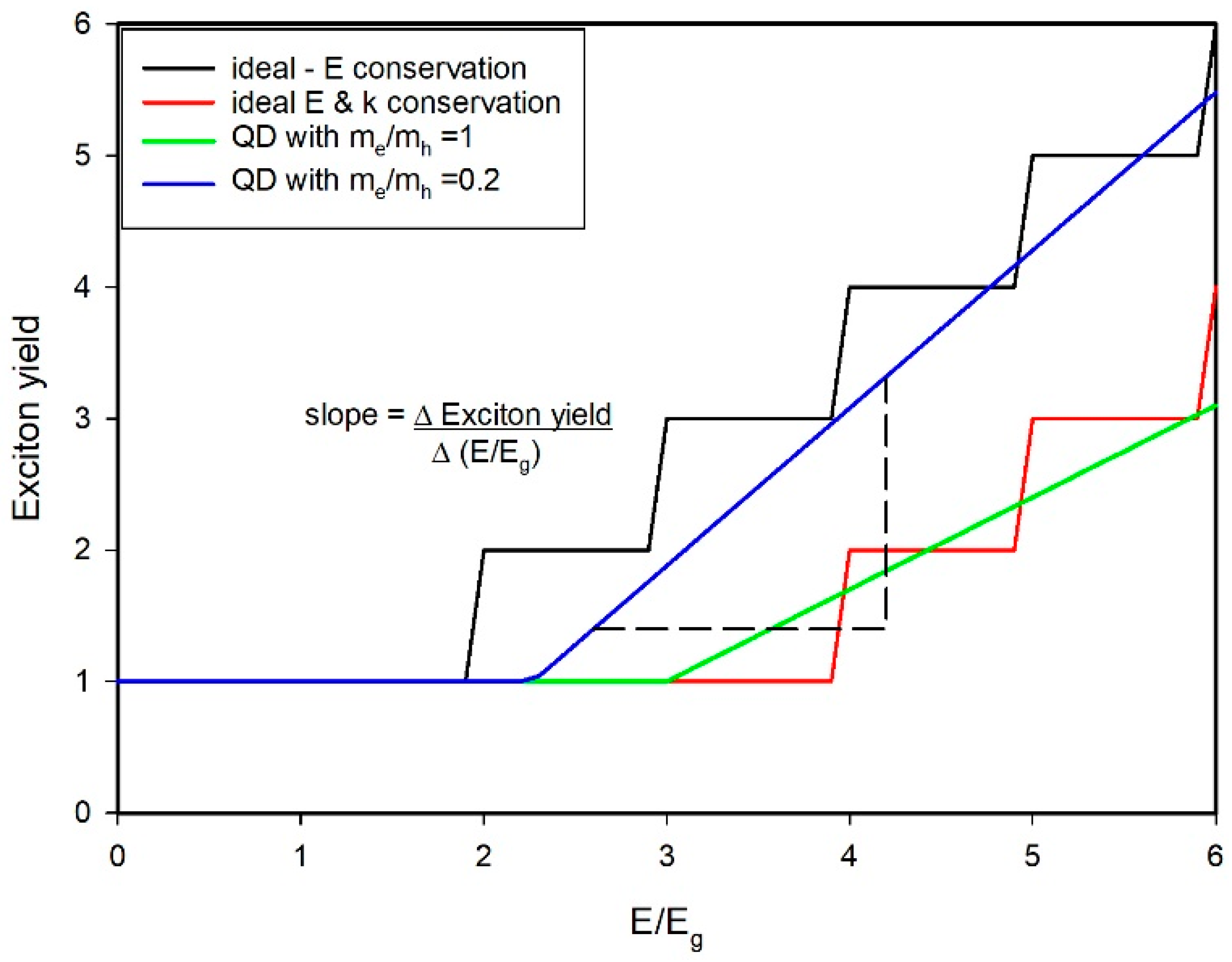
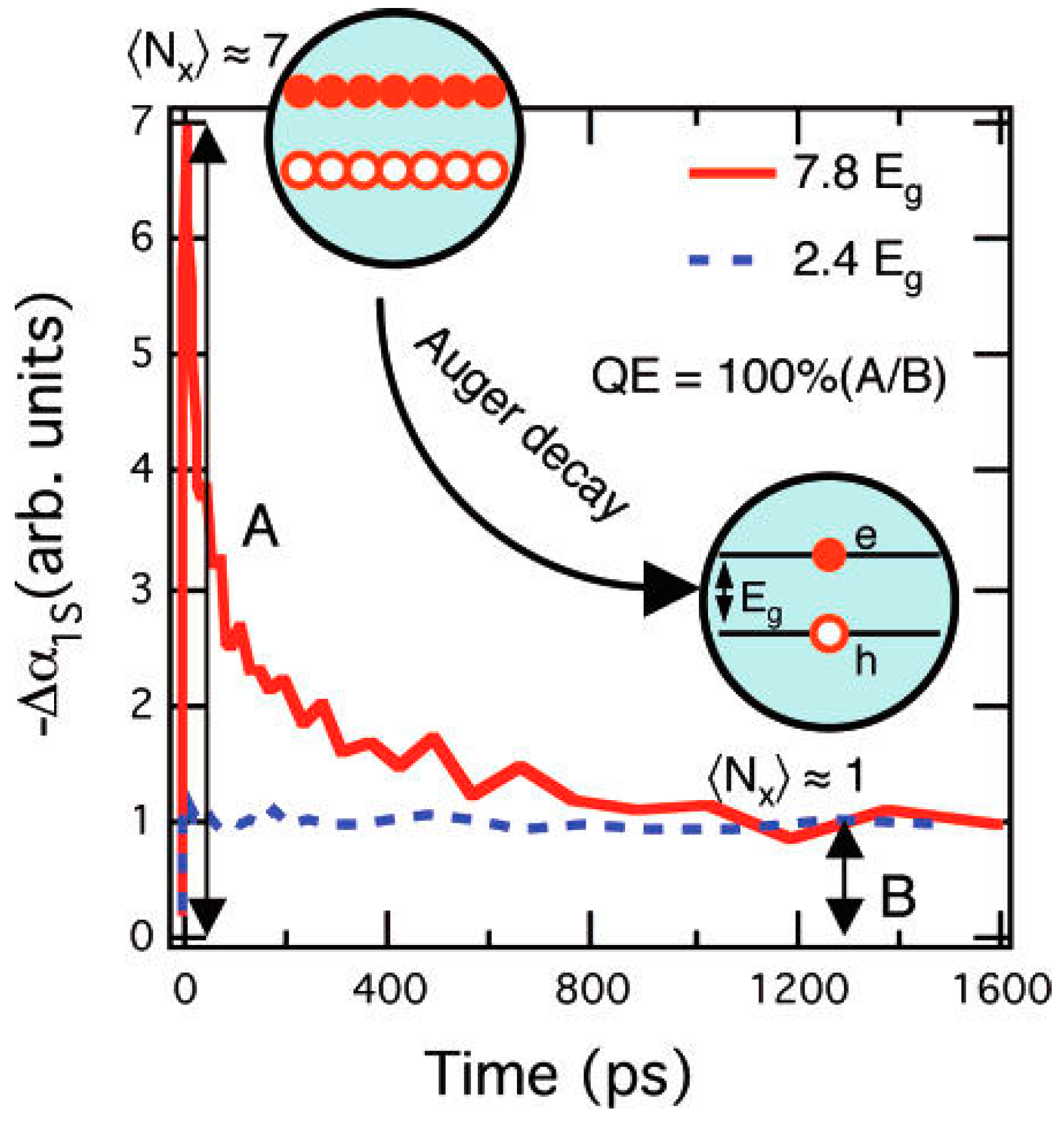
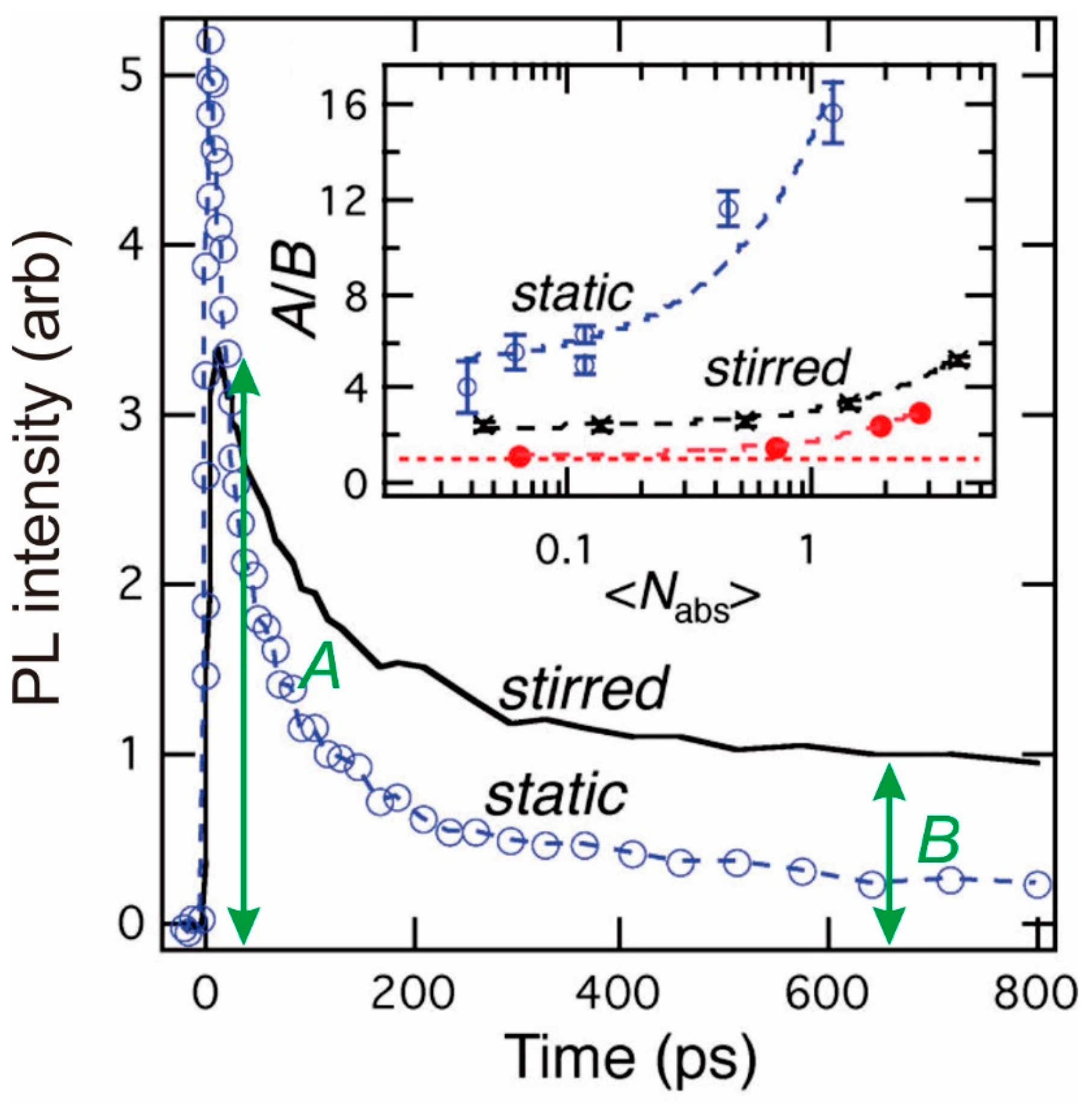
2. CM Quantum Yield Measurements
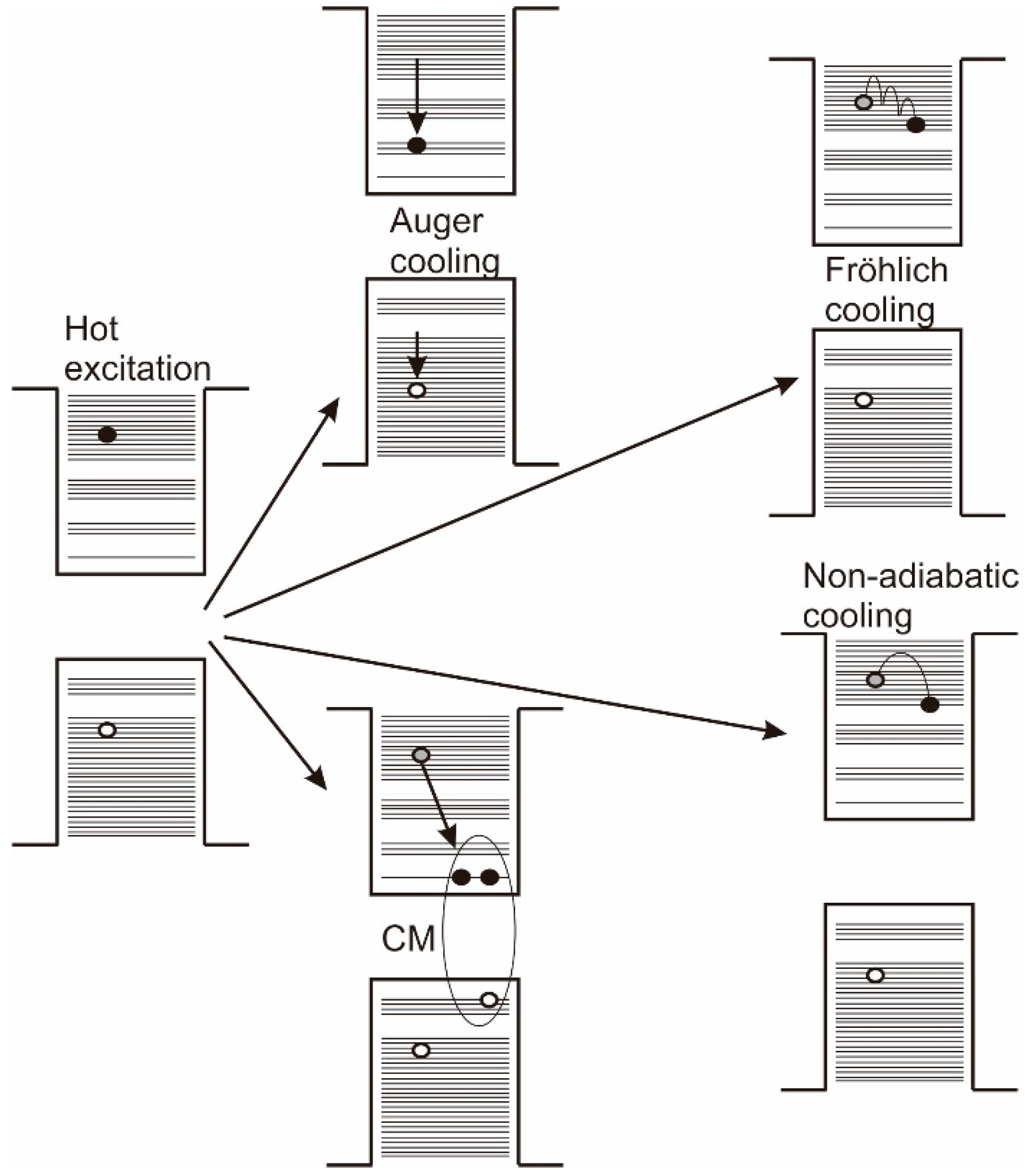
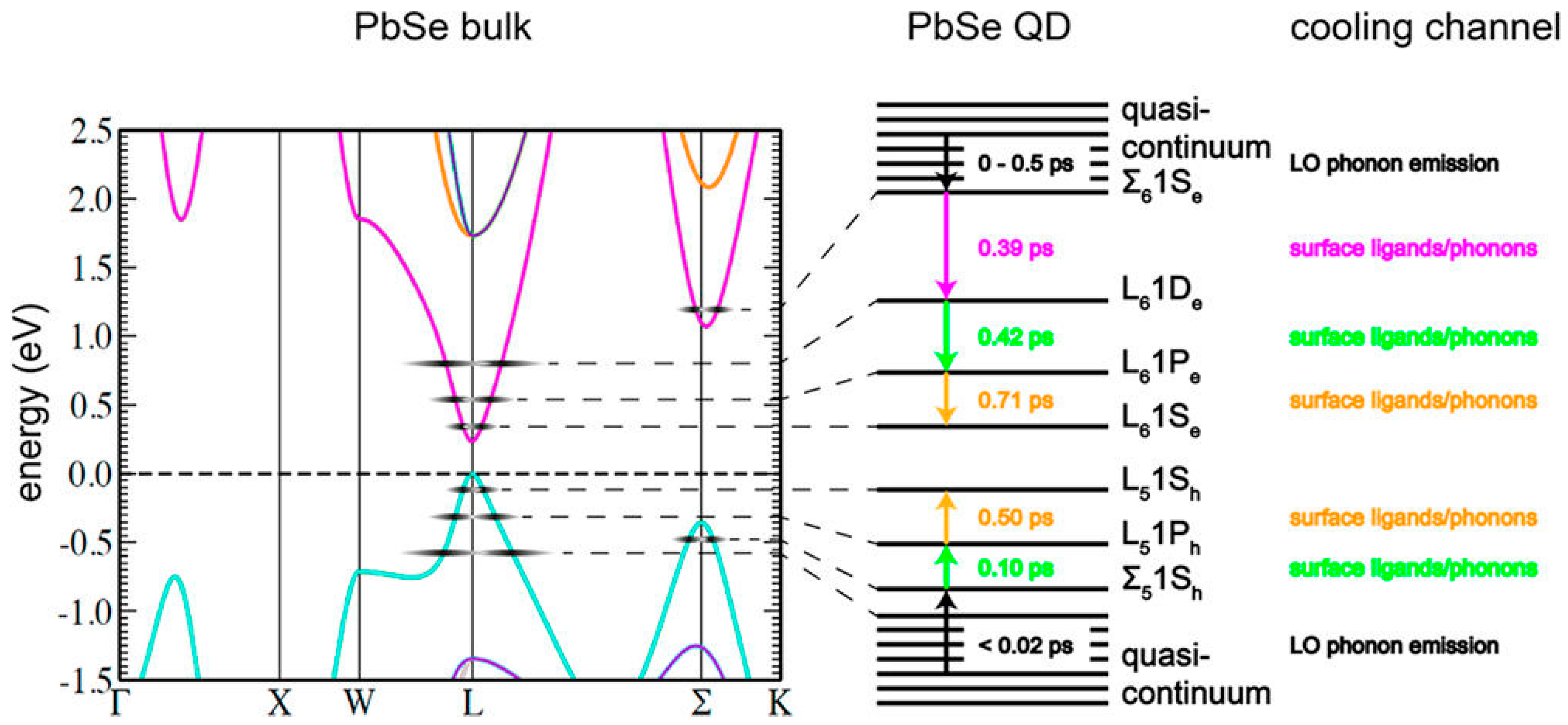
3. Carrier Cooling and CM Efficiency
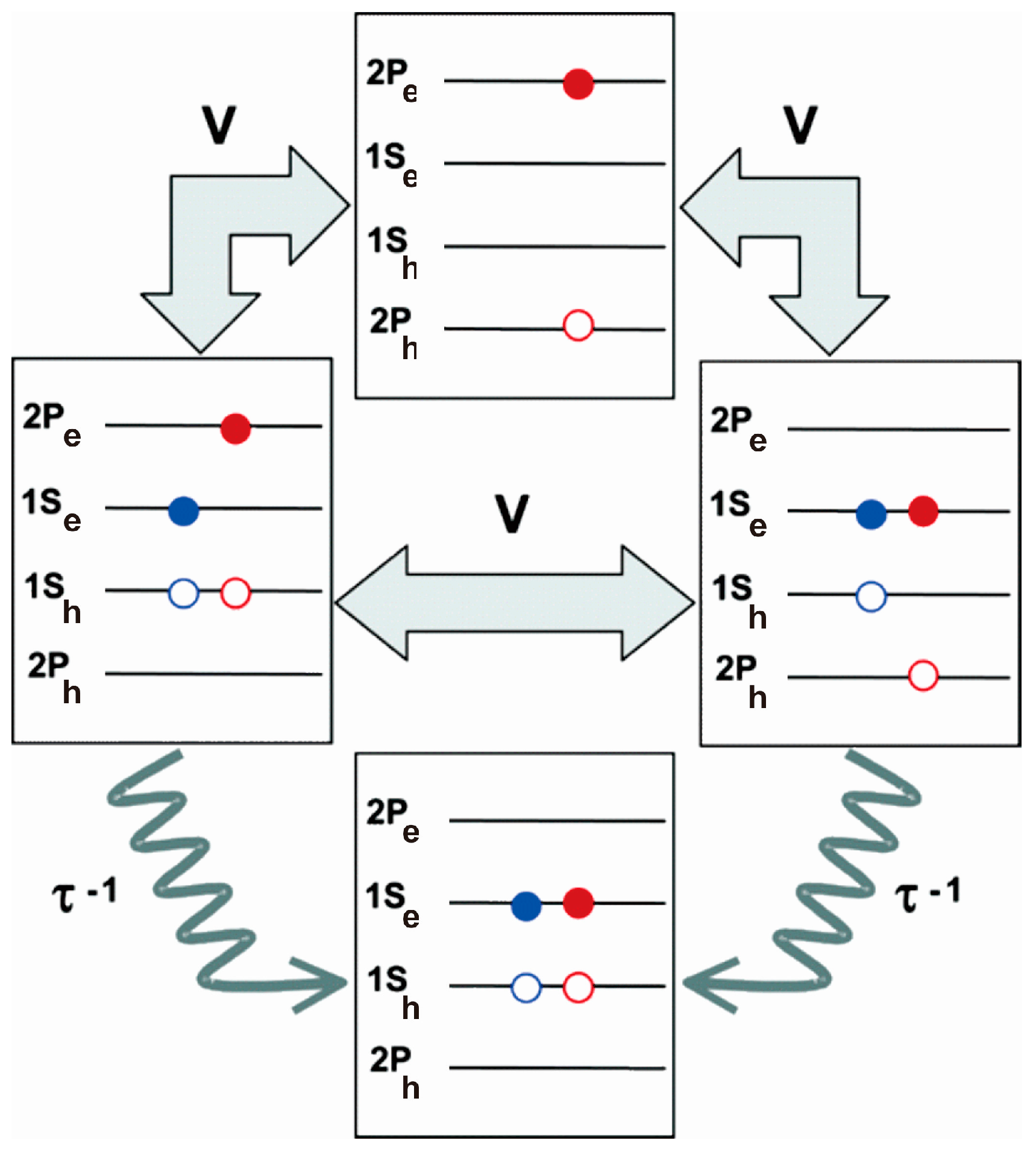
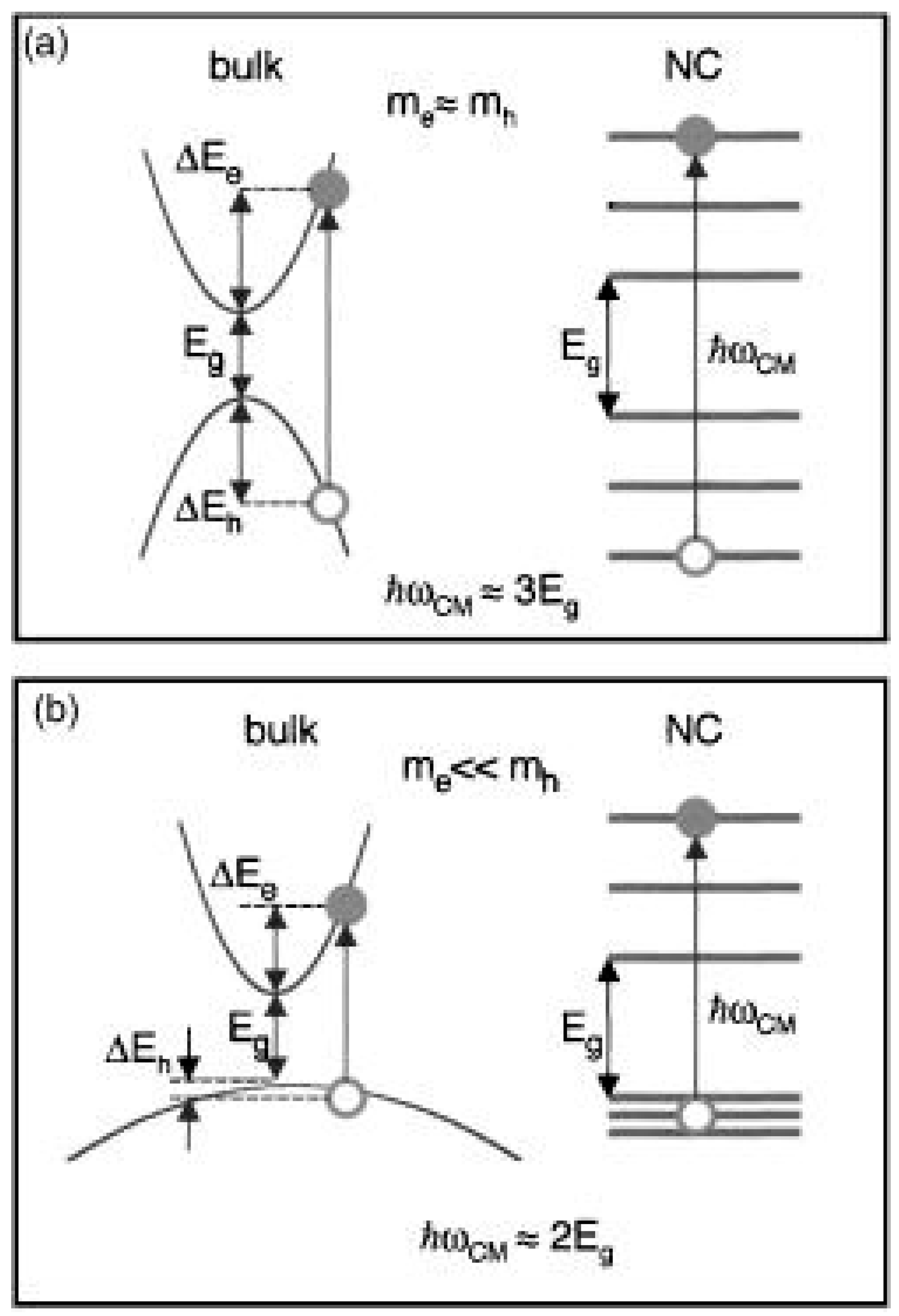
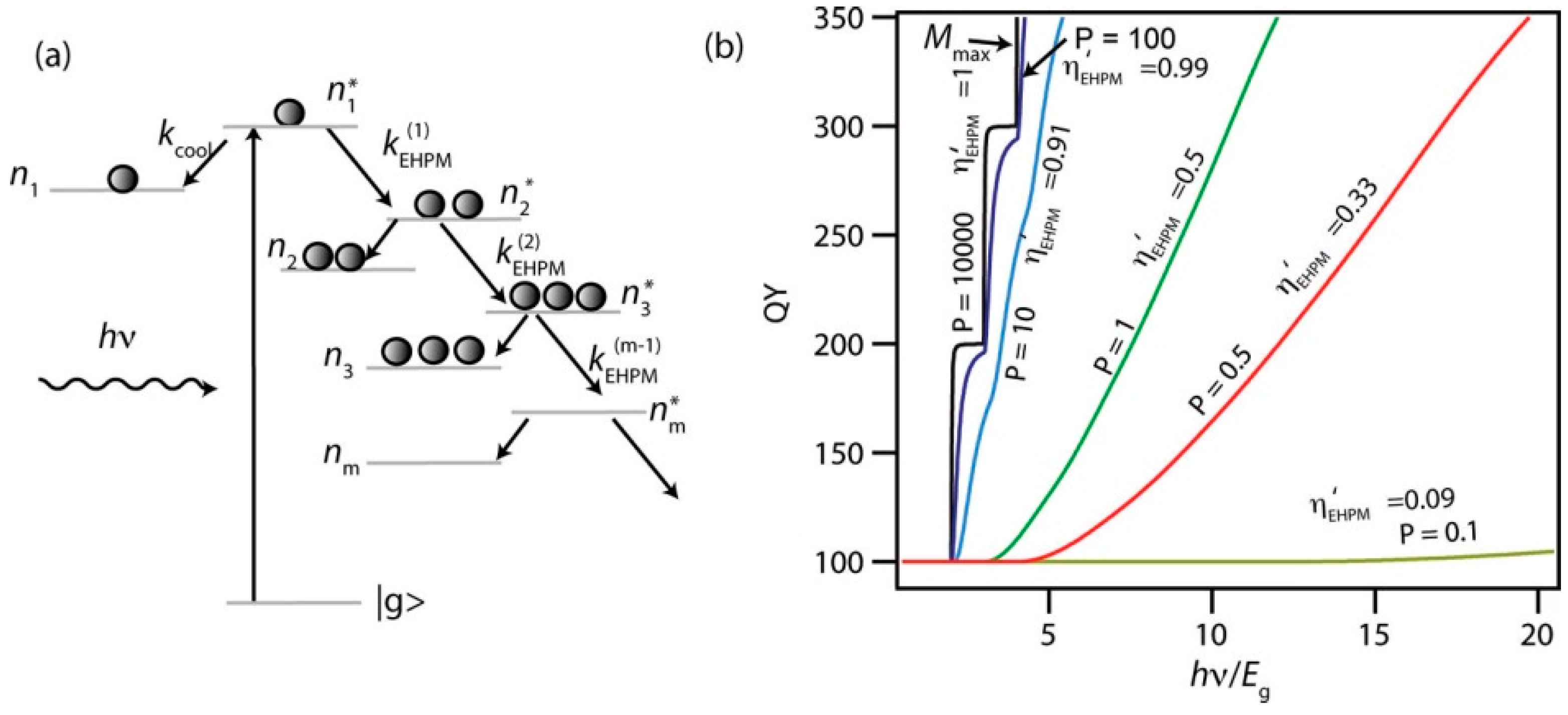
4. CM Mechanisms
5. Engineering Nanostructures to Influence the CM/Cooling Competition
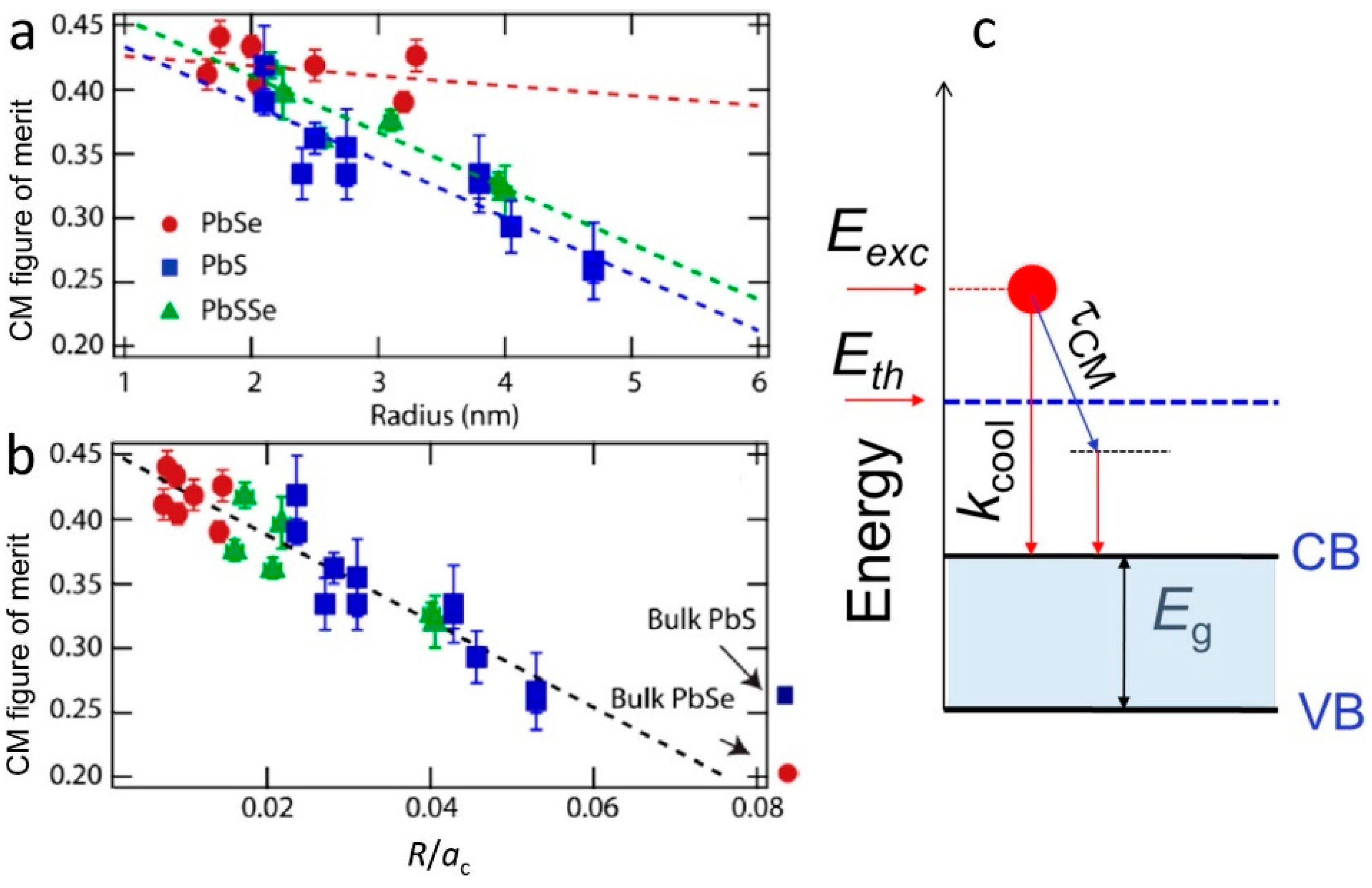
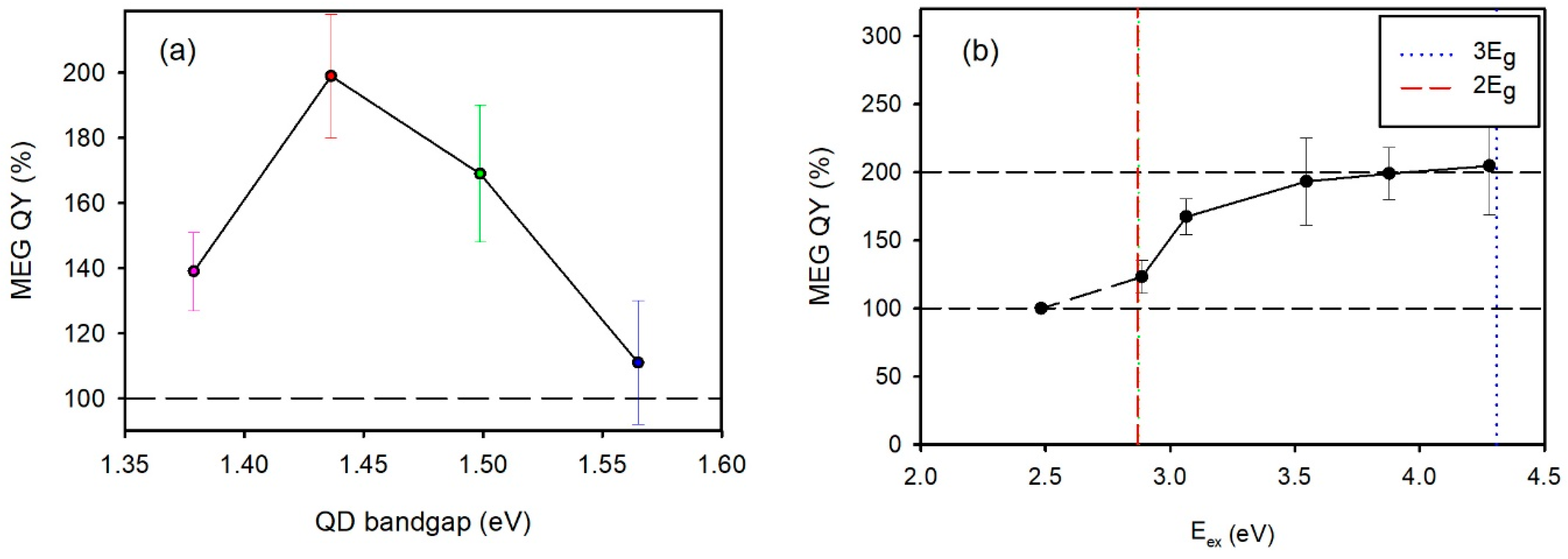
5.1. Size Effects
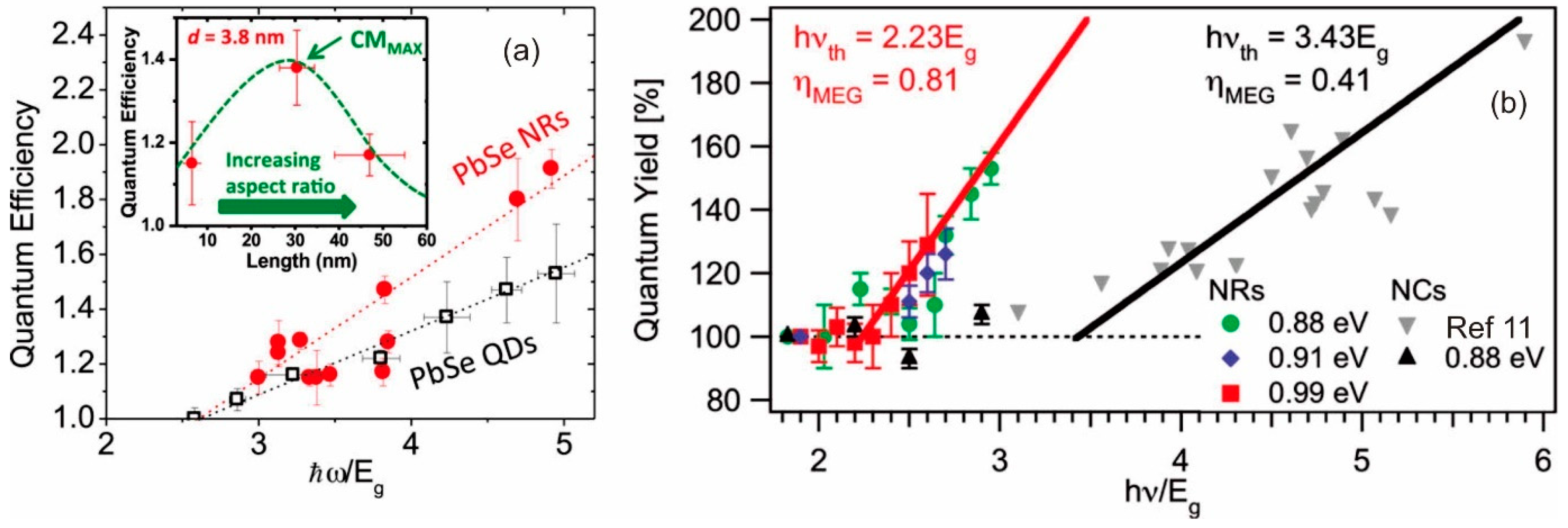
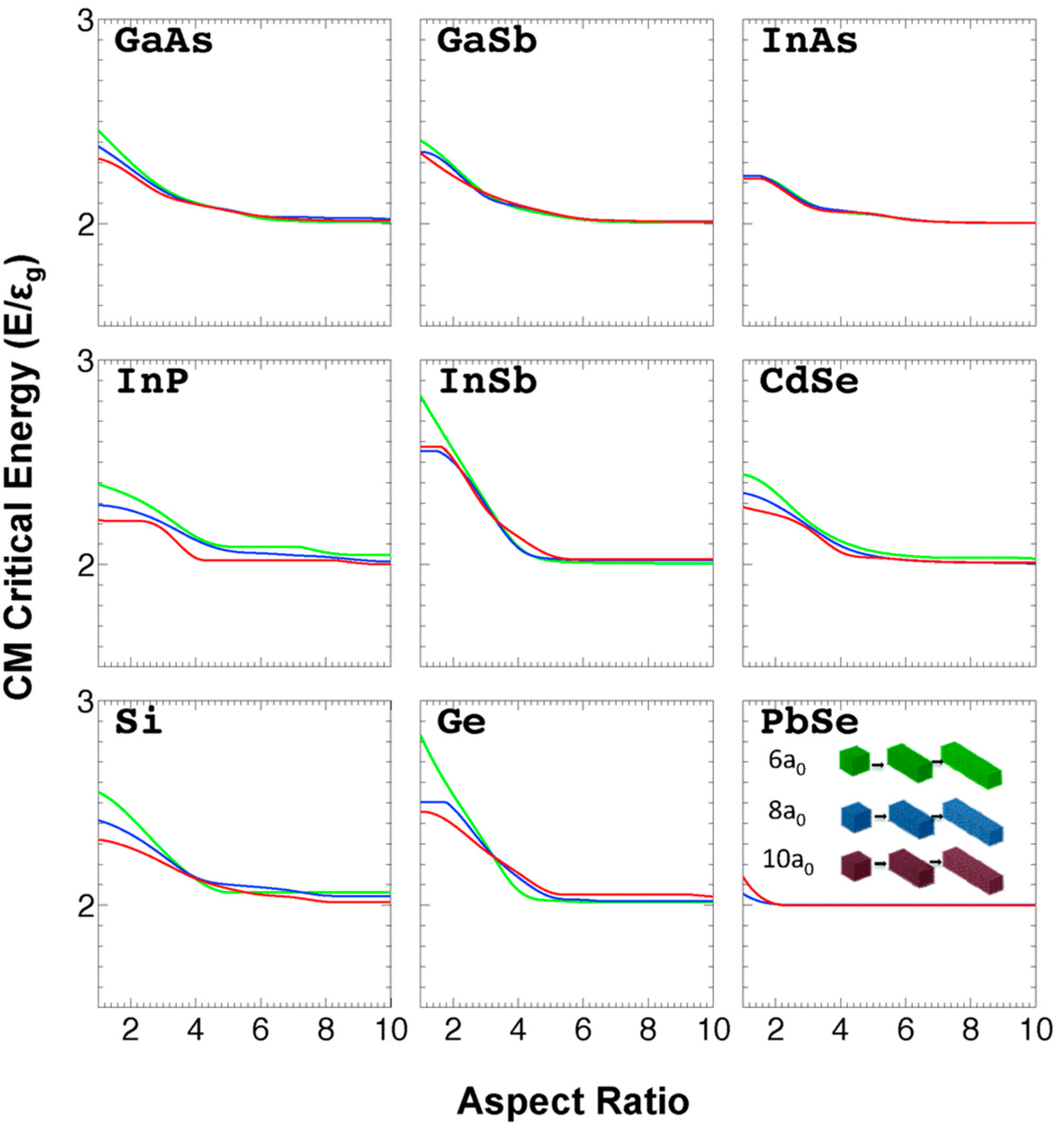
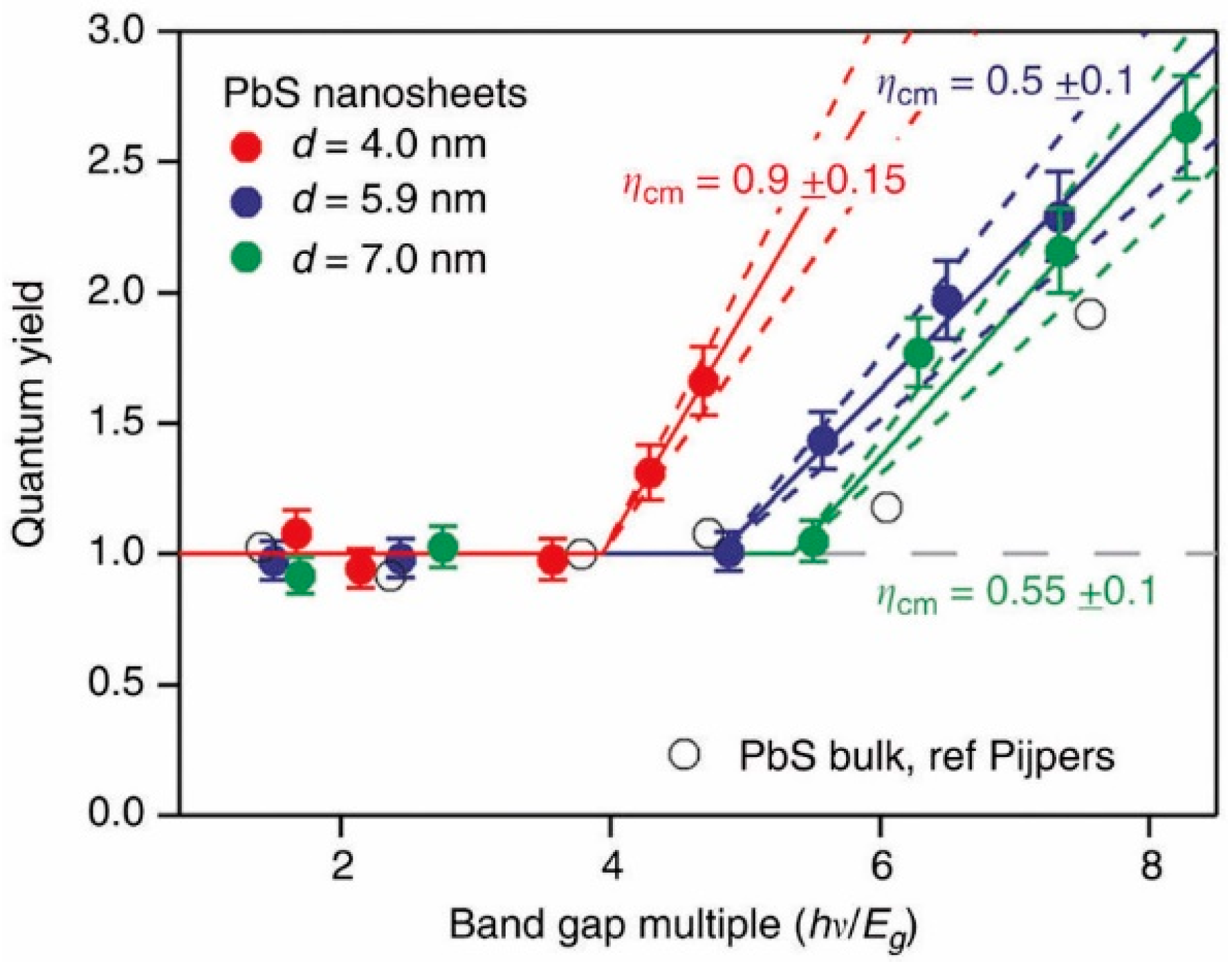
5.2. Shape and Dimensionality Effects
5.3. Heterostructures
5.4. Surface Effects
5.5. Doping/Photodoping Effects
5.6. Alloy Composition Effects
6. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Landsberg, P.T. Recombination in Semiconductors; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Capasso, F. Physics of Avalanche Photodiodes; Academic Press: London, UK, 1985; Volume 22 D. [Google Scholar]
- Pietryga, J.M.; Park, Y.-S.; Lim, J.; Fidler, A.F.; Bae, W.K.; Brovelli, S.; Klimov, V.I. Spectroscopic and device aspects of nanocrystal quantum dots. Chem. Rev. 2016, 116, 10513–10622. [Google Scholar] [CrossRef] [PubMed]
- Hildebrand, O.; Kuebart, W.; Benz, K.; Pilkuhn, M. Ga1−xAlxSb avalanche photodiodes: Resonant impact ionization with very high ratio of ionization coefficients. IEEE J. Quantum Electron. 1981, 17, 284–288. [Google Scholar] [CrossRef]
- Hollenhorst, J.N.; Webster, J.G. Avalanche diodes. In Wiley Encyclopedia of Electrical and Electronics Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1999. [Google Scholar]
- Ripoche, G.; Harari, J. Avalanche photodiodes. In Optoelectronic Sensors; ISTE: Washington, DC, USA, 2010; pp. 58–109. [Google Scholar]
- Nozik, A.J. Multiple exciton generation in semiconductor quantum dots. Chem. Phys. Lett. 2008, 457, 3–11. [Google Scholar] [CrossRef]
- Kolodinski, S.; Werner, J.H.; Wittchen, T.; Queisser, H.J. Quantum efficiencies exceeding unity due to impact ionization in silicon solar cells. Appl. Phys. Lett. 1993, 63, 2405–2407. [Google Scholar] [CrossRef]
- Ellingson, R.J.; Beard, M.C.; Johnson, J.C.; Yu, P.; Micic, O.I.; Nozik, A.J.; Shabaev, A.; Efros, A.L. Highly efficient multiple exciton generation in colloidal PbSe and PbS quantum dots. Nano Lett. 2005, 5, 865–871. [Google Scholar] [CrossRef] [PubMed]
- Wolf, M.; Brendel, R.; Werner, J.H.; Queisser, H.J. Solar cell efficiency and carrier multiplication in Si1−xGex alloys. J. Appl. Phys. 1998, 83, 4213–4221. [Google Scholar] [CrossRef]
- Beard, M.C.; Midgett, A.G.; Hanna, M.C.; Luther, J.M.; Hughes, B.K.; Nozik, A.J. Comparing multiple exciton generation in quantum dots to impact ionization in bulk semiconductors: Implications for enhancement of solar energy conversion. Nano Lett. 2010, 10, 3019–3027. [Google Scholar] [CrossRef] [PubMed]
- Shockley, W.; Queisser, H.J. Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Binks, D.J. Multiple exciton generation in nanocrystal quantum dots—Controversy, current status and future prospects. Phys. Chem. Chem. Phys. 2011, 13, 12693–12704. [Google Scholar] [CrossRef] [PubMed]
- Nair, G.; Chang, L.-Y.; Geyer, S.M.; Bawendi, M.G. Perspective on the prospects of a carrier multiplication nanocrystal solar cell. Nano Lett. 2011, 11, 2145–2151. [Google Scholar] [CrossRef] [PubMed]
- Semonin, O.E.; Luther, J.M.; Choi, S.; Chen, H.-Y.; Gao, J.; Nozik, A.J.; Beard, M.C. Peak external photocurrent quantum efficiency exceeding 100% via MEG in a quantum dot solar cell. Science 2011, 334, 1530–1533. [Google Scholar] [CrossRef] [PubMed]
- Nozik, A.J. Spectroscopy and hot electron relaxation dynamics in semiconductor quantum wells and quantum dots. Annu. Rev. Phys. Chem. 2001, 52, 193–231. [Google Scholar] [CrossRef] [PubMed]
- Nelson, C.A.; Monahan, N.R.; Zhu, X.Y. Exceeding the Shockley-Queisser limit in solar energy conversion. Energy Environ. Sci. 2013, 6, 3508–3519. [Google Scholar] [CrossRef]
- Shabaev, A.; Hellberg, C.S.; Efros, A.L. Efficiency of multiexciton generation in colloidal nanostructures. Acc. Chem. Res. 2013, 46, 1242–1251. [Google Scholar] [CrossRef] [PubMed]
- McGuire, J.A.; Sykora, M.; Robel, I.; Padilha, L.A.; Joo, J.; Pietryga, J.M.; Klimov, V.I. Spectroscopic signatures of photocharging due to hot-carrier transfer in solutions of semiconductor nanocrystals under low-intensity ultraviolet excitation. ACS Nano 2010, 4, 6087–6097. [Google Scholar] [CrossRef] [PubMed]
- Dennis, A.M.; Mangum, B.D.; Piryatinski, A.; Park, Y.-S.; Hannah, D.C.; Casson, J.L.; Williams, D.J.; Schaller, R.D.; Htoon, H.; Hollingsworth, J.A. Suppressed blinking and Auger recombination in near-infrared type-II InP/CdS nanocrystal quantum dots. Nano Lett. 2012, 12, 5545–5551. [Google Scholar] [CrossRef] [PubMed]
- Padilha, L.A.; Stewart, J.T.; Sandberg, R.L.; Bae, W.K.; Koh, W.-K.; Pietryga, J.M.; Klimov, V.I. Aspect ratio dependence of Auger recombination and carrier multiplication in PbSe nanorods. Nano Lett. 2013, 13, 1092–1099. [Google Scholar] [CrossRef] [PubMed]
- Kunneman, L.T.; Tessier, M.D.; Heuclin, H.; Dubertret, B.; Aulin, Y.V.; Grozema, F.C.; Schins, J.M.; Siebbeles, L.D.A. Bimolecular Auger recombination of electron—Hole pairs in two-dimensional CdSe and CdSe/CdZnS core/shell nanoplatelets. J. Phys. Chem. Lett. 2013, 4, 3574–3578. [Google Scholar] [CrossRef]
- Klimov, V.I.; McGuire, J.A.; Schaller, R.D.; Rupasov, V.I. Scaling of multiexciton lifetimes in semiconductor nanocrystals. Phys. Rev. B 2008, 77, 195324. [Google Scholar] [CrossRef]
- Klimov, V.I.; McBranch, D.W.; Leatherdale, C.A.; Bawendi, M.G. Electron and hole relaxation pathways in semiconductor quantum dots. Phys. Rev. B 1999, 60, 13740–13749. [Google Scholar] [CrossRef]
- Shen, Q.; Katayama, K.; Toyoda, T. Characterization of hot carrier cooling and multiple exciton generation dynamics in PbS QDs using an improved transient grating technique. J. Energy Chem. 2015, 24, 712–716. [Google Scholar] [CrossRef]
- Nair, G.; Geyer, S.M.; Chang, L.-Y.; Bawendi, M.G. Carrier multiplication yields in PbS and PbSe nanocrystals measured by transient photoluminescence. Phys. Rev. B 2008, 78, 125325. [Google Scholar] [CrossRef]
- Ten Cate, S.; Liu, Y.; Suchand Sandeep, C.S.; Kinge, S.; Houtepen, A.J.; Savenije, T.J.; Schins, J.M.; Law, M.; Siebbeles, L.D.A. Activating carrier multiplication in PbSe quantum dot solids by infilling with atomic layer deposition. J. Phys. Chem. Lett. 2013, 4, 1766–1770. [Google Scholar] [CrossRef] [PubMed]
- Klimov, V.I. Mechanisms for photogeneration and recombination of multiexcitons in semiconductor nanocrystals: Implications for lasing and solar energy conversion. J. Phys. Chem. B 2006, 110, 16827–16845. [Google Scholar] [CrossRef] [PubMed]
- Califano, M. Direct and inverse Auger processes in InAs nanocrystals: Can the decay signature of a trion be mistaken for carrier multiplication? ACS Nano 2009, 3, 2706–2714. [Google Scholar] [CrossRef] [PubMed]
- Pijpers, J.J.H.; Hendry, E.; Milder, M.T.W.; Fanciulli, R.; Savolainen, J.; Herek, J.L.; Vanmaekelbergh, D.; Ruhman, S.; Mocatta, D.; Oron, D.; et al. Carrier multiplication and its reduction by photodoping in colloidal InAs quantum dots. J. Phys. Chem. C 2007, 111, 4146–4152. [Google Scholar] [CrossRef]
- Ben-Lulu, M.; Mocatta, D.; Bonn, M.; Banin, U.; Ruhman, S. On the absence of detectable carrier multiplication in a transient absorption study of InAs/CdSe/ZnSe core/shell1/shell2 quantum dots. Nano Lett. 2008, 8, 1207–1211. [Google Scholar] [CrossRef] [PubMed]
- Nair, G.; Bawendi, M.G. Carrier multiplication yields of CdSe and CdTe nanocrystals by transient photoluminescence spectroscopy. Phys. Rev. B 2007, 76, 081304. [Google Scholar] [CrossRef]
- McGuire, J.A.; Sykora, M.; Joo, J.; Pietryga, J.M.; Klimov, V.I. Apparent versus true carrier multiplication yields in semiconductor nanocrystals. Nano Lett. 2010, 10, 2049–2057. [Google Scholar] [CrossRef] [PubMed]
- Isborn, C.M.; Prezhdo, O.V. Charging quenches multiple exciton generation in semiconductor nanocrystals: First-principles calculations on small PbSe clusters. J. Phys. Chem. C 2009, 113, 12617–12621. [Google Scholar] [CrossRef]
- Trinh, M.T.; Houtepen, A.J.; Schins, J.M.; Hanrath, T.; Piris, J.; Knulst, W.; Goossens, A.P.L.M.; Siebbeles, L.D.A. In spite of recent doubts carrier multiplication does occur in PbSe nanocrystals. Nano Lett. 2008, 8, 1713–1718. [Google Scholar] [CrossRef] [PubMed]
- Schaller, R.D.; Sykora, M.; Pietryga, J.M.; Klimov, V.I. Seven excitons at a cost of one: Redefining the limits for conversion efficiency of photons into charge carriers. Nano Lett. 2006, 6, 424–429. [Google Scholar] [CrossRef] [PubMed]
- Gdor, I.; Sachs, H.; Roitblat, A.; Strasfeld, D.B.; Bawendi, M.G.; Ruhman, S. Exploring exciton relaxation and multiexciton generation in PbSe nanocrystals using hyperspectral near-IR probing. ACS Nano 2012, 6, 3269–3277. [Google Scholar] [CrossRef] [PubMed]
- Miaja-Avila, L.; Tritsch, J.R.; Wolcott, A.; Chan, W.L.; Nelson, C.A.; Zhu, X.Y. Direct mapping of hot-electron relaxation and multiplication dynamics in PbSe quantum dots. Nano Lett. 2012, 12, 1588–1591. [Google Scholar] [CrossRef] [PubMed]
- Beard, M.C.; Midgett, A.G.; Law, M.; Semonin, O.E.; Ellingson, R.J.; Nozik, A.J. Variations in the quantum efficiency of multiple exciton generation for a series of chemically treated PbSe nanocrystal films. Nano Lett. 2009, 9, 836–845. [Google Scholar] [CrossRef] [PubMed]
- Sandberg, R.L.; Padilha, L.A.; Qazilbash, M.M.; Bae, W.K.; Schaller, R.D.; Pietryga, J.M.; Stevens, M.J.; Baek, B.; Nam, S.W.; Klimov, V.I. Multiexciton dynamics in infrared-emitting colloidal nanostructures probed by a superconducting nanowire single-photon detector. ACS Nano 2012, 6, 9532–9540. [Google Scholar] [CrossRef] [PubMed]
- Stewart, J.T.; Padilha, L.A.; Bae, W.K.; Koh, W.-K.; Pietryga, J.M.; Klimov, V.I. Carrier multiplication in quantum dots within the framework of two competing energy relaxation mechanisms. J. Phys. Chem. Lett. 2013, 4, 2061–2068. [Google Scholar] [CrossRef] [PubMed]
- Stewart, J.T.; Padilha, L.A.; Qazilbash, M.M.; Pietryga, J.M.; Midgett, A.G.; Luther, J.M.; Beard, M.C.; Nozik, A.J.; Klimov, V.I. Comparison of carrier multiplication yields in PbS and PbSe nanocrystals: The role of competing energy-loss processes. Nano Lett. 2012, 12, 622–628. [Google Scholar] [CrossRef] [PubMed]
- Kilina, S.V.; Craig, C.F.; Kilin, D.S.; Prezhdo, O.V. Ab initio time-domain study of phonon-assisted relaxation of charge carriers in a PbSe quantum dot. J. Phys. Chem. C 2007, 111, 4871–4878. [Google Scholar] [CrossRef]
- Califano, M. Model-independent determination of the carrier multiplication time constant in CdSe nanocrystals. Phys. Chem. Chem. Phys. 2009, 11, 10180–10184. [Google Scholar] [CrossRef] [PubMed]
- Califano, M. Electron relaxation following uv excitation in CdSe nanocrystals: Sub-picosecond-fast population of the 1P states across a gap wider than 10 phonon energies. J. Phys. Chem. C 2009, 113, 19859–19862. [Google Scholar] [CrossRef]
- Neukirch, A.J.; Prezhdo, O.V. Chapter 2 Charge and exciton dynamics in semiconductor quantum dots: A time domain, ab initio view. In Solar Energy Conversion: Dynamics of Interfacial Electron and Excitation Transfer; The Royal Society of Chemistry: London, UK, 2013; pp. 37–76. [Google Scholar]
- Schaller, R.D.; Pietryga, J.M.; Goupalov, S.V.; Petruska, M.A.; Ivanov, S.A.; Klimov, V.I. Breaking the phonon bottleneck in semiconductor nanocrystals via multiphonon emission induced by intrinsic nonadiabatic interactions. Phys. Rev. Lett. 2005, 95, 196401. [Google Scholar] [CrossRef] [PubMed]
- Klimov, V.I.; McBranch, D.W. Femtosecond 1p-to-1s electron relaxation in strongly confined semiconductor nanocrystals. Phys. Rev. Lett. 1998, 80, 4028–4031. [Google Scholar] [CrossRef]
- Ten Cate, S.; Liu, Y.; Schins, J.M.; Law, M.; Siebbeles, L.D.A. Phonons do not assist carrier multiplication in PbSe quantum dot solids. J. Phys. Chem. Lett. 2013, 4, 3257–3262. [Google Scholar] [CrossRef]
- Stolle, C.J.; Schaller, R.D.; Korgel, B.A. Efficient carrier multiplication in colloidal CuInSe2 nanocrystals. J. Phys. Chem. Lett. 2014, 5, 3169–3174. [Google Scholar] [CrossRef] [PubMed]
- Harbold, J.M.; Du, H.; Krauss, T.D.; Cho, K.-S.; Murray, C.B.; Wise, F.W. Time-resolved intraband relaxation of strongly confined electrons and holes in colloidal PbSe nanocrystals. Phys. Rev. B 2005, 72, 195312. [Google Scholar] [CrossRef]
- Yu, P.; Nedeljkovic, J.M.; Ahrenkiel, P.A.; Ellingson, R.J.; Nozik, A.J. Size dependent femtosecond electron cooling dynamics in CdSe quantum rods. Nano Lett. 2004, 4, 1089–1092. [Google Scholar] [CrossRef]
- Spoor, F.C.M.; Kunneman, L.T.; Evers, W.H.; Renaud, N.; Grozema, F.C.; Houtepen, A.J.; Siebbeles, L.D.A. Hole cooling is much faster than electron cooling in PbSe quantum dots. ACS Nano 2016, 10, 695–703. [Google Scholar] [CrossRef] [PubMed]
- Spoor, F.C.M.; Tomić, S.; Houtepen, A.J.; Siebbeles, L.D.A. Broadband cooling spectra of hot electrons and holes in PbSe quantum dots. ACS Nano 2017, 11, 6286–6294. [Google Scholar] [CrossRef] [PubMed]
- An, J.M.; Franceschetti, A.; Dudiy, S.V.; Zunger, A. The peculiar electronic structure of PbSe quantum dots. Nano Lett. 2006, 6, 2728–2735. [Google Scholar] [CrossRef] [PubMed]
- Kambhampati, P. Unraveling the structure and dynamics of excitons in semiconductor quantum dots. Acc. Chem. Res. 2011, 44, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Sagar, D.M.; Cooney, R.R.; Sewall, S.L.; Dias, E.A.; Barsan, M.M.; Butler, I.S.; Kambhampati, P. Size dependent, state-resolved studies of exciton-phonon couplings in strongly confined semiconductor quantum dots. Phys. Rev. B 2008, 77, 235321. [Google Scholar] [CrossRef]
- Califano, M.; Zunger, A.; Franceschetti, A. Efficient inverse Auger recombination at threshold in CdSe nanocrystals. Nano Lett. 2004, 4, 525–531. [Google Scholar] [CrossRef]
- Franceschetti, A.; An, J.M.; Zunger, A. Impact ionization can explain carrier multiplication in PbSe quantum dots. Nano Lett. 2006, 6, 2191–2195. [Google Scholar] [CrossRef] [PubMed]
- Schaller, R.D.; Agranovich, V.M.; Klimov, V.I. High-efficiency carrier multiplication through direct photogeneration of multi-excitons via virtual single-exciton states. Nat Phys 2005, 1, 189–194. [Google Scholar] [CrossRef]
- Shabaev, A.; Efros, A.L.; Nozik, A.J. Multiexciton generation by a single photon in nanocrystals. Nano Lett. 2006, 6, 2856–2863. [Google Scholar] [CrossRef] [PubMed]
- Schaller, R.D.; Petruska, M.A.; Klimov, V.I. Effect of electronic structure on carrier multiplication efficiency: Comparative study of PbSe and CdSe nanocrystals. Appl. Phys. Lett. 2005, 87, 253102. [Google Scholar] [CrossRef]
- Schaller, R.D.; Pietryga, J.M.; Klimov, V.I. Carrier multiplication in InAs nanocrystal quantum dots with an onset defined by the energy conservation limit. Nano Lett. 2007, 7, 3469–3476. [Google Scholar] [CrossRef] [PubMed]
- Achermann, M.; Hollingsworth, J.A.; Klimov, V.I. Multiexcitons confined within a subexcitonic volume: Spectroscopic and dynamical signatures of neutral and charged biexcitons in ultrasmall semiconductor nanocrystals. Phys. Rev. B 2003, 68, 245302. [Google Scholar] [CrossRef]
- Piryatinski, A.; Ivanov, S.A.; Tretiak, S.; Klimov, V.I. Effect of quantum and dielectric confinement on the exciton-exciton interaction energy in type II core/shell semiconductor nanocrystals. Nano Lett. 2007, 7, 108–115. [Google Scholar] [CrossRef] [PubMed]
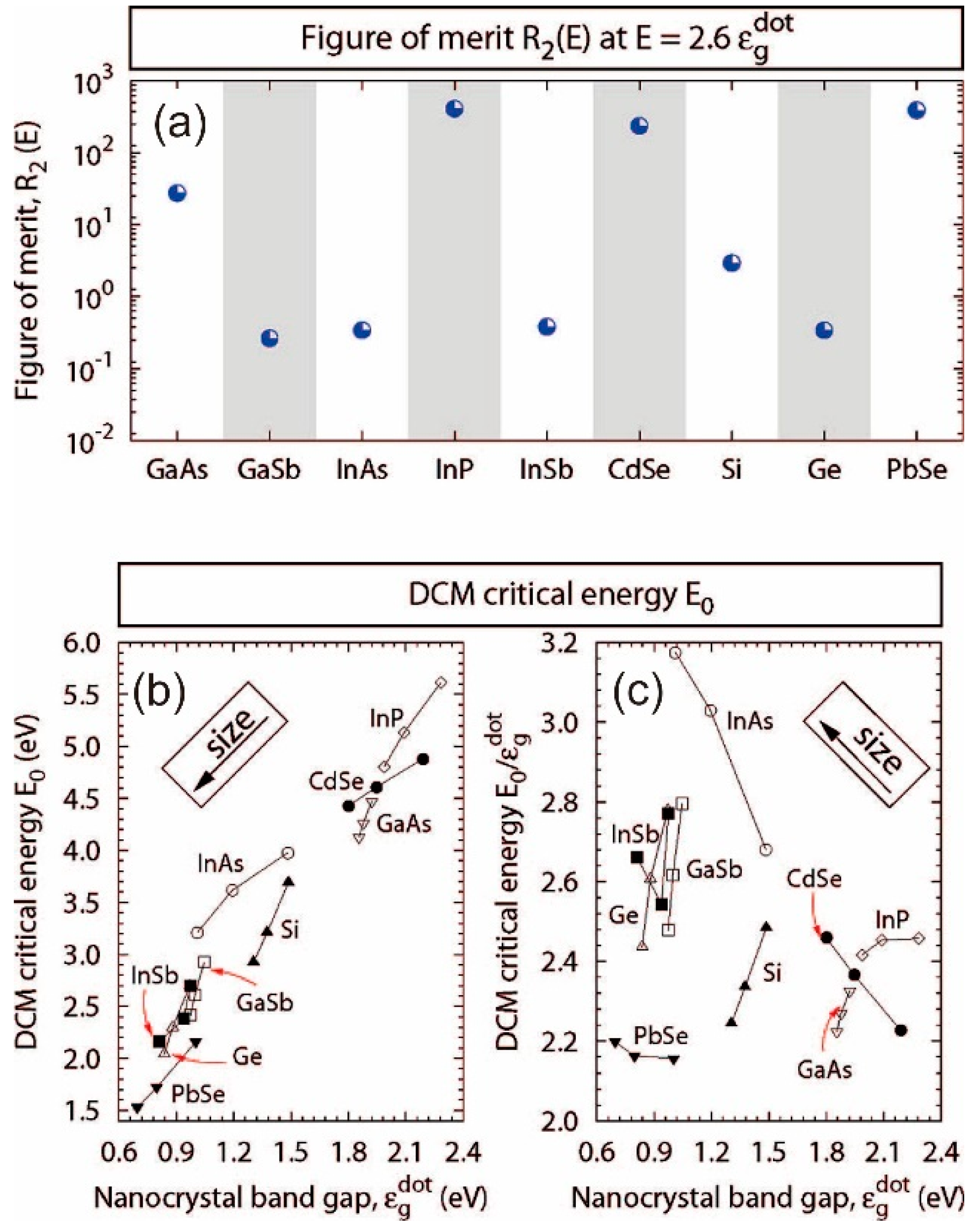
- Luo, J.-W.; Franceschetti, A.; Zunger, A. Carrier multiplication in semiconductor nanocrystals: Theoretical screening of candidate materials based on band-structure effects. Nano Lett. 2008, 8, 3174–3181. [Google Scholar] [CrossRef] [PubMed]
- Ridley, B.K. Quantum Processes in Semiconductors, 3rd ed.; Clarendon Press: Oxford, UK, 1993. [Google Scholar]
- Allan, G.; Delerue, C. Tight-binding calculations of the optical properties of HgTe nanocrystals. Phys. Rev. B 2012, 86, 165437. [Google Scholar] [CrossRef]
- Al-Otaify, A.; Kershaw, S.V.; Gupta, S.; Rogach, A.L.; Allan, G.; Delerue, C.; Binks, D.J. Multiple exciton generation and ultrafast exciton dynamics in HgTe colloidal quantum dots. Phys. Chem. Chem. Phys. 2013, 15, 16864–16873. [Google Scholar] [CrossRef] [PubMed]
- Keuleyan, S.E.; Guyot-Sionnest, P.; Delerue, C.; Allan, G. Mercury telluride colloidal quantum dots: Electronic structure, size-dependent spectra, and photocurrent detection up to 12 μm. ACS Nano 2014, 8, 8676–8682. [Google Scholar] [CrossRef] [PubMed]
- Allan, G.; Delerue, C. Role of impact ionization in multiple exciton generation in PbSe nanocrystals. Phys. Rev. B 2006, 73, 205423. [Google Scholar] [CrossRef]
- Allan, G.; Delerue, C. Influence of electronic structure and multiexciton spectral density on multiple-exciton generation in semiconductor nanocrystals: Tight-binding calculations. Phys. Rev. B 2008, 77, 125340. [Google Scholar] [CrossRef]
- Delerue, C.; Allan, G.; Pijpers, J.J.H.; Bonn, M. Carrier multiplication in bulk and nanocrystalline semiconductors: Mechanism, efficiency, and interest for solar cells. Phys. Rev. B 2010, 81, 125306. [Google Scholar] [CrossRef]
- Allan, G.; Delerue, C. Optimization of carrier multiplication for more effcient solar cells: The case of Sn quantum dots. ACS Nano 2011, 5, 7318–7323. [Google Scholar] [CrossRef] [PubMed]
- Rabani, E.; Baer, R. Distribution of multiexciton generation rates in CdSe and InAs nanocrystals. Nano Lett. 2008, 8, 4488–4492. [Google Scholar] [CrossRef] [PubMed]
- Rabani, E.; Baer, R. Theory of multiexciton generation in semiconductor nanocrystals. Chem. Phys. Lett. 2010, 496, 227–235. [Google Scholar] [CrossRef]
- Karel Čapek, R.; Moreels, I.; Lambert, K.; De Muynck, D.; Zhao, Q.; Van Tomme, A.; Vanhaecke, F.; Hens, Z. Optical properties of zincblende cadmium selenide quantum dots. J. Phys. Chem. C 2010, 114, 6371–6376. [Google Scholar] [CrossRef]
- Sills, A.; Harrison, P.; Califano, M. Exciton dynamics in InSb colloidal quantum dots. J. Phys. Chem. Lett. 2016, 7, 31–35. [Google Scholar] [CrossRef] [PubMed]
- Chang, A.Y.; Liu, W.; Talapin, D.V.; Schaller, R.D. Carrier dynamics in highly quantum-confined, colloidal indium antimonide nanocrystals. ACS Nano 2014, 8, 8513–8519. [Google Scholar] [CrossRef] [PubMed]
- Robel, I.; Gresback, R.; Kortshagen, U.; Schaller, R.D.; Klimov, V.I. Universal size-dependent trend in Auger recombination in direct-gap and indirect-gap semiconductor nanocrystals. Phys. Rev. Lett. 2009, 102, 177404. [Google Scholar] [CrossRef] [PubMed]
- Midgett, A.G.; Luther, J.M.; Stewart, J.T.; Smith, D.K.; Padilha, L.A.; Klimov, V.I.; Nozik, A.J.; Beard, M.C. Size and composition dependent multiple exciton generation efficiency in PbS, PbSe, and PbSxSe1−x alloyed quantum dots. Nano Lett. 2013, 13, 3078–3085. [Google Scholar] [CrossRef] [PubMed]
- El-Ballouli, A.A.O.; Alarousu, E.; Usman, A.; Pan, J.; Bakr, O.M.; Mohammed, O.F. Real-time observation of ultrafast intraband relaxation and exciton multiplication in PbS quantum dots. ACS Photonics 2014, 1, 285–292. [Google Scholar] [CrossRef]
- Nootz, G.; Padilha, L.A.; Levina, L.; Sukhovatkin, V.; Webster, S.; Brzozowski, L.; Sargent, E.H.; Hagan, D.J.; Van Stryland, E.W. Size dependence of carrier dynamics and carrier multiplication in PbS quantum dots. Phys. Rev. B 2011, 83, 155302. [Google Scholar] [CrossRef]
- Benisty, H.; Sotomayor-Torrès, C.M.; Weisbuch, C. Intrinsic mechanism for the poor luminescence properties of quantum-box systems. Phys. Rev. B 1991, 44, 10945–10948. [Google Scholar] [CrossRef]
- Bergren, M.R.; Palomaki, P.K.B.; Neale, N.R.; Furtak, T.E.; Beard, M.C. Size-dependent exciton formation dynamics in colloidal silicon quantum dots. ACS Nano 2016, 10, 2316–2323. [Google Scholar] [CrossRef] [PubMed]
- Padilha, L.A.; Robel, I.; Lee, D.C.; Nagpal, P.; Pietryga, J.M.; Klimov, V.I. Spectral dependence of nanocrystal photoionization probability: The role of hot-carrier transfer. ACS Nano 2011, 5, 5045–5055. [Google Scholar] [CrossRef] [PubMed]
- Blackburn, J.L.; Ellingson, R.J.; Mićić, O.I.; Nozik, A.J. Electron relaxation in colloidal InP quantum dots with photogenerated excitons or chemically injected electrons. J. Phys. Chem. B 2003, 107, 102–109. [Google Scholar] [CrossRef]
- Bartnik, A.C.; Efros, A.L.; Koh, W.K.; Murray, C.B.; Wise, F.W. Electronic states and optical properties of PbSe nanorods and nanowires. Phys. Rev. B 2010, 82, 195313. [Google Scholar] [CrossRef]
- Padilha, L.A.; Stewart, J.T.; Sandberg, R.L.; Bae, W.K.; Koh, W.-K.; Pietryga, J.M.; Klimov, V.I. Carrier multiplication in semiconductor nanocrystals: Influence of size, shape, and composition. Acc. Chem. Res. 2013, 46, 1261–1269. [Google Scholar] [CrossRef] [PubMed]
- Cunningham, P.D.; Boercker, J.E.; Foos, E.E.; Lumb, M.P.; Smith, A.R.; Tischler, J.G.; Melinger, J.S. Enhanced multiple exciton generation in quasi-one-dimensional semiconductors. Nano Lett. 2011, 11, 3476–3481. [Google Scholar] [CrossRef] [PubMed]
- Sills, A.; Califano, M. Origins of improved carrier multiplication efficiency in elongated semiconductor nanostructures. Phys. Chem. Chem. Phys. 2015, 17, 2573–2581. [Google Scholar] [CrossRef] [PubMed]
- Ten Cate, S.; Sandeep, C.S.S.; Liu, Y.; Law, M.; Kinge, S.; Houtepen, A.J.; Schins, J.M.; Siebbeles, L.D.A. Generating free charges by carrier multiplication in quantum dots for highly efficient photovoltaics. Acc. Chem. Res. 2015, 48, 174–181. [Google Scholar] [CrossRef] [PubMed]
- Pedetti, S.; Nadal, B.; Lhuillier, E.; Mahler, B.; Bouet, C.; Abécassis, B.; Xu, X.; Dubertret, B. Optimized synthesis of CdTe nanoplatelets and photoresponse of CdTe nanoplatelets films. Chem. Mater. 2013, 25, 2455–2462. [Google Scholar] [CrossRef]
- Zhou, Y.; Celikin, M.; Camellini, A.; Sirigu, G.; Tong, X.; Jin, L.; Basu, K.; Tong, X.; Barba, D.; Ma, D.; et al. Ultrasmall nanoplatelets: The ultimate tuning of optoelectronic properties. Adv. Energy Mater. 2017, 7, 1602728. [Google Scholar] [CrossRef]
- Izquierdo, E.; Robin, A.; Keuleyan, S.; Lequeux, N.; Lhuillier, E.; Ithurria, S. Strongly confined HgTe 2D nanoplatelets as narrow near-infrared emitters. J. Am. Chem. Soc. 2016, 138, 10496–10501. [Google Scholar] [CrossRef] [PubMed]
- Lesnyak, V.; George, C.; Genovese, A.; Prato, M.; Casu, A.; Ayyappan, S.; Scarpellini, A.; Manna, L. Alloyed copper chalcogenide nanoplatelets via partial cation exchange reactions. ACS Nano 2014, 8, 8407–8418. [Google Scholar] [CrossRef] [PubMed]
- Aerts, M.; Bielewicz, T.; Klinke, C.; Grozema, F.C.; Houtepen, A.J.; Schins, J.M.; Siebbeles, L.D.A. Highly efficient carrier multiplication in PbS nanosheets. Nat. Commun. 2014, 5, 3789. [Google Scholar] [CrossRef] [PubMed]
- Rowland, C.E.; Fedin, I.; Zhang, H.; Gray, S.K.; Govorov, A.O.; Talapin, D.V.; Schaller, R.D. Picosecond energy transfer and multiexciton transfer outpaces Auger recombination in binary CdSe nanoplatelet solids. Nat. Mater. 2015, 14, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Pijpers, J.J.H.; Ulbricht, R.; Tielrooij, K.J.; Osherov, A.; Golan, Y.; Delerue, C.; Allan, G.; Bonn, M. Assessment of carrier-multiplication efficiency in bulk PbSe and PbS. Nat. Phys. 2009, 5, 811–814. [Google Scholar] [CrossRef]
- Oron, D.; Kazes, M.; Shweky, I.; Banin, U. Multiexciton spectroscopy of semiconductor nanocrystals under quasi-continuous-wave optical pumping. Phys. Rev. B 2006, 74, 115333. [Google Scholar] [CrossRef]
- Deutsch, Z.; Avidan, A.; Pinkas, I.; Oron, D. Energetics and dynamics of exciton-exciton interactions in compound colloidal semiconductor quantum dots. Phys. Chem. Chem. Phys. 2011, 13, 3210–3219. [Google Scholar] [CrossRef] [PubMed]
- Pandey, A.; Guyot-Sionnest, P. Slow electron cooling in colloidal quantum dots. Science 2008, 322, 929–932. [Google Scholar] [CrossRef] [PubMed]
- Smith, C.T.; Leontiadou, M.A.; Clark, P.C.J.; Lydon, C.; Savjani, N.; Spencer, B.F.; Flavell, W.R.; O’Brien, P.; Binks, D.J. Multiple exciton generation and dynamics in InP/CdS colloidal quantum dots. J. Phys. Chem. C 2017, 121, 2099–2107. [Google Scholar] [CrossRef]
- Singhal, P.; Ghorpade, P.V.; Shankarling, G.S.; Singhal, N.; Jha, S.K.; Tripathi, R.M.; Ghosh, H.N. Exciton delocalization and hot hole extraction in CdSe QDs and CdSe/ZnS type I core shell QDs sensitized with newly synthesized thiols. Nanoscale 2016, 8, 1823–1833. [Google Scholar] [CrossRef] [PubMed]
- Lin, Q.; Makarov, N.S.; Koh, W.-K.; Velizhanin, K.A.; Cirloganu, C.M.; Luo, H.; Klimov, V.I.; Pietryga, J.M. Design and synthesis of heterostructured quantum dots with dual emission in the visible and infrared. ACS Nano 2015, 9, 539–547. [Google Scholar] [CrossRef] [PubMed]
- Cirloganu, C.M.; Padilha, L.A.; Lin, Q.; Makarov, N.S.; Velizhanin, K.A.; Luo, H.; Robel, I.; Pietryga, J.M.; Klimov, V.I. Enhanced carrier multiplication in engineered quasi-type-II quantum dots. Nat. Commun. 2014, 5, 4148. [Google Scholar] [CrossRef] [PubMed]
- Gachet, D.; Avidan, A.; Pinkas, I.; Oron, D. An upper bound to carrier multiplication efficiency in type II colloidal quantum dots. Nano Lett. 2010, 10, 164–170. [Google Scholar] [CrossRef] [PubMed]
- Stubbs, S.K.; Hardman, S.J.O.; Graham, D.M.; Spencer, B.F.; Flavell, W.R.; Glarvey, P.; Masala, O.; Pickett, N.L.; Binks, D.J. Efficient carrier multiplication in InP nanoparticles. Phys. Rev. B 2010, 81, 081303. [Google Scholar] [CrossRef]
- Wen, Q.; Kershaw, S.V.; Kalytchuk, S.; Zhovtiuk, O.; Reckmeier, C.; Vasilevskiy, M.I.; Rogach, A.L. Impact of D2O/H2O solvent exchange on the emission of HgTe and CdTe quantum dots: Polaron and energy transfer effects. ACS Nano 2016, 10, 4301–4311. [Google Scholar] [CrossRef] [PubMed]
- Aharoni, A.; Oron, D.; Banin, U.; Rabani, E.; Jortner, J. Long-range electronic-to-vibrational energy transfer from nanocrystals to their surrounding matrix environment. Phys. Rev. Lett. 2008, 100, 057404. [Google Scholar] [CrossRef] [PubMed]
- Keuleyan, S.; Kohler, J.; Guyot-Sionnest, P. Photoluminescence of mid-infrared HgTe colloidal quantum dots. J. Phys. Chem. C 2014, 118, 2749–2753. [Google Scholar] [CrossRef]
- Allan, G.; Delerue, C. Fast relaxation of hot carriers by impact ionization in semiconductor nanocrystals: Role of defects. Phys. Rev. B 2009, 79, 195324. [Google Scholar] [CrossRef]
- Konstantatos, G.; Howard, I.; Fischer, A.; Hoogland, S.; Clifford, J.; Klem, E.; Levina, L.; Sargent, E.H. Ultrasensitive solution-cast quantum dot photodetectors. Nature 2006, 442, 180–183. [Google Scholar] [CrossRef] [PubMed]
- Konstantatos, G.; Clifford, J.; Levina, L.; Sargent, E.H. Sensitive solution-processed visible-wavelength photodetectors. Nat. Photonics 2007, 1, 531–534. [Google Scholar] [CrossRef]
- Hardman, S.J.O.; Graham, D.M.; Stubbs, S.K.; Spencer, B.F.; Seddon, E.A.; Fung, H.-T.; Gardonio, S.; Sirotti, F.; Silly, M.G.; Akhtar, J.; et al. Electronic and surface properties of PbS nanoparticles exhibiting efficient multiple exciton generation. Phys. Chem. Chem. Phys. 2011, 13, 20275–20283. [Google Scholar] [CrossRef] [PubMed]
- Tyagi, P.; Kambhampati, P. False multiple exciton recombination and multiple exciton generation signals in semiconductor quantum dots arise from surface charge trapping. J. Chem. Phys. 2011, 134, 094706. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Yu, W.; Usman, A.; Isimjan, T.T.; Dgobbo, S.; Alarousu, E.; Takanabe, K.; Mohammed, O.F. Generation of multiple excitons in Ag2S quantum dots: Single high-energy versus multiple-photon excitation. J. Phys. Chem. Lett. 2014, 5, 659–665. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Ikezawa, M.; Wang, X.; Jing, P.; Li, H.; Zhao, J.; Masumoto, Y. Photocarrier recombination dynamics in ternary chalcogenide CuInS2 quantum dots. Phys. Chem. Chem. Phys. 2015, 17, 11981–11989. [Google Scholar] [CrossRef] [PubMed]
- Erwin, S.C.; Zu, L.J.; Haftel, M.I.; Efros, A.L.; Kennedy, T.A.; Norris, D.J. Doping semiconductor nanocrystals. Nature 2005, 436, 91–94. [Google Scholar] [CrossRef] [PubMed]
- Norris, D.J.; Efros, A.L.; Erwin, S.C. Doped nanocrystals. Science 2008, 319, 1776–1779. [Google Scholar] [CrossRef] [PubMed]
- Yu, D.; Wehrenberg, B.L.; Jha, P.; Ma, J.; Guyot-Sionnest, P. Electronic transport of n-type CdSe quantum dot films: Effect of film treatment. J. Appl. Phys. 2006, 99, 104315. [Google Scholar] [CrossRef]
- Roest, A.L.; Kelly, J.J.; Vanmaekelbergh, D.; Meulenkamp, E.A. Staircase in the electron mobility of a ZnO quantum dot assembly due to shell filling. Phys. Rev. Lett. 2002, 89, 036801. [Google Scholar] [CrossRef] [PubMed]
- Houtepen, A.J.; Vanmaekelbergh, D. Orbital occupation in electron-charged CdSe quantum-dot solids. J. Phys. Chem. B 2005, 109, 19634–19642. [Google Scholar] [CrossRef] [PubMed]
- Jeong, K.S.; Deng, Z.; Keuleyan, S.; Liu, H.; Guyot-Sionnest, P. Air-stable n-doped colloidal HgS quantum dots. J. Phys. Chem. Lett. 2014, 5, 1139–1143. [Google Scholar] [CrossRef] [PubMed]
- Yoon, B.; Jeong, J.; Jeong, K.S. Higher quantum state transitions in colloidal quantum dot with heavy electron doping. J. Phys. Chem. C 2016, 120, 22062–22068. [Google Scholar] [CrossRef]
- Deng, Z.; Jeong, K.S.; Guyot-Sionnest, P. Colloidal quantum dots intraband photodetectors. ACS Nano 2014, 8, 11707–11714. [Google Scholar] [CrossRef] [PubMed]
- Bejaoui, A.; Alonso, M.I.; Garriga, M.; Campoy-Quiles, M.; Goñi, A.R.; Hetsch, F.; Kershaw, S.V.; Rogach, A.L.; To, C.H.; Foo, Y.; et al. Evaluation of the dielectric function of colloidal Cd1−xHgxTe quantum dot films by spectroscopic ellipsometry. Appl. Surf. Sci. 2017, 421, 295–300. [Google Scholar] [CrossRef]
- Rinnerbauer, V.; Hingerl, K.; Kovalenko, M.; Heiss, W. Quantum confinement in layer-by-layer deposited colloidal HgTe nanocrystals determined by spectroscopic ellipsometry. Appl. Surf. Sci. 2007, 254, 291–294. [Google Scholar] [CrossRef]
- Kershaw, S.V.; Kalytchuk, S.; Zhovtiuk, O.; Shen, Q.; Oshima, T.; Yindeesuk, W.; Toyoda, T.; Rogach, A.L. Multiple exciton generation in cluster-free alloy CdxHg1−xTe colloidal quantum dots synthesized in water. Phys. Chem. Chem. Phys. 2014, 16, 25710–25722. [Google Scholar] [CrossRef] [PubMed]
- Kershaw, S.V.; Abdelazim, N.M.; Zhao, Y.; Susha, A.S.; Zhovtiuk, O.; Teoh, W.Y.; Rogach, A.L. Investigation of the exchange kinetics and surface recovery of CdxHg1−xTe quantum dots during cation exchange using a microfluidic flow reactor. Chem. Mater. 2017, 29, 2756–2768. [Google Scholar] [CrossRef]
- Shen, Q.; Oshima, T.; Yindeesuk, W.; Toyoda, T. CM and threshold data for CdxHg1−xTe sample. Personal communication, 2017. [Google Scholar]
- Chen, G.; Seo, J.; Yang, C.; Prasad, P.N. Nanochemistry and nanomaterials for photovoltaics. Chem. Soc. Rev. 2013, 42, 8304–8338. [Google Scholar] [CrossRef] [PubMed]
- Basché, T.; Bottin, A.; Li, C.; Müllen, K.; Kim, J.-H.; Sohn, B.-H.; Prabhakaran, P.; Lee, K.-S. Energy and charge transfer in nanoscale hybrid materials. Macromol. Rapid Commun. 2015, 36, 1026–1046. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.-H.; Fafarman, A.T.; Oh, S.J.; Ko, D.-K.; Kim, D.K.; Diroll, B.T.; Muramoto, S.; Gillen, J.G.; Murray, C.B.; Kagan, C.R. Bandlike transport in strongly coupled and doped quantum dot solids: A route to high-performance thin-film electronics. Nano Lett. 2012, 12, 2631–2638. [Google Scholar] [CrossRef] [PubMed]
- Kagan, C.R.; Murray, C.B. Charge transport in strongly coupled quantum dot solids. Nat. Nanotechnol. 2015, 10, 1013–1026. [Google Scholar] [CrossRef] [PubMed]
- Talapin, D.V.; Lee, J.-S.; Kovalenko, M.V.; Shevchenko, E.V. Prospects of colloidal nanocrystals for electronic and optoelectronic applications. Chem. Rev. 2010, 110, 389–458. [Google Scholar] [CrossRef] [PubMed]
- Talgorn, E.; Gao, Y.; Aerts, M.; Kunneman, L.T.; Schins, J.M.; Savenije, T.J.; van HuisMarijn, A.; van der ZantHerre, S.J.; Houtepen, A.J.; SiebbelesLaurens, D.A. Unity quantum yield of photogenerated charges and band-like transport in quantum-dot solids. Nat. Nanotechnol. 2011, 6, 733–739. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Du, Z.; Hu, J.-S.; Pan, Z.; Shen, Q.; Sun, J.; Long, D.; Dong, H.; Sun, L.; Zhong, X.; et al. Zn-Cu-In-Se quantum dot solar cells with a certified power conversion efficiency of 11.6%. J. Am. Chem. Soc. 2016, 138, 4201–4209. [Google Scholar] [CrossRef] [PubMed]
- Stavrinadis, A.; Pradhan, S.; Papagiorgis, P.; Itskos, G.; Konstantatos, G. Suppressing deep traps in PbS colloidal quantum dots via facile iodide substitutional doping for solar cells with efficiency >10%. ACS Energy Lett. 2017, 2, 739–744. [Google Scholar] [CrossRef]
- Polavarapu, L.; Nickel, B.; Feldmann, J.; Urban, A.S. Advances in quantum-confined perovskite nanocrystals for optoelectronics. Adv. Energy Mater. 2017, 7, 1700267. [Google Scholar] [CrossRef]
- Kang, J.; Wang, L.-W. High defect tolerance in lead halide perovskite CsPbBr3. J. Phys. Chem. Lett. 2017, 8, 489–493. [Google Scholar] [CrossRef] [PubMed]
- Steirer, K.X.; Schulz, P.; Teeter, G.; Stevanovic, V.; Yang, M.; Zhu, K.; Berry, J.J. Defect tolerance in methylammonium lead triiodide perovskite. ACS Energy Lett. 2016, 1, 360–366. [Google Scholar] [CrossRef]
- Dirin, D.N.; Protesescu, L.; Trummer, D.; Kochetygov, I.V.; Yakunin, S.; Krumeich, F.; Stadie, N.P.; Kovalenko, M.V. Harnessing defect-tolerance at the nanoscale: Highly luminescent lead halide perovskite nanocrystals in mesoporous silica matrixes. Nano Lett. 2016, 16, 5866–5874. [Google Scholar] [CrossRef] [PubMed]
- Hu, F.; Yin, C.; Zhang, H.; Sun, C.; Yu, W.W.; Zhang, C.; Wang, X.; Zhang, Y.; Xiao, M. Slow Auger recombination of charged excitons in nonblinking perovskite nanocrystals without spectral diffusion. Nano Lett. 2016, 16, 6425–6430. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Wen, X.; Xia, H.; Sheng, R.; Ma, Q.; Kim, J.; Tapping, P.; Harada, T.; Kee, T.W.; Huang, F.; et al. Acoustic-optical phonon up-conversion and hot-phonon bottleneck in lead-halide perovskites. Nat. Commun. 2017, 8, 14120. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Ostrowski, D.P.; France, R.M.; Zhu, K.; van de Lagemaat, J.; Luther, J.M.; Beard, M.C. Observation of a hot-phonon bottleneck in lead-iodide perovskites. Nat. Photonics 2016, 10, 53–59. [Google Scholar] [CrossRef]
- Kawai, H.; Giorgi, G.; Marini, A.; Yamashita, K. The mechanism of slow hot-hole cooling in lead-iodide perovskite: First-principles calculation on carrier lifetime from electron-phonon interaction. Nano Lett. 2015, 15, 3103–3108. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Bhaumik, S.; Goh, T.W.; Kumar, M.S.; Yantara, N.; Grätzel, M.; Mhaisalkar, S.; Mathews, N.; Sum, T.C. Slow cooling and highly efficient extraction of hot carriers in colloidal perovskite nanocrystals. Nat. Commun. 2017, 8, 14350. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Bhaumik, S.; Veldhuis, S.A.; Xing, G.; Xu, Q.; Grätzel, M.; Mhaisalkar, S.; Mathews, N.; Sum, T.C. Giant five-photon absorption from multidimensional core-shell halide perovskite colloidal nanocrystals. Nat. Commun. 2017, 8, 15198. [Google Scholar] [CrossRef] [PubMed]
- Bhaumik, S.; Veldhuis, S.A.; Ng, Y.F.; Li, M.; Muduli, S.K.; Sum, T.C.; Damodaran, B.; Mhaisalkar, S.; Mathews, N. Highly stable, luminescent core-shell type methylammonium-octylammonium lead bromide layered perovskite nanoparticles. Chem. Commun. 2016, 52, 7118–7121. [Google Scholar] [CrossRef] [PubMed]
- Weidman, M.C.; Goodman, A.J.; Tisdale, W.A. Colloidal halide perovskite nanoplatelets: An exciting new class of semiconductor nanomaterials. Chem. Mater. 2017, 29, 5019–5030. [Google Scholar] [CrossRef]
- Protesescu, L.; Yakunin, S.; Kumar, S.; Bär, J.; Bertolotti, F.; Masciocchi, N.; Guagliardi, A.; Grotevent, M.; Shorubalko, I.; Bodnarchuk, M.I.; et al. Dismantling the “red wall” of colloidal perovskites: Highly luminescent formamidinium and formamidinium-cesium lead iodide nanocrystals. ACS Nano 2017, 11, 3119–3134. [Google Scholar] [CrossRef] [PubMed]
- Castañeda, J.A.; Nagamine, G.; Yassitepe, E.; Bonato, L.G.; Voznyy, O.; Hoogland, S.; Nogueira, A.F.; Sargent, E.H.; Cruz, C.H.B.; Padilha, L.A. Efficient biexciton interaction in perovskite quantum dots under weak and strong confinement. ACS Nano 2016, 10, 8603–8609. [Google Scholar] [CrossRef] [PubMed]
- Makarov, N.S.; Guo, S.; Isaienko, O.; Liu, W.; Robel, I.; Klimov, V.I. Spectral and dynamical properties of single excitons, biexcitons, and trions in cesium-lead-halide perovskite quantum dots. Nano Lett. 2016, 16, 2349–2362. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kershaw, S.V.; Rogach, A.L. Carrier Multiplication Mechanisms and Competing Processes in Colloidal Semiconductor Nanostructures. Materials 2017, 10, 1095. https://doi.org/10.3390/ma10091095
Kershaw SV, Rogach AL. Carrier Multiplication Mechanisms and Competing Processes in Colloidal Semiconductor Nanostructures. Materials. 2017; 10(9):1095. https://doi.org/10.3390/ma10091095
Chicago/Turabian StyleKershaw, Stephen V., and Andrey L. Rogach. 2017. "Carrier Multiplication Mechanisms and Competing Processes in Colloidal Semiconductor Nanostructures" Materials 10, no. 9: 1095. https://doi.org/10.3390/ma10091095