A Review of Recent Advances towards the Development of (Quantitative) Structure-Activity Relationships for Metallic Nanomaterials
Abstract
:1. Introduction
- to provide fast and inexpensive high-throughput screening methods estimating the toxicity of chemical entity;
- to assist the classification of chemicals according to their toxicity;
- to help understand the underlying toxic mechanisms.
2. Literature Search and Analysis
3. Sources of Data for Modeling
3.1. Cellular Uptake Assays
3.2. Toxicity to Various Cell Lines
3.3. Toxicity to E. coli
4. Existing Nano-(Q)SARs
4.1. Linear Regression Models
Q2EXT = 0.83, RMSEP = 0.13
4.2. Logistic Regression Models
4.3. Support Vector Machine Models
- Cluster I: n = 13, sensitivity = 0.5, specificity = 0.8;
- Cluster II: n = 18, sensitivity = 0.78, specificity = 0.78;
- Cluster III: n = 13, sensitivity = 0.7, specificity = 0.4,
4.4. Artificial Neural Network Models
4.5. k-Nearest Neighbor Models
4.6. Other Models
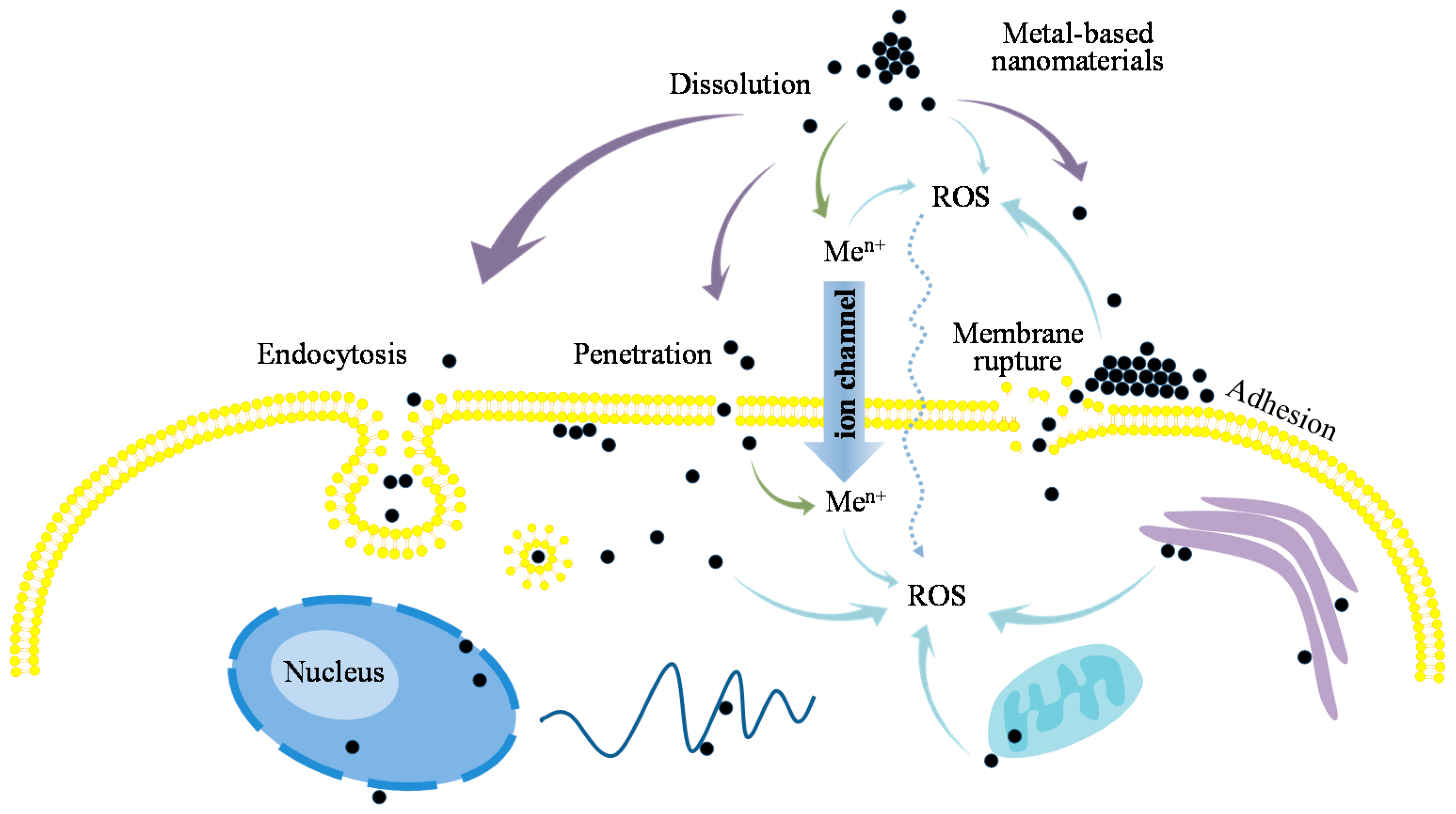
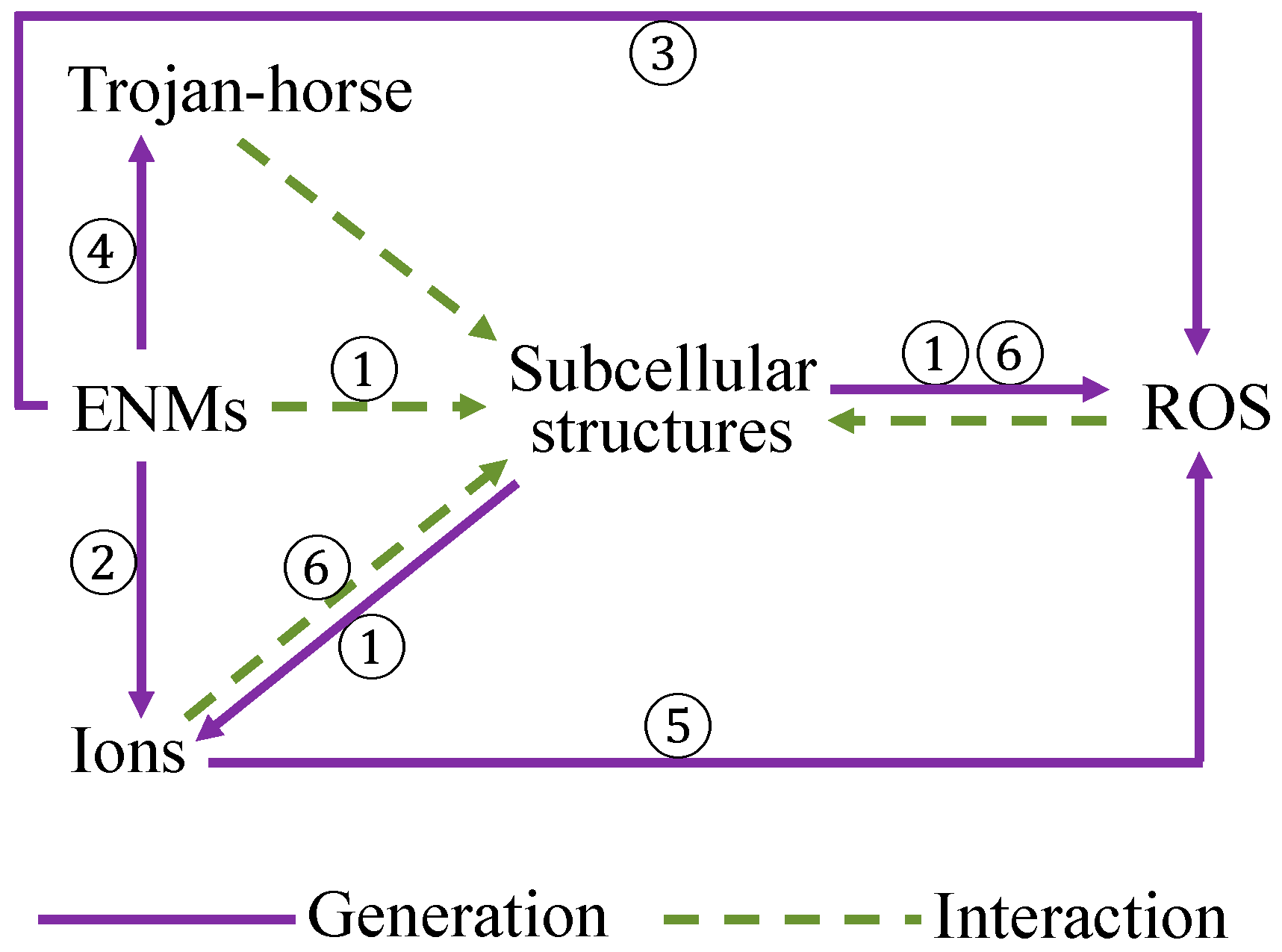
5. Interpret Mechanisms of ENM Biological Activities with Developed Models
5.1. Cellular Uptake of ENMs
5.2. ENMs-Induced Biological Effects
6. Conclusions and Outlook
- (i)
- A general overview is provided of the datasets being widely used in nano-(Q)SAR studies, and the characterization of ENMs in these datasets is discussed. Experimental data are shown to be mainly available concerning the cellular uptake by different cell lines (e.g., PaCa2, HUVEC), cytotoxicity to cells (e.g., HaCaT, BEAS-2B), and the toxicity to E. coli. A limited usage of existing data in relevant investigations was observed.
- (ii)
- An overview of nano-(Q)SARs so far developed, based on a variety of modeling techniques such as linear and non-linear regressions (MLR, PLS, and logistic regression), SVM, ANN, and kNN, is presented.
- (iii)
- An interpretation of the underlying mechanisms of ENM toxicity and cellular uptake is provided on the basis of the descriptors discussed in nano-(Q)SAR studies. The surface properties of ENMs are deemed vital for the uptake of ENMs by different cell lines, such as lipophilicity, hydrogen bonding capacity, electronegativity, shape, and size of surface modifiers. The capability of releasing ions and generating ROS, surface redox properties of ENMs are concluded to be important indicators for evaluating the toxicity of ENMs.
- (iv)
- An outlook is presented regarding the experimental data needed for future modeling and the need of proper characterization of ENMs. Owing to the limited data availability, optimizing the usage of existing information of nanotoxicity should be deliberately considered; integrating relevant available data thus becomes vital for the development of nano-(Q)SARs. Meanwhile, whether or not the dynamic transformations of ENMs in media play a vital role in the computer-aided nanotoxicity also ought to be further discussed.
Acknowledgments
Conflicts of Interest
References
- Puzyn, T.; Leszczynska, D.; Leszczynski, J. Toward the Development of “Nano-QSARs”: Advances and Challenges. Small 2009, 5, 2494–2509. [Google Scholar] [CrossRef] [PubMed]
- Linkov, I.; Steevens, J.; Adlakha-Hutcheon, G.; Bennett, E.; Chappell, M.; Colvin, V.; Davis, J.M.; Davis, T.; Elder, A.; Foss Hansen, S.; et al. Emerging methods and tools for environmental risk assessment, decision-making, and policy for nanomaterials: Summary of NATO Advanced Research Workshop. J. Nanopart. Res. 2009, 11, 513–527. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Winkler, D.A. Recent advances, and unresolved issues, in the application of computational modelling to the prediction of the biological effects of nanomaterials. Toxicol. Appl. Pharmacol. 2016, 299, 96–100. [Google Scholar] [CrossRef] [PubMed]
- Asare, N.; Instanes, C.; Sandberg, W.J.; Refsnes, M.; Schwarze, P.; Kruszewski, M.; Brunborg, G. Cytotoxic and genotoxic effects of silver nanoparticles in testicular cells. Toxicology 2012, 291, 65–72. [Google Scholar] [CrossRef] [PubMed]
- Nirmala, R.; Park, H.M.; Kalpana, D.; Kang, H.S.; Navamathavan, R.; Lee, Y.S.; Kim, H.Y. Bactericidal activity and in vitro cytotoxicity assessment of hydroxyapatite containing gold nanoparticles. J. Biomed. Nanotechnol. 2011, 7, 342–350. [Google Scholar] [CrossRef] [PubMed]
- Wiesner, M.R.; Lowry, G.V.; Alvarez, P.; Dionysiou, D.; Biswas, P. Assessing the risks of manufactured nanomaterials. Environ. Sci. Technol. 2006, 40, 4336–4345. [Google Scholar] [CrossRef] [PubMed]
- Long, T.C.; Saleh, N.; Tilton, R.D.; Lowry, G.V.; Veronesi, B. Titanium dioxide (P25) produces reactive oxygen species in immortalized brain microglia (BV2): Implications for nanoparticle neurotoxicity. Environ. Sci. Technol. 2006, 40, 4346–4352. [Google Scholar] [CrossRef] [PubMed]
- Win-Shwe, T.T.; Fujimaki, H. Nanoparticles and neurotoxicity. Int. J. Mol. Sci. 2011, 12, 6267–6280. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Wang, C.; Sun, J.; Xue, Y. Neurotoxicity of silica nanoparticles: Brain localization and dopaminergic neurons damage pathways. ACS Nano 2011, 5, 4476–4489. [Google Scholar] [CrossRef] [PubMed]
- Kumari, M.; Khan, S.S.; Pakrashi, S.; Mukherjee, A.; Chandrasekaran, N. Cytogenetic and genotoxic effects of zinc oxide nanoparticles on root cells of Allium cepa. J. Hazard Mater. 2011, 190, 613–621. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V.; Singh, S.K.; Anderson, D.; Tobin, D.J.; Dhawan, A. Zinc oxide nanoparticle induced genotoxicity in primary human epidermal keratinocytes. J. Nanosci. Nanotechnol. 2011, 11, 3782–3788. [Google Scholar] [CrossRef] [PubMed]
- Ellegaard-Jensen, L.; Jensen, K.A.; Johansen, A. Nano-silver induces dose–response effects on the nematode Caenorhabditis elegans. Ecotoxicol. Environ. Saf. 2012, 80, 216–223. [Google Scholar] [CrossRef] [PubMed]
- Thill, A.; Zeyons, O.; Spalla, O.; Chauvat, F.; Rose, J.; Auffan, M.; Flank, A.M. Cytotoxicity of CeO2 nanoparticles for E. coli. Physico-chemical insight of the cytotoxicity mechanism. Environ. Sci. Technol. 2006, 40, 6151–6156. [Google Scholar] [CrossRef] [PubMed]
- Tran, N.; Mir, A.; Mallik, D.; Sinha, A.; Nayar, S.; Webster, T.J. Bactericidal effect of iron oxide nanoparticles on Staphylococcus aureus. Int. J. Nanomed. 2010, 5, 277–283. [Google Scholar]
- Gajewicz, A.; Rasulev, B.; Dinadayalane, T.C.; Urbaszek, P.; Puzyn, T.; Leszczynska, D.; Leszczynski, J. Advancing risk assessment of engineered nanomaterials: Application of computational approaches. Adv. Drug Deliv. Rev. 2012, 64, 1663–1693. [Google Scholar] [CrossRef] [PubMed]
- Worth, A.P. The role of QSAR methodology in the regulatory assessment of chemicals. In Recent Advances in QSAR Studies: Methods and Applications; Puzyn, T., Leszczynski, J., Cronin, M.T.D., Eds.; Springer: Heidelberg, Germany, 2010; pp. 367–382. ISBN 978-1-4020-9783-6. [Google Scholar]
- Puzyn, T.; Rasulev, B.; Gajewicz, A.; Hu, X.; Dasari, T.P.; Michalkova, A.; Hwang, H.M.; Toropov, A.; Leszczynska, D.; Leszczynski, J. Using nano-QSAR to predict the cytotoxicity of metal oxide nanoparticles. Nat. Nanotechnol. 2011, 6, 175–178. [Google Scholar] [CrossRef] [PubMed]
- Russell, W.M.S.; Burch, R.L. The Principles of Humane Experimental Technique; Methuen & Co. Ltd.: London, UK, 1959. [Google Scholar]
- Fernández, A.; Lombardo, A.; Rallo, R.; Roncaglioni, A.; Giralt, F.; Benfenati, E. Quantitative consensus of bioaccumulation models for integrated testing strategies. Environ. Int. 2012, 45, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Kar, S.; Roy, K. QSAR modeling of toxicity of diverse organic chemicals to Daphnia magna using 2D and 3D descriptors. J. Hazard Mater. 2010, 177, 344–351. [Google Scholar] [CrossRef] [PubMed]
- Kar, S.; Roy, K. First report on development of quantitative interspecies structure-carcinogenicity relationship models and exploring discriminatory features for rodent carcinogenicity of diverse organic chemicals using OECD guidelines. Chemosphere 2012, 87, 339–355. [Google Scholar] [CrossRef] [PubMed]
- Toropova, A.P.; Toropov, A.A.; Leszczynska, D.; Leszczynski, J. CORAL and Nano-QFAR: Quantitative feature—Activity relationships (QFAR) for bioavailability of nanoparticles (ZnO, CuO, Co3O4, and TiO2). Ecotoxicol. Environ. Saf. 2017, 139, 404–407. [Google Scholar] [CrossRef] [PubMed]
- Toropov, A.A.; Achary, P.G.R.; Toropova, A.P. Quasi-SMILES and nano-QFPR: The predictive model for zeta potentials of metal oxide nanoparticles. Chem. Phys. Lett. 2016, 660, 107–110. [Google Scholar] [CrossRef]
- Toropova, A.P.; Toropov, A.A.; Rallo, R.; Leszczynska, D.; Leszczynski, J. Optimal descriptor as a translator of eclectic data into prediction of cytotoxicity for metal oxide nanoparticles under different conditions. Ecotoxicol. Environ. Saf. 2015, 112, 39–45. [Google Scholar] [CrossRef] [PubMed]
- Peijnenburg, W. Structure-activity relationships for biodegradation: A critical review. Pure Appl. Chem. 2009, 66, 1931–1941. [Google Scholar] [CrossRef]
- Raymond, J.W.; Rogers, T.N.; Shonnard, D.R.; Kline, A.A. A review of structure-based biodegradation estimation methods. J. Hazar.d Mater. 2001, 84, 189–215. [Google Scholar] [CrossRef]
- Ivask, A.; Juganson, K.; Bondarenko, O.; Mortimer, M.; Aruoja, V.; Kasemets, K.; Blinova, I.; Heinlaan, M.; Slaveykova, V.; Kahru, A. Mechanisms of toxic action of Ag, ZnO and CuO nanoparticles to selected ecotoxicological test organisms and mammalian cells in vitro: A comparative review. Nanotoxicology 2014, 8, 57–71. [Google Scholar] [CrossRef] [PubMed]
- Guidance Document on the Validation of (Quantitative) Structure Activity Relationship [(Q)SAR] Models. OECD Series on Testing and Assessment; Organization for Economic Cooperation and Development Posted May 30, 2007. Available online: http://www.keepeek.com/Digital-Asset-Management/oecd/environment/guidance-document-on-the-validation-of-quantitative-structure-activity-relationship-q-sar-models_9789264085442-en#.WaYqP1IYPEY (accessed on 23 March 2017).
- Burello, E.; Worth, A.P. A theoretical framework for predicting the oxidative stress potential of oxide nanoparticles. Nanotoxicology 2011, 5, 228–235. [Google Scholar] [CrossRef] [PubMed]
- Chau, Y.T.; Yap, C.W. Quantitative Nanostructure-Activity Relationship modelling of nanoparticles. RSC Adv. 2012, 2, 8489–8496. [Google Scholar] [CrossRef]
- Chen, G.; Peijnenburg, W.J.; Kovalishyn, V.; Vijver, M.G. Development of nanostructure-activity relationships assisting the nanomaterial hazard categorization for risk assessment and regulatory decision-making. RSC Adv. 2016, 6, 52227–52235. [Google Scholar] [CrossRef]
- Epa, V.C.; Burden, F.R.; Tassa, C.; Weissleder, R.; Shaw, S.; Winkler, D.A. Modeling Biological Activities of Nanoparticles. Nano Lett. 2012, 12, 5808–5812. [Google Scholar] [CrossRef] [PubMed]
- Fourches, D.; Pu, D.; Tassa, C.; Weissleder, R.; Shaw, S.Y.; Mumper, R.J.; Tropsha, A. Quantitative Nanostructure-Activity Relationship Modeling. ACS Nano 2010, 4, 5703–5712. [Google Scholar] [CrossRef] [PubMed]
- Gajewicz, A.; Schaeublin, N.; Rasulev, B.; Hussain, S.; Leszczynska, D.; Puzyn, T.; Leszczynski, J. Towards understanding mechanisms governing cytotoxicity of metal oxides nanoparticles: Hints from nano-QSAR studies. Nanotoxicology 2015, 9, 313–325. [Google Scholar] [CrossRef] [PubMed]
- Ghorbanzadeh, M.; Fatemi, M.H.; Karimpour, M. Modeling the Cellular Uptake of Magnetofluorescent Nanoparticles in Pancreatic Cancer Cells: A Quantitative Structure Activity Relationship Study. Ind. Eng. Chem. Res. 2012, 51, 10712–10718. [Google Scholar] [CrossRef]
- Kar, S.; Gajewicz, A.; Puzyn, T.; Roy, K. Nano-quantitative structure-activity relationship modeling using easily computable and interpretable descriptors for uptake of magnetofluorescent engineered nanoparticles in pancreatic cancer cells. Toxicol. In Vitro 2014, 28, 600–606. [Google Scholar] [CrossRef] [PubMed]
- Kar, S.; Gajewicz, A.; Puzyn, T.; Roy, K.; Leszczynski, J. Periodic table-based descriptors to encode cytotoxicity profile of metal oxide nanoparticles: A mechanistic QSTR approach. Ecotoxicol. Environ. Saf. 2014, 107, 162–169. [Google Scholar] [CrossRef] [PubMed]
- Kleandrova, V.V.; Luan, F.; González-Díaz, H.; Ruso, J.M.; Speck-Planche, A.; Cordeiro, M.N. Computational tool for risk assessment of nanomaterials: Novel QSTR-perturbation model for simultaneous prediction of ecotoxicity and cytotoxicity of uncoated and coated nanoparticles under multiple experimental conditions. Environ. Sci. Technol. 2014, 48, 14686–14694. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Rallo, R.; George, S.; Ji, Z.; Nair, S.; Nel, A.E.; Cohen, Y. Classification NanoSAR development for cytotoxicity of metal oxide nanoparticles. Small 2011, 7, 1118–1126. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Rallo, R.; Weissleder, R.; Tassa, C.; Shaw, S.; Cohen, Y. Nano-SAR development for bioactivity of nanoparticles with considerations of decision boundaries. Small 2013, 9, 1842–1852. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Zhang, H.Y.; Ji, Z.X.; Rallo, R.; Xia, T.; Chang, C.H.; Nel, A.; Cohen, Y. Development of structure-activity relationship for metal oxide nanoparticles. Nanoscale 2013, 5, 5644–5653. [Google Scholar] [CrossRef] [PubMed]
- Luan, F.; Kleandrova, V.V.; González-Díaz, H.; Ruso, J.M.; Melo, A.; Speck-Planche, A.; Cordeiro, M.N. Computer-aided nanotoxicology: Assessing cytotoxicity of nanoparticles under diverse experimental conditions by using a novel QSTR-perturbation approach. Nanoscale 2014, 6, 10623–10630. [Google Scholar] [CrossRef] [PubMed]
- Mu, Y.; Wu, F.; Zhao, Q.; Ji, R.; Qie, Y.; Zhou, Y.; Hu, Y.; Pang, C.; Hristozov, D.; Giesy, J.P.; et al. Predicting toxic potencies of metal oxide nanoparticles by means of nano-QSARs. Nanotoxicology 2016, 10, 1207–1214. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Li, T.; Cheng, J.; Telesca, D.; Zink, J.I.; Jiang, J. Nano-QSAR modeling for predicting the cytotoxicity of metal oxide nanoparticles using novel descriptors. RSC Adv. 2016, 6, 25766–25775. [Google Scholar] [CrossRef]
- Papa, E.; Doucet, J.P.; Doucet-Panaye, A. Linear and non-linear modelling of the cytotoxicity of TiO2 and ZnO nanoparticles by empirical descriptors. SAR QSAR Environ. Res. 2015, 26, 647–665. [Google Scholar] [CrossRef] [PubMed]
- Pathakoti, K.; Huang, M.J.; Watts, J.D.; He, X.; Hwang, H.M. Using experimental data of E. coli to develop a QSAR model for predicting the photo-induced cytotoxicity of metal oxide nanoparticles. J. Photochem. Photobiol. B 2014, 130, 234–240. [Google Scholar] [CrossRef] [PubMed]
- Singh, K.P.; Gupta, S. Nano-QSAR modeling for predicting biological activity of diverse nanomaterials. RSC Adv. 2014, 4, 13215–13230. [Google Scholar] [CrossRef]
- Sizochenko, N.; Rasulev, B.; Gajewicz, A.; Kuz’min, V.; Puzyn, T.; Leszczynski, J. From basic physics to mechanisms of toxicity: The “liquid drop” approach applied to develop predictive classification models for toxicity of metal oxide nanoparticles. Nanoscale 2014, 6, 13986–13993. [Google Scholar] [CrossRef] [PubMed]
- Sizochenko, N.; Rasulev, B.; Gajewicz, A.; Mokshyna, E.; Kuz’min, V.E.; Leszczynski, J.; Puzyn, T. Causal inference methods to assist in mechanistic interpretation of classification nano-SAR models. RSC Adv. 2015, 5, 77739–77745. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P.; Benfenati, E.; Gini, G.; Puzyn, T.; Leszczynska, D.; Leszczynski, J. Novel application of the CORAL software to model cytotoxicity of metal oxide nanoparticles to bacteria E. coli. Chemosphere 2012, 89, 1098–1102. [Google Scholar] [CrossRef] [PubMed]
- Toropov, A.A.; Toropova, A.P.; Puzyn, T.; Benfenati, E.; Gini, G.; Leszczynska, D.; Leszczynski, J. QSAR as a random event: Modeling of nanoparticles uptake in PaCa2 cancer cells. Chemosphere 2013, 92, 31–37. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Ji, Z.; Xia, T.; Meng, H.; Low-Kam, C.; Liu, R.; Pokhrel, S.; Lin, S.; Wang, X.; Liao, Y.P.; et al. Use of metal oxide nanoparticle band gap to develop a predictive paradigm for oxidative stress and acute pulmonary inflammation. ACS Nano 2012, 6, 4349–4368. [Google Scholar] [CrossRef] [PubMed]
- Weissleder, R.; Kelly, K.; Sun, E.Y.; Shtatland, T.; Josephson, L. Cell-specific targeting of nanoparticles by multivalent attachment of small molecules. Nat. Biotechnol. 2005, 23, 1418–1423. [Google Scholar] [CrossRef] [PubMed]
- Shaw, S.Y.; Westly, E.C.; Pittet, M.J.; Subramanian, A.; Schreiber, S.L.; Weissleder, R. Perturbational profiling of nanomaterial biologic activity. Proc. Natl. Acad. Sci. USA 2008, 105, 7387–7392. [Google Scholar] [CrossRef] [PubMed]
- Sayes, C.; Ivanov, I. Comparative study of predictive computational models for nanoparticle-induced cytotoxicity. Risk Anal. 2010, 30, 1723–1734. [Google Scholar] [CrossRef] [PubMed]
- Fourches, D.; Pu, D.; Tropsha, A. Exploring Quantitative Nanostructure-Activity Relationships (QNAR) Modeling as a Tool for Predicting Biological Effects of Manufactured Nanoparticles. Comb. Chem. High Throughput Screen. 2011, 14, 217–225. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Cook, S.; Wang, P.; Hwang, H.M. In vitro evaluation of cytotoxicity of engineered metal oxide nanoparticles. Sci. Total Environ. 2009, 407, 3070–3072. [Google Scholar] [CrossRef] [PubMed]
- Gramatica, P. Principles of QSAR models validation: Internal and external. QSAR Comb. Sci. 2007, 26, 694–701. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemometr. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods. V. Modification of NDDO approximations and application to 70 elements. J. Mol. Model. 2007, 13, 1173–1213. [Google Scholar] [CrossRef] [PubMed]
- MOPAC, version 2009; Stewart Computational Chemistry: Colorado Springs, CO, USA, 2009.
- Netzeva, T.I.; Worth, A.; Aldenberg, T.; Benigni, R.; Cronin, M.T.; Gramatica, P.; Jaworska, J.S.; Kahn, S.; Klopman, G.; Marchant, C.A.; et al. Current status of methods for defining the applicability domain of (quantitative) structure–activity relationships. Altern. Lab. Anim. 2005, 33, 155–173. [Google Scholar] [PubMed]
- Chen, G.; Vijver, M.G.; Peijnenburg, W.J. Summary and analysis of the currently existing literature data on metal-based nanoparticles published for selected aquatic organisms: Applicability for toxicity prediction by (Q)SARs. Altern. Lab. Anim. 2015, 43, 221–240. [Google Scholar] [PubMed]
- Sushko, I.; Novotarskyi, S.; Körner, R.; Pandey, A.K.; Rupp, M.; Teetz, W.; Brandmaier, S.; Abdelaziz, A.; Prokopenko, V.V.; Tanchuk, V.Y.; et al. Online chemical modeling environment (OCHEM): Web platform for data storage, model development and publishing of chemical information. J. Comput. Aided Mol. Des. 2011, 25, 533–554. [Google Scholar] [CrossRef] [PubMed]
- Zhao, F.; Zhao, Y.; Liu, Y.; Chang, X.; Chen, C.; Zhao, Y. Cellular uptake, intracellular trafficking, and cytotoxicity of nanomaterials. Small 2011, 7, 1322–1337. [Google Scholar] [CrossRef] [PubMed]
- Unfried, K.; Albrecht, C.; Klotz, L.; von Mikecz, A.; Grether-Beck, S.; Schins, R. Cellular responses to nanoparticles: Target structures and mechanisms. Nanotoxicology 2007, 1, 52–71. [Google Scholar] [CrossRef]
- Yue, T.; Zhang, X. Molecular understanding of receptor-mediated membrane responses to ligand-coated nanoparticles. Soft Matter 2011, 7, 9104–9112. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, H.; Chen, Z.; Zheng, Y. Penetration of Lipid Membranes by Gold Nanoparticles: Insights into Cellular Uptake, Cytotoxicity, and Their Relationship. ACS Nano 2010, 4, 5421–5429. [Google Scholar] [CrossRef] [PubMed]
- Xia, T.; Rome, L.; Nel, A. Nanobiology: Particles slip cell security. Nat. Mater. 2008, 7, 519–520. [Google Scholar] [CrossRef] [PubMed]
- Van de Waterbeemd, H.; Smith, D.A.; Jones, B.C. Lipophilicity in PK design: Methyl, ethyl, futile. J. Comput. Aided Mol. Des. 2001, 15, 273–286. [Google Scholar] [CrossRef] [PubMed]
- Thevenot, P.; Cho, J.; Wavhal, D.; Timmons, R.B.; Tang, L. Surface chemistry influences cancer killing effect of TiO2 nanoparticles. Nanomedicine 2008, 4, 226–236. [Google Scholar] [CrossRef] [PubMed]
- Von Moos, N.; Slaveykova, V.I. Oxidative stress induced by inorganic nanoparticles in bacteria and aquatic microalgae-state of the art and knowledge gaps. Nanotoxicology 2014, 8, 605–630. [Google Scholar] [CrossRef] [PubMed]
- Limbach, L.K.; Wick, P.; Manser, P.; Grass, R.N.; Bruinink, A.; Stark, W.J. Exposure of engineered nanoparticles to human lung epithelial cells: Influence of chemical composition and catalytic activity on oxidative stress. Environ. Sci. Technol. 2007, 41, 4158–4163. [Google Scholar] [CrossRef] [PubMed]
- Franklin, N.M.; Rogers, N.J.; Apte, S.C.; Batley, G.E.; Gadd, G.E.; Casey, P.S. Comparative toxicity of nanoparticulate ZnO, bulk ZnO, and ZnCl2 to a freshwater microalga (Pseudokirchneriella subcapitata): The importance of particle solubility. Environ. Sci. Technol. 2007, 41, 8484–8490. [Google Scholar] [CrossRef] [PubMed]
- Heinlaan, M.; Ivask, A.; Blinova, I.; Dubourguier, H.-C.; Kahru, A. Toxicity of nanosized and bulk ZnO, CuO and TiO2 to bacteria Vibrio fischeri and crustaceans Daphnia magna and Thamnocephalus platyurus. Chemosphere 2008, 71, 1308–1316. [Google Scholar] [CrossRef] [PubMed]
- Wiench, K.; Wohlleben, W.; Hisgen, V.; Radke, K.; Salinas, E.; Zok, S.; Landsiedel, R. Acute and chronic effects of nano- and non-nano-scale TiO2 and ZnO particles on mobility and reproduction of the freshwater invertebrate Daphnia magna. Chemosphere 2009, 76, 1356–1365. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Zhu, L.; Lin, D. Toxicity of ZnO nanoparticles to E. coli: Mechanism and the influence of medium components. Environ. Sci. Technol. 2011, 45, 1977–1983. [Google Scholar] [CrossRef] [PubMed]
- Bondarenko, O.; Ivask, A.; Kakinen, A.; Kahru, A. Sub-toxic effects of CuO nanoparticles on bacteria: Kinetics, role of Cu ions and possible mechanisms of action. Environ. Pollut. 2012, 169, 81–89. [Google Scholar] [CrossRef] [PubMed]
- Stohs, S.J.; Bagchi, D. Oxidative mechanisms in the toxicity of metal ions. Free Radic. Biol. Med. 1995, 18, 321–336. [Google Scholar] [CrossRef]
- Portier, J.; Hilal, H.S.; Saadeddin, I.; Hwang, S.J.; Subramanian, M.A.; Campet, G. Thermodynamic correlations and band gap calculations in metal oxides. Prog. Solid State Chem. 2004, 32, 207–217. [Google Scholar] [CrossRef]
- Portier, J.; Campet, G.; Poquet, A.; Marcel, C.; Subramanian, M.A. Degenerate semiconductors in the light of electronegativity and chemical hardness. Int. J. Inorg. Mater. 2001, 3, 1039–1043. [Google Scholar] [CrossRef]
- Xiao, Y.; Vijver, M.G.; Chen, G.; Peijnenburg, W.J.G.M. Toxicity and Accumulation of Cu and ZnO nanoparticles in Daphnia magna. Environ. Sci. Technol. 2015, 49, 4657–4664. [Google Scholar] [CrossRef] [PubMed]
- Hua, J.; Vijver, M.G.; Richardson, M.K.; Ahmad, F.; Peijnenburg, W.J. Particle-specific toxic effects of differently shaped zinc oxide nanoparticles to zebrafish embryos (Danio rerio). Environ. Toxicol. Chem. 2014, 33, 2859–2868. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Palma, S.; Fisher, N.S.; Wong, S.S. Effect of morphology of ZnO nanostructures on their toxicity to marine algae. Aquat. Toxicol. 2011, 102, 186–196. [Google Scholar] [CrossRef] [PubMed]
- Suresh, A.K.; Pelletier, D.A.; Doktycz, M.J. Relating nanomaterial properties and microbial toxicity. Nanoscale 2013, 5, 463–474. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Aker, W.G.; Leszczynski, J.; Hwang, H.M. Using a holistic approach to assess the impact of engineered nanomaterials inducing toxicity in aquatic systems. J. Food Drug Anal. 2014, 22, 128–146. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Peijnenburg, W.J.; Xiao, Y.; Vijver, M.G. Developing species sensitivity distributions for metallic nanomaterials considering the characteristics of nanomaterials, experimental conditions, and different types of endpoints. Food Chem. Toxicol. 2017. [Google Scholar] [CrossRef] [PubMed]
| Reference | Brief Description |
|---|---|
| Cellular uptake | |
| [30] | Developed a final consensus model based on top 5 candidate models constructed by naive Bayes, logistic regression, k-nearest neighbor (kNN), and support vector machine (SVM), predicting the cellular uptake of 105 ENMs (single metal core) by PaCa2 pancreatic cancer cells (PaCa2) |
| [32] | Modeled cellular uptake of 108 ENMs in human umbilical vein endothelial cells (HUVEC) and PaCa2 cells using multiple linear regression (MLR) with the expectation maximization method |
| [33] | Generated models predicting the cellular uptake of 109 ENMs in PaCa2 cells using the kNN method |
| [35] | Cellular uptake of 109 magnetofluorescent ENMs in PaCa2 cells was modeled using MLR and multilayered perceptron neural network, descriptor selection was performed by combining the self-organizing map and stepwise MLR |
| [36] | Developed a model establishing the cellular uptakes of 109 magnetofluorescent ENMs in PaCa2 cells |
| [47] | Predictive models were built based on cellular uptake of 109 ENMs in PaCa2 cells |
| [51] | Cellular uptake of 109 ENMs with the same core but different surface modifiers in the PaCa2 cells was modeled based on SMILES-based optimal descriptors |
| Cytotoxicity | |
| [29] | A model was proposed to show that the oxidative stress potential of metal oxide ENMs could be possibly predicted by looking at their band gap energy |
| [32] | Modeled cytotoxicity of 31 ENMs to vascular smooth muscle cells based on MLR and Bayesian regularized artificial neural network |
| [33] | Generated models predicting the cytotoxicity of 44 ENMs with diverse metal cores using the SVM method |
| [34] | Applied the MLR method combined with a genetic algorithm to describe the toxicity of 18 metal oxide ENMs to the human keratinocyte cell line (HaCaT) |
| [39] | Classification models (logistic regression) were developed to predict the cytotoxicity of nine ENMs to the transformed bronchial epithelial cells (BEAS-2B) |
| [40] | A nano-SAR was developed classifying 44 iron-based ENMs into bioactive or inactive, using a naive Bayesian classifier based on 4 descriptors: primary size, spin-lattice, and spin-spin relaxivities, and zeta potential |
| [41] | SVM nano-SAR model was constructed on basis of the cytotoxicity data of 24 metal oxide ENMs to BEAS-2B cells and murine myeloid (RAW 264.7) cells |
| [42] | Perturbation model was presented predicting the cytotoxicity of ENMs against several mammalian cell lines; influence of molar volume, polarizability, and size of the particles was indicated |
| [44] | Models were constructed to predict the cytotoxicity in HaCaT cells of 18 different metal oxide ENMs. The factors of molecular weight, cationic charge, mass percentage of metal elements, individual and aggregation sizes were discussed |
| [45] | Cytotoxicity of TiO2 and ZnO ENMs was modeled by MLR and C4.5 algorithm |
| [47] | Predictive models were built based on cytotoxicity of different ENMs (with diverse metal cores) in four cell lines (endothelial and smooth muscle cells, monocytes, and hepatocytes) |
| [48] | Based on random forest regression, developed predictive classification models for cytotoxicity of 18 metal oxide ENMs to HaCaT cells |
| [49] | Structure-activity relationship models (random forest) were introduced for the toxicity of 24 metal oxide ENMs towards BEAS-2B and RAW 264.7 cell lines |
| [52] | A classification model was built for 24 metal oxide ENMs based on the dissolution of metals and energy of conduction band (Ec) |
| Toxicity to Escherichia coli (E. coli) | |
| [31] | Global classification models were developed to predict the ecotoxicity of metallic ENMs to different species; classification models were also built for Danio rerio, Daphnia magna, Pseudokirchneriella subcapitata, and Staphylococcus aureus |
| [37] | Using the toxicity dataset of 17 metal oxide ENMs to E. coli, models were built with the MLR and partial least squares methods |
| [38] | Perturbation model was introduced for the prediction of ecotoxicity and cytotoxicity of ENMs; molar volume, electronegativity, polarizability, size of the particles, hydrophobicity, and polar surface area were involved in the model |
| [43] | A quantitative model was developed based on the toxicity data of 16 metal oxide ENMs to E. coli using enthalpy of formation of a gaseous cation (ΔHMe+) and polarization force (Z/r). The toxicity of 35 other metal oxide ENMs was predicted and depicted in the periodic table |
| [44] | Models were constructed to predict the toxicity of 17 metal oxide ENMs to E. coli. The factors of molecular weight, cationic charge, mass percentage of metal elements, individual and aggregation sizes were discussed |
| [46] | Toxicity and photo-induced toxicity of 17 metal oxide ENMs to E. coli was assessed using a self-written least-squares fitting program |
| [17] | Predicted the cytotoxicity of 17 metal oxide ENMs to E. coli with only one descriptor: enthalpy of formation of a gaseous cation having the same oxidation state as that in the metal oxide structure |
| [47] | Predictive models were built based on the toxicity of 17 different metal oxide ENMs to E. coli |
| [48] | Based on random forest regression, developed predictive classification models for the toxicity of 17 metal oxide ENMs to E. coli |
| [50] | Estimated the toxicity of 17 metal oxide ENMs to E. coli by employing the SMILES-based (simplified molecular input line entry system) optimal descriptors |
| Nano-(Q)SAR | Dataset Used | Number of ENMs | Core of ENMs | Tested Organism |
|---|---|---|---|---|
| [37] | [17] | 17 | Metal oxide | Escherichia coli (E. coli) |
| [43] | ||||
| [44] | ||||
| [17] | ||||
| [47] | ||||
| [48] | ||||
| [50] | ||||
| [30] | [53] | 146 | Metal oxide | PaCa2 pancreatic cancer cells (PaCa2) |
| [32] | ||||
| [33] | ||||
| [35] | ||||
| [36] | ||||
| [47] | ||||
| [51] | ||||
| [32] | [54] | 50 | Metal oxide and quantum dots | Endothelial cells, vascular smooth muscle cells, human HepG2 cells, RAW 264.7 cells |
| [33] | ||||
| [40] | ||||
| [47] | ||||
| [34] | [34] | 18 | Metal oxide | HaCaT cells |
| [44] | ||||
| [48] | ||||
| [41] | [52] | 24 | Metal oxide | BEAS-2B cells; RAW 264.7 cells |
| [49] | ||||
| [52] | ||||
| [39] | [39] | 9 | Metal oxide | BEAS-2B cells |
| [45] | [55] | 24 TiO2, 18 ZnO ENMs | TiO2, ZnO ENMs | Rat L2 lung epithelial cells; rat lung alveolar macrophages |
| [46] | [46] | 17 | Metal oxide | E. coli |
| [29] | Others | |||
| [31] | ||||
| [38] | ||||
| [42] | ||||
| Reference | Method of ENM Characterization | Data Accessibility | ENM Number | Other Information |
|---|---|---|---|---|
| [53] | 146 | Molecular weight and structures | ||
| [30] | 679 one-dimensional (1D), two-dimensional (2D) chemical descriptors of modifiers were calculated using PaDEL-Descriptor (v2.8) | Values of PaCa2 pancreatic cancer cells (PaCa2) cellular uptake were available (unit: number of ENMs per cell) | 109 | SMILES (simplified molecular input line entry system) |
| [32] | 691 molecular descriptors of modifiers from DRAGON (v5.5), ADRIANA (v2.2) and an in-house modeling software package | 108 | List of modifiers | |
| [33] | MOE descriptors for modifiers were used, including physical properties, surface areas, atom and bond counts, Kier & Hall connectivity indices, kappa shape indices, adjacency and distance matrix descriptors, pharmacophore feature descriptors, and molecular charges | Values of PaCa2 cellular uptake were available (log10[ENM]/cell pM) | 109 | SMILES |
| [35] | Hyperchem program (v7) for constructing molecular structure of modifiers; geometry was optimized with the Austin Model 1 (AM1) semiempirical method; DRAGON for descriptor calculation | Values of PaCa2 cellular uptake were available (log10[ENM]/cell pM ) | 109 | List of modifiers and SMILES |
| [36] | A pool of 307 descriptors of modifiers was calculated using Cerius 2 (v4.10), DRAGON 6 and PaDEL-Descriptor (v2.11) | Values of PaCa2 cellular uptake were available (log10[ENM]/cell pM) | 109 | List of modifiers |
| [47] | 174 molecular descriptors for the modifiers (topological, electronic, geometrical, and constitutional) were calculated using Chemistry Development Kit (CDK v1.0.3) | 109 | List of modifiers, chemical structures and SMILES | |
| [51] | SMILES-based optimal descriptors were used | 109 | SMILES, correlation weights (CWs) of SMILES attributes (SA) |
| Quantum-Mechanical Descriptors | Image Descriptors |
|---|---|
|
|
| Endpoint or Descriptor a | Al2O3 | Bi2O3 | CoO | Cr2O3 | CuO | Fe2O3 | In2O3 | La2O3 | NiO | Sb2O3 | SiO2 | SnO2 | TiO2 | V2O3 | Y2O3 | ZnO | ZrO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Effect concentrations and descriptor information from the study by Puzyn et al. [17] | |||||||||||||||||
| log 1/EC50 (mol/L) | 2.49 | 2.82 | 3.51 | 2.51 | 3.2 | 2.29 | 2.81 | 2.87 | 3.45 | 2.64 | 2.2 | 2.01 | 1.74 | 3.14 | 2.87 | 3.45 | 2.15 |
| HoF (kcal/mol) | −8244 | −1966 | −8800 | −2829 | −955 | −1051 | −3088 | N/A b | 64 | −2141 | −4118 | −2611 | −9826 | −3193 | −11,486 | −5307 | −9835 |
| TE (au c) | −31,466 | −36,108 | −17,007 | −20,104 | −45,632 | −6971 | −40,745 | N/A | −28,053 | −18,039 | −21,060 | −41,962 | −31,518 | −26,083 | −30,634 | −23,158 | −23,405 |
| EE (au) | −63,0309 | −695,663 | −298,812 | −307,815 | −874,569 | −44,000 | −872,315 | N/A | −432,596 | −221,602 | −321,879 | −874,369 | −576,824 | −441,766 | −511,019 | −379,005 | −358,169 |
| Core (au) | 598,843 | 659,555 | 281,806 | 287,711 | 828,937 | 37,029 | 831,570 | N/A | 404,543 | 203,563 | 300,818 | 832,407 | 545,306 | 415,683 | 480,385 | 355,847 | 334,764 |
| CA (A^2) | 1109 | 1551 | 1072 | 659 | 639 | 243 | 1314 | N/A | 659 | 975 | 753 | 1734 | 1100 | 1130 | 1805 | 855 | 1055 |
| CV (A^3) | 2260 | 4107 | 1548 | 1161 | 1108 | 319 | 3095 | N/A | 1088 | 1797 | 1467 | 3959 | 2340 | 2426 | 5401 | 1849 | 2403 |
| HOMO (eV) | −4.9 | −4.1 | −10.5 | −6.9 | −6.1 | −7.1 | −8.2 | N/A | −5.8 | −8.3 | −7.1 | −6.1 | −10.3 | −3.5 | −1.3 | −10.8 | −6.2 |
| LUMO (eV) | −0.29 | −1.4 | −8.28 | −0.49 | −2.25 | −0.68 | −3.37 | N/A | −1.03 | −1.03 | −3.89 | −2.29 | −2.86 | 0.64 | 1.2 | −6.89 | −4.54 |
| GAP (eV) | −4.59 | −2.71 | −2.2 | −6.41 | −3.85 | −6.45 | −4.79 | N/A | −4.73 | −7.27 | −3.23 | −3.85 | −7.47 | −4.17 | −2.48 | 3.87 | −1.65 |
| ΔHClust (kcal/mol) | −8017 | −1601 | −8318 | −2264 | −759 | −140 | −3190 | N/A | 325 | −1526 | −3295 | −2091 | −8731 | −3157 | −11,485 | −5357 | −8956 |
| ΔHMe+ (kcal/mol) | 1188 | 1137 | 602 | 1269 | 706 | 1408 | 1271 | 1017 | 597 | 1233 | 1686 | 1717 | 1576 | 1098 | 837 | 662 | 1358 |
| ΔHL (kcal/mol) | −3695 | −3199 | −933 | −3645 | −992 | −3589 | −3449 | −2969 | −965 | −3281 | −3158 | −2821 | −2896 | −3555 | −3111 | −971 | −2641 |
| Descriptor information from the study by Kar et al. [37] | |||||||||||||||||
| χ | 1.61 | 2.02 | 1.88 | 1.66 | 1.9 | 1.83 | 1.78 | 1.1 | 1.91 | 2.05 | 1.9 | 1.96 | 1.54 | 1.63 | 1.22 | 1.65 | 1.33 |
| ∑χ | 3.22 | 4.04 | 1.88 | 3.32 | 1.9 | 3.66 | 3.56 | 2.2 | 1.91 | 4.1 | 1.9 | 1.96 | 1.54 | 3.26 | 2.44 | 1.65 | 1.33 |
| ∑χ/nO | 1.073 | 1.347 | 1.880 | 1.107 | 1.900 | 1.220 | 1.187 | 0.733 | 1.910 | 1.367 | 0.95 | 0.98 | 0.77 | 1.087 | 0.813 | 1.650 | 0.665 |
| MW | 102.0 | 466.0 | 74.9 | 152.0 | 79.5 | 159.6 | 277.6 | 325.8 | 74.7 | 291.5 | 60.1 | 150.7 | 79.9 | 149.9 | 225.8 | 81.4 | 123.2 |
| NMetal | 2 | 2 | 1 | 2 | 1 | 2 | 2 | 2 | 1 | 2 | 1 | 1 | 1 | 2 | 2 | 1 | 1 |
| NOxygen | 3 | 3 | 1 | 3 | 1 | 3 | 3 | 3 | 1 | 3 | 2 | 2 | 2 | 3 | 3 | 1 | 2 |
| χox | 3 | 3 | 2 | 3 | 2 | 3 | 3 | 3 | 2 | 3 | 4 | 4 | 4 | 3 | 3 | 2 | 4 |
| Descriptor information from the studies of Singh and Gupta [47] and Toropov et al. [50] | |||||||||||||||||
| SMILES notation | O = [Al]O[Al] = O | O = [Bi]O[Bi] = O | [Co] = O | O = [Cr]O[Cr] = O | [Cu] = O | O = [Fe]O[Fe] = O | O = [In]O[In] = O | O = [La]O[La] = O | [Ni] = O | O = [Sb]O[Sb] = O | O = [Si] = O | O = [Sn] = O | O = [Ti] = O | O = [V]O[V] = O | O = [Y]O[Y] = O | O = [Zn] | O = [Zr] = O |
| Descriptor information from the study by Sizochenko et al. [48] | |||||||||||||||||
| Size (nm) | 44 | 90 | 100 | 60 | N/A | 32 | 30 | 46 | 30 | 20 | 150 | 15 | 46 | 15 | 38 | 71 | 47 |
| Aggregation size (nm) | 372 | 2029 | 257 | 617 | N/A | 298 | 224 | 673 | 291 | 223 | 640 | 810 | 265 | 1307 | 1223 | 189 | 661 |
| Effect concentrations and descriptor information from the study by Pathakoti et al. [46] | |||||||||||||||||
| toxicity under darkness, log 1/EC50 (mol/L) | 2.42 | 3.55 | 3.13 | 2.06 | 4.24 | 2.4 | 2.83 | 4.96 | 3.79 | 3.12 | 2.54 | 2.53 | 2.14 | 3.48 | 5.79 | 5.8 | 2.58 |
| toxicity under sunlight exposure, log 1/EC50 (mol/L) | 2.75 | 4.02 | 3.33 | 2.06 | 5.71 | 2.54 | 3.48 | 5.56 | 3.87 | 3.66 | 2.92 | 3.24 | 4.68 | 3.78 | 5.84 | 6.23 | 3.04 |
| Particle size (vendor) (nm) | <50 | 90–210 | <100 | <100 | <50 | <50 | <100 | <100 | <50 | 90–210 | 10–20 | <100 | <100 | N/A | <50 | <100 | <100 |
| Particle size TEM (nm) | 55 ± 17 | 144 ± 7 | 55 ± 13 | 47 ± 27 | 28 ± 7 | 68 ± 20 | 60 ± 14 | 65 ± 19 | 14 ± 9 | 84 ± 23 | 20 ± 5 | 15 ± 4 | 42 ± 9 | N/A | 38 ± 9 | 71 ± 17 | 27 ± 6 |
| Hydrodynamic size (nm) | 330 | 4084 | 262 | 426 | 285 | >6000 | 308 | 508 | 399 | 619 | 1230 | 3971 | 748 | 307 | 357 | 1614 | 2337 |
| Zeta potential (mV) (H2O) | 30.3 ± 1.3 | −(16.5 ± 0.8) | 17.5 ± 1.5 | −(12.0 ± 1.3) | 24.4 ± 0.6 | −(6.3 ± 1.0) | 22.6 ± 0.4 | −(3.6 ± 1.1) | 26.0 ± 0.4 | −20.7 ± 1.3 | −29.8 ± 1.9 | −21.1 ± 0.4 | −(10.7 ± 2.5) | −(27.9 ± 0.9) | 16.3 ± 0.9 | −(20.9 ± 0.5) | −(6.9 ± 0.5) |
| Zeta potential (mV) (KCl) | 25.3 ± 1.1 | −(4.9 ± 0.1) | 26.0 ± 0.5 | 23.3 ± 1.0 | 19.1 ± 0.3 | −(19.5 ± 1.9) | 28.7 ± 0.4 | 22.3 ± 1.7 | 26.8 ± 1.2 | −(12.7 ± 0.4) | −(33.7 ± 1.6) | −(16.7 ± 0.2) | −(2.2 ± 0.4) | −(32.6 ± 0.5) | 17.9 ± 1.0 | −(24.9 ± 0.3) | 4.0 ± 2.7 |
| Surface area (m2/g) | 37 | N/A | >8 | N/A | 33 | 36 | 28 | 20 | 80 | N/A | N/A | 18.6 | 36 | N/A | 31 | 15 | 22 |
| HHOMO (au) | −0.283 | −0.253 | −0.221 | −0.245 | −0.236 | −0.283 | −0.265 | −0.187 | −0.241 | −0.262 | −0.343 | −0.305 | −0.265 | −0.219 | −0.189 | −0.228 | −0.243 |
| LZELEHHO (au) | 0.211 | 0.184 | 0.169 | 0.199 | 0.178 | 0.175 | 0.196 | 0.121 | 0.180 | 0.174 | 0.245 | 0.224 | 0.195 | 0.174 | 0.129 | 0.132 | 0.184 |
| LUMOA (au) | −0.138 | −0.116 | −0.116 | −0.152 | −0.121 | −0.066 | −0.127 | −0.054 | −0.120 | −0.086 | −0.147 | −0.143 | −0.125 | −0.129 | −0.068 | −0.036 | −0.125 |
| LUMOB (au) | −0.138 | −0.116 | −0.131 | −0.117 | −0.119 | −0.163 | −0.127 | −0.054 | −0.114 | −0.086 | −0.147 | −0.143 | −0.125 | −0.106 | −0.068 | −0.139 | −0.125 |
| ALZLUMO (au) | −0.138 | −0.116 | −0.123 | −0.135 | −0.120 | −0.114 | −0.127 | −0.054 | −0.117 | −0.086 | −0.147 | −0.143 | −0.125 | −0.117 | −0.068 | −0.087 | −0.125 |
| Cp (J mol−1 K−1) | 79.04 | 113.51 | 55.23 | 118.74 | 42.3 | 103.85 | 92 | 108.78 | 44.31 | 101.63 | 44.43 | 52.59 | 55.48 | 103.22 | 102.51 | 40.25 | 56.19 |
| MHOMOA (au) | −0.218 | −0.319 | −0.232 | −0.222 | −0.289 | −0.229 | −0.202 | −0.188 | −0.236 | −0.334 | −0.301 | −0.267 | −0.232 | −0.247 | −0.211 | −0.293 | −0.232 |
| MLUMOA (au) | 0.017 | 0.114 | 0.036 | 0.027 | 0.036 | 0.031 | 0.010 | 0.015 | 0.035 | 0.130 | −0.007 | −0.017 | 0.021 | 0.024 | 0.018 | 0.043 | 0.016 |
| QMELECT (au) | 0.101 | 0.103 | 0.098 | 0.097 | 0.126 | 0.099 | 0.096 | 0.086 | 0.101 | 0.102 | 0.154 | 0.142 | 0.106 | 0.111 | 0.097 | 0.125 | 0.108 |
| Reference | Descriptor or Identified Factor by Developed Models | Dataset |
|---|---|---|
| Studies of modeling cellular take of ENMs | ||
| [30] | Number of CH2 groups, primary, secondary and tertiary nitrogen, halogens (fluorine, bromine, iodine), sulfur atoms, fused rings, hydrogen bonding | [53] |
| [32] | Number of 10 membered rings (nR10), molecular asphericity (ASP), d COMMA2 value/weighted by atomic masses (DISPm), Qzz COMMA2 value/weighted by atomic masses (QZZm), number of secondary amides, aliphatic (nRCONHR), number of (thio-) carbamates, aromatic (nArOCON), CH3X (C-005), number of circuits (nCIR), number of N atoms (nN), average molecular span R (SPAM), Qyy COMMA2 value/weighted by atomic polarizabilities (QYYp), number of total secondary C sp3 (nCs), number of aromatic hydroxyls (nArOH), H attached to C0(sp3) with 2X attached to next C (H-053), =O (O-058) | |
| [33] | Surface area “owned” with SlogP weight −10 to −0.40 (SlogP_VSA0), surface area “owned” with SlogP weight −0.40 to −0.20 (SlogP_VSA1), surface area “owned” with SlogP weight −0.20 to 0 (SlogP_VSA2), surface area “owned” with SlogP weight −0.15 to −0.20 (SlogP_VSA5), van der Waals surface area surface area of hydrogen-bond donors (vsa_don), van der Waals surface area of nondonor/-acceptor atoms (vsa_other), van der Waals surface area surface area of basic atoms (vsa_base), sum of the van der Waals surface area of atoms whose PEOE partial charge is positive, divided by the total surface area (PEOE_VSA_FPOS), van der Waals surface area where atomic partial charge 0.05 < q < 0.10 (PEOE_VSA+1), number of double bonds, aromatic bonds are not considered (b_double) | |
| [35] | Number of donor atoms for H-bonds (nHDon), Geary autocorrelation of lag 1 weighted by van der Waals volume (GATS1v), 3D-MoRSE-signal 29/unweighted (Mor29u), D total accessibility index/weighted by Sanderson electronegativity (De), 3D-MoRSE-signal 14/unweighted (Mor14u), mean electrotopological state (Ms) | |
| [36] | Hydrophobicity of the N atom in primary aliphatic amine (Al-NH2) fragment (Atype-N-66), hydrophobicity of the N atom in a secondary aliphatic amine (Al2-NH) fragment (Atype-N-67), measure of electronic features of the molecule relative to molecular size (∑β'), relative positive charge surface area (Jurs-RPCS), all-path Wiener index (Wap), number of aliphatic nitro groups (nRNO2) | |
| [47] | Weighted partial negative surface area-3 (WNSA-3), weighted partial positive area-2 (WPSA-2), Chi simple path descriptor of order 5 (SP-5), Chi valance path descriptor of order 4 (VP-4), moment of inertia along X/Z-axis (MOMI-XZ), logarithmic form of octanol-water partition coefficient predicted by atomic method (XlogP), number of rotatable bonds (nRotB), number of hydrogen bond donors (nHBDon), Chi valance path cluster of order 6 (VPC-6), ionization potential (IP), number of hydrogen acceptors (nHBAcc) | |
| Studies of modeling cytotoxicity of ENMs to cell lines | ||
| [34] | Enthalpy of formation of metal oxide nanocluster representing a fragment of the surface (∆Hfc), Mulliken’s electronegativity of the nanocluster (χc) | [34] |
| [44] | Molecular weight, cationic charge, mass percentage of metal elements, individual size, aggregation size | |
| [48] | Unbonded two-atomic fragments [Me]···[Me] (S1), Wigner-Seitz radius of oxide’s molecule (rw), mass density (ρ), covalent index of the metal ion (CI), SiRMS-derived number of oxygen’s atoms in a molecule (S2), aggregation parameter (AP) | |
| [32] | Core material (IFe3O4), surface coating (Idextran), surface charge (Isurf.chg) | [54] |
| [33,40,47] | Size, R1 relaxivity, R2 relaxivity, zeta potential | |
| [52] | Conduction band energy (Ec), solubility of metals | [52] |
| [41] | Ionic index of metal cation (Z2/r), ENM conduction band energy (Ec), metal oxide ionization energy (∆HIE), metal oxide electronegativity (χMeO), atomization energy of metal oxide (EAmz), primary size (d), atomic mass of ENM metal (mMe) | |
| [49] | Mass density, molecular weight, aligned electronegativity, covalent index, cation polarizing power, Wigner-Seitz radius, surface area, surface-area-to-volume ratio, aggregation parameter, two-atomic descriptor of van der Waals interactions, tri-atomic descriptor of atomic charges, tetra-atomic descriptor of atomic charges, size in DMEM | |
| [45] | Size of ENMs (X0), size in water (X1), size in phosphate buffered saline (X2), concentration (X4), zeta potential (X5) | [55] |
| [39] | Size of ENM (d), volume concentration (θv), period of the ENM metal in the periodic table (PMe), atomization energy of the metal oxide (EMeO) | [39] |
| [42] | Molar volume, polarizability, size of ENMs, electronegativity, hydrophobicity and polar surface area of surface coatings | Others |
| Studies of modeling the toxicity of ENMs to species | ||
| [46] | Absolute electronegativity of the metal atom (QMELECT), absolute electronegativity of the metal oxide (LZELEHHO), literature molar heat capacity of the metal oxide at 298.15 K (Cp), average of the alpha and beta LUMO energies of the metal oxide (ALZLUMO) | [46] |
| [17] | Enthalpy of formation of a gaseous cation having the same oxidation state as that in the metal oxide structure (∆HMe+) | [17] |
| [37] | Charge of the metal cation corresponding to a given oxide (χox), metal electronegativity (χ) | |
| [43] | Enthalpy of formation of a gaseous cation having the same oxidation state as that in the metal oxide structure (∆HMe+), polarization force (Z/r) | |
| [44] | Molecular weight, cationic charge, mass percentage of metal elements, individual size, aggregation size | |
| [47] | Oxygen percent, molar refractivity, polar surface area | |
| [48] | Unbonded two-atomic fragments [Me]···[Me] (S1), Wigner-Seitz radius of oxide’s molecule (rw), mass density (ρ), cation polarizing power (CPP), SiRMS-derived number of oxygen’s atoms in a molecule (S2), tri-atomic fragments [Me]-[O]-[Me] (S3), proportion of surface molecules to molecules in volume (SV) | |
| [31] | Molecular polarizability, accessible surface area, solubility | Others |
| [38] | Molar volume, polarizability, size of ENMs, electronegativity, hydrophobicity and polar surface area of surface coatings | Others |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Vijver, M.G.; Xiao, Y.; Peijnenburg, W.J.G.M. A Review of Recent Advances towards the Development of (Quantitative) Structure-Activity Relationships for Metallic Nanomaterials. Materials 2017, 10, 1013. https://doi.org/10.3390/ma10091013
Chen G, Vijver MG, Xiao Y, Peijnenburg WJGM. A Review of Recent Advances towards the Development of (Quantitative) Structure-Activity Relationships for Metallic Nanomaterials. Materials. 2017; 10(9):1013. https://doi.org/10.3390/ma10091013
Chicago/Turabian StyleChen, Guangchao, Martina G. Vijver, Yinlong Xiao, and Willie J.G.M. Peijnenburg. 2017. "A Review of Recent Advances towards the Development of (Quantitative) Structure-Activity Relationships for Metallic Nanomaterials" Materials 10, no. 9: 1013. https://doi.org/10.3390/ma10091013





