Effect of the Elastic Deformation of a Point-Sharp Indenter on Nanoindentation Behavior

Abstract

The effect of the elastic deformation of a point-sharp indenter on the relationship between the indentation load P and penetration depth h (P-h curve) is examined through the numerical analysis of conical indentations simulated with the finite element method. The elastic deformation appears as a decrease in the inclined face angle β, which is determined as a function of the elastic modulus of the indenter, the parabolic coefficient of the P-h loading curve and relative residual depth, regardless of h. This indicates that nominal indentations made using an elastic indenter are physically equivalent to indentations made using a rigid indenter with the decreased β. The P-h curves for a rigid indenter with the decreased β can be estimated from the nominal P-h curves obtained with an elastic indenter by using a procedure proposed in this study. The elastic modulus, yield stress, and indentation hardness can be correctly derived from the estimated P-h curves.

1. Introduction

Nanoindentation is a form of mechanical testing characterized as a depth-sensing indentation [1] to evaluate local mechanical properties through the analysis of the indentation load P versus the penetration depth h (P-h curve, hereafter). The analysis is principally based on a geometrical definition in which the indentation is carried out on a flat surface using an indenter geometrically defined such as flat-ended, spherical, ellipsoidal, point-sharp (e.g., conical, Berkovich, Vickers, cube corner, etc.). The point-sharp indentation has an advantage in local mechanical testing owes to the analytical simplicity for the geometrical similarity [2].

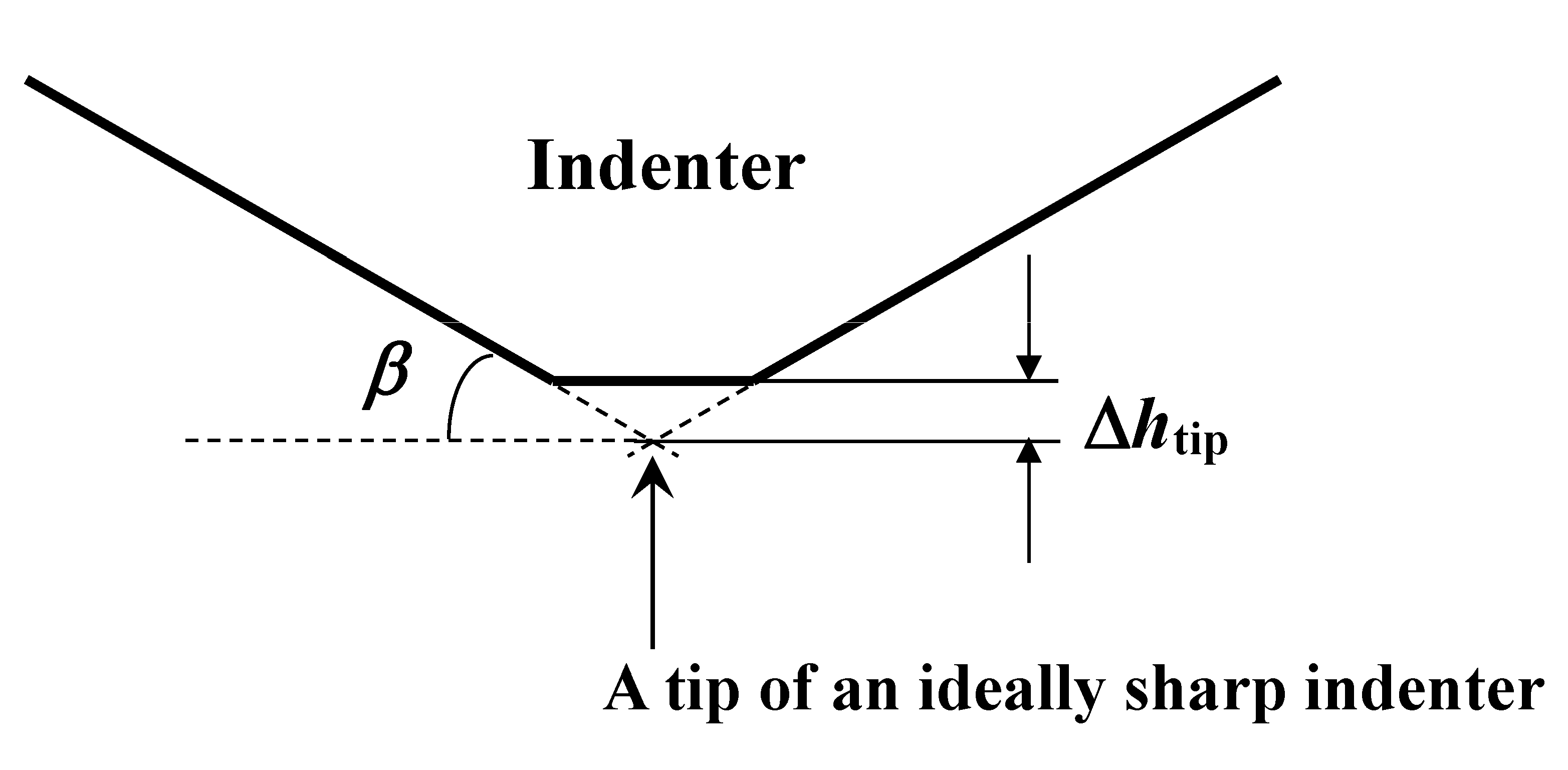
The bluntness of the indenter tip is one of the inevitable problems of undesirable tip geometry, especially for the point-sharp indentations, because it is impossible to make an ideally sharp indenter. The degree of the bluntness of a point-sharp indenter has been expressed in terms of the radius of curvature at the tip [3,4,5], but the actual geometry of a blunt tip is not guaranteed to be spherical. An area function [6,7] which gives the projected contact area at the maximum indentation load is another approach to express the bluntness of a point-sharp indenter, but the area function is theoretically valid only for hardness evaluation. A truncated tip which represents a blunt tip in an extremely poor situation [8] is a suitable model for a strict discussion on the effect of the tip bluntness on indentation behavior. According to the appendix of this paper, where a truncated tip is considered, the undesirable effect of the bluntness of a point-sharp indenter can be removed out simply if the P-h curve is shifted with Δh_tip in the h direction for indentations deeper than 2Δh_tip, where Δh_tip is the distance between ideally sharp and blunt tips (see Figure A1, Figure A2, Figure A3 and Figure A4). In addition, Δh_tip can be estimated through an extrapolation of the linear relationship between h and P*** observed in the large P and h region to P = 0 (see Figure A5).

The elastic deformation of an actual point-sharp indenter, which has been conventionally taken into account on the basis of Hertzian contact [6]; Hertzian contact was basically used for spherical indentations as a modification of the elastic modulus evaluation. It is also an inevitable problem of undesirable tip geometry, especially for indentations on a very hard material, and there is still some controversy whether the modification based on the Hertzian contact can be applied to point-sharp indentations. Moreover, there are no reports on the modifications of the indenter elastic deformation for other mechanical properties such as the indentation hardness or yield stress. The geometrical changes of a point-sharp indenter due to elastic deformation should be considered when evaluating local mechanical properties with the nanoindentation technique.

In this paper, the effect of the elastic deformation of a point-sharp indenter on a P-h curve is quantified in a numerical analysis of conical nanoindentation behaviors simulated with the finite element method (FEM). In addition, a procedure of deriving physically meaningful P-h curves, which should be utilized for mechanical property evaluation. Finally, the validity and accuracy of this method is examined.

2. FEM Simulation of Nanoindentation

A conical indentation on a cylindrical elastoplastic solid was modeled in order to avoid the difficulty of modeling a pyramidal indenter widely used for actual nanoindentations. The FEM simulation exploited the large strain elastoplastic capability of ABAQUS code (Version 5.8.1) in the same way as reported in the literature [9,10]. Indentation contact was simulated by the use of elastic cone indenters with two different inclined face angles β (19.7° and 30°). Young’s modulus of the elastic indenter was in the range of 300–1140 GPa. The finite-element mesh in the elastic indenter with β of 19.7° was composed of 775 4-node quadrilateral axisymmetric elements with 2443 nodes. The elastic indenter with β of 30° had 704 elements with 2258 nodes.

The FEM simulation used elastoplastic linear strain hardening rules, i.e., $\sigma =E\epsilon$ for $\sigma <Y$, and $\sigma =Y+E_p{\epsilon }_p$ for $\sigma \ge Y$, where σ is the stress, E the Young’s modulus and ε the strain. Here, Y is the yield stress and E_p ($\equiv d\sigma /d{\epsilon }_{\mathrm{p}}$) is the plastic strain hardening modulus, where dσ, dε, dε_e, and dε_p are, respectively, the incremental values of stress, total, elastic, and plastic strains. Indentations were simulated for E, Y and E_p ranges of 50–1000 GPa, 0.1–60 GPa, and 0–200 GPa, respectively. The von Mises criterion with isotropic hardening was used to determine the onset of yielding flow.

3. Results and Discussion

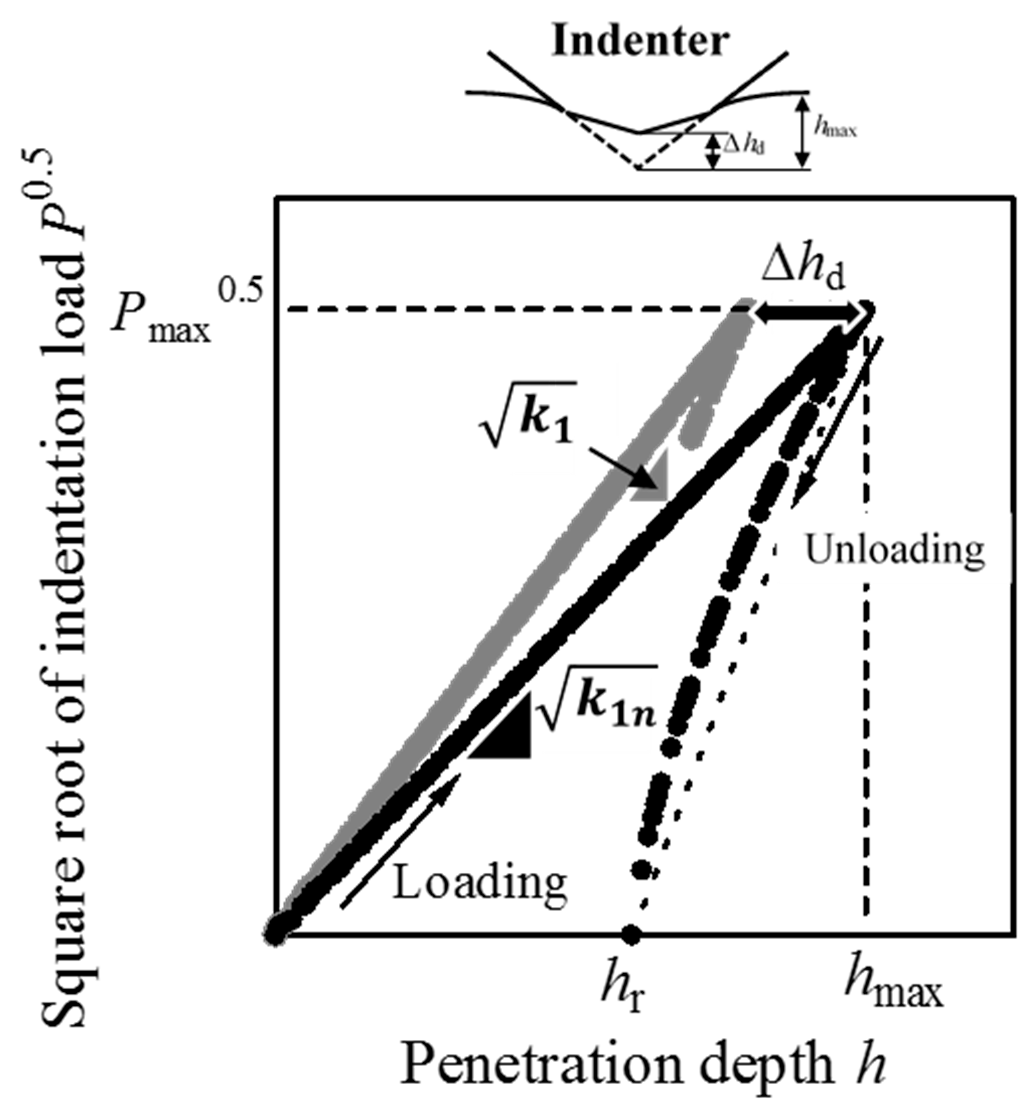
A quadratic relationship between P and h on loading is theoretically guaranteed for a point-sharp indentation on the flat surface of a homogeneous elastoplastic solid [11,12]. The quadratic relationship was also observed in simulated P-h curves made with an elastic cone indenter. This indicates that the elastic deformation of a cone indenter can be described as a decrease in β determined regardless of h. Therefore, nominal indentations made with an elastic cone indenter with an original inclined face angle β_o should be physically equivalent to indentations made with a rigid cone indenter with the decreased inclined face angle β_d.

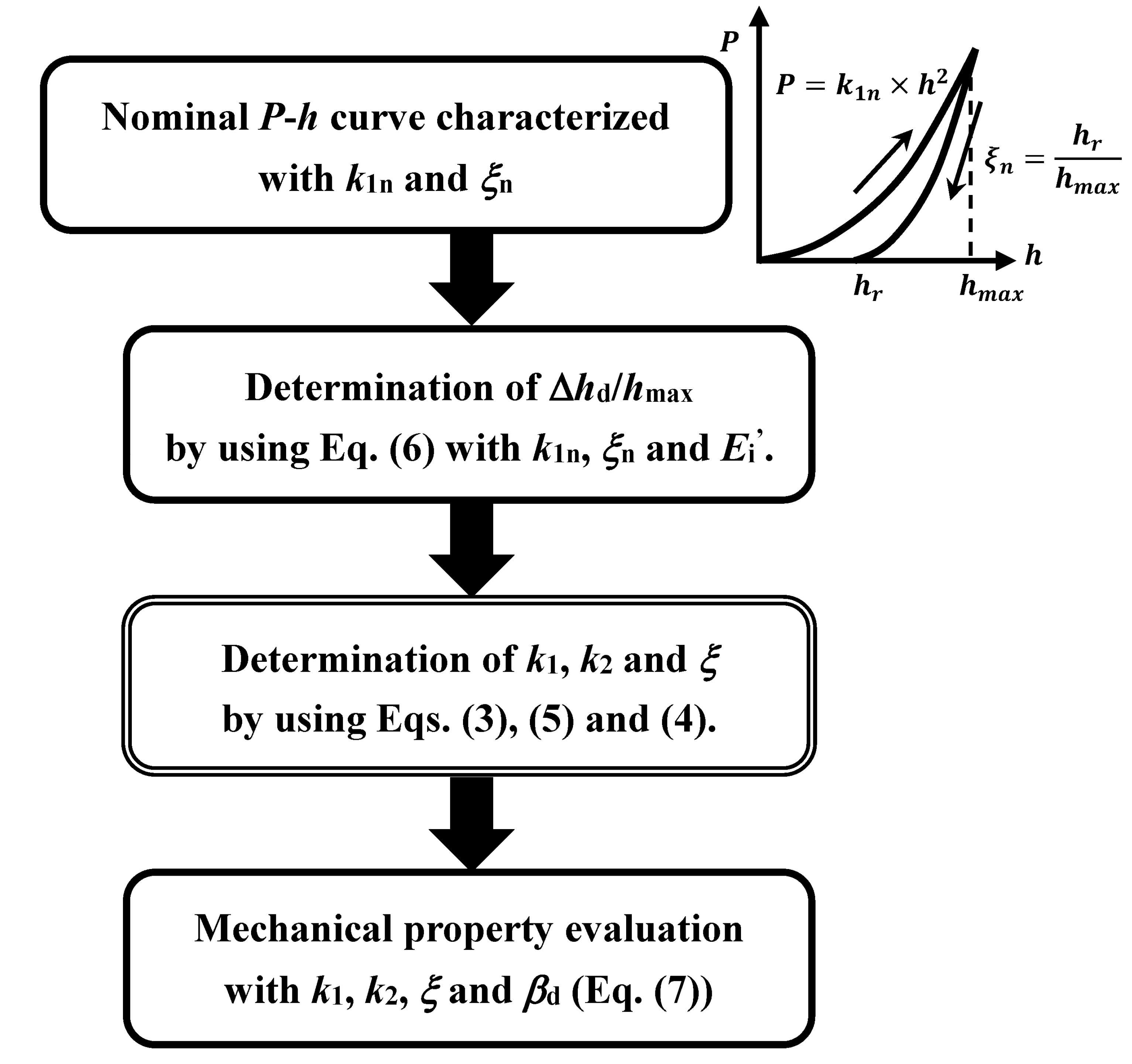
A nominal quadratic P-h relationship for an elastic cone indenter can be depicted as follows:

$$P=k_{1\mathrm{n}}{h}^2\text{ for loading},$$

(1)

where k_1n is the nominal indentation loading parameter. Here, h in Equation (1) is the nominal penetration depth because the decrease in β from β_o to β_d, due to the elastic deformation of a cone indenter, gives a decrease in real penetration depth. Thus, a physically meaningful P-h relationship can be written with a true indentation loading parameter k₁, which should be observed in a P-h loading curve using a rigid cone indenter with β_d as

$$P_{\max }=k_1{\left(h_{\max }-\Delta h_{\mathrm{d}}\right)}^2,$$

(2)

where Δh_d is the decrease in h at the maximum penetration depth h_max due to the elastic deformation of a cone indenter (see Figure 1). The combination of Equations (1) and (2) leads to the equation:

$$k_1=k_{1\mathrm{n}}{\left(1-\frac{\Delta h_{\mathrm{d}}}{h_{\max }}\right)}^{-2}.$$

(3)

This means that Δh_d/h_max is a key parameter to estimating k₁ from the nominal k_1n. In other words, Δh_d/h_max can be simulated as

$$\frac{\Delta h_{\mathrm{d}}}{h_{\max }}=1-\sqrt{\frac{k_{1\mathrm{n}}}{k_1}},$$

(3′)

where k_1n in Equation (3’) is observed in a simulated P-h loading curve with an elastic cone indenter and k₁ in Equation (3’) is evaluated with the mechanical properties inputted into the FEM model [9,10]. In the following paragraph, the effect of Δh_d/h_max on a P-h curve is examined quantitatively through numerical analysis.

In addition to k₁, the relative residual penetration depth ξ, defined as h_r/h_max, where h_r is the residual penetration depth, characterizes a P-h curve and nominally decreased by the elastic deformation of a cone indenter to be ξ_n. A true ξ-value, which should be observed in a P-h curve using a rigid cone indenter with β_d, can also be evaluated with the mechanical properties inputted into the FEM model [9,10]. The numerical analysis revealed that the evaluated ξ can be correlated with the nominal ξ_n as a function of Δh_d/h_max

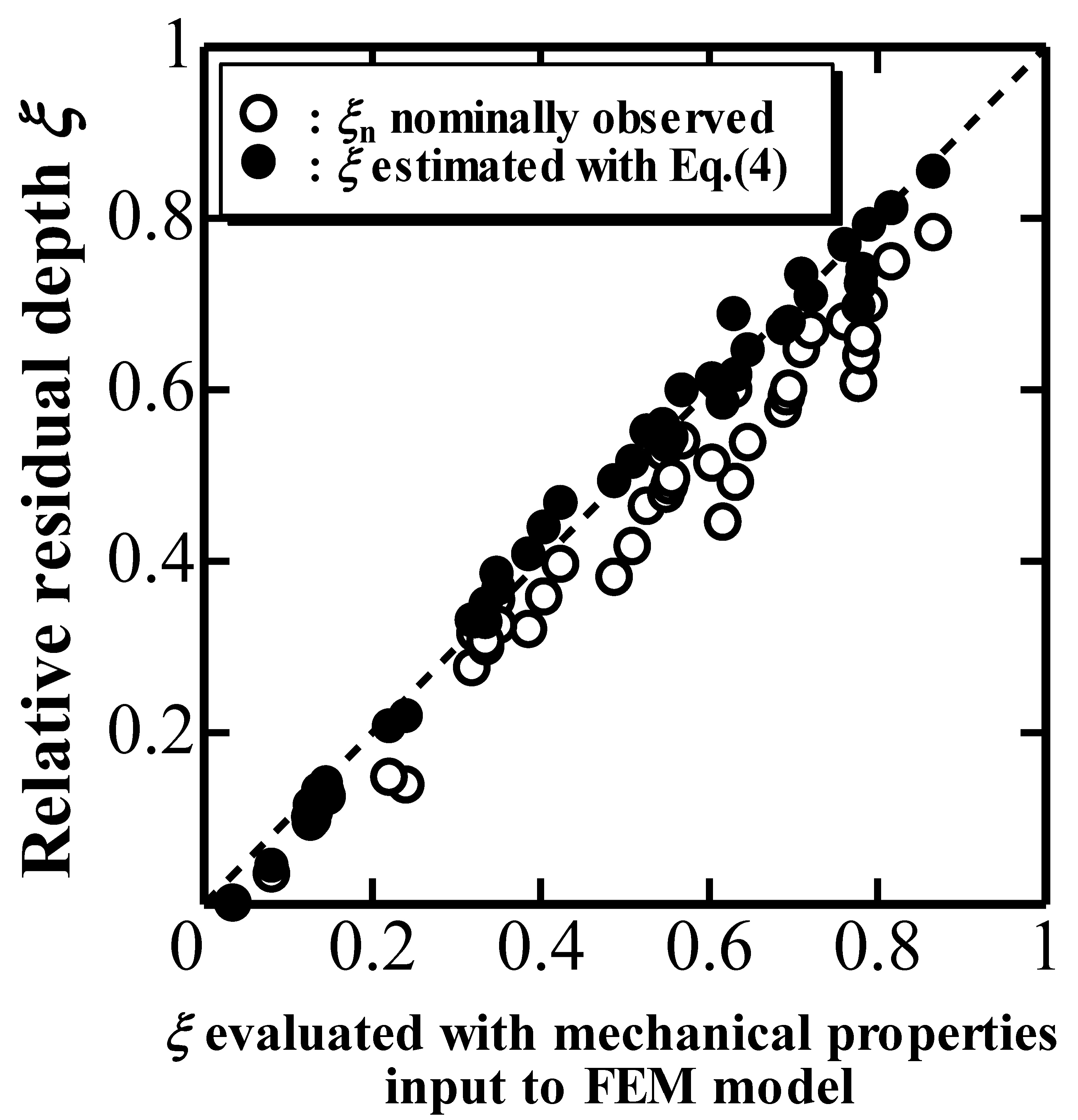
$$\xi ={\xi }_{\mathrm{n}}{\left\{1-{\left(\frac{\Delta h_{\mathrm{d}}}{h_{\max }}\right)}^{0.85}\right\}}^{-0.50}.$$

(4)

Figure 2 plots ξ estimated with Equation (4) and ξ_n against the true ξ evaluated with the mechanical properties inputted into the FEM model [9,10]. The results indicate the validity of using Equation (4) to estimate ξ from the nominal ξ_n and Δh_d/h_max. In addition, it is confirmed that ξ_n is smaller than ξ because of the overestimation of the penetration depth h due to the elastic deformation of the indenter. Moreover, a true indentation unloading parameter k₂ defined as P_max/(h_max − h_r)*, which should be observed in an P-h unloading curve using a rigid cone indenter with β_d, can be estimated from a simulated P-h curve with an elastic cone indenter characterized by k_1n and ξ_n using Equations (3) and (4) as

$$k_2=\frac{k_1}{{\left(1-\xi \right)}^2}=k_{1\mathrm{n}}{\left(1-\frac{\Delta h_{\mathrm{d}}}{h_{\max }}\right)}^{-2}{\left[1-{\xi }_{\mathrm{n}}{\left\{1-{\left(\frac{\Delta h_{\mathrm{d}}}{h_{\max }}\right)}^{0.85}\right\}}^{-0.50}\right]}^{-2}.$$

(5)

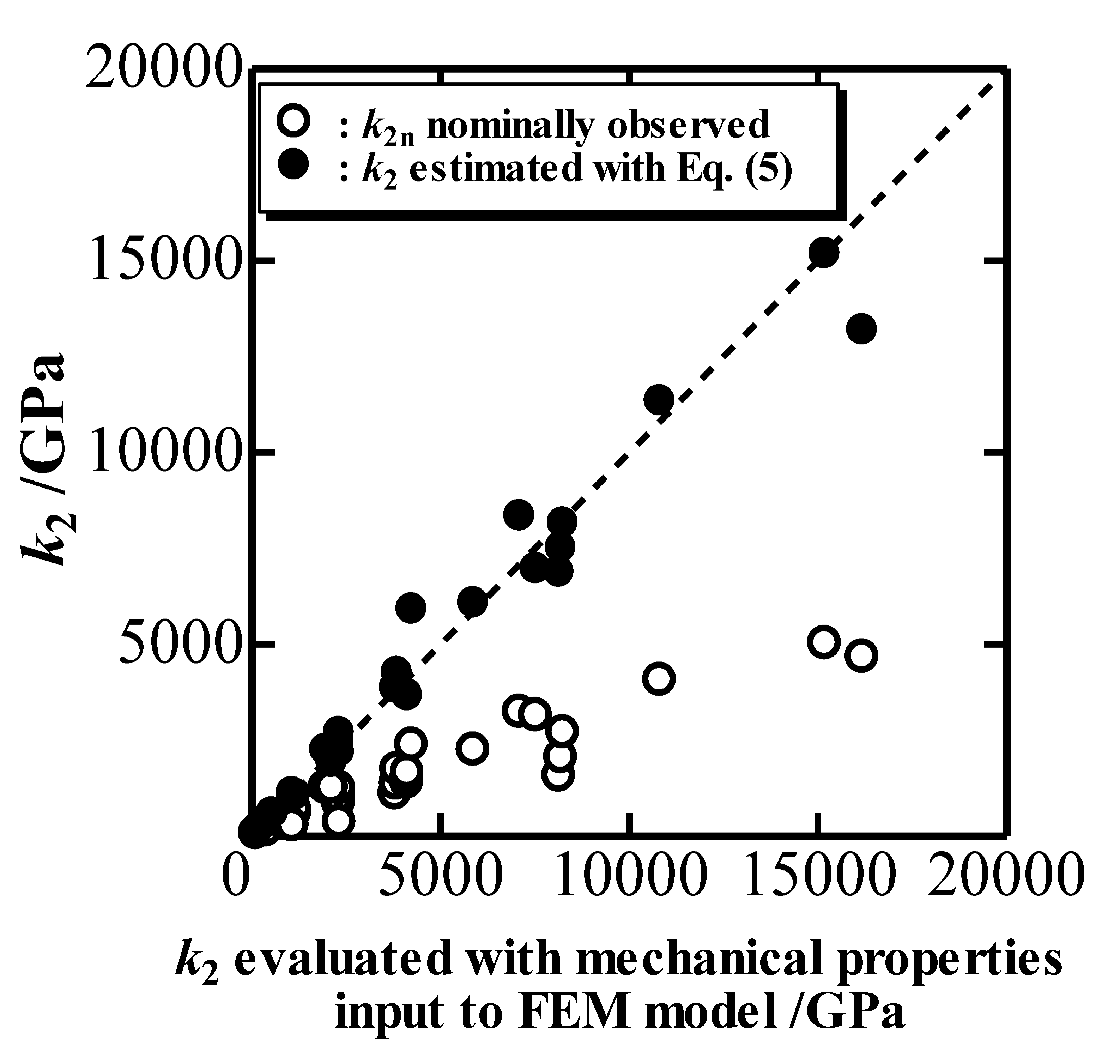
Figure 3 plots the estimated k₂ with Equation (5) as well as the nominal indentation unloading parameter k_2n determined from a simulated P-h curve with an elastic cone indenter against the true k₂ evaluated with the mechanical properties inputted into the FEM model [9,10]. Figure 3 indicates that k₂ can be estimated correctly by using Equation (5) with Δh_d/h_max, and that the nominal k_2n is quite far from k₂ owing to the overestimation of h.

The numerical analysis also revealed that Δh_d/h_max is determined to be

$$\frac{\Delta h_{\mathrm{d}}}{h_{\max }}=0.616{\left\{\frac{k_{1\mathrm{n}}}{{E_{\mathrm{i}}}^{\prime }\left(1+{{\xi }_{\mathrm{n}}}^{1.5}\right)}\right\}}^{0.84},$$

(6)

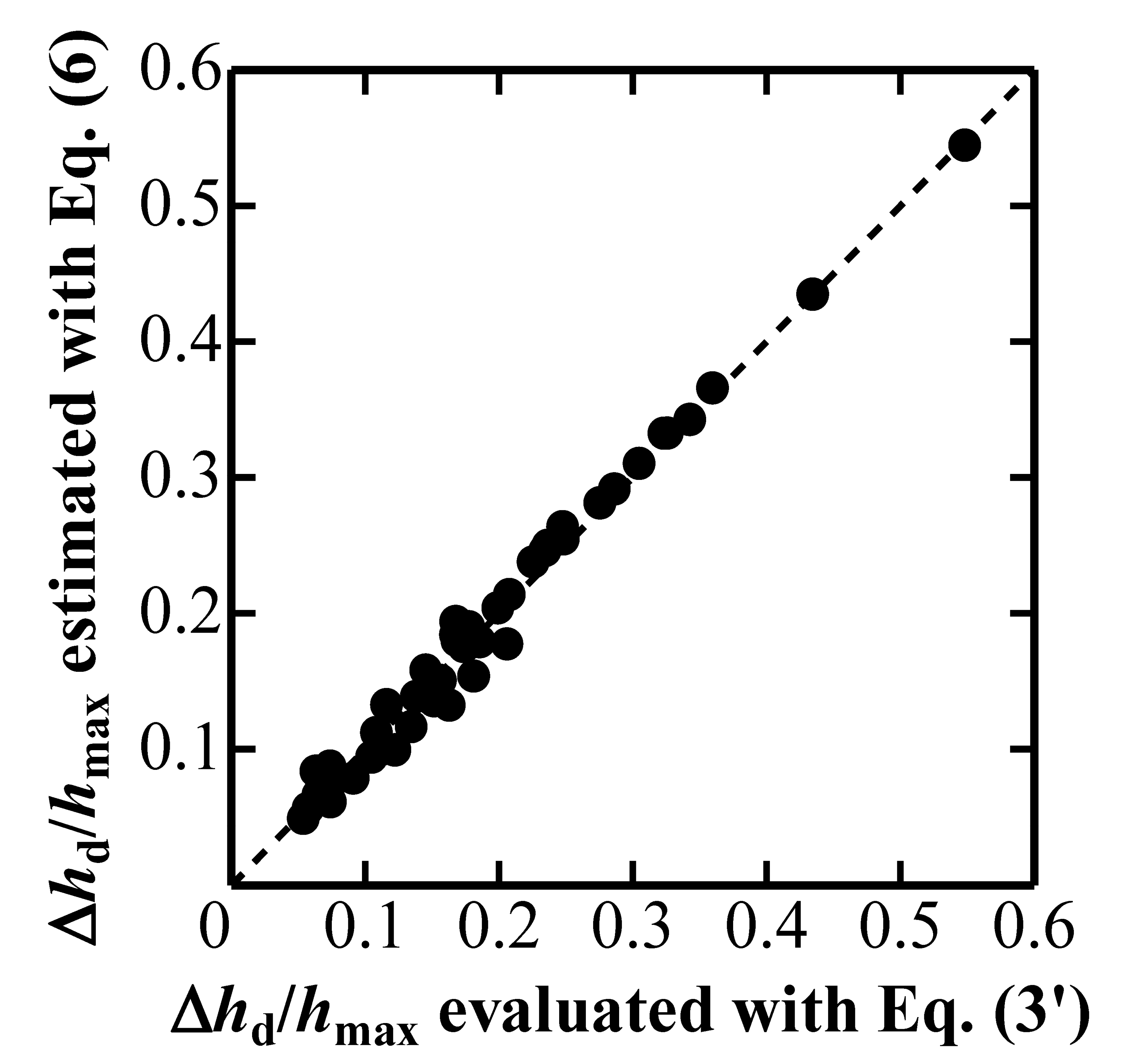
where E_i′ is defined as E_i/(1 − ν_i*) and E_i and ν_i are Young’s modulus and Poisson’s ratio of an elastic indenter, respectively. Figure 4 plots Δh_d/h_max estimated with Equation (6) against Δh_d/h_max evaluated with Equation (3’). Figure 3 indicates that Δh_d/h_max can be estimated by using Equation (6) with a nominally observed P-h curve characterized by k_1n and ξ_n, and with the elastic properties of an elastic indenter characterized by E_i and ν_i.

In order to estimate mechanical properties from a P-h curve characterized with k₁, k₂ and ξ, we should know the inclined face angle β_d of the elastically deformed indenter. Numerical analysis revealed that β_d is given as a function of β_o, ξ_n and Δh_d/h_max

$$\frac{\tan {\beta }_{\mathrm{d}}}{\tan {\beta }_{\mathrm{o}}}=1-{\left(1-{{\xi }_{\mathrm{n}}}^{0.80}\right)}^{0.83}{\left(\frac{\Delta h_{\mathrm{d}}}{h_{\max }}\right)}^{0.90}.$$

(7)

Figure 5 plots $\frac{\tan {\beta }_{\mathrm{d}}}{\tan {\beta }_{\mathrm{o}}}$ estimated with Equation (7) against $\frac{\tan {\beta }_{\mathrm{d}}}{\tan {\beta }_{\mathrm{o}}}$ observed in a simulated nanoindentation, and indicates the validity to estimate the inclined face angle β_d of the elastically deformed indenter with Δh_d/h_max.

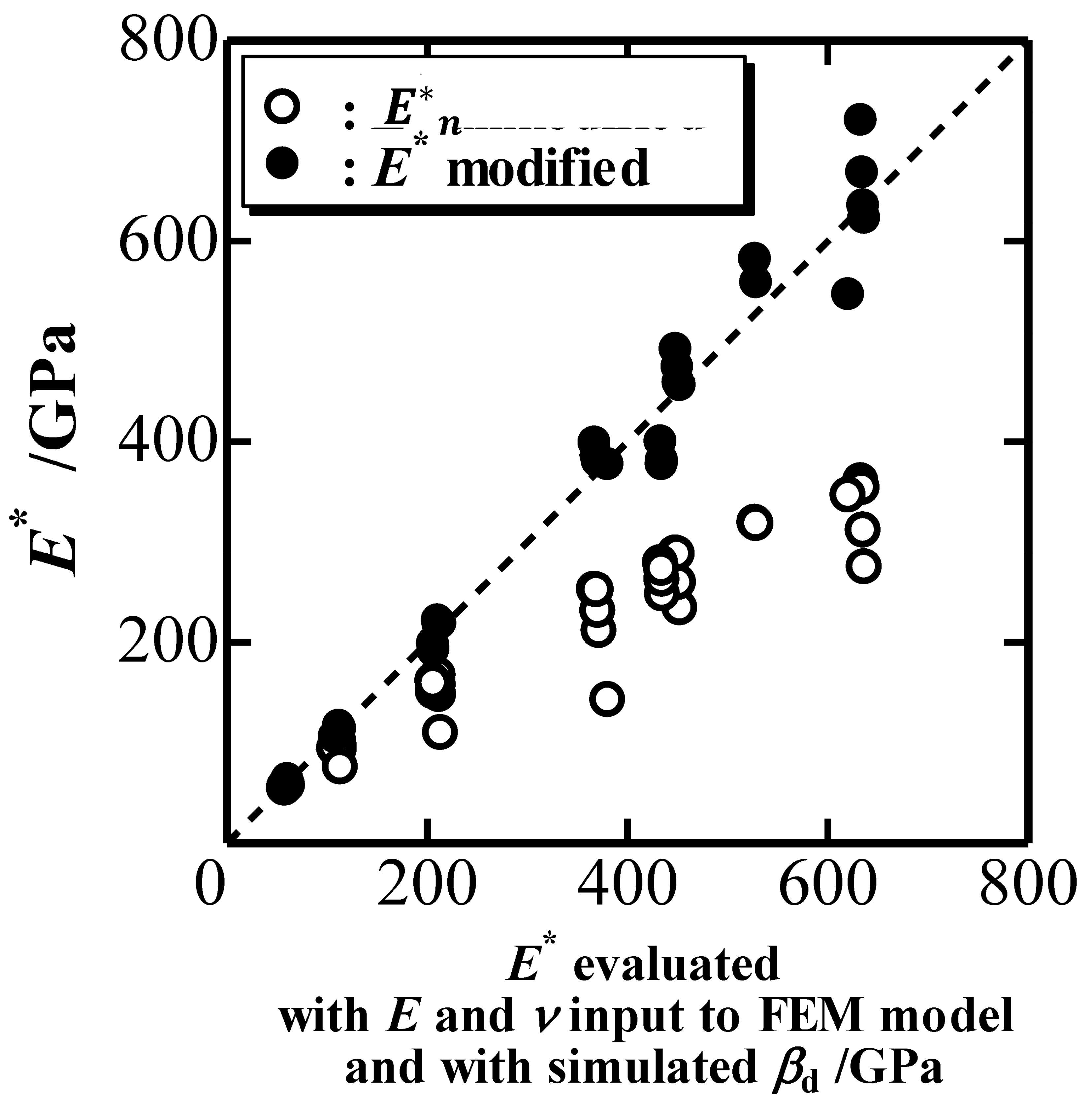
The representative indentation elastic modulus E*, defined as $E^{*}=\frac{E}{1-{\left(\nu -0.225{\tan }^{1.05}{\beta }_{\mathrm{d}}\right)}^2}$ in terms of β_d [9], can be estimated from the simulated P-h curve using Equations (3)–(7) if we know E_i and ν_i, whereas it is evaluated with E and ν inputted into the FEM model and with β_d observed in simulated nanoindentations. Figure 6 plots the estimated E* (black circles) against the evaluated E*. The white circles are E*_n estimated with the nominal values of k_2n and ξ_n [9], which means that the elastic deformation of an indenter is not modified for the estimation of E*. Figure 6 indicates the modification of the elastic deformation of an indenter can determine E* correctly. The underestimation of E* without the modification (the white circles in Figure 6) is caused by the overestimation of the elastic rebound during the unloading process because the extrinsic elastic deformation of the indenter is added to the intrinsic elastic deformation of the indented material.

The representative indentation yield stress Y*, defined as $Y^{*}=\frac{Y+0.25E_{\mathrm{p}}\tan {\beta }_{\mathrm{d}}}{1-\left(\nu -0.225{\tan }^{1.05}{\beta }_{\mathrm{d}}\right)}$ in terms of β_d [10], can also be estimated using a simulated P-h curve and Equations (3)–(7) if we know E_i and ν_i. Moreover, it can be evaluated with Y, E_p and ν inputted into the FEM model and with β_d of the simulated indentation. 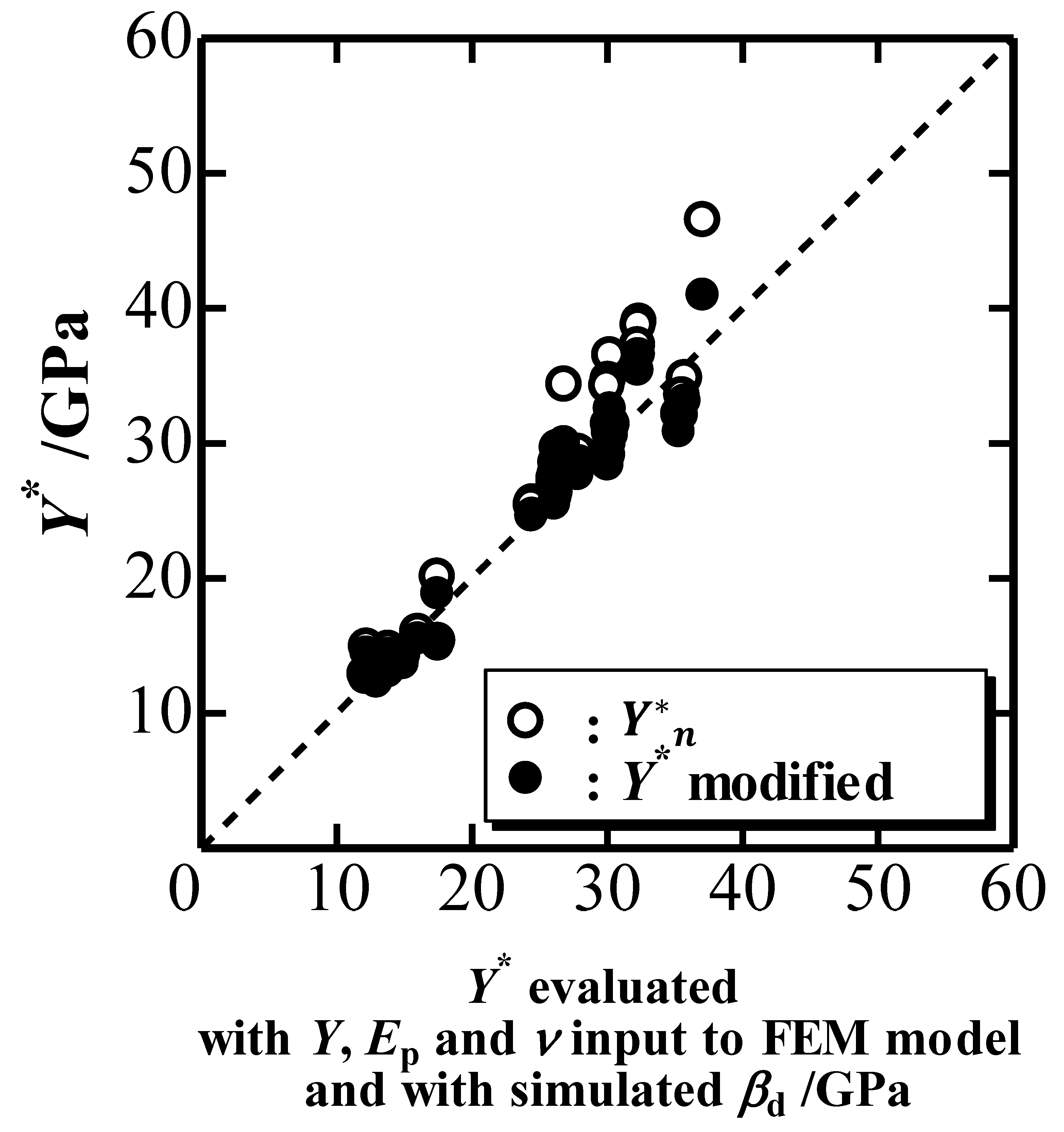Figure 7 plots the estimated Y* (black circles) against the evaluated Y*. Y*_n estimated with E*_n, ξ_n and β_o is plotted for comparison. This figure shows that the modification of the elastic deformation of an indenter more or less correctly estimates Y* although the difference between the modified and unmodified Y* is not so large with respect to the difference observed in E* (see Figure 6). A relatively large difference in Y* is typically found in the range of ξ less than 0.1, where plastic deformation is not dominant. The small difference observed in Figure 7 is attributed to the decrease in k_1n and ξ_n due to elastic deformation of an elastic indenter, where the former decreases Y* nominally while the latter increases Y* apparently.

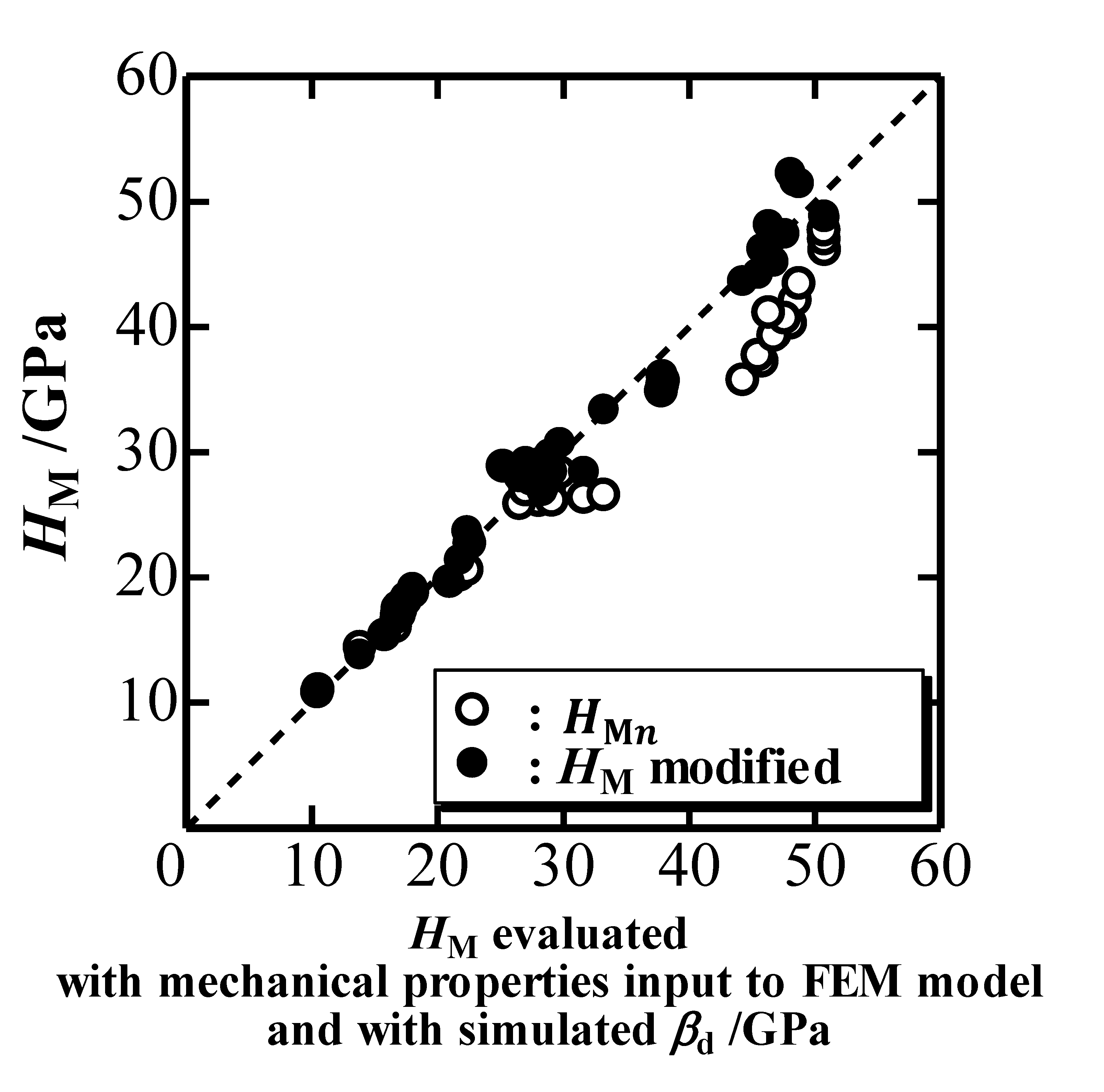
A previous study on the indentation hardness H_M found that it can be evaluated with the mechanical properties inputted into the FEM model and with the simulated β_d [9,10]. On the other hand, H_M can be estimated from a true P-h curve characterized with k₁, k₂ and ξ. Figure 8 plots the estimated H_M (black circles) against the evaluated H_M. The nominal H_Mn estimated with the nominal P-h curve is plotted as white circles in Figure 8, and a comparison reveals that the modification more or less correctly estimates H_M, although the difference between the estimated H_M and the nominal H_Mn is not so large with respect to the difference observed in E* (see Figure 6). The difference is rather high in the large H_M region, where elastic deformation of the indenter is most severe. The small difference observed in Figure 8 owes to the decrease in k_1n and ξ_n due to elastic deformation of an elastic indenter, where the former decreases H_M nominally while the latter increases H_M apparently through the decrease of nominal contact depth.

We conducted nanoindentation experiments and reported E*, Y* and H_M for several materials [9,10]. These values were evaluated with modified P-h curves (see Figure 9) considering elastic deformation of a diamond indenter with Young’s modulus and a Poisson’s ratio of 1140 GPa and 0.07, respectively.

Table 1. Effect of elastic deformation of diamond indenter on mechanical property evaluations.

Materials	Δhd/hmax	βd/βo (deg.)	k2/k2n (10 3 GPa)	ξ/ξn	E* (GPa)	Y* (MPa)	HM (GPa)
					(Modified Value/Unmodified Value)
Brass	0.020	19.6/19.7	7.65/4.78	0.930/0.913	102/81	584/597	1.26/1.29
Duralumin	0.020	19.6/19.7	4.37/3.03	0.909/0.893	77/64	605/618	1.31/1.33
Beryllium copper alloy	0.027	19.6/19.7	9.49/5.44	0.925/0.904	136/103	841/863	1.82/1.86
Fused silica	0.065	19.0/19.7	0.615/0.477	0.550/0.522	74/65	5.21 × 103/5.35 × 103	8.56/8.40
Alumina	0.158	18.3/19.7	4.90/2.25	0.690/0.614	340/225	12.6 × 103/12.9 × 103	24.3/22.8

shows these mechanical properties as well as those evaluated with a nominal P-h curve made without considering any elastic deformation of the indenter. Δh_d/h_max and β_d estimated with the numerical analysis developed in this study are shown in order to examine the degree of the elastic deformation of the indenter. Δh_d/h_max and the change in β (Δβ = β_o − β_d) are large for relatively hard materials (e.g., fused silica and alumina), which would cause a large elastic deformation of the indenter. Even in that case, the changes in Y* and H_M due to the elastic deformation of the indenter are not so large. In contrast, the change in E* is so large that it cannot be ignored. The underestimation of E* without the modification is caused by the overestimation of the elastic deformation during the unloading process because the extrinsic elastic deformation of the indenter is added to the intrinsic elastic deformation of the indented material.

According to Equation (6), the following equation can be derived

$$\frac{H_M}{E_i\prime }=\frac{{\gamma }^2}{g}\left(1+{{\xi }_{\mathrm{n}}}^{1.5}\right){\left(\frac{\Delta h_{\mathrm{d}}}{0.616h_{\max }}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$0.84$}\right.}$$

(8)

When indentation hardness is not affected much by the indenter elastic deformation, where γ is the surface profile parameter defined as γ = h_max/h_c, h_c is the contact depth, and g is the geometrical factor of a point-sharp indenter to be 24.5 for β = 19.7°. E_i’ is required to be about 250 times larger than H_M for Δh_d/h_max smaller than 0.05, where the effect of the indenter elastic deformation on a P-h curve may be ignored for indentations with Berkovich-type indenter.

4. Conclusions

The effect of the geometrical changes due to the elastic deformation of a point-sharp indenter was examined by conducting a numerical analysis of P-h curves simulated with FEM. The effect appears as a decrease in the inclined face angle β. The key parameter Δh_d/h_max, which can be utilized to derive the physically meaningful P-h curve and the decreased β, can be estimated with an equation derived by numerical analysis. The mechanical properties of indented materials, such as E*, Y* and H_M, can be estimated by using the P-h curve and β characterized by k₁, k₂ and ξ estimated with the key parameter Δh_d/h_max. The modification of a P-h curve and β with Δh_d/h_max is most effective for the estimation of the accurate E* with respect to Y* and H_M.