Optimal Coordinated Management of a Plug-In Electric Vehicle Charging Station under a Flexible Penalty Contract for Voltage Security

Abstract

The increasing penetration of plug-in electric vehicles (PEVs) may cause a low-voltage problem in the distribution network. In particular, the introduction of charging stations where multiple PEVs are simultaneously charged at the same bus can aggravate the low-voltage problem. Unlike a distribution network operator (DNO) who has the overall responsibility for stable and reliable network operation, a charging station operator (CSO) may schedule PEV charging without consideration for the resulting severe voltage drop. Therefore, there is a need for the DNO to impose a coordination measure to induce the CSO to adjust its charging schedule to help mitigate the voltage problem. Although the current time-of-use (TOU) tariff is an indirect coordination measure that can motivate the CSO to shift its charging demand to off-peak time by imposing a high rate at the peak time, it is limited by its rigidity in that the network voltage condition cannot be flexibly reflected in the tariff. Therefore, a flexible penalty contract (FPC) for voltage security to be used as a direct coordination measure is proposed. In addition, the optimal coordinated management is formulated. Using the Pacific Gas and Electric Company (PG&E) 69-bus test distribution network, the effectiveness of the coordination was verified by comparison with the current TOU tariff.

1. Introduction

Plug-in electric vehicles (PEVs) have been attracting interest as an alternative solution to manage the increasing amount of CO₂ emission. Authorities in a number of countries have set ambitious goals for integrating a large number of PEVs [1,2]. However, the charging demands for PEVs are relatively larger than the household loads, and are inherently uncoordinated due to the unpredictable behavior of the consumers. Consequently, the high penetration of PEVs may threaten the stable and reliable operation of the distribution network. Specifically, there can be severe voltage drops, fluctuation problems, and degradation in the system efficiency [3,4,5].

To address these concerns, various PEV charging methods have been suggested from the perspective of a distribution network operator (DNO). In [6], the DNO manages the charging demands of PEVs to minimize the line losses of the distribution network. A similar charging method is suggested to minimize the line losses in [7], but it uses stochastic programming to consider the uncertainty of loads in the optimization problem. In [8], a real-time charging strategy for managing the uncoordinated and uncertain charging demands of PEVs is presented to minimize the total operating cost of the distribution network, including the line losses. In order to minimize the operating costs, the authors of [9] propose a method in which the inputs for optimization are continuously updated, and the optimization results are periodically renewed at each time step to reflect the difference between the forecasted value and the actual inputs. In the literature [6,7,8,9], the DNO directly manages the charging schedules of multiple PEVs considering the network constraints to pursue efficient and reliable operation of the distribution network. However, due to operational complexity and burden from the increasing numbers of PEVs, it seems to be difficult for the DNO to directly manage the charging of multiple PEVs in the distribution network [10,11]. Moreover, various concepts of intermediate entities that are independent of the DNO have been emerging in practice [12,13]. For these reasons, many studies assume that an intermediate entity is delegated to manage PEV charging demands. The intermediate entity does not have any responsibility for the stable and reliable operation of the distribution network, unlike the DNO, but the entity simply aims to maximize its profit with a proper method for managing the PEV charging demand [14,15,16,17]. This conflict of interest can be mitigated by various types of coordination measures. The coordination measure should enable the DNO to inform the intermediate entity of the network status or to motivate the intermediate entity to shift its charging demand to another time. However, methods for coordination between the DNO and the intermediate entity have not been thoroughly investigated in the literature.

This study assumes that the PEV charging station is located at a specific bus in the distribution network and that hundreds of PEVs request to be provided with charging service at the same station. Furthermore, it is assumed that the intermediate entity, the so-called charging station operator (CSO), is delegated to manage the charging demands of PEVs. In this circumstance, the CSO only seeks to profit from providing charging service to the PEVs without considering the stability and reliability of the distribution network. Therefore, the hundreds of PEVs in the charging station can significantly drop the voltage of the following bus in the same feeder as well as the bus where the station is located. For this reason, this study suggests a flexible penalty contract (FPC) as a coordination measure, which is designed to induce the CSO not to compromise the voltage conditions of the distribution network. In this scheme, the DNO notices hourly the recommended charging power that does not cause voltages below the lower limit for the CSO, and imposes a penalty price for exceeding the maximum power as an addition to the current electricity tariff, such as the time-of-use (TOU) rate. Furthermore, a formulation for the optimal coordinated charging management of the CSO under the FPC is proposed in this paper.

The remainder of this paper is structured as follows: Section 2 presents the needs for coordination between the CSO and the DNO and details the coordination under the FPC; Section 3 describes the mathematical formulation for the coordinated management of a PEV charging station under the proposed FPC.; in Section 4, the proposed optimal coordinated management method under the FPC is demonstrated through case studies using simulations with the Pacific Gas and Electricity Company (PG&E) 69-bus distribution network; and concluding remarks are given in Section 5.

2. Flexible Penalty Contract for Voltage Security

2.1. Need for Coordination between the Charging Station Operator and the Distribution Network Operator

In this study, it is assumed that the stakeholders in the PEV charging business are the DNO, the CSO, and a number of PEVs. The DNO generally takes responsibility for stable and reliable operation of the distribution network, and the CSO provides charging services to PEVs at a charging station in a commercial/office building. Unlike PEV charging services for households, the CSO provides a simultaneous charging service at a commercial/industrial building for a number of PEVs. Therefore, the charging service provided to PEVs mostly operates during office hours rather than at night. For this reason, the charging demands at the station may double the current electricity loads at the peak time or when a number of PEVs simultaneously try to charge at the same location. Therefore, this type of charging service can threaten the stability of the distribution network, mostly by causing severe voltage drops in the distribution network. However, the CSO currently has no responsibility for stable network operation, but simply provides charging service via the network as a large-size customer. For this reason, there is little or no motivation for the CSO to shift its charging demands to other time slots without an additional penalty or incentive scheme. Among a number of possible solutions, this study suggests a penalty contract for voltage security.

2.2. Concept of Coordinated Operation with the Flexible Penalty Contract

This study considers an FPC between the CSO and the DNO to supplement the weakness of the TOU tariff. Although the TOU is surely one solution that can induce PEV charging demands to be shifted to off-peak times from peak times, it cannot flexibly cover the voltage problems in the distribution network according to the network status. The FPC can be useful for the DNO to induce the CSO to manage its charging demands by providing information about the network status.

Specifically, under the contract scheme, the DNO calculates the maximum available power $P_{\text{MAX}}^i(t)$ at bus i at the time slot t that ensures all bus voltages remain within the limits using day-ahead forecasted demand data. For simplicity, it is assumed that the charging service is provided in units of hours, and each time slot t is an element of set T, where $T=\{0,1,2,\cdots ,23\}$. Additionally, it is assumed that the DNO can notify the day-ahead recommended power consumption signal $P_{\mathrm{R}}^i(t)$ instead of $P_{\text{MAX}}^i(t)$ with the security margin (SM) considering the uncertainty in the charging demands of PEVs and other electricity demands. The relationship between $P_{\text{MAX}}^i(t)$ and $P_{\mathrm{R}}^i(t)$ is:

$$P_{\mathrm{R}}^i(t)=(1-SM)P_{\text{MAX}}^i(t)$$

(1)

where SM can be set according to the DNO’s attitude regarding the risk from uncertainty, and $P_{\text{MAX}}^i(t)$ can vary depending on the hourly network conditions.

Additionally, in the case when the power demand of the charging station exceeds $P_{\mathrm{R}}^i(t)$, the DNO will impose an additional penalty price β to the CSO for the amount that exceeds $P_{\mathrm{R}}^i(t)$ by the contract. On the contrary, if the power demand does not exceed the noticed $P_{\mathrm{R}}^i(t)$, the CSO is charged only at the current TOU rate. With the FPC having the described structure, the rigidity of the TOU can be supplemented and the DNO can partly charge the CSO for the cost of upgrading the network.

3. Formulation for Coordinated Management of a Plug-In Electric Vehicle Charging Station under the Flexible Penalty Contract

3.1. Specifying the Flexible Penalty Contract by the Distribution Network Operator

This study proposes the FPC as a coordination scheme for managing the conflicts of interest between the DNO and CSO. Within the FPC scheme, the DNO notifies the CSO of the day-ahead recommended power consumption signal and imposes a penalty price β, if the charging demands at each time slot exceed the recommended value at that time. The day-ahead recommended power consumption signal provides the threshold of the FPC, and it can be considered as a consumption guideline for the CSO to avoid a low-voltage problem in the network. This signal can be calculated by obtaining the decision variable vector P_MAX, which can be securely accommodated in the network and it varies according to the day-ahead forecast load data $P_{\mathrm{L}}^i(t)$, $Q_{\mathrm{L}}^i(t)$ in Equation (5). Since this study does not focus on the day-ahead forecast of demand, it is assumed that $P_{\mathrm{L}}^i(t)$, $Q_{\mathrm{L}}^i(t)$ are given data. The optimal solution for P_MAX can be determined by choosing the best solution among feasible vectors satisfying the constraint Equations (5) and (6). In this study, in terms of voltage security, the criteria for choosing the best solution is designed to maximize the voltage margin (VM) of the most vulnerable bus to the low-voltage problem. In addition, the decision variable vector TP, which means the position of tap on the main transformer, and its corresponding constraint Equations (7) and (8) are considered since the DNO can also adjust the tap position of the main transformer equipped with an on-load tap changer (OLTC) to control voltages of the network. OLTC controls the secondary side voltage magnitude of the substation transformers by adjusting the tap position. Voltage magnitudes are controlled discretely according to tap step, and OLTC can generally adjust the voltage by ±10% in 16 steps, with 17 positions [18,19,20]. Therefore, the optimization problem of the DNO on specifying the FPC can be described with the objective function described in Equation (2) subject to the Equations (5)–(8) as follows:

$$\underset{P_{MAX},\mathit{T}\mathit{P}}{\max }V{M}_{\min }=\underset{P_{MAX},\mathit{T}\mathit{P}}{\max }\left(\min \left(\left|V^i(t)\right|-V_{\text{LL}}\right)\right)$$

(2)

where the decision variable vector P_MAX, TP can be represented as:

$${\mathit{P}}_{MAX}=\left[{\mathit{P}}_{MAX}^1,\cdots ,{\mathit{P}}_{MAX}^{\mathit{n}}\right]=\left[\begin{array}{c}{P}_{\mathrm{MAX}}^1(0)\\ ⋮\\ P_{\text{MAX}}^1(23)\end{array}\begin{array}{c}\cdots \\ \ddots \\ \cdots \end{array}\begin{array}{c}{P}_{\text{MAX}}^n(0)\\ ⋮\\ P_{\text{MAX}}^n(23)\end{array}\right]$$

(3)

$$\mathit{T}\mathit{P}=[TP(0),\cdots ,TP(23)]\text{'}\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}where\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}TP(t)\in \{0,\cdots ,16\}$$

(4)

subject to:

• Power flow constraints:

  $$\begin{array}{l}{P}_{\mathrm{F}}^l(t)+P_{\mathrm{L}}^i(t)+P_{\text{MAX}}^i(t)=0,\text{ \hspace{0.17em}\hspace{0.17em}for \hspace{0.17em}}{}^{\forall }i=1,\cdots ,n\\ Q_{\mathrm{F}}^l(t)+Q_{\mathrm{L}}^i(t)=0,\text{\hspace{0.17em}\hspace{0.17em}for \hspace{0.17em}}{}^{\forall }i=1,\cdots ,n\end{array}$$

  (5)

  $$\begin{array}{l}{P}_{\mathrm{F}}^l(t)=\left|V^i(t)\right|{\displaystyle \sum _j\left|V^j(t)\right|}\left[G_{ij}\cos ({\mathsf{\delta }}^i(t)-{\mathsf{\delta }}^j(t))+B_{ij}\sin ({\mathsf{\delta }}^i(t)-{\mathsf{\delta }}^j(t))\right]\\ Q_{\mathrm{F}}^l(t)=\left|V^i(t)\right|{\displaystyle \sum _j\left|V^j(t)\right|}\left[G_{ij}\sin ({\mathsf{\delta }}^i(t)-{\mathsf{\delta }}^j(t))-B_{ij}\cos ({\mathsf{\delta }}^i(t)-{\mathsf{\delta }}^j(t))\right]\end{array}$$

  (6)

  $$|V^2(t)|=V_{\text{LL}}+\frac{V_{\text{UL}}-V_{\text{LL}}}{N_{TP}-1}\times TP(t)\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}for\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{}^{\forall }t=0,\cdots ,23$$

  (7)
• Tap operational constraints of the main transformer:

  $${\displaystyle \sum _T\left|TP(t)-TP(t+1)\right|}\le N{T}_{\text{MAX}}$$

  (8)

$P_{\mathrm{F}}^l(t)$ and $Q_{\mathrm{F}}^l(t)$ are the active and reactive power flows on the distribution line l at t, and $TP(t)$ is tap position of the main transformer. Voltage magnitude of the secondary side of the transformer is determined by the tap position $TP(t)$, and the relationship between tap position and the voltage is represented in Equation (7) where V_UL, V_LL are upper and lower voltage limits, and N_TP is the number of tap levels. Equation (8) prevents the excessive operation of the tap changer by limiting the total number of tap movements to less than the maximum number of tap movements NT_MAX. By including this integer variable and the operational constraints, the optimization problem for the objective function in Equation (2) subject to Equations (5)–(8) can be considered as non-linear integer programming.

Over the 24 h, $P_{\mathrm{R}}^i(t)$ varies depending on hourly demands of $P_{\mathrm{L}}^i(t)$ and $Q_{\mathrm{L}}^i(t)$, and can be expressed as:

$${\mathit{P}}_R^i=\left[\begin{array}{c}{P}_{\mathrm{R}}^i(0)\\ ⋮\\ P_{\mathrm{R}}^i(23)\end{array}\right]=(1-SM)\arg \underset{P_{MAX}^i}{\max }VM$$

(9)

As mentioned in Section 2, the penalty rate by the proposed FPC is imposed only when $P_{\text{CS}}^i(t)$ exceeds $P_{\mathrm{R}}^i(t)$, as follows:

$${\mathsf{\beta }}^t=\{\begin{array}{l}\mathsf{\beta }\text{\hspace{1em}if }{P}_{\text{CS}}^i(t)\ge P_{\mathrm{R}}^i(t)\\ 0\text{\hspace{1em}if else}\end{array}$$

(10)

where β^t should be set to be larger than the difference between the TOU rate at the peak time and at the part-peak time to be effective as a coordination measure. If not, the demand shift by the TOU overwhelms the effect from β^t.

3.2. Optimal Charging Management of the Charging Station Operator under the Flexible Penalty Contract Scheme

The CSO pays the cost of using electricity to provide the charging service at the TOU tariff ρ^t to the DNO. In addition to the current TOU rate ρ^t, the CSO should pay the penalty price β^t for the excess quantity when $P_{\text{CS}}^i(t)$ exceeds $P_{\mathrm{R}}^i(t)$ under the FPC scheme. The signal $P_{\mathrm{R}}^i(t)$ plays a role as the connector between the DNO and the CSO and is an obtained value from Equation (9) in Section 3.1. On the other side, the CSO generates revenue by providing the charging service to PEVs at its charging station. The charging service fee is set to be a constant value μ^t because it is not the main concern of this study. As a rational profit-seeking entity, the CSO aims to maximize its daily profit under the FPC scheme. Therefore, the objective function for the optimal charging management of the CSO can be expressed as Equation (11), considering the revenues and costs, subject to the constraints given in Equations (15)–(17):

$$\underset{{\text{ST}}^{k,i}(t)}{\max }\text{Profit}=\underset{{\text{ST}}^{k,i}(t)}{\max }{\displaystyle \sum _{t=0}^{23}\left[{\mathsf{\mu }}^t{P}_{\text{CS}}^i(t)-\left({\mathsf{\rho }}^t{P}_{\text{CS}}^i(t)+{\mathsf{\beta }}^t\left(P_{\text{CS}}^i(t)-P_{\mathrm{R}}^i(t)\right)\right)\right]}$$

(11)

where:

$$P_{\text{CS}}^i(t)=p_{\text{PEV}}\times N_{\mathrm{C}}^i(t)$$

(12)

$$N_{\mathrm{C}}^i(t)={\displaystyle \sum _{k=1}^{N_{\text{PEV}}^t}S{T}^{k,i}(t)},S{T}^{k,i}(t)\in \left\{0,1\right\}$$

(13)

$$N_{\mathrm{R}}^i(t)=\lfloor \frac{P_{\mathrm{R}}^i(t)}{p_{\text{PEV}}}\rfloor ,\lfloor x\rfloor \text{ is the largest integer less than or equal to }x$$

(14)

subject to:

$$N_{\text{PEV}}^i(t)\le N_{\text{SLOT}}$$

(15)

$$So{C}^{k,i}(t)=\{\begin{array}{l}So{C}_{\text{INI}}^{k,i}\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}for\hspace{0.17em}}{}^{\forall }t=0,\cdots ,T_{\text{ARR}}^{k,i}-1\\ So{C}^{k,i}(t-1)+S{T}^{k,i}(t-1)\times \frac{p_{\text{PEV}}}{ca{p}_{\text{PEV}}}\times \Delta t\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}for\hspace{0.17em}}{}^{\forall }t=T_{\text{ARR}}^{k,i},\cdots ,T_{\text{DEP}}^{k,i}\end{array}$$

(16)

$$So{C}_{\text{REQ}}^{k,i}\le So{C}^{k,i}(t)\le So{C}_{\text{MAX}}\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}for\hspace{0.17em}\hspace{0.17em}}{}^{\forall }t=T_{\text{DEP}}^{k,i},\cdots ,23$$

(17)

On the basis of the assumption that every PEV is provided electricity with the same charging cables, the charging demand of the charging station at t, $P_{\text{CS}}^i(t)$, can be calculated using Equation (12), where $p_{\text{PEV}}$ is the rated power of the charging cable, and $N_{\mathrm{C}}^i(t)$ is the number of PEVs that are being charged at t. $N_{\mathrm{C}}^i(t)$ is expressed in Equation (13) as the sum of charging statuses of the PEVs, $S{T}^{k,i}(t)$, which is a binary variable. The recommended number of PEVs being charged $N_{\mathrm{R}}^i(t)$, for the charging station on bus $i$ at time slot t can be represented as Equation (14). Additionally, $N_{\mathrm{C}}^i(t)$ should not exceed the number of slots procured at the charging station described in Equation (15). The state of charge (SoC) of the kth PEV, $So{C}^{k,i}(t)$ before its arrival should be maintained at the given initial SoC, $So{C}_{\text{INI}}^{k,i}$ and the relationship between the SoC of the adjacent time slot t and t − 1 can be formulated as Equation (16) where ∆t is a size of a time slot, which is 1 h, and $ca{p}_{\text{PEV}}$ is the capacity of the PEV’s battery. Equation (17) indicates that $So{C}^{k,i}(t)$ should fulfill the required SoC, $So{C}_{\text{REQ}}^{k,i}$ before the PEV’s departure and $So{C}^{k,i}(t)$ must be smaller than the upper limit, $So{C}_{\text{MAX}}$.

4. Case Studies

4.1. Simulation Settings

4.1.1. Network Configuration and Data

The proposed optimal coordinated management method under the FPC was demonstrated through simulations with the PG and E 69-bus test distribution network in [21]. The structure of the network is shown in Figure 1. The substation transformer located between buses 1 and 2 is equipped with OLTC, which controls the voltage magnitude of bus 2. The operating range of the OLTC was set to vary from −5% to 5%, in 16 steps, and the interval of tap movement was set to 0.625% [18,19,20]. As shown in Figure 1, three shunt capacitors are located at buses 14, 61, and 62, with capacities of 600 kVAR, 500 kVAR, and 450 kVAR, respectively. The base values of power and voltage were set to 10 MVA and 12.66 kV, respectively.

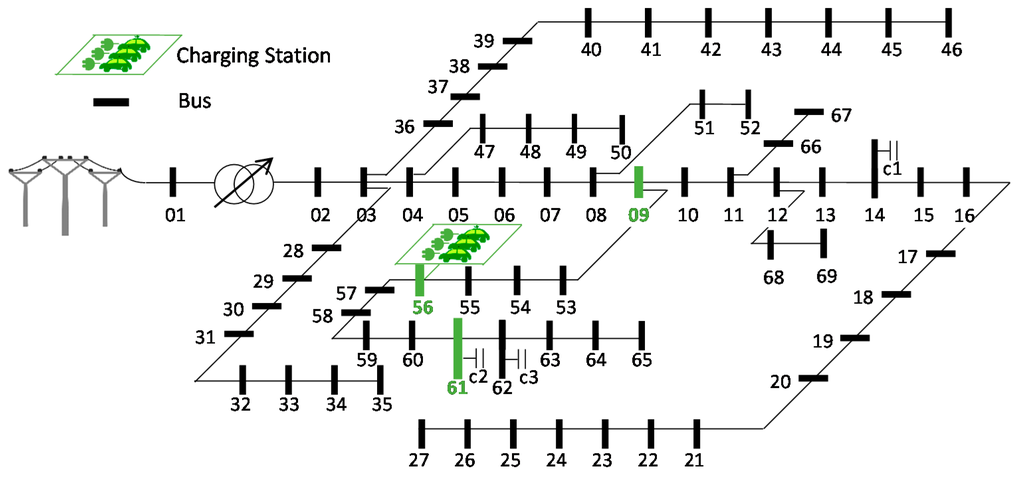
Figure 1. PG and E 69-bus test distribution network [21].

The peak demand of the network was set to 3791 kW; the forecasted hourly demands (%) in the network are shown in Figure 2 [22]. The active/reactive power demand of each bus is assumed to be distributed according to the data in [21]. It is assumed that the ratio of the forecasted hourly demand is the same for all buses.

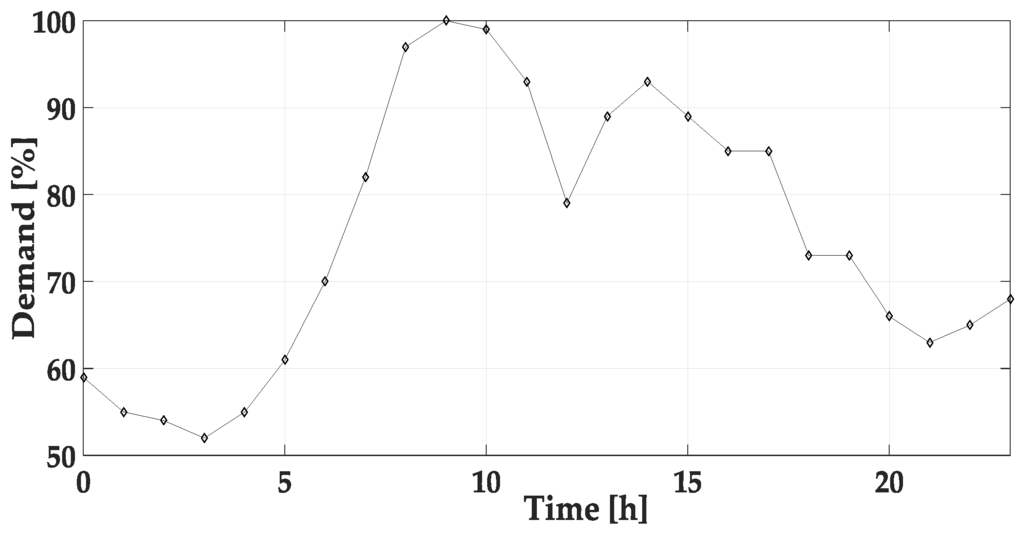
Figure 2. Forecasted hourly demand (%) over 24 h [22].

4.1.2. Characteristic Data of the Plug-in Electric Vehicles

This simulation considered PEVs with a battery capacity of 21.6 kWh and a charging cable with a charging rate of 3.3 kW. Table A1 in the Appendix summarizes the randomly-generated information for 100 PEVs based on Table 1, including arrival and departure time, initial SoC, and required SoC. All data were generated assuming a normal distribution. The arrival time is the time when a PEV arrives at the charging station, and the departure time is the time when a PEV leaves the charging station. The initial SoC denotes the SoC of a PEV at arrival, and the required SoC indicates the level SoC that a PEV needs to reach until its departure time.

Table 1. Basic data for generating the information of 100 plug-in electric vehicles (PEVs). SoC: state of charge.

Information	Arrival Time	Departure Time	Initial SoC	Required SoC
Average Value	9:00	19:00	30%	70%
Standard Deviation	1 h	1 h	20%	20%

4.1.3. Time-of-use Rates for the Charging Station Operator

In this study, it is assumed that the DNO charges the CSO according to the PG and E EV E-9A TOU pricing scheme, especially for PEVs in the summer season, as summarized in Table 2 [23].

Table 2. Summer PG and E time-of-use (TOU) rates ($/kWh) [23].

Time	Rates	Time
On-peak	0.361	13:00–20:00
Part-peak	0.145	06:00–13:00
		20:00–23:00
Off-peak	0.092	00:00–06:00
		23:00–24:00

4.1.4. Others

The values of the other simulation parameters are listed in Table 3.

Table 3. Other parameters.

Parameter	Acronym	Value
Security margin	SM	10%
Maximum SoC for a PEV	SoCMAX	100%
Upper voltage limit of the network	VUL	1.05 p.u.
Lower voltage limit of the network	VLL	0.95 p.u.
Number of charging slots at the charging station	NSLOT	100
Number of PEVs assumed for the simulation	NPEV	100
Number of Tap levels	NTP	17
Penalty price for the FPC	β	$0.24/kWh

If the penalty price is smaller than the gaps between the TOU rates at each time (off-peak, part-peak, and on-peak), the effect of the penalty price is overwhelmed by the effect of the TOU scheme. In this case, the FPC will not be an effective supplementary scheme for the TOU with respect to the voltage security. Therefore, the penalty price must be greater than the difference between the TOU rates. For the same reason, once the penalty price is greater than the rate gap between the TOU rates, the coordination results of the CSO will almost be the same, regardless of the penalty price value. However, the CSO’s charging service cost will increase proportionally with the penalty price. Hence, the penalty price is determined to be larger than the rate gap ($0.216/kWh) between the on-peak rate ($0.361/kWh) and the part-peak rate ($0.145/kWh).

4.2. Simulation Cases

The simulation cases were configured as listed in Table 4. In order to verify the effectiveness of the proposed FPC, a comparison was conducted among three tariff conditions in each simulation case. Three simulation Cases, A, B, and C, were configured to investigate the effects of different locations of the charging station on the simulation results. In Case B, the charging station was located at bus 61, which is closer to the main substation at bus 1 compared to the location at bus 56 in Case A. In Case C, the charging station was located at bus 9, which is farther from the main substation at bus 1, compared to bus 56 in Case A.

Table 4. Simulation cases.

Simulation Cases	Condition	Tariff	Charging Station Location
Case A	I	Flat rate	Bus 56
	II	PG&E EV-9A TOU
	III	PG&E EV-9A TOU + FPC
Case B	I	Flat rate	Bus 61
	II	PG&E EV-9A TOU
	III	PG&E EV-9A TOU + FPC
Case C	I	Flat rate	Bus 9
	II	PG&E EV-9A TOU
	III	PG&E EV-9A TOU + FPC

In each simulation case, Condition I is a flat-rate tariff, which means that there is no hour-to-hour rate variation. For Condition I, the DNO has no measure to induce the CSO to shift its charging demand from peak times to other times. Condition II is the PG and E EV-9A TOU tariff. This type of tariff indirectly helps the DNO maintain network stability but cannot flexibly reflect the network status. The authors consider Condition II as a “rigid” tariff condition that is not suitable for an environment with a high penetration of PEVs. Condition III is the proposed scheme, which applies the FPC described in Section 2 and Section 3 on the basis of PG and E EV-9A TOU tariff to motivate the CSO to shift its charging demand at certain times when a voltage problem is expected.

4.3. Simulation Results

The DNO’s optimization problem presented in Section 3.1 is solved using MATLAB’s (The MathWorks, Natick, MA, USA) built-in genetic algorithm solver, and the CSO’s optimization problem presented in Section 3.2 is solved using MATLAB’s built-in fmincon solver. All of the simulations were conducted using a personal computer (PC) with 3.10-GHz Intel^® Core i5-4440 central processing unit (CPU), 8 GB of random-access memory (RAM), and 64-bit Windows^® 7 operating system. Both optimization routines are time-consuming mixed-integer nonlinear problems. The actual computation times of the simulation cases are listed in Table 5, and it is found that each case takes a few hours. Since the proposed FPC scheme is designed to be conducted a day ahead, the computation times in Table 5 seem to be implementable in practice. It should be noted that more time is consumed in case B than other cases, which means that the problem becomes more difficult as the charging station is located further from the main substation (bus 1).

Table 5. Computation times of the simulation cases (s). DNO: distribution network operator; and CSO: charging station operator.

Simulaiton Cases	DNO‘s Optimization	CSO’s Optimization
		I. Flat Rate	II. PG andE EV-9A TOU	III. PG andE EV-9A TOU + FPC
Case A (Bus 56)	282	1	651	2259
Case B (Bus 61)	397	1	841	8689
Case C (Bus 9)	278	1	835	1366

Under Condition I in Case A (Case A-I), where the flat rate is applied, the CSO is not motivated to adjust its charging schedule because there is no difference in the electricity tariff at each time. Therefore, the CSO only considers the required energy for the PEVs when it determines its charging schedule. The profile of $N_{\mathrm{C}}^i(t)$ for 24 h resulting from Case A-I is shown in Figure 3a. $N_{\mathrm{C}}^i(t)$ is observed to exceed $N_{\mathrm{R}}^i(t)$ in Figure 3a, and the minimum voltage of the distribution network is below the low voltage limit V_LL during the same period as shown in Figure 4.

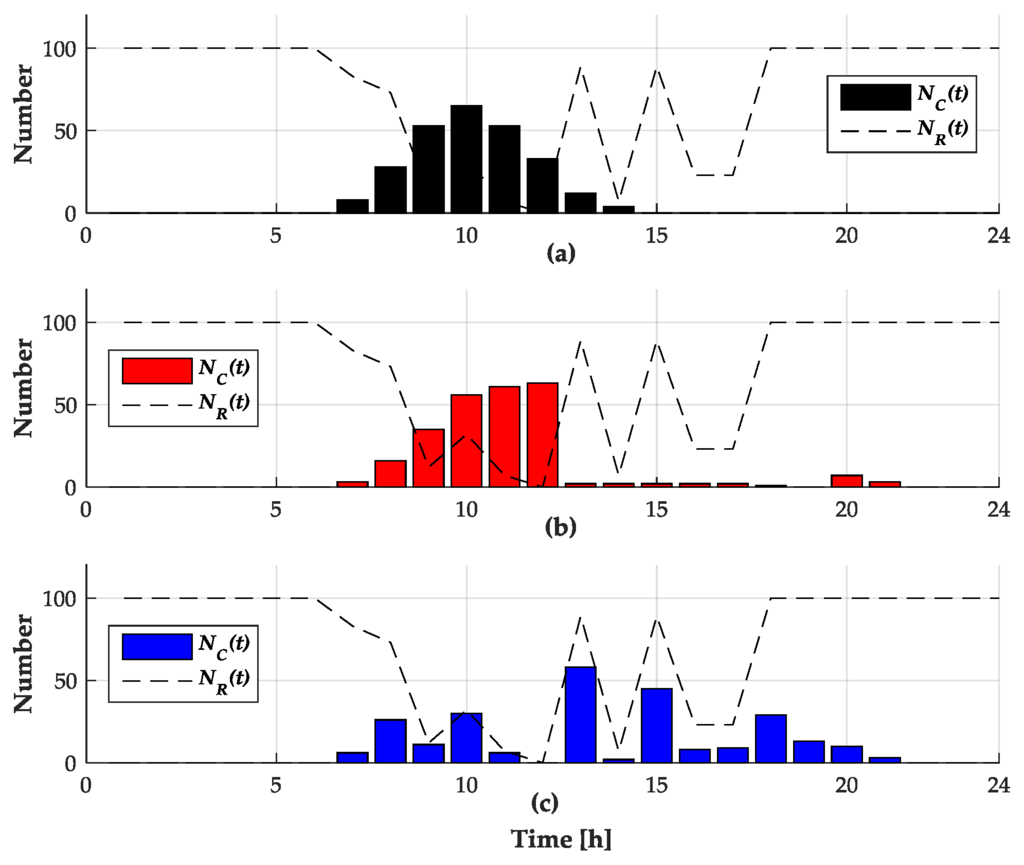
Figure 3. $N_{\mathrm{C}}^i(t)$ for (a) Case A-I; (b) Case A-II; and (c) Case A-III, with $N_{\mathrm{R}}^i(t)$ (dashed line) for each hours.

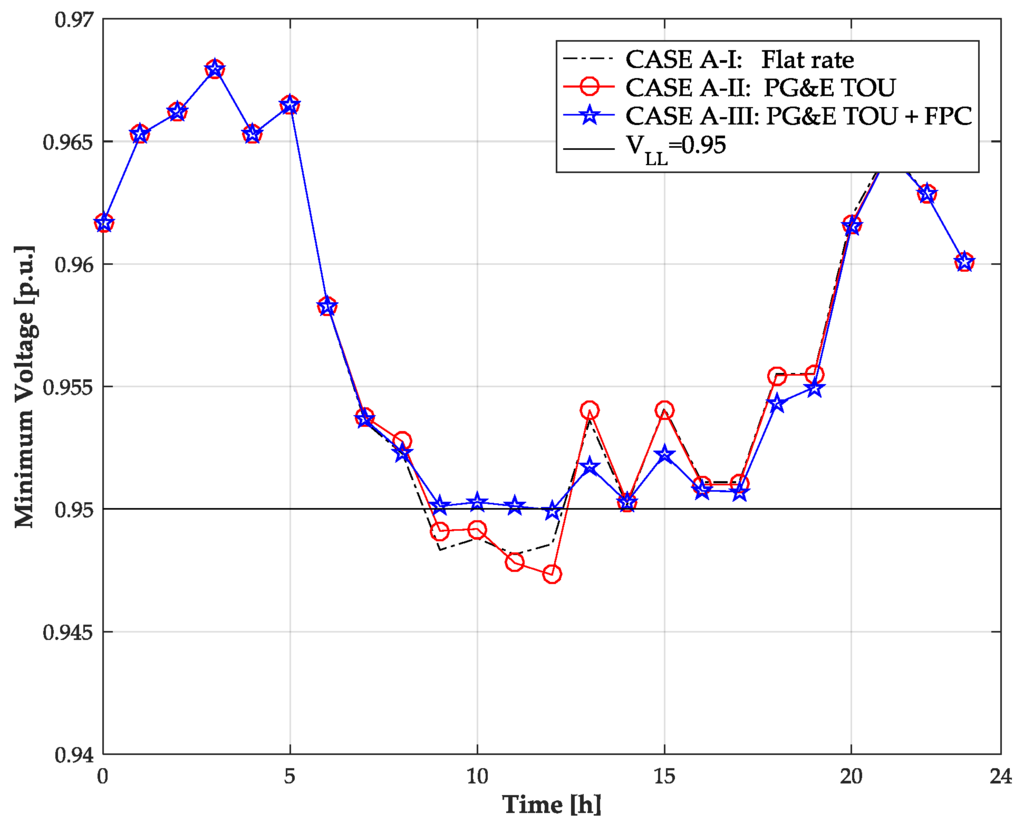
Figure 4. Minimum voltage of the test distribution network for Case A over 24 h.

Applying Condition II in Case A (Case A-II), where the PG and E EV-9A TOU tariff is used, the CSO shifts the charging demand from the peak time to other times because the rate at the peak time is higher than the rates of the other times. For this reason, it can be observed that the charging demand at 13 h and 14 h in Case A-I is moved to other time slots before the peak time and after the peak time, as presented in Figure 3b. Additionally, it is observed in Figure 3b that $N_{\mathrm{C}}^i(t)$ violates $N_{\mathrm{R}}^i(t)$ between 9 h and 12 h, because there is no coordination measure for delivering information on the voltage condition of the network to the CSO from the DNO. A noteworthy point is that the minimum voltage in Case A-II, with the TOU rate, is less than the minimum voltage in Case A-I, with the flat rate, as seen in Figure 4. In particular, the minimum voltage in Case A-II occurs at 12 h, unlike in case A-I, which occurs at 11 h. The reason for this result is that the charging demand at 12 h increases by a strategic act of the CSO for avoiding the peak rate of the TOU rate. Furthermore, this result implies that the charging scheduling of the CSO considering the TOU rate can aggravate the voltage condition of the network.

For Condition III in Case A (Case A-III), where the proposed FPC for voltage security is assumed, in addition to the PG and E EV-9A TOU tariff, the CSO evenly deconcentrates the charging demand to other times, as shown in Figure 3c, in order to avoid the potential penalty cost that might be imposed on the excess of $N_{\mathrm{C}}^i(t)$ to $N_{\mathrm{R}}^i(t)$. Additionally, it is shown that $N_{\mathrm{C}}^i(t)$ for all times do not exceed $N_{\mathrm{R}}^i(t)$ in Figure 3c, and the low voltage problems that occur in Case A-I and Case A-II are mitigated well in Case A-III, as presented in Figure 4.

In Case B, the location of the charging station (bus 61) is set to be farther from the main substation, compared to the location of the charging station (bus 56) in Case A. This means that Case B is configured to observe the changes in the simulation results when the voltage problem becomes more severe than in Case A. As a result of the calculation of $N_{\mathrm{R}}^i(t)$ with the method described in Section 3.1 for Case B, $N_{\mathrm{R}}^i(t)$ for 24 h is represented by the dashed lines in Figure 5. It is clearly observed that the values of $N_{\mathrm{R}}^i(t)$ for Case B are stricter than those for Case A by comparing Figure 3 and Figure 5. In addition, it is observed by comparing Figure 4 and Figure 6 that the voltage problems are more effectively mitigated in Case B than in Case A. However, the minimum voltage values of a few time slots of Case B-III are just below the voltage lower limit V_LL, which is a result of the CSO’s excessive charging over $N_{\mathrm{R}}^i(t)$ in order to comply with contract with the PEVs. In other words, even if the proposed FPC improves the voltage security and mitigates the low-voltage problem, there is still a limit of total charging loads depending on the bus location of the charging station and the distribution network condition.

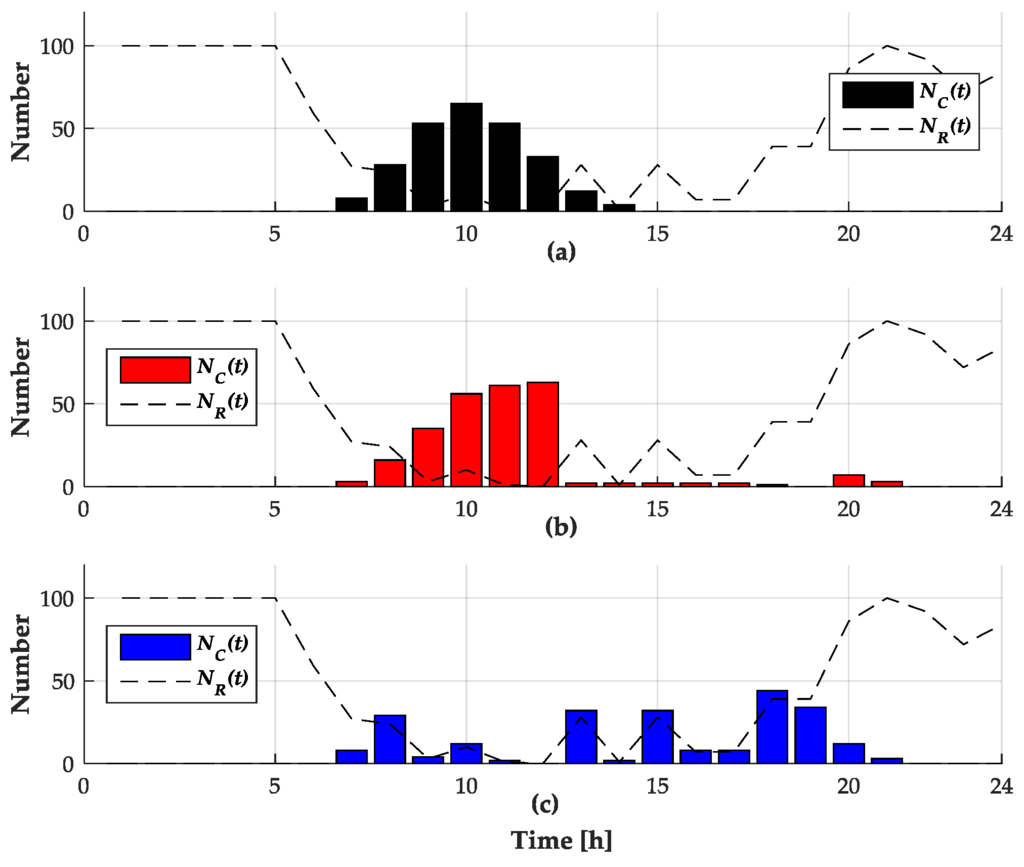
Figure 5. $N_{\mathrm{C}}^i(t)$ for (a) Case B-I; (b) Case B-II; and (c) Case B-III, with $N_{\mathrm{R}}^i(t)$ (dashed line) for each hour.

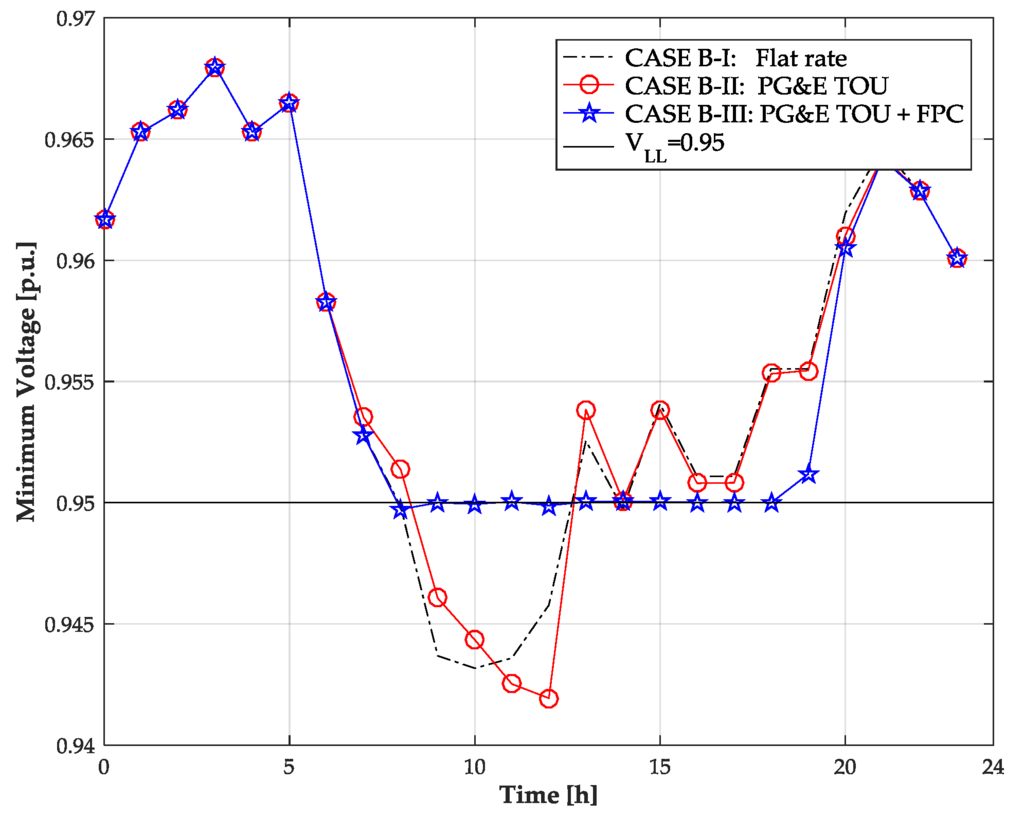
Figure 6. Minimum voltage of the test distribution network for Case B over 24 h.

In Case C, the location of the charging station (bus 9) is set to be closer to the main station compared to the location of the charging station (bus 56) in Case A. This means that Case C is configured to analyze the changes in the simulation results if the voltage problem is less serious than that in Case A. Figure 7 shows that the values of $N_{\mathrm{R}}^i(t)$ for 24 h have more generous values in Case C compared to those in Case A. As seen in Figure 8, the mitigation of the voltage problem is not as effective in Case C as in Case A or Case B. Consequently, considering the results of Case B and Case C, it can be said that the proposed FPC becomes more effective as stricter $N_{\mathrm{R}}^i(t)$ conditions are imposed.

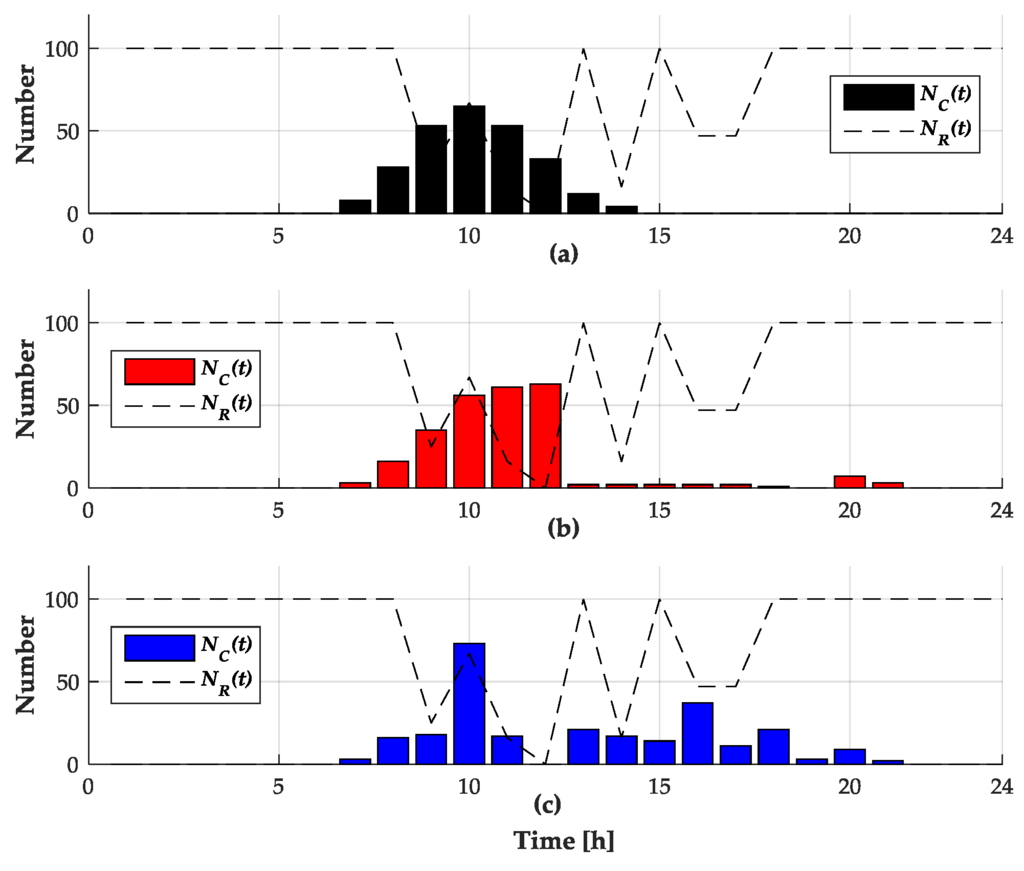
Figure 7. $N_{\mathrm{C}}^i(t)$ for (a) Case C-I; (b) Case C-II; and (c) Case C-III, with $N_{\mathrm{R}}^i(t)$ (dashed line) for each hour.

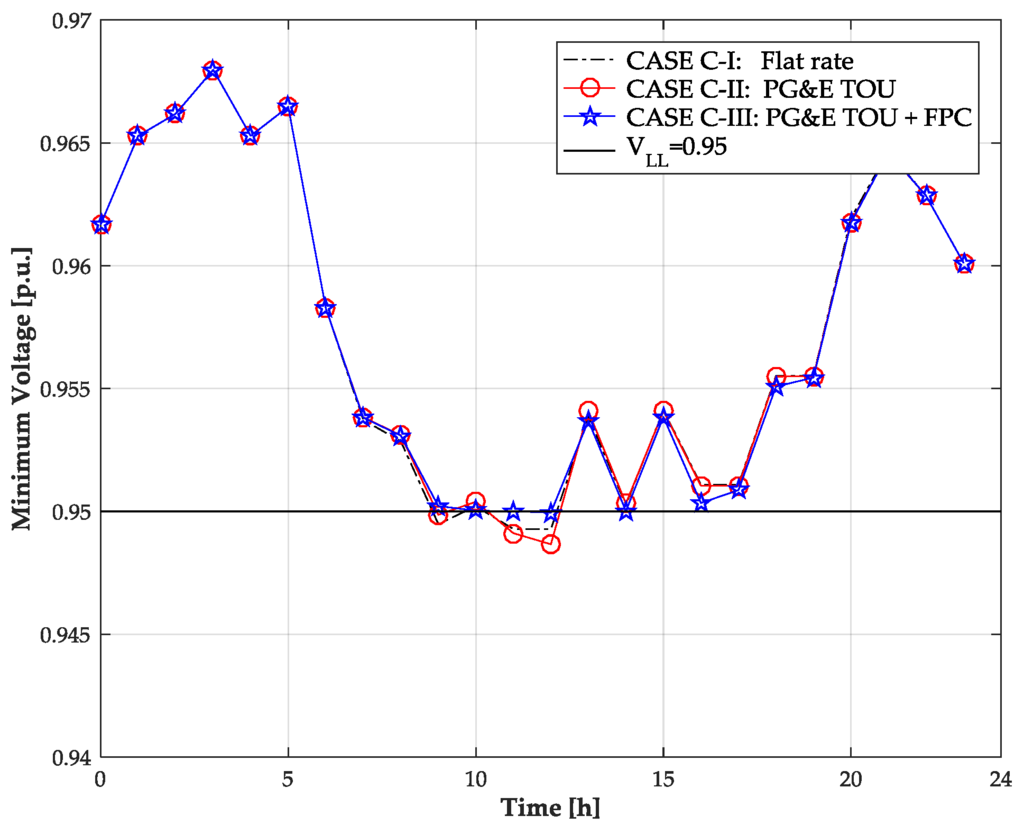
Figure 8. The minimum voltage of the test distribution network for Case C over 24 h.

5. Conclusions

This study proposes an FPC for voltage security as a coordination measure between the DNO and the CSO, which helps the DNO mitigate the low-voltage problem caused by the existence of a charging station. In this paper, a method for calculating $N_{\mathrm{R}}^i(t)$, and a formulation for the optimal coordinate management of the CSO under the FPC scheme are proposed. Using the PG and E 69-bus test distribution network, the proposed scheme is verified to be effective as a coordination measure to handle the voltage security. In other words, the FPC can play a role as a measure to pass on the DNO’s cost for maintaining stable operation of the network to the CSO. In addition, the effect of the FPC can be altered according to the location of the charging station. Specifically, it is more effective to use the FPC when a bus is more vulnerable to voltage drops. Although this study does not obtain the optimal penalty price to maximize the social welfare under the FPC scheme, this can be addressed in depth in future work.