Analysis and Minimization of Output Current Ripple for Discontinuous Pulse-Width Modulation Techniques in Three-Phase Inverters
Abstract
:1. Introduction
2. Problem Statement and Basic Equations
2.1. Load Model and Current Ripple Definitions
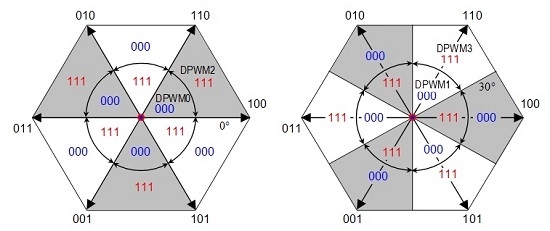
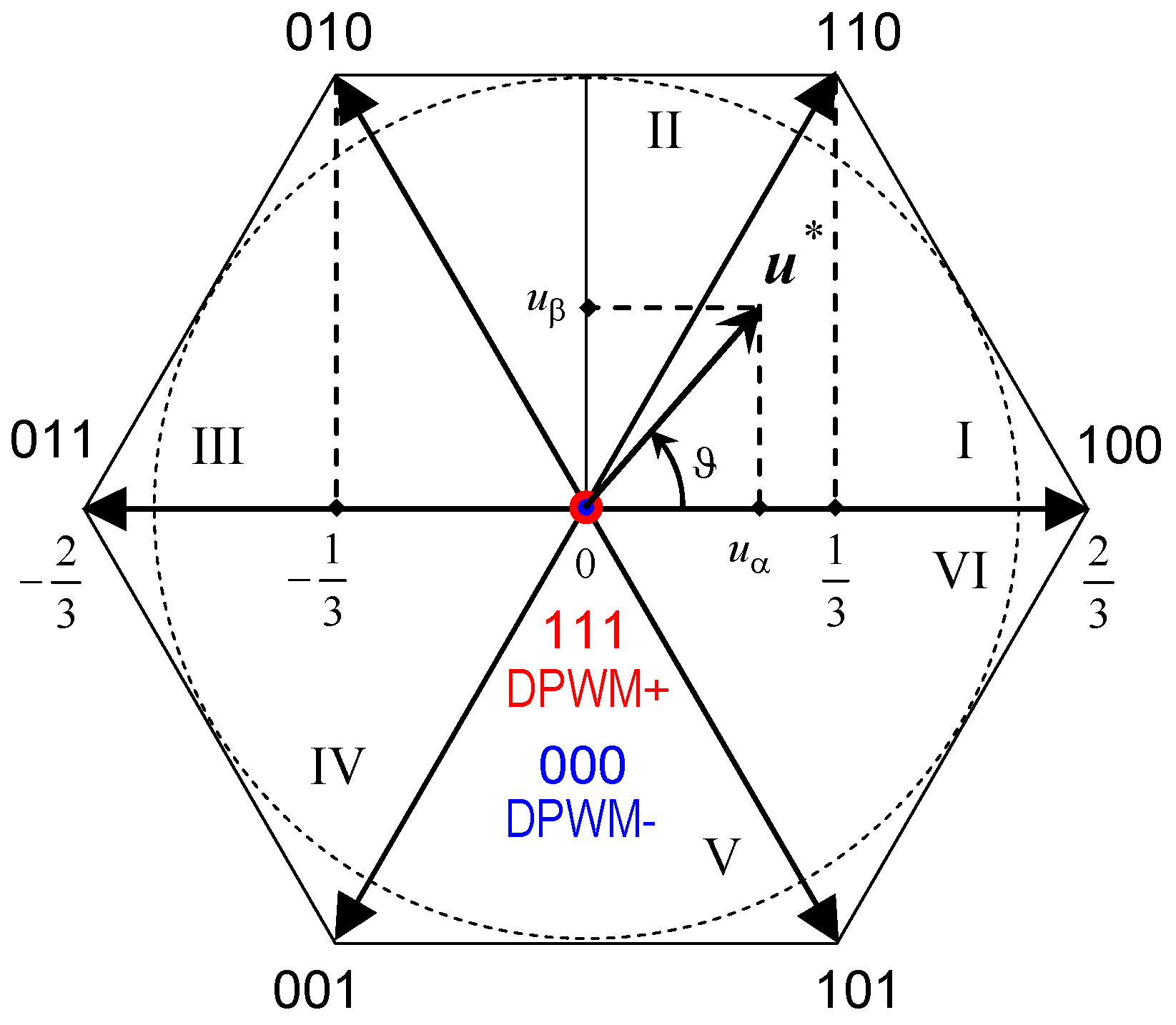
2.2. Space Vector Discontinuous Pulse-Width Modulation
3. Evaluation of Output Current Ripple
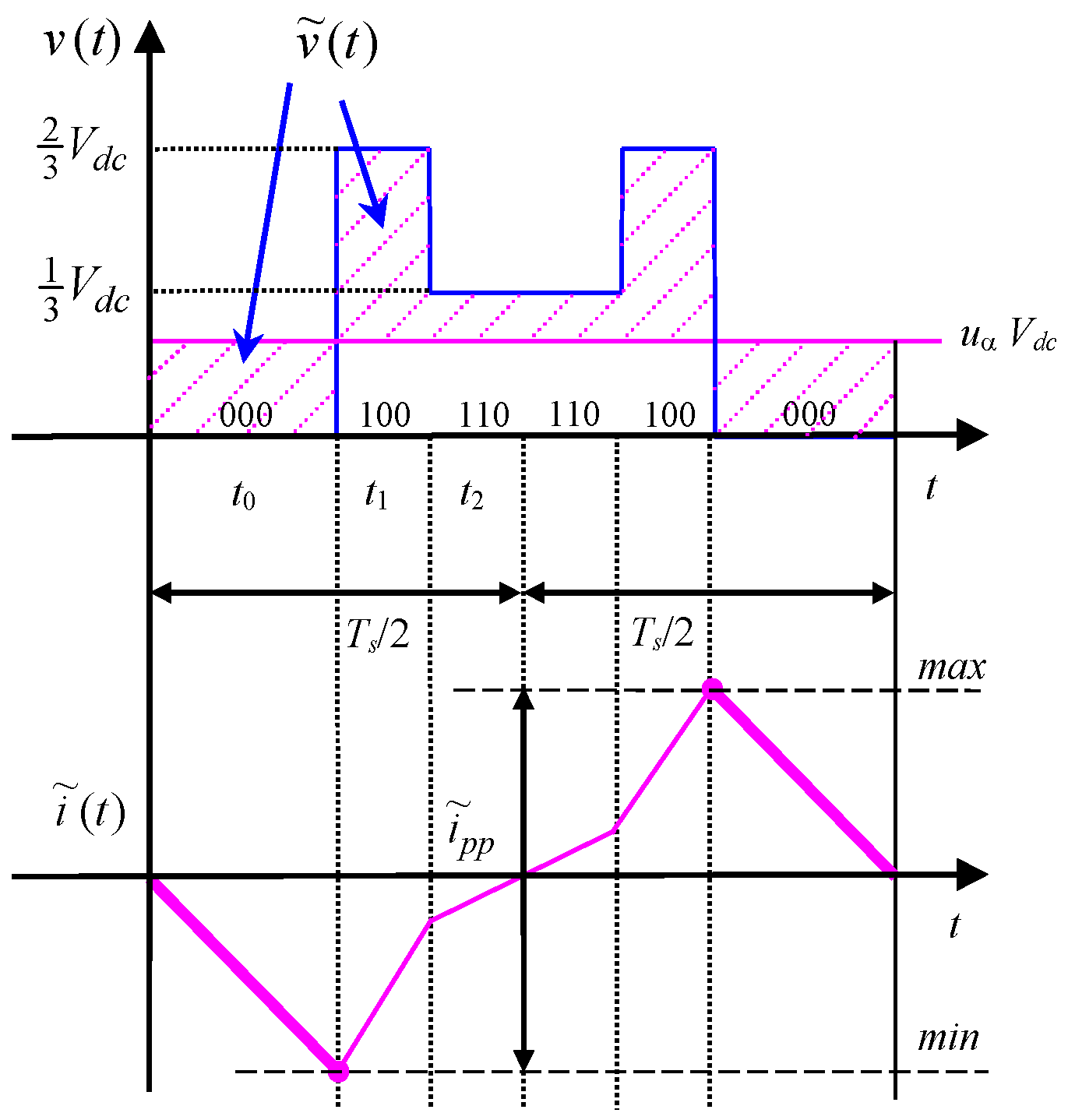
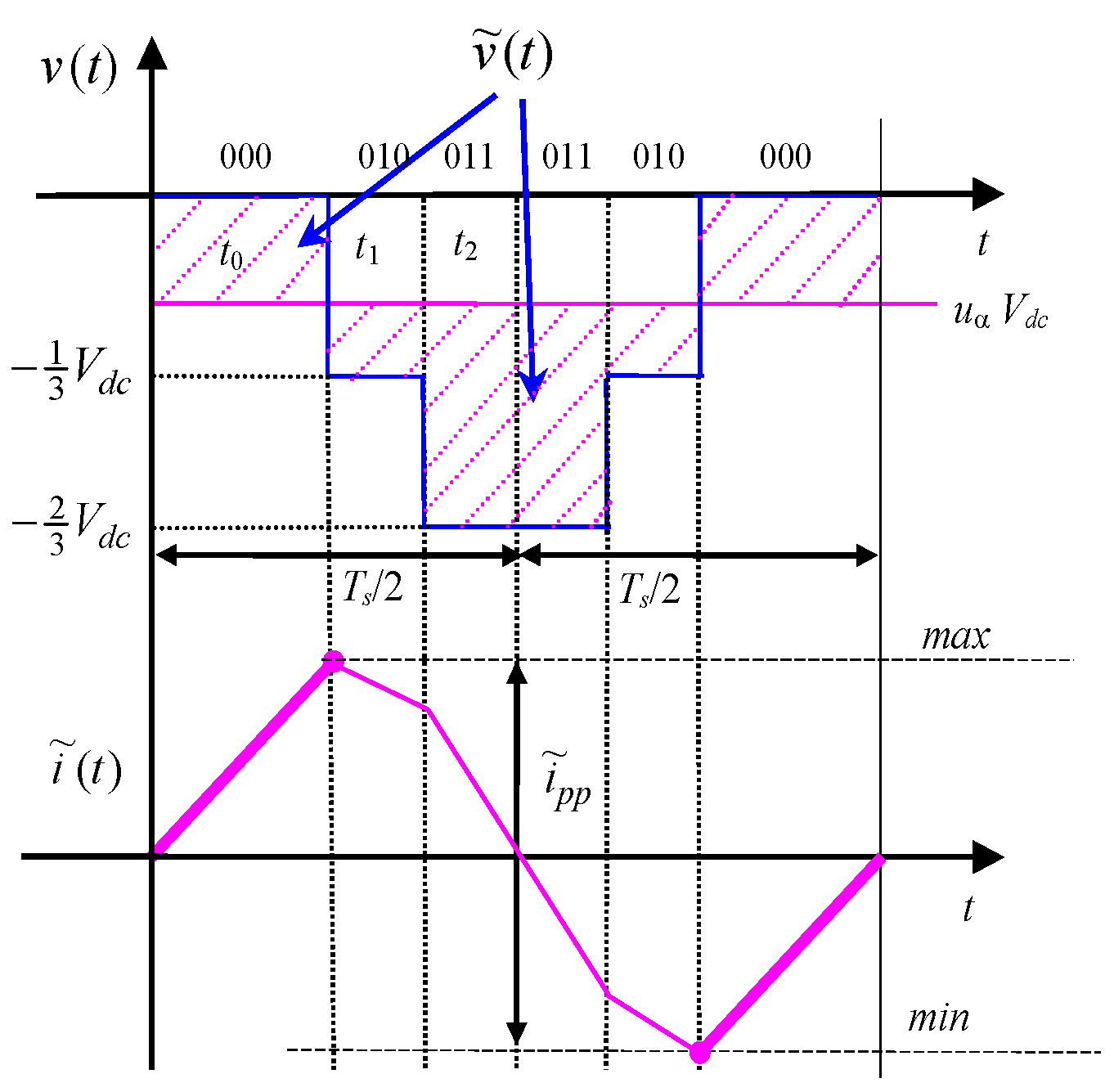
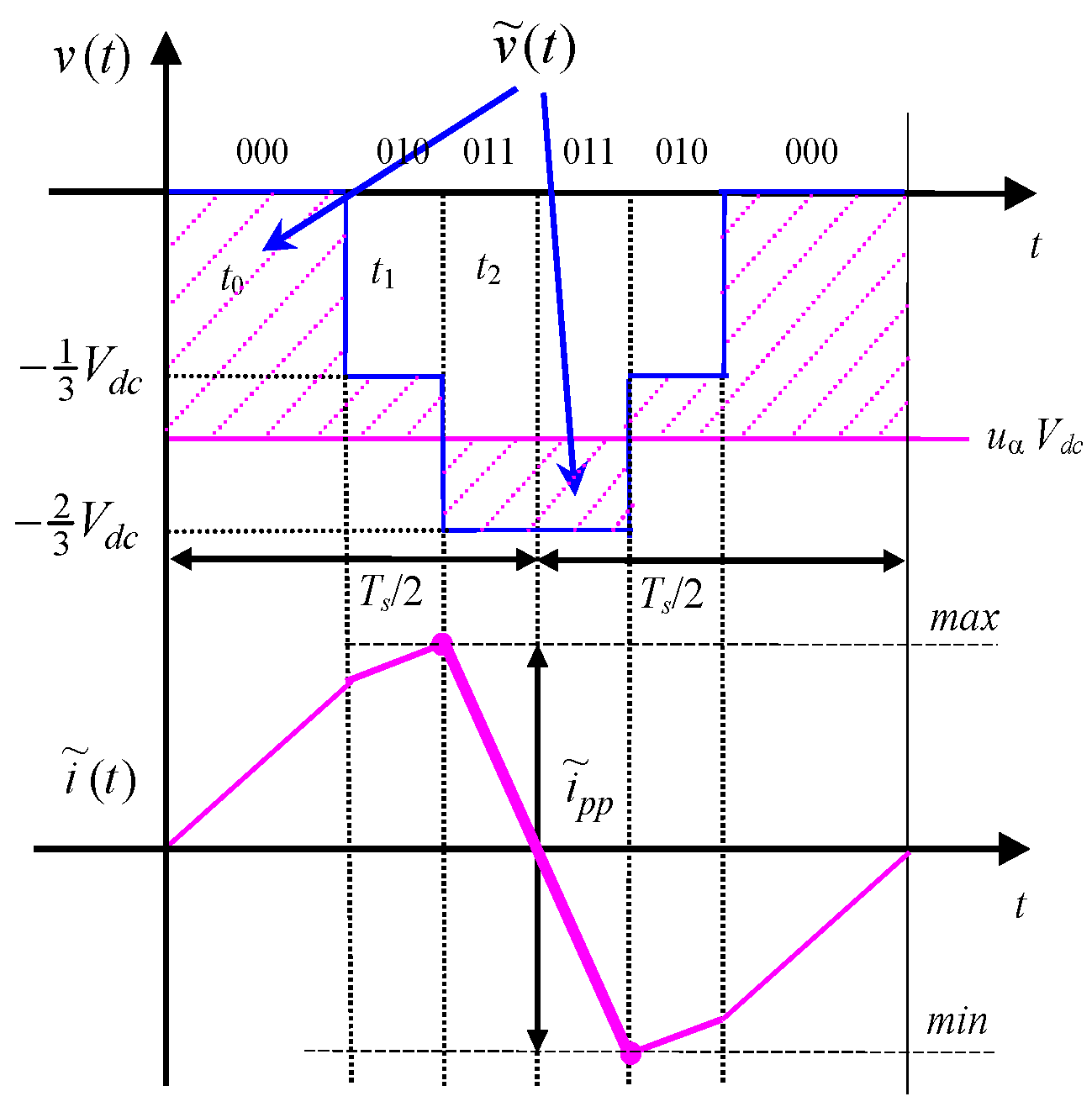
3.1. Negative Clamped Discontinuous Pulse-Width Modulation (DPWM−)
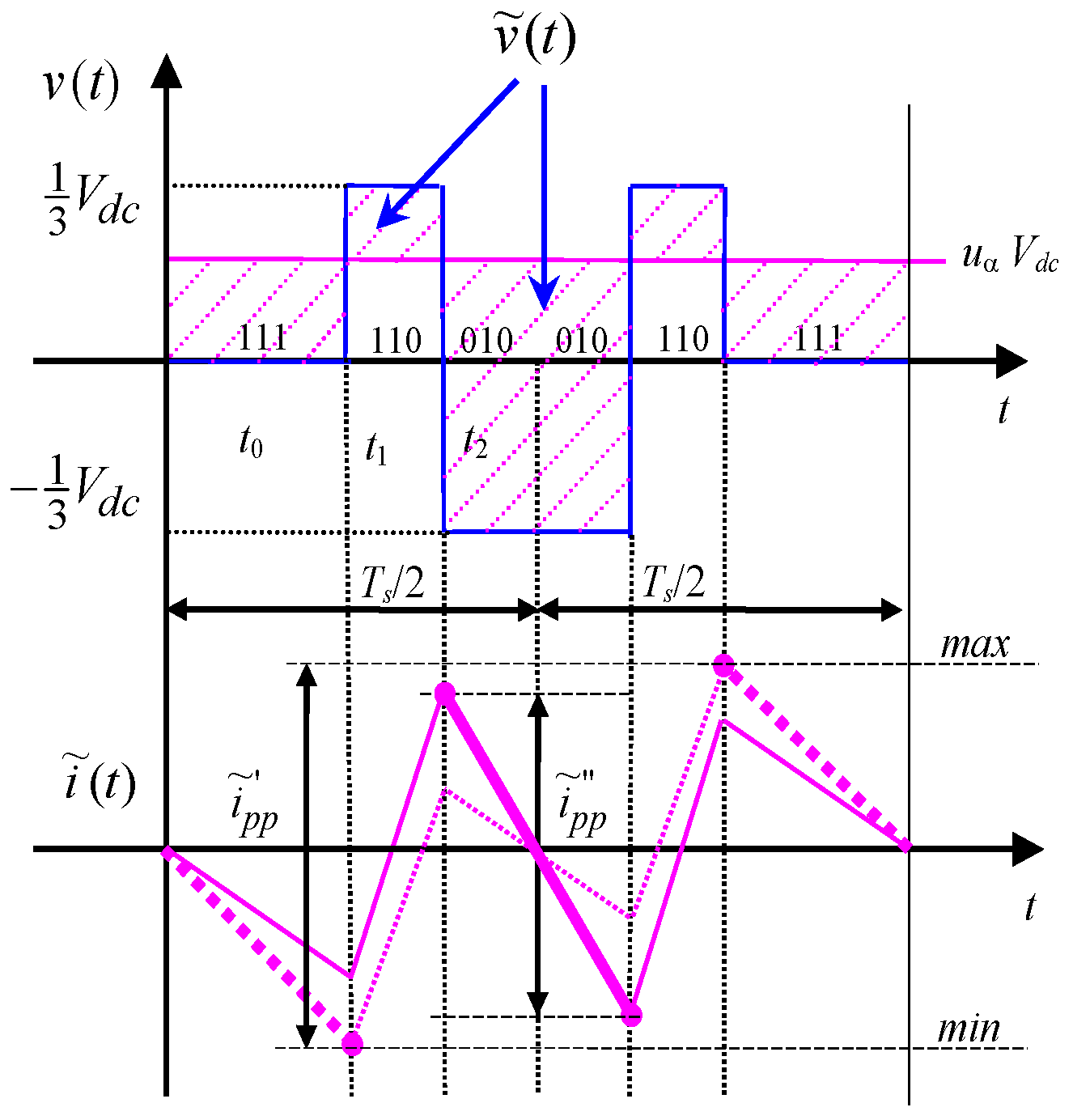
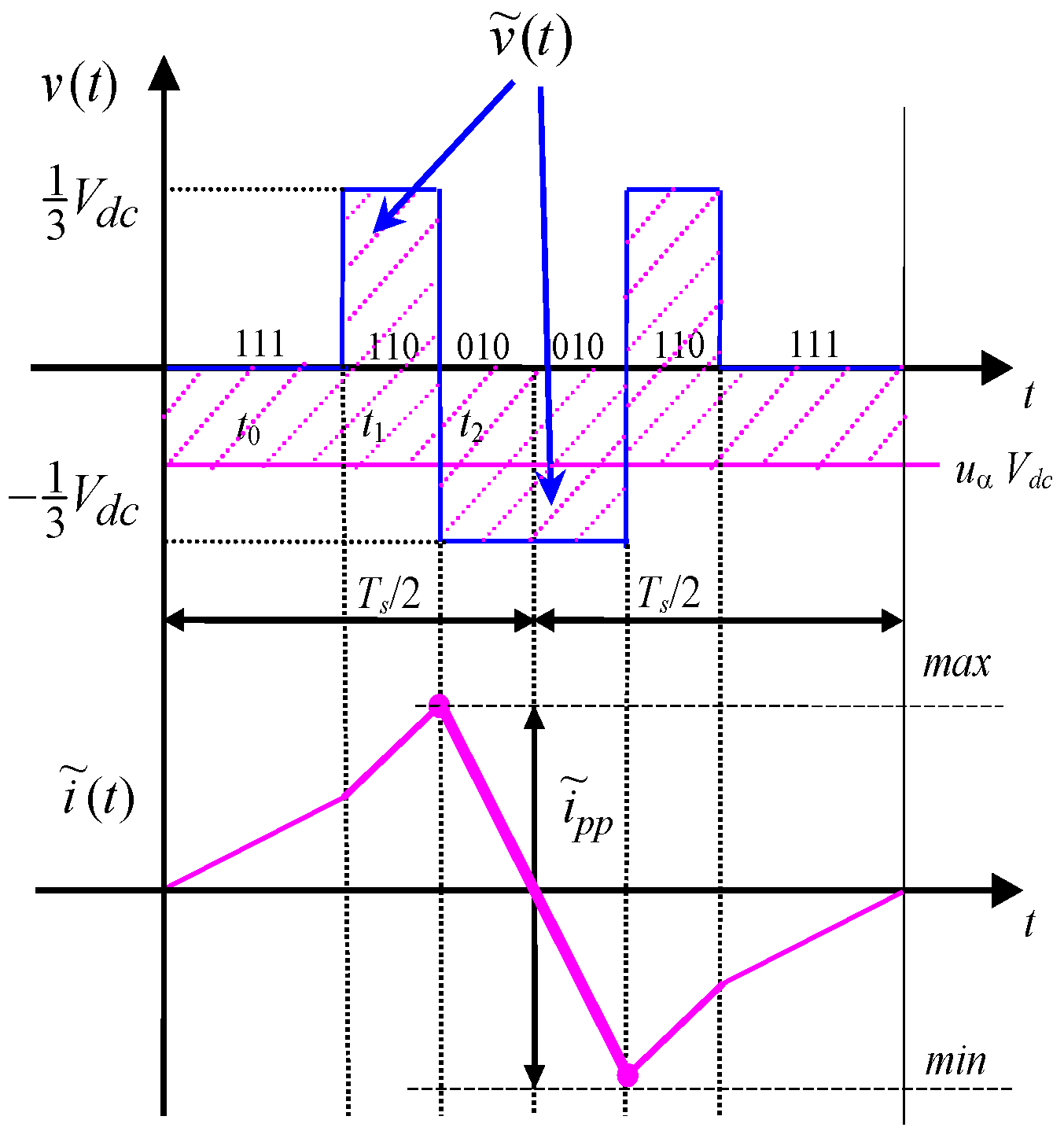
3.1.1. Evaluation of Current Ripple in Sector I
3.1.2. Evaluation of Current Ripple in Sector II
3.1.3. Evaluation of Current Ripple in Sector III
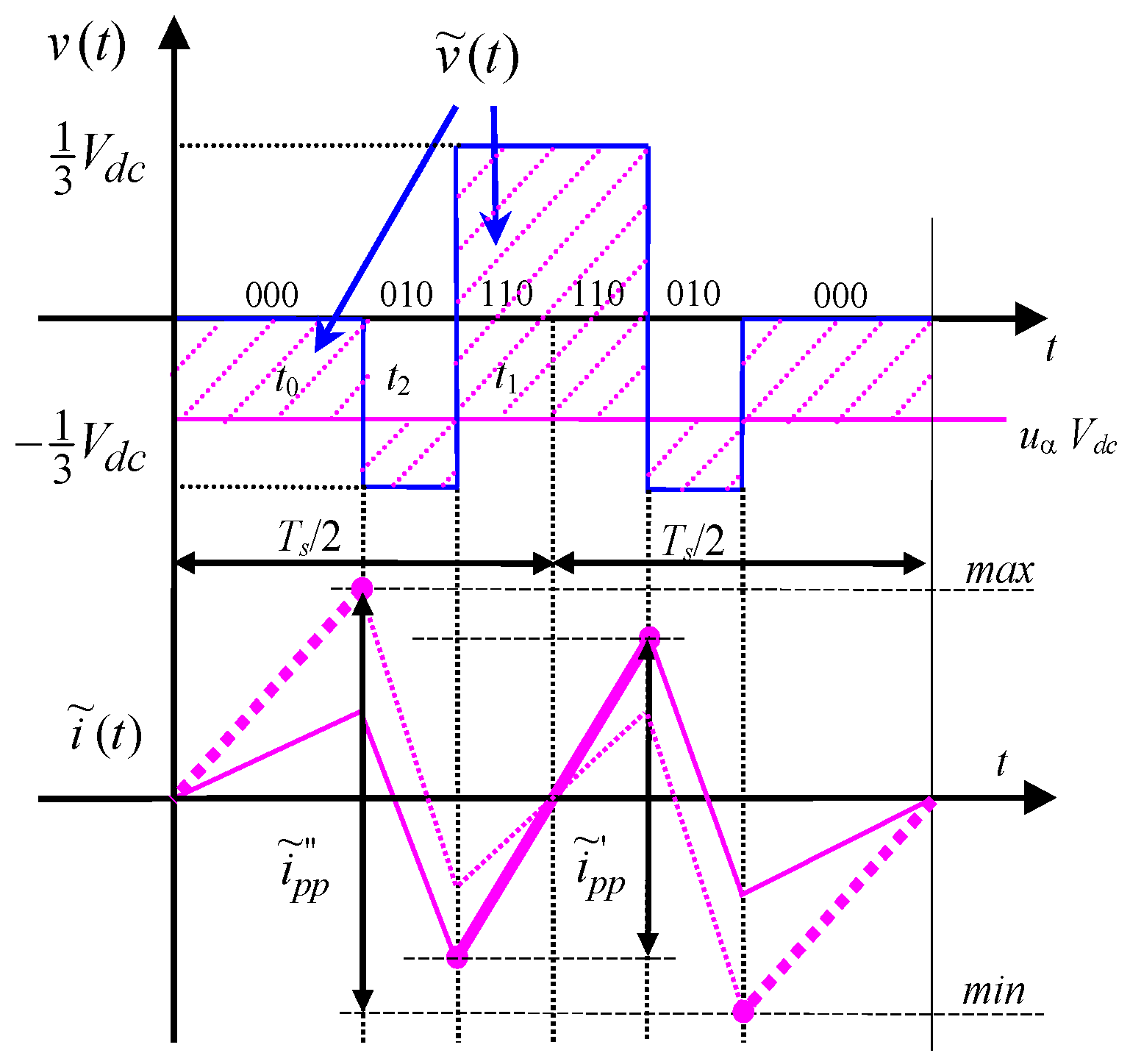
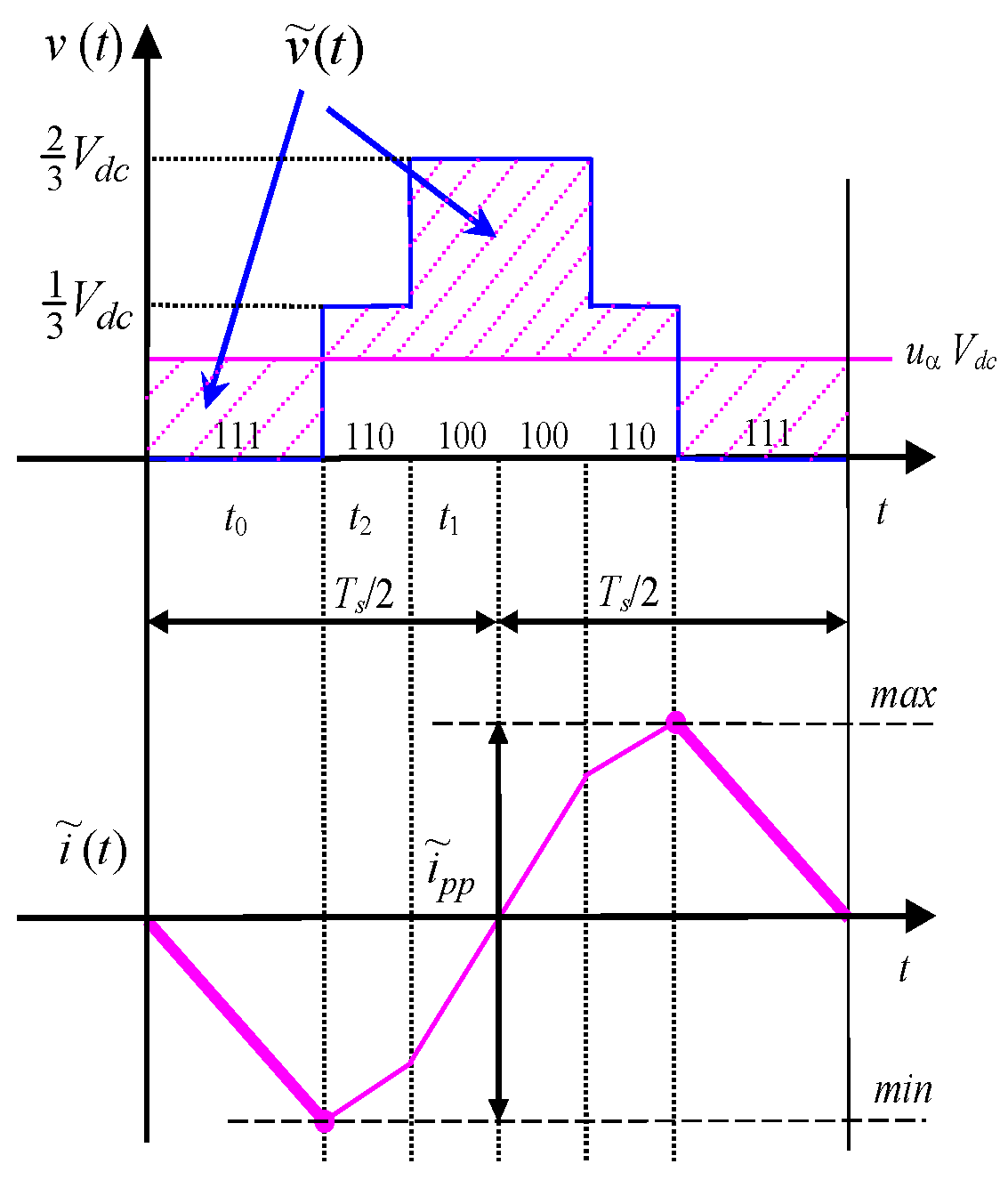
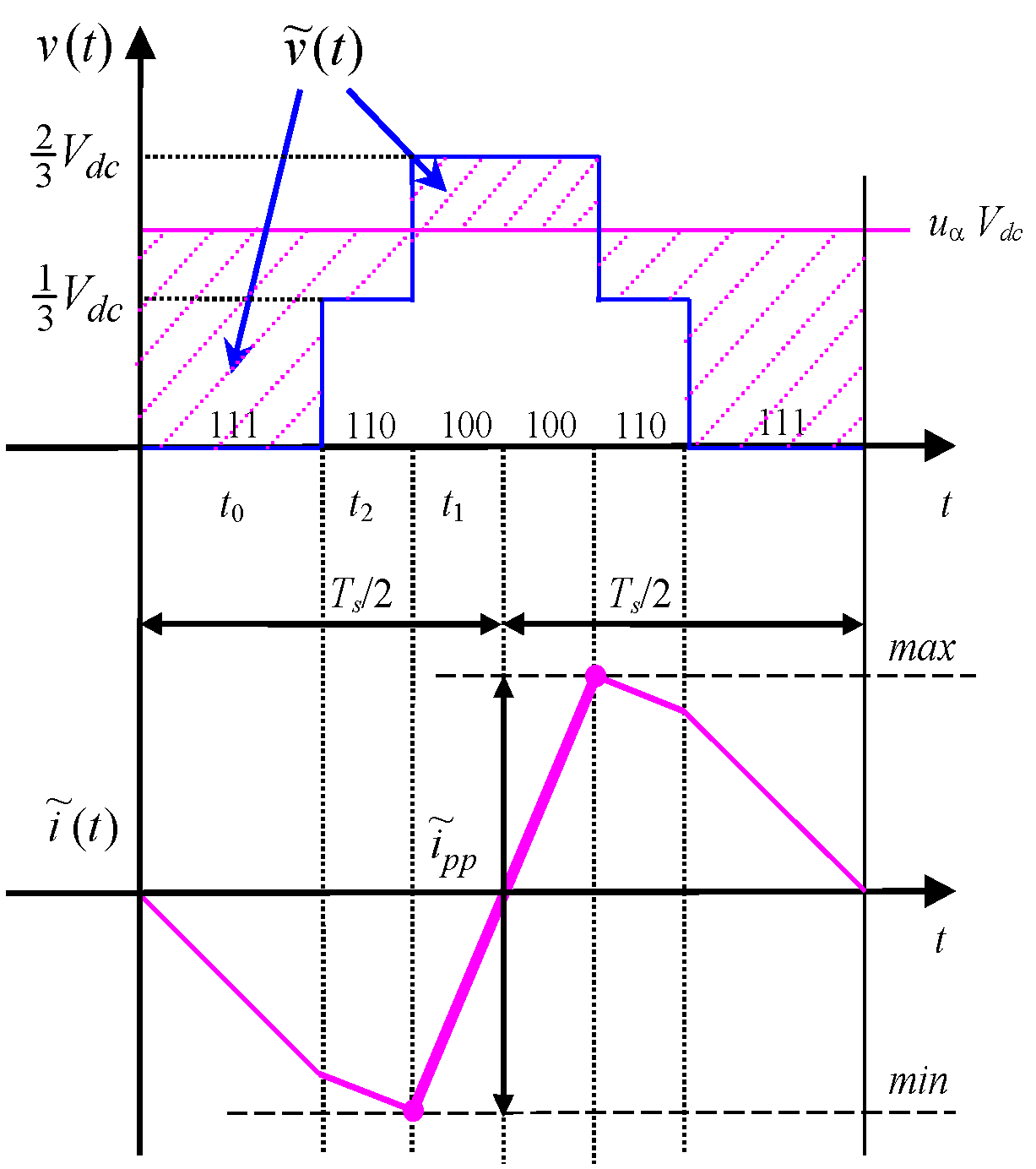
3.2. Positive Clamped Discontinuous Pulse-Width Modulation (DPWM+)
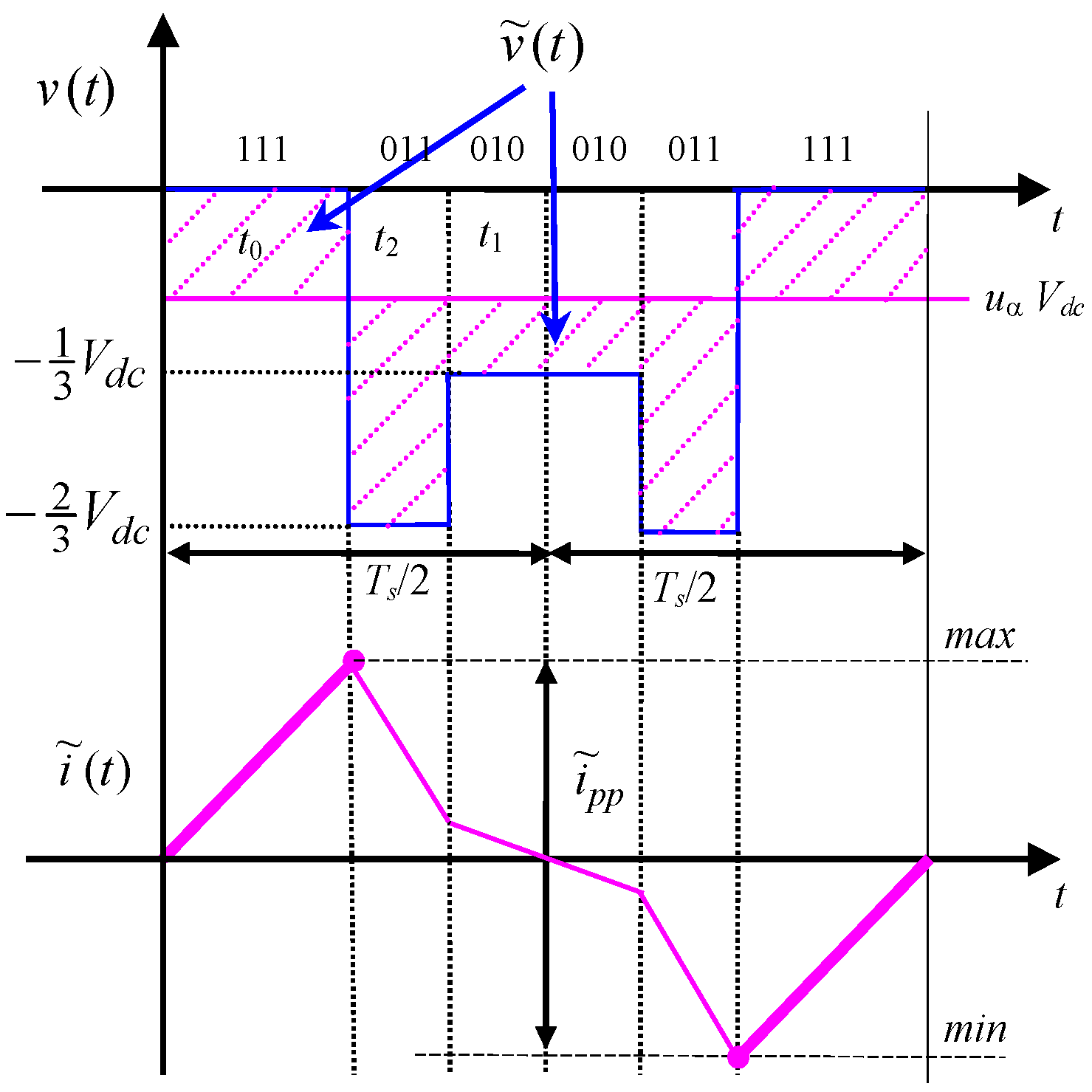
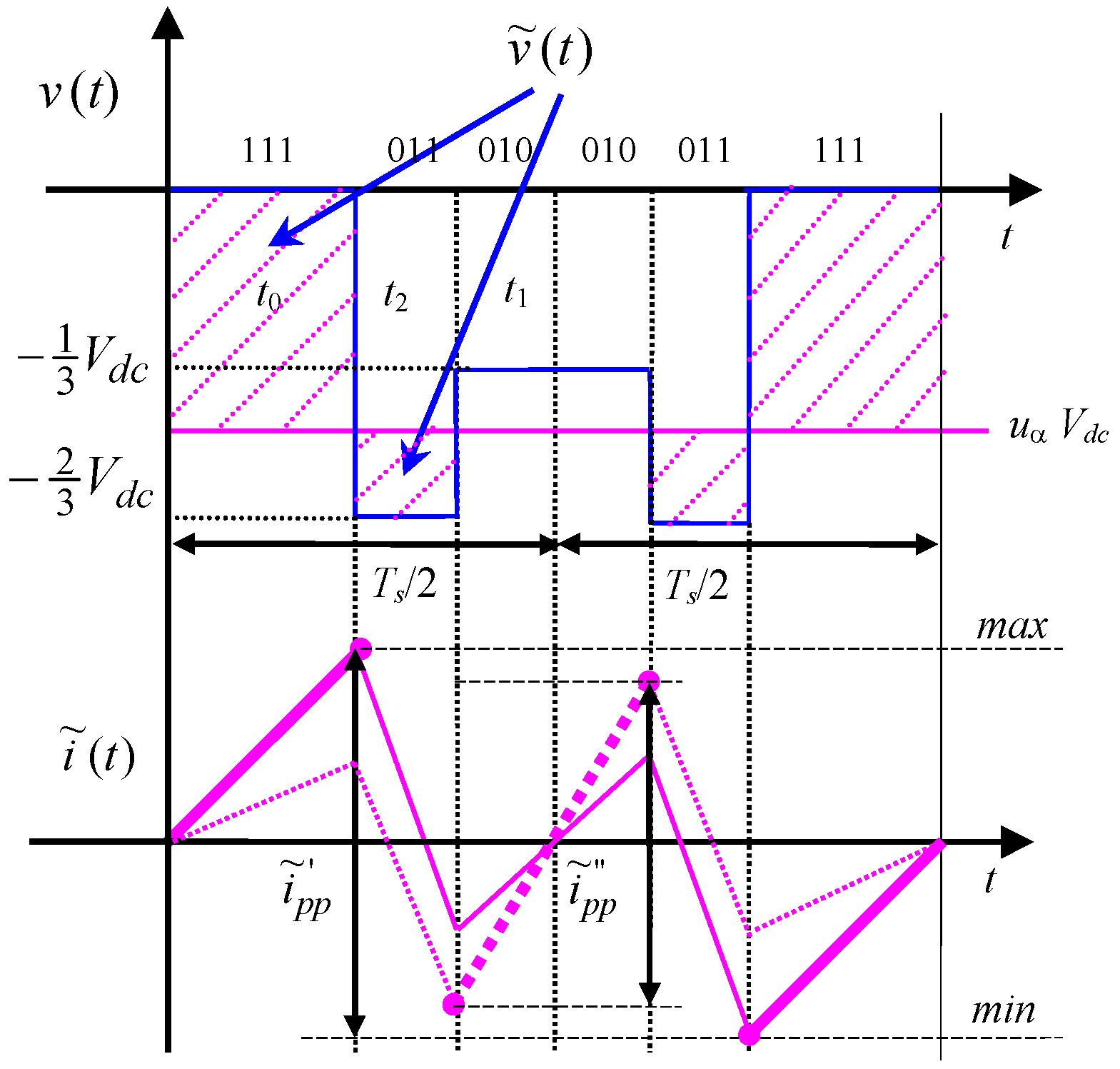
3.2.1. Evaluation of Current Ripple in Sector I
3.2.2. Evaluation of Current Ripple in Sector II
3.2.3. Evaluation of Current Ripple in Sector III
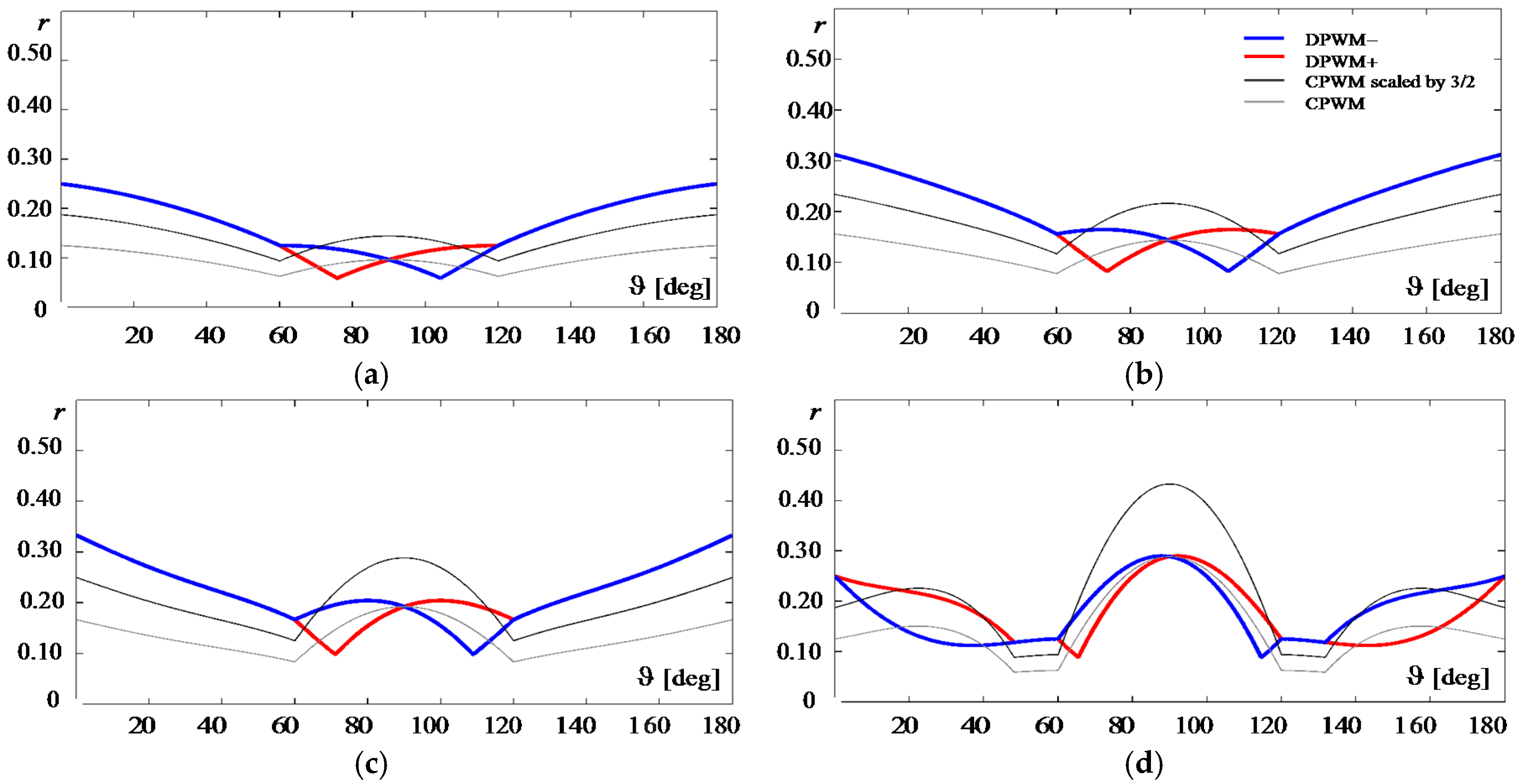
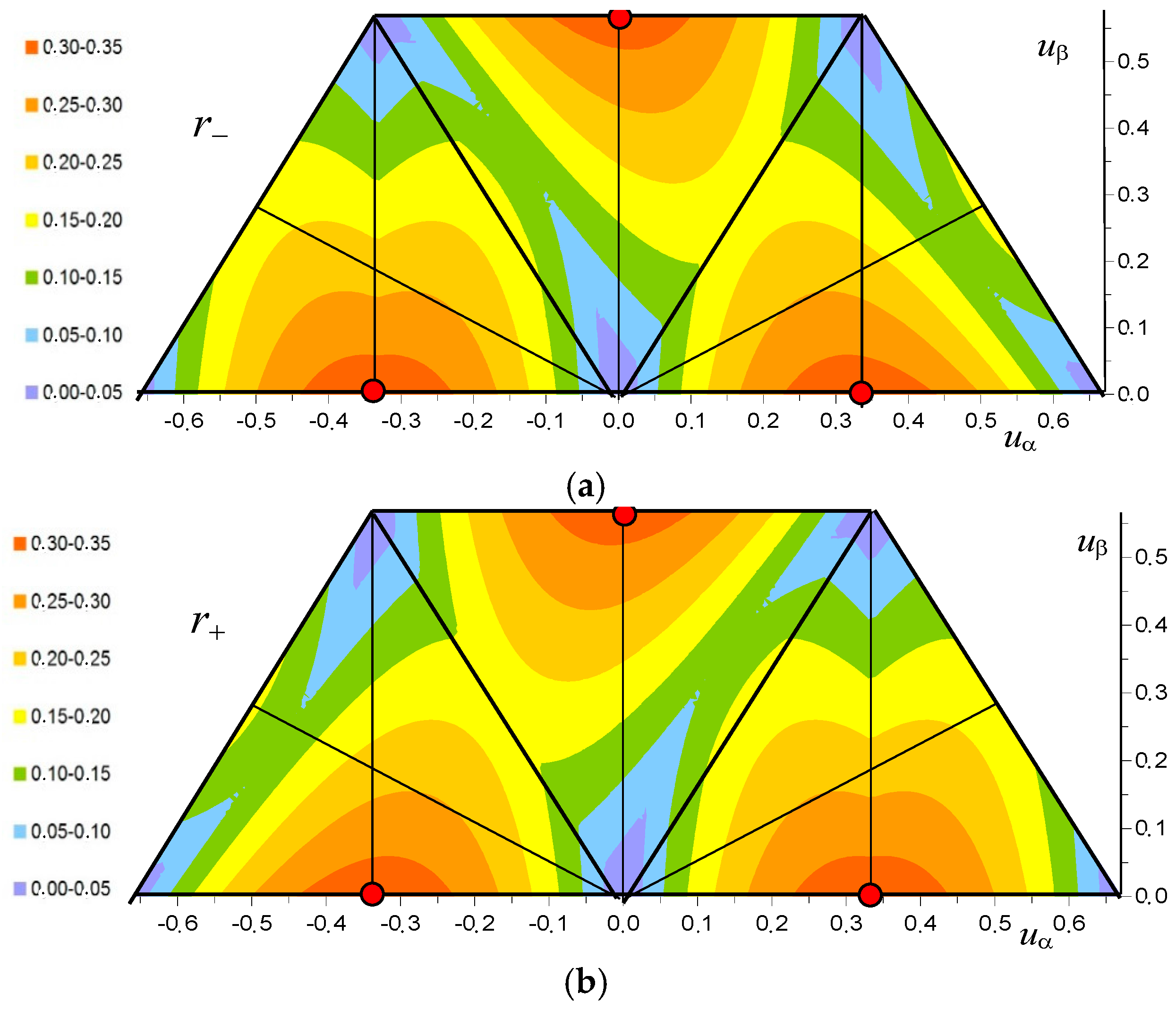
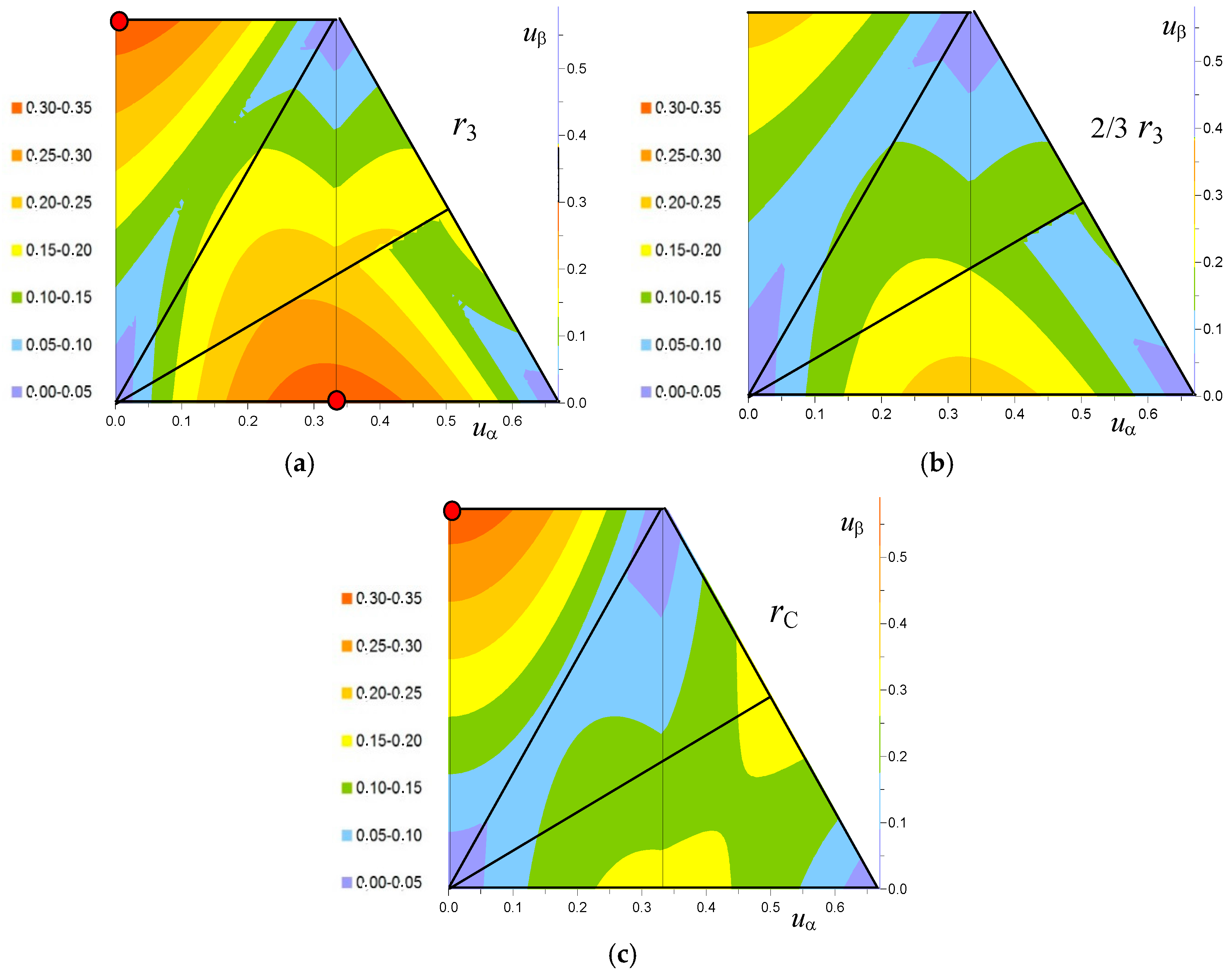
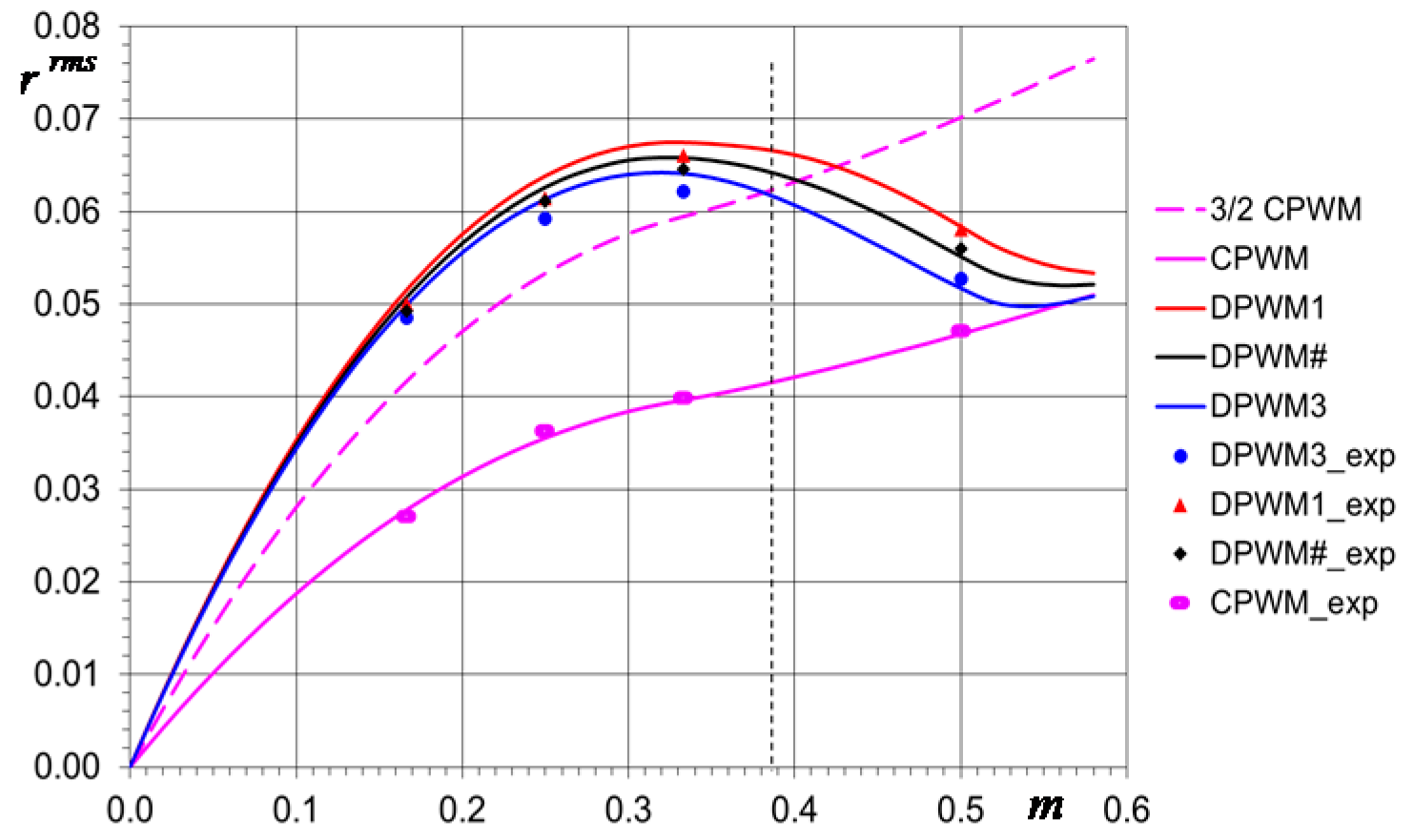
4. Ripple Diagrams and Discussion
4.1. Peak-to-Peak Current Ripple Amplitude
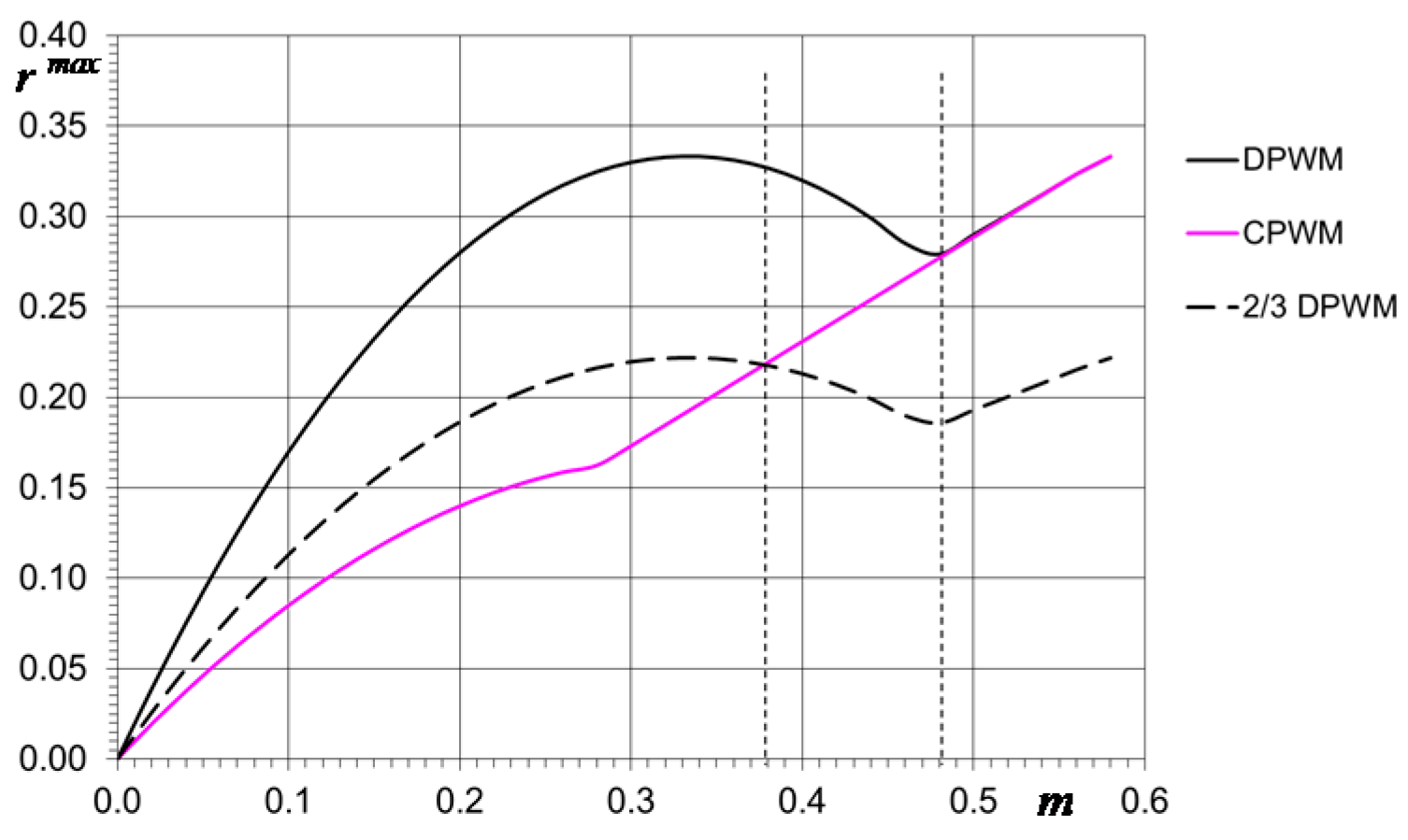
4.2. Maximum of the Current Ripple
4.3. Average Peak-to-Peak Current Ripple
4.4. Relation Between Peak-to-Peak and Current Ripple Rms
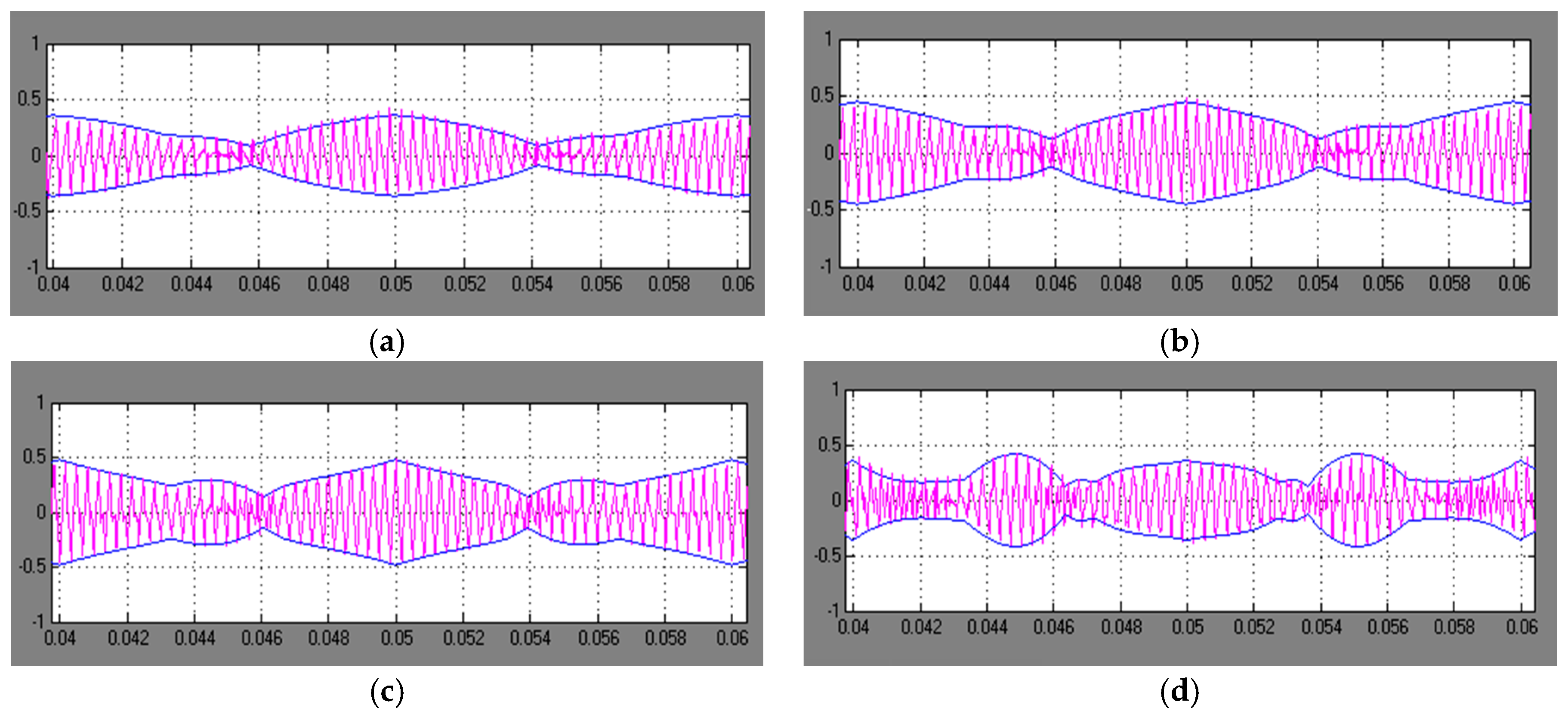
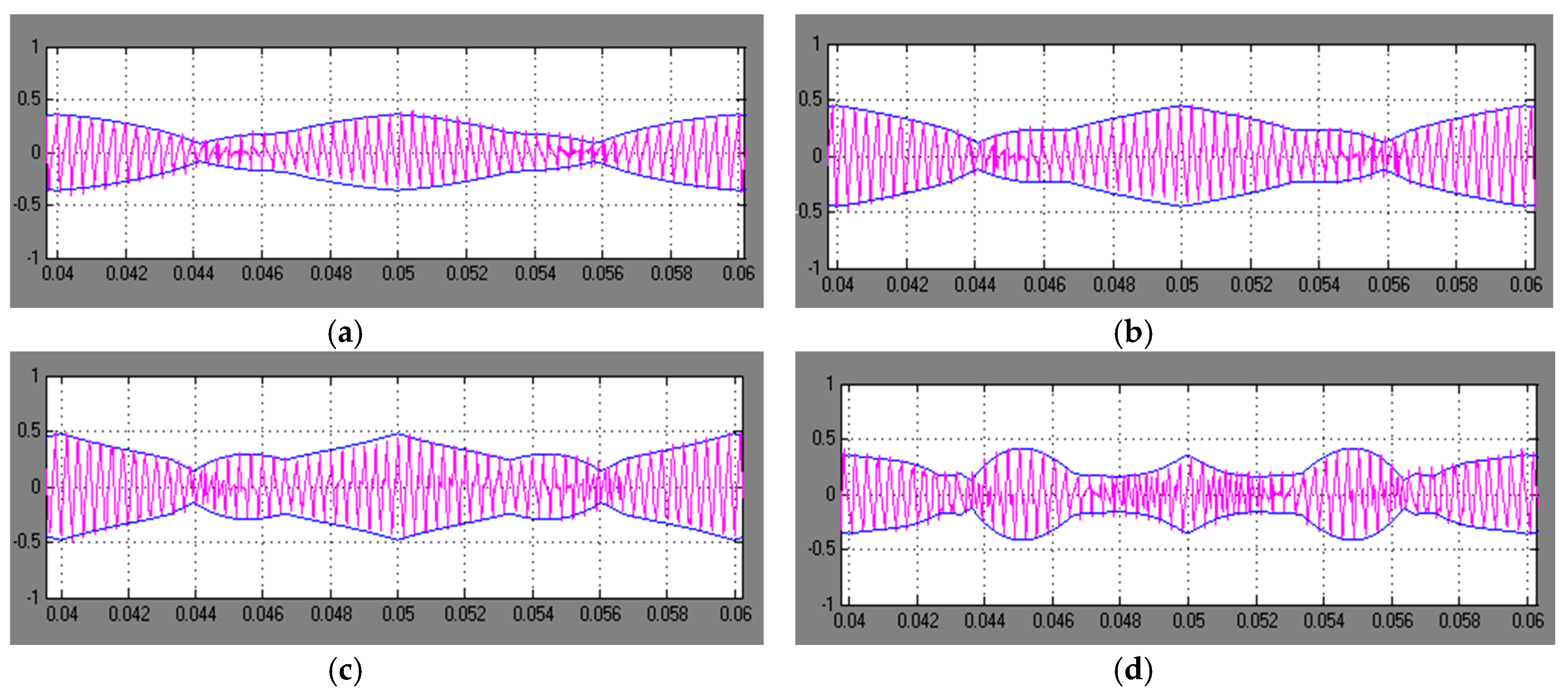
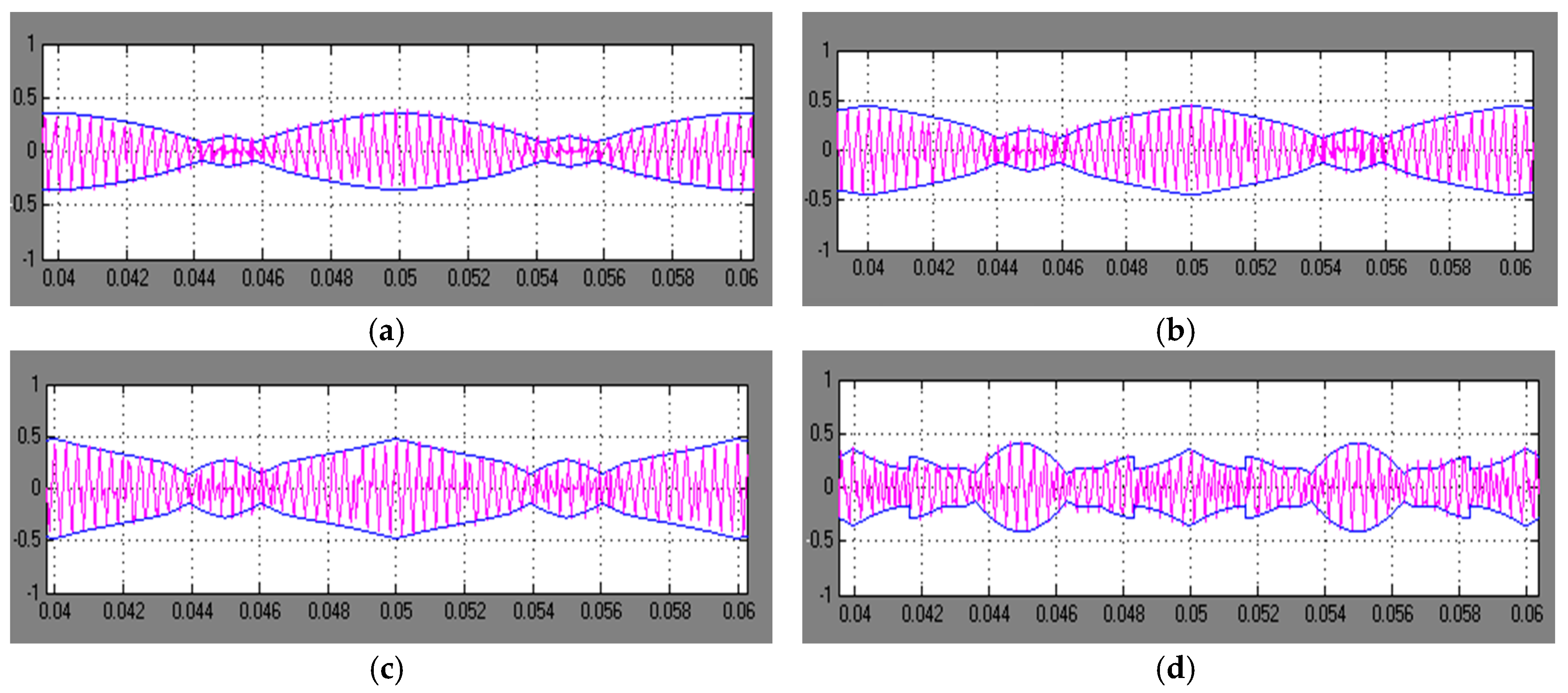
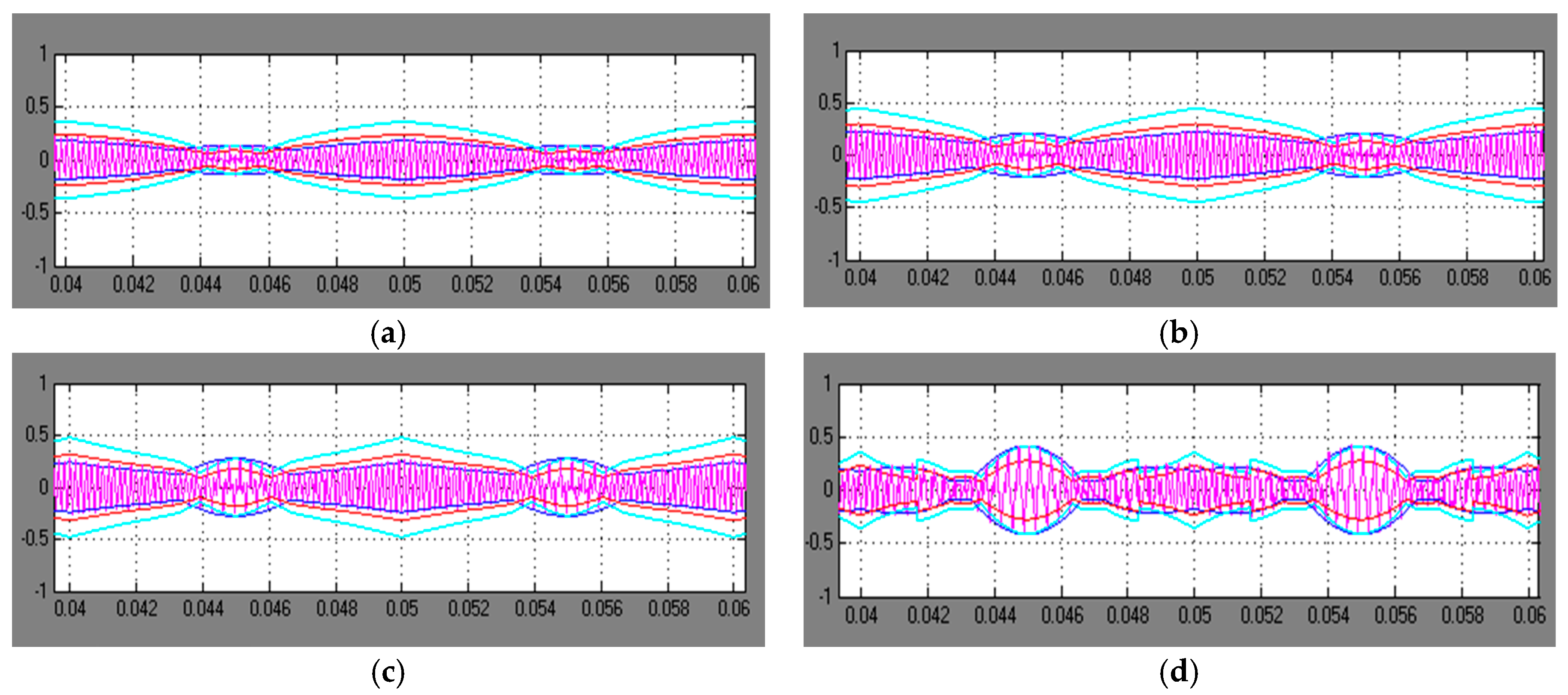
5. Experimental Results
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Van der Broeck, H.W.; Skudelny, H.-C.; Stanke, G.V. Analysis and realization of a pulse width modulator based on voltage space vectors. IEEE Trans. Ind. Appl. 1988, 24, 142–150. [Google Scholar] [CrossRef]
- Hava, A.M.; Kerkman, R.J.; Lipo, T.A. Carrier-Based PWM-VSI Overmodulation strategies: Analysis, comparison, and design. IEEE Trans. Power Electron. 1998, 13, 674–689. [Google Scholar] [CrossRef]
- Hava, A.M.; Kerkman, R.J.; Lipo, T.A. Simple analytical and graphical methods for carier-based PWM-VSI drives. IEEE Trans. Power Electron. 1999, 14, 49–61. [Google Scholar] [CrossRef]
- Holmes, G.D.; Lipo, T.A. Pulse width modulation for power converters: Principles and practice. In IEEE Press Series on Power Engineering; John Wiley & Sons: Oxford, UK, 2003. [Google Scholar]
- Kolar, J.W.; Ertl, H.; Zach, F.C. Influence of the modulation method on the conduction and switching losses of a PWM converter system. IEEE Trans. Ind. Appl. 1991, 27, 1063–1075. [Google Scholar] [CrossRef]
- Casadei, D.; Serra, G.; Tani, A.; Zarri, L. Theoretical and experimental analysis for the RMS current ripple minimization in induction motor drives controlled by SVM technique. IEEE Trans. Ind. Electron. 2004, 51, 1056–1065. [Google Scholar] [CrossRef]
- Holtz, J. Pulsewidth modulation for electric power conversion. IEEE Proc. 1994, 82, 1194–1214. [Google Scholar] [CrossRef]
- Depenbrock, M. Pulse Width Control of a 3-Phase Inverter with Nonsinusoidal Phase Voltages. In Proceedings of the IEEE International Semiconductor Power Converter Conference Record, New York, NY, USA, 1977; pp. 399–403.
- Ogasawara, S.; Nabae, A.; Akagi, H. A novel PWM scheme of voltage source inverter based on space vector theory. Arch. Elektrotech. 1990, 74, 33–41. [Google Scholar] [CrossRef]
- Hava, A.M.; Kerkman, R.J.; Lipo, T.A. A high-performance generalized discontinuous PWM algorithm. IEEE Trans. Ind. Appl. 1998, 34, 1059–1071. [Google Scholar] [CrossRef]
- Ojo, O. The generalized discontinuous PWM scheme for three-phase voltage source inverters. IEEE Trans. Ind. Electron. 2004, 51, 1280–1289. [Google Scholar] [CrossRef]
- Beig, A.R.; Kanukollu, S.; Hosani, K.A.; Dekka, A. Space-vector-based synchronized three-level discontinuous PWM for medium-voltage high-power VSI. IEEE Trans. Ind. Electron. 2014, 61, 3891–3901. [Google Scholar] [CrossRef]
- Sekhar, K.R.; Srinivas, S. Discontinuous decoupled PWMs for reduced current ripple in a dual two-level inverter fed open-end winding induction motor drive. IEEE Trans. Power Electron. 2013, 28, 2493–2502. [Google Scholar] [CrossRef]
- Charumit, C.; Kinnares, V. Discontinuous SVPWM techniques of three-leg VSI-fed balanced Two-phase loads for reduced switching losses and current ripple. IEEE Trans. Power Electron. 2015, 30, 2191–2204. [Google Scholar] [CrossRef]
- Dujic, D.; Jones, M.; Levi, E. Analysis of output current ripple rms in multiphase drives using space vector approach. IEEE Trans. Power Electron. 2009, 24, 1926–1938. [Google Scholar] [CrossRef]
- Dujic, D.; Jones, M.; Levi, E.; Prieto, J.; Barrero, F. Switching ripple characteristics of space vector PWM schemes for five-phase two-level voltage source inverters—Part 2: Flux harmonic distortion factors. IEEE Trans. Ind. Electron. 2011, 58, 2789–2808. [Google Scholar] [CrossRef]
- Ruderman, A.; Wang, F. Understanding PWM current ripple in star-connected AC motor drive. IEEE Power Electron. Soc. Newsl. 2009, 21, 14–17. [Google Scholar]
- Grandi, G.; Loncarski, J. Evaluation of Current Ripple Amplitude in Three-Phase PWM Voltage Source Inverters. In Proceedings of the 8th International Conference on Compatibility Power Electronics, Ljubljana, Slovenia, 5–7 June 2013; pp. 156–161.
- Park, J.-H.; Jeong, H.-G.; Lee, K.-B. Output current ripple reduction algorithms for home energy storage systems. Energies 2013, 6, 5552–5569. [Google Scholar] [CrossRef]
- Jiang, D.; Wang, F. Current-ripple prediction for three-phase PWM converters. IEEE Trans. Ind. Appl. 2014, 50, 531–538. [Google Scholar] [CrossRef]
- Grandi, G.; Loncarski, J.; Dordevic, O. Analysis and comparison of peak-to-peak current ripple in two-level and multilevel PWM inverters. IEEE Trans. Ind. Electron. 2015, 62, 2721–2730. [Google Scholar] [CrossRef]
- Loncarski, J.; Leijon, M.; Srndovic, M.; Rossi, C.; Grandi, G. Comparison of output current ripple in single and dual three-phase inverters for electric vehicle motor drives. Energies 2015, 8, 3832–3848. [Google Scholar] [CrossRef]
- Grandi, G.; Loncarski, J. Analysis of peak-to-peak current ripple amplitude in seven-phase PWM voltage source inverters. Energies 2013, 6, 4429–4447. [Google Scholar] [CrossRef]
- Lewicki, A. Dead-time effect compensation based on additional phase current measurements. IEEE Trans. Ind. Electron. 2015, 62, 4078–4085. [Google Scholar] [CrossRef]
- Grandi, G.; Loncarski, J.; Seebacher, R. Effects of Current Ripple on Dead-Time Distortion in Three-Phase Voltage Source Inverters. In Proceedings of the 2012 IEEE International Energy Conferences and Exhibition, Florence, Italy, 9–12 September 2012; pp. 207–212.
- Wu, F.; Feng, F.; Luo, L.; Duan, J.; Sun, L. Sampling period online adjusting-based hysteresis current control without band with constant switching frequency. IEEE Trans. Ind. Electron. 2015, 62, 270–277. [Google Scholar] [CrossRef]
- Jiang, D.; Wang, F.F. Variable switching frequency PWM for three-phase converters based on current ripple prediction. IEEE Trans. Power Electron. 2013, 28, 4951–4931. [Google Scholar] [CrossRef]
- Asiminoaei, L.; Rodriguez, P.; Blaabjerg, F.; Malinowski, M. Reduction of switching losses in active power filters with a new generalized discontinuous-PWM strategy. IEEE Trans. Ind. Electron. 2008, 55, 467–471. [Google Scholar] [CrossRef]







| Sector | δ1 | δ2 | δ0 |
|---|---|---|---|
| I | |||
| II | |||
| III |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grandi, G.; Loncarski, J.; Srndovic, M. Analysis and Minimization of Output Current Ripple for Discontinuous Pulse-Width Modulation Techniques in Three-Phase Inverters. Energies 2016, 9, 380. https://doi.org/10.3390/en9050380
Grandi G, Loncarski J, Srndovic M. Analysis and Minimization of Output Current Ripple for Discontinuous Pulse-Width Modulation Techniques in Three-Phase Inverters. Energies. 2016; 9(5):380. https://doi.org/10.3390/en9050380
Chicago/Turabian StyleGrandi, Gabriele, Jelena Loncarski, and Milan Srndovic. 2016. "Analysis and Minimization of Output Current Ripple for Discontinuous Pulse-Width Modulation Techniques in Three-Phase Inverters" Energies 9, no. 5: 380. https://doi.org/10.3390/en9050380