Application of Hybrid Quantum Tabu Search with Support Vector Regression (SVR) for Load Forecasting
Abstract
:1. Introduction
2. Methodology of Support Vector Regression Quantum Tabu Search (SVRQTS) Model
2.1. Support Vector Regression (SVR) Model
2.2. Chaotic Quantum Tabu Search Algorithm
2.2.1. Tabu Search (TS) Algorithm and Quantum Tabu Search (QTS) Algorithm
2.2.2. Chaotic Mapping Function for Quantum Tabu Search (QTS) Algorithm
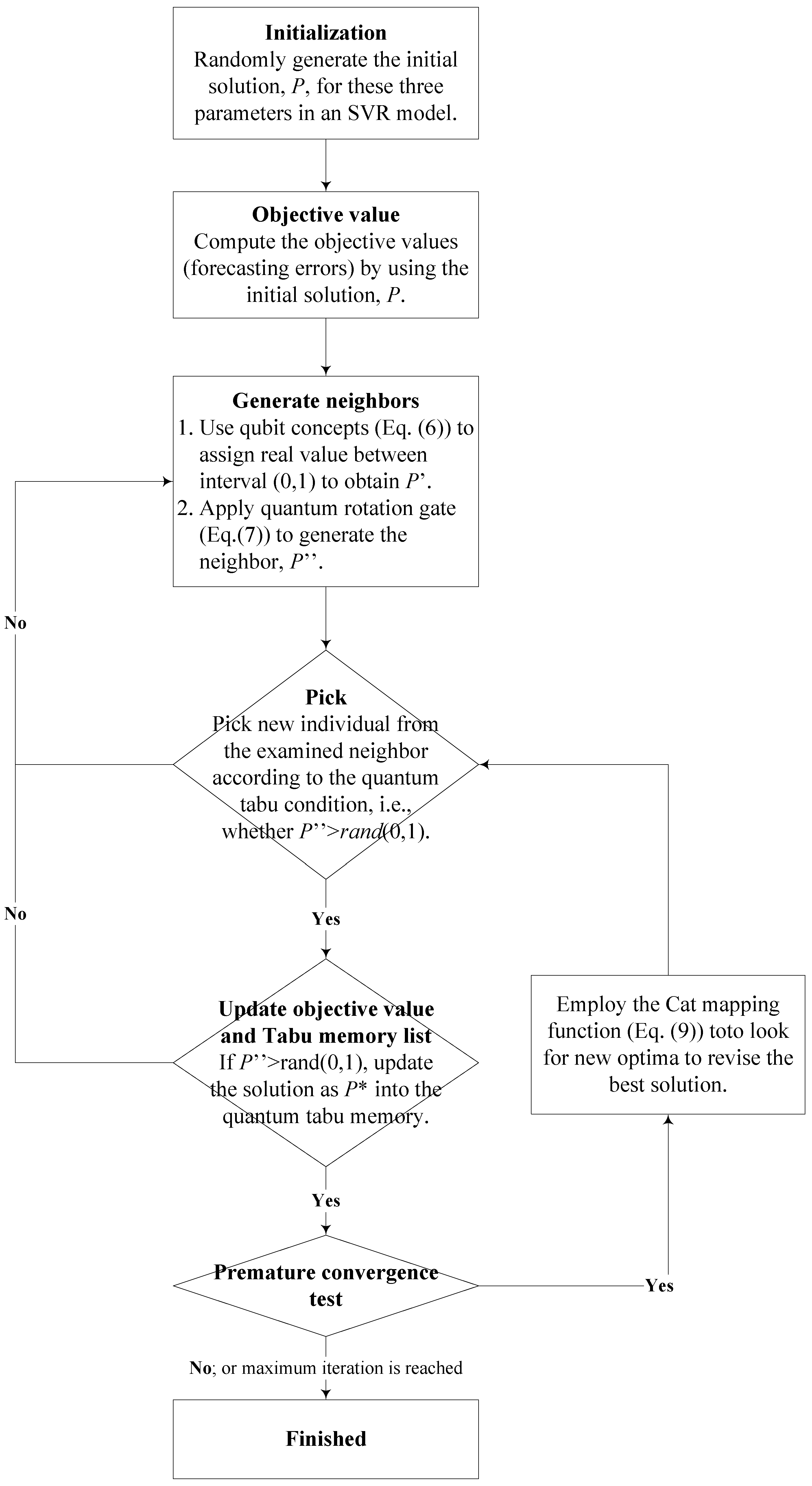
2.2.3. Implementation Steps of Chaotic Quantum Tabu Search (CQTS) Algorithm
3. Numerical Examples
3.1. Data Set of Numerical Examples
3.1.1. The First Example: Taiwan Regional Load Data
3.1.2. The Second Example: Taiwan Annual Load Data
3.1.3. The Third Example: 2014 Global Energy Forecasting Competition (GEFCOM 2014) Load Data
3.2. The SVRCQTS Load Forecasting Model
3.2.1. Parameters Setting in CQTS Algorithm
3.2.2. Forecasting Results and Analysis for Example 1
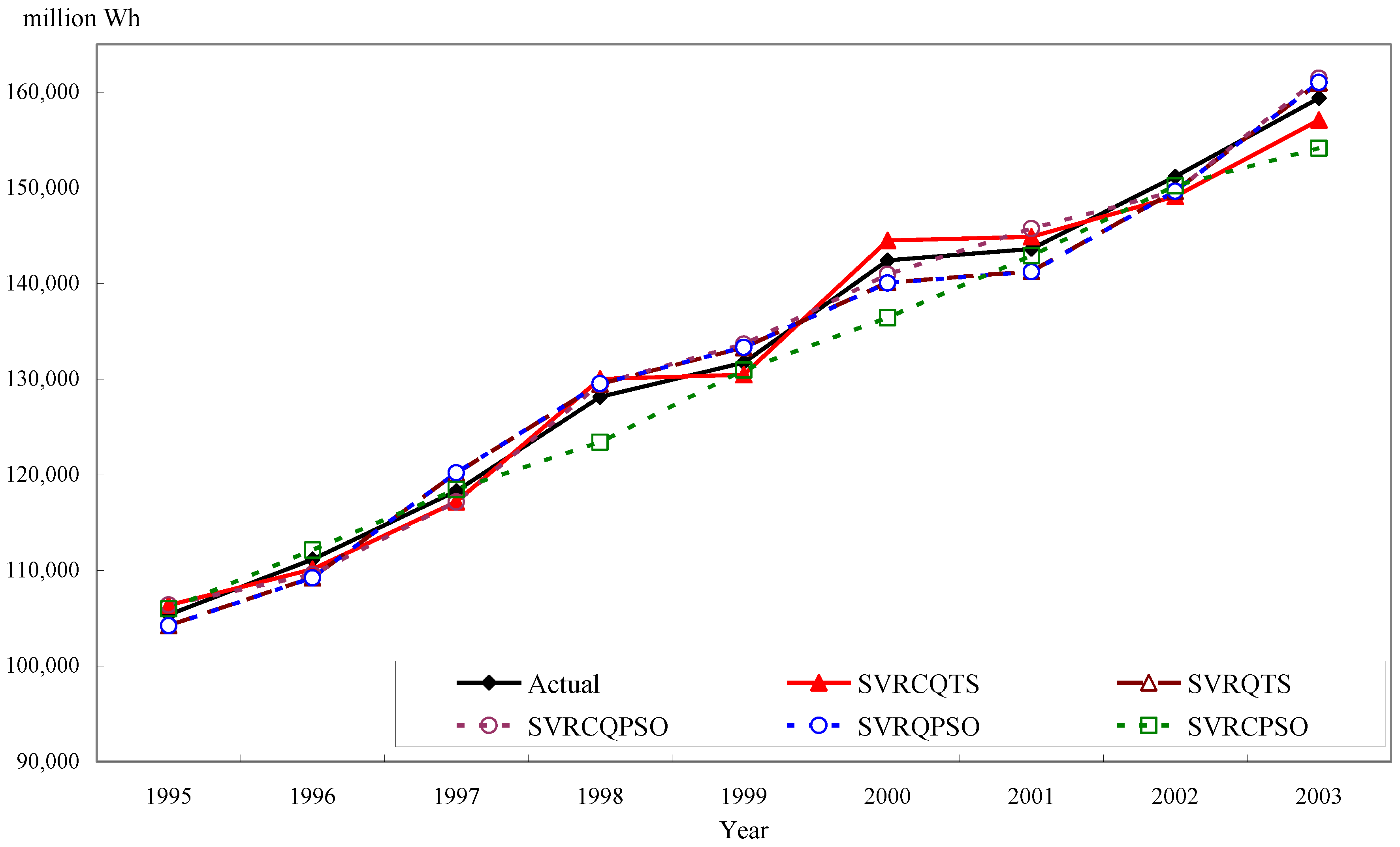
3.2.3. Forecasting Results and Analysis for Example 2
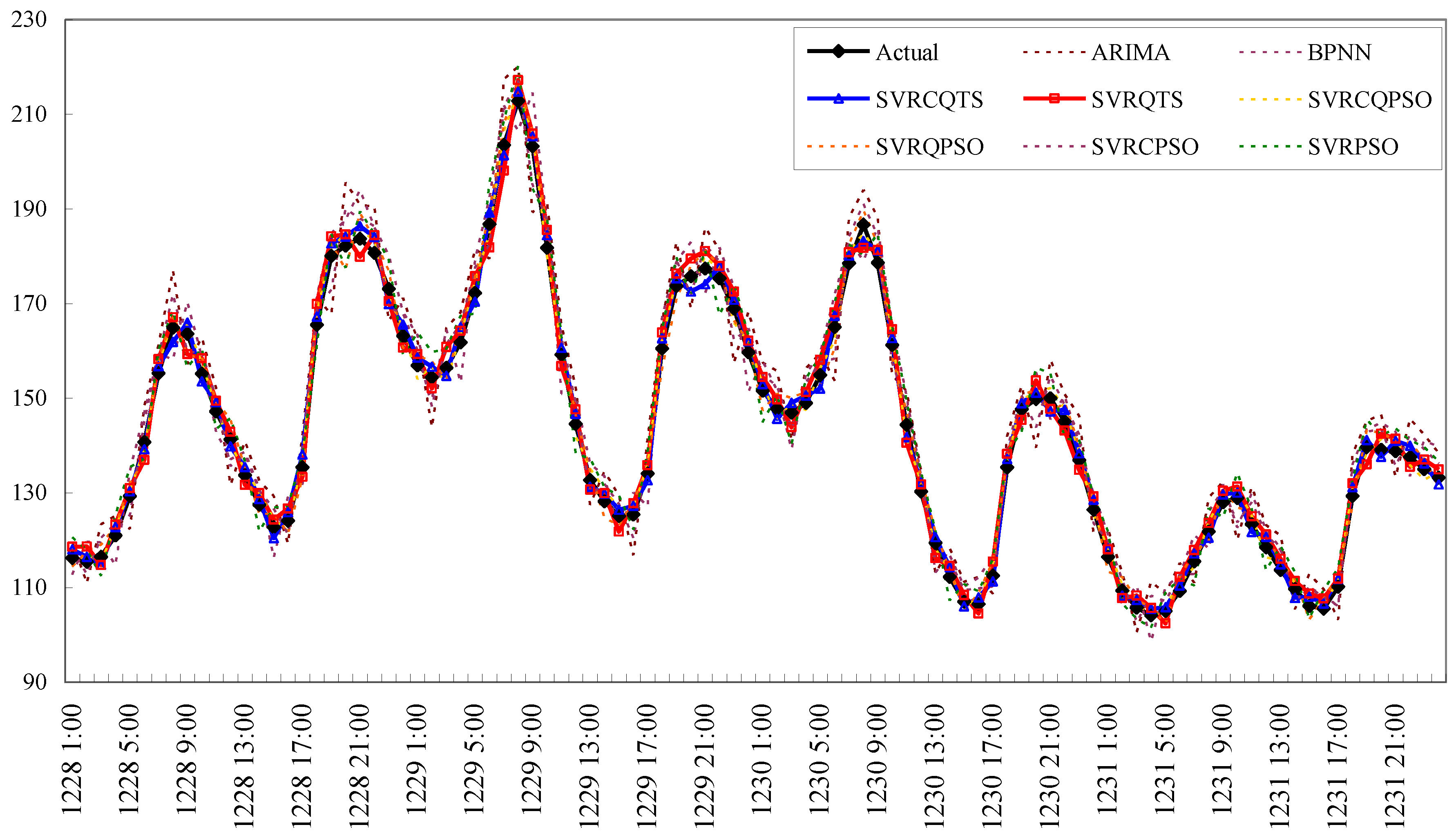
3.2.4. Forecasting Results and Analysis for Example 3
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Bunn, D.W.; Farmer, E.D. Comparative models for electrical load forecasting. Int. J. Forecast. 1986, 2, 241–242. [Google Scholar]
- Fan, S.; Chen, L. Short-term load forecasting based on an adaptive hybrid method. IEEE Trans. Power Syst. 2006, 21, 392–401. [Google Scholar] [CrossRef]
- Morimoto, R.; Hope, C. The impact of electricity supply on economic growth in Sri Lanka. Energy Econ. 2004, 26, 77–85. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, J.; Lu, H. Combining forecasts of electricity consumption in China with time-varying weights updated by a high-order Markov chain model. Omega 2014, 45, 80–91. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Li, Y.; Zhu, S.; Zhao, J. Techniques of applying wavelet de-noising into a combined model for short-term load forecasting. Int. J. Electr. Power Energy Syst. 2014, 62, 816–824. [Google Scholar] [CrossRef]
- Hussain, A.; Rahman, M.; Memon, J.A. Forecasting electricity consumption in Pakistan: The way forward. Energy Policy 2016, 90, 73–80. [Google Scholar] [CrossRef]
- Maçaira, P.M.; Souza, R.C.; Oliveira, F.L.C. Modelling and forecasting the residential electricity consumption in Brazil with pegels exponential smoothing techniques. Procedia Comput. Sci. 2015, 55, 328–335. [Google Scholar] [CrossRef]
- Al-Hamadi, H.M.; Soliman, S.A. Short-term electric load forecasting based on Kalman filtering algorithm with moving window weather and load model. Electr. Power Syst. Res. 2004, 68, 47–59. [Google Scholar] [CrossRef]
- Zheng, T.; Girgis, A.A.; Makram, E.B. A hybrid wavelet-Kalman filter method for load forecasting. Electr. Power Syst. Res. 2000, 54, 11–17. [Google Scholar] [CrossRef]
- Blood, E.A.; Krogh, B.H.; Ilic, M.D. Electric power system static state estimation through Kalman filtering and load forecasting. In Proceedings of the Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008.
- Hippert, H.S.; Taylor, J.W. An evaluation of Bayesian techniques for controlling model complexity and selecting inputs in a neural network for short-term load forecasting. Neural Netw. 2010, 23, 386–395. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Yang, J. Forecasting natural gas consumption in China by Bayesian model averaging. Energy Rep. 2015, 1, 216–220. [Google Scholar] [CrossRef]
- Chai, J.; Guo, J.E.; Lu, H. Forecasting energy demand of China using Bayesian combination model. China Popul. Resour. Environ. 2008, 18, 50–55. [Google Scholar]
- Vu, D.H.; Muttaqi, K.M.; Agalgaonkar, A.P. A variance inflation factor and backward elimination based robust regression model for forecasting monthly electricity demand using climatic variables. Appl. Energy 2015, 140, 385–394. [Google Scholar] [CrossRef]
- Dudek, G. Pattern-based local linear regression models for short-term load forecasting. Electr. Power Syst. Res. 2016, 130, 139–147. [Google Scholar] [CrossRef]
- Wu, J.; Wang, J.; Lu, H.; Dong, Y.; Lu, X. Short term load forecasting technique based on the seasonal exponential adjustment method and the regression model. Energy Convers. Manag. 2013, 70, 1–9. [Google Scholar] [CrossRef]
- Hernández, L.; Baladrón, C.; Aguiar, J.M.; Carro, B.; Sánchez-Esguevillas, A.; Lloret, J. Artificial neural networks for short-term load forecasting in microgrids environment. Energy 2014, 75, 252–264. [Google Scholar] [CrossRef]
- Ertugrul, Ö.F. Forecasting electricity load by a novel recurrent extreme learning machines approach. Int. J. Electr. Power Energy Syst. 2016, 78, 429–435. [Google Scholar] [CrossRef]
- Quan, H.; Srinivasan, D.; Khosravi, A. Uncertainty handling using neural network-based prediction intervals for electrical load forecasting. Energy 2014, 73, 916–925. [Google Scholar] [CrossRef]
- Li, P.; Li, Y.; Xiong, Q.; Chai, Y.; Zhang, Y. Application of a hybrid quantized Elman neural network in short-term load forecasting. Int. J. Electr. Power Energy Syst. 2014, 55, 749–759. [Google Scholar] [CrossRef]
- Sousa, J.C.; Neves, L.P.; Jorge, H.M. Assessing the relevance of load profiling information in electrical load forecasting based on neural network models. Int. J. Electr. Power Energy Syst. 2012, 40, 85–93. [Google Scholar] [CrossRef]
- Lahouar, A.; Slama, J.B.H. Day-ahead load forecast using random forest and expert input selection. Energy Convers. Manag. 2015, 103, 1040–1051. [Google Scholar] [CrossRef]
- Bennett, C.J.; Stewart, R.A.; Lu, J.W. Forecasting low voltage distribution network demand profiles using a pattern recognition based expert system. Energy 2014, 67, 200–212. [Google Scholar] [CrossRef]
- Santana, Á.L.; Conde, G.B.; Rego, L.P.; Rocha, C.A.; Cardoso, D.L.; Costa, J.C.W.; Bezerra, U.H.; Francês, C.R.L. PREDICT—Decision support system for load forecasting and inference: A new undertaking for Brazilian power suppliers. Int. J. Electr. Power Energy Syst. 2012, 38, 33–45. [Google Scholar] [CrossRef]
- Efendi, R.; Ismail, Z.; Deris, M.M. A new linguistic out-sample approach of fuzzy time series for daily forecasting of Malaysian electricity load demand. Appl. Soft Comput. 2015, 28, 422–430. [Google Scholar] [CrossRef]
- Hooshmand, R.-A.; Amooshahi, H.; Parastegari, M. A hybrid intelligent algorithm based short-term load forecasting approach. Int. J. Electr. Power Energy Syst. 2013, 45, 313–324. [Google Scholar] [CrossRef]
- Akdemir, B.; Çetinkaya, N. Long-term load forecasting based on adaptive neural fuzzy inference system using real energy data. Energy Procedia 2012, 14, 794–799. [Google Scholar] [CrossRef]
- Chaturvedi, D.K.; Sinha, A.P.; Malik, O.P. Short term load forecast using fuzzy logic and wavelet transform integrated generalized neural network. Int. J. Electr. Power Energy Syst. 2015, 67, 230–237. [Google Scholar] [CrossRef]
- Liao, G.-C. Hybrid Improved Differential Evolution and Wavelet Neural Network with load forecasting problem of air conditioning. Int. J. Electr. Power Energy Syst. 2014, 61, 673–682. [Google Scholar] [CrossRef]
- Zhai, M.-Y. A new method for short-term load forecasting based on fractal interpretation and wavelet analysis. Int. J. Electr. Power Energy Syst. 2015, 69, 241–245. [Google Scholar] [CrossRef]
- Zeng, X.; Shu, L.; Huang, G.; Jiang, J. Triangular fuzzy series forecasting based on grey model and neural network. Appl. Math. Model. 2016, 40, 1717–1727. [Google Scholar] [CrossRef]
- Efendigil, T.; Önüt, S.; Kahraman, C. A decision support system for demand forecasting with artificial neural networks and neuro-fuzzy models: A comparative analysis. Expert Syst. Appl. 2009, 36, 6697–6707. [Google Scholar] [CrossRef]
- Coelho, V.N.; Coelho, I.M.; Coelho, B.N.; Reis, A.J.R.; Enayatifar, R.; Souza, M.J.F.; Guimarães, F.G. A self-adaptive evolutionary fuzzy model for load forecasting problems on smart grid environment. Appl. Energy 2016, 169, 567–584. [Google Scholar] [CrossRef]
- Khashei, M.; Mehdi Bijari, M. A novel hybridization of artificial neural networks and ARIMA models for time series forecasting. Appl. Soft Comput. 2011, 11, 2664–2675. [Google Scholar] [CrossRef]
- Ghanbari, A.; Kazemi, S.M.R.; Mehmanpazir, F.; Nakhostin, M.M. A Cooperative Ant Colony Optimization-Genetic Algorithm approach for construction of energy demand forecasting knowledge-based expert systems. Knowl.-Based Syst. 2013, 39, 194–206. [Google Scholar] [CrossRef]
- Bahrami, S.; Hooshmand, R.-A.; Parastegari, M. Short term electric load forecasting by wavelet transform and grey model improved by PSO (particle swarm optimization) algorithm. Energy 2014, 72, 434–442. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J.; De Moor, B. Optimal control by least squares support vector machines. Neural Netw. 2001, 14, 23–35. [Google Scholar] [CrossRef]
- Aras, S.; Kocakoç, İ.D. A new model selection strategy in time series forecasting with artificial neural networks: IHTS. Neurocomputing 2016, 174, 974–987. [Google Scholar] [CrossRef]
- Kendal, S.L.; Creen, M. An Introduction to Knowledge Engineering; Springer: London, UK, 2007. [Google Scholar]
- Cherroun, L.; Hadroug, N.; Boumehraz, M. Hybrid approach based on ANFIS models for intelligent fault diagnosis in industrial actuator. J. Control Electr. Eng. 2013, 3, 17–22. [Google Scholar]
- Hahn, H.; Meyer-Nieberg, S.; Pickl, S. Electric load forecasting methods: Tools for decision making. Eur. J. Oper. Res. 2009, 199, 902–907. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process Syst. 1997, 9, 155–161. [Google Scholar]
- Tay, F.E.H.; Cao, L.J. Modified support vector machines in financial time series forecasting. Neurocomputing 2002, 48, 847–861. [Google Scholar] [CrossRef]
- Hong, W.C. Electric load forecasting by seasonal recurrent SVR (support vector regression) with chaotic artificial bee colony algorithm. Energy 2011, 36, 5568–5578. [Google Scholar] [CrossRef]
- Chen, Y.H.; Hong, W.C.; Shen, W.; Huang, N.N. Electric load forecasting based on LSSVM with fuzzy time series and global harmony search algorithm. Energies 2016, 9, 70. [Google Scholar] [CrossRef]
- Fan, G.; Peng, L.-L.; Hong, W.-C.; Sun, F. Electric load forecasting by the SVR model with differential empirical mode decomposition and auto regression. Neurocomputing 2016, 173, 958–970. [Google Scholar] [CrossRef]
- Geng, J.; Huang, M.L.; Li, M.W.; Hong, W.C. Hybridization of seasonal chaotic cloud simulated annealing algorithm in a SVR-based load forecasting model. Neurocomputing 2015, 151, 1362–1373. [Google Scholar] [CrossRef]
- Ju, F.Y.; Hong, W.C. Application of seasonal SVR with chaotic gravitational search algorithm in electricity forecasting. Appl. Math. Model. 2013, 37, 9643–9651. [Google Scholar] [CrossRef]
- Fan, G.; Wang, H.; Qing, S.; Hong, W.C.; Li, H.J. Support vector regression model based on empirical mode decomposition and auto regression for electric load forecasting. Energies 2013, 6, 1887–1901. [Google Scholar] [CrossRef]
- Hong, W.C.; Dong, Y.; Zhang, W.Y.; Chen, L.Y.; Panigrahi, B.K. Cyclic electric load forecasting by seasonal SVR with chaotic genetic algorithm. Int. J. Electr. Power Energy Syst. 2013, 44, 604–614. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Hong, W.C.; Dong, Y.; Tsai, G.; Sung, J.T.; Fan, G. Application of SVR with chaotic GASA algorithm in cyclic electric load forecasting. Energy 2012, 45, 850–858. [Google Scholar] [CrossRef]
- Hong, W.C.; Dong, Y.; Lai, C.Y.; Chen, L.Y.; Wei, S.Y. SVR with hybrid chaotic immune algorithm for seasonal load demand forecasting. Energies 2011, 4, 960–977. [Google Scholar] [CrossRef]
- Hong, W.C. Application of chaotic ant swarm optimization in electric load forecasting. Energy Policy 2010, 38, 5830–5839. [Google Scholar] [CrossRef]
- Hong, W.C. Hybrid evolutionary algorithms in a SVR-based electric load forecasting model. Int. J. Electr. Power Energy Syst. 2009, 31, 409–417. [Google Scholar] [CrossRef]
- Hong, W.C. Electric load forecasting by support vector model. Appl. Math. Model. 2009, 33, 2444–2454. [Google Scholar] [CrossRef]
- Hong, W.C. Chaotic particle swarm optimization algorithm in a support vector regression electric load forecasting model. Energy Convers. Manag. 2009, 50, 105–117. [Google Scholar] [CrossRef]
- Glover, F. Tabu search, part I. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
- Glover, F. Tabu search, part II. ORSA J. Comput. 1990, 2, 4–32. [Google Scholar] [CrossRef]
- Zeng, Z.; Yu, X.; He, K.; Huang, W.; Fu, Z. Iterated tabu search and variable neighborhood descent for packing unequal circles into a circular container. Eur. J. Oper. Res. 2016, 250, 615–627. [Google Scholar] [CrossRef]
- Lai, D.S.W.; Demirag, O.C.; Leung, J.M.Y. A tabu search heuristic for the heterogeneous vehicle routing problem on a multigraph. Trans. Res. E Logist. Trans. Rev. 2016, 86, 32–52. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, Y.; Lü, Z. A tabu search based hybrid evolutionary algorithm for the max-cut problem. Appl. Soft Comput. 2015, 34, 827–837. [Google Scholar] [CrossRef]
- Kvasnicka, V.; Pospichal, J. Fast evaluation of chemical distance by tabu search algorithm. J. Chem. Inf. Comput. Sci. 1994, 34, 1109–1112. [Google Scholar] [CrossRef]
- Amaral, P.; Pais, T.C. Compromise Ratio with weighting functions in a Tabu Search multi-criteria approach to examination timetabling. Comput. Oper. Res. 2016, 72, 160–174. [Google Scholar] [CrossRef]
- Shen, Q.; Shi, W.-M.; Kong, W. Modified tabu search approach for variable selection in quantitative structure–activity relationship studies of toxicity of aromatic compounds. Artif. Intell. Med. 2010, 49, 61–66. [Google Scholar] [CrossRef] [PubMed]
- Chou, Y.H.; Yang, Y.J.; Chiu, C.H. Classical and quantum-inspired Tabu search for solving 0/1 knapsack problem. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (IEEE SMC 2011), Anchorage, AK, USA, 9–12 October 2011.
- Huang, M.L. Hybridization of chaotic quantum particle swarm optimization with SVR in electric demand forecasting. Energies 2016, 9, 426. [Google Scholar] [CrossRef]
- Amari, S.; Wu, S. Improving support vector machine classifiers by modifying kernel functions. Neural Netw. 1999, 12, 783–789. [Google Scholar] [CrossRef]
- Chen, G.; Mao, Y.; Chui, C.K. Asymmetric image encryption scheme based on 3D chaotic cat maps. Chaos Solitons Fractals 2004, 21, 749–761. [Google Scholar] [CrossRef]
- Su, H. Chaos quantum-behaved particle swarm optimization based neural networks for short-term load forecasting. Procedia Eng. 2011, 15, 199–203. [Google Scholar] [CrossRef]
- 2014 Global Energy Forecasting Competition Site. Available online: http://www.drhongtao.com/gefcom/ (accessed on 2 May 2016).
- Diebold, F.X.; Mariano, R.S. Comparing predictive accuracy. J. Bus. Econ. Stat. 1995, 13, 134–144. [Google Scholar]

| Regions | SVRCQTS Parameters | MAPE of Testing (%) | ||
| σ | C | ε | ||
| Northern | 10.0000 | 0.7200 | 1.0870 | |
| Central | 6.0000 | 0.5500 | 1.2650 | |
| Southern | 8.0000 | 0.6500 | 1.1720 | |
| Eastern | 8.0000 | 0.4300 | 1.5430 | |
| Regions | SVRQTS Parameters | MAPE of Testing (%) | ||
| σ | C | ε | ||
| Northern | 4.0000 | 0.2500 | 1.3260 | |
| Central | 12.0000 | 0.2800 | 1.6870 | |
| Southern | 10.0000 | 0.7200 | 1.3670 | |
| Eastern | 8.0000 | 0.4200 | 1.9720 | |
| Year | Northern Region | |||||
| SVRCQTS | SVRQTS | SVRCQPSO | SVRQPSO | SVRCPSO | SVRPSO | |
| 1997 | 11,123 (101) | 11,101 (121) | 11,339 (117) | 11,046 (176) | 11,232 (10) | 11,245 (23) |
| 1998 | 11,491 (151) | 11,458 (184) | 11,779 (137) | 11,787 (145) | 11,628 (14) | 11,621 (21) |
| 1999 | 12,123 (142) | 12,154 (173) | 11,832 (149) | 12,144 (163) | 12,016 (35) | 12,023 (42) |
| 2000 | 13,052 (128) | 13,080 (156) | 12,798 (126) | 12,772 (152) | 12,306 (618) | 12,306 (618) |
| MAPE (%) | 1.0870 | 1.3260 | 1.1070 | 1.3370 | 1.3187 | 1.3786 |
| Year | Central Region | |||||
| SVRCQTS | SVRQTS | SVRCQPSO | SVRQPSO | SVRCPSO | SVRPSO | |
| 1997 | 5009 (52) | 5132 (71) | 4987 (74) | 5140 (79) | 5066 (5) | 5085 (24) |
| 1998 | 5167 (79) | 5142 (104) | 5317 (71) | 5342 (96) | 5168 (78) | 5141 (105) |
| 1999 | 5301 (68) | 5318 (85) | 5172 (61) | 5130 (103) | 5232 (1) | 5236 (3) |
| 2000 | 5702 (69) | 5732 (99) | 5569 (64) | 5554 (79) | 5313 (320) | 5343 (290) |
| MAPE (%) | 1.2650 | 1.6870 | 1.2840 | 1.6890 | 1.8100 | 1.9173 |
| Year | Southern Region | |||||
| SVRCQTS | SVRQTS | SVRCQPSO | SVRQPSO | SVRCPSO | SVRPSO | |
| 1997 | 6268 (68) | 6436 (100) | 6262 (74) | 6265 (71) | 6297 (39) | 6272 (64) |
| 1998 | 6398 (80) | 6245 (73) | 6401 (83) | 6418 (100) | 6311 (7) | 6314 (4) |
| 1999 | 6343 (84) | 6338 (79) | 6179 (80) | 6178 (81) | 6324 (65) | 6327 (68) |
| 2000 | 6735 (69) | 6704 (100) | 6738 (66) | 6901 (97) | 6516 (288) | 6519 (285) |
| MAPE (%) | 1.1720 | 1.3670 | 1.1840 | 1.3590 | 1.4937 | 1.5899 |
| Year | Eastern Region | |||||
| SVRCQTS | SVRQTS | SVRCQPSO | SVRQPSO | SVRCPSO | SVRPSO | |
| 1997 | 362 (4) | 364 (6) | 353 (5) | 350 (8) | 370 (12) | 367 (9) |
| 1998 | 390 (7) | 388 (9) | 404 (7) | 390 (7) | 376 (21) | 374 (23) |
| 1999 | 395 (6) | 394 (7) | 394 (7) | 410 (9) | 411 (10) | 409 (8) |
| 2000 | 427 (7) | 429 (9) | 414 (6) | 413 (7) | 418 (2) | 415 (5) |
| MAPE (%) | 1.5430 | 1.9720 | 1.5940 | 1.9830 | 2.1860 | 2.3094 |
| Compared Models | Wilcoxon Signed-Rank Test | |||
|---|---|---|---|---|
| α = 0.025; W = 0 | α = 0.005; W = 0 | p-Value | ||
| Northern region | SVRCQTS vs. SVRPSO | 0 a | 0 a | N/A |
| SVRCQTS vs. SVRCPSO | 0 a | 0 a | N/A | |
| SVRCQTS vs. SVRQPSO | 0 a | 0 a | N/A | |
| SVRCQTS vs. SVRCQPSO | 0 a | 0 a | N/A | |
| SVRCQTS vs. SVRQTS | 1 | 1 | N/A | |
| Central region | SVRCQTS vs. SVRPSO | 0 a | 0 a | N/A |
| SVRCQTS vs. SVRCPSO | 0 a | 0 a | N/A | |
| SVRCQTS vs. SVRQPSO | 0 a | 0 a | N/A | |
| SVRCQTS vs. SVRCQPSO | 1 | 1 | N/A | |
| SVRCQTS vs. SVRQTS | 0 a | 0 a | N/A | |
| Southern region | SVRCQTS vs. SVRPSO | 0 a | 0 a | N/A |
| SVRCQTS vs. SVRCPSO | 0 a | 0 a | N/A | |
| SVRCQTS vs. SVRQPSO | 0 a | 0 a | N/A | |
| SVRCQTS vs. SVRCQPSO | 1 | 1 | N/A | |
| SVRCQTS vs. SVRQTS | 0 a | 0 a | N/A | |
| Eastern region | SVRCQTS vs. SVRPSO | 0 a | 0 a | N/A |
| SVRCQTS vs. SVRCPSO | 0 a | 0 a | N/A | |
| SVRCQTS vs. SVRQPSO | 0 a | 0 a | N/A | |
| SVRCQTS vs. SVRCQPSO | 1 | 1 | N/A | |
| SVRCQTS vs. SVRQTS | 0 a | 0 a | N/A | |
| Optimization Algorithms | Parameters | MAPE of Testing (%) | ||
|---|---|---|---|---|
| σ | C | ε | ||
| PSO algorithm [56] | 0.2293 | 10.175 | 3.1429 | |
| CPSO algorithm [56] | 0.2380 | 39.296 | 1.6134 | |
| QPSO algorithm [66] | 12.0000 | 0.380 | 1.3460 | |
| CQPSO algorithm [66] | 10.0000 | 0.560 | 1.1850 | |
| QTS algorithm | 5.0000 | 0.630 | 1.3210 | |
| CQTS algorithm | 6.0000 | 0.340 | 1.1540 | |
| Years | SVRCQTS | SVRQTS | SVRCQPSO | SVRQPSO | SVRCPSO | SVRPSO |
|---|---|---|---|---|---|---|
| 1995 | 106,353 (985) | 104,241 (1127) | 106,379 (1011) | 104,219 (1149) | 105,960 (592) | 102,770 (2598) |
| 1996 | 110,127 (1013) | 109,246 (1894) | 109,573 (1567) | 109,210 (1930) | 112,120 (980) | 109,800 (1340) |
| 1997 | 117,180 (1119) | 120,174 (1875) | 117,149 (1150) | 120,210 (1911) | 118,450 (151) | 115,570 (2729) |
| 1998 | 130,023 (1893) | 129,501 (1371) | 129,466 (1336) | 129,527 (1397) | 123,400 (4730) | 120,650 (7480) |
| 1999 | 130,464 (1262) | 133,275 (1549) | 133,646 (1920) | 133,304 (1578) | 130,940 (786) | 128,240 (3486) |
| 2000 | 144,500 (2087) | 140,099 (2314) | 140,945 (1468) | 140,055 (2358) | 136,420 (5993) | 137,250 (5163) |
| 2001 | 144,884 (1260) | 141,271 (2353) | 145,734 (2110) | 141,227 (2397) | 142,910 (714) | 140,230 (3394) |
| 2002 | 149,099 (2094) | 149,675 (1518) | 149,652 (1541) | 149,646 (1547) | 150,210 (983) | 151,150 (43) |
| 2003 | 157,099 (2281) | 161,001 (1621) | 161,458 (2078) | 161,032 (1652) | 154,130 (5250) | 146,940 (12,440) |
| MAPE (%) | 1.1540 | 1.3210 | 1.1850 | 1.3460 | 1.6134 | 3.1429 |
| Compared Models | Wilcoxon Signed-Rank Test | ||
|---|---|---|---|
| α = 0.025; W = 5 | α = 0.005; W = 8 | p-Value | |
| SVRCQTS vs. SVRPSO | 2 a | 2 a | N/A |
| SVRCQTS vs. SVRCPSO | 3 a | 3 a | N/A |
| SVRCQTS vs. SVRQPSO | 4 a | 4 a | N/A |
| SVRCQTS vs. SVRCQPSO | 4 a | 4 a | N/A |
| SVRCQTS vs. SVRQTS | 4 a | 4 a | N/A |
| Optimization Algorithms | Parameters | MAPE of Testing (%) | ||
|---|---|---|---|---|
| σ | C | ε | ||
| PSO algorithm [66] | 7.000 | 34.000 | 0.9400 | 3.1500 |
| CPSO algorithm [66] | 22.000 | 19.000 | 0.6900 | 2.8600 |
| QPSO algorithm [66] | 9.000 | 42.000 | 0.1800 | 1.9600 |
| CQPSO algorithm [66] | 19.000 | 35.000 | 0.8200 | 1.2900 |
| QTS algorithm | 25.000 | 67.000 | 0.0900 | 1.8900 |
| CQTS algorithm | 12.000 | 26.000 | 0.3200 | 1.3200 |
| Compared Models | Wilcoxon Signed-Rank Test | ||
|---|---|---|---|
| α = 0.025; W = 2328 | α = 0.05; W = 2328 | p-Value | |
| SVRCQTS vs. ARIMA | 1621 a | 1621 a | 0.00988 |
| SVRCQTS vs. BPNN | 1600 a | 1600 a | 0.00782 |
| SVRCQTS vs. SVRPSO | 2148 | 2148 a | 0.04318 |
| SVRCQTS vs. SVRCPSO | 2163 | 2163 a | 0.04763 |
| SVRCQTS vs. SVRQPSO | 1568 a | 1568 a | 0.00544 |
| SVRCQTS vs. SVRCQPSO | 1344 a | 1344 a | 0.00032 |
| SVRCQTS vs. SVRQTS | 1741 | 1741 a | 0.03156 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-W.; Lin, B.-Y. Application of Hybrid Quantum Tabu Search with Support Vector Regression (SVR) for Load Forecasting. Energies 2016, 9, 873. https://doi.org/10.3390/en9110873
Lee C-W, Lin B-Y. Application of Hybrid Quantum Tabu Search with Support Vector Regression (SVR) for Load Forecasting. Energies. 2016; 9(11):873. https://doi.org/10.3390/en9110873
Chicago/Turabian StyleLee, Cheng-Wen, and Bing-Yi Lin. 2016. "Application of Hybrid Quantum Tabu Search with Support Vector Regression (SVR) for Load Forecasting" Energies 9, no. 11: 873. https://doi.org/10.3390/en9110873
APA StyleLee, C.-W., & Lin, B.-Y. (2016). Application of Hybrid Quantum Tabu Search with Support Vector Regression (SVR) for Load Forecasting. Energies, 9(11), 873. https://doi.org/10.3390/en9110873






