2.1. Theoretical Background of the Spectral Wave Models
The model considered for performing simulations in the basin of the Black Sea is Simulating Waves Nearshore (SWAN) [
14]. This is one of the state-of-the-art wave models based on the spectrum concept. Such models integrate the energy balance Equation (1) describing the variation of the wave energy spectrum in the fifth dimensions, represented by time, geographic, and spectral spaces (the spectral space is defined by the relative frequency
and the wave direction
):
where
N is the action density spectrum defined as the ratio between the energy density and relative frequency,
and
are the components of the relative group velocity
for the geographical space (
, with
k the wave number),
and
are the propagation velocities in the spectral space and
t is the time. In the right hand side of the action balance equation, and
S is the total source expressed in terms of energy density.
In the expression of the total source term three components are significant in deep water, and they correspond to the atmospheric input (
Sin), whitecapping dissipation (
Sdis), and nonlinear quadruplet interactions (
Snl), respectively. Additional source terms are considered in shallow water (
Ssw) to account for the finite depth effects. Hence the total source becomes:
If the medium itself is moving with the velocity
the frequency of the wave passing a field point is shifted due to the Doppler Effect:
Usually, the quantity ω is called the observed or absolute frequency while σ is the relative or intrinsic frequency whose functional dependence on k (the wave number in absolute value) is known as the classical dispersion relationship. The actual versions of the spectral wave models deal mainly with the action density spectrum instead of the energy density spectrum. This is because, unlike the energy density, in the presence of the currents the action density is conserved.
In SWAN, the energy transport components over one meter of wave front (in W/m), called also the wave power (
PW) components, are computed with the relationships:
where
E represents the wave energy density spectrum,
x, y are the problem coordinate system (for the spherical coordinates,
x axis corresponds to the longitude and
y axis to the latitude), and
Cgx,
Cgy are the components of the absolute group velocity
, which is defined as:
As a result the total wave power becomes:
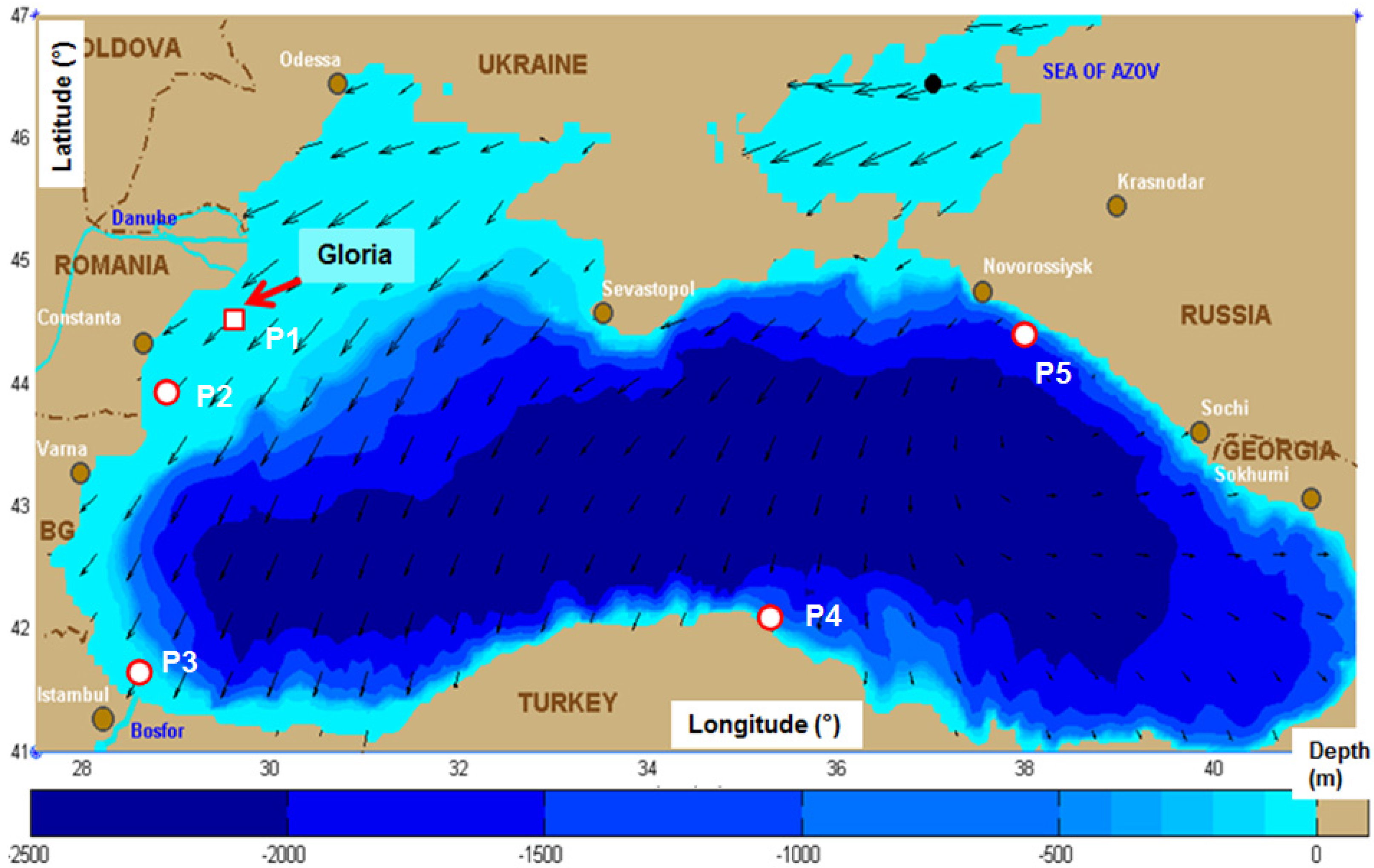
The computational domain defined for the SWAN model simulations in the basin of the Black Sea, also including the Sea of Azov, is presented in
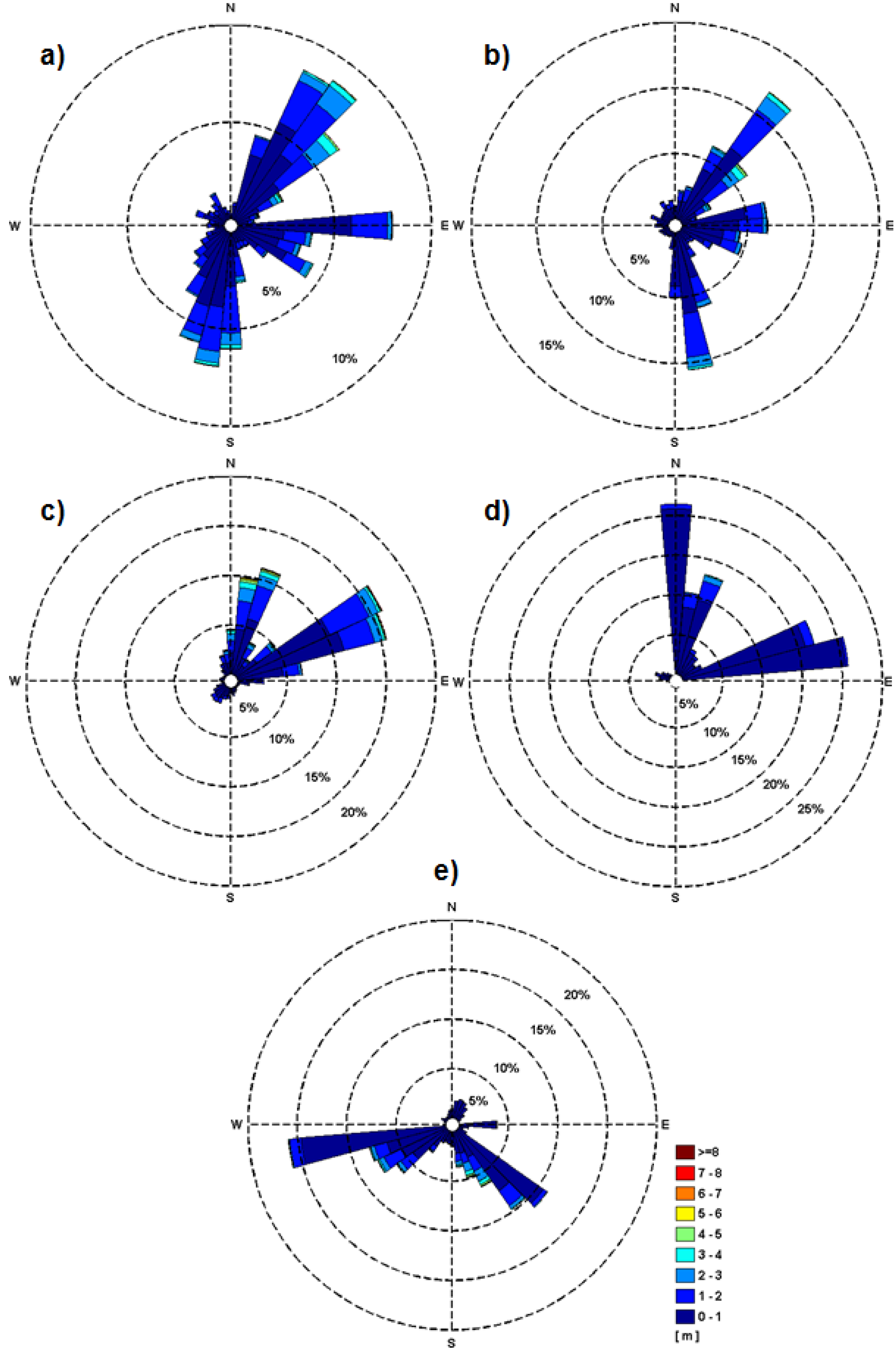
Figure 1. The background of the figure illustrates the bathymetry of the sea, while the foreground presents the wave vectors corresponding to one of the most relevant winter time wave propagation patterns. The position of the Gloria drilling platform that operates in the western sector of the Black Sea (44°31′ N, 29°34′ E) at a location where the water depth is about 50 m is indicated in the figure as also the positions of five reference points that were further considered for local analyses.
The system origin corresponds to the lower left corner point and has the coordinates (27.5° E, 41.0° N). The x direction (longitude) extends 14°, while the y direction (latitude) extends 6°. In the geographical space, the computational grid was chosen to coincide with the bathymetric grid and has 176 points in the x direction and 76 points in the y direction. The points are equally spaced with 4.5 min. In the spectral space, 36 directions and 30 frequencies were considered. The frequency range defined is between 0.05 and 1.0 Hz. Some additional details related to the input and to the physical options considered in the SWAN simulations are presented in
Table 1.
Table 1.
Input and physics considered in the SWAN simulations.
Table 1.
Input and physics considered in the SWAN simulations.
| SWAN model | Input/Process |
|---|
| Model version | 40.91ABC |
| Bathymetry | Same resolution as the computational grid |
| Wind forcing | Wind fields at 10 m from NCEP-CFSR |
| Physics | Quadruplet nonlinear interactions: fully explicit computation of the nonlinear transfer with DIA (default) |
| Exponential growth by wind (Janssen, 1991) |
| Whitecapping: Janssen formulation [15] |
| Bottom friction: JONSWAP formulation [16] |
| Computation mode | Non-stationary |
| Time step | 10 min |
| Numerical scheme | S&L [17] |
This wave prediction system was initially validated against
in situ measurements, considering for the western side of the Black Sea, especially the measurements performed at the Gloria drilling unit [
12], and some validations against remotely-sensed data [
18] have been also performed. The results of the above wave prediction system were found, in general, more reliable than those coming from other similar wave modeling systems based on spectral models that were implemented in the basin of the Black Sea [
19] and also in line with some other implementations in enclosed, or semi-enclosed, sea environments [
20,
21,
22]. Nevertheless, direct comparisons against
in situ measurements, as those performed at the Gloria drilling unit, show that there are still some situations when the accuracy of the wave predictions needs to be substantially improved. That is why, in order to increase the reliability of the wave predictions, some data assimilation (DA) techniques have been developed and associated to the wave modeling system herewith implemented. The methodology considered will be briefly described next.
2.2. Techniques Considered for Assimilation of the Satellite Data
As it is widely known, the main target behind the implementation of the data assimilation techniques is to reduce the systematic errors that may occur in the results provided by the numerical models, taking advantage of the existing measurements. Thus, the basic philosophy of the data assimilation is to combine the complementary information from measurements and the results of the numerical models into an optimal estimate of the geophysical fields of interest [
23,
24]. The assimilation of the wave data is usually performed in terms of significant wave height (
Hs). Measurements of this wave parameter are available locally (generally coming from buoys) and widespread (altimeter data). The sequential methods combine all the observations falling within a particular time window and update the model solution without reference to the model dynamics. The most widely adopted DA schemes are based either on instantaneous sequential procedures, like the optimal interpolation (OI) [
25,
26], or the successive correction method (SCM) [
27]. These methods are attractive, especially due to their lower computational demands, such DA schemes based on OI being widely used in the centers for wave forecasting. In fact, most of the weather prediction centers with wave modelling capabilities are assimilating nowadays altimeter measurements, respectively
Hs, using assimilation procedures based on the OI or SCM techniques.
For the current SWAN-based wave modeling system implemented in the basin of the Black Sea, such an algorithm based on OI techniques was considered. This is formulated in the observational space, with the following definitions [
25,
26]:
in which
O represents the observation vector that contains all the observations available within the time window considered for assimilation (for satellite data, the observations made on the geographical domain defined by the wave model grid are considered);
Vb is the background vector (
Hs wave model results);
Va is the analysis vector (corrected
Hs wave model results); (
F,
F) represent the forward observational operator and the linear observation operator matrix, respectively,
Co is the observation error covariance; and
Cb is the background error covariance.
The
Forward Operator represents a method of converting a forecast model variable to an observed variable. In our case, the observations and predicted variables are the same (significant wave height,
Hs), and the method reduces to a spatial interpolation of the predictions to the observation locations. The analysis increment is equivalently defined by the relationship
where the quantity
represents the weight matrix (which is also commonly called the Kalman gain matrix). The horizontal correlation is computed with the relation:
in which
is the horizontal distance between two locations (observations or observation and a grid point) and
Lmax is the correlation length of the prediction errors for the wave parameter assimilated [
26].
Various studies [
28] recommend at about 45° latitude (the Black Sea area being centered on this latitude) a value for the parameter
Lmax of around 400 km, which represents about 4° degrees. First, this value was used but since, in the Black Sea, the wind-sea waves are dominant, it was considered necessary to also test some lower values for this parameter and to calculate the statistical results obtained after the DA application [
29].
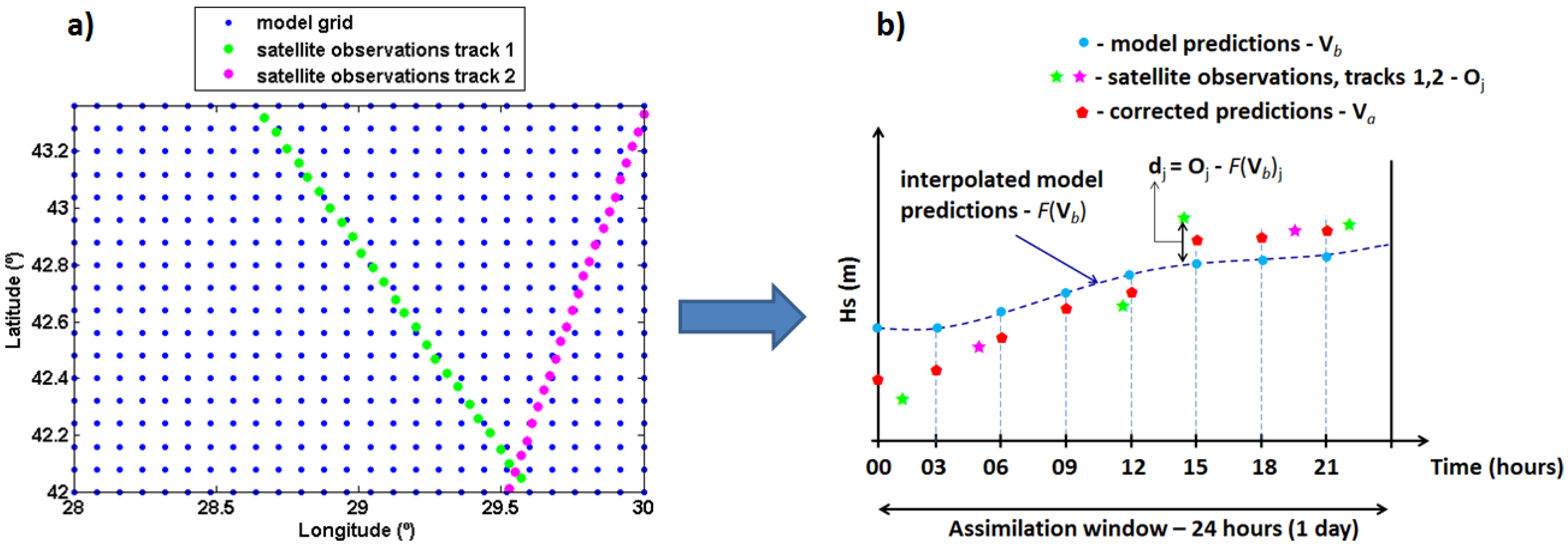
It has to also be highlighted that the effectiveness of the DA techniques are highly dependent on the number of the measured data that are assimilated. For the large areas, the available measurements are only those coming from satellites, which in the recent years have become increasingly more accurate, representing the most viable source for the use in the DA techniques. For the implementation of the DA algorithm in the Black Sea, the measurements from the following satellites have been considered ERS-2, ENVISAT, TOPEX, Poseidon, JASON-1, JASON-2, GEOSAT Follow-On (GFO), Cryosat-2, and SARAL. The assimilation of the altimeter measurements is applied to a window of 24 h (1 day), as shown schematically in
Figure 2.
After performing corrections of the significant wave heights in the grid points (
G) that are affected by the assimilation process, in order to interact with the wave model, the next step is to transfer this correction in the spectral space. In the SWAN model, the 2D wave energy density spectrum corresponding to a certain simulation (
) is discretized in a matrix form as follows:
where the index
n (
n = 1
, nf, with
nf the number of frequencies) defines the distribution of the wave energy along the frequencies and the index
m (
m = 1,
nd, with
nd the number of directions) defines the distribution of the wave energy along the wave directions. Thus,
represents the wave energy density (or variance density in m
2/Hz/degr) corresponding to the frequency number
n and to the direction number
m (as defined in the model settings) corresponding to the grid point
G and to the simulation performed for the time instant (
t). The above spectral matrix can be written in a normalized form as follows:
in which
is the maximum value of the energy variance and
represents the normalized form of the spectral matrix obtained by dividing the elements of the genuine spectral matrix by the maximum value of the energy variance.
Figure 2.
(a) Schematic presentation of a computational domain for which wave model predictions exist in the grid points and the satellite tracks crossing the respective area in 24 h; (b) Calculation of the difference dj between the observation Oj and the prediction interpolated to the observation position F(Vb)j made at the time of observation, considering the values of the observations recorded in the 1-day assimilation window.
Figure 2.
(a) Schematic presentation of a computational domain for which wave model predictions exist in the grid points and the satellite tracks crossing the respective area in 24 h; (b) Calculation of the difference dj between the observation Oj and the prediction interpolated to the observation position F(Vb)j made at the time of observation, considering the values of the observations recorded in the 1-day assimilation window.
Finally, in order to propagate the
Hs correction in the spectral space, the following approach is considered:
The spectral correction
is defined as:
Following this approach, the correction of the significant wave height is propagated in the spectral space, keeping as invariant the normalized spectral matrix defined before. This means that while the significant wave height is corrected, the shape of the spectrum is kept unchanged. Thus, the model is updated daily via the hot-files, where the corrections are operated in the spectral space for all the points affected by the assimilation process. Some results in relationship with the changes induced in the wave predictions by this DA scheme are discussed in the next section.
2.3. Reliability of the Wave Predictions with Data Assimilation
Considering the optimal interpolation assimilation technique presented above, [
29] performed a preliminary evaluation of the wave energy patterns in the basin of the Black Sea corresponding to the 10-year time interval (1999–2008). Nevertheless, in the above-mentioned work, for reasons of computational effectiveness, the information was not propagated in the spectral space. This means that the process consisted only in blending daily the satellite data with the model predictions without reinitiating each day the model simulations with updated initial conditions. From this perspective, the present work continues the above-mentioned study, but this time the hindcast was extended to a 15-year period (1999–2013) and the assimilation process was also completed by propagating the information in the spectral space, following the approach described in the previous section and on this basis the initial conditions were updated daily.
Since the amount of data assimilated represents an essential issue in improving the quality of the assimilation results, some information on the number of the existing observations in the period under consideration are provided in
Table 2. For the case of each altimeter, the period in which observations are available in the 15-year interval was also specified.
Table 2.
The number of existing satellite observations in the 15-year time interval under consideration, structured in the number of observations used for assimilation and for validation, respectively.
Table 2.
The number of existing satellite observations in the 15-year time interval under consideration, structured in the number of observations used for assimilation and for validation, respectively.
| Satellite | Nr. observations for assimilation | Nr. observations for validation |
|---|
| ERS-2 (until 04-07-2011) | 197,136 | |
| ENVISAT (14-05-2002 to 08-04-2012) | | 126,736 |
| TOPEX (until 08-10-2005) | | 132,615 |
| Poseidon (until 08-10-2005) | 3821 | |
| JASON-1 (15-01-2002 to 21-06-2013) | 193,849 | |
| GFO GFO (07-01-2000 to 07-09-2008) | 101,693 | |
| JASON-2 (from 04-07-2008) | 102,038 | |
| Cryosat-2 (from 14-03-2013) | | 57,569 |
| SARAL (from 14-07-2010) | 16,910 | |
| Total | 615,447 | 316,920 |
The statistical parameters considered to analyze the influence of the DA scheme on the quality of the
Hs predictions are: mean measured and simulated values of the significant wave height, bias, mean absolute error, RMS error, scatter index (
SI), correlation coefficient (
R), and the regression slope (
S), all of them being computed according to their standard definitions. First, the statistical parameters corresponding to the comparison between the
Hs simulated by SWAN (Hs-SWAN) and the altimeter measurements considered for validation (ENVISAT, Topex, and Cryosat-2) were calculated. These statistical results are considered as a reference to evaluate the influence of the DA scheme on the quality of the wave predictions and they are presented in
Table 2 (where
N represents the number of pairs of data used in the statistical calculations). The statistical results obtained after applying the DA are also presented in
Table 2. Although various values for the correlation length have been tested (4°, 3.5°, and 3.2°, respectively), since there were not essential differences between the results [
29], only the first case (corresponding to a correlation length of 4°) will be considered next.
The analysis of the results presented in
Table 3 clearly show that by applying the DA scheme all the statistical parameters are improved, while significant improvements in terms of the parameters
MAE,
RMSE,
SI, and
R are noticed. Scatter diagrams have been also designed and they are presented in
Figure 3.
Table 3.
Statistical results obtained for the Hs values simulated with SWAN and the Hs values obtained after the application of the DA method, against altimeter measurements used for validation across the Black Sea, results corresponding to the 15-year time interval (1999–2013).
Table 3.
Statistical results obtained for the Hs values simulated with SWAN and the Hs values obtained after the application of the DA method, against altimeter measurements used for validation across the Black Sea, results corresponding to the 15-year time interval (1999–2013).
| Parameter | MeanObs (m) | MeanSim (m) | Bias (m) | MAE (m) | RMSE (m) | SI | R | S | N |
|---|
| SWAN Hs (m) | 1.04 | 0.97 | −0.07 | 0.27 | 0.35 | 0.35 | 0.88 | 0.98 | 316,920 |
| SWAN-DA Hs (m) | 1.01 | −0.03 | 0.21 | 0.29 | 0.28 | 0.91 | 0.99 |
Figure 3.
Scatter diagrams presenting the observed Hs (data from ENVISAT, Topex and Cryosat-2 satellites) against the predicted Hs computed using the SWAN model without DA (a) and with DA (b), corresponding to the 15-year period (1999–2013). The different colors indicate different quantities of data in the single pixels. The solid lines denote the perfect fit to the modelled and observed values and the dashed lines represent the best-fit slope.
Figure 3.
Scatter diagrams presenting the observed Hs (data from ENVISAT, Topex and Cryosat-2 satellites) against the predicted Hs computed using the SWAN model without DA (a) and with DA (b), corresponding to the 15-year period (1999–2013). The different colors indicate different quantities of data in the single pixels. The solid lines denote the perfect fit to the modelled and observed values and the dashed lines represent the best-fit slope.
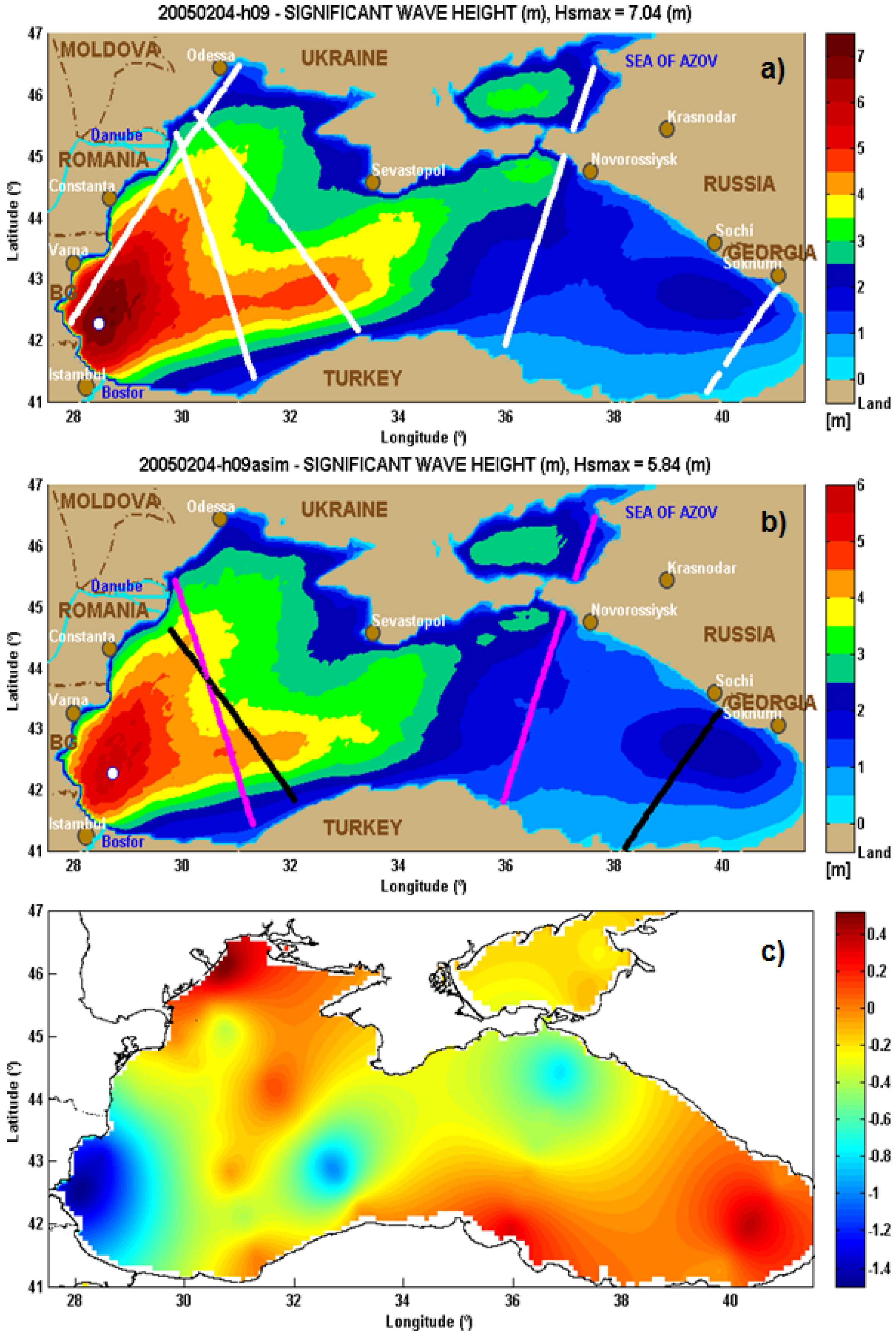
In
Figure 4, an example of the results obtained before and after the application of the DA technique is presented. Thus,
Figure 4a illustrates the results of the SWAN simulations in the Black Sea in terms of significant wave height scalar fields for the time frame 2005.02.04-h09. In the same
Figure 4a, the satellite tracks for the entire day 4 February 2005, corresponding to the data considered for the assimilation process are represented with white color.
Figure 4b presents the new significant wave height scalar fields, as obtained after applying the DA technique, and also the satellite tracks considered for validations, which are represented with black and magenta color, respectively. Finally,
Figure 4c illustrates the differences in terms of the
Hs scalar fields, which means significant wave height with DA minus significant wave height without DA. Comparisons along the satellite tracks, SWAN without DA, SWAN with DA and satellite measurements (ENVISAT and TOPEX) are presented in
Figure 5. The graphs clearly show that after assimilation the values of the parameter
Hs are significantly closer to the measurements.
Figure 4.
Significant wave height (Hs) scalar fields corresponding to the time frame 2005.02.04-h09: (a) SWAN Hs fields (without DA), the satellite tracks considered for the assimilation process (corresponding to the entire day on 4 February 2005) are represented with white color; (b) SWAN Hs fields with DA, the satellite tracks considered for the validation process (ENVISAT—tracks with magenta color, TOPEX—tracks with black color); and (c) Hs scalar fields, differences Hs with DA against Hs without DA.
Figure 4.
Significant wave height (Hs) scalar fields corresponding to the time frame 2005.02.04-h09: (a) SWAN Hs fields (without DA), the satellite tracks considered for the assimilation process (corresponding to the entire day on 4 February 2005) are represented with white color; (b) SWAN Hs fields with DA, the satellite tracks considered for the validation process (ENVISAT—tracks with magenta color, TOPEX—tracks with black color); and (c) Hs scalar fields, differences Hs with DA against Hs without DA.
Figure 5.
Comparisons between: Hs measured, Hs simulated with SWAN, and Hs obtained after applying DA along the satellite tracks, corresponding to the entire day 4 February 2005. (a) Tracks of ENVISAT; (b) Tracks of TOPEX.
Figure 5.
Comparisons between: Hs measured, Hs simulated with SWAN, and Hs obtained after applying DA along the satellite tracks, corresponding to the entire day 4 February 2005. (a) Tracks of ENVISAT; (b) Tracks of TOPEX.