Recent Progress on the Resilience of Complex Networks
Abstract
:1. Introduction

2. Framework for a Network Formed of Interdependent Networks
2.1. General Framework
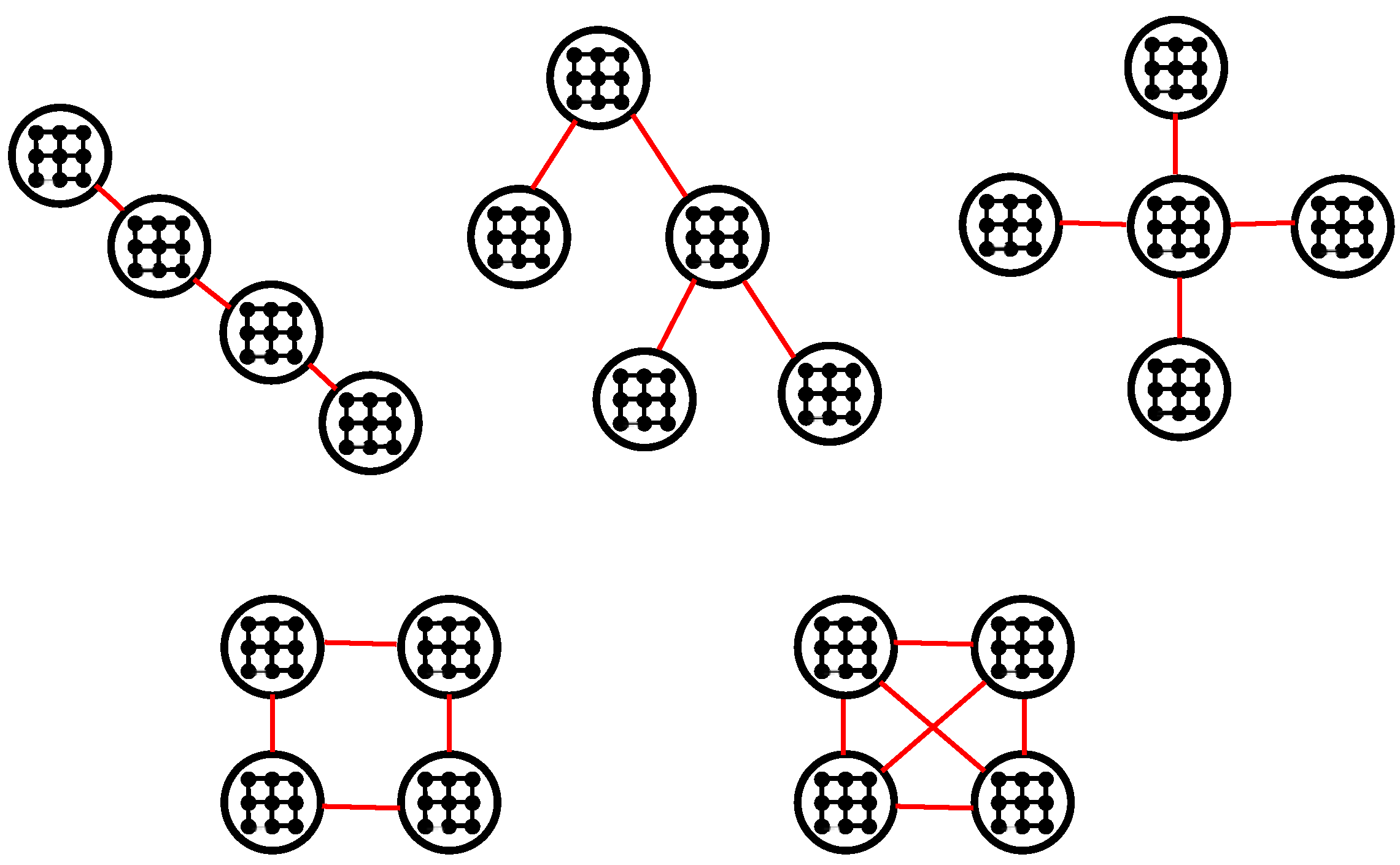
2.2. Percolation Laws
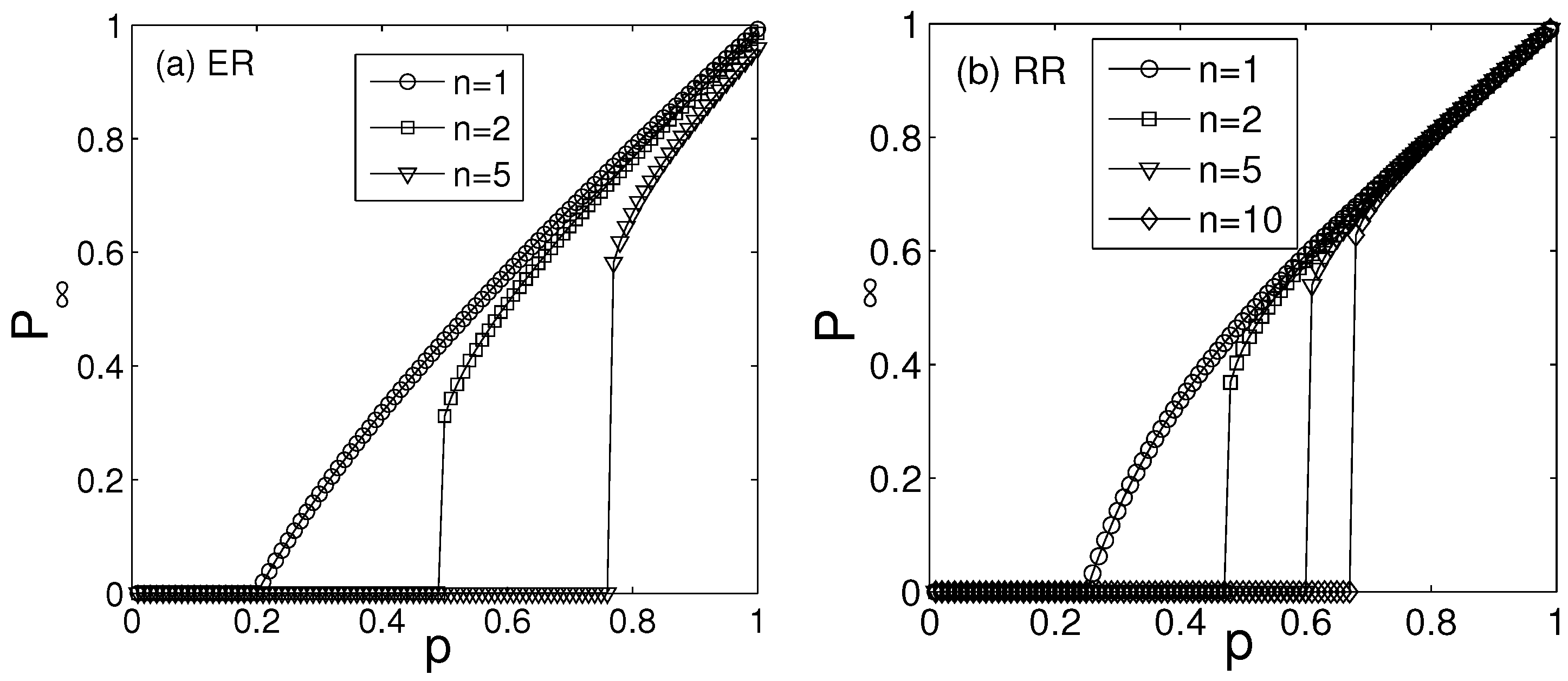

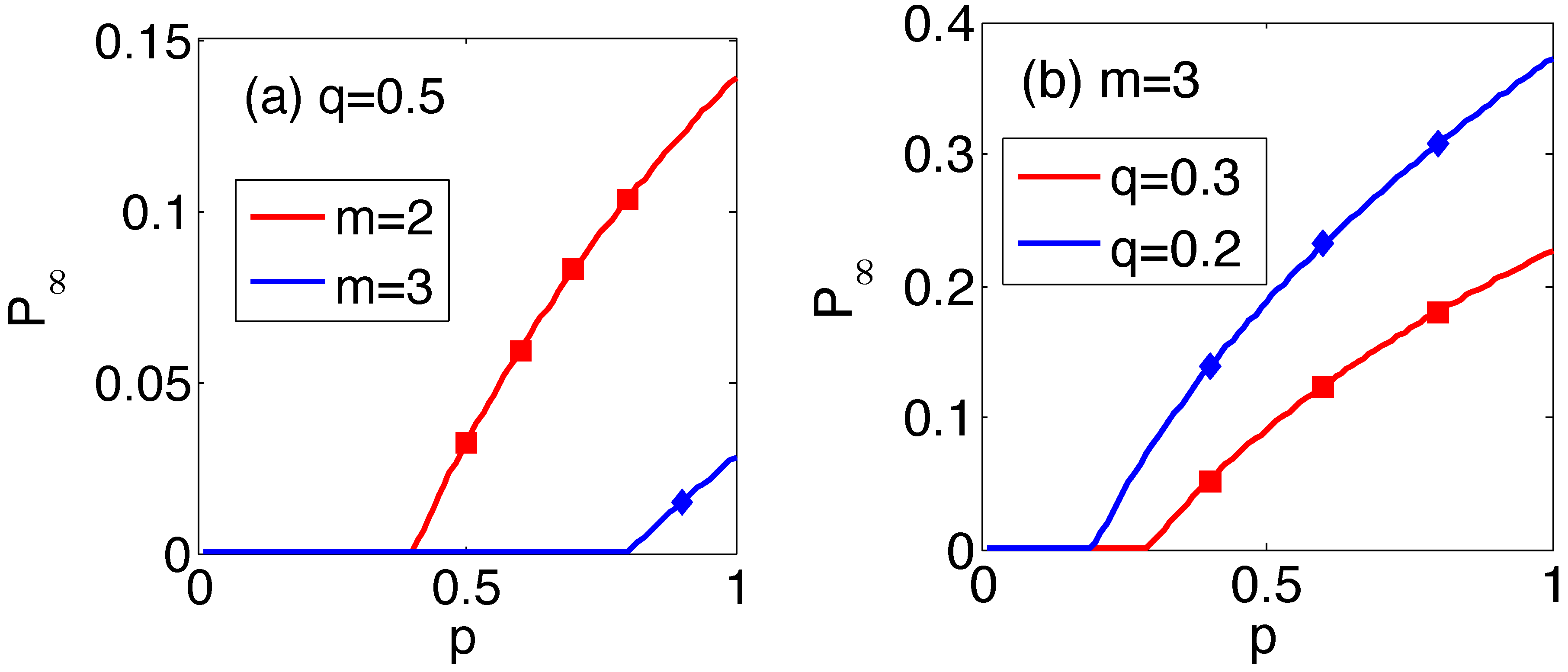
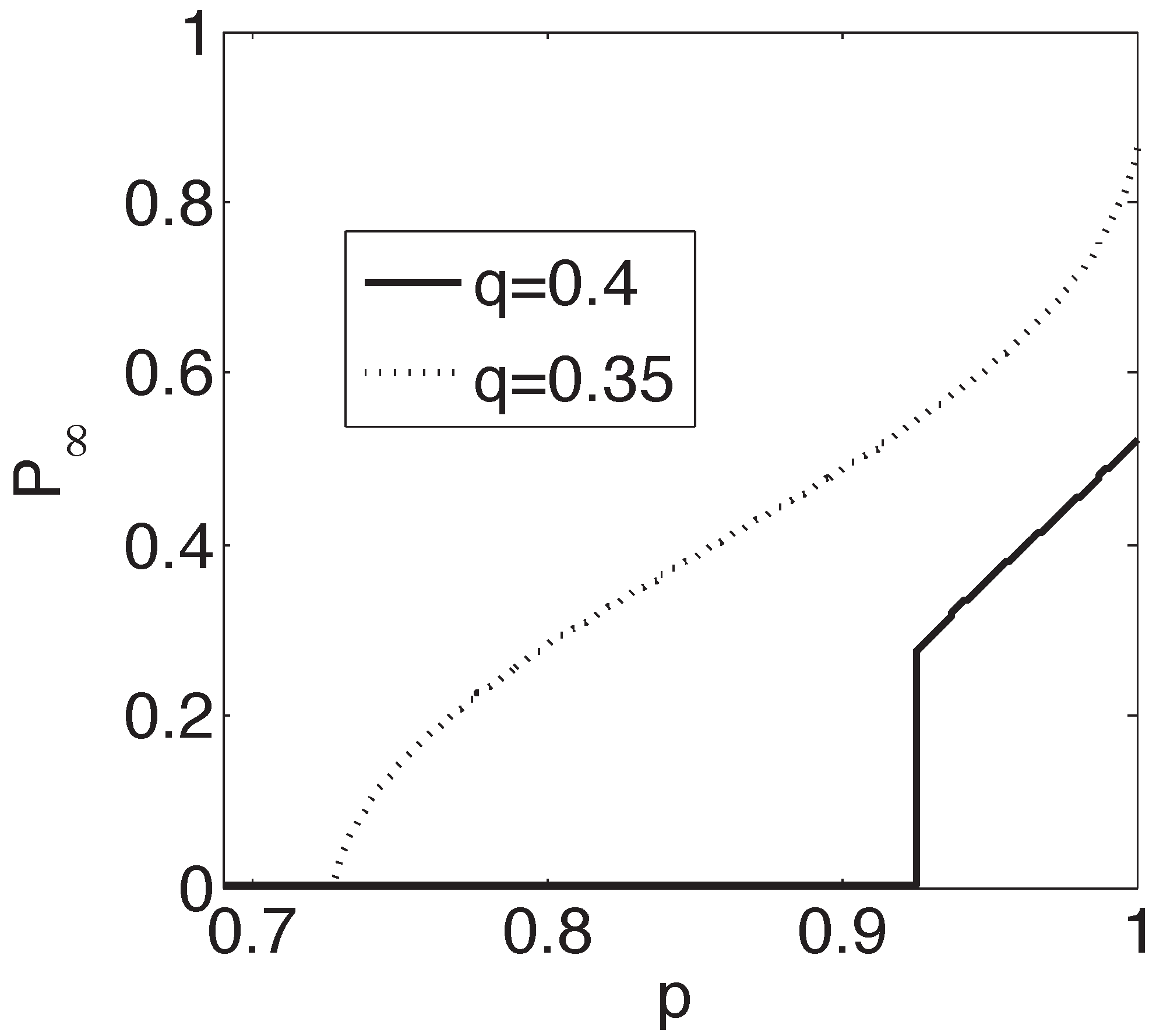
3. Extreme Vulnerability of Interdependent Spatially-Embedded Networks
3.1. Pair of Spatially-Embedded Networks
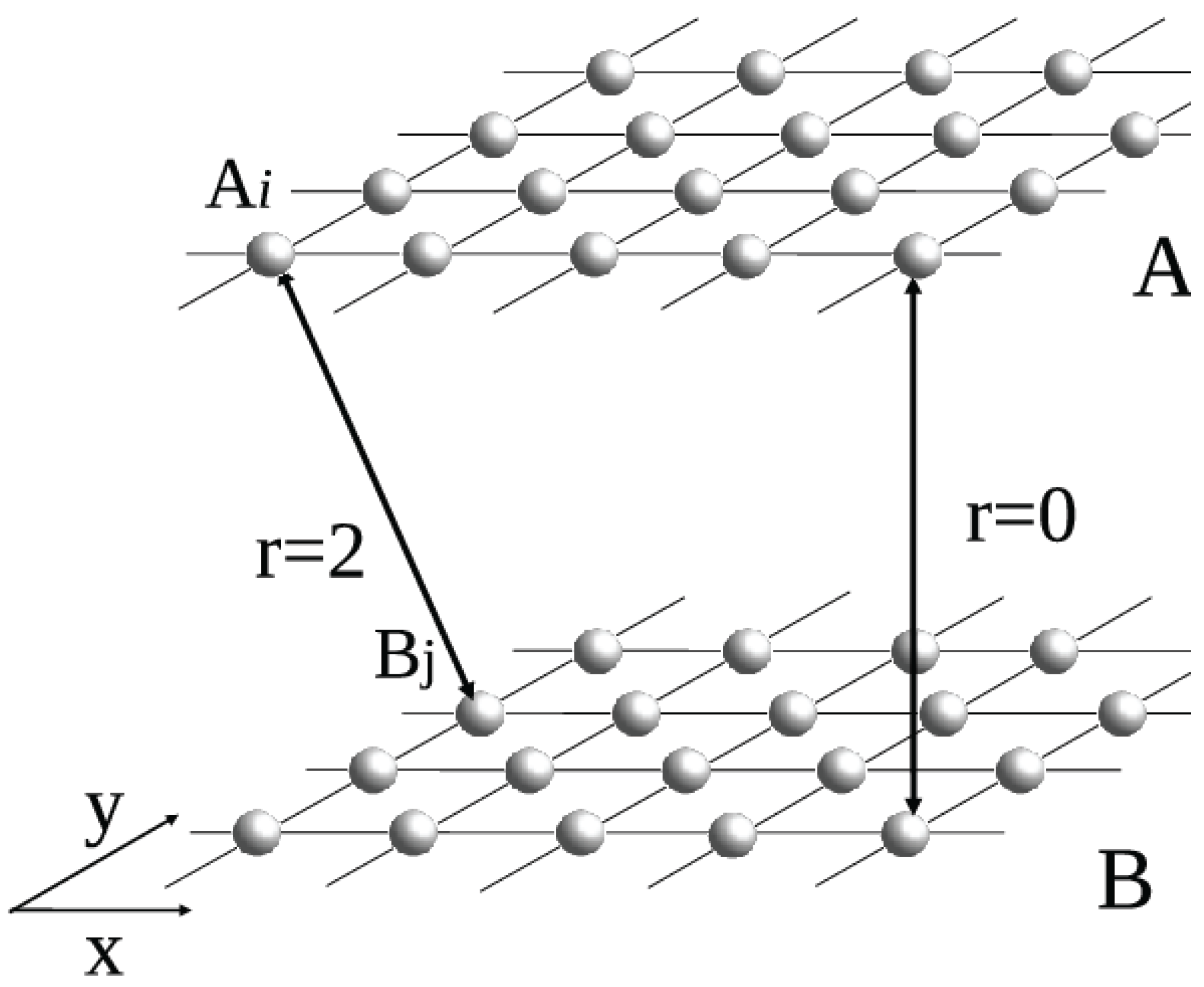

3.2. Network of Spatially-Embedded Networks
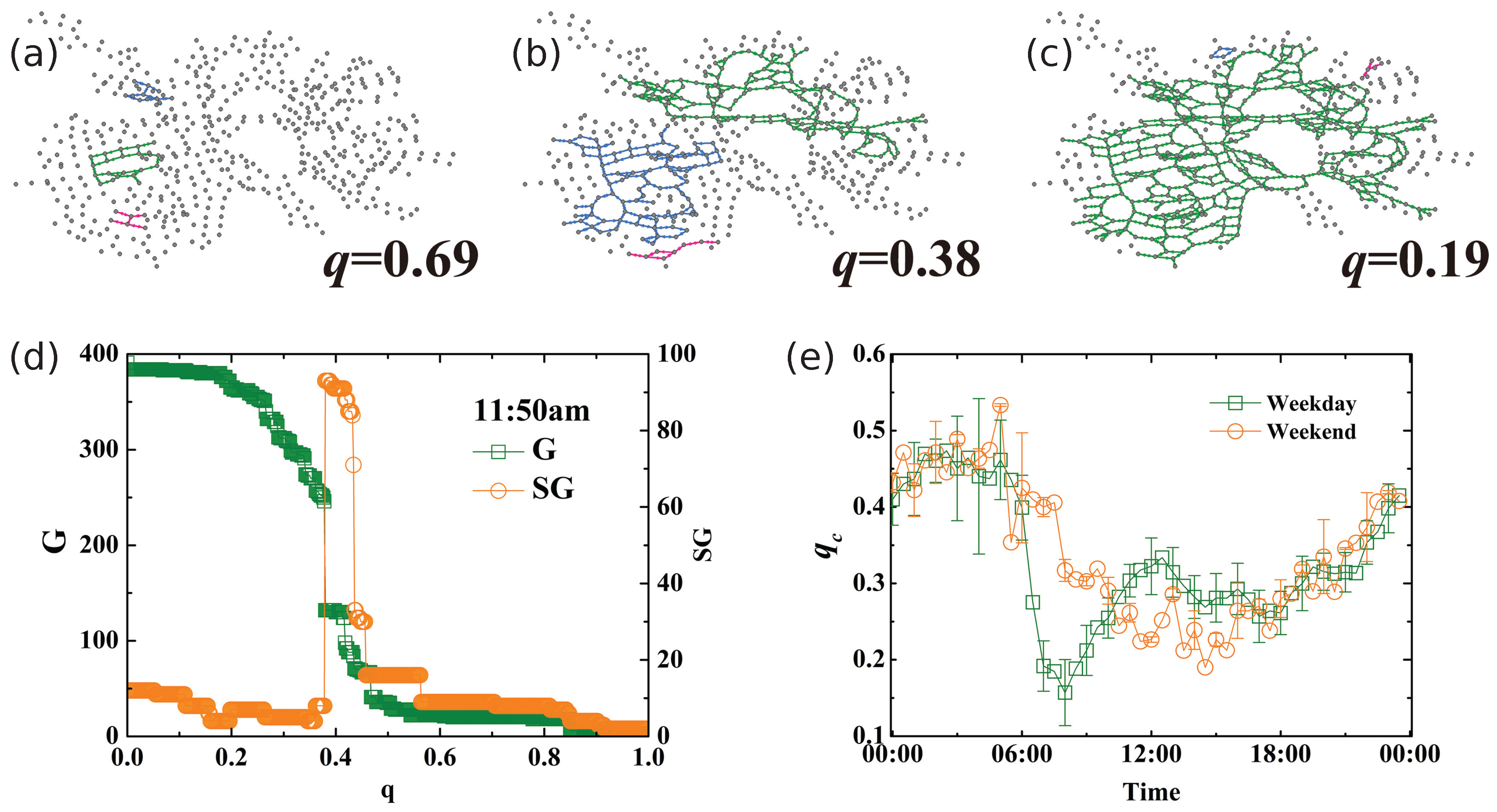
4. Percolation in a Dynamic Traffic Network
5. Spontaneous Recovery in Dynamical Networks

6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [PubMed]
- Albert, R.; Jeong, H.; Barabási, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef] [PubMed]
- Cohen, R.; Erez, K.; Ben-Avraham, D.; Havlin, S. Resilience of the Internet to random breakdowns. Phys. Rev. Lett. 2000, 85, 4626–4628. [Google Scholar] [CrossRef] [PubMed]
- Callaway, D.S.; Newman, M.E.; Strogatz, S.H.; Watts, D.J. Network robustness and fragility: Percolation on random graphs. Phys. Rev. Lett. 2000, 85. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Barrat, A.; Barthelemy, M.; Pastor-Satorras, R.; Vespignani, A. The architecture of complex weighted networks. Proc. Natl. Acad. Sci. USA 2004, 101, 3747–3752. [Google Scholar] [CrossRef] [PubMed]
- Gallos, L.K.; Cohen, R.; Argyrakis, P.; Bunde, A.; Havlin, S. Stability and topology of scale-free networks under attack and defense strategies. Phys. Rev. Lett. 2005, 94. [Google Scholar] [CrossRef]
- Song, C.; Havlin, S.; Makse, H.A. Self-similarity of complex networks. Nature 2005, 433, 392–395. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.; Barabási, A.L.; Watts, D.J. The Structure and Dynamics of Networks; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Cohen, R.; Havlin, S. Complex Networks: Structure, Stability and Function; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Daqing, L.; Kosmidis, K.; Bunde, A.; Havlin, S. Dimension of spatially embedded networks. Nat. Phys. 2011, 7, 481–484. [Google Scholar] [CrossRef]
- Newman, M.E.J. Networks: An Introduction; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Dorogovtsev, S.N.; Mendes, J.F. Evolution of Networks: From Biological Nets to the Internet and WWW (Physics); Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Satorras, R.P.; Vespignani, A. Evolution and Structure of the Internet: A Statistical Physics Approach; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Caldarelli, G.; Vespignani, A. Large scale Structure and Dynamics of Complex Webs; World Scientific: New York, NY, USA, 2007. [Google Scholar]
- Barrat, A.; Barthelemy, M.; Vespignani, A. Dynamical Processes on Complex Networks; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Barthélemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar] [CrossRef]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef] [PubMed]
- Bashan, A.; Bartsch, R.P.; Kantelhardt, J.W.; Havlin, S.; Ivanov, P.C. Network physiology reveals relations between network topology and physiological function. Nat. Commun. 2012, 3. [Google Scholar] [CrossRef] [PubMed]
- Ludescher, J.; Gozolchiani, A.; Bogachev, M.I.; Bunde, A.; Havlin, S.; Schellnhuber, H.J. Improved El Niño forecasting by cooperativity detection. Proc. Natl. Acad. Sci. USA 2013, 110, 11742–11745. [Google Scholar] [CrossRef] [PubMed]
- Faloutsos, M.; Faloutsos, P.; Faloutsos, C. On power-law relationships of the internet topology. In Proceedings of the ACM SIGCOMM 1999 Conference on Applications, Technologies, Architectures, and Protocols for Computer Communication, Cambridge, MA, USA, 30 August–3 September 1999; Volume 29, pp. 251–262.
- Handcock, M.S.; Raftery, A.E.; Tantrum, J.M. Model-based clustering for social networks. J. R. Statist. Soc. A 2007, 170, 301–354. [Google Scholar] [CrossRef]
- Jackson, M.O.; Rogers, B.W. Meeting Strangers and Friends of Friends: How Random are Social Networks? Am. Econ. Rev. 2007, 97, 890–915. [Google Scholar] [CrossRef]
- Borgatti, S.P.; Mehra, A.; Brass, D.J.; Labianca, G. Network Analysis in the Social Sciences. Science 2009, 323, 892–895. [Google Scholar] [CrossRef] [PubMed]
- Borgatti, S.P. Identifying sets of key players in a network. Comput. Math. Organ. Theory 2006, 12, 21–34. [Google Scholar] [CrossRef]
- Onnela, J.P.; Saramäki, J.; Hyvönen, J.; Szabó, G.; Lazer, D.; Kaski, K.; Kertész, J.; Barabási, A.L. Structure and tie strengths in mobile communication networks. Proc. Natl. Acad. Sci. USA 2007, 104, 7332–7336. [Google Scholar] [CrossRef] [PubMed]
- Faust, K. Comparing social networks: Size, density and local structure. Metodol. Zv. 2006, 3, 185–216. [Google Scholar]
- Colizza, V.; Barrat, A.; Barthélemy, M.; Vespignani, A. The role of the airline transportation network in the prediction and predictability of global epidemics. Proc. Natl. Acad. Sci. USA 2006, 103, 2015–2020. [Google Scholar] [CrossRef] [PubMed]
- Milo, R.; Shen-Orr, S.; Itzkovitz, S.; Kashtan, N.; Chklovskii, D.; Alon, U. Network motifs: Simple building blocks of complex networks. Science 2002, 298, 824–827. [Google Scholar] [CrossRef] [PubMed]
- Alon, U. Biological Networks: The Tinkerer as an Engineer. Science 2003, 301, 1866–1867. [Google Scholar] [CrossRef] [PubMed]
- Bollobás, B. Random Graphs; Cambridge University Press: London, UK, 1985. [Google Scholar]
- Cohen, R.; Erez, K.; Ben-Avraham, D.; Havlin, S. Breakdown of the Internet under intentional attack. Phys. Rev. Lett. 2001, 86, 3682–3685. [Google Scholar] [CrossRef] [PubMed]
- Schneider, C.M.; Moreira, A.A.; Andrade, J.S.; Havlin, S.; Herrmann, H.J. Mitigation of malicious attacks on networks. Proc. Natl. Acad. Sci. USA 2011, 108, 3838–3841. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Fu, B.; Wang, Y.; Lu, G.; Berezin, Y.; Stanley, H.E.; Havlin, S. Percolation transition in dynamical traffic network with evolving critical bottlenecks. Proc. Natl. Acad. Sci. USA 2015, 112, 669–672. [Google Scholar] [CrossRef] [PubMed]
- Dickison, M.; Havlin, S.; Stanley, H.E. Epidemics on interconnected networks. Phys. Rev. E 2012, 85. [Google Scholar] [CrossRef]
- Crucitti, P.; Latora, V.; Marchiori, M. Model for cascading failures in complex networks. Phys. Rev. E 2004, 69. [Google Scholar] [CrossRef]
- Ash, J.; Newth, D. Optimizing complex networks for resilience against cascading failure. Phys. A Stat. Mech. Appl. 2007, 380, 673–683. [Google Scholar] [CrossRef]
- Majdandzic, A.; Podobnik, B.; Buldyrev, S.V.; Kenett, D.Y.; Havlin, S.; Stanley, H.E. Spontaneous recovery in dynamical networks. Nat. Phys. 2014, 10, 34–38. [Google Scholar] [CrossRef]
- Herrmann, H.J.; Schneider, C.M.; Moreira, A.A.; Andrade, J.S., Jr.; Havlin, S. Onion-like network topology enhances robustness against malicious attacks. J. Stat. Mech. Theory Exp. 2011, 2011. [Google Scholar] [CrossRef]
- Bunde, A.; Havlin, S. Fractals and Disordered Systems; Springer: New York, NY, USA, 1996. [Google Scholar]
- Gao, J.; Buldyrev, S.V.; Stanley, H.E.; Havlin, S. Networks formed from interdependent networks. Nat. Phys. 2012, 8, 40–48. [Google Scholar] [CrossRef]
- Cohen, R.; Havlin, S. Complex Networks: Structure, Robustness and Function; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Chen, Y.; Paul, G.; Havlin, S.; Liljeros, F.; Stanley, H.E. Finding a better immunization strategy. Phys. Rev. Lett. 2008, 101. [Google Scholar] [CrossRef]
- Cohen, R.; Havlin, S.; Ben-Avraham, D. Efficient immunization strategies for computer networks and populations. Phys. Rev. Lett. 2003, 91. [Google Scholar] [CrossRef]
- Braunstein, L.A.; Buldyrev, S.V.; Cohen, R.; Havlin, S.; Stanley, H.E. Optimal paths in disordered complex networks. Phys. Rev. Lett. 2003, 91. [Google Scholar] [CrossRef]
- Zimmerman, R. Decision-making and the vulnerability of interdependent critical infrastructure. In Proceedings of the 2004 IEEE International Conference on Systems, Man and Cybernetics, The Hague, The Netherlands, 10–13 October 2004; Volume 5, pp. 4059–4063.
- Mendonça, D.; Wallace, W.A. Impacts of the 2001 World Trade Center attack on New York city critical infrastructures. J. Infrastruct. Syst. 2006, 12, 260–270. [Google Scholar] [CrossRef]
- Robert, B.; Morabito, L. The operational tools for managing physical interdependencies among critical infrastructures. Int. J. Crit. Infrastruct. 2008, 4, 353–367. [Google Scholar] [CrossRef]
- Reed, D.A.; Kapur, K.C.; Christie, R.D. Methodology for assessing the resilience of networked infrastructure. IEEE Syst. J. 2009, 3, 174–180. [Google Scholar] [CrossRef]
- Mansson, D.; Thottappillil, R.; Backstrom, M. Methodology for classifying facilities with respect to intentional EMI. IEEE Trans. Electromagn. Compat. 2009, 51, 46–52. [Google Scholar] [CrossRef]
- Rosato, V.; Issacharoff, L.; Tiriticco, F.; Meloni, S.; Porcellinis, S.; Setola, R. Modeling interdependent infrastructures using interacting dynamical models. Int. J. Crit. Infrastruct. 2008, 4, 63–79. [Google Scholar] [CrossRef]
- D’Agostino, G.; Scala, A. Networks of Networks: The Last Frontier of Complexity; Springer: Berlin, Germany, 2014. [Google Scholar]
- Rinaldi, S.M.; Peerenboom, J.P.; Kelly, T.K. Identifying, understanding, and analyzing critical infrastructure interdependencies. IEEE Control Syst. 2001, 21, 11–25. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Parshani, R.; Paul, G.; Stanley, H.E.; Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 2010, 464, 1025–1028. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.; Strogatz, S.H.; Watts, D.J. Random graphs with arbitrary degree distributions and their applications. Phys. Rev. E 2001, 64. [Google Scholar] [CrossRef]
- Shao, J.; Buldyrev, S.V.; Braunstein, L.A.; Havlin, S.; Stanley, H.E. Structure of shells in complex networks. Phys. Rev. E 2009, 80. [Google Scholar] [CrossRef]
- U.S.-Canada Power System Outage Task Force. Final Report on the August 14th 2003 Blackout in the United States and Canada: Causes and Recommendations; U.S. Department of Energy: Washington, DC, USA, 2004. [Google Scholar]
- Gao, J.; Li, D.; Havlin, S. From a single network to a network of networks. Natl. Sci. Rev. 2014, 1, 346–356. [Google Scholar] [CrossRef]
- Parshani, R.; Buldyrev, S.V.; Havlin, S. Interdependent networks: Reducing the coupling strength leads to a change from a first to second order percolation transition. Phys. Rev. Lett. 2010, 105. [Google Scholar] [CrossRef]
- Shao, J.; Buldyrev, S.V.; Havlin, S.; Stanley, H.E. Cascade of failures in coupled network systems with multiple support-dependence relations. Phys. Rev. E 2011, 83. [Google Scholar] [CrossRef]
- Baxter, G.; Dorogovtsev, S.; Goltsev, A.; Mendes, J. Avalanche collapse of interdependent networks. Phys. Rev. Lett. 2012, 109. [Google Scholar] [CrossRef]
- Cellai, D.; López, E.; Zhou, J.; Gleeson, J.P.; Bianconi, G. Percolation in multiplex networks with overlap. Phys. Rev. E 2013, 88. [Google Scholar] [CrossRef]
- Leicht, E.A.; D’Souza, R.M. Percolation on Interacting Networks; Cornell University: Ithaca, NY, USA, 2011. [Google Scholar]
- Parshani, R.; Buldyrev, S.V.; Havlin, S. Critical effect of dependency groups on the function of networks. Proc. Natl. Acad. Sci. USA 2011, 108, 1007–1010. [Google Scholar] [CrossRef] [PubMed]
- Bashan, A.; Parshani, R.; Havlin, S. Percolation in networks composed of connectivity and dependency links. Phys. Rev. E 2011, 83. [Google Scholar] [CrossRef]
- Zhao, J.H.; Zhou, H.J.; Liu, Y.Y. Inducing effect on the percolation transition in complex networks. Nat. Commun. 2013, 4. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Ksherim, B.; Cohen, R.; Havlin, S. Percolation in interdependent and interconnected networks: Abrupt change from second to first order transition. Phys. Rev. E 2011, 84. [Google Scholar] [CrossRef]
- Amin, S.M.; Wollenberg, B.F. Toward a smart grid: Power delivery for the 21st century. IEEE Power Energy Mag. 2005, 3, 34–41. [Google Scholar] [CrossRef]
- Farhangi, H. The path of the smart grid. IEEE Power Energy Mag. 2010, 8, 18–28. [Google Scholar] [CrossRef]
- Gungor, V.C.; Lu, B.; Hancke, G.P. Opportunities and challenges of wireless sensor networks in smart grid. IEEE Trans. Ind. Electron. 2010, 57, 3557–3564. [Google Scholar] [CrossRef]
- Parshani, R.; Rozenblat, C.; Ietri, D.; Ducruet, C.; Havlin, S. Inter-similarity between coupled networks. Europhys. Lett. 2010, 92. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Shere, N.W.; Cwilich, G.A. Interdependent networks with identical degrees of mutually dependent nodes. Phys. Rev. E 2011, 83. [Google Scholar] [CrossRef]
- Hu, Y.; Zhou, D.; Zhang, R.; Han, Z.; Rozenblat, C.; Havlin, S. Percolation of interdependent networks with intersimilarity. Phys. Rev. E 2013, 88. [Google Scholar] [CrossRef]
- Gao, J.; Buldyrev, S.V.; Havlin, S.; Stanley, H.E. Robustness of a network of networks. Phys. Rev. Lett. 2011, 107. [Google Scholar] [CrossRef]
- Gao, J.; Buldyrev, S.V.; Havlin, S.; Stanley, H.E. Robustness of a network formed by n interdependent networks with a one-to-one correspondence of dependent nodes. Phys. Rev. E 2012, 85. [Google Scholar] [CrossRef]
- Son, S.W.; Bizhani, G.; Christensen, C.; Grassberger, P.; Paczuski, M. Percolation theory on interdependent networks based on epidemic spreading. Europhys. Lett. 2012, 97. [Google Scholar] [CrossRef]
- Gao, J.; Buldyrev, S.V.; Stanley, H.E.; Xu, X.; Havlin, S. Percolation of a general network of networks. Phys. Rev. E 2013, 88. [Google Scholar] [CrossRef]
- Brummitt, C.D.; DâĂŹSouza, R.M.; Leicht, E. Suppressing cascades of load in interdependent networks. Proc. Natl. Acad. Sci. USA 2012, 109, E680–E689. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Qin, P.; Wang, H.; Liu, C.; Jiang, Y. Epidemics on interconnected lattices. Europhys. Lett. 2014, 105. [Google Scholar] [CrossRef]
- Pocock, M.J.; Evans, D.M.; Memmott, J. The robustness and restoration of a network of ecological networks. Science 2012, 335, 973–977. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, K.; Bianconi, G. Percolation on interacting, antagonistic networks. J. Stat. Mech. Theory Exp. 2013, 2013. [Google Scholar] [CrossRef]
- Morris, R.G.; Barthelemy, M. Transport on coupled spatial networks. Phys. Rev. Lett. 2012, 109. [Google Scholar] [CrossRef]
- Zhang, P.; Cheng, B.; Zhao, Z.; Li, D.; Lu, G.; Wang, Y.; Xiao, J. The robustness of interdependent transportation networks under targeted attack. Europhys. Lett. 2013, 103. [Google Scholar] [CrossRef]
- Gomez, S.; Diaz-Guilera, A.; Gomez-Gardeñes, J.; Perez-Vicente, C.J.; Moreno, Y.; Arenas, A. Diffusion dynamics on multiplex networks. Phys. Rev. Lett. 2013, 110. [Google Scholar] [CrossRef]
- Nagler, J.; Levina, A.; Timme, M. Impact of single links in competitive percolation. Nat. Phys. 2011, 7, 265–270. [Google Scholar] [CrossRef]
- Aguirre, J.; Papo, D.; Buldú, J.M. Successful strategies for competing networks. Nat. Phys. 2013, 9, 230–234. [Google Scholar] [CrossRef]
- Kivelä, M.; Arenas, A.; Barthelemy, M.; Gleeson, J.P.; Moreno, Y.; Porter, M.A. Multilayer networks. J. Complex Netw. 2014, 2, 203–271. [Google Scholar] [CrossRef]
- Radicchi, F.; Arenas, A. Abrupt transition in the structural formation of interconnected networks. Nat. Phys. 2013, 9, 717–720. [Google Scholar] [CrossRef]
- Li, D.; Jiang, Y.; Kang, R.; Shlomo, H. Spatial correlation analysis of cascading failures: Congestions and Blackouts. Sci. Rep. 2014, 4. [Google Scholar] [CrossRef]
- Danziger, M.M.; Shekhtman, L.M.; Berezin, Y.; Havlin, S. Two Distinct Transitions in Spatially Embedded Multiplex Networks; Cornell University: Ithaca, NY, USA, 2015. [Google Scholar]
- Peerenboom, J.P.; Fisher, R.; Whitfield, R.G. Recovering from disruptions of interdependent critical infrastructures. In Proceedings of the CRIS/DRM/IIIT/NSF Workshop on Mitigating the Vulnerability of Critical Infrastructures to Catastrophic Failures, Alexandria, VA, USA, 10–11 September 2001.
- Emmerich, T.; Bunde, A.; Havlin, S.; Li, G.; Li, D. Complex networks embedded in space: Dimension and scaling relations between mass, topological distance, and Euclidean distance. Phys. Rev. E 2013, 87. [Google Scholar] [CrossRef]
- Emmerich, T.; Bunde, A.; Havlin, S. Diffusion, annihilation, and chemical reactions in complex networks with spatial constraints. Phys. Rev. E 2012, 86. [Google Scholar] [CrossRef]
- Li, W.; Bashan, A.; Buldyrev, S.V.; Stanley, H.E.; Havlin, S. Cascading failures in interdependent lattice networks: The critical role of the length of dependency links. Phys. Rev. Lett. 2012, 108. [Google Scholar] [CrossRef]
- Bashan, A.; Berezin, Y.; Buldyrev, S.V.; Havlin, S. The extreme vulnerability of interdependent spatially embedded networks. Nat. Phys. 2013, 9, 667–672. [Google Scholar] [CrossRef]
- Berezin, Y.; Bashan, A.; Danziger, M.M.; Li, D.; Havlin, S. Localized attacks on spatially embedded networks with dependencies. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed]
- Segal, E.; Shapira, M.; Regev, A.; Pe’er, D.; Botstein, D.; Koller, D.; Friedman, N. Module networks: Identifying regulatory modules and their condition-specific regulators from gene expression data. Nat. Genet. 2003, 34, 166–176. [Google Scholar] [CrossRef] [PubMed]
- Majdandzic, A.; Braunstein, L.A.; Curme, C.; Vodenska, I.; Levy-Carciente, S.; Stanley, H.E.; Havlin, S. Multiple Tipping Points and Optimal Repairing in Interacting Networks; Cornell University: Ithaca, NY, USA, 2015. [Google Scholar]
- Shekhtman, L.M.; Berezin, Y.; Danziger, M.M.; Havlin, S. Robustness of a network formed of spatially embedded networks. Phys. Rev. E 2014, 90. [Google Scholar] [CrossRef]
- Danziger, M.M.; Bashan, A.; Berezin, Y.; Havlin, S. Interdependent Spatially Embedded Networks: Dynamics at Percolation Threshold. In Proceedings of the 2013 International Conference on Signal-Image Technology & Internet-Based Systems (SITIS), Kyoto, Japan, 2–5 December 2013; pp. 619–625.
- Shao, S.; Huang, X.; Stanley, H.E.; Havlin, S. Percolation of localized attack on complex networks. New J. Phys. 2015, 17, 1367–2630. [Google Scholar] [CrossRef]
- Jelasity, M.; Montresor, A.; Babaoglu, O. Gossip-based aggregation in large dynamic networks. ACM Trans. Comput. Syst. 2005, 23, 219–252. [Google Scholar] [CrossRef]
- Steglich, C.; Snijders, T.A.; Pearson, M. Dynamic networks and behavior: Separating selection from influence. Sociol. Methodol. 2010, 40, 329–393. [Google Scholar] [CrossRef]
- Goh, K.I.; Kahng, B.; Kim, D. Universal behavior of load distribution in scale-free networks. Phys. Rev. Lett. 2001, 87. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Blanchard, O.J.; Summers, L.H. Hysteresis and the European unemployment problem. In NBER Macroeconomics Annual 1986; MIT Press: Cambridge, MA, USA, 1986; pp. 15–90. [Google Scholar]
- Ding, F.; Dokholyan, N.V.; Buldyrev, S.V.; Stanley, H.E.; Shakhnovich, E.I. Direct molecular dynamics observation of protein folding transition state ensemble. Biophys. J. 2002, 83, 3525–3532. [Google Scholar] [CrossRef]
- Kesselring, T.A.; Lascaris, E.; Franzese, G.; Buldyrev, S.V.; Herrmann, H.J.; Stanley, H.E. Finite-size scaling investigation of the liquid-liquid critical point in ST2 water and its stability with respect to crystallization. J. Chem. Phys. 2013, 138. [Google Scholar] [CrossRef] [PubMed]
- Motter, A.E.; Myers, S.A.; Anghel, M.; Nishikawa, T. Spontaneous synchrony in power-grid networks. Nat. Phys. 2013, 9, 191–197. [Google Scholar] [CrossRef]
- Zhou, D.; Bashan, A.; Cohen, R.; Berezin, Y.; Shnerb, N.; Havlin, S. Simultaneous first-and second-order percolation transitions in interdependent networks. Phys. Rev. E 2014, 90. [Google Scholar] [CrossRef]
- Schneider, C.M.; Yazdani, N.; Araújo, N.A.; Havlin, S.; Herrmann, H.J. Towards designing robust coupled networks. Sci. Rep. 2013, 3. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Liu, S.; Zhan, M. Dynamical robustness analysis of weighted complex networks. Phys. A Stat. Mech. Appl. 2013, 392, 4181–4191. [Google Scholar] [CrossRef]
- Tanaka, G.; Morino, K.; Aihara, K. Dynamical robustness in complex networks: The crucial role of low-degree nodes. Sci. Rep. 2012, 2. [Google Scholar] [CrossRef] [PubMed]
- Morino, K.; Tanaka, G.; Aihara, K. Efficient recovery of dynamic behavior in coupled oscillator networks. Phys. Rev. E 2013, 88. [Google Scholar] [CrossRef]
- Zou, W.; Senthilkumar, D.; Nagao, R.; Kiss, I.Z.; Tang, Y.; Koseska, A.; Duan, J.; Kurths, J. Restoration of rhythmicity in diffusively coupled dynamical networks. Nat. Commun. 2015, 6. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Gao, J.; Buldyrev, S.V.; Havlin, S.; Stanley, H.E. Robustness of interdependent networks under targeted attack. Phys. Rev. E 2011, 83. [Google Scholar] [CrossRef]
- Dong, G.; Gao, J.; Tian, L.; Du, R.; He, Y. Percolation of partially interdependent networks under targeted attack. Phys. Rev. E 2012, 85. [Google Scholar] [CrossRef]
- Dong, G.; Gao, J.; Du, R.; Tian, L.; Stanley, H.E.; Havlin, S. Robustness of network of networks under targeted attack. Phys. Rev. E 2013, 87. [Google Scholar] [CrossRef]
- Yagan, O.; Qian, D.; Zhang, J.; Cochran, D. Optimal allocation of interconnecting links in cyber-physical systems: Interdependence, cascading failures, and robustness. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 1708–1720. [Google Scholar] [CrossRef]
- Gu, C.G.; Zou, S.R.; Xu, X.L.; Qu, Y.Q.; Jiang, Y.M.; Liu, H.K.; Zhou, T. Onset of cooperation between layered networks. Phys. Rev. E 2011, 84. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Liu, X.; Li, D.; Havlin, S. Recent Progress on the Resilience of Complex Networks. Energies 2015, 8, 12187-12210. https://doi.org/10.3390/en81012187
Gao J, Liu X, Li D, Havlin S. Recent Progress on the Resilience of Complex Networks. Energies. 2015; 8(10):12187-12210. https://doi.org/10.3390/en81012187
Chicago/Turabian StyleGao, Jianxi, Xueming Liu, Daqing Li, and Shlomo Havlin. 2015. "Recent Progress on the Resilience of Complex Networks" Energies 8, no. 10: 12187-12210. https://doi.org/10.3390/en81012187






