Abstract
The main advantage of hybrid powertrains is based on the efficient transfer of power and torque from power sources to the powertrain as well as recapturing of reversible energies without effecting the vehicle performance. The benefits of hybrid hydraulic powertrains can be better utilized with an appropriate power management. In this paper, different types of power management algorithms like off-line and on-line methods are briefly reviewed and classified. Finally, the algorithms are evaluated and compared. Therefore, different related criteria are evaluated and applied.1. Introduction
Hybrid powertrain technology as a potential solution for reduction of vehicle fuel consumption is the central topic in the context of green powertrain technologies. By definition, hybrid powertrain includes two or more power sources combined with either a conventional transmission system or a hydraulic/electric transmission system to overcome power demand of the vehicle [1]. Characteristics of hybrid powertrains are defined by certain aspects like engine operation efficiency, power transfer efficiency, and regeneration of reversible energies. The efficiency of the entire hybrid powertrain drastically depends on the complex dynamics of the subsystems. Therefore, the design and application of an optimal controller to hybrid powertrains is necessary. Power or energy management in hybrid powertrains acts as a supervisory control algorithm to control the power split between engine and motor. Supplying vehicle power demand, objective functions such as vehicle fuel consumption, are optimized. Therefore, the task of the power management is the most important subject after topology design and components sizing.
In the context of vehicle longitudinal dynamics, different definitions for the performance of the vehicle exist. Acceleration rate, maximum vehicle velocity, and gradeability are known as typical criteria defining vehicle performance in practice. In the context of hybrid vehicles, one of the typical definitions describing vehicle performance is reference velocity tracking. In other words, for the improvement of vehicle performance, it can be expected that the hybrid vehicle can also track the expected drive cycle. For this reason, one of the objective functions in optimal control of power management is related to vehicle velocity and reference velocity difference minimization.
Typical researches in the field of hybrid powertrains deal with topologies design, comparison between different topologies, and the evaluation of different topologies on the vehicle's performance [2–4]. An approach for optimizing component size and topology-design for hybrid hydraulic vehicle (HHV) is presented in [5]. For this reason, using a general model, three different configurations of the power split topology are modeled. The comparison of the optimization results show that the input coupled power split HHV is the most fuel efficient topology. Despite the components size optimization, here the size of the accumulator is not optimized. The same method is applied to compare the performance and fuel consumption of the typical topologies of HHV, namely series, parallel, and power split [6]. According to the results, the capability of power split topology to reduce fuel consumption is higher than two other topologies discussed. The characteristics of a hybrid mechanic powertrain (HMP) which is a combination of a continuous variable transmission and flywheel, are investigated in [7]. The size of the key components is optimized considering the given constraints, in order to optimize several functionalities of the hybrid powertrain e.g., braking energy regeneration and efficient operation of the engine. The results demonstrate the potential of HMP to reduce fuel consumption. It can be concluded that the power management approaches as well as the performance and efficiency of the powertrain strongly depend on the topology of the powertrain.
Furthermore, methodologies to optimize components size by means of performance and efficiency improvement of hybrid powertrain are given in [8–10]. Besides application of a new power management optimization method to a hybrid electric vehicle (HEV), the effect of operational costs such as vehicle acceleration requirement on the component size and cost of the system are studied [8]. Generalization of this method for design of HEV is claimed. The same approach is applied to a HHV [10]. A multi-objective multi-parametric global optimization strategy is developed in [9] for optimization of HHV component size including a globally optimized power management technique. The results show the most optimal size of components with consideration of optimal power management. In [11], the effect of key parameters such as initial pressure of the accumulator to HHV are studied. The results show the effect of components' size on both performance and efficiency of the powertrain.
In review papers, different classifications for power management are given. In [12], optimal power management approaches are additionally classified based on the used mathematical optimization methods into two categories namely, numerical optimization methods such as dynamic programming (DP) and analytical optimization methods such as Pontryagins minimum principle [13]. Static optimization, DP, quadratic programming (QP), model predictive control (MPC), linear programming, Hamilton-Jacobi-Bellman equation are introduced as the usual optimization methods used for power management optimization. In [14], power managements are classified into optimal and sub-optimal control strategies. The global optimization methods such as DP are proposed as reference for other algorithms done to their reliable solutions. The other categories include heuristic control, rule-based power management control, and equivalent consumption minimization strategy (ECMS) [15,16].
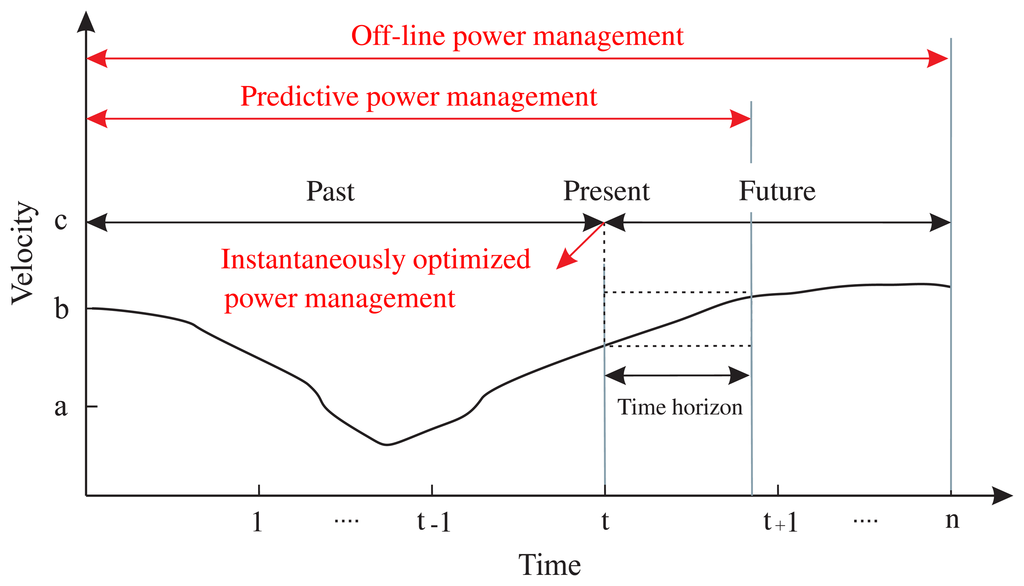
Whether a power management is applicable to an on-line hybrid powertrain depends on the available information regarding vehicle power demand as well as the future vehicle velocity. For off-line power management optimization, the past, present, future information about the vehicle velocity is needed as depicted in Figure 1. While for the on-line instantaneously optimized power management, just the instantaneous information at present is needed. Availability of partial information about vehicle velocity in the future makes it feasible to optimize the power management in future time. Therefore, using predictive approaches, vehicle velocity can be predicted for a specific time horizon. Power management can consequently be optimized in a limited time. The relation between different power management approaches like off-line, predictive, and instantaneous approaches are illustrated in Figure 1. An overview about the proposed power management classification is presented in Table 1.

In this contribution, typical topologies and types of hybrid vehicles are briey introduced and compared. The direct comparison of HEV and HHV is not within the focus of this paper. Different developed power management approaches are investigated and partially compared. A new classification based on the real-time applicability of the power management approaches is proposed. Typical off-line power management optimization methods and algorithms are explained. Further, on-line and real-time power management methods are reviewed, the introduced power management approaches are rule-based controller, fuzzy logic controller, equivalent consumption minimization strategy. Moreover, typical approaches for estimation of the vehicle velocity are discussed. Finally, the power management approaches are evaluated and compared analytically, based on different criteria, and published results. Because of the quantities of the discussed power management approaches and using different models, drive cycles, and topologies in different literatures, a numerical comparison of the results is not possible.
2. Hybrid Hydraulic and Electric Vehicle Topologies
Typical topologies of hybrid powertrains are series, parallel, and power split. The parallel hybrid vehicle is also known as power assist topology. It contains a hydraulic/electric motor coupled to the conventional transmission system. The accumulator charging can be realized by recapturing during braking or deceleration (regenerative braking mode) or parallel during driving by the power of the engine (power split mode). Also possible is the use of the power of the engine only for charging the accumulator (stationary charging mode).
In series topology, the mechanical connection between engine and vehicle is replaced by a hydraulic/electric transmission system using direct coupling of the hydraulic/electric motor to the drive shaft and the hydraulic pump/electric generator to the flywheel. Because of the mechanical decoupling of vehicle and engine, optimal operation of the engine with an appropriate controller is realizable. To recapture braking energy, the hydraulic/electric motor connected to the drive shaft changes its operating mode to hydraulic pump/electric generator during deceleration. By using the valves in HHV and DC/DC-converters in HEV, different topologies for series hybrid vehicles can be realized. However, each topology has its individual characteristic and control strategy. In Figure 2 the topologies of fully controllable series HEV and HHV topologies are illustrated. Keeping the topologies and controllers constant, the proposed HEV and HHV can be compared. Electric generator, electric motor/generator, and buffer (battery, super cap, etc.), are the main components of HEV whereas, the main components of HHV are pump, motor/pump, and accumulator. The functionality of both proposed HEV and HHV are the same, despite a different dynamics of the system components. Considering hydraulic accumulator and electric batteries as the most important elements of HHV and HEV respectively, hydraulic accumulators have lower capacity but higher power density compared to those of electric batteries. Due to chemical transportation processes the charging and discharging processes of electric batteries cannot be compared with those of hydraulic accumulators. Here a compressible gas is compressed more or less ideally and more important, very fast. From an energy point of view it should also be stated that energy conversion efficiency using electrochemical processes (charging and discharging of batteries) is about 70% to 90% (per charging). In case of charging with high dynamics (fast charging/discharging) the efficiency is reduced, which is known as rate-efficiency according to Peukert limited due to cell-chemistry. For these reasons, dynamic response of hydraulic accumulators is faster than those of electric batteries and can be used to improve the dynamic behavior of the vehicle significantly. In contrast, the low capacity of the hydraulic accumulator reduces its functionally to boost operations of short duration.
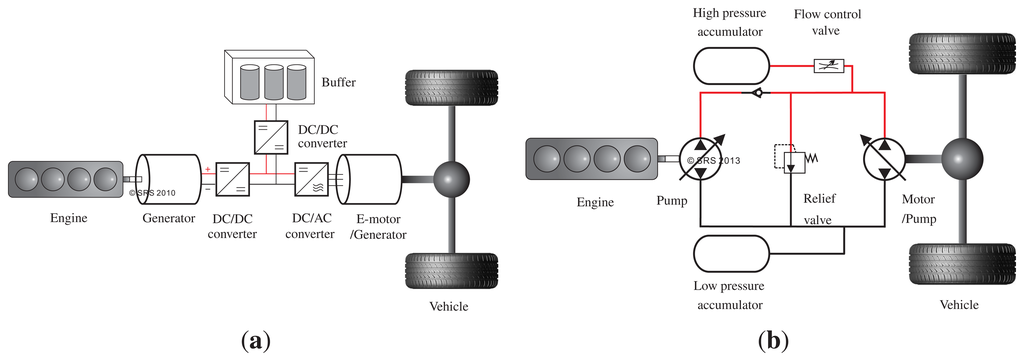
According to Figure 2 use of a variable displacement pump, motor, and control valve for the accumulator makes the system fully controllable. Here, fully controllable includes decoupled control of the power sources according to the vehicle power demand. The same statement is true for the proposed HEV topology because of the implementation of DC/DC-converters. Although the dynamics of the HEV and HHV are different, the same power management control concepts can be applied.
The comparison of HEV and HHV is discussed in [17,18]. In [17] fuel consumption and vehicle performance of three parallel hybrid powertrains applied to a bus are compared. The proposed hybrid vehicles are: a super capacitor-based HEV, a battery-based HEV, and a HHV. According to the results, HEV is more efficient than HHV. In addition, vehicle performance is compared for three criteria, maximum vehicle velocity, gradeability, and acceleration time. The super capacitor-based HEV can realize higher accelerating rate than HHV, while accelerating rate of the HHV is higher than battery-based HEV. However, gradeability of battery-based HEV is more than HHV and super capacitor-based HEV. In addition to the system characteristics and power management control strategy, the effect of the drive cycle on the performance and efficiency of the HHV and HEV is worth considering. Due to the low power capacity of the hydraulic accumulator, its acts a temporary power source. In other words, hydraulic accumulator can be charged and discharged very fast. It is appropriate for the drive cycles that include periodic acceleration and deceleration. City drive cycles such as ECE-15 include more acceleration and deceleration phases in each period of time and the maximum velocity value is also lower compared to highway drive cycles. Therefore, HHV is suitable for vehicles undergoing 'stop and go'-modes such as shuttle buses. In contrast, charge sustainability of electric batteries as well as their large capacity are the reasons for better fuel economy of the HEV in highway drive cycles.
3. Off-Line Power Management
Off-line power management is usually used to define optimal power-management control parameters in advance. Therefore, the approaches use knowledge of the vehicle drive cycle, briefly speaking: it is assumed that the knowledge is exact and known in advance. Depending on the class of power management, both static and dynamic optimization methods can be applied to off-line power management. Static optimization methods use the quasi-static model of the powertrain to be controlled, such as instantaneous power balance method. In contrast, dynamic optimization methods such as DP, use dynamic models of the subsystems during the optimization process [18,19]. In this case, the mathematical formulation of the dynamics of the subsystem such as engine, vehicle, pump, motor, and accumulator are used to realize the dynamical model of the powertrain topology The dynamic model of hybrid powertrain is complex and nonlinear. The nonlinearity results from the multi-mode operation of the hybrid powertrain. Due to the dynamical complexity of the power train, simplification of power management optimization, linearization, and discretization of the model are unavoidable. Feasibility of the solution is the other problem of power management optimization. Due to limited optimal operation of powertrain components and restrictions dictated by objective functions, different equality as well as inequality constrains are applied to this optimization problem. As some of these constrains depend on the states of the problem, they change during time. Therefore, feasibility check of the solution is also unavoidable.
Because of the necessity of prior knowledge about the vehicle drive cycle, in off-line power management strategies, both global and local optimization algorithms are applicable. However off-line globally optimized power managements are more optimal in comparison to the locally optimized power management, because global optimization methods use a wide range of input information for optimization, while local optimization methods define the optimal control based on individual working points.
3.1. Dynamic Programming-Based Power Management
Dynamic programming is a numerical sequential global optimization approach based on Bellman's principle of optimality [20]. The underlying concept of DP is optimization of a sequence of decisions to optimize each related subsequence. Therefore, DP results in an optimal trajectory of sequential decisions within predefined initial and final conditions, realizing a global optimization of the objective functions as depicted in Figure 3.
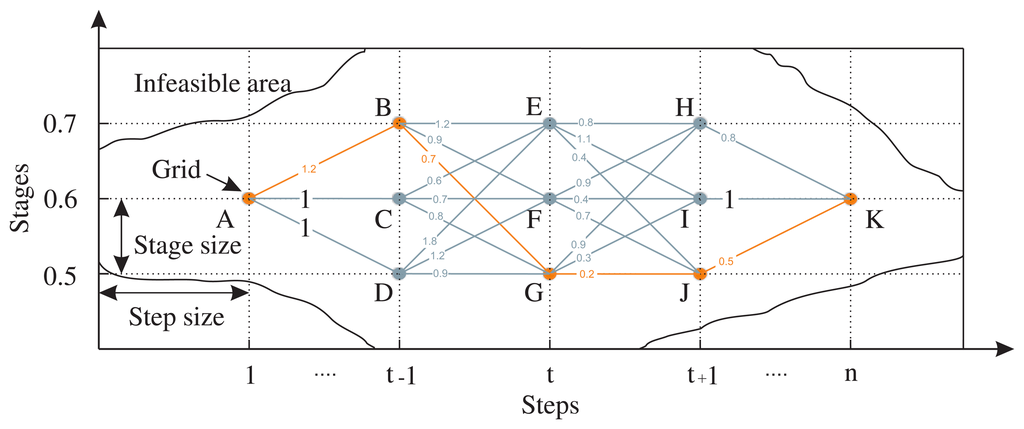
The optimality resulting from DP depends on the number of grid points on the trajectory plan of the state of the system. Decrement of the size of stages as well as steps increase the number of grid points and the optimality of the DP is increased consequently. However, the increase in the number of grid points leads to an increment of the computation load. To decrease the computation load, infeasible states can be omitted as depicted in Figure 3. Although DP-based power management belongs to the category of off-line power management approaches, it establishes a benchmark for evaluation of the optimality of the other developed power management approaches, particularly rule-based power management [21]. Moreover, the results of DP-based power management are typically used for improving the optimality of the hierarchical power management controllers [22].
In [23], the formulation of DP-based power management optimization for application to three typical topologies of HEVs, namely series, parallel, and power split, is given. Additionally, the sensitivity of the optimality of DP-optimized power management to the initial and final values of the system states is investigated. The results such as desired trajectories of accumulator state of charge (SoC) for different drive cycles are saved in a lookup table to be implemented as real-time power management. A rule-based power management is developed and optimized with the help of the lookup table. The comparison of the tuned rule-based controller and DP-optimized power management confirm the improvement of the system's efficiency, showing closeness of the results to the DP-optimized power management. In [24], the same comparison between three typical topologies of hybrid hydraulic powertrain with DP-optimized power management is realized. For parallel topology transmission, gear ratio and engine state are considered as the control variables, while for series topology, engine state and engine speed are the control variables. For power-spit, control variables of both parallel topology as well as series topology are considered as control variables. The results show that the power-split appears to be the worse topology with respect to fuel consumption reduction for both urban and highway drive cycles. These results are in contradiction to the conclusion given in [6]. One reason for this conflict may be the consideration of subsystem efficiencies in both modeling and optimization in [6]. In [24], fuel consumption of the power split topology is reported to be close to series topology, while in [6], fuel consumption of both series and parallel topologies are significantly more than power split. Based on these results, parallel topology is slightly more efficient than series in the urban drive cycle but is significantly more efficient than series in the highway drive cycle [24]. The reason for low efficiency of both series and parallel topologies in highway drive cycle is the unavailability of braking energy for regeneration. The reason for different result in [6,24] may be due to the differences in the models. Furthermore, the substantial difference between fuel consumption of parallel and series topologies is not justified.
In [25,26], stochastic DP (SDP) method is used for optimization of the power management of a parallel hybrid hydraulic truck. Using this method, instead of using prior knowledge about drive cycle, the drive cycle is approximated by a Markov chain. A Markov chain is a qualitative mathematical approach to describe finite states of systems, assuming stochastic transition probabilities between the states. Using Markov chains, the probability to reach upcoming states can be calculated, the main assumption is, that the transition only depends on the state itself (and not on the former transitions history). The result of power management optimization for different drive cycles are calculated and saved in a lookup table. For the application of the results to a real-time power management, the instantaneous velocity of the vehicle is recognized to be close to those in the lookup table [27]. Thereafter, the related control inputs are extracted with the help of interpolation techniques.
A comparison between rule-based power management and two variables SDP power management applied to a parallel hybrid hydraulic powertrain in [25], shows a significant fuel consumption reduction for SDP power management. The control inputs are the power distribution and gear shifting ratios. In [28], the performance of SDP-based power management and ESMC are compared with a DP-based power management, applied to a power split HEV. A two level controller approach consisting of power distribution control and engine optimization control is implemented. Vehicle velocity and SoC are considered as the state variables of the powertrain system. According to the results, both SDP and ECMS decrease the fuel consumption significantly close to benchmark.
In [29], a new boundary-line DP power management is developed. The new one-dimensional DP approach explicitly solves the issues of infeasibility, accuracy, and computational load. It is demonstrated that using pre-calculation and elimination of infeasible state variables, the computation load as well as the feasibility problem can be solved. As depicted in Figure 3, boundary lines of the infeasible areas do not pass necessarily over the grid point of the system state. By definition, grid points are the intersection of stage and step lines which contain the values of the state variables. Therefore, an exact interpolation between grid values improves the accuracy of the DP-based power management. For this reason, the boundary line method is proposed for the exact extrapolation of the values of state variable as well as cost function. The accuracy of the DP optimization depends on the grid size of the state-space. It is investigated that by using boundary line method, the effect of state-space resolution can be minimized. Finally, the computational effort to calculate the values of the states on grid points in infeasible area is decreased by the elimination of infeasible areas of the state. Therefore, the computational load of the boundary-line DP power management is less than usual DP power management.
3.2. Genetic Algorithm-Based Power Management
Genetic algorithm (GA) is a numerical optimization approach for constrained, multi-objective multi-parametric, and complex nonlinear problems. In the process of GA optimization, instead of using analytical methods, techniques such as selection, encoding, mutation, and crossover are used. Through an iterative loop, a batch of variable is generated and for each batch, the objective function is evaluated with respect to a given objective function. Finally, during a multi-loop iteration process, the algorithm defines those samples which converge to the optimal solution with respect to the given objective function. Although, GA can be used for the optimization of complex nonlinear multi-input multi-output (MIMO) hybrid powertrains, its computational load is high. Because of convergence toward an optimal answer, all possible combinations of samples must be iteratively evaluated. For this reason, GA is only appropriate for application in off-line power management [18,30]. It is also used for the adjustment of the parameters of other control strategies.
A GA-QP-based power management for a power split HEV is developed in [30]. By using the QP method, the relation between the battery current and fuel-rate is defined. Using the relation between two variables of the problem, the problem can be simplified by reducing the number of variables. The GA is used to find the power threshold of the engine in combination with the Lagrange method. The outputs of the controller are engine-on power threshold and the accumulator power current. This algorithm is applied to optimize the power management instantaneously in both urban and highway drive cycles. The efficiency of the new power management is demonstrated by comparing the results with that of conventional powertrain. Lack of validation of the new simplified model reduces the reliability of the results. Additionally, GA parameters, namely number of population, elitist amount, and mutation rate, influence the optimality of the problem. Therefore, optimization of the GA parameters instead of their experimental-base selection may improve the efficiency of power management.
The threshold-based energy control strategy is a rule-based on-line power management discussed in the on-line power management section. This strategy involves two parameters, torque difference and pressure limit of active-charging-pressure, related to the output torque of the engine and demanded torque, as well as pressure of the hydraulic accumulator. In [31], GA is implemented for the static adjustment of the parameters of the threshold-based energy control strategy. The results show substantial reduction in fuel consumption compared to the conventional threshold-based energy control strategy. The parameters of the controller are adjusted off-line. Nevertheless, due to the dependency of the results on the drive cycle, the controller cannot to be used in combination with unknown drive cycles.
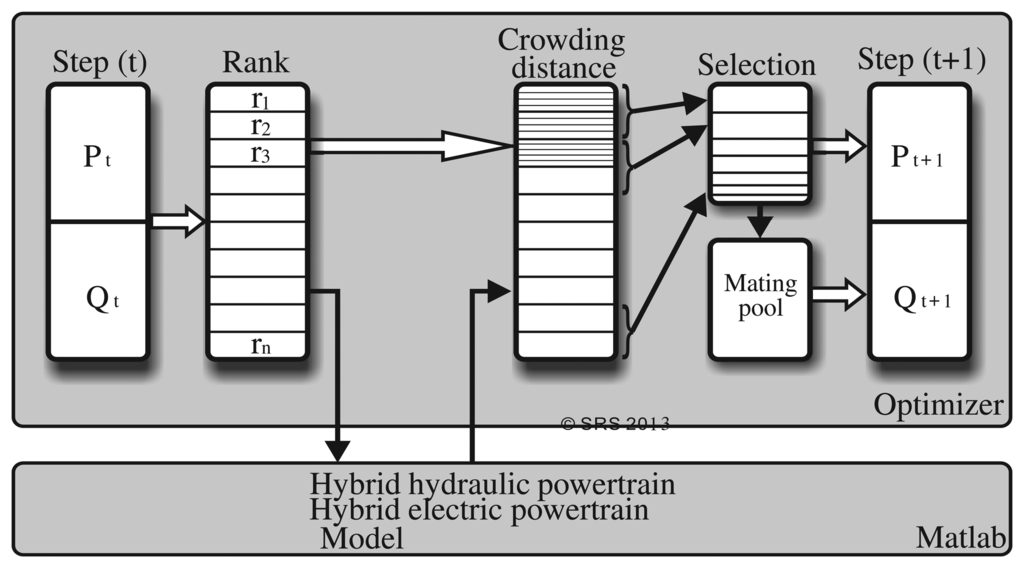
A non-dominated sorting genetic algorithm (NSGA) based on GA is applied for optimization of power management of parallel HEV and HHV as depicted in Figure 4 [18,32]. The control variables are the power distribution ratio between the engine and the secondary power source and the parameters of PI driver controller. Vehicle performance and fuel consumption are the objective functions of the considered optimization problem. The results show a substantial improvement in vehicle performance and fuel consumption reduction. The same control strategy using conventional GA is applied to a HHV in [33] for sizing of the components. The objective functions are weighted using Decision Alternative Ratio Evaluation System (DARE) law. The simulation results show that the bigger accumulator size improves the fuel economy but decreases the vehicle performance. Moreover, bigger pump/motor size improves the fuel economy and vehicle performance.
4. On-Line Power Management
The application of power management strategies to on-line or real-time systems involves solving basic problems, namely those of unknown upcoming power demand trajectory and computational load. Lack of the knowledge of future power demand trajectories, makes global optimization of the power management impossible in real-time. Therefore, only optimization methods based on instantaneous vehicle speed data can be implemented. However, efficiency and performance of the on-line power management strategies are consequently lower than those resulting from off-line power management strategies. Development of on-line power managements start with realization of rule-based controllers [34]. Conventional rule-based power managements are non-optimal with respect to off-line globally optimized power management. The optimization of rule-based power management using off-line methods results in a desirable solution but it depends strongly on the information used to describe the upcoming driving requirements, briefly speaking the drive cycle necessary for optimization is unknown resulting in a decrease in system efficiency. In the following sections, the most important on-line power management strategies are explained in detail.
4.1. Rule-Based Power Management
Rule-based power managements are simple to design and implement. Based on an on-line controller for implementation of supervisory power management strategies, the rules can be typical heuristic experiences or results combining if-then conditions. The concept of rule-based power management is an instantaneous determination of power split ratio based on logical rules and local constrains. Therefore, rule-based power management cannot be optimal. As the logical rules depend on the system characteristics, topology, and design goals, an unique method for synthesizing the rules does not exist. The first step to design a rule-based power management is often based on the determination of vehicle operational modes. Using driver command the operational mode of the vehicle is divided to four modes, namely acceleration, deceleration, stop, and constant velocity. Depending on the SoC and demanded torque, different sub-modes may be selected e.g., braking energy regeneration and conventional braking combination during deceleration, accumulator charging during acceleration, using only the engine in acceleration mode etc. [35].
The threshold-based energy control strategy is one of the conventional rule-based power management controller. In [31], a threshold-based energy control strategy is developed based on the thresholds of the engine efficient operation and SoC. In this power management controller, the engine efficiency map is divided into three areas with the help of two constant power lines, namely engine-on and motor-assist power lines as depicted in Figure 5. These two reference power lines are used to control the state of the engine in acceleration mode. If the vehicle power demand is between zero and engine-on power line, only the motor supplies power. If the power demand is between engine-on and motor-assist power, only the engine supplies power. Finally, if the power demand is more than motor-assist power line, motor assists the engine to dominate the power demand. In deceleration mode, braking energy must be recaptured to charge the accumulator as much as possible. Accordingly, the most efficient operating point of the engine is around the point with engine speed 2250 rpm, engine torque 280 Nm, and engine power about 66 kW.
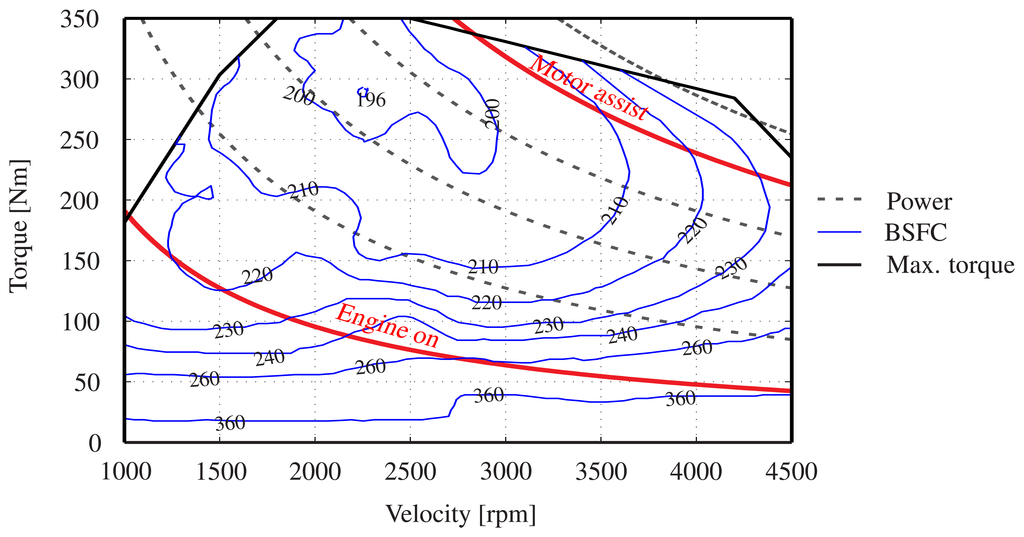
In [36], a map-based power management controller is developed based on a DP-based power management and using comprehensive extraction method. In addition to fuel consumption, emission of the engine is considered to be minimized. Therefore, emission is modeled using engine thermal dynamic and after-treatment dynamic models. Three control strategies namely engine bang-bang, gear-shifting, and power split based on the DP optimization map are proposed. The thresholds of these controllers are cold-start and hot-start emission of the engine. The results justify the emission reduction of the vehicle using map-based power management controller.
Optimization of the applied logic of rule-based power management using the results of globally optimized power management such as DP is usual. The difference between demanded torque and efficient torque of the engine as well as the SoC threshold are the main control variables of rule-based power management [31]. According to the results, fuel consumption and dynamic performance of the power management are improved. Moreover, optimization of the rule-based power management controller using DP-based power management is realized in [37]. Based on the DP optimization results, a new gear-shift strategy is extracted for the HHV powertrain. Moreover, the logic-based rules for switching between operational modes are tuned using the DP results. For example if the SOC is high, charging of the accumulator with engine power must be avoided. The result shows a possible reduction of fuel consumption up to more than fifty percent using the optimized rule-based power management.
The bang-bang controller (also known as two points switching control, is in [1,38] denoted as thermostat strategy) is based on accumulator power preservation. In this control strategy, an effort is made to operate the engine at the most efficient points subject to the SoC of the accumulator [39]. The engine on and off strategy is based on hitting the minimum and maximum SoC of the accumulator respectively. However, in this strategy, engine switches between either idle/supply modes or on/off modes. The frequent switching of the engine is undesirable because it increases fuel consumption due to transient operation of the engine. To overcome this drawback, the charging threshold of the accumulator can be limited by using a SoC dead band [39]. In Figure 6, the key parameters of the thermostat strategy namely, dead band, threshold power, and threshold SoC are presented. The critical SoC is the value in which the engine starts to charge the accumulator. In other words, when the SoC is higher than critical value, accumulator is the only power source while for values lower than critical SoC, the only power supply is the engine. To charge the accumulator, the engine operates at the shown maximum power point which is the most optimal operating point of the engine.
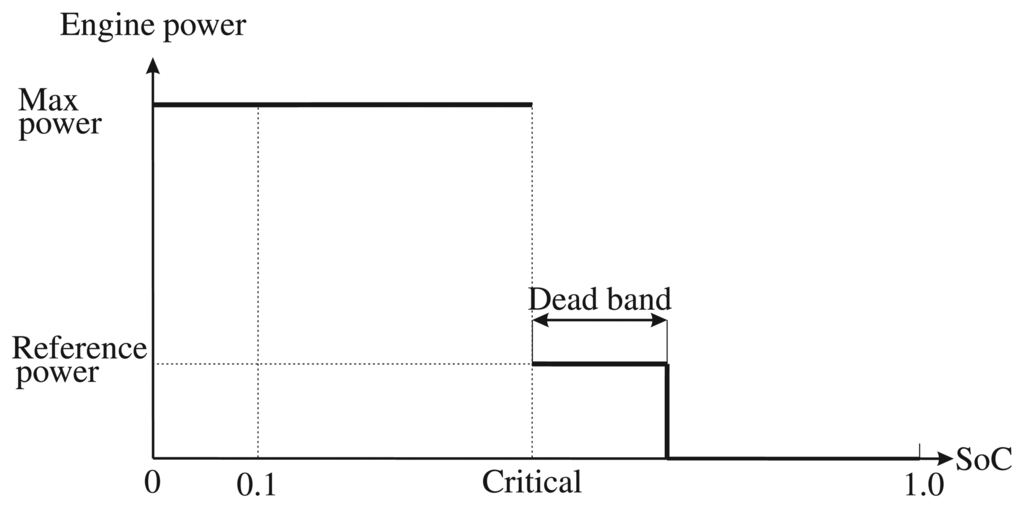
In [38], the effects of key parameters of the two points control strategy on the performance and efficiency of the power management are investigated. Accordingly, increase in the reference power value increases the number of undesirable switching of the engine between on/off modes or idle/supply modes at a certain time. An increase in dead band value, however, results in fuel consumption reduction. Moreover, the value of critical SoC has a significant effect on the amount of braking energy that is captured during deceleration mode. In other words, in two points control strategy, effort should be made in keeping the minimum SoC as low as the critical SoC. Therefore, depletion of the accumulator just before braking phase by means of increment of capturing braking energy may not be guaranteed. Consequently, algorithms defining the optimal values of control parameters are needed. For this reason, a static adjustment of control parameters is proposed in [38]. Although, this method improves the fuel economy relative to the conventional threshold strategy, using optimization algorithms may improve the performance and efficiency of the two points control strategy.
In [40], three rule-based power management strategies are developed called namely by the authors: pure-thermostatic, acceleration-thermostatic, and with-idle-thermostatic strategies. The pure-thermal strategy uses SoC as the only state variable of the powertrain. In this case, the accumulator is charged with the engine whenever the accumulator has enough capacity. In the acceleration-thermostatic strategy, both SoC and driver command are used as state variables. In this case, in addition to the accumulator capacity, the powertrain must operate in acceleration mode to charge the accumulator. The only difference between acceleration-thermostatic and with-idle-thermostatic strategies is that, in the second strategy, the accumulator can be charged whenever the vehicle drives with constant velocity. The results justify the superiority of the with-idle-thermostatic strategies to decrease fuel consumption. The reason is that the accumulator can be charged in engine idle mode and it has enough capacity at the beginning of deceleration for capturing the braking energy.
Although rule-based power management controller is applicable to on-line and even real-time power management, it is not an optimal power management. Despite ability to improve the efficiency of the rule-based power management, the efficiency of the explained method is always less than both global and local optimization algorithms. Therefore, the rule-based power management controller is a sub-optimal, on-line and real-time-applicable power management.
4.2. Fuzzy Logic Controller
In contrast to rule-based power management, fuzzy-based power management controller is based on partially true logics. In other words, the rules are not necessarily true or false rules. Fuzzy controller contains a series of linguistic rules and each rule contains one antecedent and two consequents. The fuzzy logic controller consists of fuzzification, inference engine, rule base, and defuzzification. Application of partially true logics in fuzzy-based power management, causes a smooth transition of the dynamic behavior of the powertrain in contrast to true or false logics in the rule-based power management. Therefore, fuzzy controller may guarantee the robustness of the power management.
In [41], three different control strategies are combined. The first strategy reduces fuel consumption by optimization of the power split ratio. The second control strategy maximizes the braking energy captured during deceleration mode, and the last control strategy sustains the SoC to increase the robustness of the control system. Three sub fuzzy controllers are designed to control the operation of the engine, on/off switching of the engine, and braking energy distribution. Based on accumulator energy level, different membership functions are selected which define the switch time between operation modes. The number of membership functions for braking energy distribution controller is five while for the two other controllers is seven.
The fuzzy controller uses driver command as well as SoC as the control inputs. By definition, the relation of captured braking energy to the available braking energy is regeneration ratio. The effect of this factor on the efficiency of the power management is studied and on-line control of this factor by means of vehicle performance improvement is confirmed. The control strategy is applied to Toyota Pirus model, the used drive cycle is the combination of three different drive cycles by means of long trip realization. Simulation results show efficient operation of the engine. The undesirable engine on/off switching is detected in the one segment of the drive cycle which contains more stop and go maneuvers. Comparison of the SoC shows better sustainability of SoC in the fuzzy-based power management in comparison with Prius HEV. The similar controller is used in [42] to reduce the fuel consumption and emission.
A generalized fuzzy logic-based power management controller for three typical topologies of the HEV, namely parallel, series, power split is developed in [43]. The state of the engine is determined by the power demand of a scaled vehicle, as well as engine velocity, engine temperature, SoC, vehicle speed, and acceleration. Vehicle power demand as well as vehicle torque are determined by PID driver controller. Each hybrid topology needs its individual power management. Therefore, for each topology individual power management is developed based on sustaining SoC strategy. These power management algorithms are combined with the help of fuzzy rules to form a generalized power management. The power split ratio is the output of the generalized fuzzy logic-based power management. The results show that power split topology increases the fuel economy more than that by series and parallel topologies. Although the approach is a generalized power management controller, application of it to other topologies requires many modifications. A generalized fuzzy logic-based power management controller for three typical topologies of the HEV, namely parallel, series, power split is developed in [43].
A new fuzzy logic controller based on travel distance information is developed in [44]. The two inputs of the controller are SoC and vehicle power demand, the output of the controller is power split ratio. Considering the dependency of the SoC to the travel distance necessitates the need for using GPS data. The results show a comparable fuel consumption with engine on/off strategy. Comparison of the results shows substantial fuel consumption decrement. The presented results for a drive cycle show depletion of the accumulator at the end of the drive cycle and sustain requirement of SoC for the next drive cycle. Moreover, each drive cycle ends with braking so that brake energy is captured at the end of the drive cycle. Due to the point that brake energy losses are accepted and included, this approach cannot really be accepted as an hybrid powertrain approach.
4.3. Equivalent Consumption Minimization Strategy
The equivalent consumption minimization strategy (ECMS) is an instantaneously optimized power management strategy. In ECMS, the accumulator is considered as a subsidiary reversible fuel tank. Based on the ECMS strategy, the fluctuation of the energy level in secondary power source will be compensated by replacement of the equivalent fuel power in the future [45]. For equivalency of the fuel power and accumulator power, the instantaneous efficiency of the power line must be calculated as depicted in Figure 7. Accordingly, the equivalent amount of fuel to compensate the used accumulator energy in discharging mode and equivalent amount of fuel to produce as much as power saved in the accumulator in charging modes is calculated. For this reason, energy losses at certain operating points of the system must be considered. Based on this definition, the power management is optimized by minimization of both engine fuel consumption and equivalent fuel consumption of the secondary power source. In contrast to other power management optimization methods, the control variable in ECMS is the equivalency factor. By definition, the equivalency factor is the relation between the used energy of the secondary power source to the power demand. Therefore, increase in the value of equivalency factor, increases the use of the auxiliary power source energy and vise versa.
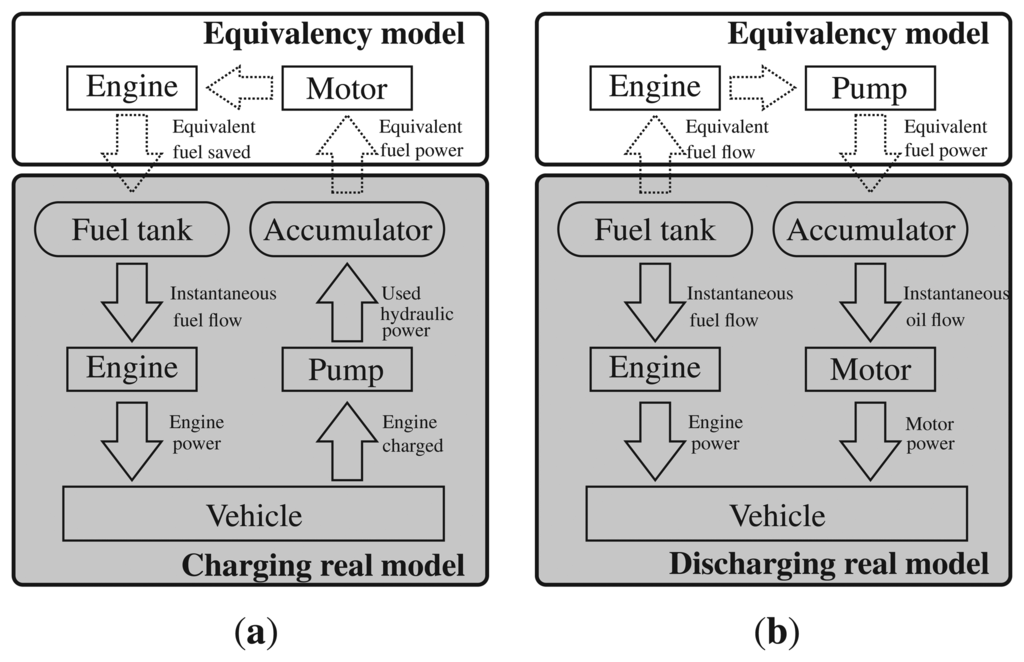
By using the equivalency factor as the only control variable, proper charge and discharge of the accumulator considering variable boundary conditions cannot be guaranteed. In other words, accumulator may be overcharged or undercharged. To avoid this problem, with the help of an iterative loop, the value of SoC is compared to the boundary values and if needed the equivalency factor is corrected. Due to difference between efficiency of the power transmission in charge and discharge operational modes, a method is developed to distinguish equivalency factor in charge and discharge modes of the secondary power source in [46]. For an on-line application of this method, two different equivalency factors are converted to one variable which is the probability factor. The evaluation of the probability factor without using prediction methods results in on-line calculation of the equivalence factor for ECMS. However, the presented method increases substantially the performance and optimality of the powertrain, it is not applicable to real-time power management, because the power management is optimized for a specific drive cycle.
Performance of ECMS is preferred in comparison with the global optimization algorithms such as simulated annealing in [45,47] and DP in [46]. An adaptive equivalent consumption minimization strategy (A-ECMS) is developed in [48] to increase the optimality of ECMS. Using GPS data and comparing with vehicle velocity, the equivalency factor can be adjusted instantaneously with this adaptive ECMS strategy. To decrease the computational load by means of real-time application of A-ECSM, the two dimensional adaptive problem is converted to an one dimensional one by substitution of a unique equivalency factor. The real-time implementation of this method is approved by using vehicle velocity prediction method and GPS data for evaluation of the road load. The results of A-ECMS are compared with DP-based power management as well as a conventional ECMS. The comparison shows less fuel consumption for A-ECMS relative to conventional ECMS. Furthermore, results justify the computational load decrement of the A-ECMS without alteration of the optimality.
A new strategy to improve the efficiency of the ECMS is presented in [49]. The improvement is brought about by relating the equivalent factor and the vehicle speed by using more accumulator power. The results show relative fuel consumption reduction for city drive cycle, but not for the urban drive cycle. In [50], a new A-ECMS with predictive dynamic programming approach is developed which is called DP-ECMS. In this approach, power and torque demand of the vehicle are predicted. The gear ratio and SoC of the accumulator are considered as the two states of the controlled system to decrease fuel consumption. The comparison of the results with DP-based power management approves the near optimal fuel consumption of the new A-ECMS. Besides the robustness of this approach, its optimality is shown on comparison with a number of other A-ECMS approaches. However, high computational load of DP makes it inappropriate to be used for real-time power management. To overcome this drawback, an iterative method based on Pontryagins approach is developed in [51] called global Pontryagin optimization (GPO). Between different methods proposed to solve this problem, bisection method is proposed as the simplest and the most robust one. Comparison between the results of DP-ECMS and GPO for seven different drive cycles shows substantial decrement in computational load but no effect to fuel consumption reduction. Although low computation load of the GPO makes it appropriate in real-time power management, both GPO and DP-ECMS are off-line power management approaches and therefore not applicable.
In [52], the equivalency factor is estimated based on the recognition of driving pattern. The driving pattern is estimated with the help of the past drive patterns. Based on recognition of the driving pattern, the equivalency factor is controlled adaptively. In addition, a PI controller is utilized to sustain SoC close to nominal value. The results show good recognition of the drive cycle as well as SoC control. However, high computational load hinders the application of this method for real-time power management. Three different A-ECMS, namely adaptive PI controller approach, discrete time method, and proportional controller, are compared together using SoC feedback [53]. The results confirm the robustness and optimality of the adaptive PI controller and discrete time method. Although, the results of drive cycle recognition approach are close to those resulting from model predictive approaches, the applicability of this method depends on the size of the accumulator. In other words, this method is valid in operational situations where the accumulator does not fully charge and discharge.
5. Real-Time Power Management
Inaccessibility of the drive cycle in future is a crucial problem for the realization of real-time power management approaches. The assumption of prior-knowledge about the “drive cycle” is unrealistic and it is used just for off-line optimization of power management. To overcome this drawback, methods such as drive cycle recognition [54], and the use of GPS data [55,56] are developed and applied to real-time power management. However, they are based on the past and present vehicle velocity information. Furthermore, only local power management optimizations are realizable with the help of these approaches. Finally, there is a time delay between current power demand signal and output controls of the power management.
5.1. Telematics Technology-Based Predictive Approach
Telematics technology is one of the new developments within the field of intelligent vehicle technologies. In general, this technology realizes the communication of the vehicles with other vehicles and environment. With the help of information getting through this system, different intelligent systems such as vehicle tracking can be realized. Telematics technology can be used for adjustment of instantaneous vehicle velocity in urban environment [55]. The comparison between telematics-equipped vehicle with conventional vehicles shows a significant reduction in fuel consumption [55]. Also the efficiency of the telematics-equipped vehicle and HEV are comparable. Based on the information gathered from telematics technology, the vehicle velocity in the next partial time is provided [56]. Combination of these information with the ECMS power management results in an on-line power management. The power management formulation is solved using sequential QP. Comparison of the results for different traffic preview lengths, show higher fuel economy in short time preview. The combination of the vehicle velocity and vehicle position to predict the power demand is presented in [57]. It is shown experimentally that the position and velocity profiles of the stop and go vehicle such as garbage trucks follow a pattern. Based on this consideration, other factors such as driver behavior, road grade variation, and vehicle mass variation effect the power demand of the vehicle. The iterative learn prediction profile method calculates the vehicle power demand by comparison of driver behavior to the given data. At the stopping phase of the vehicle, using the GPS data, the next velocity and position profile for prediction of vehicle power demand is searched. Additional to predictive power management, a conventional power management is considered where the prediction of vehicle velocity is impossible. For application of predictive power management in real-time, synchronization of the predictive velocity and reference velocity is very important. If the data interval of the vehicle acceleration is bigger than the predicted one, acceleration mode control will be applied in real-time instead of braking mode control. Therefore, power management does not operate appropriately.
5.2. Model Predictive Approach
Model predictive control is a mathematical method for calculation of the system input trajectory to optimize the output of the system in the future. Based on the current dynamics of the system, the future of the system for a specific prediction horizon is predicted and the control inputs are calculated. The performance of the MPC drastically depends on the prediction window. The application of this method to hybrid powertrain can decrease the fuel consumption by prediction of the system inputs such as power split factor. If the computation load of this method is decreased, this method can be used as a real-time power management.
A two level nonlinear model predictive power management controller is developed for a power split HEV [58]. To ensure simplicity, vehicle velocity and power distribution controllers are decoupled. In the supervisory or high level control, power demand of the vehicle is predicted with a linear model predictive algorithm while in low level control, the power distribution is optimized instantaneously. To increase the accuracy of the power management as well as the application of linear MPC, the internal model, which is used for vehicle velocity prediction, is linearized around the instantaneous operating points. The parameters of the MPC are adjusted with a rule-based controller. Although the results demonstrate significant decrease of fuel consumption in comparison with rule-based power management, the results are not validated and just simulation results are presented. Moreover, the efficiency of this MPC-based power management can be improved by optimal adjustment of MPC parameters. The same control scheme with small differences is used in [59] to a series HHV. Engine torque, pump, and motor displacement ratios are the input variables of the system. The goal of the controller is optimal operation of the engine in drive mode. Tracking the desired vehicle velocity has more priority than fuel consumption reduction. Limiting the operation of the engine to a constant torque, consideration of constant efficiency for hydraulic elements, lack of optimal adjustment of MPC parameters are the problems associated with this MPC-based power management. In [60] the relation between dwell time, accumulator size, and engine on and off switch frequency is investigated. Higher dwell time increases the engine durability. Moreover, bigger dwell time requires larger accumulator capacity.
The performance of nonlinear MPC-based power management in association with an adaptive prediction time horizon is presented in [61]. If the predictive velocity matched well with the reference velocity, time horizon is increased and vice versa. Therefore, the computational load of the power management can be decreased adaptively while the performance and efficiency of power management are increased. Comparison of the MPC power management with DP as well as a conventional controller shows substantial improvement in both fuel consumption and vehicle performance. An integrated predictive power management controller is developed in [62]. In this approach, velocity prediction method is combined with ECMS supervisory control by means of fuel consumption optimization. In this power management, the equivalency factor is the control variable. The weighting ratios of the objective functions are the inputs to the power management strategy. In addition, the equivalency factor controller is heuristic. Although, the velocity prediction method is not accurate, the simulation results for eight different drive cycles justify the potential of the new integrated predictive power management to reduce fuel consumption. Moreover, comparison of the results with a non-predictive ECMS power management as well as a DP-based power management shows improvement in optimality of the power management respectively.
5.3. Stochastic Model Predictive Approach
In contrast to the MPC, which uses prior knowledge about drive cycle, stochastic model predictive control (SMPC) uses random information about vehicle velocity for optimization of power management. Using a Markov chain, the distribution of the power demand in the future can be assumed based on previous experiences. The integration of the stochastic power demand prediction with DP is already explained. Because of the high computation load of DP, it is not implementable as real-time power management. However, SMPC uses supervisory optimization methods such as linear or QP with low computational load. Therefore, it is a real-time power management strategy.
In [63], SMPC approach is applied to a series hybrid powertrain as on-line power management. With the help of a two level integrated power management approach, the power demand of the vehicle is predicted stochastically and power distribution is optimized in the second level. At each time step using all possible Markov states, all possible power demand distribution in the next step are generated iteratively. Based on the known power demand, power distributions is optimized using quadratic optimization approach. The results of SMPC power management are compared to two other MPC approaches, namely frozen-time MPC and prescient MPC. In frozen-time MPC, a prior knowledge about drive cycle is necessary while prescient MPC uses constant actual power demand for the prediction of power demand in future. Therefore, frozen-time MPC is a deterministic approach. Comparison of the results shows the optimality of prescient MPC, SMCP, and frozen-time MPC respectively.
Similar power management is applied to a HHV. The control variables are pump/motor displacement ratio as well as engine power variation. The objective functions are operation of the engine, vehicle performance, and the brake energy regeneration. Based on two operational modes of the engine, namely engine on and off, two predictive models are developed. The states of the prediction model are vehicle velocity, SoC, and output power of the engine. For simplicity, the complex model of the powertrain is linearized and discretized. Comparison of the results with frozen-time MPC, and prescient MPC verifies the results presented in [63].
6. Discussion and Evaluation
Comparison of different power management approaches show that except optimization of the power management, computation load, ability to easily implement, and information about upcoming vehicle velocity are the other important criteria for realization of a real-time power management. The first problem associated with the implementation of power management to real-time systems, regardless of control strategy, is the lack of information about upcoming vehicle power demand. Additionally, backward model of the powertrain is needed to calculate power demand regarding the vehicle velocity. The complexity and non-linearity of the powertrain model must be simplified by linearization, and simplification of the model. Although the recommended methods are able to solve these problems theoretically, reduction of computation load is unavoidable for real-time implementation of power management. Use of powerful processors or simplification of e.g., predictive model to decrease the computation load, sequentially increase the cost and inaccuracy. Therefore, between simplicity and accuracy of the powertrain backward model a weighted balance has to be considered. Nevertheless, optimality of power management is usually sacrificed. Moreover, unavailability of experimental results or even possibility of comparison respect to practical oriented benchmarks results makes it impossible to judge about power management strategies. Different power management optimization strategies have their individual drawbacks. In Table 2, discussed power management algorithms are compared from the real-time applicability and optimality points of views. In real-time applicable power management, the calculation time is short enough that can be realized in real time steps. In contrast, on-line power management has the same structure as the real- time power management but the calculation time is longer. In conditional cases, the power management algorithm definitively cannot be applied as real-time power management. It depends on its ability to impose conditions, such as calculation load reduction which are discussed in detail.

Rule-based power managements are based on predefined constant logical rules and real-time applicable. Performance and efficiency of rule-based controller depend on a wide variety of rules, logics, and conditions. Rule-based controller improves the optimal operation of the individual components without consideration of the overall efficiency of the powertrain. Near optimal point and near optimal line operation of the engine, on and off switching of the engine, reducing transient operation of the engine, engine constant speed with variable torque, SoC bound control, and maximum recapturing of braking energy are usual control strategies. Applicability of a specific strategy depends on the type of hybrid powertrain, degree of hybridization, size of the components, and drive cycle. To improve the efficiency and performance of the rule-based power management, controller adjustment is unavoidable. However optimization of power management depends on drive cycle. Therefore, generalization of a unique rule-based power management to all drive cycles and driver behavior is impossible. These types of power management are simple to implement. It can be applied as on-line and real-time power management. Nevertheless, it is not an optimal power management. Moreover, the time-delay between the feedback signal of vehicle velocity and output signal of power management is unavoidable. This drawback proves the superiority of predictive power management to the instantaneous power management optimization. All in all, rule-based as an instantaneous and sub-optimal control approach, is the usual real-time power management in context of hybrid powertrains.
The type of optimization method which is used for development of power management of hybrid vehicles, depends on the availability of vehicle power demand. Using prior-knowledge about drive cycle, both local and global optimization algorithms such as GA, DP, and ECMS without consideration of computation load, are applicable. A usual instantaneous power management strategy is ECMS and it is applicable as both off-line and on-line power management strategy. In contrast to rule-based controller, ECMS provides optimal power management. However, the method is very sensitive to the control parameters mainly equivalency factor. It is a robust power management in context of sustaining SoC. For this reason, SoC must be penalized with an additional objective function. The optimality of ECMS in off-line application is close to globally optimized power managements. Although different approaches such as A-ECMS are developed to increase the optimality of ECMS, their computation load is huge. Therefore, other such optimization methods, suffer lack of optimality due to simplicity. Model predictive control is proposed as on-line and real-time power management. Unlike rule-based, which is sub-optimal power management and such as ECMS, MPC-based power management is optimal power management. Same as other optimization methods, MPC leads to large calculation load. However, simplicity of the model decreases the complexity and computation load while decreasing the optimality.
As global optimization methods such as DP need more time for computation effort involved, mostly they are not applicable as real-time power management. Among all developed optimal power managements, DP-based approaches show the most optimal power distribution. Therefore it can be used as benchmark for evaluation of other power managements. However, it is based on backward calculation of power distribution using deterministic drive cycle with mostly time consuming computational load.
Unlike numerical optimization methods, analytical optimization methods based on minimum principals such as Pontryagins minimum principle reduce the computational load substantially [61]. Nevertheless, formulation of a complex nonlinear MIMO hybrid power management for application of analytical methods requires model simplification. In this case, optimal model simplification methods may decrease unavoidable errors [64], therefore, the result is sub-optimal. Moreover, it requires no prior knowledge about optimization horizon.
7. Summary and Conclusions
In this contribution, different power management strategies including both off-line to on-line are briefly introduced, explained, and compared. Global optimization methods can be used only for off-line power management optimization. They are used to survey the potential of the powertrain to reduce fuel consumption. Therefore, the results can be used for topology design, parameter adjustment, component size adjustment, and evaluation of other power management as benchmark. Among off-line power managements, deterministic DP is the most appropriate method. With a sequential decision, the trajectory of the system state as well as control input among all possible trajectories is selected which results in the least objective function value. Nevertheless, it is not directly appropriate for a real-time powertrain.
A rule-based and fuzzy-logic based controller, and ECMS are discussed in detail as on-line power management solutions which are implementable to the real-time powertrain. Although the fuzzy logic controller does not have the disadvantages possessed by a rule-based controller, computational effort is more than rule-based controller. Implementation of ECMS to a real-time powertrain is subject to parameter sensitivity as well as adjustment of the equivalency factor. Predictive power managements are introduced in detail and their superiority to the other power management is discussed. Moreover, different methods for prediction of vehicle velocity are reviewed. Finally, we discuss the evaluatuation of real-time implementable power managements. For the future work, based on the review of power managements, an appropriate power management for different topologies of a HHV will be designed.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ehsani, M.; Gao, Y.; Gay, S.E.; Emadi, A. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles; CRC Press: New York, NY, USA, 2005. [Google Scholar]
- Capata, R.; Coccia, A. Procedure for the Design of a Hybrid-Series Vehicle and the Hybridization Degree Choice. Energies 2010, 3, 450–461. [Google Scholar]
- Shankar, R.; Marco, J.; Assadian, F. The Novel Application of Optimization and Charge Blended Energy Management Control for Component Downsizing within a Plug-in Hybrid Electric Vehicle. Energies 2012, 5, 4892–4923. [Google Scholar]
- Fang, L.; Qin, S.; Xu, G.; Li, T.; Zhu, K. Simultaneous Optimization for Hybrid Electric Vehicle Parameters Based on Multi-Objective Genetic Algorithms. Energies 2011, 4, 532–544. [Google Scholar]
- Cheong, K.L.; Li, P.Y.; Chase, T.R. Optimal Design of Power-Split Transmissions for Hydraulic Hybrid Passenger Vehicles. Proceedings of the American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 3295–3300.
- Du, Z.; Cheong, K.L.; Li, P.Y.; Chase, T.R. Fuel Economy Comparisons of Series, Parallel and HMT Hydraulic Hybrid Architectures. Proceedings of the American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 5954–5959.
- Van Berkel, K.; Römers, L.; Vroemen, B.; Hofman, T.; Steinbuch, M. Design of a Low-Cost Hybrid Powertrain with Large Fuel Savings. Proceedings of the 25th World Battery, Hybrid and Fuel Cell Electric Vehicle Symposium & Exhibition, Shenzhen, China, 5–9 November 2010.
- Pourabdollah, M.; Murgovski, N.; Grauers, A.; Egardt, B. Optimal Sizing of a Parallel PHEV Powertrain. IEEE Trans. Veh. Technol. 2013, 62, 2469–2480. [Google Scholar]
- Moulik, B.; Karbaschian, M.A.; Söffker, D. Size and Parameter Adjustment of a Hybrid Hydraulic Powertrain Using a Global Multi-Objective Optimization Algorithm. Proceedings of the IEEE Vehicle Power and Propulsion Conference, Beijing, China, 15–18 October 2013; pp. 1–6.
- Mensing, F.; Li, P.Y. Sizing and Optimal Operation of a Power Split Hydraulic Hybrid Drive Train. Proceedings of the International Fluid Power Exhibition, Las Vegas, NV, USA, 22–26 March 2011.
- Karbaschian, M.A.; Söffker, D. Performance and Efficiency of a Hydraulic Hybrid Powertrain. Proceedings of the 2nd International Energy Efficient Vehicles Conference, Dresden, Germany, 18–19 June 2012; pp. 174–187.
- Sciarreta, A.; Guzzella, L. Control of Hybrid Electric Vehicles. IEEE Control Syst. 2007, 27, 60–70. [Google Scholar]
- Yuan, Z.; Teng, L.; Fengchun, S.; Peng, H. Comparative Study of Dynamic Programming and Pontryagin's Minimum Principle on Energy Management for a Parallel Hybrid Electric Vehicle. Energies 2013, 6, 2305–2318. [Google Scholar]
- Hofman, T.; Steinbuch, M.; van Druten, R.M.; Serrarens, A.F.A. Rule-based energy management strategies for hybrid vehicles. Int. J. Electr. Hybrid Veh. 2007, 1, 71–97. [Google Scholar]
- Wang, X.; He, H.; Sun, F.; Sun, X.; Tang, H. Comparative Study on Different Energy Management Strategies for Plug-in Hybrid Electric Vehicles. Energies 2013, 6, 5656–5675. [Google Scholar]
- Xu, Q.; Cui, S.; Song, L.; Zhang, Q. Research on the Power Management Strategy of Hybrid Electric Vehicles Based on Electric Variable Transmissions. Energies 2014, 7, 934–960. [Google Scholar]
- Louvigny, Y.; Duysinx, J.N.P. Analysis of hybrid hydraulic vehicles and comparison with hybrid electric vehicles using batteries or super capacitors. Proceedings of the EET-2008 European Ele-Drive Conference, International Advanced Mobility Forum, Geneva, Switzerland, 11–13 March 2008.
- Karbaschian, M.A.; Marx, M.; Moulik, B.; Söffker, D. Multiobjective NSGA II-based control optimization of hydraulic and electric hybrid propulsion systems with respect to their dynamic behavior in time domain. Proceedings of the 14nd Antriebstechnisches Kolloquium (ATK), Aachen, Germany, 19–20 March 2013; pp. 641–657.
- Wu, B.; Lin, C.C.; Filipi, Z.; Peng, H.; Assanis, D. Optimal Power Management for a Hydraulic Hybrid Delivery Truck. Int. J. Veh. Mech. Mobil. 2004, 42, 23–40. [Google Scholar]
- Bellman, R.E.; Dreyfus, S.E. Applied Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1962. [Google Scholar]
- Lai, L.; Ehsani, M. Dynamic Programming Optimized Constrained Engine on and off Control Strategy for Parallel HEV. Proceedings of the IEEE Vehicle Power and Propulsion Conference, Beijing, China, 15–18 October 2013; pp. 422–426.
- Lin, C.C.; Kang, J.M.; Grizzle, J.; Peng, H. Energy Management Strategy for a Parallel Hybrid Electric Truck. Proceedings of the American Control Conference, Arlington, VA, USA, 25–27 June 2001; Volume 4, pp. 2878–2883.
- Wang, R.; Lukic, S.M. Dynamic Programming Technique in Hybrid Electric Vehicle Optimization. Proceedings of the IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012; pp. 1–8.
- Stelson, K.A.; Meyer, J.J.; Alleyne, A.G.; Hencey, B. Optimization of a Passenger Hydraulic Hybrid Vehicle to Improve Fuel Economy. Proceedings of the 7th JFPS International Symposium on Fluid Power, Toyama, Japan, 15–18 September 2008.
- Johri, R.; Baseley, S.; Filipi, Z. Simultaneous Optimization of Supervisory Control and Gear shift Logic for a Parallel Hydraulic Hybrid Refuse Truck Using Stochastic Dynamic Programming. Proceedings of the ASME Dynamic Systems and Control Conference an Bath/ASME Symposium on Power and Motion Control, Arlington, VA, USA, 31 October–2 November 2011; Volume 1, pp. 99–106.
- Tate, D.T.; Grizzle, J.; Peng, H. Shortest path stochastic control for hybrid electric vehicles. Int. J. Robust Nonlinear Control 2008, 18, 1409–1429. [Google Scholar]
- Moura, S.J.; Fathy, H.K.; Callaway, D.S. A Stochastic Optimal Control Approach for Power Management in Plug-in Hybrid Electric Vehicles. IEEE Trans. Control Syst. Technol. 2011, 19, 545–555. [Google Scholar]
- Liu, J.; Peng, H. Modeling and Control of a Power-Split Hybrid Vehicle. IEEE Trans. Control Syst. Technol. 2008, 16, 1242–1251. [Google Scholar]
- Sundström, O.; Guzzella, L. A Generic Dynamic Programming Matlab Function. Proceedings of the18th IEEE International Conference on Control Applications Part of 2009 IEEE Multi-conference on Systems and Control, Saint Petersburg, Russia, 8–10 July 2009; pp. 1625–1630.
- Chen, Z.; Mi, C.C.; Xiong, R.; Xu, J.; You, C. Energy management of a power-split plug-in hybrid electric vehicle based on genetic algorithm and quadratic programming. J. Power Sources 2013, 248, 416–426. [Google Scholar]
- Tao, L.; Jincheng, Z.; Shuwen, W.; Fangde, G. Logic Threshold Based Energy Control Strategy for Parallel Hydraulic Hybrid Vehicles. Res. J. Appl. Sci. Eng. Technol. 2013, 6, 2339–2344. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multi objective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar]
- Qing, L.G.; Jie, C.; Fang, X.F. Optimal Design for a Hydraulic Regeneration Propel System of the Hydraulic Hybrid Bus. J. WSEAS Trans. Syst. 2010, 9, 453–462. [Google Scholar]
- Lin, C.C.; Filipi, Z.; Louca, L.; Peng, H.; Assanis, D.; Stein, J. Modelling and control of a medium-duty hybrid electric truck. Int. J. Veh. Des. 2004, 11, 349–370. [Google Scholar]
- Pisu, P.; Rizzoni, G. A Comparative Study Of Supervisory Control Strategies for Hybrid Electric Vehicles. IEEE Trans. Control Syst. Technol. 2007, 15, 506–518. [Google Scholar]
- Kum, D.; Peng, H.; Bucknor, N.K. Supervisory Control of Parallel Hybrid Electric Vehicles or Fuel and Emission Reduction. J. Dyn. Syst. Meas. Control 2011, 133, 102–112. [Google Scholar]
- Filipi, Z.; Louca, L.; Daran, B.; Lin, C.C.; Yildir, U.; Wu, B.; Kokkolaras, M.; Assanis, D.; Peng, H.; Papalambros, P.; et al. Combined optimisation of design and power management of the hydraulic hybrid propulsion system for the 6X6 medium truck. Int. J. Heavy Veh. Syst. 2004, 11, 372–402. [Google Scholar]
- Feng, D.; Huang, D. Modeling and Control of a Series Hydraulic Hybrid Vehicle. J. Comput. Inf. Syst. 2012, 8, 1805–1819. [Google Scholar]
- Kim, Y.; Filipi, Z. Series Hydraulic Hybrid Propulsion for a Light Truck—Optimizing the Thermostatic Power Management. SAE Trans. J. Engines 2007, 116, 1597–1609. [Google Scholar]
- Chen, C.K.; Vu, T.V.; Hung, C.W. System Modeling and Control Strategy Development for a Series Hydraulic Hybrid Vehicle. Proceedings of the International Multi Conference of Engineers and Computer Scientists, Hong Kong, 13–15 March 2013.
- Abdelsalam, A.; Cu, S. A Fuzzy Logic Global Power Management Strategy for Hybrid Electric Vehicles Based on a Permanent Magnet Electric Variable Transmission. Energies 2012, 5, 1175–1198. [Google Scholar]
- Khoucha, F.; Benbouzid, M.E.H.; Kheloui, A. An Optimal Fuzzy Logic Power Sharing Strategy for Parallel Hybrid Electric Vehicles. Proceedings of the IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; pp. 1–5.
- Cheng, C.; McGordon, A.; Jones, R.; Jennings, P.A. Generalised Fuzzy-Logic-Based Power Management Strategy for Various Hybrid Electric Vehicle Powertrain Architectures. Proceedings of the International Conference on Control, Coventry, UK, 7–10 September 2010; pp. 1–6.
- Alipour, H.; Asaei, B.; Farivar, G. Fuzzy Logic Based Power Management Strategy for Plug-in Hybrid Electric Vehicles with Parallel Configuration. Proceedings of the International Conference on Renewable Energies and Power Quality, Santiago de Compostela, Spain, 28–30 March 2012.
- Paganelli, G.; Guerra, T.M.; Delprat, S.; Santin, J.J.; Delhom, M.; Combes, E. Simulation and assessment of power control strategies for a parallel hybrid car. J. Automob. Eng. 2000, 214, 705–717. [Google Scholar]
- Sciarretta, A.; Back, M.; Guzzella, L. Optimal Control of Parallel Hybrid Electric Vehicles. IEEE Trans. Control Syst. Technol. 2004, 12, 352–363. [Google Scholar]
- Delpratm, S.; Guerra, T.M.; Paganelli, G.; Lauber, J.; Delhom, M. Control strategy optimization for an hybrid parallel powertrain. Proceedings of the American Control Conference, Arlington, VA, USA, 25–27 June 2001; Volume 2, pp. 1315–1320.
- Musardo, C.; Rizzoni, G.; Staccia, B. A-ECMS: An Adaptive Algorithm for Hybrid Electric Vehicle Energy Management. Proceedings of the 44th IEEE Conference on Decision and Control and 2005 European Control Conference, Seville, Spain, 12–15 December 2005; pp. 1816–1823.
- Liu, J.; Peng, H. Control Optimization for a Power-Split Hybrid Vehicle. Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006.
- Kutter, S.; Bäker, B. Predictive Online Control for Hybrids: Resolving the Conflict Between Global Optimality, Robustness and Real-Time Capability. Proceedings of the IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; pp. 1–7.
- Kutter, S.; Bäker, B. An Iterative Algorithm for the Global Optimal Predictive Control of Hybrid Electric Vehicles. Proceedings of the IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011; pp. 1–7.
- Gu, B.; Rizzoni, G. An adaptive algorithm for hybrid electric vehicle energy management based on driving pattern recognition. Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Chicago, IL, USA, 5–10 November 2006; pp. 249–358.
- Onori, S.; Serrao, L. On Adaptive-ECMS strategies for hybrid electric vehicles. Proceedings of the International Scientific Conference on Hybrid and Electric Vehicles, Malmaison, France, 6–7 December 2011.
- Lin, C.C.; Peng, H.; Jeon, S.; Lee, J.M. Driving Pattern Recognition for Control of Hybrid Electric Trucks. Int. J. Veh. Mech. Mobil. 2004, 42, 41–58. [Google Scholar]
- Manzie, C.; Watson, H.; Halgamuge, S. Fuel economy improvements for urban driving: Hybrid vs. intelligent vehicles. Transp. Res. Part C 2007, 15, 1–16. [Google Scholar]
- Kim, T.S.; Manzie, C.; Sharma, R. Model Predictive Control of Velocity and Torque Split in a Parallel Hybrid Vehicle. Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 2014–2019.
- Bender, F.A.; Kaszynski, M.; Sawodny, O. Drive Cycle Prediction and Energy Management Optimization for Hybrid Hydraulic Vehicles. IEEE Trans. Veh. Technol. 2013, 62, 3581–3592. [Google Scholar]
- Borhan, H.A.; Vahidi, A.; Phillips, A.M.; Kuang, M.L.; Kolmanovsky, I.V. Predictive Energy Management of a Power-Split Hybrid Electric Vehicle. Proceedings of the American Control Conference, Louis, MO, USA, 10–12 June 2009; pp. 3970–3976.
- Deppen, T.O.; Alleyne, A.G.; Stelson, K.; Meyer, J. Predictive Energy Management for Parallel Hydraulic Hybrid Passenger. Proceedings of the ASME Dynamic Systems and Control Conference, Cambridge, MA, USA, 13–15 September 2010.
- Deppen, T.O.; Alleyne, A.G.; Stelson, K.; Meyer, J. A Model Predictive Control Approach for a Parallel Hydraulic Hybrid Powertrain. Proceedings of the American Control Conference, m, CA, USA, 29 June–1 July 2011; pp. 2713–2718.
- Marx, M.; Söffker, D. Optimization of the Powerflow Control of a Hybrid Electric Powertrain including Load Profile Prediction. Proceedings of the IEEE Vehicle Power and Propulsion Conference, Seoul, Korea, 9–12 October 2012; pp. 395–400.
- Cassebaum, O.; Bäker, B. Predictive Supervisory Control Strategy for Parallel HEVs Using Former Velocity Trajectories. Proceedings of the IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011; pp. 1–6.
- Ripaccioli, G.; Bernardini, D.; Cairano, S.D.; Bemporad, A.; Kolmanovsky, I.V. A Stochastic Model Predictive Control Approach for Series Hybrid Electric Vehicle Power Management. Proceedings of the American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 5844–5849.
- Rizzoni, G.; Guzzella, L.; Baumann, B. Unified modeling of hybrid electric vehicle drivetrains. IEEE/ASME Trans. Mechatron. 1999, 4, 246–257. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).