Fast Estimation of State of Charge for Lithium-Ion Batteries

Abstract

This paper presents a novel impedance-based approach to efficiently estimate the state of charge (SOC) of a Li-ion battery. By using an AC impedance analyzer, a database is constructed, containing records of AC impedance versus SOC. In practical applications, the SOC values can be found instantly once the contents of the database are referenced. For validation purposes, AC impedance comparisons are conducted using AC impedance analyzer as a benchmark at SOC of 0%, 50% and 100%, which indicate errors of 8.636%, 2.604% and 0.600%, respectively.

1. Introduction

As environmental pollution worsens, the development of various types of electric vehicles such as electric bicycles, hybrid vehicles, electric cars, and electric motorcycles, is receiving plenty of attention like never before. All these vehicles are battery powered, and Li-ion batteries are one of the most popular choices for this task. Li-ion batteries have the advantages of high energy density, high power density, low self-discharge, fast charging, high energy weight ratios, no memory effect and high durability [1]. However, there is no easy way to accurately display the battery SOC and acquire information on the current battery status. Definitely, SOC can serve as an indicator to remind users to recharge batteries and to prevent batteries from overcharging [2].

There are a variety of approaches to estimate the SOC for Li-ion batteries. The Coulomb counting method is a commonly seen rechargeable battery capacity estimation method, using an open-loop algorithm and counting the battery charge and discharge capacity. However, this method requires a high accuracy current measurement device and is incapable of performing real-time SOC measurements. Moreover, there is no easy way to acquire the initial SOC values and the defects of larger measurement error accumulation due to uncertain disturbances, leading to an inaccurate estimation [3,4]. The open circuit voltage method measures a family of open circuit voltage curves with the SOC value as a parameter in advance, but it doesn't consider parameter variations in electrochemical batteries and aging effects. Since it requires a long period of rest time after each measurement, it is hence inapplicable to hybrid vehicles applications [5,6]. The Kalman filter method has to build an accurate battery model first, which considers both the open circuit voltage and internal resistance of the battery. Using the built battery model, the open circuit voltage can be formulated, but this model cannot practically simulate the nonlinear dynamic behavior of the plant. In an attempt to achieve high accuracy in SOC estimation, the major disadvantages of the Kalman filter method are that it necessitates an accurate battery model and a complex mathematic operation [7–10].

This paper presents an efficient SOC estimation approach for Li-ion batteries. Using records of the AC impedance versus the SOC value contained in a pre-built database, the SOC value corresponding to the measured AC impedance, can be found instantly. AC impedance comparisons are made with an AC impedance analyzer as a benchmark at SOC of 0%, 50% and 100%, which indicates errors of 8.636%, 2.604% and 0.600%, respectively.

2. AC Impedance Analysis

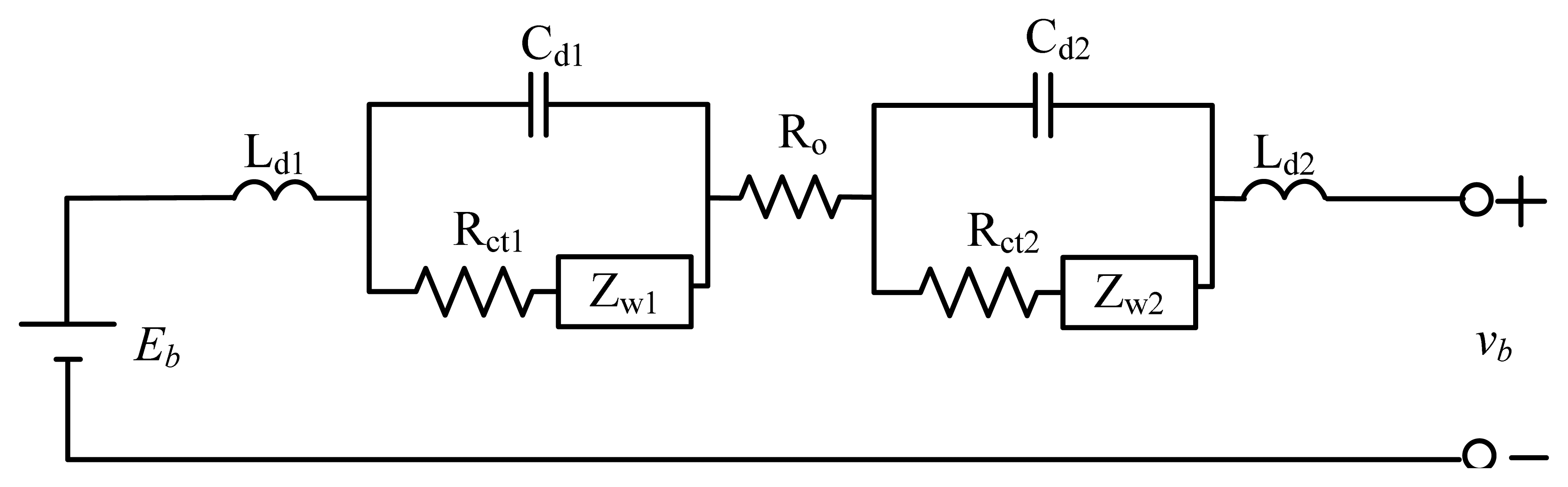
This paper aims are to explore the AC impedance influence of a 18650 Li-ion battery on SOC. Presented in Figure 1 is the complete Li-ion battery AC impedance model for an electrolyte battery where the equivalent AC impedance in the electrochemical process between the anode and cathode is described in detail. In most cases, electrodes are made of porous materials, partially accounting for the electrode impedance at high frequencies [11–13]. Furthermore, curled electrodes used for manufacturing purposes inevitably yield electrode inductances L_d1 and L_d2. R_o represents the ohmic resistance caused by electrode metals, electrolyte and battery terminals. The charge transfer resistance, R_ct1 and R_ct2, indicate the rate of charge delivery on the electrode surface, (i.e., the chemical reaction rate and activation energy on electrodes dominated by materials). The double-layer capacitances, C_d1 and C_d2, refer to the capacitance caused by the valence charges on the electrode surface immersed in electrolyte and ions with opposite charge attached to surface. Double-layer capacitances exist across the electrode-electrolyte interfaces, and vary with temperature, ion concentration and electrode roughness. The Warburg impedance Z_w1 and Z_w2 denotes the reactance caused by ion diffusion, when reactant approaches or combustion products escapes from electrode surface [14–16]. Finally, a battery is modeled as an ideal voltage source E_b in series with the above-stated AC impedance [17–19].

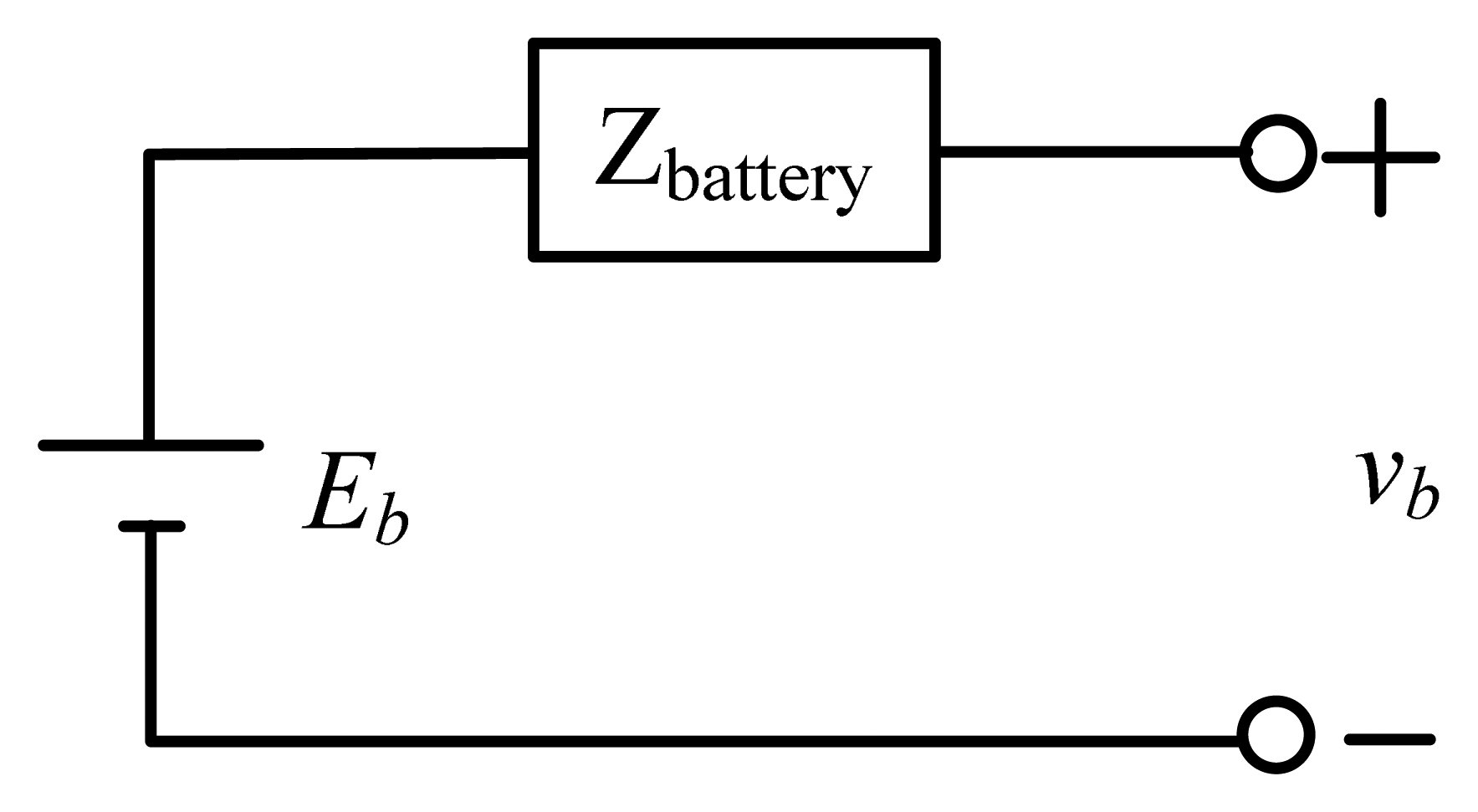
A simplified model of the complete one in Figure 1 is illustrated in Figure 2. Accordingly, a battery is modeled as a cascade of a charge transfer resistance R_ct and a Warburg impedance Z_w, connected in parallel with a double-layer capacitance C_d, then connected in series with an ohmic resistance R_o, an electrode inductance L_d and an ideal voltage source E_b [20].

The Warburg coefficient is expressed as:

$${\overline{Z}}_w={\delta }_w{\mathrm{\omega }}^{-\frac{1}{2}}+j{\delta }_w{\mathrm{\omega }}^{-\frac{1}{2}}$$

(1)

where δ_w and ω denote the ion diffusion coefficient and the angular frequency, respectively. The equivalent impedance of the battery in Figure 2 is written as:

$${\overline{Z}}_{\text{battery}}=\text{R}+j\text{X}$$

(2)

where R and X respectively represent the real and the imaginary parts, and rewritten as:

$$\text{R}={\text{R}}_{\text{o}}+\frac{{\left(\frac{1}{{\mathrm{\omega }\text{C}}_{\text{d}}}\right)}^2\left({\text{R}}_{\text{ct}}+{\delta }_w{\mathrm{\omega }}^{-\stackrel{1}{}/\underset{2}{}}\right)}{{\left({\text{R}}_{\text{ct}}+{\delta }_w{\mathrm{\omega }}^{-\stackrel{1}{}/\underset{2}{}}\right)}^2+{\left({\delta }_w{\mathrm{\omega }}^{-\stackrel{1}{}/\underset{2}{}}-\frac{1}{{\mathrm{\omega }\text{C}}_{\text{d}}}\right)}^2}$$

(3)

$$\text{X}={\mathrm{\omega }\text{L}}_{\text{d}}-\frac{\frac{1}{{\mathrm{\omega }\text{C}}_{\text{d}}}\left[{\left({\delta }_w{\mathrm{\omega }}^{-\stackrel{1}{}/\underset{2}{}}\right)}^2+\left({\delta }_w{\mathrm{\omega }}^{-\stackrel{1}{}/\underset{2}{}}\right)\left(\frac{1}{{\mathrm{\omega }\text{C}}_{\text{d}}}\right)+{\left({\text{R}}_{\text{ct}}+{\delta }_w{\mathrm{\omega }}^{-\stackrel{1}{}/\underset{2}{}}\right)}^2\right]}{{\left({\text{R}}_{\text{ct}}+{\delta }_w{\mathrm{\omega }}^{-\stackrel{1}{}/\underset{2}{}}\right)}^2+{\left({\delta }_w{\mathrm{\omega }}^{-\stackrel{1}{}/\underset{2}{}}-\frac{1}{{\mathrm{\omega }\text{C}}_{\text{d}}}\right)}^2}$$

(4)

The Warburg impedance Z_w is found to demonstrate very little influence on the overall equivalent impedance at high frequencies. The battery can be divided into three frequency parts: a high frequency region at frequencies >1 kHz; an intermediate frequency region frequency between 10 Hz and 1 kHz; a low frequency region at frequency <1 Hz [21]. Since the battery discussed in this work is operated at frequencies beyond 1 Hz, Z_w is hence not taken into account in the simplified model, as illustrated in Figure 3. The simplified model is employed herein for subsequent simulations, as illustrated in Figure 4.

A battery is modeled as an ideal voltage source connected in series with an equivalent impedance, represented as:

$${\overline{\text{Z}}}_{\text{battery}}=\left[{\text{R}}_{\text{o}}+\frac{\frac{{\text{R}}_{\text{ct}}}{{\left({\mathrm{\omega }}_s{\text{C}}_{\text{d}}\right)}^2}}{{{\text{R}}_{\text{ct}}}^2+{\left(\frac{1}{{\mathrm{\omega }}_s{\text{C}}_{\text{d}}}\right)}^2}\right]+j\left[{\mathrm{\omega }}_s{\text{L}}_{\text{d}}-\frac{\frac{{{\text{R}}_{\text{ct}}}^2}{{\mathrm{\omega }}_s{\text{C}}_{\text{d}}}}{{{\text{R}}_{\text{ct}}}^2+{\left(\frac{1}{{\mathrm{\omega }}_s{\text{C}}_{\text{d}}}\right)}^2}\right]$$

(5)

3. Experimental Analysis

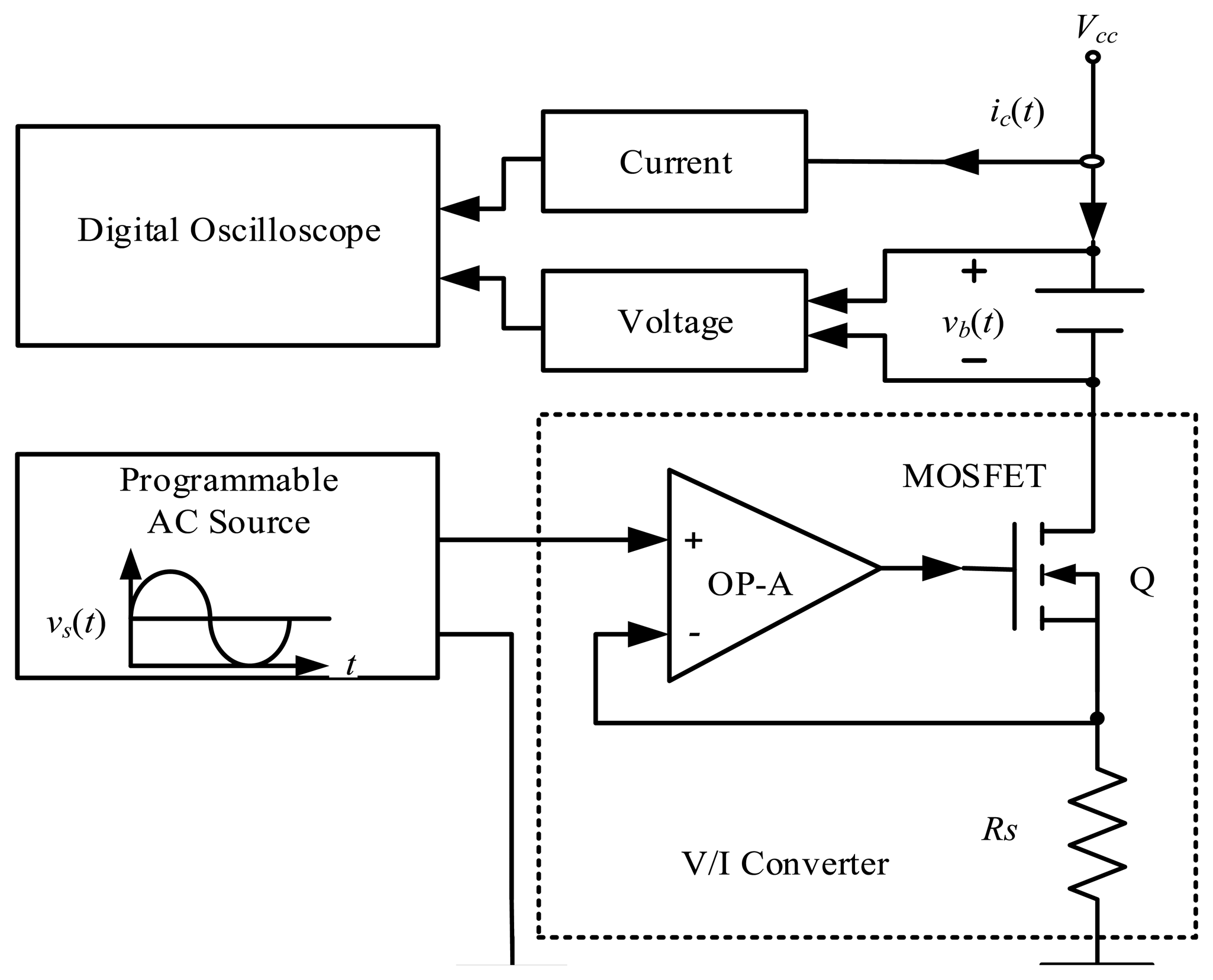
Figure 5 shows the battery SOC test platform. It mainly involves a digital oscilloscope, a current amplifier, a current shunt, a voltage probe(s), a programmable AC source, and a voltage/current converter.

The programmable AC source consists of a signal produced as a unit to specify the charging frequency, while the voltage/current converter is composed of an MOSFET and an operational amplifier (OPA).

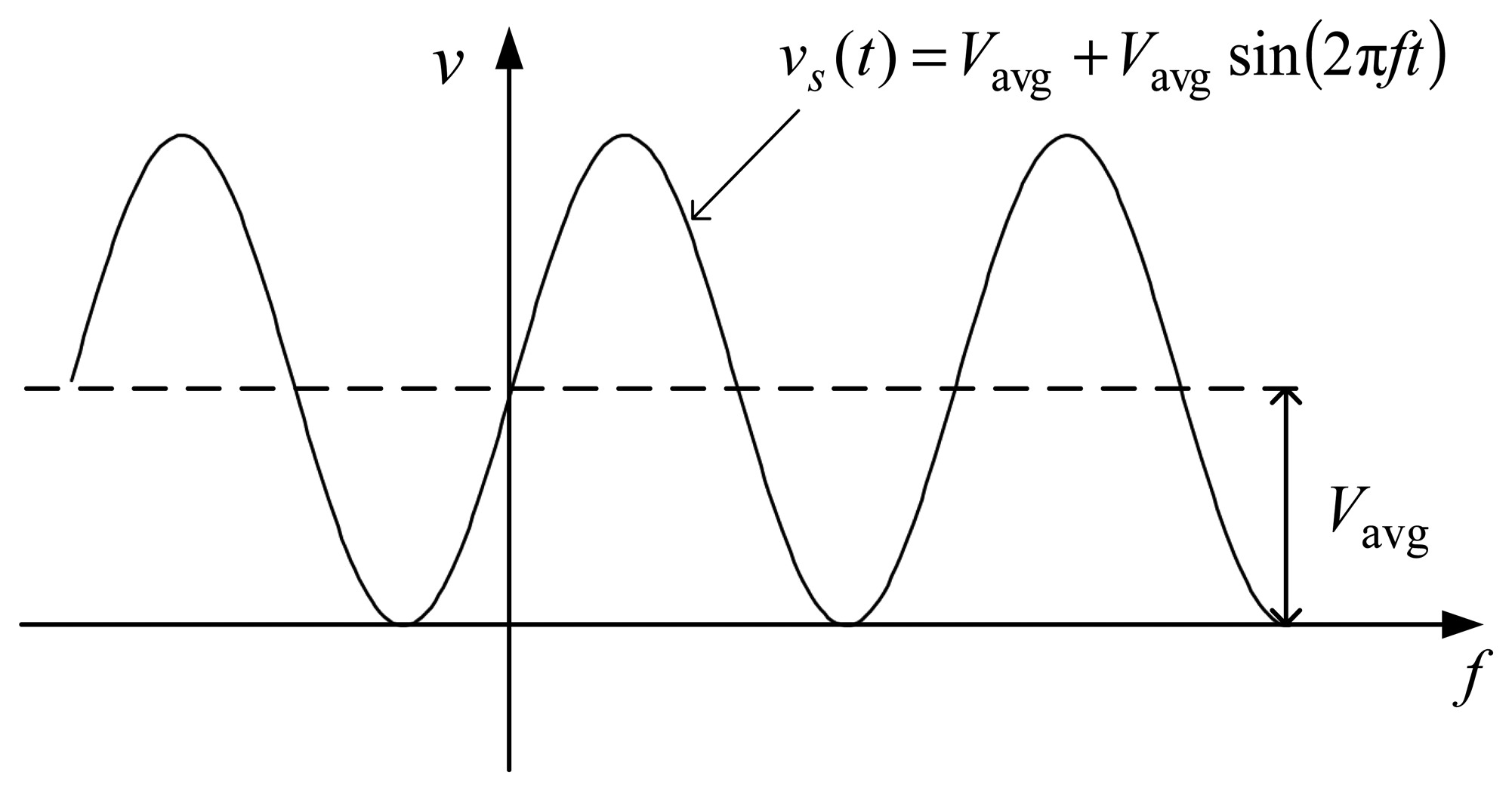
The test platform works as follows: the programmable AC source produces a sinusoidal ripple voltage v_s(t) as follows:

$$v_s(t)=V_{\text{avg}}+V_{\text{avg}}sin\left(2\pi ft\right)$$

(6)

where V_avg stands for the average voltage level. The waveform is shown in Figure 6 Through the voltage/current converter, a sinusoidal ripple current i_c(t) is obtained as:

$$i_c(t)=\frac{v_s(t)}{R_s}=\frac{V_{\text{avg}}+V_{\text{avg}}sin\left(2\pi ft\right)}{R_s}$$

(7)

where R_s is the series resistance in the battery SOC test platform.

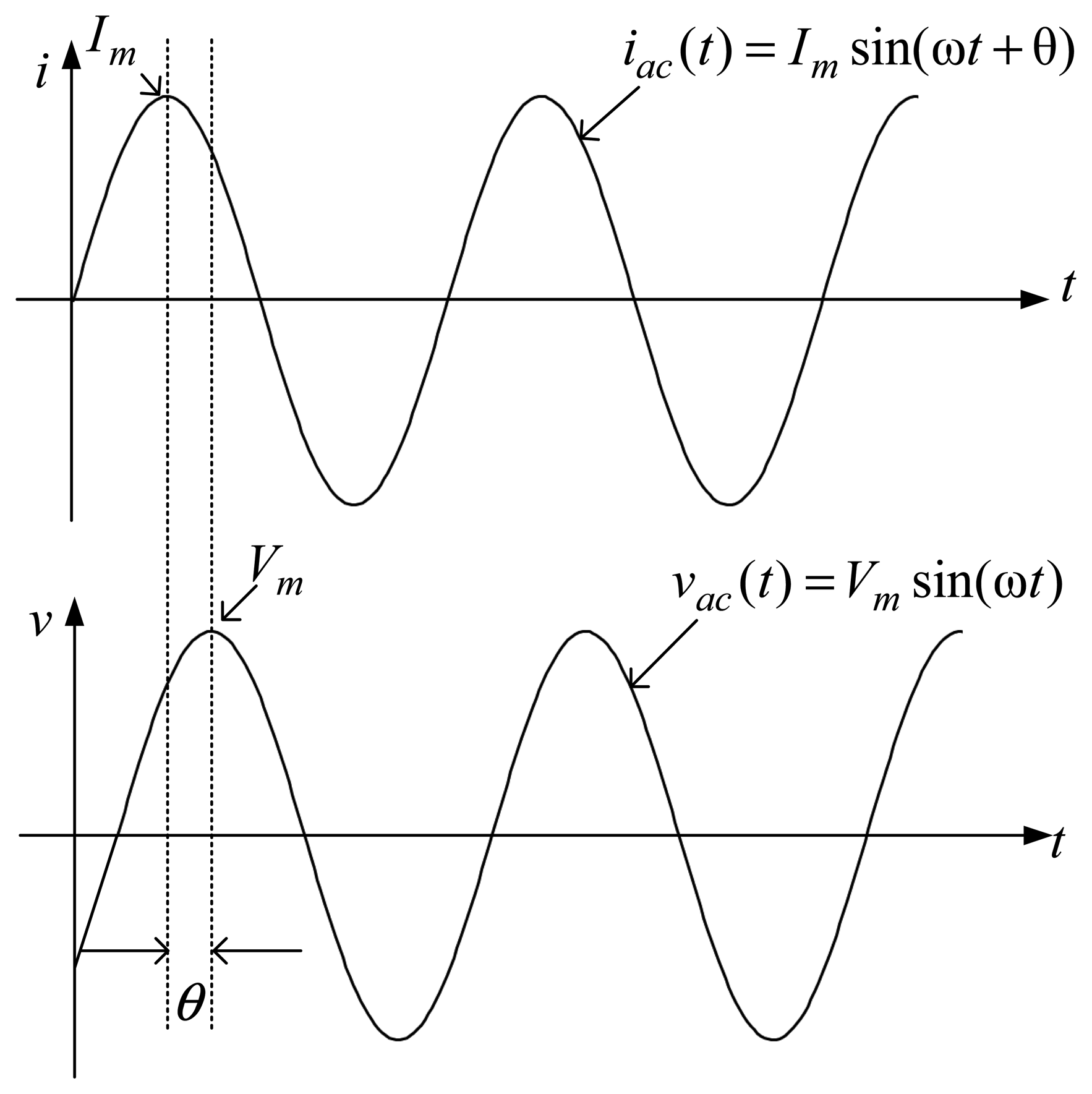
Figure 7 shows the charge current and battery voltage waveforms containing DC components, a low AC current signal, as expressed in Equation (8) and then applied to the battery, sets off an output voltage, as represented in Equation (9):

$$i(t)=I_{dc}+I_{m}sin(\mathrm{\omega }t+\mathrm{\theta })$$

(8)

$$v(t)=V_{dc}+V_{m}sin(\mathrm{\omega }t)$$

(9)

where I_dc is equal to I_m.

The filtered waveforms, i_ac(t) and v_ac(t), are illustrated in Figure 8, respectively expressed as:

$$i_{ac}(t)=I_{m}sin(\mathrm{\omega }t+\mathrm{\theta })$$

(10)

$$v_{ac}(t)=V_{m}sin(\mathrm{\omega }t)$$

(11)

According to Equations (10) and (11), the ratio of v_ac(t) to i_ac(t) gives the AC impedance, represented as:

$$\overline{Z}=\frac{V_m}{I_m}\angle -\mathrm{\theta }$$

(12)

Expressing Equation (12) in complex form, the battery impedance can be expressed as:

$$\overline{Z}=Z^{\prime }-j{Z}^{″}=\left|Z\right|\angle -\mathrm{\theta }$$

(13)

where Z′ represents the real part of the complex; Z″ represents the imaginary part of the complex; |Z| represents the magnitude of AC impedance; and θ represents the angle of AC impedance [22–24].

The AC impedance of an 18650 battery can be expressed on the complex plane in several forms. Figure 9 exhibits the Nyquist plot of a battery. A review of Figure 9 reveals that the battery internals are resistive, inductive and capacitive components, and the capacitive components of the Nyquist plot of a battery is presented in a semicircle case [25–27].

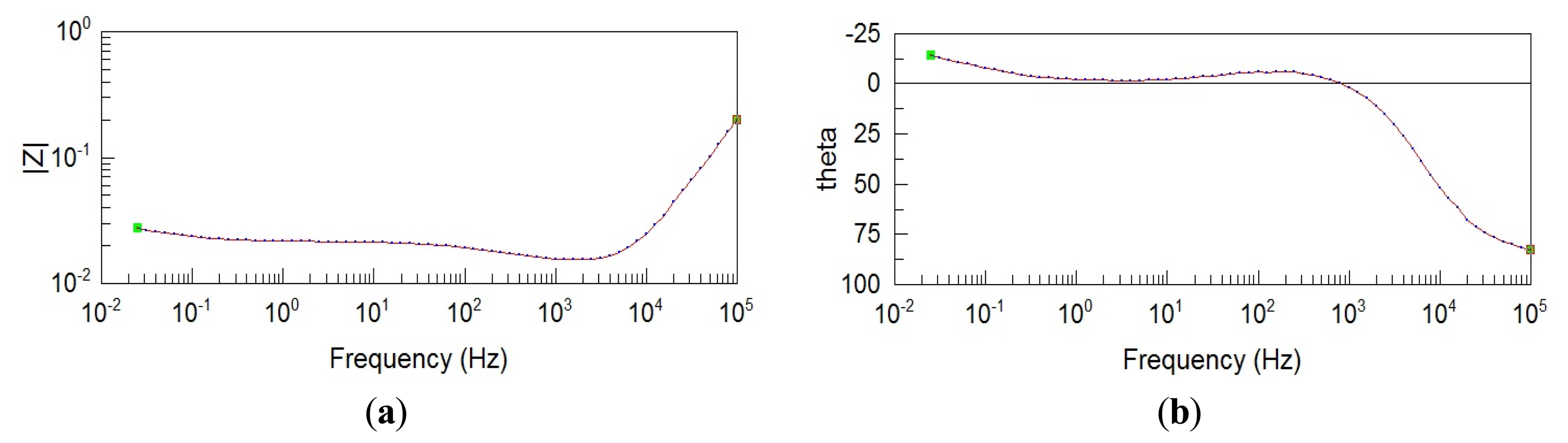
Figure 10a,b shows the AC impedance spectrum of test battery measured by the Solartron 1280 B AC impedance Bode plot analyzer.

4. Experimental Process

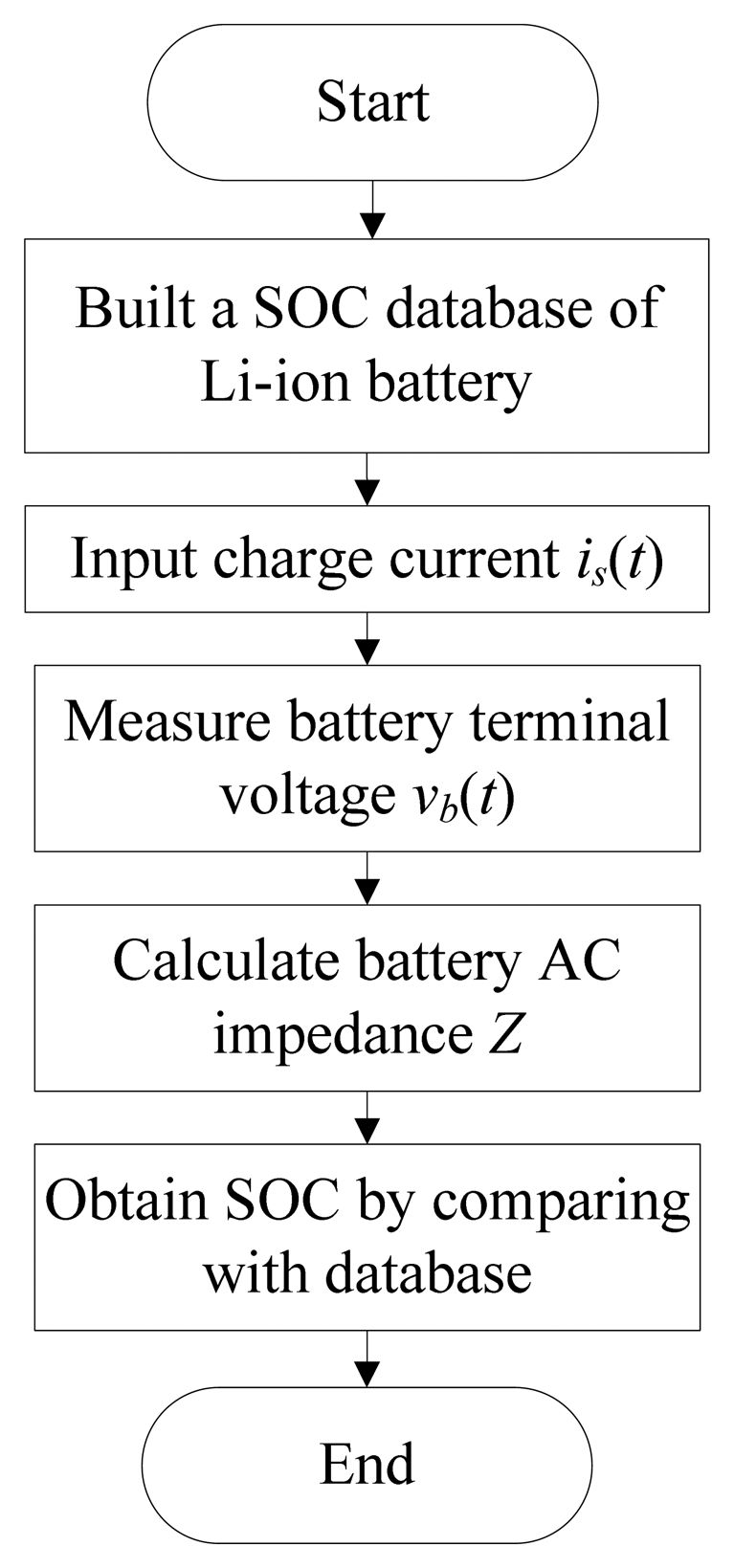
Figure 11 shows the flow chart of the presented SOC estimation approach for Li-ion battery proposed in this paper. As the first step, a database containing records of AC impedance versus SOC for a 18650 Li-ion battery is built using an AC impedance analyzer. Subsequently, the impedance Z, as stated in the preceding section and then measured in the presented test platform, is compared with the contents in the constructed database for the corresponding SOC value. Since the SOC value is fully determined by the measured AC impedance in this work, there is a definite need to perform high accuracy measurements. Tabulated in

Table 1. Apparatus.

Apparatus	Type
Digital Oscilloscope	GW GDS-1152A-U
Programmable AC Source	GW AFG-2025
Power Supply	GW GPS-3303
Shunt	SH-0002A-200
AC Impedance Analyzer	Solartron 1280B
Digital Oscilloscope	GW GDS-1152A-U
Programmable AC Source	GW AFG-2025

are the measurement facilities employed, and presented in Figure 12 is a photo of the experimental setup. Besides, exhibited in Figure 13 is a photo of the AC impedance analyzer employed for a database construction, a device comprising an impedance recorder and a voltage and current perturbator.

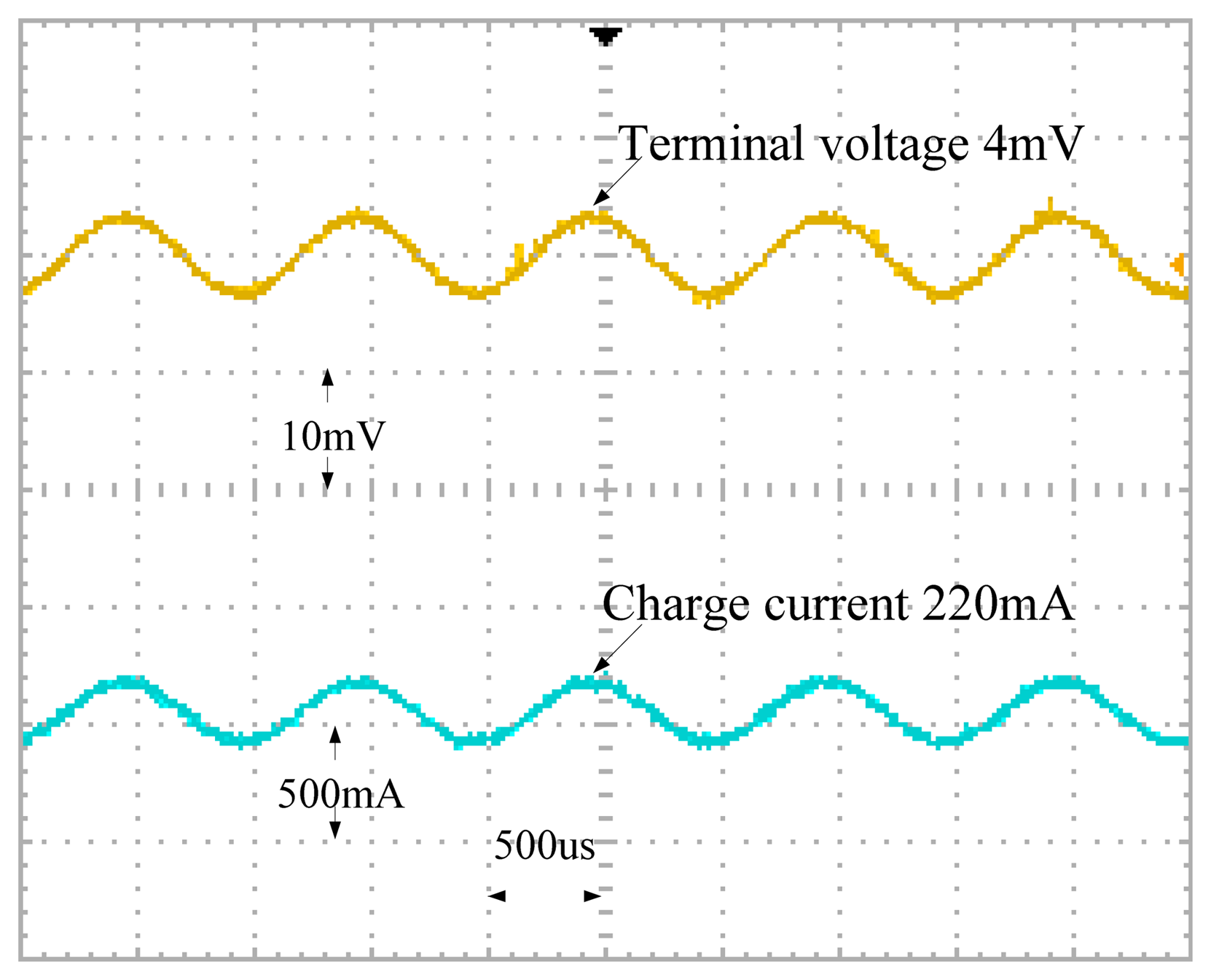
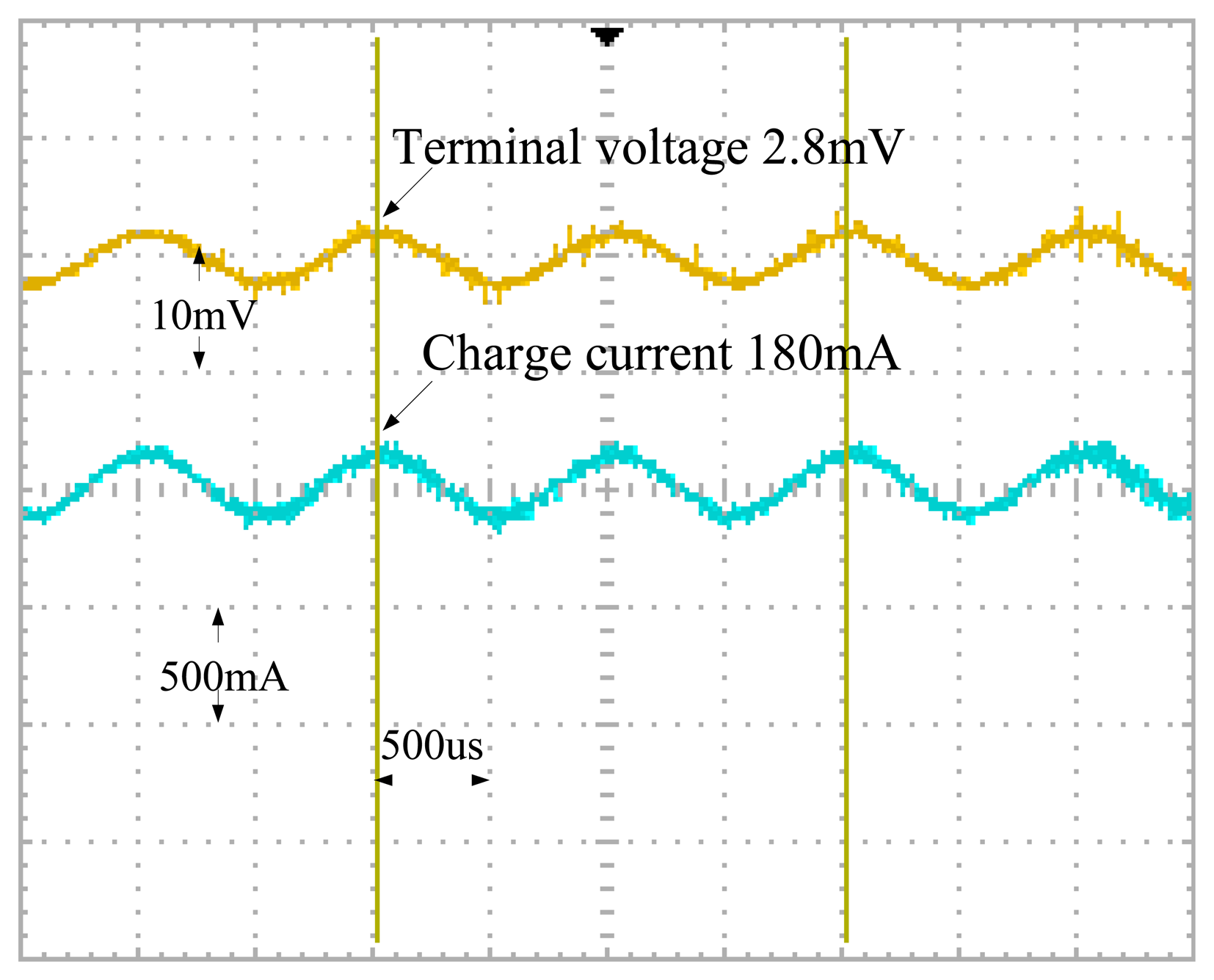
Figure 14 shows an illustration of the charge current and the battery terminal voltage waveforms in an AC impedance measurement. Enlargement of the waveforms in Figure 14 with DC components filtered indicates that both waveforms only contain AC components, as demonstrated in Figure 15.

The AC impedance measurement of an 18650 Li-ion battery can be made in real time using the charge current and the battery voltage waveforms, and the SOC is available instantly once the contents of a pre-built database are referenced.

5. Experiment Result

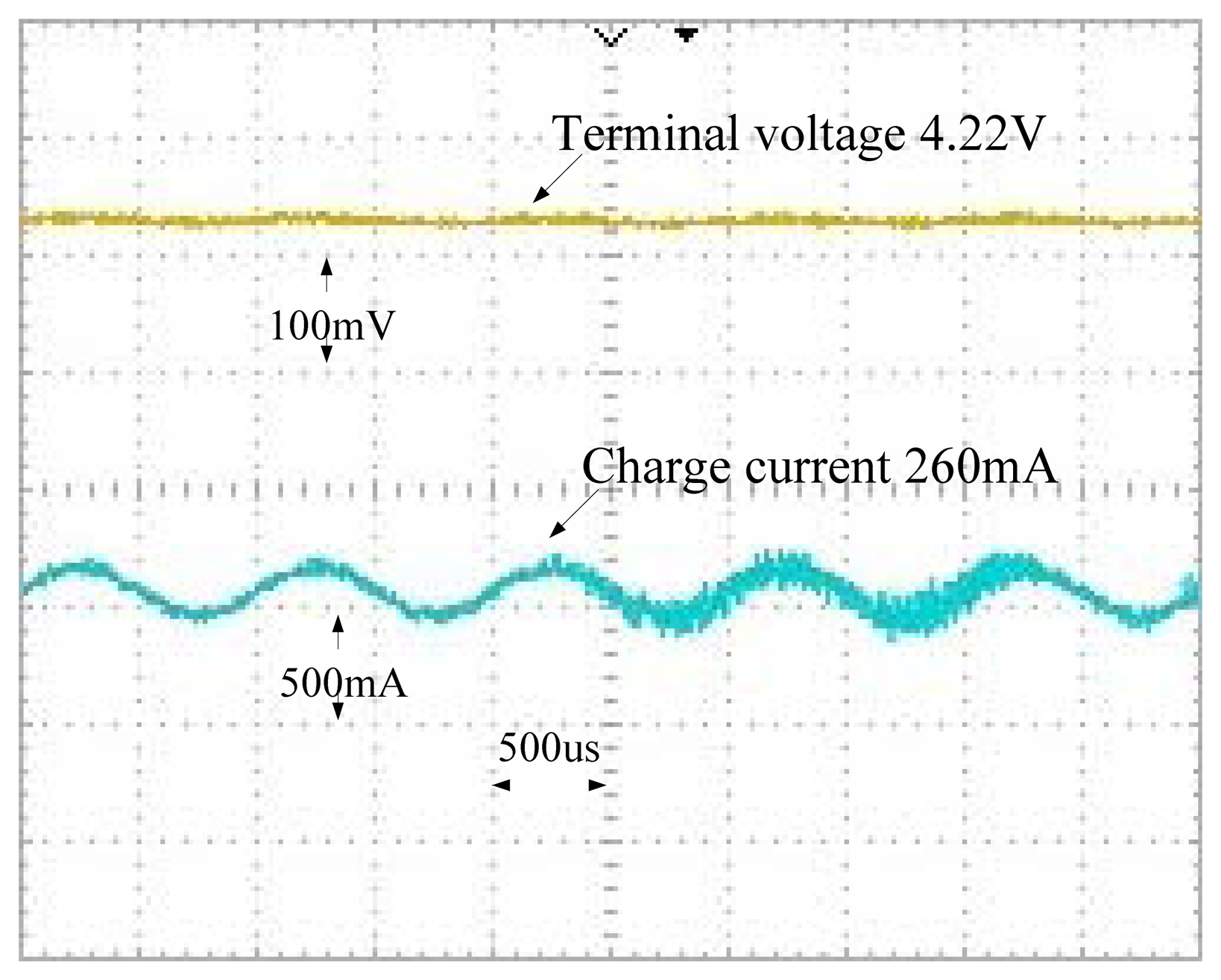
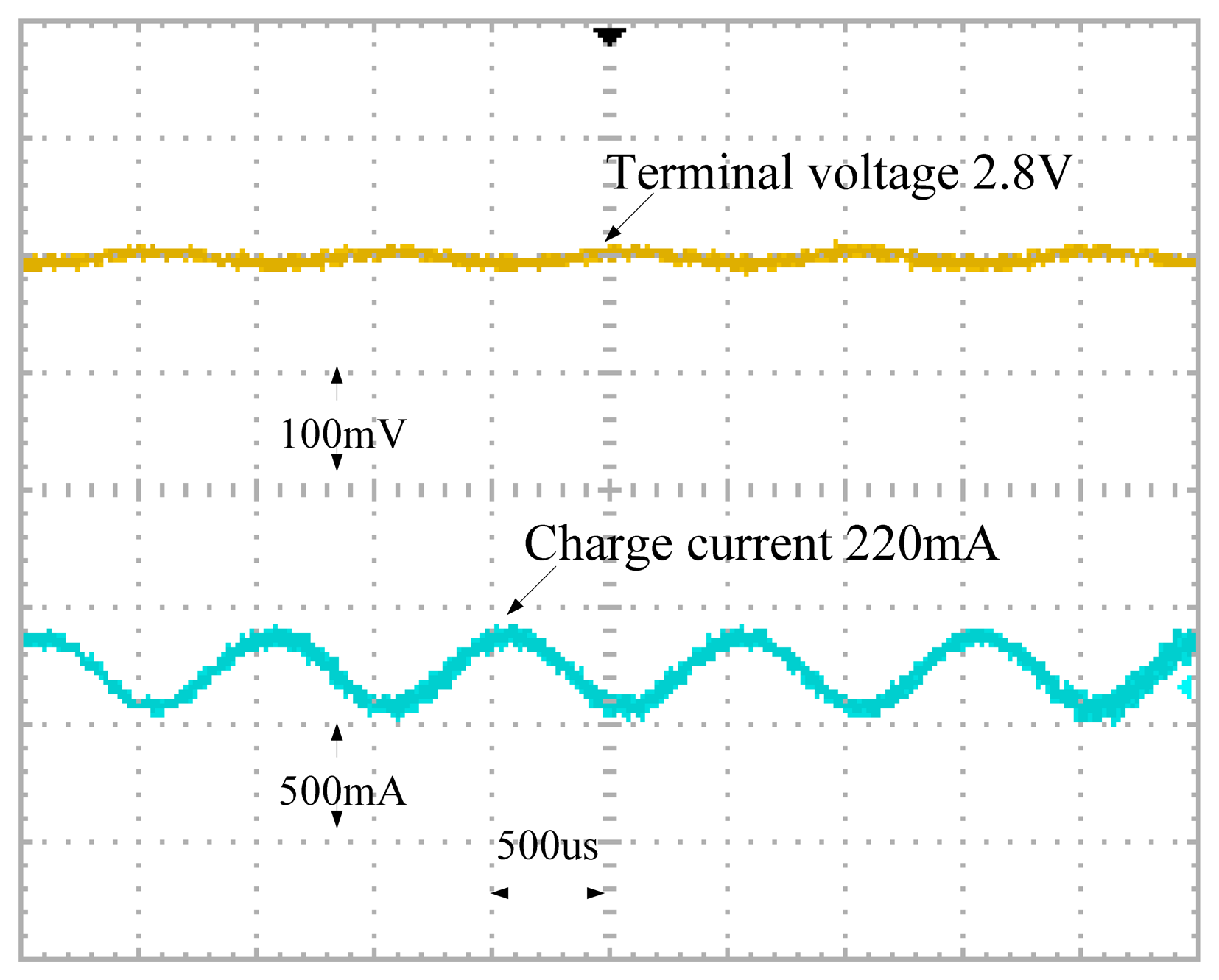
An IBR18650BC Li-ion battery is employed as a battery under test in this work. Cases with open circuit output voltage of 2.8 V, 3.7 V and 4.2 V are treated as the 0%, 50% and 100% SOC cases, respectively. Figures 16 and 17 show the unfiltered and filtered charge current and battery output voltage waveforms in the 0% SOC case, respectively.

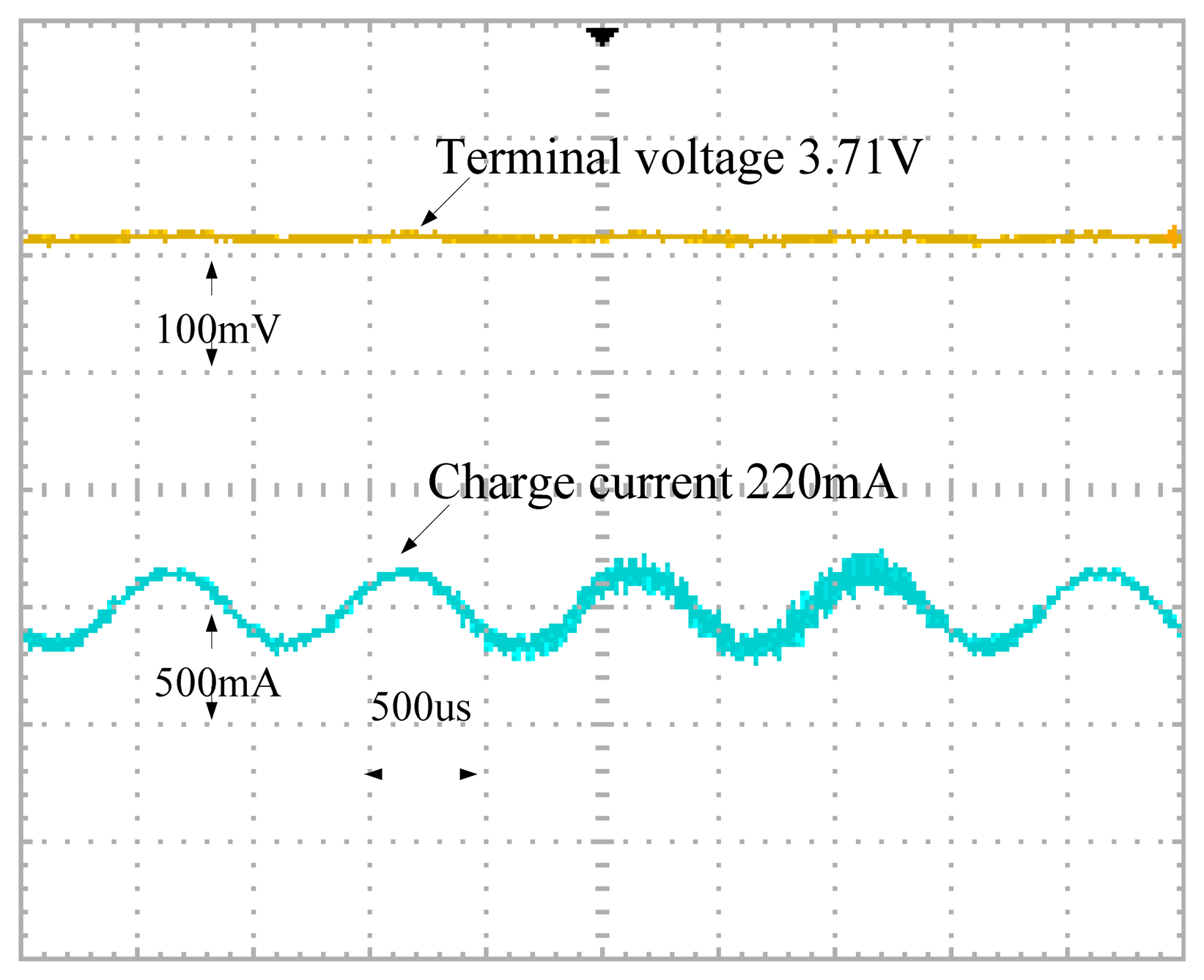
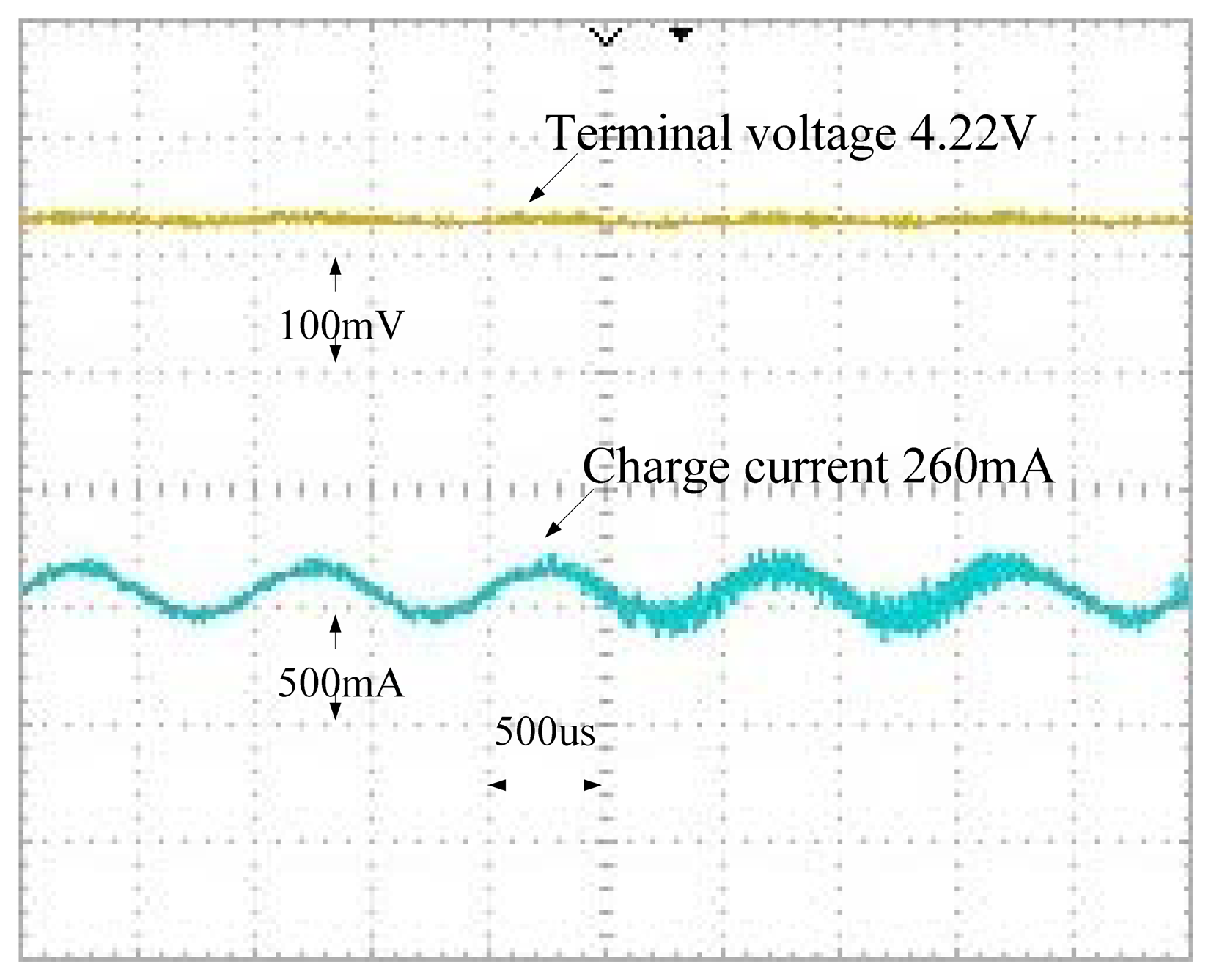
Figures 18 and 19 are the unfiltered charge current and battery output voltage waveforms in the 50% and 100% SOC cases, while in Figures 20 and 21 are the filtered versions of Figures 18 and 19, respectively.

Figure 20 shows the filtered waveforms corresponding to an AC impedance of 0.01556 Ω. Figure 21 shows the filtered waveforms corresponding to an AC impedance of 0.01556 Ω.

Table 2. Accuracy comparison of proposal method and ITRI database.

SOC	Proposal values (Ω)	Database values (Ω)	Error (%)
SOC 0%	0.02000	0.018410	8.636
SOC 50%	0.01556	0.015165	2.604
SOC 100%	0.01556	0.015654	0.600

shows the AC impedance compared with a database, provided by the Industrial Technology Research Institute (ITRI), Taiwan, as a benchmark. AC impedance errors are 8.636%, 2.604% and 0.6% in the 0%, 50% and 100% SOC cases, respectively.

Figure 22 shows the accuracy comparison of AC impedance values measured by the proposed method and ITRI at various battery SOC. Figure 23 shows the estimation errors of the AC impedance value.

6. Conclusions

This paper presents a novel approach to efficiently estimate SOC. As the first step, the AC impedance measurement of an 18650 Li-ion battery is made in a test platform at various values of SOC, and then a database is built accordingly. In practical uses, the pre-built database is referenced instantly to locate the corresponding SOC value, once the AC impedance of a battery under test is found experimentally. For validation purposes, an impedance comparison between this proposal and ITRI database is made in three cases. AC impedance errors of 8.636%, 2.604% and 0.600% are seen at SOC of 0%, 50% and 100%, respectively.