Influence of Three Dynamic Predictive Clothing Insulation Models on Building Energy Use, HVAC Sizing and Thermal Comfort
Abstract
: In building energy simulation, indoor thermal comfort condition, energy use and equipment size are typically calculated based on the assumption that the clothing insulation is equal to a constant value of 0.5 clo during the cooling season and 1.0 clo during the heating season. The assumption is not reflected in practice and thus it may lead to errors. In reality, occupants frequently adjust their clothing depending on the thermal conditions, as opposed to the assumption of constant clothing values above, indicating that the clothing insulation variation should be captured in building simulation software to obtain more reliable and accurate results. In this study, the impact of three newly developed dynamic clothing insulation models on the building simulation is quantitatively assessed using the detailed whole-building energy simulation program, EnergyPlus version 6.0. The results showed that when the heating ventilation and air conditioning system (HVAC) is controlled based on indoor temperature the dynamic clothing models do not affect indoor operative temperatures, energy consumption and equipment sizing. When the HVAC is controlled based on the PMV model the use of a fixed clothing insulation during the cooling (0.5 clo) and heating (1.0 clo) season leads to the incorrect estimation of the indoor operative temperatures, energy consumption and equipment sizing. The dynamic clothing models significantly (p < 0.0001) improve the ability of energy simulation tools to assess thermal comfort. The authors recommend that the dynamic clothing models should be implemented in dynamic building energy simulation software such as EnergyPlus.1. Introduction
The amount of thermal insulation worn by a person has significant influences on thermal comfort [1]. The thermal insulation provided by garments and clothing ensembles is measured in clo. 1.0 clo is equal to 0.155 m2 °C/W. For near-sedentary activities where the metabolic rate is approximately 1.2 met, the effect of changing clothing insulation on the optimum operative temperature is approximately 6 °C/clo [1], indicating that clothing is one of the most important thermal comfort adjustments available to building occupants [2]. Clothing value is one of the six variables affecting the determination of the predicted mean vote (PMV) and predicted percentage of dissatisfied (PPD) [3] and thus it is an important input for thermal comfort determination in a variety of international thermal comfort standards [1,4,5].
Due to the significance of the clothing in thermal comfort and HVAC system operation, a number of studies on the topic have been carried out thus far. Havenith et al. [6] discussed the representation and measurement of clothing parameters and metabolic rate in the PMV context. It was observed that the impacts of body motion and air movement are relevant and thus they must be taken into account for the comfort prediction related to the clothing insulation [6]. Gauthier and Shipworth showed that in the PMV-PPD calculations the most influential parameter are the metabolic activity and the clothing insulation [7]. Morgan and de Dear examined clothing behaviour and its relationship with thermal environments in shopping mall and call centre [8]. They found that day-to-day variation in clothing levels changed significantly in the shopping mall where a dress code was not in place, compared to the call centre where a dress code was forced. For the shopping mall they developed a linear regression equation to relate the daily average clothing value with daily mean outdoor dry bulb temperature [8]. Toftum et al. [9] evaluated the consequences for occupant performance and energy consumption of controlling the indoor condition according to the adaptive comfort model and conventional PMV model. The adaptive comfort model takes into account the adaptation of occupants to the outdoor conditions in naturally ventilated buildings such as changing their clothing insulations. For the quantitative evaluation of the occupant performance, Bayesian Network theory, suggested by Jensen et al. [10], was combined with dynamic simulation of the indoor environment and of the energy consumption as well as with dose–response relationships between indoor climate parameters and mental performance. As a result of simulations for two building configurations with and without mechanical cooling, it was found that occupant performance differed only modestly between configurations despite the significant difference in indoor temperatures and that energy consumption was always lower in buildings without mechanical cooling, indicating that determining acceptable indoor thermal environments with the adaptive comfort model may result in significant energy savings without having large consequences for the occupant performance [10]. De Carli et al. [11] developed single variable linear regression models to predict the clothing insulation as a function of the outdoor air temperature measured at 6 o'clock in the morning. They concluded that a variation of 0.1 clo is sufficient to significantly change the comfort evaluation in mechanically conditioned buildings [11].
In most building energy simulations, thermal comfort condition is calculated based on the assumption that the clothing insulation is equal to a constant value of 0.5 clo during the cooling season and 1.0 clo during the heating season. Usually those two values are used and the change from 0.5 to 1 or vice-versa is made suddenly from one day to another. In addition, there is no standardized guideline on how to set clothing insulation schedules in the international standards. This simplified assumption may lead to systems that are incorrectly sized and operated. In reality, occupants frequently adjust their clothing depending on the thermal conditions around them as discussed in other literature above, as opposed to the assumption of constant clothing values. Therefore, the clothing insulation variation should be captured during the building simulation to realistically model HVAC systems. In order to overcome the limitations of the constant clothing insulation assumption, three new predictive clothing insulation models were developed by Schiavon and Lee based on 6333 selected observations taken from ASHRAE RP-884 and RP-921 databases [12–15]. The first and third models vary the clothing insulation as a function of outdoor air temperature measured at 6 o'clock and the second model takes into account both 6 o'clock outdoor air temperature and indoor operative temperature when adjusting the clothing insulation [13].
In this study, the three newly developed predictive clothing insulation models are implemented into a customized version of the detailed whole-building energy simulation program, EnergyPlus version 6.0. The aim of this study is to assess the influence of the three dynamic models on energy use, equipment size and thermal comfort.
2. Predictive Model Description and Implementation into EnergyPlus
2.1. Predictive Clothing Models Description
Two new predictive clothing insulation models were developed by Schiavon and Lee [13] based on 6333 selected observations taken from the ASHRAE RP-884 and RP-921 databases. There are a variety of possible variables that may affect the clothing insulation such as metabolic activity, sex, HVAC system type, indoor operative temperature, relative humidity, outdoor condition, air velocity, season and location, etc. The full list of the variables that were investigated for the screening process is summarized in [13]. A multivariable mixed model method was used to develop the regression equations. Among the variables that can possibly affect occupants' clothing, outdoor air temperature measured at 6 o'clock and indoor operative temperature were chosen due to their highest ability to predict the clothing insulation level. Two predictive models are reported in Equations (1) and (2):
2.2. A Clothing Insulation Model for Thermal Comfort Standards
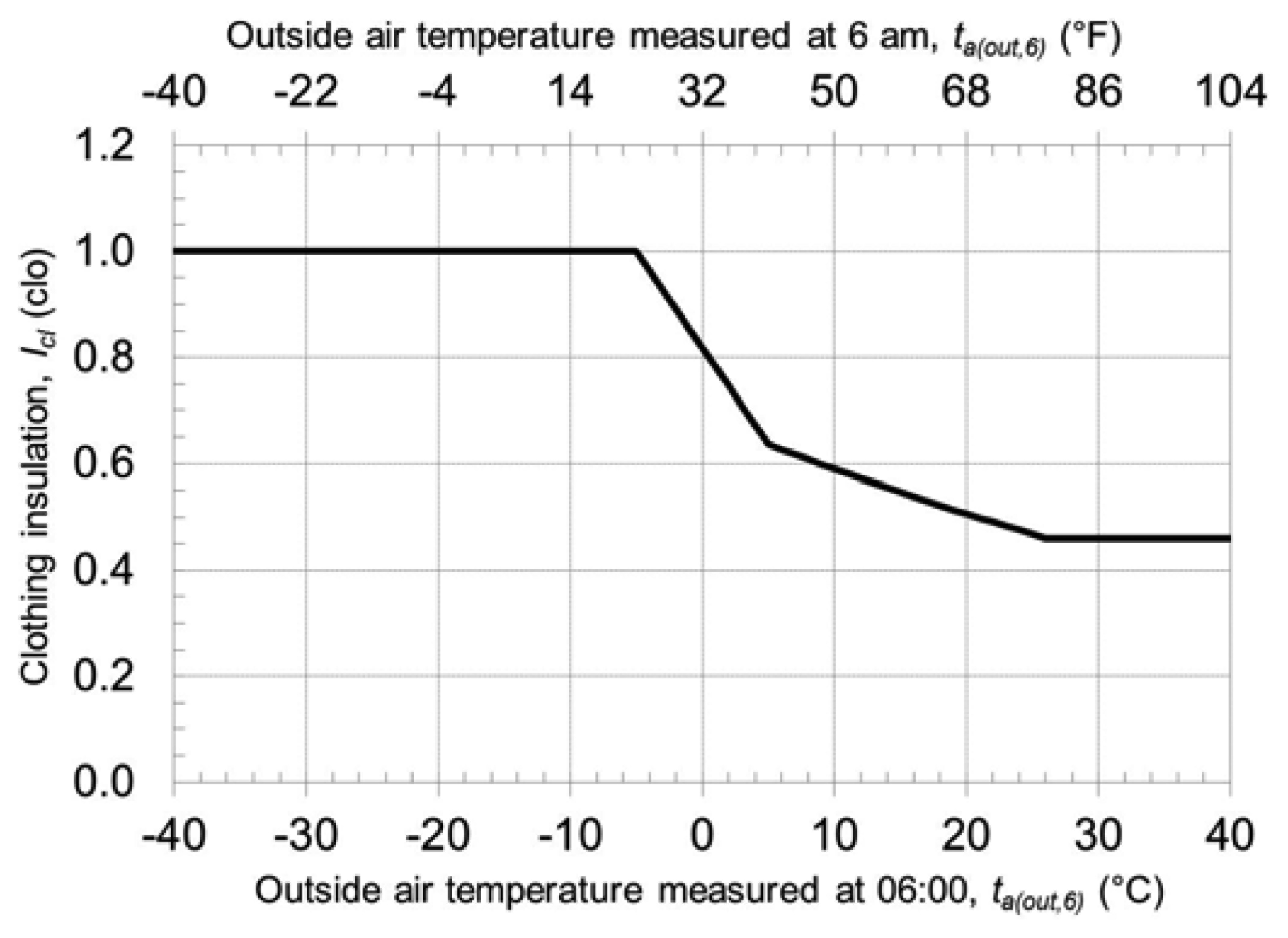
In thermal comfort standards is suggested to use 1 clo for winter conditions and 0.5 clo for summer conditions. A dynamic model to predict clothing insulation is needed but the models proposed in the previous paragraph are not suited to be implemented directly in thermal comfort as explained in [1]. The following adapted model is proposed for being implemented in thermal comfort standards:
The proposed model is plotted in Figure 1.
2.3. Implementation into EnergyPlus
The three models have been implemented into EnergyPlus. EnergyPlus is a relatively new building performance simulation program having greater capabilities than other software [16]. It calculates the surface temperatures in each time step by performing a detailed heat balance including the radiant heat exchange between surfaces and occupants, which directly affects the thermal comfort. EnergyPlus automatically performs the detailed heat, air, surface and energy balances within the whole building. All the modes of heat loss from the body are automatically taken into account including the convection and radiant heat loss from the outer surface of the clothing, the heat loss by water vapor diffusion through the skin, the heat loss by evaporation of sweat from the skin surface, the latent and dry respiration heat loss and the heat transfer from the skin to the outer surface of the clothing [17].
It should be noted that the three new models are not implemented into the official release version of EnergyPlus but into the customized version used only for this study. Despite the implementation into the customized version, the source codes written in Fortran 90 programming language were successfully modified and validated. The unexpected hurdle during the implementation process was coupling the clothing insulation with 6 o'clock outdoor air temperature. Since 6 o'clock temperature is not the value that varies in each time-step, i.e., it is a fixed value every day based on the outdoor air temperature at a specific time, unlike other parameters such as indoor operative temperature which varies hourly or sub-hourly, coupling clothing value and 6 o'clock temperature was not straightforward in EnergyPlus code structure. On the other hand, the source code related to the complicated system and plant modules did not need to be modified. Only the thermal comfort related modules and subroutines needed to be modified to implement the new predictive models. To assess the correctness of the implementation of the three models into EnergyPlus they were validated against the results obtained using Equations (1)–(3) implemented in a Microsoft Excel worksheet. The three clothing value sets exactly matched each other without any discrepancies, indicating that the new models are properly implemented into EnergyPlus.
3. Methods
3.1. Description of the Simulated Building
A three-story prototype office building located in Chicago (IL, USA) having a rectangular shape and aspect ratio of 1.5 was chosen for this study. The floor plate size is 2000 m2 (total floor area is 6000 m2) and each floor is composed of an interior zone and four perimeter zones with a perimeter zone depth of 4.6 m. The floor to floor height is 3.96 m and the return plenum height is 1.2 m. Strip windows are evenly distributed in the walls and the window-to-wall ratio is 40%. The constructions and the thermal properties of windows comply with ASHRAE 90.1-2010 [18].
3.2. Internal Heat Gains
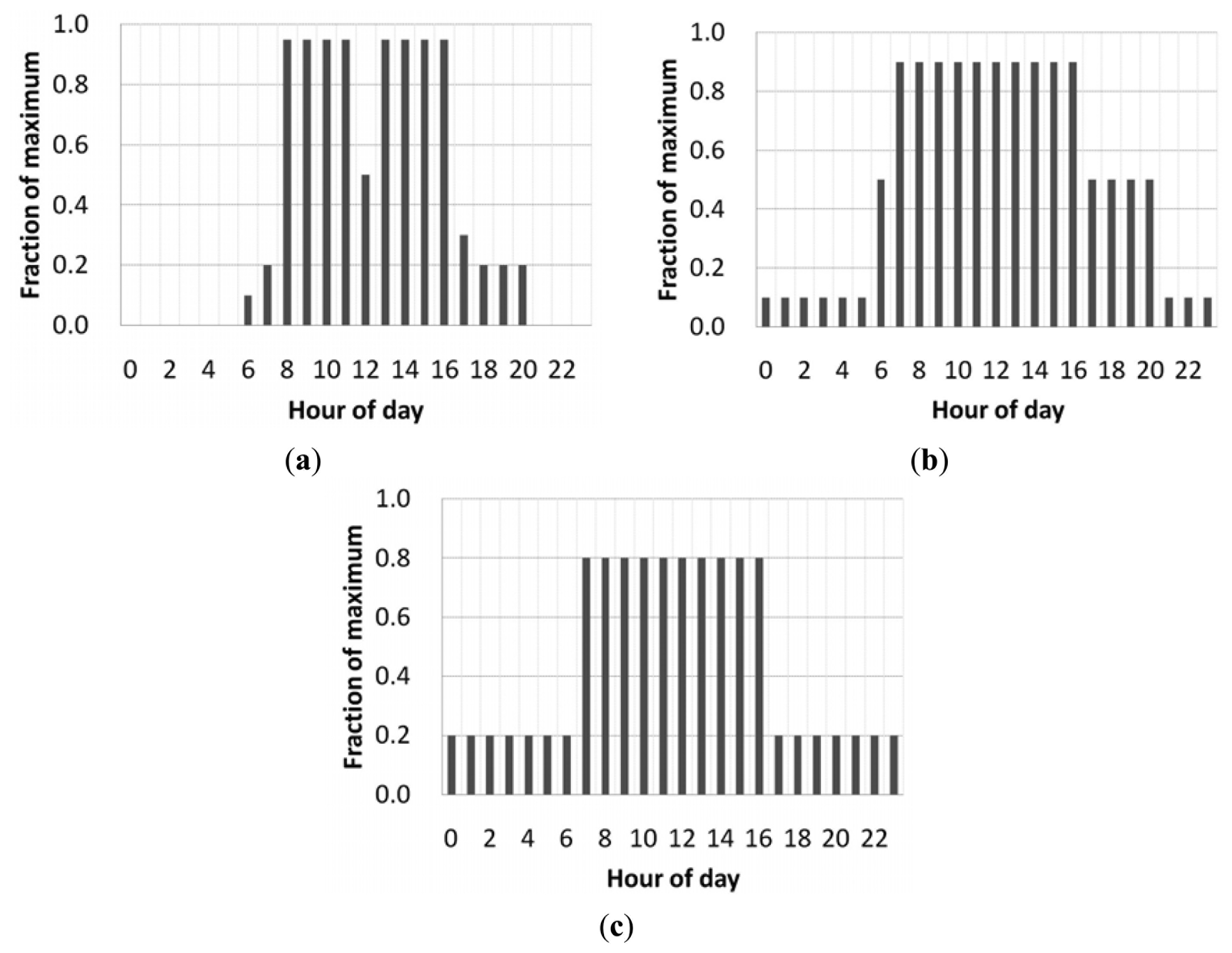
The peak internal load levels of the baseline case are summarized in Table 1 and the hourly variations of the internal loads for the typical office building follow the schedules specified in ASHRAE Standard 90.1 [18], which are shown in Figure 2. The metabolic rate for office workers was assumed to be 100 W/person in Table 1. HVAC systems operate from 5:00 to 19:00 during the weekdays. It is off during weekends.
3.3. HVAC System, Ventilation Rate and Indoor Set-points
The HVAC system is switched off during the nighttime. The infiltration was assumed equal to 3.33 × 10−4 m3/(sm2) (flow per exterior surface area) which was equal to 0.26 ACH in perimeter zones. The minimum outdoor air flow rate was set to be 0.762 L/(sm2) at both system and zone levels which was equal to 7.08 L/s per person and was provided whenever the system was turned on [16]. Each zone is served by the conventional variable air volume (VAV) terminal unit. EnergyPlus object of AirTerminal:SingleDuct:VAV:Reheatis used for the realistic modeling of VAV unit [19]. After getting the conditioned air supplied from the central air handling unit (AHU), VAV unit in each zone have slightly different control logics between cooling and heating mode. In the cooling mode, the airflow is adjusted to meet the cooling load with the discharge air temperature fixed at the AHU supply air temperature (SAT) set-point. In the heating mode, the hot water flow through the reheat coil and the resultant discharge air temperature are adjusted with the airflow fixed at the minimum airflow of 0.762 L/(sm2). At the system level, a single variable-speed central station AHU serves the building and is composed of economizer, chilled water cooling coil, hot water heating coil and supply fan. AHU SAT was set to be 14.0 °C. The central plant consists of a centrifugal chiller, a gas fired boiler, variable speed pumps and a two-speed cooling tower. Details of system and plant inputs are summarized in Table 2. In Cases 1–4 (see Table 3) PMV is used as the indoor set-point to control the occupant space to quantitatively assess the impact of the predictive clothing insulation models. EnergyPlus uses an iteration method over the entire HVAC system in order to converge the system controllers based on the PMV set-point [17]. The iteration proceeds and the system controllers are simulated in sequence until the calculated PMV value in each thermal zone matches the set-point within the specified tolerance. During this sequence of iterative solutions, the supply air and water mass flow rates are held constant. The controllers are converged by the method of interval halving, which was chosen for its robustness [17]. The cooling and heating PMV set-points were set at 0.5 and −0.5, respectively. In cases 5 to 11 the HVAC system is trying to keep the operative temperature between 20 °C and 26 °C. These cases represent a more common control of buildings.
3.4. Simulated Cases
Eleven cases were studied. The baselines are the Cases 1 and 5 in which the assumption of constant clothing values was used. In Case 2 the model relating the clothing insulation to the outdoor air temperature measured at 6 o'clock (Equation (1)) is studied. In Case 3 the model relating the clothing insulation to both 6 o'clock outdoor air and indoor operative temperatures (Equation (2)) is studied. In Case 4 the model suggested for implementation in thermal comfort standards (Equation (3)) is studied. Cases 5–8 are equal to Cases 1–4 respectively except for the control of the system. In Cases 1–4 the zone temperature is controlled based on PMV. This control gives the same comfort conditions and allows assessing the influences of the models on the energy use and equipment size. The thermal comfort variable is kept out. This is not a realist method of controlling buildings. In Cases 5–8 the zone operative temperature is kept between 20 °C and 26 °C. These are more realistic cases. The energy use and the size of the equipment will be the same and the thermal comfort would be different. In Cases 9–11 the influences of adding a chair to clothing insulation values calculated with Equations (1)–(3) are investigated. In all the eleven simulation, the met activity was fixed equal to 1.15 met and air velocity to 0.2 m/s. The simulated cases are summarized in Table 3.
3.5. Sensitivity Analysis
As a final step of this study, a sensitivity analysis is performed for the parameters that could affect the difference in the energy performance related to two clothing assumptions, Schedule and Equation (2). The parameters under consideration are climatic condition, internal load level and window-to-wall ratio. Four climatic conditions are investigated: Chicago characterized by cool and humid, Houston characterized by hot and humid, Minneapolis characterized by cold and humid and San Francisco characterized by warm and marine condition. The four climates and their denominations are summarized in Table 4 [16]. U-values of walls and window properties were adjusted depending on different climates based on ASHRAE Standard 90.1 [18]. Similarly, three different internal load levels are investigated. Load levels of overhead lighting, occupancy and plug equipment for each case is summarized in Table 5. As stated earlier, the metabolic rate for office workers was assumed to be 100 W/person in Table 5. Finally, three window-to-wall ratios (WWRs) of 30%, 50% and 70% were investigated. Strip windows are evenly distributed in the walls and different WWRs are achieved by varying the window height.
3.6. Statistical Analysis
The data distributions are plotted as frequency histograms. If not otherwise specified the data are reported as median [25th percentile:75th percentile] unit, e.g., 12 (10:15) m/s. The normal distribution of the data was tested with the Shapiro-Wilk normality test or visual analysis of the Q-Q plots [20]. To compare means and to test statistical difference t-test and ANOVA were used when appropriate. For all tests the results were considered statistically significant when p < 0.05. The statistical analysis was performed with R version 2.15.2 [21].
4. Results and Discussion
4.1. Hourly Clothing Insulation Variations
Hourly clothing insulation values for a typical day in winter, summer and middle seasons are illustrated in Figure 3. Results for Cases 9–11 are not reported because the values are similar to the one of Cases 6–8 plus the insulation of the chair (0.1 clo). Each figure includes clothing variations in both west perimeter and interior zones for eight simulations cases summarized in Table 3. Regardless of the season and zone orientation, Case 1 and Case 5 showed the same clothing insulation due to the fact that both cases used the assumption of constant clothing values. Similarly, Case 2 and Case 6 showed the same clothing insulation due to the fact that both cases related the clothing insulation to the outdoor air temperature measured at 6 o'clock. The same is for Case 4 and Case 8. Since the same weather conditions were used, those two couple of cases should show the same clothing insulations as shown in the figure. Cases 1, 2, 4, 5, 6, 8, 9 and 11 have constant values during the whole day. Cases 1 and 5 assumed a fixed clothing value depending on the season and Cases 2, 4, 6, 8, 9 and 11 adjusted the clothing insulation as a function of 6 o'clock outdoor air temperature, which changed on the daily basis instead of hourly or sub-hourly basis. On the other hand, in Cases 3, 7, and 10 where the clothing insulation changed as a function of both 6 o'clock outdoor air and indoor operative temperatures, it changed hourly as shown in Figure 3 (Cases 3 and 7) since the indoor operative temperature changed every time-step, which, in turn, directly affected clothing values in each time-step.
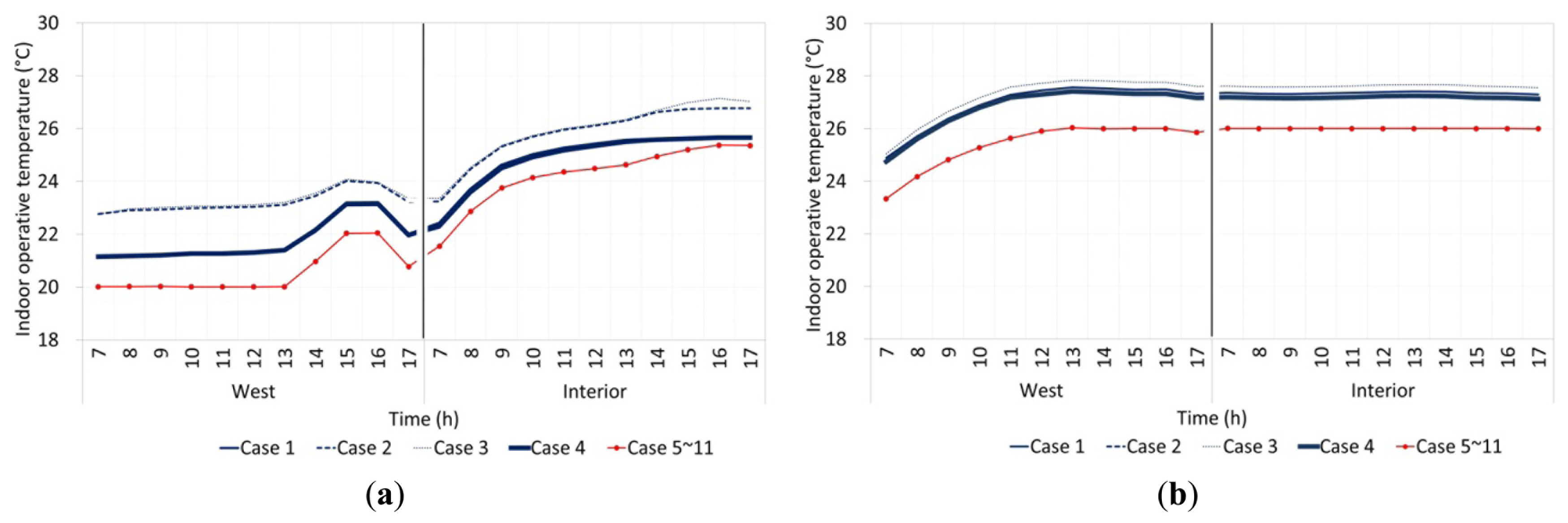
The clothing insulation models are significantly different (p < 0.001).The clothing insulation is equal to Icl = 0.65 [0.57:0.73] clo for cases controlled by Equation (1), Icl = 0.61 [0.51:0.74] clo for cases controlled by Equation (2), and to Icl = 0.66 [0.57:0.86] clo for cases controlled by Equation (3). Equation (3) has the widest inter-quantile range (0.29, compared to 0.16 and 0.22 of Equations (1) and (2) respectively). The wider variation implies that Equation (3) allows the wider flexibility in clothing insulation. The wider variations happen mainly in cold months. The operative temperature in the interior zone (26.0 [25.2:26.3] °C) was 1.7 K higher than the median temperature in the perimeter zones (24.3 °C) as shown in Figure 4. Operative temperature and clothing insulation have the reverse relationship as expressed in Equation (2) and thus the higher operative temperature in the interior zone reduced the clothing value in Figure 3.
The zone thermal control strategy is significantly affecting the operative temperature (p < 0.001), for the PMV control (Cases 1–4) top = 25.6 [23.4:27.4] °C, for the control based on operative temperature (Cases 5–11) top = 24.6 [21.1:26.0] °C. Therefore the operative temperature is in average 1 K higher in the cases with PMV control. This affects energy consumption as described later. For the given clothing, air velocity and metabolic activity those temperature satisfy the requirement of standards, but they are slightly higher than common values found in practice in commercial buildings where, for cultural reasons, clothing values suggested by standards may not always be used. Cases 5 through 11 showed similar operative temperature variations due to the fact that those cases controlled the system based on the indoor operative temperature, regardless of different clothing models. Therefore, the dynamic clothing models do not affect indoor operative temperatures when the HVAC is controlled based on indoor temperature.
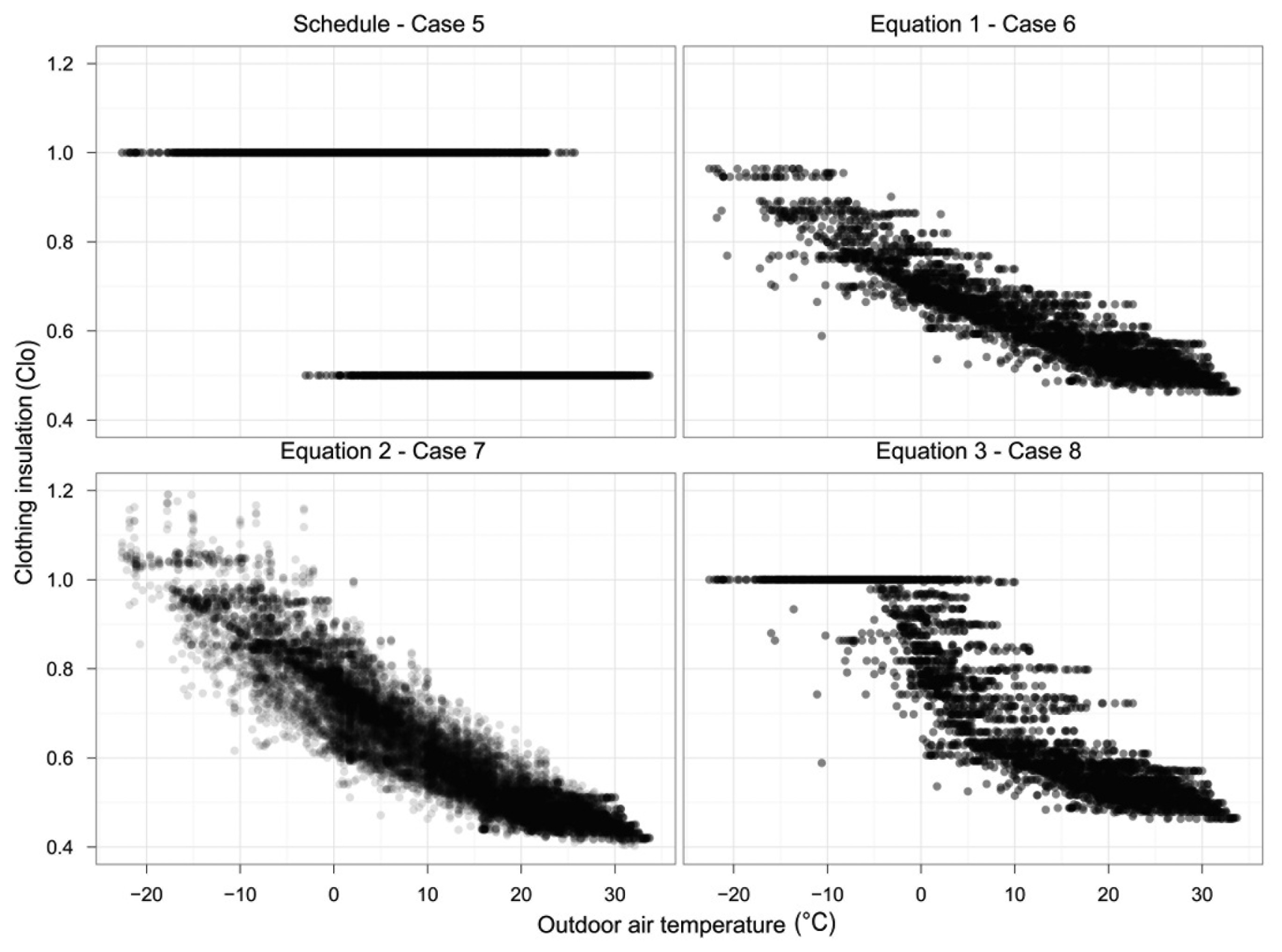
In Figure 5 are shown the outside air temperature vs. the clothing insulation for the Case 5 (Scheduled), 6 (Equation (1)), 7 (Equation (2)) and 8 (Equation (3)). Each data point is plotted with a transparency of 90%. Therefore only if there is at least 10 points one over the other the point is fully black. We used this technique to avoid overemphasize outliers. From the figure it can be clearly seen when the scheduled approach is used (Case 5) the clothing insulation is not related to the outdoor air temperature, indeed for the same outdoor temperature is possible to have the clothing insulation equal to 1 or 0.5 clo. When we look at Cases 6, 7 and 8 we need to keep in mind that the clothing insulation is calculated using the outdoor air temperature measured at 6 o'clock in the morning. Equation (2) give the wider range of clothing insulations. As expected Equation (3) has higher clothing insulation values when the outdoor air temperature is less than 5 °C compared to Equation (1).
4.2. Heating and Cooling Rate
Heating rate have been plotted with box plots for all the factor analyzed (zone, month, day, hour, case, equation implemented and zone thermostat control). Heating rates for zone, month, day, hour were following expected profiles and therefore are not reported here. The difference in heating rate between the 11 studied case is statistically significant (p < 0.001) but from engineering point of view. Cases 5 through 11 showed identical heating supply rate due to the fact that those cases controlled the system based on the indoor operative temperature regardless of different clothing assumptions and therefore can be summarized in value, that is 1823 [552:4235] W. For the Cases 1–4 the heating rate distribution is slightly lower and equal to 1509 [446:3923] W. This indicates that the zone thermal control strategy does slightly affect the heating rate. If the zone is control base on the temperature (common practice) the clothing model used does not affect the heating rate.
Similar results were been obtained for the cooling rate. The main difference was related to the fact that the interior zone had cooling rate much higher than the perimeter zones (interior = 12,258) [8743:20,044] W, perimeter = 2942 [2007:4878] W. This is due to the high internal gains.
4.3. Annual Energy Breakdown
The annual site and source HVAC energy breakdown for each simulated case is illustrated in Figure 6a,b. The secondary to primary conversion factors of 3.167 and 1.084 were assumed for the electricity and natural gas, respectively [19].
Cases 5 through 11 showed identical energy. Therefore, the clothing models do not affect energy use if the temperature control is done based on zone indoor temperature. As shown in the figure, Cases 5 through 11 showed the lowest total HVAC site and source energy consumption compared to Cases 1, 2 and 3 mainly due to the lowest annual boiler energy. The annual heating energy of Cases 5 through 11 was 41.0 kWh/m2, while they were 49.0 kWh/m2, 55.8 kWh/m2, 56.4 kWh/m2 and 51.6 kWh/m2 in Cases1, 2, 3 and 4, respectively. This is due to the fact that the minimum indoor temperatures in Cases 5 through 11 were lower than those of Cases 1, 2, 3 and 4.
In terms of the comparison among Cases 1, 2, 3 and 4 where the system was controlled based on PMV set-point, Case 1 showed the lowest total HVAC energy consumption due to the lowest annual boiler energy. This is due to the higher clothing insulation. This suggests that, for PMV based control, the constant clothing insulation assumption can lead to the under-prediction of the annual heating energy consumption by 15% and therefore the predictive clothing model taking into account the surrounding thermal environment should be used during the simulation.
On the other hand, Cases 5 through 11 showed the highest cooling energy compared to Cases 1–4. The annual site cooling energy of Cases 5 through 11 was 8.8 kWh/m2, while they were 7.9 kWh/m2, 7.9 kWh/m2, 7.5 kWh/m2 and 7.9 kWh/m2 in Cases 1, 2, 3 and 4, respectively. This is due to the fact that the indoor temperature in Cases 5 through 11 was controlled to 26 °C, while in the Cases 1–4 max temperature were slightly higher. In terms of the comparison among Cases 1, 2, 3 and 4, Case 3 showed the lowest cooling energy as shown in Figure 6. This is due to the lower clothing insulation.
4.4. Equipment Size
Similar to the impact on energy discussed previously, occupant's clothing can have the impact on the HVAC system sizing as well. In this study, instead of fully relying on auto-sizing function of EnergyPlus, a simple work-around was used to ensure that the system sizing was correctly determined for each simulation case. A dummy full year simulation was run first, and then the annual profiles of the plant heating demand for the boiler, the plant cooling demand for the chiller and the supply airflow for the AHU fan was screened. Based on the screening process, for each equipment the proper size was selected and a sizing factor of 1.2 was applied for the final run. Then, the annual simulation was performed based on the boiler, chiller and fan sizes determined from this work around.
The final sizing of the boiler, chiller and central AHU supply fan is summarized in Table 6 for the eleven simulated cases. As presented in the table, the difference in the boiler sizing can be easily observed among simulated cases. In terms of the comparison between Cases 1, 2, 3 and 4 having the same control logic based on PMV set-point, Cases 2–4 applying the new predictive clothing insulation models showed the boiler sizing of 248 kW, 252 kW and 239 kW, respectively, which were 7.8%, 9.5% and 3.9% larger than that of the baseline (Case 1—constant clothing insulation assumption). Chiller and AHU fan sizing also showed the difference among simulated cases, but the discrepancies were not as relevant as the one for the boiler. Chiller size turned out to be 254 kW in Case 1, which is less than 1.6% different from Cases 2, 3 and 4. AHU fan size showed 11.3 m3/s in Case 1, which was also less than 2.6% different from the other three cases. When the PMV control is applied, assuming the fixed clothing insulation at 1.0 clo during the heating season can lead to the under-estimation of the boiler size.
On the other hand, Cases 5 through 11 have identical equipment size. Therefore, the dynamic clothing models do not affect equipment sizing when the HVAC system is controlled based on indoor temperature. Cases 5 through 11 showed smaller boiler size and bigger chiller size compared to Cases 1, 2, 3 and 4, showing a similar pattern to the energy consumption results above. This is due to the fact that operative temperatures were lower than the other cases in both heating and cooling seasons as shown in Figure 7.
4.5. Thermal Comfort (Based on PMV)
In this section, the possible impacts of the new predictive clothing models on occupant comfort are described. Thermal comfort was evaluated with the Fanger's PMV value [3]. The zone thermal control based on the PMV method (Cases 1–4 = −0.15 [−0.48:0.50] PMV) was able to provide a better comfort (p < 0.0001) than the zone thermal control based on operative temperature (Cases 5–8 = −0.24 [−0.84:0.02] PMV). This is an expected result. It is interesting to notice that the zone thermal control based on operative temperature tend to overcool the zone (median value is −0.24 PMV). This is due to the fact that for the air velocity selected (0.2 m/s) and for the metabolic activity used (1.15 met) the operative temperature that gives PMV = 0.50 is 27.1 °C if Icl = 0.5 clo and the operative temperature that gives PMV = −0.5 is 20.4 °C if Icl = 1 clo. Metabolic activity is a parameter that strongly affects PMV calculations. PMV control provides better comfort but its implementation in practice is unlikely due to technical barriers (e.g., measuring air velocity, assessing clothing and metabolic activity).
In Figure 7 are shown the histograms for Cases 5–8, which correspond to the use of the schedule, Equation (1)–(3), respectively for summer and winter. According to the PMV index, the lowest percentage of dissatisfied people is obtained when PMV = 0. The four PMV distributions are different (p < 0.0001). If each case is analyzed together (without separating in summer and winter) the following results are obtained: Case 5 = −0.14 [−0.71:0.03] PMV, Case 6 = −0.28 [−1.09:0.05] PMV; Case 7 = −0.35 [−0.97:−0.07] PMV; and Case 8 = −0.21 [−0.80:0.06] PMV. Case 5 generated an higher PMV than the one found in the other three cases. Using the simplest clothing model (Case 5—0.5 clo in cooling and 1 clo in heating) underestimate thermal comfort problems and provide an incorrect prediction of thermal comfort. From Figure 7 can be noticed that the distribution in summer is around PMV = 0 and skewed toward the cold side. For the winter, the distribution is centered around zero for Case 5 and colder for the other three cases. The difference among Cases 6, 7, and 8 is not strong, but Cases 7 and 6 are the most alike. Case 7 can be arguably considered the most precise (it use Equation (2) that gives the best predict abilities [13]).
4.6. Sensitivity Analysis
In the sensitivity analysis, the percentage difference between Case 1 and Case 3 was evaluated to investigate the impact of the considered parameters on energy discrepancies. The results of the sensitivity analysis as a function of three parameters are illustrated in Figure 8. Chiller, boiler and total HVAC energy percentage differences are presented. Positive value indicates that Case 3 applying the new predictive clothing model consumes more energy than Case 1 of constant clothing insulation assumption. As shown in the figure, the percentage difference in the boiler energy is significantly increased under hot and warm conditions due to the fact that the annual energy intensity itself was not big and thus the percentage difference accordingly increased. The percentage difference in the total HVAC energy showed the highest value in San Francisco where the annual energy intensity was the lowest among investigated climates.
In case of the sensitivity analysis for WWR shown in Figure 8c, both boiler and total HVAC energy difference were reduced with the higher WWR. The reduced percentage difference in the boiler energy was because of the reduced boiler energy intensity as the WWR increased due to greater solar radiant penetration into the building. In case of the sensitivity analysis for internal load level shown in Figure 8c, the boiler energy percentage difference significantly increased from 15.5% to 22.5% due to the fact that as the internal load increased, the heating energy decreased similar to the reason for the climatic condition above. On the other hand, the total HVAC energy difference was reduced from 10.4% to 7.1%. It could be concluded that WWR did not have big impact on the percentage difference in all the boiler, chiller and total HVAC energies between Case 1 and Case 3. However, the percentage difference in the boiler energy can be clearly observed with regard to climatic conditions and internal load level. Clear tendency in the percentage difference in both chiller and total HVAC energies could not be observed wither regard to the three parameters that were taken into account in the sensitivity analysis.
4.7. Limitations and Future Work
The main limitation of this study is related to the selection of the cases to be simulated. The impact of the new predictive clothing insulation models on energy and comfort was investigated for only one particular climate (Chicago, IL, USA) and one particular system type (conventional forced air system equipped with variable speed central AHU and VAV box with reheat coil in each zone). In addition, the different settings in the HVAC system from this study such as different AHU SATs, minimum airflow settings and plant curves have not been investigated.
If the HVAC system is controlled base on the PMV method then the dynamic clothing models affect energy use and equipment size. If it is controlled base on indoor temperature then the dynamic clothing models affect thermal comfort assessment. Therefore based on the results reported in this study the authors recommend that the dynamic clothing models should be implemented in dynamic building energy simulation software such as EnergyPlus.
5. Conclusions
The conclusions of this research are:
When the HVAC is controlled based on indoor temperature the dynamic clothing models do not affect indoor operative temperatures, energy consumptions and equipment sizes.
When the HVAC is controlled based on the PMV model the use of a fixed clothing insulation during the cooling (0.5 clo) and heating (1.0 clo) season leads to the incorrect estimation of the indoor operative temperatures, energy consumptions and equipment sizes.
The dynamic clothing models significantly (p < 0.0001) improve thermal comfort estimation.
The authors recommend that the dynamic clothing models should be implemented in dynamic building energy simulation software such as EnergyPlus.
Acknowledgments
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (2012R1A1A1003730). This research was also supported by the Center for the Built Environment (CBE), University of California Berkeley, United States. For the help with data analysis, the authors would like to thank Yeo Beom Yoon, Graduate Student Researcher at Hanbat National University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- American Society of Heating, Refrigerating and Air-Conditioning Engineers. In Thermal Environmental Conditions for Human Occupancy; ANSI/ASHRAE 55-2010; ANSI/ASHRAE: Atlanta, GA, USA, 2010.
- Newsham, G.R. Clothing as a thermal comfort moderator and the effect on energy consumption. Energy Build. 1997, 26, 283–291. [Google Scholar]
- Fanger, P.O. Thermal Comfort, Copenhagen; Danish Technical Press: Copenhagen, Denmark, 1970. [Google Scholar]
- European Committee for Standardization. In Criteria for the Indoor Environment including Thermal, Indoor Air Quality, Light and Noise; EN 15251–2007; CEN: Brussels, Belgium, 2007.
- International Organization for Standardization. In Moderate Thermal Environment—Determination of the PMV and PPD Indices and Specification of the Conditions for Thermal Comfort; ISO 7730; ISO: Geneva, Switzerland, 2005.
- Havenith, G.; Holmer, I.; Parsons, K. Personal Factors in thermal comfort assessment: Clothing properties and metabolic heat production. Energy Build. 2002, 34, 581–591. [Google Scholar]
- Gauthier, S.; Shipworth, D. Predictive Thermal Comfort Model: Are the Field Studies Measuring the Most Influential Variables? Proceedings of the 7th Windsor Conference 2012, Windsor, UK, 12–15 April 2012.
- Morgan, C.; de Dear, R. Weather, clothing and thermal adaptation to indoor climate. Clim. Res. 2003, 24, 267–284. [Google Scholar]
- Toftum, J.; Andersen, R.V.; Jensen, K.L. Occupant performance and building energy consumption with different philosophies of determining acceptable thermal conditions. Build. Environ. 2009, 44, 2009–2016. [Google Scholar]
- Jensen, K.L.; Toftum, J.; Friis-Hansen, P. A bayesian network approach to the evaluation of building design and its consequences for employee performance and operational cost. Build. Environ. 2009, 44, 456–462. [Google Scholar]
- De Carli, M.; Olesen, B.W.; Zarrella, A.; Zecchin, R. People's clothing behavior according to external weather and indoor environment. Build. Environ. 2007, 42, 3965–3973. [Google Scholar]
- De Dear, R.; Brager, G. Developing an Adaptive Model of Thermal Comfort and Preference; Final Report ASHRAE RP-884; ASHRAE: Atlanta, GA, USA, 1997. [Google Scholar]
- Schiavon, S.; Lee, K.H. Dynamic predictive clothing insulation models based on outdoor air and indoor operative temperatures. Build. Environ. 2013, 59, 250–260. [Google Scholar]
- Cena, K.; de Dear, R.J. Field study of occupant comfort and office thermal environments in a hot, arid climate. ASHRAE Trans. Res. 1999, 105, 204–217. [Google Scholar]
- De Dear, R.; Brager, G. The adaptive model of thermal comfort and energy conservation in the built environment. Int. J. Biometeorol. 2011, 45, 100–108. [Google Scholar]
- Crawley, D.; Lawrie, L.; Winkelmann, F.; Buhl, W.F.; Huang, H.J.; Pedersen, C. EnergyPlus: Creating a new-generation building energy simulation program. Energy Build. 2001, 33, 319–331. [Google Scholar]
- EnergyPlus, 2012. EnergyPlus Engineering Reference. The Reference to EnergyPlus Calculations. Available online: http://apps1.eere.energy.gov/buildings/energyplus/pdfs/engineeringreference.pdf (accessed on 29 October 2012).
- American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc. In Energy Standard for Buildings except Low Rise Residential Buildings; ASHRAE Standard 90.1-2004; ASHRAE: Atlanta, GA, USA, 2010.
- The U. S. DOE, 2012. EnergyPlus Input Output Reference. The Encyclopedic Reference to EnergyPlus Input and Output. Available online: http://apps1.eere.energy.gov/buildings/energyplus/pdfs/inputoutputreference.pdf (accessed on 29 October 2012).
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar]
- R Development Core Team. In R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2012.




| Internal load type | Maximum value | Internal load type | Maximum value |
|---|---|---|---|
| Overhead lighting, W/m2 | 10.8 | Equipment, W/m2 | 8.6 |
| Peak occupancy, m2/person | 22.3 | Total, W/m2 | 23.9 |
| HVAC | Values | HVAC | Values |
|---|---|---|---|
| AHU supply temperature | 14.0 °C | Minimum outside air rate | 0.762 L/s·m2 |
| AHU fan design static pressure | 1125 Pa | Chiller design COP | 5.0 |
| AHU fan efficiency | 75% | Boiler design efficiency | 80% |
| AHU part load shutoff | 125 Pa |
| Case | Clothing insulation model | Zone thermal control | Chair | Description |
|---|---|---|---|---|
| 1 | Scheduled | −0.5 < PMV < 0.5 | Not used | Fixed at 1.0 from 1 January to 31 March Fixed at 0.5 from 1 April to 30 September Fixed at 1.0 from 1 October to 31 December |
| 2 | Equation (1) | −0.5 < PMV < 0.5 | Not used | Clothing insulation as a function of 6 o'clock outdoor air temperature |
| 3 | Equation (2) | −0.5 < PMV < 0.5 | Not used | Clothing insulation as a function of both 6 o'clock outdoor air and indoor operative temperatures |
| 4 | Equation (3) | −0.5 < PMV < 0.5 | Not used | Clothing insulation as a function of 6 o'clock outdoor air temperature |
| 5 | Scheduled | 20 °C < top < 26 °C | Not used | Fixed at 1.0 from 1 January to 31 March Fixed at 0.5 from 1 April to 30 September Fixed at 1.0 from 1 October to 31 December |
| 6 | Equation (1) | 20 °C < top < 26 °C | Not used | Clothing insulation as a function of 6 o'clock outdoor air temperature |
| 7 | Equation (2) | 20 °C < top < 26 °C | Not used | Clothing insulation as a function of both 6 o'clock outdoor air and indoor operative temperatures |
| 8 | Equation (3) | 20 °C < top < 26 °C | Not used | Clothing insulation as a function of 6 o'clock outdoor air temperature |
| 9 | Equation (1) | 20 °C < top < 26 °C | 0.1 clo | Clothing insulation as a function of 6 o'clock outdoor air temperature |
| 10 | Equation (2) | 20 °C < top < 26 °C | 0.1 clo | Clothing insulation as a function of both 6 o'clock outdoor air and indoor operative temperatures |
| 11 | Equation (3) | 20 °C < top < 26 °C | 0.1 clo | Clothing insulation as a function of 6 o'clock outdoor air temperature |
| Denomination | City | Climatic condition |
|---|---|---|
| CGO | Chicago (IL) | cool and humid |
| HTX | Houston (TX) | hot and humid |
| MNA | Minneapolis (MN) | cold and humid |
| SFA | San Francisco (CA) | warm and marine |
| Denomination | INT_22.6 | INT_33.9 | INT_50.8 |
|---|---|---|---|
| Overhead lighting, W/m2 | 10.8 | 16.2 | 24.3 |
| Peak occupancy, m2/person | 22.3 | 14.9 | 9.9 |
| Equipment, W/m2 | 8.6 | 12.9 | 19.3 |
| Total, W/m2 | 23.9 | 35.8 | 53.7 |
| HVAC component | Case 1 | Case 2 | Case 3 | Case 4 | Case 5∼11 |
|---|---|---|---|---|---|
| Boiler (kW) | 230 | 248 (7.8%) | 252 (9.6%) | 239 (3.9%) | 209 (−9.1%) |
| Chiller (kW) | 254 | 258 (1.6%) | 250 (−1.6%) | 252 (−0.8%) | 270 (6.3%) |
| Central AHU fan (m3/s) | 11.3 | 11.1 (−1.8%) | 11.0 (−2.7%) | 11.1 (−1.8%) | 12.4 (9.7%) |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lee, K.H.; Schiavon, S. Influence of Three Dynamic Predictive Clothing Insulation Models on Building Energy Use, HVAC Sizing and Thermal Comfort. Energies 2014, 7, 1917-1934. https://doi.org/10.3390/en7041917
Lee KH, Schiavon S. Influence of Three Dynamic Predictive Clothing Insulation Models on Building Energy Use, HVAC Sizing and Thermal Comfort. Energies. 2014; 7(4):1917-1934. https://doi.org/10.3390/en7041917
Chicago/Turabian StyleLee, Kwang Ho, and Stefano Schiavon. 2014. "Influence of Three Dynamic Predictive Clothing Insulation Models on Building Energy Use, HVAC Sizing and Thermal Comfort" Energies 7, no. 4: 1917-1934. https://doi.org/10.3390/en7041917




