Numerical Simulation on Head-On Binary Collision of Gel Propellant Droplets
Abstract
:1. Introduction
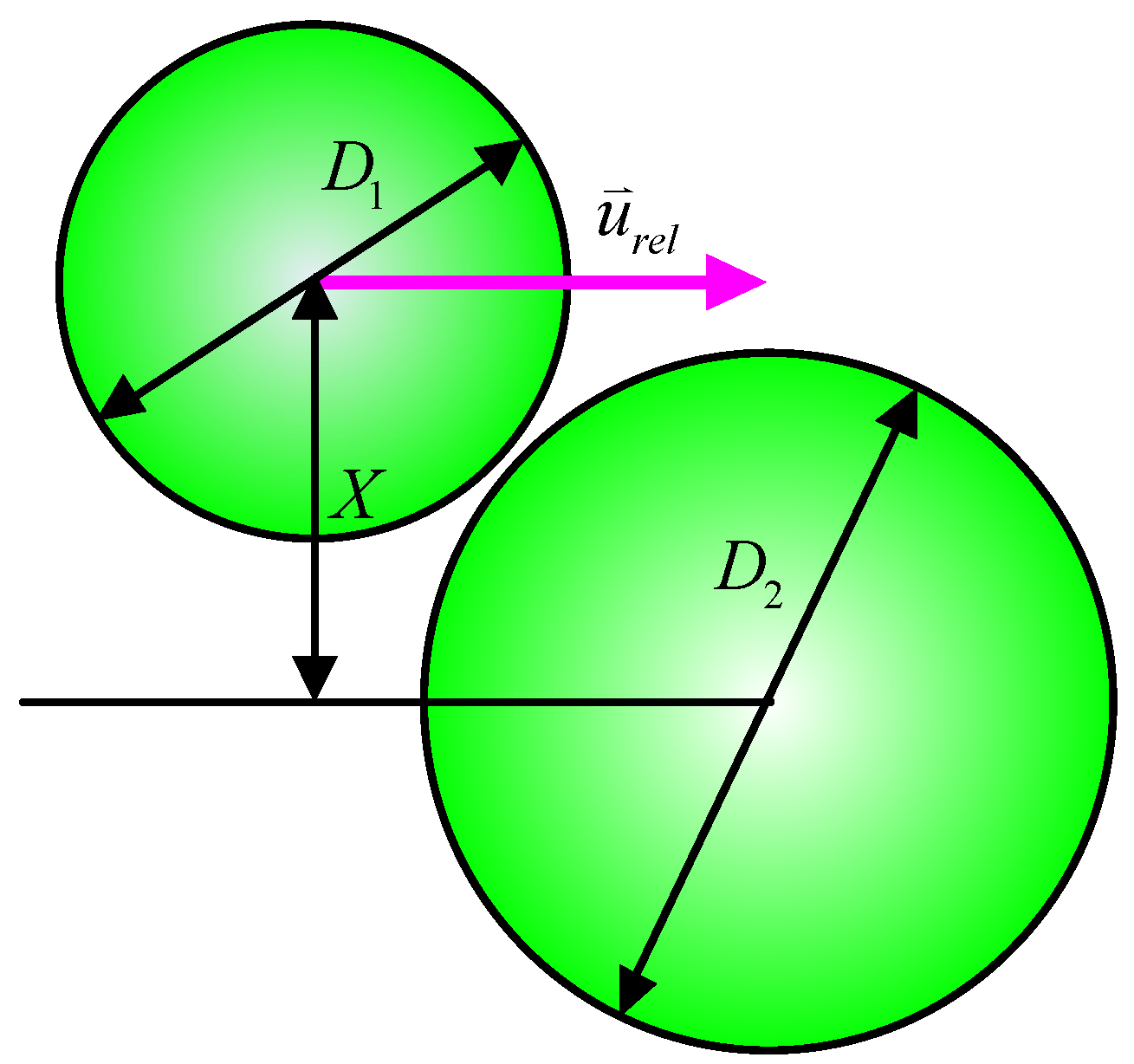
2. Model Description
2.1. Mathematical Formulation
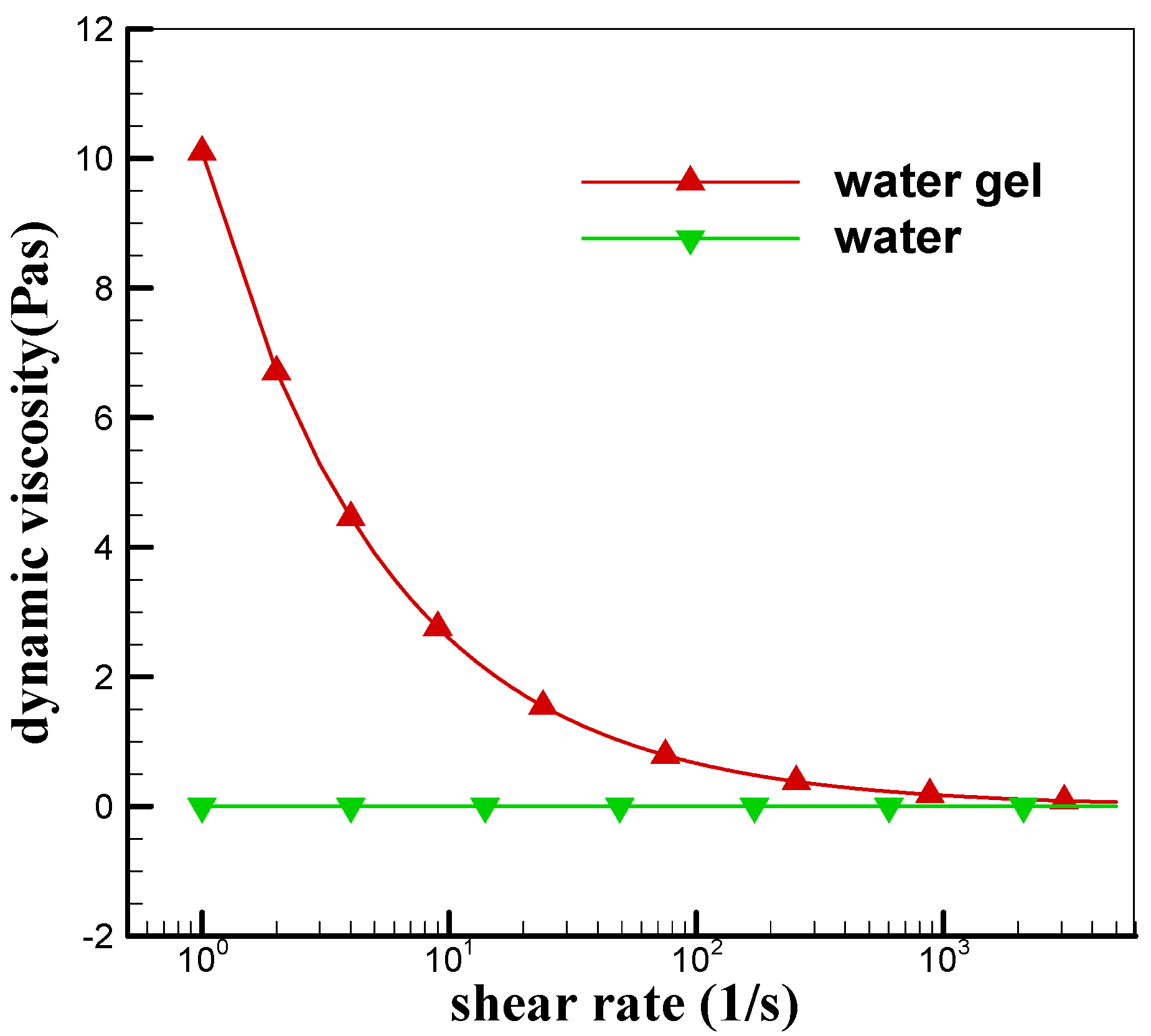
2.2. Gel Propellant Rheology
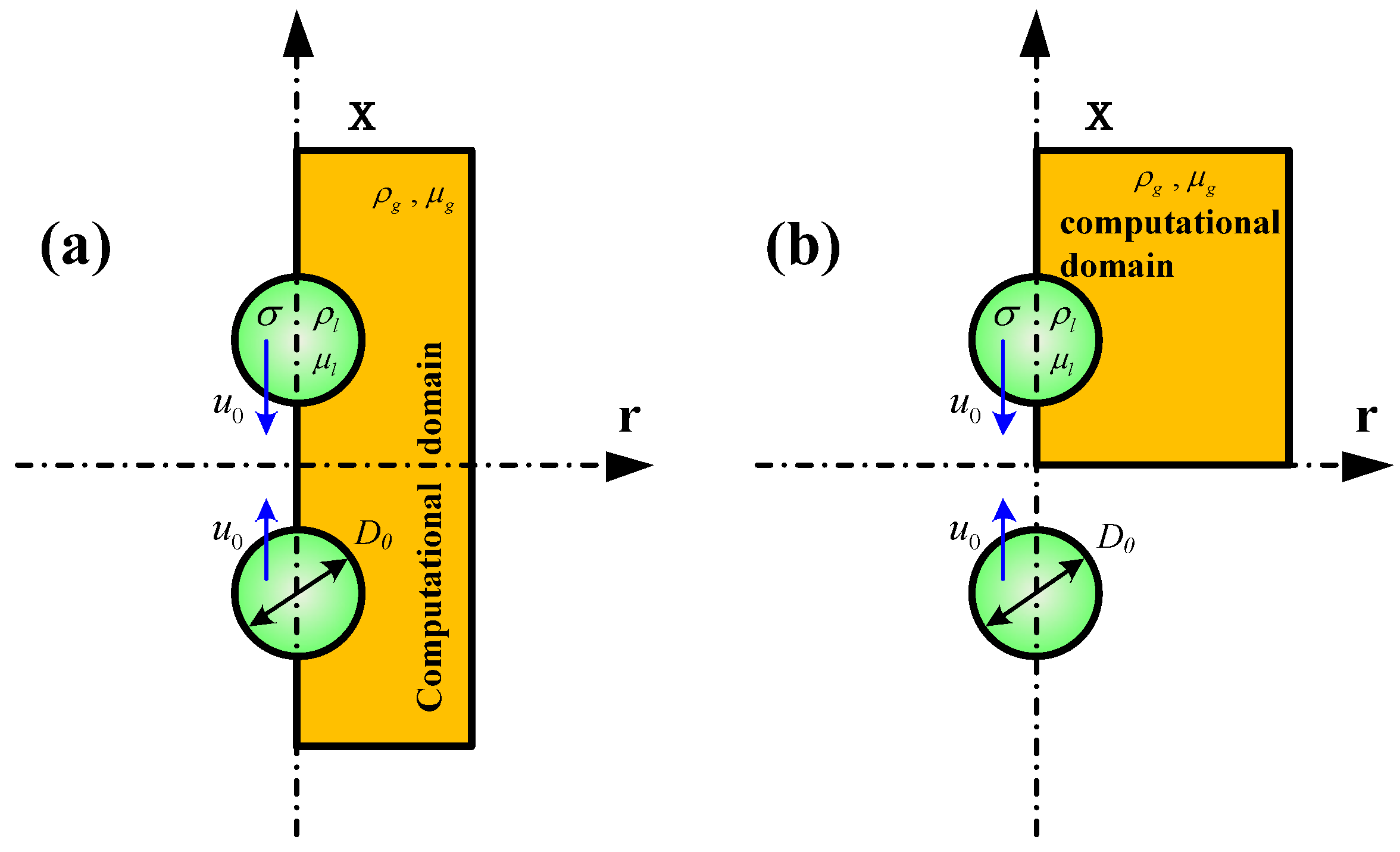
3. Model Validations
3.1. Newtonian Droplet Coalescence

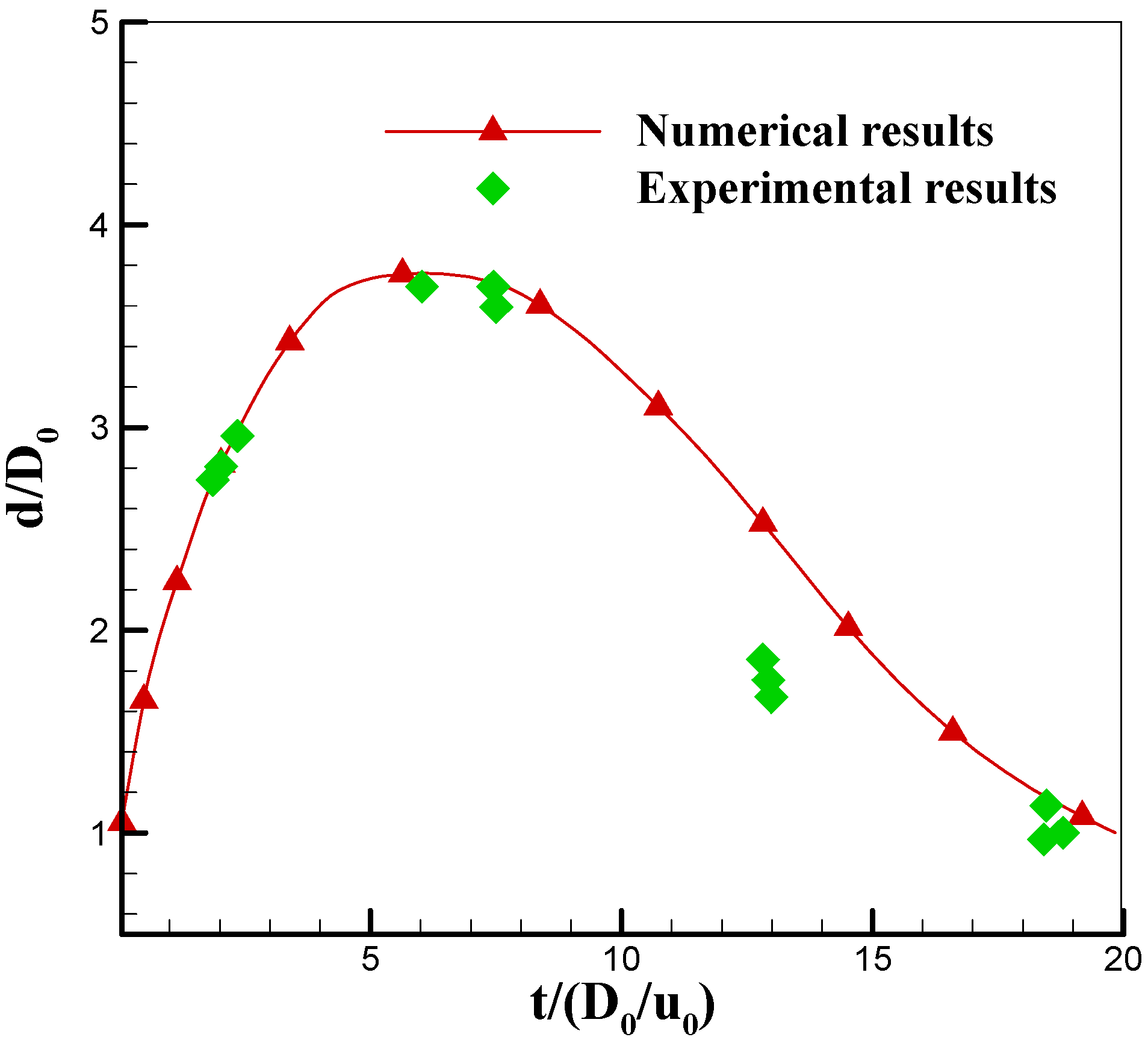
3.2. Shear-Thinning Droplet Collision
3.3. Grid and Time Step Independence Study
4. Results and Discussion
4.1. Bouncing Collision
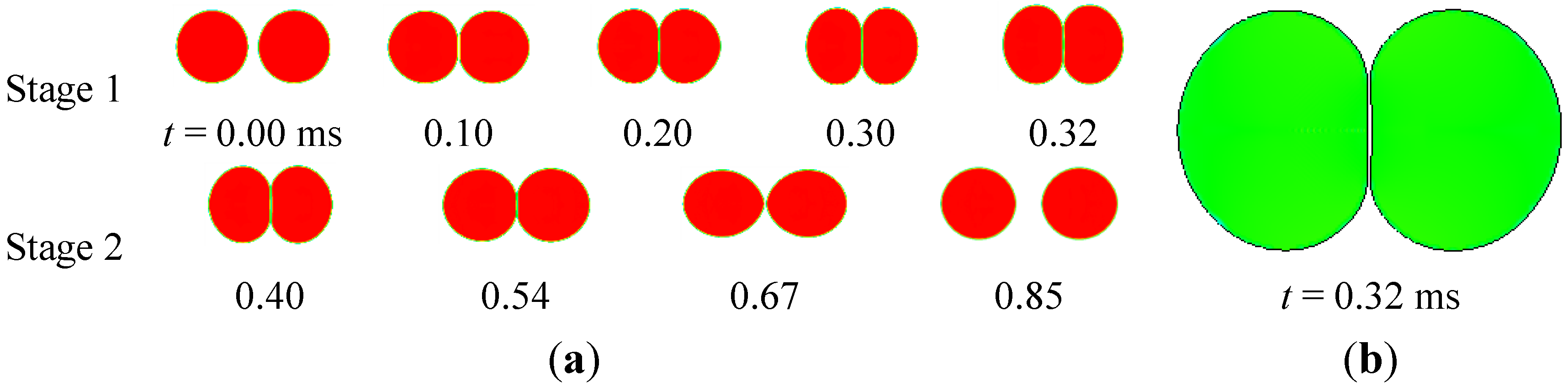
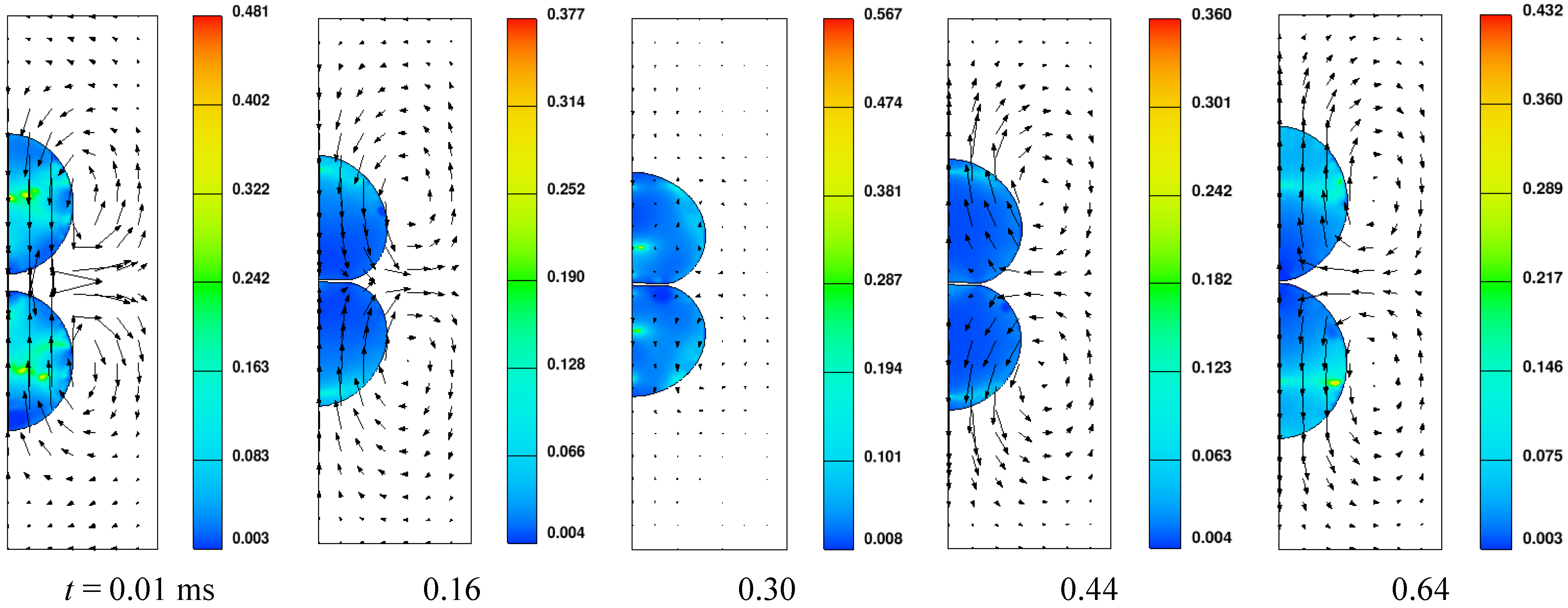
4.2. Coalescence Collision
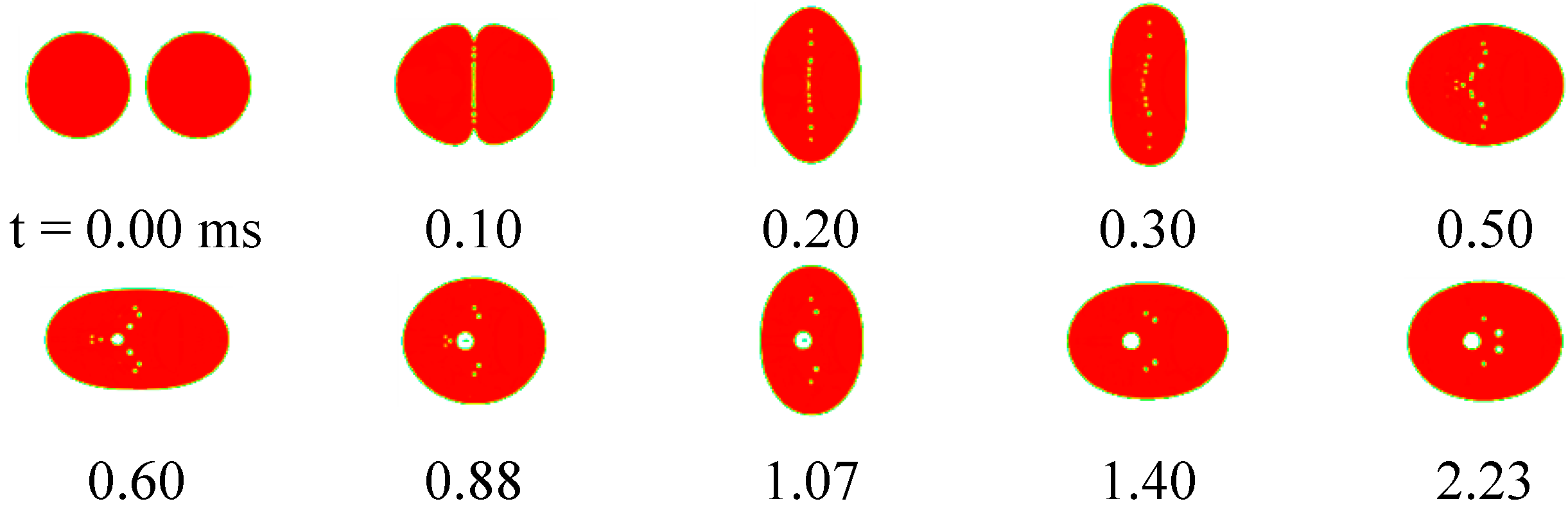
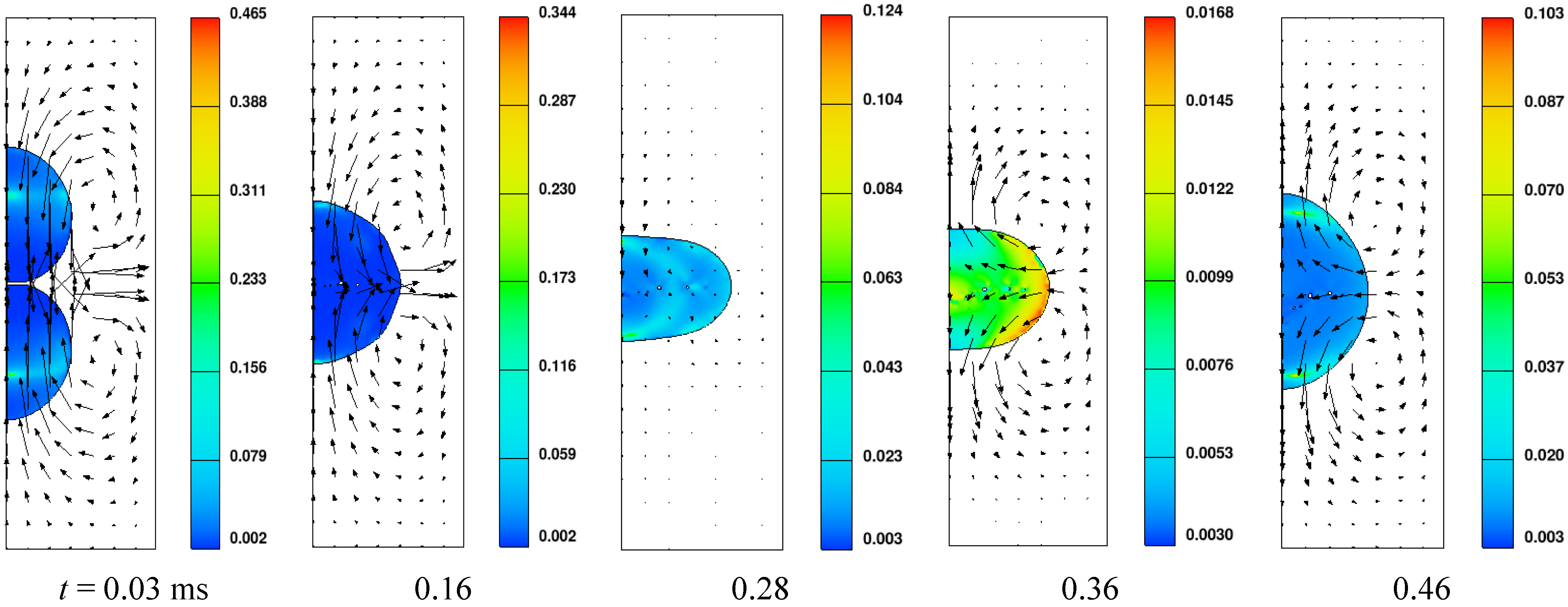
4.3. Reflexive Separation Collision
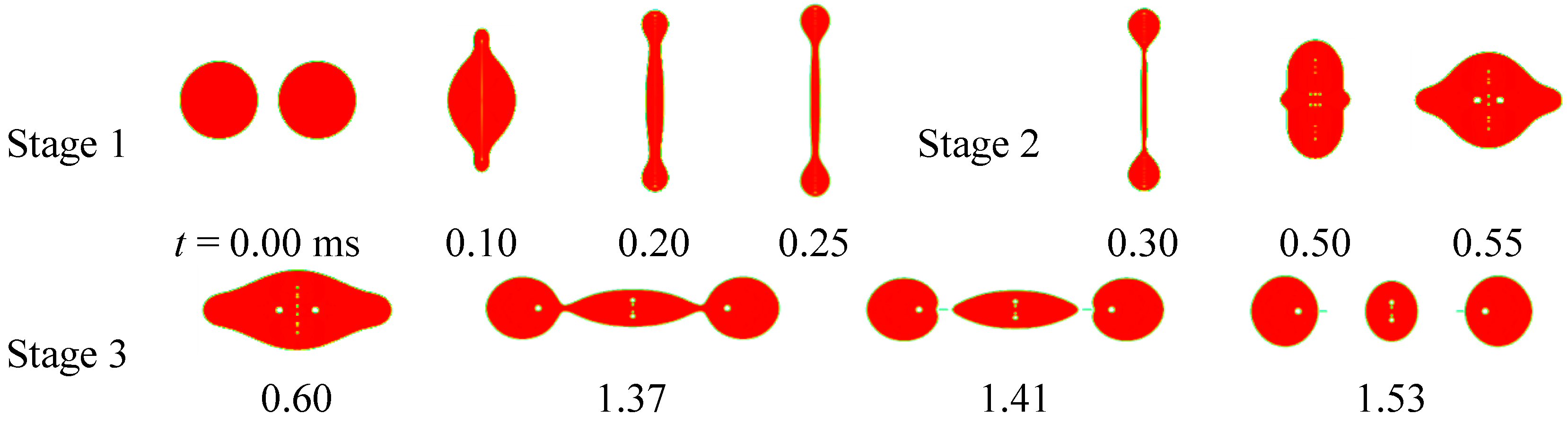
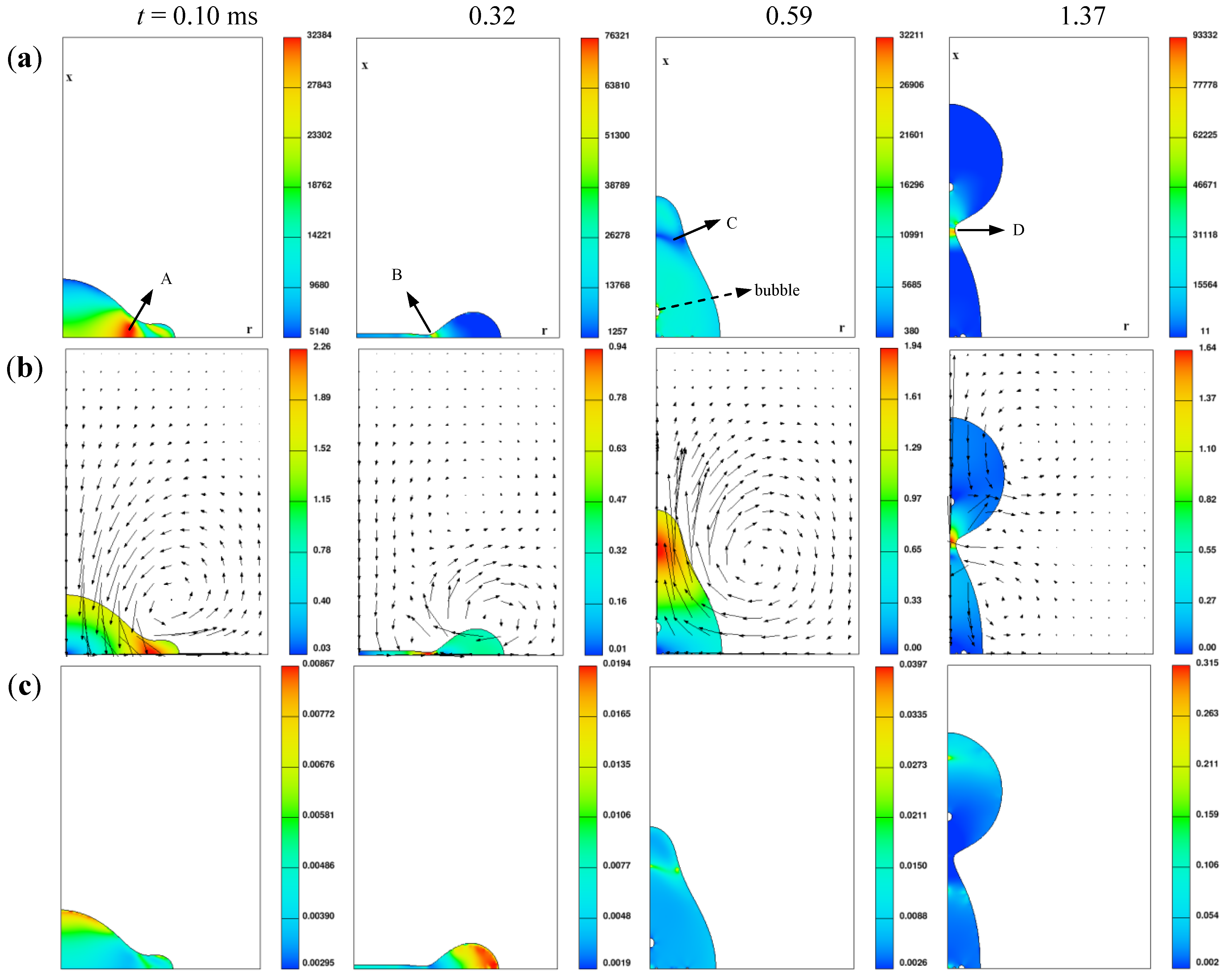
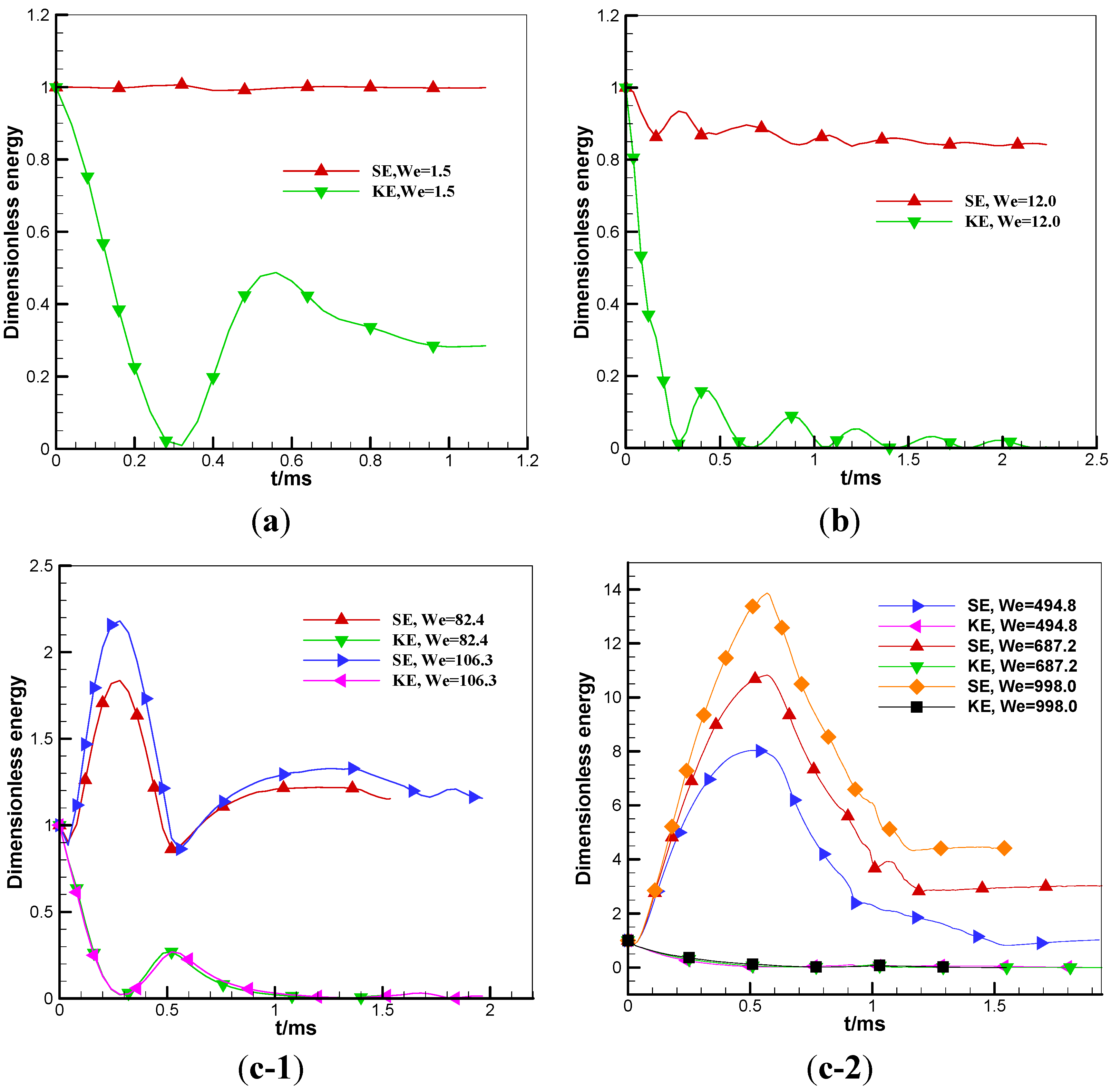
4.4. Evolution of the Energy Budget
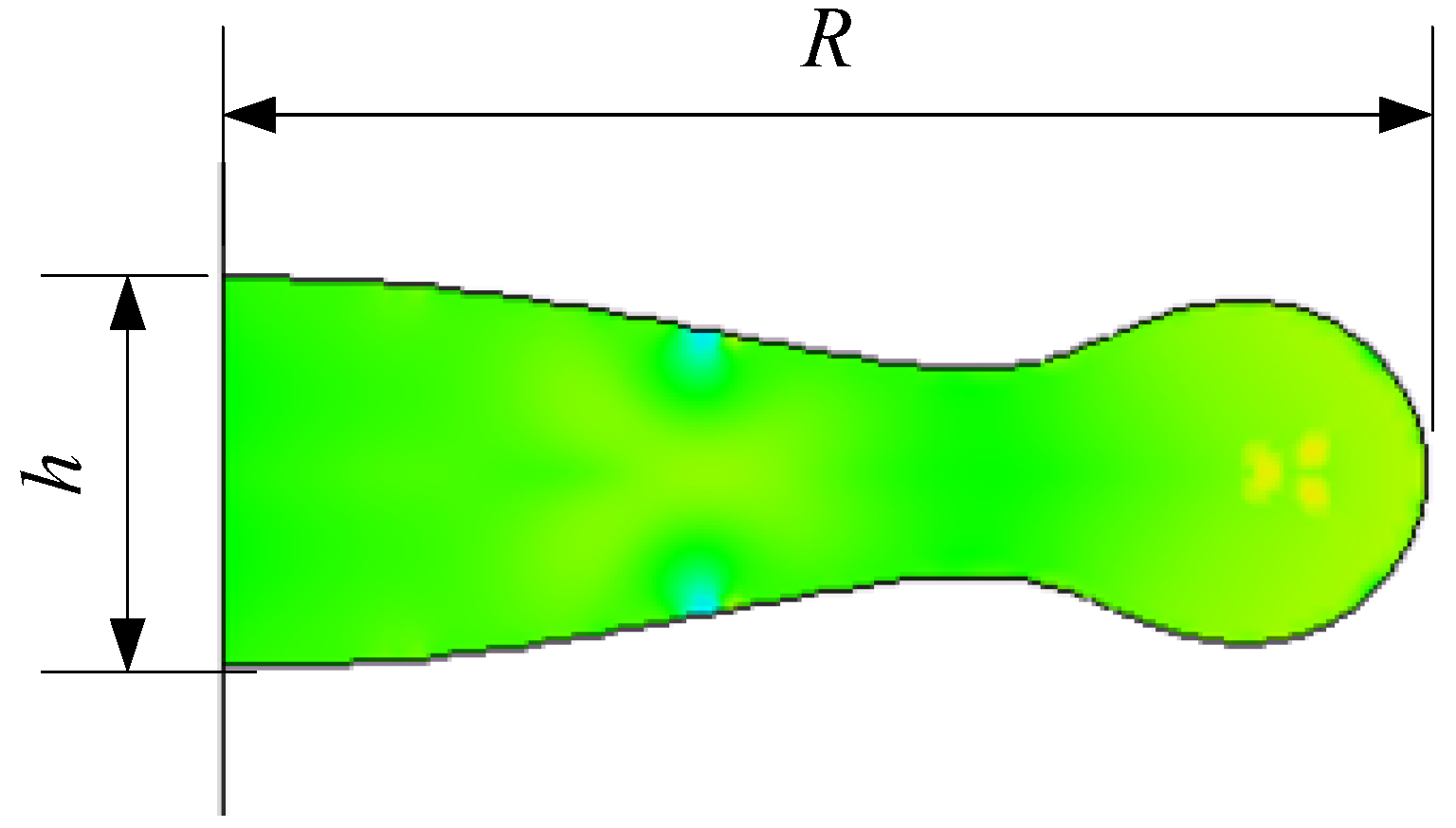
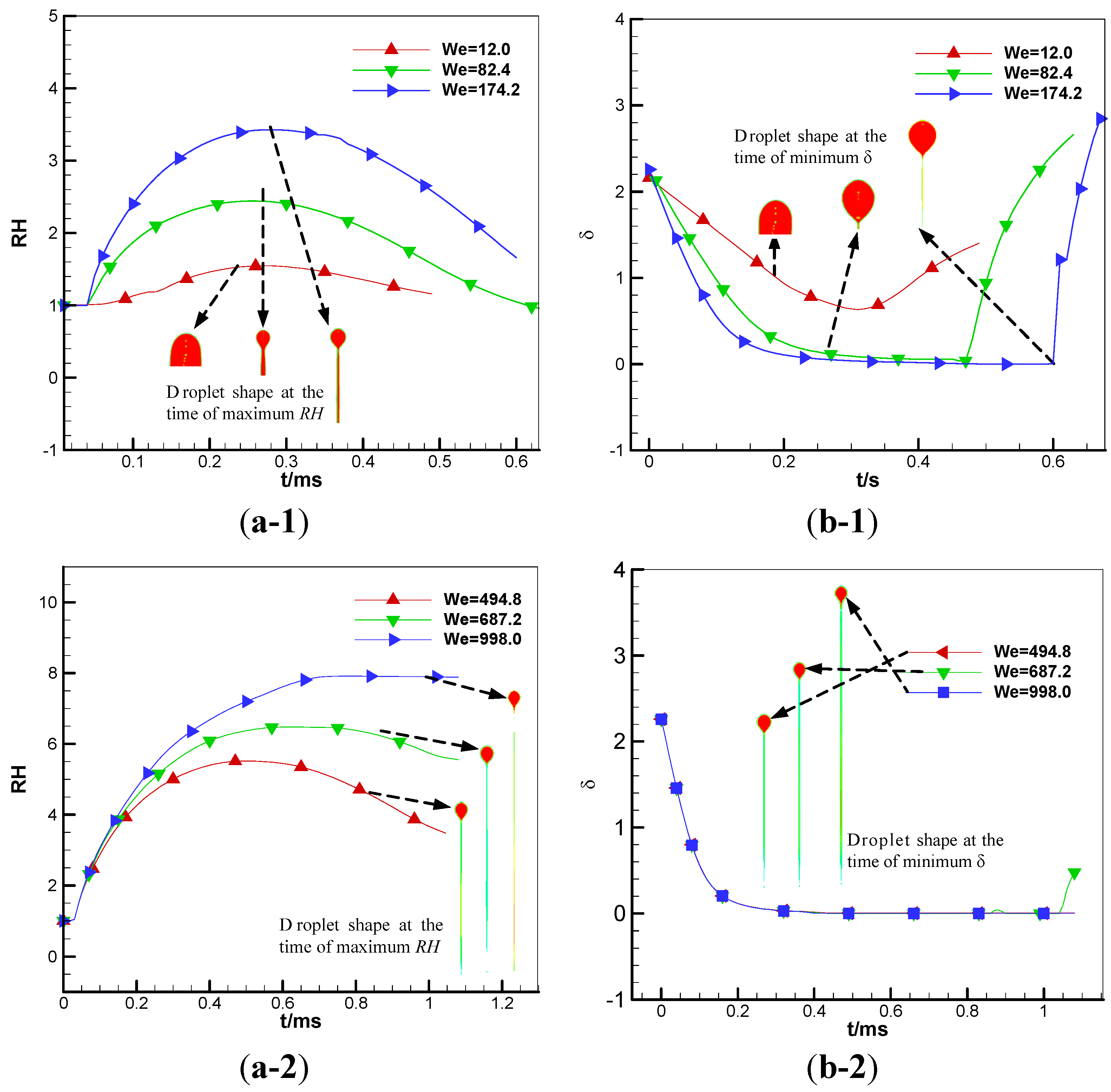
4.5. Maximum Deformation
5. Conclusions
- (1)
- The VOF methodology is capable of predicting the details of complex flow configurations, like the evolution of the gas-liquid free interface, gas bubbles entrapment and coalescence, and ligament formation.
- (2)
- The maximum shear rate occurs at the point where the flow is redirected and accelerated, and minimum effective viscosity occurs at the corresponding point. Rebound of droplets is determined by the Weber number and viscosity of the fluid together. At the time of maximum droplet deformation, the fluid within droplets is at the stagnant state, and dynamic viscosity increases, leading to easier rebound in comparison with the base fluid droplets. The alternant appearance along with the deformation of droplets in the radial and axial direction is the main characteristic of the droplet coalescence process, and the deformation amplitude attenuates gradually. Three distinctive stages (radial expansion, recovery of the spherical shape, and the axial extension and reflexive separation) were identified for reflexive separation process of droplets.
- (3)
- During the rebound process of droplets, the kinetic energy decreases remarkably, whilst the surface energy increases slightly. The kinetic energy and surface energy take on opposite variation trends for the process of droplet coalescence. The influence of Weber number on variation of surface energy is more remarkable, while the influence on variation of kinetic energy is small.
- (4)
- In the case of a low Weber number, the radial velocity of rim reverses its direction towards the center of the disc; the flow within the thin disc continues to accumulate in the boundary ring, which results in the minimum central thickness of a droplet appearance later than its maximum deformation. However, this result is contrary to the case of a high Weber number, because the dimensionless center thickness δ becomes zero during the process of RH increasing.
Acknowledgments
References
- Zhang, P.; Law, C.K. An analysis of head-on droplet collision with large deformation in gaseous medium. Phys. Fluids 2011, 23, 042102:1–042102:22. [Google Scholar]
- Natan, B.; Rahimi, S. The status of gel propellants in year 2000. Int. J. Energy Mater. Chem. Propuls. 2002, 5, 172–194. [Google Scholar]
- Liu, Z.J.; Wu, J.J.; He, Z. Investigation of Organic-gellant Droplets Evaporation Characteristics in the Static Environment. In Proceedings of 62nd International Astronautical Congress, Cape Town, South Africa, 3–7 October 2011; Volume 8, pp. 6336–6344.
- Solomon, Y.; Natan, B.; Cohen, Y. Combustion of gel fuels based on organic gellants. Combust. Flame 2009, 156, 261–268. [Google Scholar] [CrossRef]
- Liu, Z.J.; Hu, X.P.; He, Z.; Wu, J.J. Experimental study on the combustion and microexplosion of freely falling gelled unsymmetrical dimethylhydrazine (UDMH) fuel droplets. Energies 2012, 5, 3126–3136. [Google Scholar] [CrossRef]
- Klaus, M.; Helmut, K.C. Some Aspects of Rheological and Flow Characteristics of Gel Fuels with Regard to Propulsion Application. In Proceedings of 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Denver, CO, USA, 2–5 August 2009.
- Chen, X.D.; Ma, D.J.; Vigor, Y. Collision Outcome and Mass Transfer of Unequal-sized Droplet Collision. In Proceedings of 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012.
- Chen, X.D.; Ma, D.J.; Khare, P.; Vigor, Y. Energy and Mass Transfer during Binary Droplet Collision. In Proceedings of 49th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011.
- Ashgriz, N.; Poo, J.Y. Coalescence and separation in binary collision of liquid drops. J. Fluid Mech. 1990, 221, 183–204. [Google Scholar] [CrossRef]
- Brenn, G.; Frohn, A. Collision and coalescence of droplets of various liquids. J. Aerosol Sci. 1989, 20, 1027–1030. [Google Scholar] [CrossRef]
- Qian, J.; Law, C.K. Regimes of coalescence and separation in droplet collision. J. Fluid Mech. 1997, 331, 59–80. [Google Scholar] [CrossRef]
- Gotaas, C.; Havelka, P.; Jakobsen, H.A.; Svendsen, H.F. Effect of viscosity on droplet-droplet collision outcome: Experimental study and numerical comparison. Phys. Fluids 2007, 19, 102106:1–102106:17. [Google Scholar]
- Pan, K.; Law, C.K.; Zhou, B. Experimental and mechanistic description of merging and bouncing in head-on binary droplet collision. J. Appl. Phys. 2008, 103, 064901:1–064901:11. [Google Scholar]
- Focke, C.; Bothe, D. Computational analysis of binary collisions of shear-thinning droplets. J. Non-Newton. Fluid Mech. 2011, 166, 799–810. [Google Scholar] [CrossRef]
- Dupuy, P.M.; Lin, Y.; Fernandino, M.; Jakobsen, M.H.; Svendsen, H.M. Modeling of high pressure binary droplet collisions. Comput. Math. Appl. 2011, 61, 3564–3576. [Google Scholar] [CrossRef]
- Nikolopoulos, N.; Nikas, K.-S.; Bergeles, G. A numerical investigation of central binary collision of droplets. Comput. Fluids 2009, 38, 1191–1202. [Google Scholar] [CrossRef]
- Melissa, O. Experiments on droplet collisions, bounce, coalescence and disruption. Prog. Energy Combust. Sci. 1997, 23, 65–79. [Google Scholar] [CrossRef]
- Nikolopoulos, N.; Theodorakakos, A.; Bergeles, G. Off-centre binary collision of droplets: A numerical investigation. Int. J. Heat Mass Transf. 2009, 52, 4160–4174. [Google Scholar] [CrossRef]
- Nikolopoulos, N.; Strotos, G.; Nikas, K.-S.; Bergeles, G. The effect of Weber number on the central binary collision outcome between unequal-sized droplets. Int. J. Heat Mass Transf. 2012, 55, 2137–2150. [Google Scholar] [CrossRef]
- Dai, M.; Schmidt, D.P. Numerical simulation of head-on droplet collision: Effect of viscosity on maximum deformation. Phys. Fluids 2005, 17, 041701:1–041701:4. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, D.B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Rahimi, S.; Peretz, A.; Natan, B. On shear rheology of gel propellants. Propellants Explos. Pyrotech. 2007, 32, 165–174. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liu, Z.; Wu, J.; Zhen, H.; Hu, X. Numerical Simulation on Head-On Binary Collision of Gel Propellant Droplets. Energies 2013, 6, 204-219. https://doi.org/10.3390/en6010204
Liu Z, Wu J, Zhen H, Hu X. Numerical Simulation on Head-On Binary Collision of Gel Propellant Droplets. Energies. 2013; 6(1):204-219. https://doi.org/10.3390/en6010204
Chicago/Turabian StyleLiu, Zejun, Jianjun Wu, He Zhen, and Xiaoping Hu. 2013. "Numerical Simulation on Head-On Binary Collision of Gel Propellant Droplets" Energies 6, no. 1: 204-219. https://doi.org/10.3390/en6010204



