1. Introduction
Recent years have seen a particular focus on renewable energies such as solar, wind energy, biomass, geothermal and waste heat recovery from industrial processes. In addition to their economic advantages from reducing fossil fuel consumption, the use of these energies contributes to the reduction of atmospheric emissions of greenhouse gases.
Exothermic processes offer more than final products for which they are incurred, exergy flows in excess from the effluents. These quantities of exergy have not been subject of transfer or conversion, or even destruction during the previous evolutions and therefore remain in thermal form present in dry or moist flue gases before they are totally destroyed through exhaust or via gas coolers when the effluent is re-employed in downstream process.
With regards to the specificities of release conditions of the resource, its molar composition and the thermodynamic constraints that it may have, no fluid can be presented a priori as the best recovery solution, especially when comparing dry exergy resources and highly moist ones. Therefore, as a first step, available resources will be characterized.
Liu
et al. [
1] have studied analytically the influence of the working fluid, by its properties and its operating conditions, on system performances and highlighted, when calling to thermodynamic optimization, the interest of focusing studies on global efficiency of the whole system rather than thermal efficiency of the working cycle. Other studies, performed by Madhawa
et al. [
2] and Kanoglu
et al. [
3] are based on exergy approaches to properly parameterize ORCs for geothermal applications. Schuster
et al. [
4] have pointed out that R-245fa, a hydrofluorocarbon (HFC), is suitable for a power plant recovering heat from a thermal source at an initial temperature of 210 °C. This fluid is studied in this paper for lower hot source inlet levels and compared to other alternatives.
2. Resources Characterization
Waste heat recovery related to ENERCO_LT project covers various gas production plants, such as air separation units, Steam Methane Reforming plants (SMR) and oxy-combustion processes.
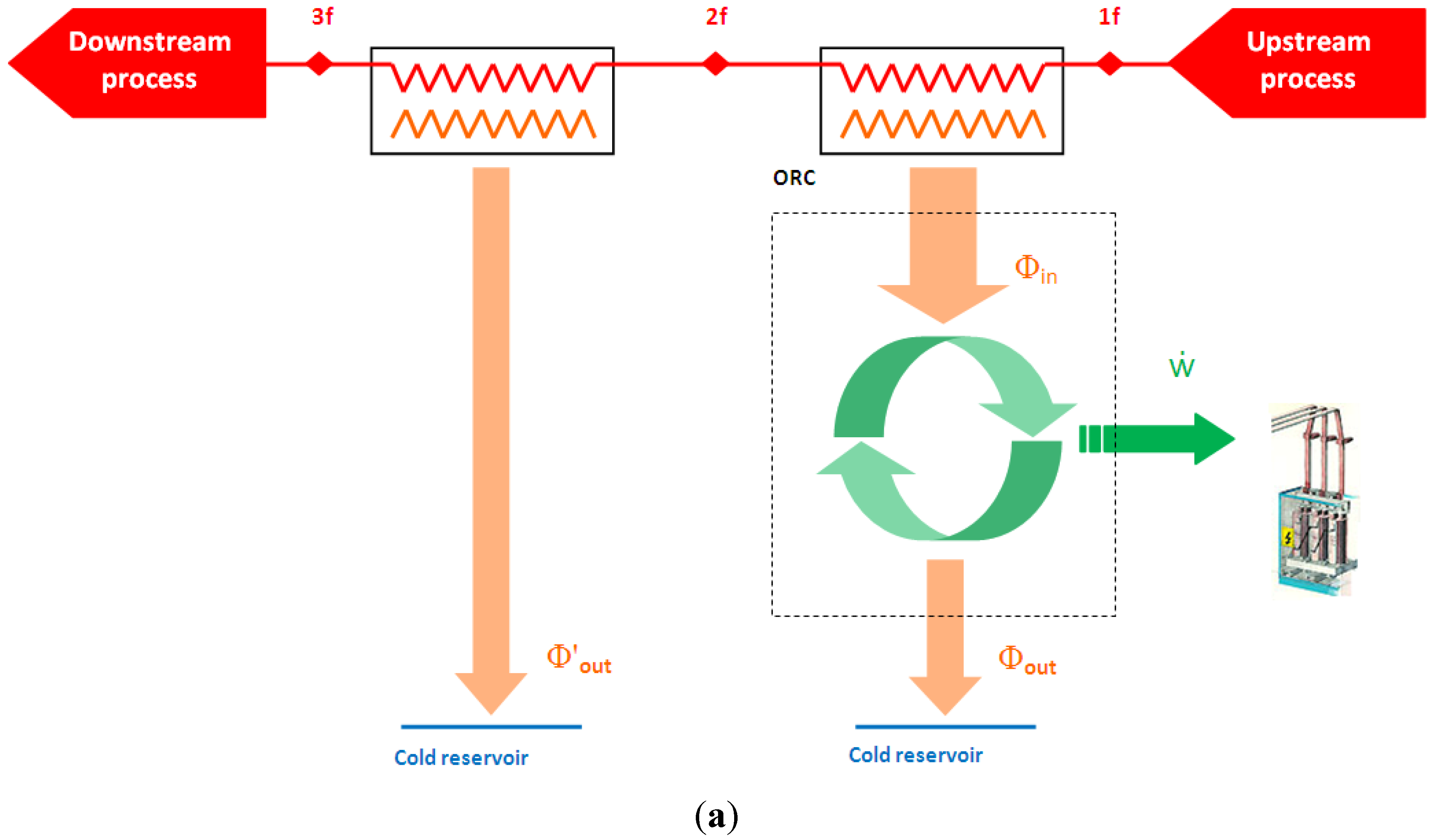
When considering an ordinary recovery system, as shown in
Figure 1a, the overall available resource is defined as bounded by the upstream process outlet 1
f and the downstream process inlet 3
f. Overall exergy resources are determined according to the cooling conditions of effluents and their molar compositions as expressed below:
Two resources are considered, summarized in
Table 1. Exergy calculations take as reference the ambient temperature
To of 15 °C.
Figure 1.
(a) Scheme of one cycle recovery process; (b) Scheme of two-cycle cascade recovery process.
Figure 1.
(a) Scheme of one cycle recovery process; (b) Scheme of two-cycle cascade recovery process.
Table 1.
Resource characteristics.
Table 1.
Resource characteristics.
| Resource | T1f [°C] | P [bar] | Water molarfraction [%] | Mass flowrate [kg/s] | Dew point [°C] | Ėx3f1f [kW] |
|---|
| almost dry | 165 | 25 | 2 | 152.2 | 75 | 4950 |
| moist | 150 | 1 | 20 | 130.2 | 60 | 6148 |
The first resource, with low humidity content, is cooled from 165 °C to 25 °C and shows an exergy flow about 4.9 MW thanks to a high mass flow rate. The second resource, highly moist, is cooled from 150 °C to 25 °C and shows an exergy flow about 6.1 MW thanks to an additional latent heat provided by the condensation of water vapour at low temperature.
From these exergy resources, work production can be evaluated from the exergy efficiency of the engine cycles
ηex. For a single recovery engine cycle (
Figure 1a):
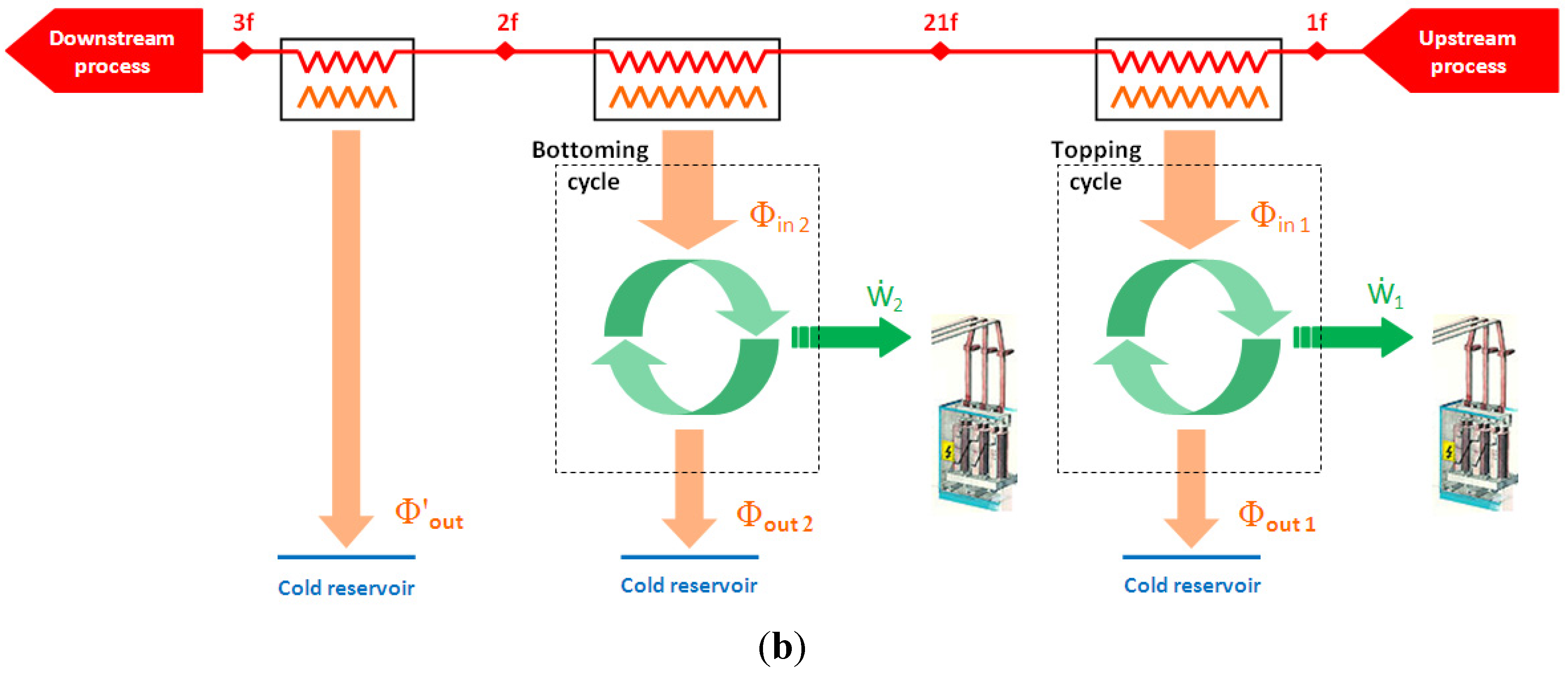
For a cascading recovery engine cycle (
Figure 1b):
Figure 2 estimates the production of work according to the discharge temperature
T2f for a fixed exergy efficiency of the cycle equal to 50%. The representation shows that the best global performance is achieved with low discharge temperature
T2f. Moreover, it can be seen that condensing process significantly increases the exergy resource, and then the work production. For the moist resource, the change of slope when crossing the dew point is particularly important.
Nevertheless, this first study does not take into account the fitting between the cooled flow (the resource) temperature profile and the working fluid temperature profile which could be difficult to match with a single recovery engine cycle. As a consequence, 50% exergy efficiency could be not reachable with such a cycle, and would require a cascading cycle (
Figure 1b); the first one working on the right of the dew point (
T21f ≈
Tdew), and the second one taking advantage of the condensing process.
Figure 2.
Produced power calculated for 50% cycle exergy efficiency.
Figure 2.
Produced power calculated for 50% cycle exergy efficiency.
3. Exergy Analysis
It is well known that exergy efficiency of an engine can be expressed according to the exergy destructions Ėxd,i of the constituting components: heat exchangers, pumps, turbines, ducts, etc.
For a single cycle, exergy efficiency (Equation 2) can also be written as:
This form is particularly interesting because it emphasizes which processes are mainly responsible of the exergy efficiency degradation. In a vapour power plant, the irreversibilities are generally qualified as internal or external irreversibilities. The internal exergy destruction is caused by:
friction forces at the origin of pressure losses in the internal structures of the system, where the work of these forces is transformed into heat,
internal heat transfer at finite difference temperature, in case of internal heat recovery.
The external irreversibilities are caused by:
heat transfers at finite difference temperatures between the working fluid and external hot or cold sources,
mechanical transfer of work.
The cycle exergy destruction covers the internal and external irreversibilities that occur inside the working cycle, basically in feed pump, vapour generator, turbine, condenser and eventually the regenerator when adopted [
5]. Moreover, it is denoted by exergy loss, the irreversibility occurring outside the working cycle; that is the exergy flow
Ėx3f2f excluded from the recovery process.
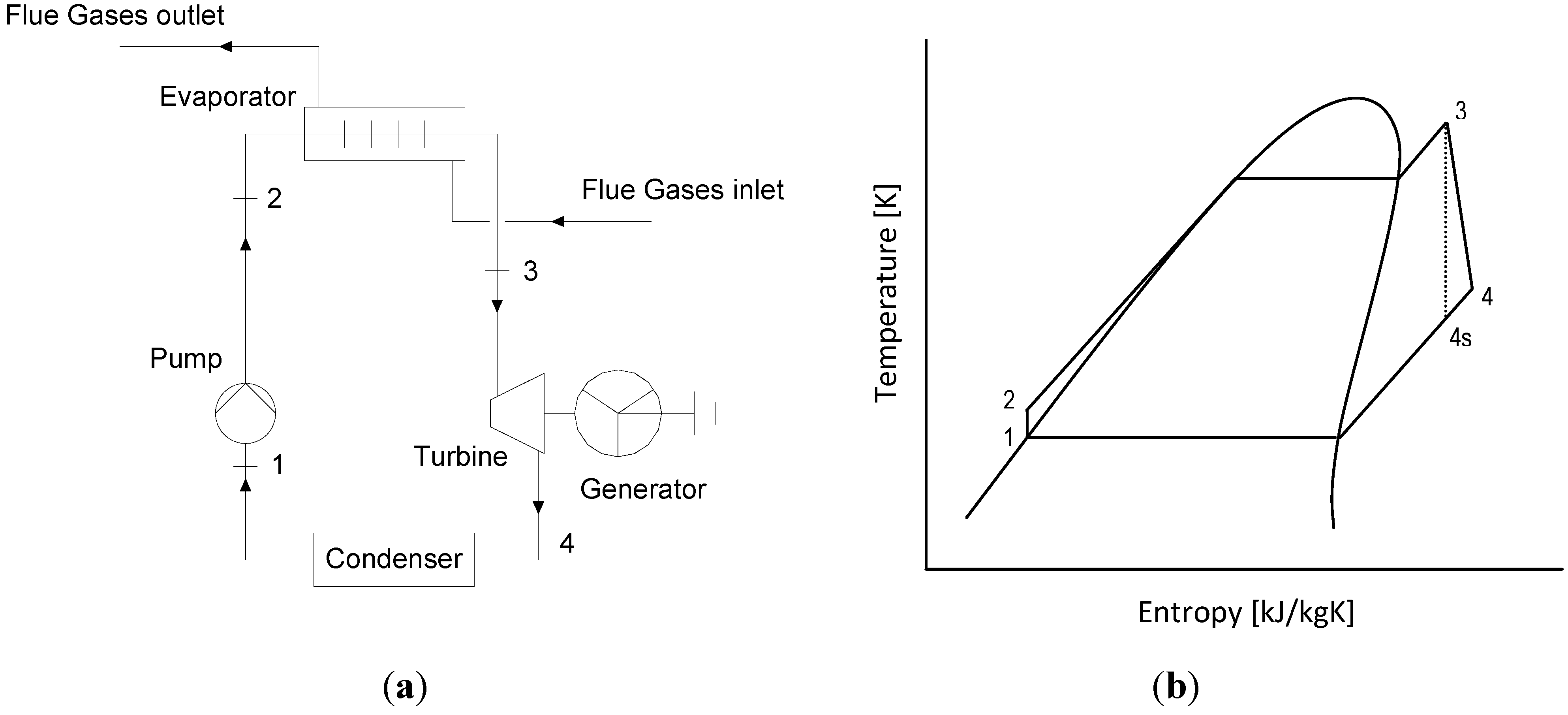
The evolution of working fluid into the investigated cycle can be summarized in four unitary operations as shown in
Figure 3. The working fluid leaves the condenser as a saturated liquid at temperature
T1 and condensation pressure
PL (point 1), then it is compressed into a feed pump to an evaporation pressure
PH (point 2) with a proper isentropic efficiency
ηs,p. At the outlet of the pump, the fluid is heated at constant pressure in the evaporator until it becomes saturated in vapour or superheated, and reaches
T3 temperature (point 3). The vapour is then expanded in a turbine to the condenser pressure
PL (point 4). During expansion, the fluid delivers mechanical work with a proper isentropic efficiency
ηs,t. Finally, the fluid passes through the condenser releasing heat at constant pressure until it becomes saturated in liquid.
Figure 3.
Simple ORC. (a) Schematic diagram; (b) (T–s) diagram.
Figure 3.
Simple ORC. (a) Schematic diagram; (b) (T–s) diagram.
For each unitary process (i.e., for each component), thermal and/or mechanical power and exergy destruction is evaluated from the energy and exergy balances, assuming stationary regime.
Pump (1 to 2): Assuming adiabatic compression, energy and exergy balances can be written as:
Isentropic efficiency is defined as the ratio of ideal mechanical power (
i.e., reversible pump) and actual mechanical power:
The power consumed by the pump then becomes:
Equation 5 gives then the specific enthalpy of point 2 (which is then completely defined, pressure
P2 being known). Equation 6 gives the exergy destruction by the pumping process:
Vapour generator (2 to 3): Isobaric transformation is assumed for the working fluid. For the hot source, gas stream is cooled to an outlet temperature
T2f, taking as design parameter. Energy and exergy balances are given by:
Introducing the equivalent temperature of transformation (2 to 3) and (1
f to 2
f), and the heat power transferred from the hot gas to the cycle
Φin:
Exergy destruction in the vapour generator can be expressed by:
with:
Turbine (3 to 4): Except for the isentropic efficiency definition, energy and exergy balance are similar to those write to the pump. For a turbine, isentropic efficiency is defined as the ratio of actual mechanical power and ideal mechanical power:
Then, actual power, specific enthalpy
h4 and exergy destruction are:
Condenser (4 to 1): Isobaric operation is assumed, and condensing heat is transferred to cooling water, supposed at exergy reference temperature
To. Energy and exergy balances are:
Equivalent temperature can also be introduced here:
and exergy destruction in the condenser could be expressed as follows:
The total exergy destroyed into the working cycle is equal to the sum of the irreversibilities generated within each component:
Finally, the global destruction is equal to the sum of the exergy destroyed inside and outside the cycle:
and the global exergy efficiency
ηex,g can be written as:
According to the Second Law of Thermodynamics, within a system having real evolutions, it is impossible to convert the whole available thermal energy into useful work. The contribution to the exergy destruction in the system differs from one component to another; it is dictated in part by the properties of the employed fluid and in another part by the evolution conditions of this fluid within components of the system. Exergy analysis shows also that it is not recommended to optimize separately the components as if each treated process was isolated from the others. Thus, in order to reach a final design with minimum overall irreversibilities, the working fluid should be selected with care and operating conditions shall be subject to systemic optimization based on simultaneous analysis of all the alterations produced.
4. Static Studies of Recovery Solutions
Calculation tools for recovery process simulation and optimization were created and developed according to the distinctive investigated designs and in convenience with the operating static regimes (subcritical and supercritical), from the Prosim Plus 3.1 simulator [
6,
7]. The working fluid properties are calculated using REFPROP 8.0 developed by the National Institute of Standards and Technology [
8].
The challenge of technico-economic optimization consists in developing sensitivity analysis on cost variations around the pinch while thermodynamic optimization of energy systems requires that the pinch be as small as possible by bringing system near a limit case. Following calculations have been done for a quasi-limit case of 10 K pinch in vapour generator without incurring additional need for heat in the endothermic zone. Isentropic efficiencies of feed pump and turbine are set respectively to 0.9 and 0.85. As for cooling conditions, cold isobar has been fixed to a liquid saturation temperature of 25 °C.
4.1. Results and Discussion for Almost Dry Resource
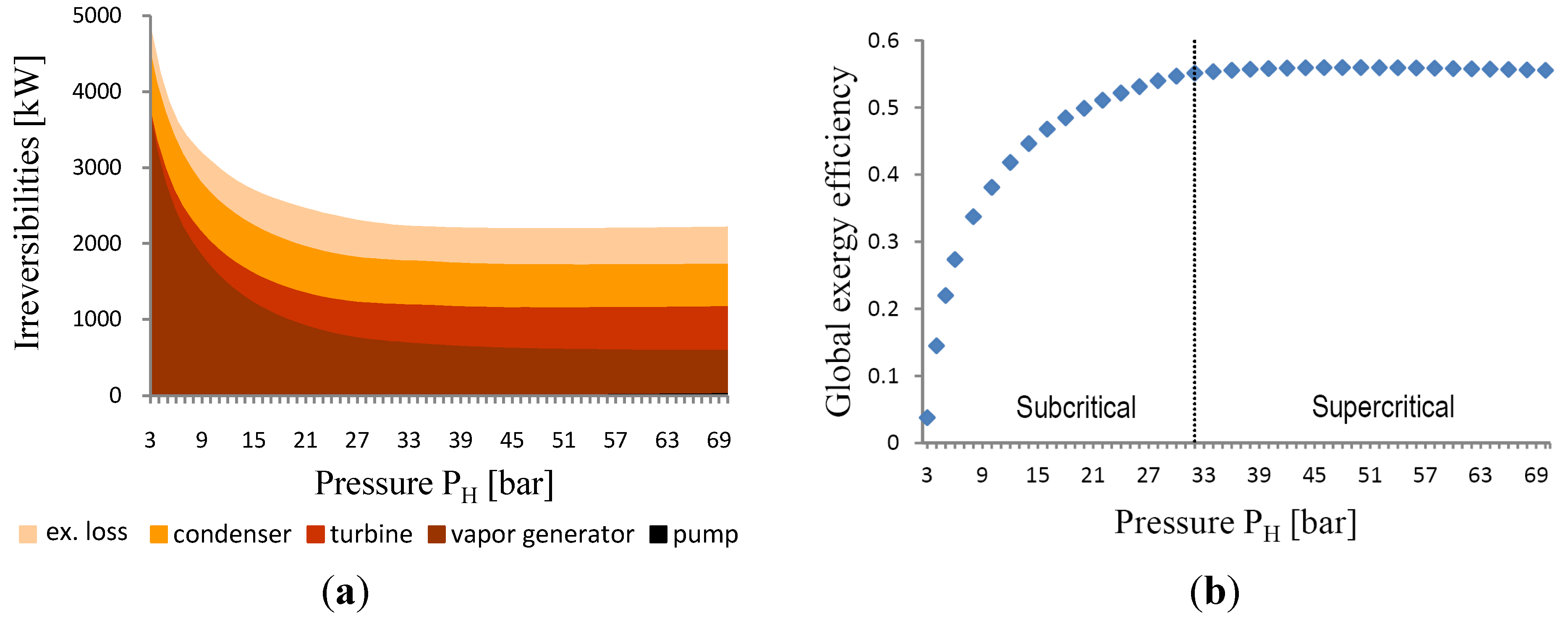
The existence in itself of pinch is at the origin of exergy destruction accompanying the cooling of hot gases. Although a minimized pinch contributes to a better cooling, however its location on the composite curve remains a sensitive point able to degrade global performances of the system.
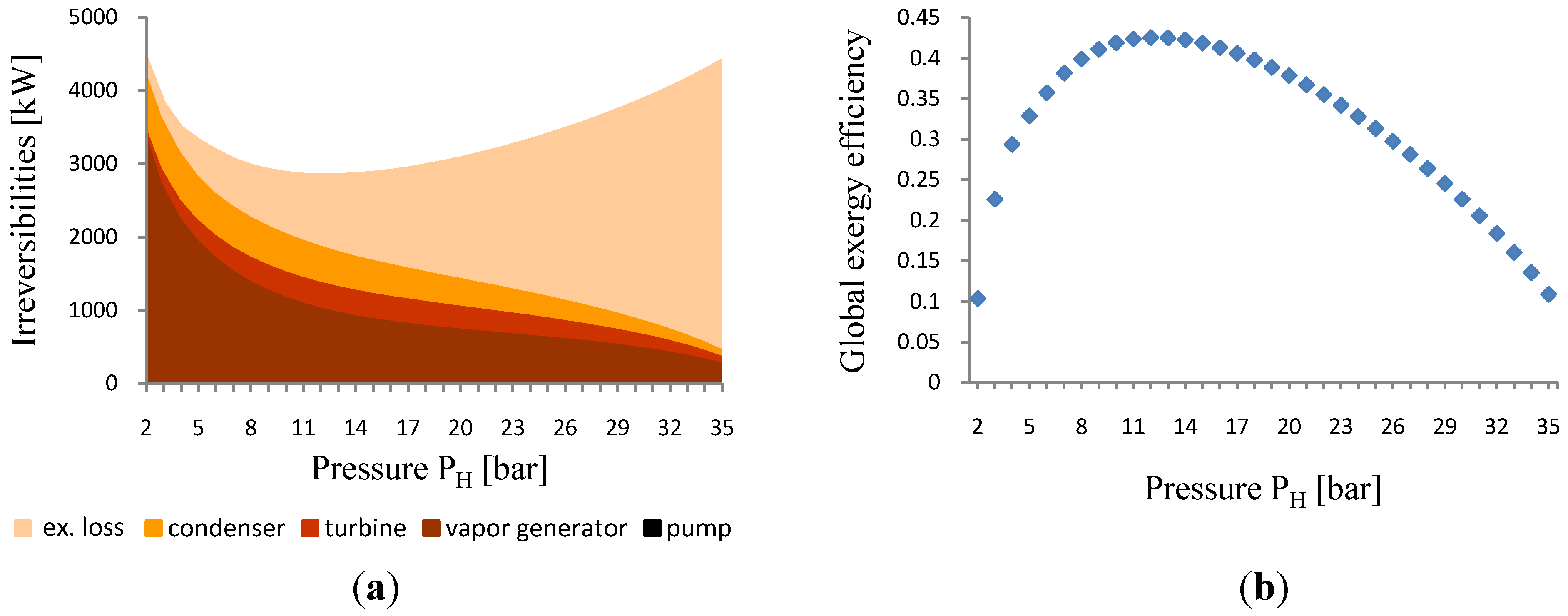
When studying a working cycle using R-245fa,
Figure 4a shows that the variation of the vaporization pressure (leading to the variation of pinch location on the composite curves and therefore the discharge temperature
T2f) does not affect the cycle exergy destruction and the exergy loss in the same manner,
i.e., if it reduces the exergy loss outside of the working cycle, it amplifies the exergy destruction inside of it and vice versa. As the final objective is to reduce the overall irreversibility of the entire system, a compromise should be found between these two irreversibilities reductions.
Otherwise, in
Figure 4b, the global exergy efficiency shows a maximum value obtained at a subcritical pressure, below which the cycle exergy destruction appears dominant and above which, the exergy loss
Ėx3f2f becomes dominant. Such significant optimum corresponds to an appropriate phase change temperature, not very high and not close to the hot source inlet temperature.
Figure 4.
R-245fa global performance from almost dry resource. (a) Irreversibilities diagram; (b) Global exergy efficiency behavior.
Figure 4.
R-245fa global performance from almost dry resource. (a) Irreversibilities diagram; (b) Global exergy efficiency behavior.
Figure 4 clearly illustrates the contribution of exergy analysis in optimization problems. As for the choice of the working fluid to use, this will depend on its thermophysical properties and on the resource requirement, mainly the critical temperature, latent heat and the slopes of both saturation lines on the (
T–s) diagram.
As seen in
Figure 6a, R-245fa cannot be regarded as an appropriate solution since its critical temperature is slightly lower than the hot source inlet temperature. This prevents adequate temperature matching between the flue gases and the working fluid. It results in an acute pinch at the end of the preheating zone. In this case, and because of the high critical temperature, systemic optimization seeking to maximize the global efficiency leads to a ratio between the vaporization latent and sensible preheating heat close to one. However, even at the optimum, both cycle exergy destruction and exergy loss remain important.
As seen in
Figure 6b, R-236fa is identified as an interesting working fluid according to the almost dry resource. Thanks to its properties, this fluid leads to a better temperature matching between the hot and cold flows with a high temperature level at the entrance to turbine. In this case, sensible preheating, far exceeding vaporization latent heat, leads to high subcritical temperature, close to the critical one, limiting therefore the vapour generator irreversibilities.
Figure 5.
R-236fa global performance from almost dry resource. (a) Irreversibilities diagram; (b) Global exergy efficiency behavior.
Figure 5.
R-236fa global performance from almost dry resource. (a) Irreversibilities diagram; (b) Global exergy efficiency behavior.
Moreover, it can be seen from
Figure 5, that the maximum value of global exergy efficiency is spotted at supercritical pressure where the cycle reaches a triangular shape. In this case, the optimum issue is no longer of such significance, especially when operating at high supercritical pressures.
Table 2 indicates that R-236fa, leads to an increase of the optimal global efficiency of only 2% compared to subcritical design
i.e., net power gain of 62 kW.
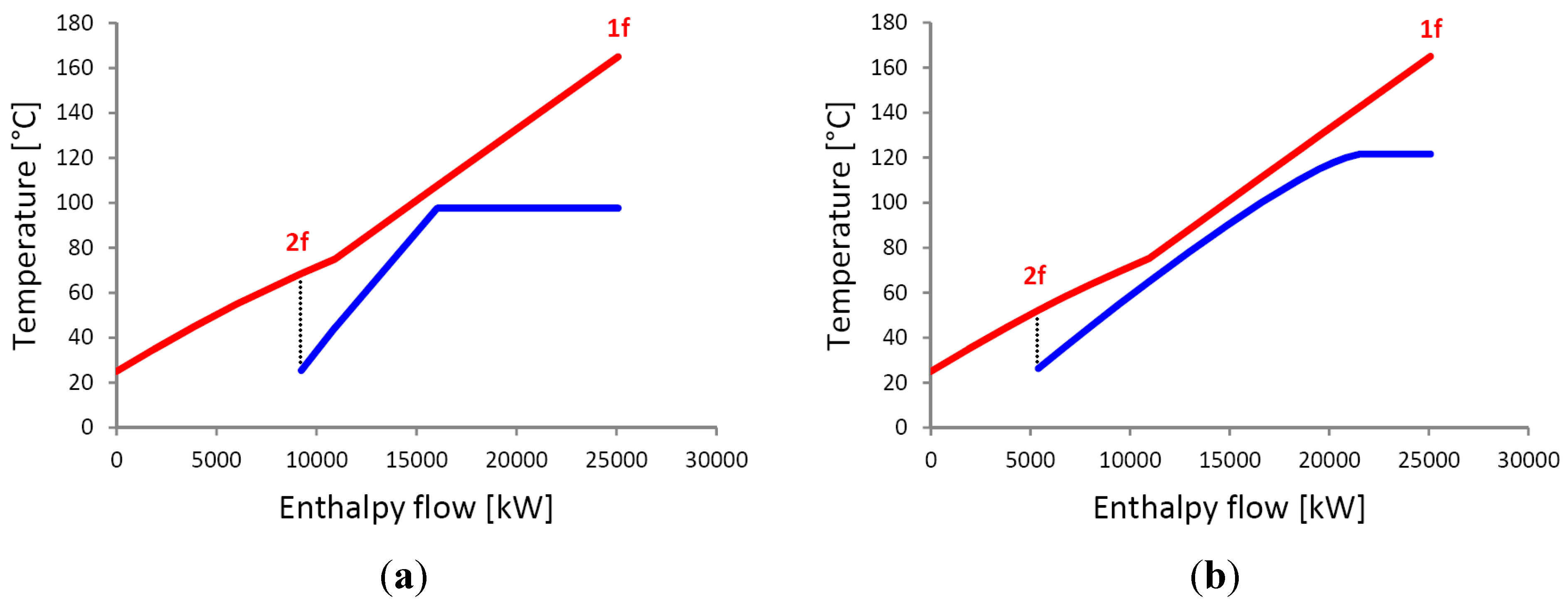
Figure 6.
Almost dry resource composite curves. (a) R-245fa solution; (b) R-236fa solution.
Figure 6.
Almost dry resource composite curves. (a) R-245fa solution; (b) R-236fa solution.
Using dry and isentropic fluids with high boiling point is interesting because they will not require superheat, especially when this latter is able to degrade global system performances by amplifying the exergy loss. For that reason, both subcritical cycles using the R-245fa and R-236fa do not foresee superheat. As for transcritical cycle, the rise of vapour temperature increases the exergy loss and should be subject to exergy analysis.
The ORC employing R-236fa, even proved as the better solution for the recovery problem, cannot be used in practice, due to its high Global Warming Potential value (GWP). Despite a critical temperature slightly outside the appropriate range, R-1234yf, an environmentally friendly hydrofluoro-olefin (HFO), is a good compromise between environmental impact and performance and is applicable for the dry resource recovery process. Performances of subcritical and transcritical cycles using this fluid are summarized in
Table 2.
Table 2.
Almost dry resource: cycle performances.
Table 2.
Almost dry resource: cycle performances.
| Fluid | GWP | PC [bar] | TC [°C] | PL [bar] | PH [bar] | TIT [°C] | TET [°C] | T2f [°C] | C [kJ/m3] | W [kW] | ηex [%] | ηex,g [%] |
|---|
| R-245fa | 950 | 36.5 | 154 | 1.4 | 12 | 97.7 | 43.3 | 68.6 | 2248 | 2107 | 52.5 | 42.6 |
| R-236fa | 9400 | 32 | 124.9 | 2.7 | 30 | 121.6 | 33.9 | 52.2 | 9801 | 2710 | 59.7 | 54.7 |
| 2.7 | 48 | 143.4 | 29.9 | 52.8 | 19,741 | 2772 | 61.2 | 56 |
| R-1234yf | 4 | 32.6 | 94.8 | 6.7 | 32 | 95.6 | 25.2 | 44.9 | 5352 | 2376 | 50.6 | 48 |
| 6.7 | 70* | 142.6 | 37.5 | 54.7 | 16,440 | 2676 | 59.8 | 54.1 |
5. Conclusions
Systemic optimization by extension of pinch method, although it correctly optimizes the system, does not adapt it to the specificities of the available resource, since the fluid has influence on system performance not only by its operating conditions, but also by its thermophysical properties.
It has been demonstrated that, when facing a recovery problem, a priori bets on designs and fluids cannot be made before assessing their adequacy to the requirements of the particular problem. Based on the First and Second Law of Thermodynamics, the optimized solution can be identified via an appropriate design, an adequate working fluid and under suitable working conditions, able to overcome pinch problem dictated by fluid properties and thermodynamic constraints imposed by the resource itself. However, other constraints, predominately technological and environmental, come into consideration and have to be included in the optimization process.
In particular, it can be noted that the presence of contaminants and the possible condensation process involved for the moist resource will require high quality materials for the heat exchangers. Thus, an economic analysis is very important after the thermodynamically optimized configuration is set. Furthermore, a multi-objective optimization would be interesting to look at the trade-offs of the system between efficiency and cost.