A New Uncertainty-Based Control Scheme of the Small Modular Dual Fluid Reactor and Its Optimization
Abstract
:1. Introduction
2. Description of SMDFR and Control System
2.1. Small Modular Dual Fluid Reactor
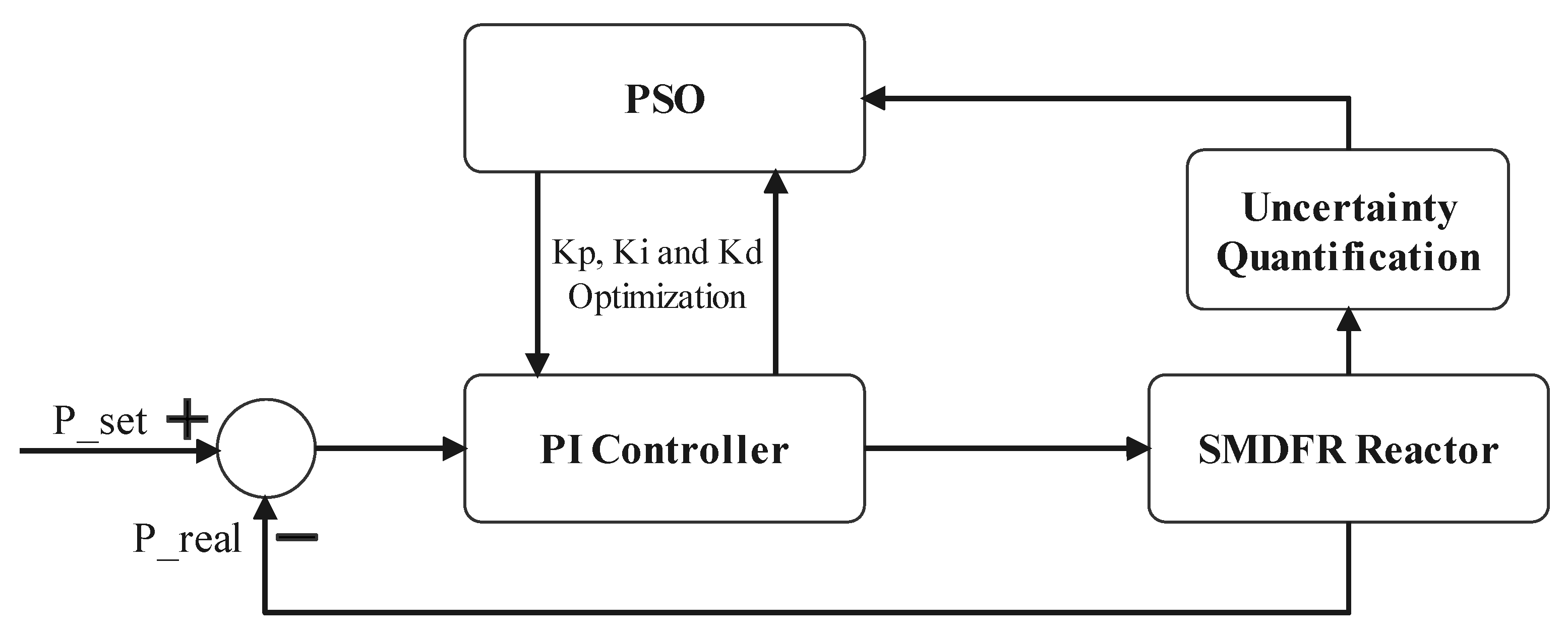
2.2. Uncertainty-Based Particle Swarm Optimization of the Control System
3. Methodology
3.1. Reactor Core Modeling
3.1.1. Data Used for Analysis
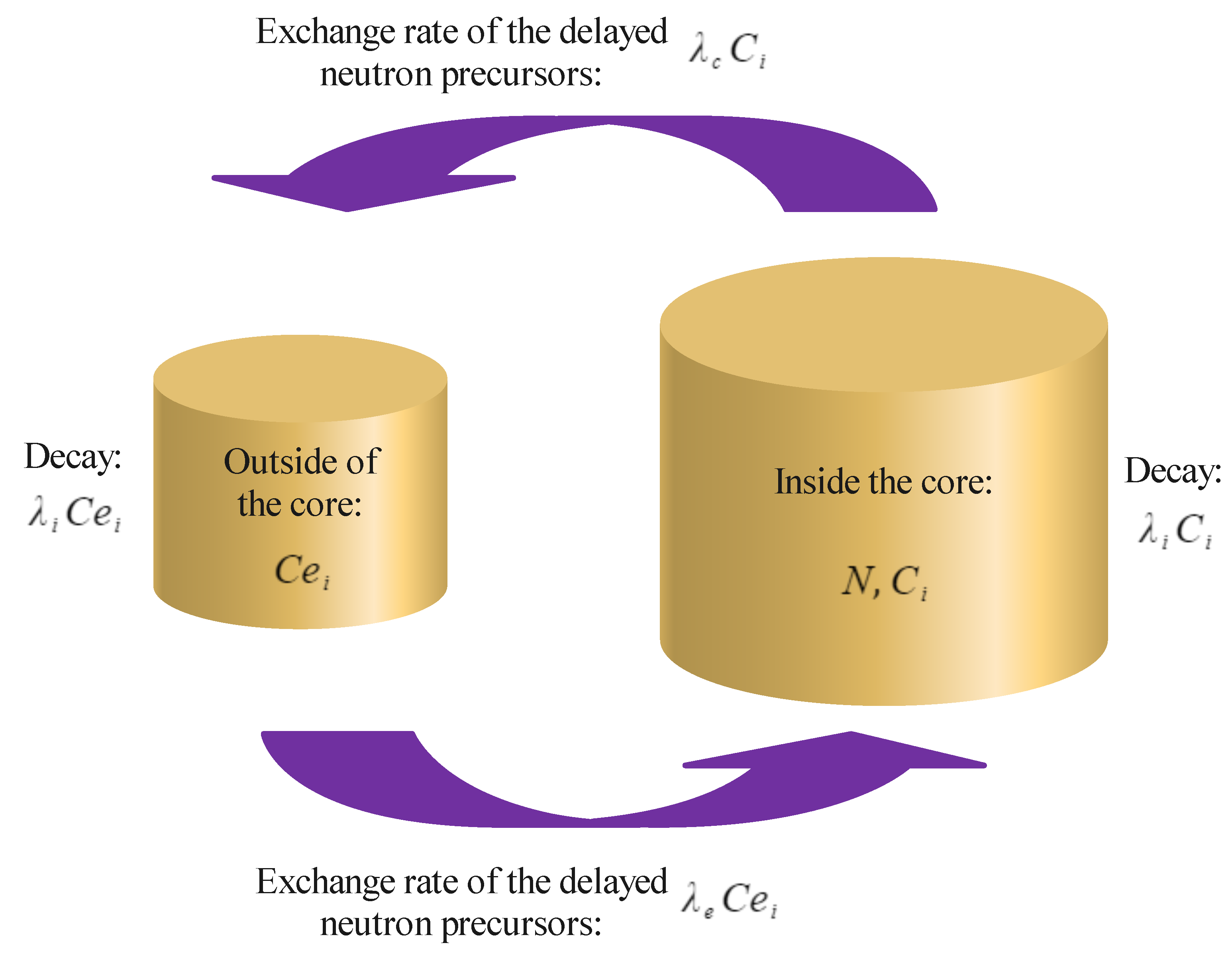
3.1.2. Modified Point Kinetic Model
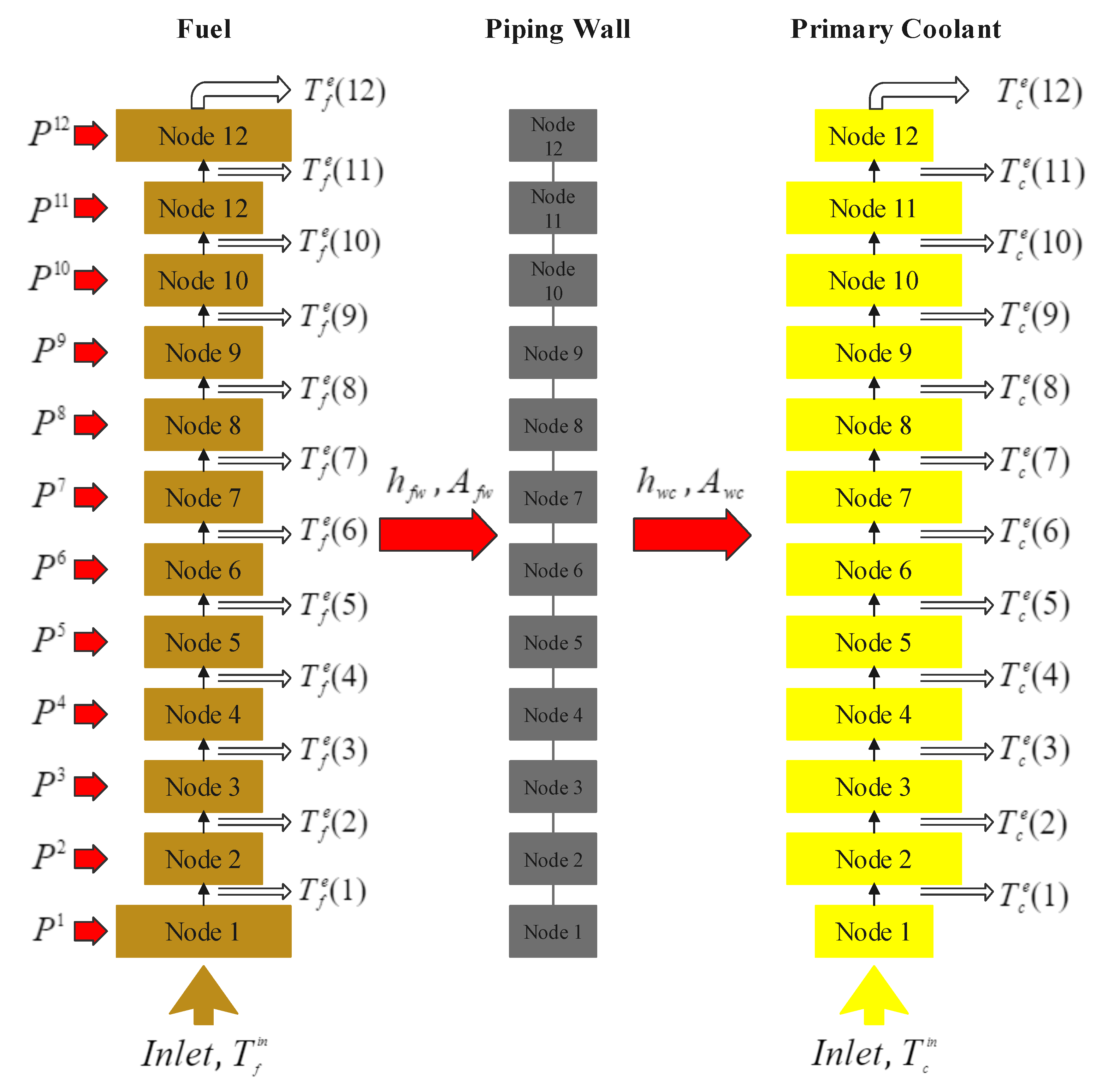
3.1.3. Thermodynamic Model
3.1.4. Reactivity Feedback
3.2. PI Controller
3.3. Uncertainty Quantification
3.3.1. Input Uncertainties of the Numerical Model
- Thermal power, mass flow rates, and inlet temperatures are specified with reference to the reported experimental uncertainty in the literature [18].
- The heat capacity of liquid lead (coolant) is specified according to the uncertainty bounds found in [19].
- The heat capacity of molten salt (fuel) is specified referring to the value of liquid lead. Since no data are available for the molten salt, and there is a heat transfer process between the two fluids, a consistent uncertainty range is applied to both of them in order to achieve a conservative assumption for the heat transfer process. In the future, its value will be adapted when experimental data of the molten salt are generated/available.
- Temperature feedback coefficients and heat transfer coefficients are taken with a ±10% uncertainty range from the default value. Since no data are available, this assumption is considered to be sufficiently conservative. When more data are obtained, their ranges will be updated accordingly.
3.3.2. Tolerance Limits
3.3.3. Sensitivity Quantification
3.4. PSO Optimization with Uncertainties
4. Results and Discussion
4.1. Verification
4.2. Feasibility of the Control System
4.3. Optimization
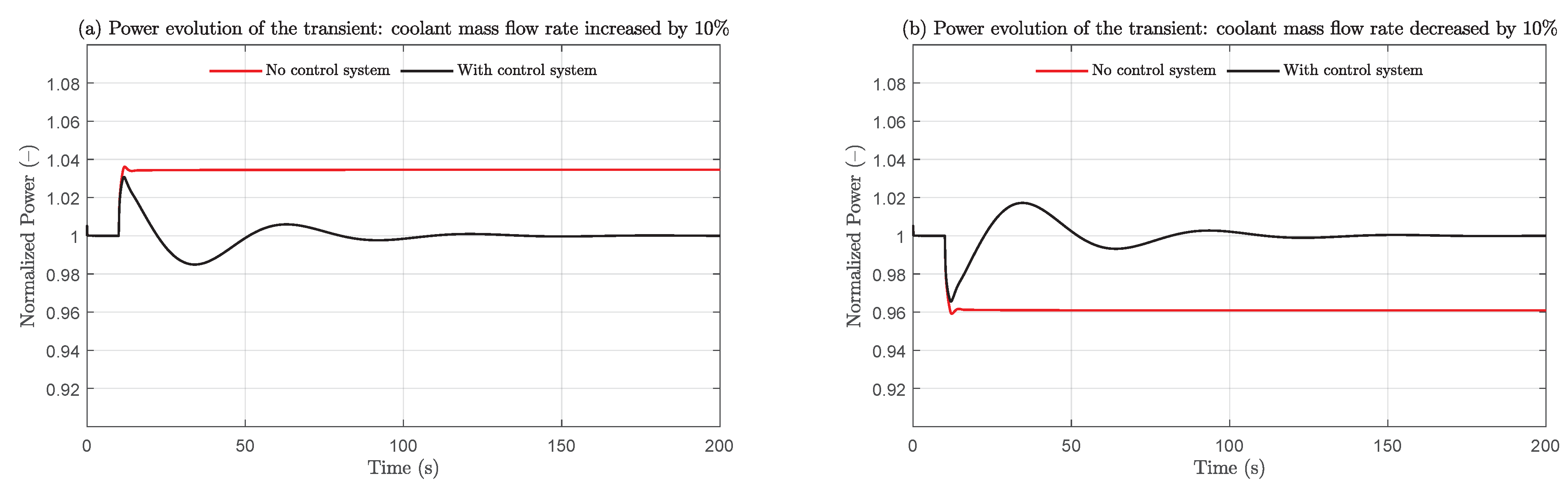
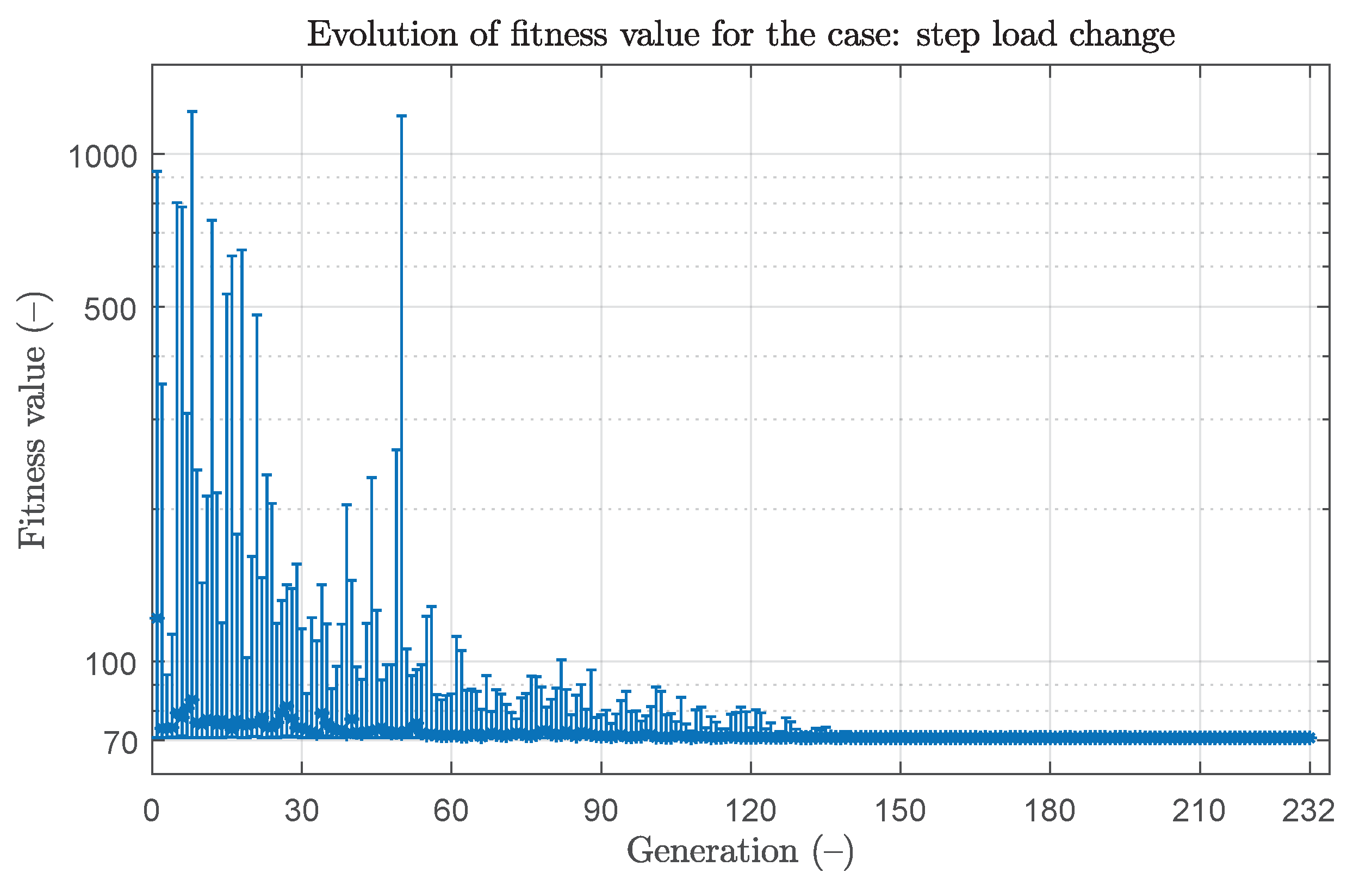
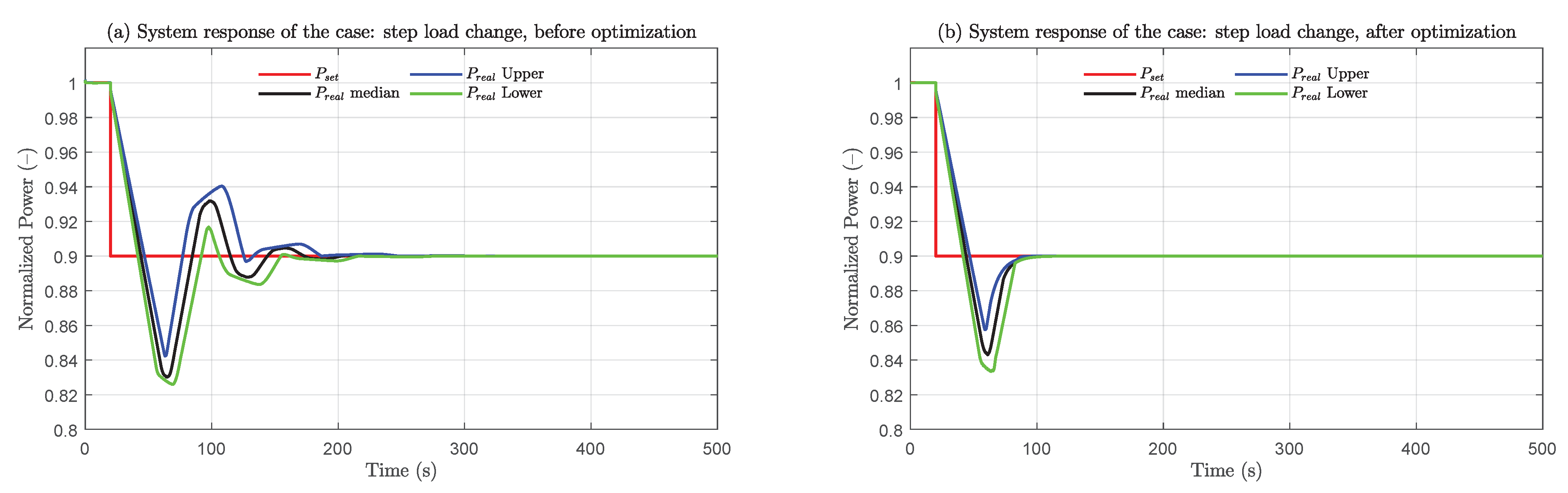
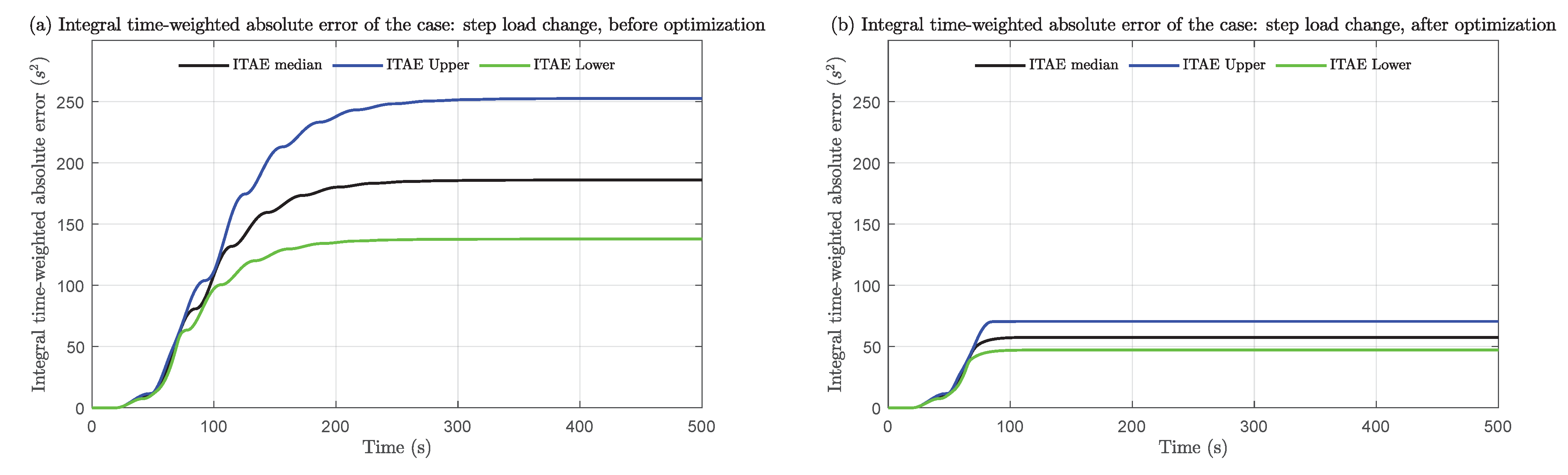
4.3.1. Step Load Change
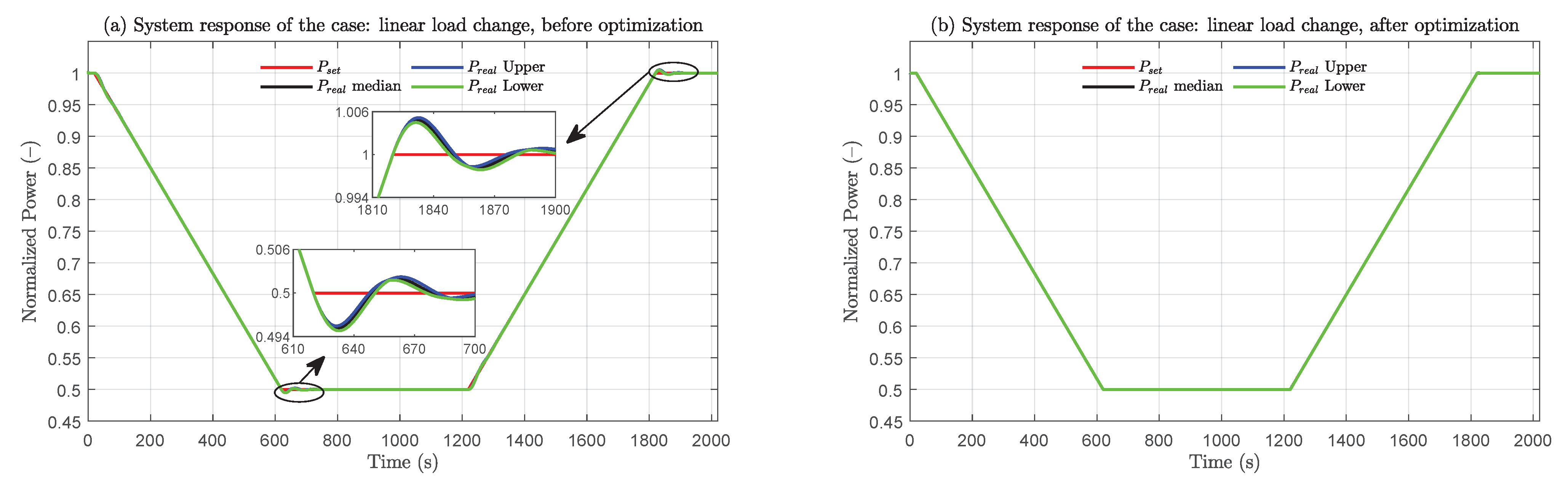
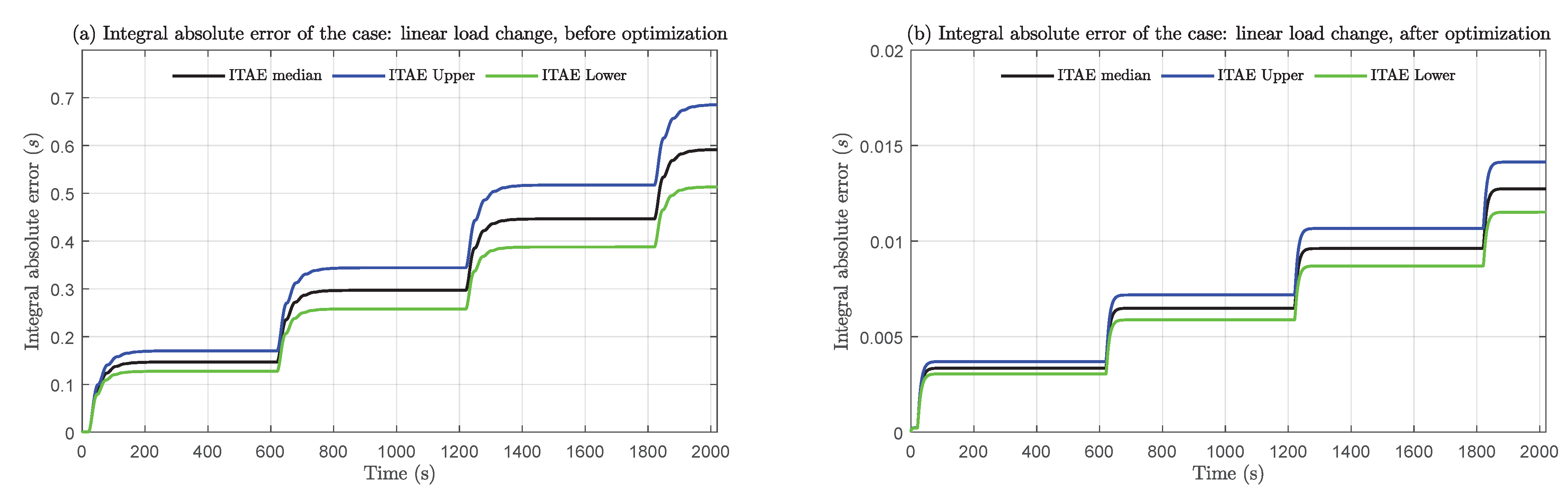
4.3.2. Linear Load Change
4.4. Performance Assessment
4.5. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SMDFR | Small modular dual fluid reactor |
| PSO | Particle swarm optimization |
| DNP | Delayed neutron precursors |
| FP | Full power |
| IAE | Integral absolute error |
| ITAE | Integral time-weighted absolute error |
| CFD | Computational fluid dynamics |
| SRC | Standardized regression coefficient |
| S1 | First-order sensitivity index |
| ST | Total effect index |
| Mean neutron generation time | |
| Fraction of the i-th DNP group | |
| Overall fraction of the DNP groups | |
| Decay constant | |
| Total neutron flux | |
| Inverse of the neutron velocity | |
| Initial neutron density | |
| Nominal power | |
| Transit time inside the core | |
| Transit time outside of the core | |
| Drifting-induced decay constant inside the core | |
| Drifting-induced decay constant outside of the core | |
| Reactivity feedback coefficient of fuel | |
| Reactivity feedback coefficient of coolant | |
| Initial reactivity | |
| Initial concentration of the i-th DNP group inside the core | |
| Initial concentration of the i-th DNP group outside of the core | |
| Heat transfer area between fuel and pipe wall | |
| Heat transfer area between coolant and pipe wall | |
| Mass flow rate of fuel | |
| Mass flow rate of coolant | |
| Mass of fuel | |
| Mass of pipe wall | |
| Mass of coolant | |
| Heat capacity of fuel | |
| Heat capacity of pipe wall | |
| Heat capacity of coolant | |
| Heat transfer coefficient between fuel and pipe wall | |
| Heat transfer coefficient between coolant and pipe wall | |
| Fuel temperature | |
| Pipe wall temperature | |
| Coolant temperature | |
| Fuel inlet temperature | |
| Coolant inlet temperature | |
| Difference between the set value and the real (measured) value | |
| Proportional gain | |
| Integral gain |
References
- Robertson, R.; Briggs, R.; Smith, O.; Bettis, E. Two-Fluid Molten-Salt Breeder Reactor Design Study (Status as of 1 January 1968); Technical Report; Oak Ridge National Lab: Oak Ridge, TN, USA, 1970. [Google Scholar]
- Singh, V.; Lish, M.R.; Wheeler, A.M.; Chvála, O.; Upadhyaya, B.R. Dynamic modeling and performance analysis of a two-fluid molten-salt breeder reactor system. Nucl. Technol. 2018, 202, 15–38. [Google Scholar] [CrossRef]
- Taube, M.; Ligou, J. Molten plutonium chlorides fast breeder reactor cooled by molten uranium chloride. Ann. Nucl. Sci. Eng. 1974, 1, 277–281. [Google Scholar] [CrossRef]
- Huke, A.; Ruprecht, G.; Weißbach, D.; Gottlieb, S.; Hussein, A.; Czerski, K. The Dual Fluid Reactor—A novel concept for a fast nuclear reactor of high efficiency. Ann. Nucl. Energy 2015, 80, 225–235. [Google Scholar] [CrossRef]
- Wang, X.; Macian-Juan, R. Steady-state reactor physics of the dual fluid reactor concept. Int. J. Energy Res. 2018, 42, 4313–4334. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Q.; He, X.; Du, Z.; Seidl, M.; Macian-Juan, R.; Czerski, K.; Dabrowski, M. Neutron physical feasibility of small modular design of Dual Fluid Reactor. In Proceedings of the International Conference on Nuclear Engineering (ICONE) 2019.27; The Japan Society of Mechanical Engineers: Tsukuba, Ibaraki, Japan, 2019; p. 1229. [Google Scholar]
- Sierchuła, J.; Weissbach, D.; Huke, A.; Ruprecht, G.; Czerski, K.; Da¸browski, M.P. Determination of the liquid eutectic metal fuel dual fluid reactor (DFRm) design—Steady state calculations. Int. J. Energy Res. 2019, 43, 3692–3701. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Macian-Juan, R. Preliminary hydraulic analysis of the distribution zone in the Dual Fluid Reactor concept. Prog. Nucl. Energy 2019, 110, 364–373. [Google Scholar] [CrossRef]
- Liu, C.; Li, X.; Luo, R.; Macian-Juan, R. Thermal Hydraulics Analysis of the Distribution Zone in Small Modular Dual Fluid Reactor. Metals 2020, 10, 1065. [Google Scholar] [CrossRef]
- Liu, C.; Papukchiev, A.; Macián-Juan, R. Uncertainty and sensitivity analysis of coupled multiscale simulations in the context of the SESAME EU-Project. Int. J. Adv. Nucl. React. Des. Technol. 2020, 2, 117–130. [Google Scholar] [CrossRef]
- Luo, R.; Liu, C.; Macián-Juan, R. Investigation of Control Characteristics for a Molten Salt Reactor Plant under Normal and Accident Conditions. Energies 2021, 14, 5279. [Google Scholar] [CrossRef]
- Introduction to COMSOL Multiphysics. COMSOL. 2020. Available online: https://cdn.comsol.com/doc/5.5/IntroductionToCOMSOLMultiphysics.pdf (accessed on 10 October 2021).
- CFD Module User’s Guide. COMSOL. 2020. Available online: https://doc.comsol.com/5.4/doc/com.comsol.help.cfd/CFDModuleUsersGuide.pdf (accessed on 10 October 2021).
- Heat Transfer Module User’s Guide. COMSOL. 2020. Available online: https://doc.comsol.com/5.4/doc/com.comsol.help.heat/HeatTransferModuleUsersGuide.pdf (accessed on 10 October 2021).
- Keepin, G. Physics of Nuclear Kinetics; Addison-Wesley Series in Nuclear Science and Engineering; Addison-Wesley Publishing Company: Boston, MA, USA, 1965. [Google Scholar]
- Wang, X.; Liu, C.; Macián-Juan, R. Dynamics and stability analysis of DFT using U-Pu and Tru fuel salts. In Proceedings of the 2018 International Congress on Advances in Nuclear Power Plants, ICAPP 2018, Charlotte, NC, USA, 8–11 April 2018. [Google Scholar]
- Glaeser, H. GRS method for uncertainty and sensitivity evaluation of code results and applications. Sci. Technol. Nucl. Install. 2008, 2008. [Google Scholar] [CrossRef] [Green Version]
- Grishchenko, D.; Papukchiev, A.; Liu, C.; Geffray, C.; Polidori, M.; Kööp, K.; Jeltsov, M.; Kudinov, P. TALL-3D open and blind benchmark on natural circulation instability. Nucl. Eng. Des. 2020, 358, 110386. [Google Scholar] [CrossRef]
- Fazio, C.; Sobolev, V.; Aerts, A.; Gavrilov, S.; Lambrinou, K.; Schuurmans, P.; Gessi, A.; Agostini, P.; Ciampichetti, A.; Martinelli, L.; et al. Handbook on Lead-Bismuth Eutectic Alloy and Lead Properties, Materials Compatibility, Thermal-Hydraulics and Technologies-2015 Edition; Organisation for Economic Co-Operation and Development: Paris, France, 2015. [Google Scholar]
- Krishnamoorthy, K.; Mathew, T. Statistical Tolerance Regions: Theory, Applications, and Computation; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 744. [Google Scholar]
- Noether, G.E. Elements of Nonparametric Statistics; Wiley: Hoboken, NJ, USA, 1967. [Google Scholar]
- Helton, J.C.; Johnson, J.D.; Sallaberry, C.J.; Storlie, C.B. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliab. Eng. Syst. Saf. 2006, 91, 1175–1209. [Google Scholar] [CrossRef] [Green Version]
- Glaeser, H.; Krzykacz-Hausmann, B.; Luther, W.; Schwarz, S.; Skorek, T. Methodenentwicklung und exemplarische Anwendungen zur Bestimmung der Aussagesicherheit von Rechenprogrammergebnissen. GRS Rep. 2008, 1, 86–90. [Google Scholar]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Bonyadi, M.R.; Michalewicz, Z. Particle Swarm Optimization for Single Objective Continuous Space Problems: A Review. Evol. Comput. 2017, 25, 1–54. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Chen, S. Constrained Particle Swarm Optimization. MATLAB File Exch. 2009–2018. Available online: https://www.mathworks.com/matlabcentral/fileexchange/25986 (accessed on 10 October 2021).












| Parameters | Values |
|---|---|
| Core zone D × H (m) | 0.95 × 2.0 |
| Distribution zone D × H (m) | 0.95 × 0.2 |
| Collection zone D × H (m) | 0.95 × 0.2 |
| Height of core (m) | 2.4 |
| Outer reflector diameter (m) | 1.25 |
| Tank D × H (m) | 1.65 × 3.4 |
| Number of fuel tubes | 1027 |
| Fuel pin pitch (m) | 0.025 |
| Outer/interior fuel tube diameter (m) | 0.008/0.007 |
| Outer/interior coolant tube diameter (m) | 0.005/0.004 |
| Mean linear power density (W/cm) | 609 |
| Fuel inlet/outlet temperature (K) | 1300/1300 |
| Coolant inlet/outlet temperature (K) | 973/1100 |
| Fuel inlet/in-core velocity (m/s) | 3/0.5225 |
| Coolant inlet/in-core velocity (m/s) | 5/1.3488 |
| Parameters | Value |
|---|---|
| ( ) | |
| ( ) | |
| ( ) | |
| 5.43 | |
| 10.0 | |
| 0.184 | |
| 0.1 | |
| ( ) | |
| ( ) |
| Parameters | Distribution Zone | Core Zone (1 from 10 Nodes) | Collection Zone |
|---|---|---|---|
| Fuel pipes (#) | - | - | 1027 |
| Coolant pipes (#) | 2166 | 2166 | - |
| 13.6 | 9.0 | 13.6 | |
| 10.9 | 10.3 | 10.9 | |
| 327.7 | 327.7 | 327.7 | |
| 5550.5 | 5550.5 | 5550.5 | |
| 307.7 | 116.4 | 307.7 | |
| 39.3 | 31.1 | 39.3 | |
| 219.9 | 770.5 | 219.9 | |
| 400 | 400 | 400 | |
| 690 | 690 | 690 | |
| 140.2 | 140.2 | 140.2 | |
| Heat taken by coolant (J) | 18,744,000 | 5,970,000 | 16,956,000 |
| 6546.0 | 4305.1 | 7629.5 | |
| 27,405.4 | 13,833.4 | 32,177.3 | |
| 1300.0 | - | - | |
| 973.0 | - | - |
| # | Parameters | Probability Density Function | Min. | Max. |
|---|---|---|---|---|
| 1 | Thermal power (factor) | Uniform | 0.98 | 1.02 |
| 2 | Temperature feedback coefficient of fuel (factor) | Uniform | 0.9 | 1.1 |
| 3 | Temperature feedback coefficient of coolant (factor) | Uniform | 0.9 | 1.1 |
| 4 | Mass flow rate of fuel (factor) | Uniform | 0.95 | 1.05 |
| 5 | Mass flow rate of coolant (factor) | Uniform | 0.95 | 1.05 |
| 6 | Heat capacity of fuel (factor) | Uniform | 0.95 | 1.05 |
| 7 | Heat capacity of coolant (factor) | Uniform | 0.95 | 1.05 |
| 8 | Heat transfer coefficient between fuel and wall (factor) | Uniform | 0.9 | 1.1 |
| 9 | Heat transfer coefficient between wall and coolant (factor) | Uniform | 0.9 | 1.1 |
| 10 | Fuel inlet temperature (additive) | Uniform | –2.2 | 2.2 |
| 11 | Coolant inlet temperature (additive) | Uniform | –2.2 | 2.2 |
| Parameters | Value |
|---|---|
| Fitness function | |
| Number of variables | 2 |
| Constraints | none |
| Kp | 10~10,000 |
| Ki | 10~1000 |
| Population size | 20 |
| Generations | 300 |
| Social attraction | 1.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Luo, R.; Macián-Juan, R. A New Uncertainty-Based Control Scheme of the Small Modular Dual Fluid Reactor and Its Optimization. Energies 2021, 14, 6708. https://doi.org/10.3390/en14206708
Liu C, Luo R, Macián-Juan R. A New Uncertainty-Based Control Scheme of the Small Modular Dual Fluid Reactor and Its Optimization. Energies. 2021; 14(20):6708. https://doi.org/10.3390/en14206708
Chicago/Turabian StyleLiu, Chunyu, Run Luo, and Rafael Macián-Juan. 2021. "A New Uncertainty-Based Control Scheme of the Small Modular Dual Fluid Reactor and Its Optimization" Energies 14, no. 20: 6708. https://doi.org/10.3390/en14206708






