Comprehensive Second-Order Adjoint Sensitivity Analysis Methodology (2nd-ASAM) Applied to a Subcritical Experimental Reactor Physics Benchmark: IV. Effects of Imprecisely Known Source Parameters
Abstract
:1. Introduction
2. Computation of 1st- and 2nd-Order Sensitivities of the PERP Leakage Response to Source Parameters
2.1. First-Order Sensitivities
2.2. Second-Order Sensitivities
3. Mixed Second-Order Sensitivities of the PERP Total Leakage Response with Respect to the Benchmark’s Source Parameters and Total Cross Sections
3.1. Computing the Second-Order Sensitivities
3.2. Alternative Path: Computing the Second-Order Sensitivities
3.3. Numerical Results for
3.3.1. Second-Order Relative Sensitivities , , and
3.3.2. Second-Order Relative Sensitivities , , and
4. Mixed Second-Order Sensitivities of the PERP Total Leakage Response with Respect to the Parameters Underlying the Benchmark’s Source Parameters and Scattering Cross Sections
4.1. Computing the Second-Order Sensitivities
4.1.1. Second-Order Sensitivities
4.1.2. Second-Order Sensitivities
4.2. Alternative Path: Computing the Second-Order Sensitivities
4.2.1. Second-Order Sensitivities
4.2.2. Second-Order Sensitivities
4.3. Numerical Results for
4.3.1. Results for the Relative Sensitivities
4.3.2. Results for the Relative Sensitivities
4.3.3. Results for the Relative Sensitivities
4.3.4. Results for the Relative Sensitivities
5. Mixed Second-Order Sensitivities of the PERP Total Leakage Response with Respect to the Benchmark’s Source Parameters and Fission Cross Sections
5.1. Computing the Second-Order Sensitivities
5.2. Alternative Path: Computing the Second-Order Sensitivities
5.3. Numerical Results for
6. Mixed Second-Order Sensitivities of the PERP Total Leakage Response with Respect to the Benchmark’s Source Parameters and the Average Number of Neutrons per Fission
6.1. Computing the Second-Order Sensitivities
6.2. Alternative Path: Computing the Second-Order Sensitivities
6.3. Numerical Results for
7. Mixed Second-Order Sensitivities of the PERP Total Leakage Response with Respect to the Benchmark’s Source Parameters and Isotopic Number Densities
7.1. Computing the Second-Order Sensitivities
7.2. Alternative Path: Computing the Second-Order Sensitivities
7.3. Numerical Results for
8. Quantification of Uncertainties in the PERP Leakage Response due to Uncertainties in Source Parameters
9. Discussions and Conclusions Related to the Sensitivities and Uncertainties to the Source Parameters
- (1)
- The 1st-order relative sensitivities of the PERP leakage response with respect to the source parameters for the fissionable isotopes are all positive, signifying that an increase in the source parameters will cause an increase in the total neutron leakage from the PERP sphere.
- (2)
- The 1st-order relative sensitivities for , , and for have the same value, although their absolute sensitivities differ from each other. The 1st-order relative sensitivities with respect to the source parameters of isotope 239Pu are very small, of the order of 10−4 or less. However, the 1st-order relative sensitivities with respect to the source parameters , , , and of isotope 240Pu are quite large, with values close to 1.0.
- (3)
- The following relations hold for the 1st- and 2nd-order sensitivities to the source parameters: ; and for .
- (4)
- The 2nd-order sensitivities are all positive. The 2nd-order relative sensitivities of the leakage response with respect to the source parameters of isotope 239Pu are very small, of the order of 10−4 or less. However, several mixed 2nd-order relative sensitivities of the leakage response with respect to the source parameters of isotope 240Pu are quite large, having values close to 1.0. The unmixed 2nd-order sensitivities in the matrix are mostly zero, except for and . Moreover, the unmixed 2nd-order relative sensitivity with respect to the Watt’s coefficient , namely, , is about 50% larger than the corresponding 1st-order one; whereas the value of the 2nd-order relative sensitivity with respect to the Watt’s coefficient , namely, , is about 1/7 of the value of the corresponding 1st-order sensitivity .
- (5)
- For the 2nd-order mixed sensitivities , among the elements of the matrix , 32 elements have relative sensitivities greater than 1.0. These large sensitivities involve the total cross sections of isotopes 239Pu or 1H. However, when the source parameters or , or the total cross sections of isotopes 240Pu, 69Ga, 71Ga and C are involved, the absolute values of the mixed 2nd-order relative sensitivities are all smaller than 1.0. The largest absolute values in the matrix are . Also, all the elements in the submatrices , , and have negative values; whereas the elements in submatrices and can have positive or negative values, depending on the energy group as well as the isotope of the microscopic total cross sections.
- (6)
- For the 2nd-order mixed sensitivities , the corresponding relative sensitivities are all smaller than 1.0. The overall largest value in the matrix is . All of these (largest) sensitivities are related to the 0th-order self-scattering cross section for the 12th energy group of isotope 5 (C). For the 2nd-order mixed relative sensitivities with respect to the source parameters and the 0th-order (i.e., ) scattering microscopic cross sections, the values of the relative sensitivities can be positive or negative, but there are more positive values than negative ones. For the 2nd-order mixed relative sensitivities with respect to the source parameters and the 1st-order (i.e., ) scattering microscopic cross sections, the overall largest (absolute) value is ; these sensitivities involve the 1st-order out-scattering cross section of isotope 1H. In addition, for the scattering order , the values of the relative sensitivities can also be positive or negative, but there are more negative values than positive ones. The values for the 2nd-order mixed relative sensitivities of the leakage response with respect to the source parameters of isotope 240Pu and the higher-order (i.e., ) scattering cross sections for all isotopes in the PERP benchmark are all very small, in the order of 10−2 or less.
- (7)
- For the 2nd-order mixed sensitivities , it has been found that the values of the corresponding relative sensitivities are all smaller than 1.0. The single largest relative value is . All elements in the submatrices , , and have positive values, and the element with the maximum absolute value in each of these submatrices relates to the microscopic fission cross sections for the 12th energy group of isotopes 239Pu and 240Pu (namely, ). For the submatrices and , the values of the elements can be positive or negative., and the element with the maximum absolute value in each of the submatrices and relates to the microscopic fission cross sections for the 7th energy group of isotopes 239Pu and 240Pu (i.e., ).
- (8)
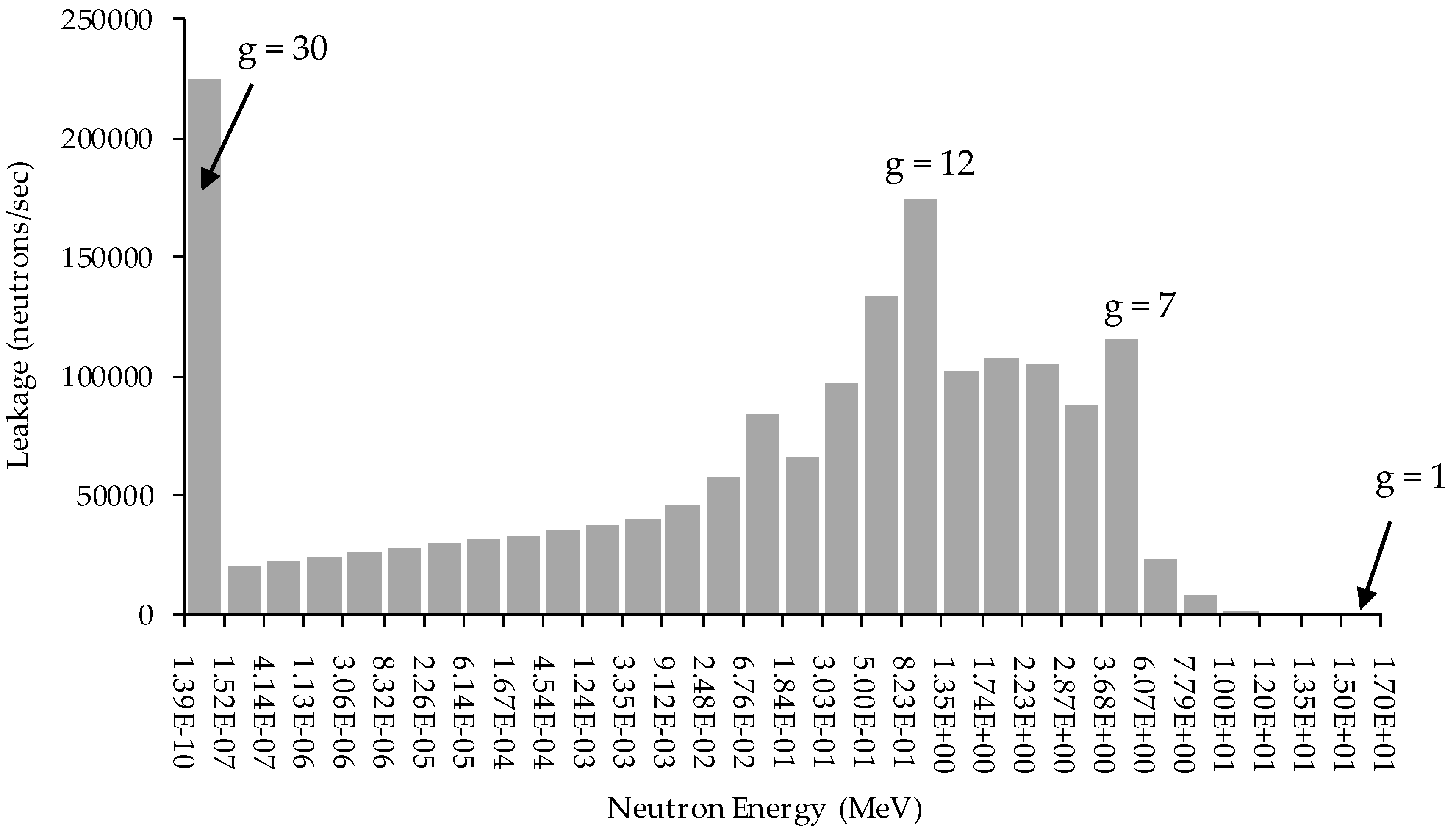
- For the 2nd-order mixed sensitivities , the corresponding relative sensitivities are mostly smaller than 1.0; only 4 elements with absolute values greater than 1.0, which are . Similarly, all elements in the submatrices , , and for have positive values, and the element with the maximum absolute value in each of these submatrices relates to the average number of neutrons per fission for the 12th energy group of the isotopes (namely, ). The elements in submatrices and have positive values for , and have negative values for . The elements having the maximum absolute value in each of the submatrices and pertain to the average number of neutrons per fission for the 7th energy group of the isotopes 239Pu and 240Pu (namely, ). The reason that the maximum absolute value in each of submatrices mostly relates to energy groups 7 and 12 is because those groups have high leakage, as shown in Figure 1. The high leakage in those groups is due to the fission spectrum of the isotopes 239Pu and 240Pu, as illustrated in Figure 4 from Part III [3], where most of the spectrum is concentrated in the energy region , with the largest portion contained in group 12, and the next largest contained in group 7.
- (9)
- For the 2nd-order mixed sensitivities , it has been found that among the 60 elements in the relative sensitivity matrix , there are 9 elements having values greater than 1.0; these are: ; ; and . The elements , , and , , have identical values. Also, all of the mixed 2nd-order sensitivities of the leakage response with respect to the source parameters and the isotopic number densities are positive, except for and , which have negative values.
- (9)
- By considering typical values for the standard deviations for the uncorrelated source parameters, it has been found that the effects of both the first- and second-order sensitivities on the expected response value, its standard deviation and skewness are negligible. However, many mixed 2nd-order sensitivities in matrices , and are significantly larger than the unmixed 2nd-order sensitivities of the leakage response with respect to the source parameters. Therefore, it would be very important to obtain correlations among the various model parameters, since the correlations among the source parameters and other model parameters (e.g., total cross sections, average number of neutrons per fission, and isotopic number densities) could provide significantly larger contributions to the response moments than the standard deviations of the source parameters.
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Definitions of PERP Model Parameters
References
- Cacuci, D.G.; Fang, R.; Favorite, J.A. Comprehensive Second-Order Adjoint Sensitivity Analysis Methodology (2nd-ASAM) Applied to a Subcritical Experimental Reactor Physics Benchmark: I. Effects of Imprecisely Known Microscopic Total and Capture Cross Sections. Energies 2019, 12, 4219. [Google Scholar] [CrossRef] [Green Version]
- Fang, R.; Cacuci, D.G. Comprehensive second-order adjoint sensitivity analysis methodology (2nd-ASAM) applied to a subcritical experimental reactor physics benchmark: II. Effects of imprecisely known microscopic scattering cross sections. Energies 2019, 12, 4114. [Google Scholar] [CrossRef] [Green Version]
- Cacuci, D.G.; Fang, R.; Favorite, J.A.; Badea, M.C.; di Rocco, F. Comprehensive second-order adjoint sensitivity analysis methodology (2nd-ASAM) applied to a subcritical experimental reactor physics benchmark: III. Effects of imprecisely known microscopic fission cross sections and average number of neutrons per fission. Energies 2019, 12, 4100. [Google Scholar] [CrossRef] [Green Version]
- Cacuci, D.G. Second-Order Adjoint Sensitivity Analysis Methodology (2nd-ASAM) for Computing Exactly and Efficiently First- and Second-Order Sensitivities in Large-Scale Linear Systems: I. Computational Methodology. J. Comput. Phys. 2015, 284, 687–699. [Google Scholar] [CrossRef] [Green Version]
- Cacuci, D.G. The Second-Order Adjoint Sensitivity Analysis Methodology; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2018. [Google Scholar]
- Cacuci, D.G. Application of the Second-Order Comprehensive Adjoint Sensitivity Analysis Methodology to Compute 1st- and 2nd-Order Sensitivities of Flux Functionals in a Multiplying System with Source. Nucl. Sci. Eng. 2019, 193, 555–600. [Google Scholar] [CrossRef] [Green Version]
- Valentine, T.E. Polyethylene-Reflected Plutonium Metal Sphere Subcritical Noise Measurements, SUB-PU-METMIXED-001. In International Handbook of Evaluated Criticality Safety Benchmark Experiments, NEA/NSC/DOC(95)03/I-IX; Report NEA/NSC/DOC(95)03/I, OECD-NEA (2008); Organization for Economic Co-operation and Development, Nuclear Energy Agency: Paris, France, 2008. [Google Scholar]
- Fang, R.; Cacuci, D.G. Comprehensive second-order adjoint sensitivity analysis methodology (2nd-ASAM) applied to a subcritical experimental reactor physics benchmark: V. Computation of mixed 2nd-order sensitivities involving isotopic number densities. Energies. submitted.
- Cacuci, D.G.; Fang, R.; Favorite, J.A. Comprehensive second-order adjoint sensitivity analysis methodology (2nd-ASAM) applied to a subcritical experimental reactor physics benchmark: VI. Overall impact of 1st- and 2nd-order sensitivities on response uncertainties. Energies. submitted.
- Wilson, W.B.; Perry, R.T.; Shores, E.F.; Charlton, W.S.; Parish, T.A.; Estes, G.P.; Brown, T.H.; Arthur, E.D.; Bozoian, M.; England, T.R.; et al. SOURCES4C: A Code for Calculating (α,n), Spontaneous Fission, and Delayed Neutron Sources and Spectra. In Proceedings of the 12th Biennial Topical Meeting of the Radiation Protection and Shielding Division of the American Nuclear Society, Santa Fe, NM, USA, 14–18 April 2002. LA-UR-02-1839. [Google Scholar]
- Alcouffe, R.E.; Baker, R.S.; Dahl, J.A.; Turner, S.A.; Ward, R. PARTISN: A Time-Dependent, Parallel Neutral Particle Transport Code System; LA-UR-08-07258; Los Alamos National Laboratory: Los Alamos, NM, USA, 2008. [Google Scholar]
- Conlin, J.L.; Parsons, D.K.; Gardiner, S.J.; Gray, M.; Lee, M.B.; White, M.C. MENDF71X: Multigroup Neutron Cross-Section Data Tables Based upon ENDF/B-VII.1X; Los Alamos National Laboratory Report LA-UR-15-29571 (October 7, 2013); Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2013. [Google Scholar]
- Chadwick, M.B.; Herman, M.; Obložinský, P.; Dunn, M.E.; Danon, Y.; Kahler, A.C.; Smith, D.L.; Pritychenko, B.; Arbanas, G.; Arcilla, R.; et al. ENDF/B-VII.1: Nuclear Data for Science and Technology: Cross Sections, Covariances, Fission Product Yields and Decay Data. Nuclear Data Sheets 2011, 112, 2887–2996. [Google Scholar] [CrossRef]
- Cacuci, D.G. BERRU Predictive Modeling: Best Estimate Results with Reduced Uncertainties; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
| Materials | Isotopes | Weight Fraction | Density (g/cm3) | Zones |
|---|---|---|---|---|
| Material 1 (plutonium metal) | Isotope 1 (239Pu) | 9.3804 × 10−1 | 19.6 | Material 1 is assigned to zone 1, which has a radius of 3.794 cm. |
| Isotope 2 (240Pu) | 5.9411 × 10−2 | |||
| Isotope 3 (69Ga) | 1.5152 × 10−3 | |||
| Isotope 4 (71Ga) | 1.0346 × 10−3 | |||
| Material 2 (polyethylene) | Isotope 5 (C) | 8.5630 × 10−1 | 0.95 | Material 2 is assigned to zone 2, which has an inner radius of 3.794 cm and an outer radius of 7.604 cm. |
| Isotope 6 (1H) | 1.4370 × 10−1 |
| Quantity | Values (neutrons/s) |
|---|---|
| Integral source | 2.7839 × 105 |
| Integral fission | 2.4584 × 106 |
| Integral absorption | 9.7201 × 105 |
| Integral in-scattering | 8.3842 × 106 |
| Integral self-scattering | 1.3558 × 107 |
| Integral out-scattering | 8.3842 × 106 |
| Integral net leakage | 1.7648 × 106 |
| Integral particle balance | 8.3526 × 10−6 |
| Parameters | [1/sec] | [-] | [-] | [-] | [-] | [atoms/cm3] |
| Values | 9.11029 × 10−13 | 3.0 × 10−12 | 0.885247 | 3.80269 | 2.16 | 4.631644 × 1022 |
| Parameters | [1/sec] | [-] | [-] | [-] | [-] | [atoms/cm3] |
| Values | 3.35340 × 10−12 | 5.75 × 10−8 | 0.794930 | 4.68927 | 2.16 | 2.921242 × 1021 |
| values | 2.252 × 10−4 | 2.252 × 10−4 | 1.119 × 10−5 | 2.801 × 10−6 | 2.252 × 10−4 | 2.252 × 10−4 |
| values | 9.998 × 10−1 | 9.998 × 10−1 | 4.372 × 10−2 | 1.165 × 10−2 | 9.998 × 10−1 | 9.998 × 10−1 |
= 0 | = 9.998 × 10−1 | = 4.373× 10−2 | = 1.165 × 10−2 | = 9.998 × 10−1 | = 9.998 × 10−1 | |
= 0 | = 4.373 × 10−2 | = 1.165 × 10−2 | = 9.998 × 10−1 | = 9.998 × 10−1 | ||
= 6.594 × 10−2 | = 3.179 × 10−2 | = 4.373 × 10−2 | = 4.373 × 10−2 | |||
= 1.571× 10−3 | = 1.165 × 10−2 | = 1.165 × 10−2 | ||||
| = 0 | = 9.998 × 10−1 | |||||
= 0 |
2 elements with absolute values >1.0 | Min. value = −8.36 × 10−2 at g = 12 | Min. value = −3.76 × 10−3 at g = 12 | Min. value = −2.55 × 10−3 at g = 12 | Min. value = −7.85 × 10−1 at g = 30 | 6 elements with absolute values >1.0 | |
2 elements with absolute values >1.0 | Min. value = −8.36 × 10−2 at g = 12 | Min. value = −3.76 × 10−3 at g = 12 | Min. value = −2.55 × 10−3 at g = 12 | Min. value = −7.85 × 10−1 at g = 30 | 6 elements with absolute values >1.0 | |
Min. value = −2.54 × 10−1 at g = 7 | Min. value = −1.60 × 10−2 at g = 7 | Min. value = −6.79 × 10−4 at g = 7 | Min. value = −4.50 × 10−4 at g = 7 | Max. value = 3.47 × 10−2 at g = 30 | Max. value = 4.14 × 10−1 at g = 30 | |
Min. value = −6.72 × 10−2 at g = 7 | Min. value = −4.22 × 10−3 at g = 7 | Min. value = −1.79 × 10−4 at g = 7 | Min. value = −1.19 × 10−4 at g = 7 | Max. value = 1.24 × 10−2 at g = 30 | Max. value = 1.48 × 10−1 at g = 30 | |
2 elements with absolute values >1.0 | Min. value = −8.36 × 10−2 at g = 12 | Min. value = −3.76 × 10−3 at g = 12 | Min. value = −2.55 × 10−3 at g = 12 | Min. value = −7.85 × 10−1 at g = 30 | 6 elements with absolute values >1.0 | |
2 elements with absolute values >1.0 | Min. value = −8.36 × 10−2 at g = 12 | Min. value = −3.76 × 10−3 at g = 12 | Min. value = −2.55 × 10−3 at g = 12 | Min. value = −7.85 × 10−1 at g = 30 | 6 elements with absolute values >1.0 |
| g | Relative Sensitivities | g | Relative Sensitivities |
|---|---|---|---|
| 1 | −0.0003 | 16 | −0.779 |
| 2 | −0.0006 | 17 | −0.364 |
| 3 | −0.002 | 18 | −0.227 |
| 4 | −0.009 | 19 | −0.181 |
| 5 | −0.046 | 20 | −0.155 |
| 6 | −0.135 | 21 | −0.137 |
| 7 | −0.789 | 22 | −0.099 |
| 8 | −0.725 | 23 | −0.081 |
| 9 | −0.843 | 24 | −0.051 |
| 10 | −0.845 | 25 | −0.060 |
| 11 | −0.775 | 26 | −0.063 |
| 12 | −1.320 | 27 | −0.017 |
| 13 | −1.154 | 28 | −0.003 |
| 14 | −0.952 | 29 | −0.035 |
| 15 | −0.690 | 30 | −0.462 |
| g | Relative Sensitivities | g | Relative Sensitivities |
|---|---|---|---|
| 1 | −4.440 × 10−6 | 16 | −1.164 |
| 2 | −1.169 × 10−5 | 17 | −1.173 |
| 3 | −4.108 × 10−5 | 18 | −1.141 |
| 4 | −2.555 × 10−4 | 19 | −1.094 |
| 5 | −1.735 × 10−3 | 20 | −1.032 |
| 6 | −7.360 × 10−3 | 21 | −0.969 |
| 7 | −0.067 | 22 | −0.892 |
| 8 | −0.085 | 23 | −0.826 |
| 9 | −0.128 | 24 | −0.749 |
| 10 | −0.158 | 25 | −0.709 |
| 11 | −0.183 | 26 | −0.653 |
| 12 | −0.437 | 27 | −0.584 |
| 13 | −0.523 | 28 | −0.547 |
| 14 | −0.576 | 29 | −0.544 |
| 15 | −0.582 | 30 | −9.364 |
Max. value = 1.34 × 10−1 g′ = 12, g = 12 | Max. value = 8.89 × 10−3 g′ = 12, g = 12 | Max. value = 5.14 × 10−4 g′ = 12, g = 12 | Max. value = 3.30 × 10−4 g′ = 12, g = 12 | Max. value = 6.81 × 10−1 g′ = 12, g = 12 | Max. value = 1.26 × 10−1 g′ = 16, g = 17 | |
Max. value = 1.34 × 10−1 g′ = 12, g = 12 | Max. value = 8.89 × 10−3 g′ = 12, g = 12 | Max. value = 5.14 × 10−4 g′ = 12, g = 12 | Max. value = 3.30 × 10−4 g′ = 12, g = 12 | Max. value = 6.81 × 10−1 g′ = 12, g = 12 | Max. value = 1.26 × 10−1 g′ = 16, g = 17 | |
Max. value = 3.43 × 10−2 g′ = 7, g = 7 | Max. value = 2.00 × 10−3 g′ = 7, g = 7 | Max. value = 8.67 × 10−5 g′ = 7, g = 7 | Max. value = 5.43 × 10−5 g′ = 7, g = 7 | Max. value = 8.35 × 10−3 g′ = 7, g = 7 | Min. value = −9.22 × 10−3 g′ = 16, g = 17 | |
Max. value = 9.10 × 10−3 g′ = 7, g = 7 | Max. value = 5.32 × 10−4 g′ = 7, g = 7 | Max. value = 2.30 × 10−5 g′ = 7, g = 7 | Max. value = 1.44 × 10−5 g′ = 7, g = 7 | Max. value = 2.19 × 10−3 g′ = 7, g = 7 | Min. value = −3.34 × 10−3 g′ = 16, g = 17 | |
Max. value = 1.34 × 10−1 g′ = 12, g = 12 | Max. value = 8.89 × 10−3 g′ = 12, g = 12 | Max. value = 5.14 × 10−4 g′ = 12, g = 12 | Max. value = 3.30 × 10−4 g′ = 12, g = 12 | Max. value = 6.81 × 10−1 g′ = 12, g = 12 | Max. value = 1.26 × 10−1 g′ = 16, g = 17 | |
Max. value = 1.34 × 10−1 g′ = 12, g = 12 | Max. value = 8.89 × 10−3 g′ = 12, g = 12 | Max. value = 5.14 × 10−4 g′ = 12, g = 12 | Max. value = 3.30 × 10−4 g′ = 12, g = 12 | Max. value = 6.81 × 10−1 g′ = 12, g = 12 | Max. value = 1.26 × 10−1 g′ = 16, g = 17 |
Min. value = −8.72 × 10−2 g′ = 7, g = 7 | Min. value = −5.24 × 10−3 g′ = 7, g = 7 | Min. value = −1.76 × 10−4 g′ = 7, g = 7 | Min. value = −1.07 × 10−4 g′ = 7, g = 7 | Min. value = −2.74 × 10−2 g′ = 12, g = 12 | Min. value = −1.04 × 10−1 g′ = 12, g = 13 | |
Min. value = −8.72 × 10−2 g′ = 7, g = 7 | Min. value = −5.24 × 10−3 g′ = 7, g = 7 | Min. value = −1.76 × 10−4 g′ = 7, g = 7 | Min. value = −1.07 × 10−4 g′ = 7, g = 7 | Min. value = −2.74 × 10−2 g′ = 12, g = 12 | Min. value = −1.04 × 10−1 g′ = 12, g = 13 | |
Min. value = −2.91 × 10−2 g′ = 7, g = 7 | Min. value = −1.75 × 10−3 g′ = 7, g = 7 | Min. value = −5.88 × 10−5 g′ = 7, g = 7 | Min. value = −3.57 × 10−5 g′ = 7, g = 7 | Min. value = −7.36 × 10−3 g′ = 7, g = 7 | Max. value = 7.46 × 10−3 g′ = 16, g = 16 | |
Min. value = −7.73 × 10−3 g′ = 7, g = 7 | Min. value = −4.65 × 10−4 g′ = 7, g = 7 | Min. value = −1.56 × 10−5 g′ = 7, g = 7 | Min. value = −9.48 × 10−6 g′ = 7, g = 7 | Min. value = −1.93 × 10−3 g′ = 7, g = 7 | Max. value = 2.71 × 10−3 g′ = 16, g = 16 | |
Min. value = −8.72 × 10−2 g′ = 7, g = 7 | Min. value = −5.24 × 10−3 g′ = 7, g = 7 | Min. value = −1.76 × 10−4 g′ = 7, g = 7 | Min. value = −1.07 × 10−4 g′ = 7, g = 7 | Min. value = −2.74 × 10−2 g′ = 12, g = 12 | Min. value = −1.04 × 10−1 g′ = 12, g = 13 | |
Min. value = −8.72 × 10−2 g′ = 7, g = 7 | Min. value = −5.24 × 10−3 g′ = 7, g = 7 | Min. value = −1.76 × 10−4 g′ = 7, g = 7 | Min. value = −1.07 × 10−4 g′ = 7, g = 7 | Min. value = −2.74 × 10−2 g′ = 12, g = 12 | Min. value = −1.04 × 10−1 g′ = 12, g = 13 |
(239Pu) | (240Pu) | |
|---|---|---|
Max. value = 8.82 × 10−1, at g = 12 | Max. value = 4.57 × 10−2, at g = 12 | |
Max. value = 8.82 × 10−1, at g = 12 | Max. value = 4.57 × 10−2, at g = 12 | |
Max. value = 1.90 × 10−1, at g = 7 | Max. value = 1.07 × 10−2, at g = 7 | |
Max. value = 5.02 × 10−1, at g = 7 | Max. value = 2.84 × 10−3, at g = 7 | |
Max. value = 8.82 × 10−1, at g = 12 | Max. value = 4.57 × 10−2, at g = 12 | |
Max. value = 8.82 × 10−1, at g = 12 | Max. value = 4.57 × 10−2, at g = 12 |
1 element with absolute value >1.0 | Max. value = 6.31 × 10−2, at g = 12 | |
1 element with absolute value >1.0 | Max. value = 6.31 × 10−2, at g = 12 | |
Max. value = 2.47 × 10−1, at g = 7 | Max. value = 1.40 × 10−2, at g = 7 | |
Max. value = 6.53 × 10−2, at g = 7 | Max. value = 3.70 × 10−3, at g = 7 | |
1 element with absolute value >1.0 | Max. value = 6.31 × 10−2, at g = 12 | |
1 element with absolute value >1.0 | Max. value = 6.31 × 10−2, at g = 12 |
| g | Relative Sensitivities | g | Relative Sensitivities |
|---|---|---|---|
| 1 | 5.265 × 10−4 | 16 | 0.297 |
| 2 | 1.069 × 10−3 | 17 | 0.117 |
| 3 | 3.064 × 10−3 | 18 | 0.068 |
| 4 | 0.014 | 19 | 0.060 |
| 5 | 0.067 | 20 | 0.065 |
| 6 | 0.169 | 21 | 0.071 |
| 7 | 0.762 | 22 | 0.063 |
| 8 | 0.658 | 23 | 0.064 |
| 9 | 0.802 | 24 | 0.042 |
| 10 | 0.842 | 25 | 0.055 |
| 11 | 0.786 | 26 | 0.051 |
| 12 | 1.214 | 27 | 0.026 |
| 13 | 0.847 | 28 | 0.012 |
| 14 | 0.555 | 29 | 0.034 |
| 15 | 0.321 | 30 | 0.461 |
(239Pu) | (240Pu) | (69Ga) | (71Ga) | (C) | (1H) | |
|---|---|---|---|---|---|---|
= 5.967 | = 1.219 | = 2.228 × 10−3 | = 1.364 × 10−3 | = 6.310 × 10−1 | = 1.001 | |
= 5.967 | = 1.219 | = 2.228 × 10−3 | = 1.364 × 10−3 | = 6.310 × 10−1 | = 1.001 | |
= 3.065 × 10−1 | = 2.592 × 10−2 | = 7.758 × 10−5 | = 7.537 × 10−5 | = 1.078 × 10−2 | = −1.709 × 10−2 | |
= 8.202 × 10−2 | = 7.648 × 10−3 | = 1.934 × 10−5 | = 2.083 × 10−5 | = 2.386 × 10−3 | = −6.788 × 10−3 | |
= 5.967 | = 1.219 | = 2.228 × 10−3 | = 1.364 × 10−3 | = 6.310 × 10−1 | = 1.001 |
| Relative Standard Deviation | 10% | 5% | 1% |
|---|---|---|---|
| 1.7648 × 106 | 1.7648 × 106 | 1.7648 × 106 | |
| 5.9586 × 102 | 1.4897 × 102 | 5.9586 × 100 | |
| 1.7654 × 106 | 1.7649 × 106 | 1.7648 × 106 | |
| 1.2459 × 1011 | 3.1147 × 1010 | 1.2459 × 109 | |
| 6.7741 × 105 | 4.2338 × 104 | 6.7741 × 101 | |
| 1.2459 × 1011 | 3.1147 × 1010 | 1.2459 × 109 | |
| 2.0825 × 1011 | 1.3016 × 1010 | 2.0825 × 107 | |
| 4.7356 × 10−6 | 2.3678 × 10−6 | 4.7356 × 10−7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, R.; Cacuci, D.G. Comprehensive Second-Order Adjoint Sensitivity Analysis Methodology (2nd-ASAM) Applied to a Subcritical Experimental Reactor Physics Benchmark: IV. Effects of Imprecisely Known Source Parameters. Energies 2020, 13, 1431. https://doi.org/10.3390/en13061431
Fang R, Cacuci DG. Comprehensive Second-Order Adjoint Sensitivity Analysis Methodology (2nd-ASAM) Applied to a Subcritical Experimental Reactor Physics Benchmark: IV. Effects of Imprecisely Known Source Parameters. Energies. 2020; 13(6):1431. https://doi.org/10.3390/en13061431
Chicago/Turabian StyleFang, Ruixian, and Dan Gabriel Cacuci. 2020. "Comprehensive Second-Order Adjoint Sensitivity Analysis Methodology (2nd-ASAM) Applied to a Subcritical Experimental Reactor Physics Benchmark: IV. Effects of Imprecisely Known Source Parameters" Energies 13, no. 6: 1431. https://doi.org/10.3390/en13061431






