A Novel DC-Coil-Free Hybrid-Excited Machine with Consequent-Pole PM Rotor

Abstract

This paper proposes a new DC coil free hybrid excited machine concept, which has no external field windings. The technical novelty is the integration of field windings and armature windings. DC bias current is injected into the excitation and the field windings in the traditional hybrid excited machine are eliminated. Compared with traditional hybrid-excited machines with additional field windings, the proposed machine can realize a higher slot utilization ratio, hence achieve a higher torque density and a wider flux adjusting range. Another advantage of the proposed machine is that the voltage drop associated with flux regulation is small due to the small DC resistance, and the torque generating capability at the flux regulating region can be improved accordingly. The rotor is specifically designed with magnet-iron sequences and a consequent-pole, in which the permanent magnet and iron pole are alternatively employed. A bi-directional flux modulating effect can be achieved, which can contribute to the magnetic coupling in the air-gap. Analytical derivation is used to describe the operating principle, and the proposed machine was optimally designed using the Tabu search algorithm. A prototype was made, and its performances investigated through experimental tests.

1. Introduction

Permanent magnet (PM) machines have shown significant advantages over electrically excited machines. Generally, PM machines have high efficiency and large torque density when employed with a rare earth magnet, which makes them more competitive than electrically excited machines (EEMs) in large-torque traction applications [1,2,3,4,5,6,7]. Fixed PM excitation is one major drawback of PM machines which means that the air-gap flux cannot be easily regulated as in the EEMs by controlling the excitation current. A well-known flux weakening method of PM machines is to apply negative d-axis current, but the voltage drop involved with the d-axis current reduces the output torque and efficiency accordingly [8,9,10].

Hybrid excited machines (HEMs) have been proposed to integrate the advantages of good flux regulating capability of EEMs and the high torque density of PM machines [11,12,13,14,15,16,17]. There are two kinds of excitation sources employed in HEMs, one is magnetic and the other is field current. The air-gap field is mainly generated by the magnets and field current is used to adjust the air-gap field. According to the investigation reported in [18], HEMs can realize a wide constant power speed range, as well as higher efficiency at the flux weakening region.

Many researches have been reported on HEMs and various novel topologies proposed, and their applications in electric traction widely investigated [19,20,21,22,23]. In order to increase reliability, brushless structure is desirable and the field windings are better being employed on the stator. The magnet can be employed either on the rotor [24,25,26] or on the stator [27,28,29]. Although employing magnet excitation on the stator can result in robust rotor structure, the magnet inevitably takes up some stator space and the space for electric loading is reduced, which reduces the torque density accordingly. Meanwhile, the magnets are located in the stator thermal field, which increases the demagnetization risk of the magnets. Therefore, from the point of achieving good distribution of electric loading and magnetic loading, and reducing the demagnetization risk of magnets, employing magnets on the rotor and field coils on the stator is a better choice for HEMs. Since the field coils of HEMs are only used during flux regulation, and reduce the effective slot area for armature coils, the torque density of HEMs is reduced by the field coils, especially during low-speed operation. The same goes for the flux regulating capability, which is limited by the slot area used for the field windings.

A novel DC-coil-free HEM (DCF-HEM) is proposed in this paper. Compared with traditional HEMs with additional DC coils, the proposed DCF-HEM can achieve higher torque density and wider field adjusting range. The field windings and armature windings in the proposed design are integrated, and DC bias current is injected into the integrated stator winding to achieve flux regulation. The rotor consists of magnet poles and iron segments, namely a magnet-iron consequent-pole rotor, which has a flux modulating effect and can provide PM excitation. The operating principle and field adjusting theory of the proposed DCF-HEM are here analytically investigated. The Tabu search algorithm is used to conduct design optimization of the proposed DCF-HEM. The electromagnetic performances are studied through both the finite element method (FEM) and experimental tests.

2. Machine Configuration

The configuration of the proposed DCF-HEM is shown in Figure 1a. Concentrated windings are employed to reduce the end winding length and copper loss. Different from traditional HEMs with additional field windings, the proposed DCF-HEM has integrated stator winding, and a DC bias component is injected into the armature current to achieve flux regulation. The AC component is responsible for electromagnetic torque production. According to the flux direction of the DC bias current, each phase winding is separated into two parts which are excited by a synchronous sinusoidal current with an opposite DC bias component. Generally, the DC bias current is responsible for flux weakening. However, flux strengthening can also be realized by changing the direction of the DC bias current. The adjacent stator teeth are specifically designed with uneven height to create uneven reluctance distribution, so as to modulate the magnetic field produced by the rotor magnets. The rotor is designed with magnet-iron sequences, and all the magnets are magnetized in a radially outward direction. A rotor magnetic pole-pair consists of a rotor iron pole and its adjacent magnet. Although the magnets are located on the rotor, some specific rotor PM harmonics can be adjusted by the DC bias current due to the effect of the bidirectional flux modulating, therefore the electromagnetic torque and back-EMF can be regulated accordingly. It should be noted that this machine can also be connected as a traditional HEM with additional DC windings, as shown in Figure 1b.

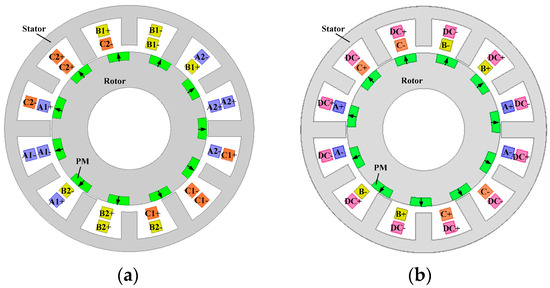
Figure 1. Machine Configurations. (a) The proposed DC-coil-free hybrid excited machine (DCF-HEM). (b) Connected with additional DC windings.

In order to restrict copper loss, an equivalent current $I_e$ expressed in Equation (1) is defined.

$$I_e=\sqrt{\frac{1}{T}{\displaystyle \underset{0}{\overset{T}{\int }}{\left[\sqrt{2}{I}_a\cos \left(\omega t\right)+I_d\right]}^{2}dt}}=\sqrt{{I_a}^2+{I_d}^2}$$

(1)

where $I_a$ and $\omega$ represent the RMS value and angular frequency of the armature current, respectively, $I_d$ refers to the RMS value of the DC bias current. When the stator windings are applied with DC bias current, the equivalent current $I_e$ is kept unchanged by reducing the RMS value of the armature current. In conditions where the speed of DCF-HEM is lower than the rated speed, no DC bias current is applied since flux regulation is not needed in this region, and all the inverter voltage is used to generate AC current to produce electromagnetic torque. For traditional HEMs with additional field coils, since the field coils are open circuited and useless when flux regulating is not needed, the maximum electromagnetic torque can be expressed as in Equation (2).

$$T_{HEM}=K_{slot}{A}_{slot}J{\psi }_f\frac{N_a}{N_d+N_a}$$

(2)

where $K_{slot}$ is the slot filling factor, $A_{slot}$ is the slot area, $J$ is the current density, ${\psi }_f$ is the total PM flux linkage, and $N_a$ and $N_d$ refer to the turns of armature coils and field coils, respectively. Since the armature coils and field coils are incorporated in the proposed DCF-HEM, all the coils can be excited to generate electromagnetic torque. Compared with traditional HEMs, the maximum output torque of the proposed machine is increased and can be expressed as

$$T_{pro}=K_{slot}{A}_{slot}J{\psi }_f$$

(3)

In order to operate in the high speed region, flux weakening is needed and realized by injecting DC bias current into the windings. For traditional HEMs, only field coils can be used to generate a flux weakening current, and its maximum value is given by

$$I_{HEM}=A_{slot}J{K}_{slot}\frac{N_d}{N_d+N_a}$$

(4)

In the proposed machine, all the coils can be excited to generate a flux regulating current and the flux regulating capability is increased. The theoretical maximum flux regulating current can be expressed in Equation (5), in which stator windings are only excited by DC bias current and the AC component is zero.

$$I_{pro}=A_{slot}J{K}_{slot}$$

(5)

3. Mathematical Modeling

The principle of flux modulating caused by uneven permeance distribution is reported in [30]. In the proposed DCF-HEM, bi-directional flux modulating effect is the operating basis. Similar to the pole-pair combination of magnetic gear, the pole-pair number (PPN) of AC current p_α, PPN of DC bias current p_f and PPN of rotor PMs p_r are governed by

$$p_r=p_a+p_f$$

(6)

Since the stator windings are concentrated, the PPN of the DC bias current p_f equals half of the stator slot number N_s.

$$p_f=\frac{N_s}{2}$$

(7)

It can be easily observed that the air-gap field has three components, which are generated by the armature current, DC bias current, and rotor PMs, respectively. In order to give a deep insight into the operating principle and flux adjusting theory of the proposed DCF-HEM, the coupling mechanism of these three magnetic fields was analytically studied through harmonic analysis.

3.1. Air-Gap Flux Generated by Rotor PMs

Through multiplying air-gap permeance and magnetomotive force (MMF), the air-gap flux density is obtained. The MMF of rotor PMs can be assumed as square waveform, and can be expressed in the Fourier series, as given in Equation (8).

$$F_{PM}\left(\theta ,t\right)={\displaystyle \sum _{i=1,3,5}^{\infty }{F}_{PMi}\cos i{p}_r\left(\theta -{\Omega }_{r}t-{\theta }_0\right)}$$

(8)

where $i$ refers to the harmonic order, $F_{PMi}$ refers to the MMF amplitude of the ith harmonic, $\theta$ is the circumferential position, ${\Omega }_r$ and ${\theta }_0$ are the angular speed and initial position of the rotor, respectively. The bi-directional flux modulating effect can be realized because both the stator and rotor have uneven permeance distribution. The air-gap permeance function of the stator and rotor can be expressed in the Fourier series, as given in Equations (9) and (10), respectively.

$${\Lambda }_s\left(\theta \right)={\Lambda }_{s0}-{\displaystyle \sum _{v=1}^{\infty }{\Lambda }_{sv}\cos \left(v\frac{N_s}{2}\theta \right)}$$

(9)

$${\Lambda }_r\left(\theta ,t\right)={\Lambda }_{r0}-{\displaystyle \sum _{n=1}^{\infty }{\Lambda }_{rn}\cos \left(n{p}_r\left(\theta -{\Omega }_{r}t-{\theta }_0\right)\right)}$$

(10)

where ${\Lambda }_{s0}$ and ${\Lambda }_{sv}$ refer to the average value and amplitude of the νth harmonic of stator permeance, respectively. ${\Lambda }_{r0}$ and ${\Lambda }_{rn}$ refer to the average value and amplitude of the nth harmonic of rotor permeance, respectively. With Equations (9) and (10), the air-gap permeance function of the proposed DCF-HEM can be obtained, as given in Equation (11).

$$\begin{array}{l}\Lambda \left(\theta ,t\right)={\Lambda }_s\left(\theta \right){\Lambda }_r\left(\theta ,t\right)\\ ={\Lambda }_{s0}{\Lambda }_{r0}-{\Lambda }_{r0}{\displaystyle \sum _{v=1}^{\infty }{\Lambda }_{sv}\cos \left(v\frac{N_s}{2}\theta \right)}\\ -{\Lambda }_{s0}{\displaystyle \sum _{n=1}^{\infty }{\Lambda }_{rn}\cos \left(n{p}_r\theta -n{p}_r\left({\Omega }_{r}t+{\theta }_0\right)\right)}\\ +\frac{1}{2}{\displaystyle \sum _{v=1}^{\infty }{\displaystyle \sum _{n=1}^{\infty }{\Lambda }_{sv}{\Lambda }_{rn}\cos \left(\left(n{p}_r\pm v\frac{N_s}{2}\right)\theta -n{p}_r\left({\Omega }_{r}t+{\theta }_0\right)\right)}}\end{array}$$

(11)

Therefore, the air-gap flux density generated by rotor PMs can be obtained by multiplying Equations (8) and (11), as given in Equation (12).

$$\begin{array}{l}{B}_{PM}\left(\theta ,t\right)=F_{PM}\left(\theta ,t\right)\Lambda \left(\theta ,t\right)\\ ={\Lambda }_{s0}{\Lambda }_{r0}{\displaystyle \sum _{i=1,3,5}^{\infty }{F}_{PMi}\cos \left(i{p}_r\theta -i{p}_r\left({\Omega }_{r}t+{\theta }_0\right)\right)}\\ -\frac{1}{2}{\Lambda }_{r0}{\displaystyle \sum _{i=1,3,5}^{\infty }{\displaystyle \sum _{v=1}^{\infty }{F}_{PMi}{\Lambda }_{sv}}\cos \left(\left(i{p}_r\pm v\frac{N_s}{2}\right)\theta -i{p}_r\left({\Omega }_{r}t+{\theta }_0\right)\right)}\\ -\frac{1}{2}{\Lambda }_{s0}{\displaystyle \sum _{i=1,3,5}^{\infty }{\displaystyle \sum _{n=1}^{\infty }{F}_{PMi}{\Lambda }_{rn}}\cos \left(\left(i{p}_r\pm n{p}_r\right)\theta -\left(i{p}_r\pm n{p}_r\right)\left({\Omega }_{r}t+{\theta }_0\right)\right)}\\ +\frac{1}{4}{\displaystyle \sum _{i=1,3,5}^{\infty }{\displaystyle \sum _{v=1}^{\infty }{\displaystyle \sum _{n=1}^{\infty }{F}_{PMi}{\Lambda }_{sv}{\Lambda }_{rn}\cos \left(\left(i{p}_r\pm n{p}_r\pm v\frac{N_s}{2}\right)\theta -\left(i{p}_r\pm n{p}_r\right)\left({\Omega }_{r}t+{\theta }_0\right)\right)}}}\end{array}$$

(12)

It can be seen that the air-gap flux density of rotor PMs has four harmonic groups. The first and third items, as well as the second and fourth items can be combined, and Equation (12) can be rewritten as:

$$\begin{array}{l}{B}_{PM}\left(\theta ,t\right)={\displaystyle \sum _{n=1}^{\infty }{B}_{PMn}\cos \left(n{p}_r\theta -n{p}_r\left({\Omega }_{r}t+{\theta }_0\right)\right)}\\ +{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{v=1}^{\infty }{B}_{PMnv}}\cos \left(\left(n{p}_r\pm v\frac{N_s}{2}\right)\theta -n{p}_r\left({\Omega }_{r}t+{\theta }_0\right)\right)}\end{array}$$

(13)

The first item in Equation (13) refers to the rotor PM harmonics considering rotor saliency, and the second item refers to additional harmonics introduced by the flux modulating effect of the stator.

3.2. Air-Gap Flux Generated by DC Bias Current

The air-gap flux density of the DC bias current can be obtained in the same way as the air-gap flux density of rotor PMs. Equation (14) gives the expression of the MMF of the DC bias current

$$\{\begin{array}{l}{F}_f\left(\theta \right)={\displaystyle \sum _{j=1,3,5}^{\infty }{F}_{fj}\cos \left(j\frac{N_s}{2}\theta \right)}\\ F_{fj}=\frac{4N{I}_d}{j\pi }\sin \left(j{b}_{so}\frac{\pi }{2}\right)\end{array}$$

(14)

where $N$ is the stator winding turns, and $b_{so}$ refers to the stator slot opening. By multiplying Equations (11) and (14), the air-gap flux density of the DC bias current can be obtained, as given in Equation (15).

$$\begin{array}{l}{B}_f\left(\theta ,t\right)={\displaystyle \sum _{v=1}^{\infty }{B}_{fv}\cos \left(v\frac{N_s}{2}\theta \right)}\\ +{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{v=1}^{\infty }{B}_{fnv}}\cos \left(\left(n{p}_r\pm v\frac{N_s}{2}\right)\theta -n{p}_r\left({\Omega }_{r}t+{\theta }_0\right)\right)}\end{array}$$

(15)

In which the first item refers to the DC bias current harmonics considering stator saliency, and the second item refers to additional harmonics introduced by the flux modulating effect of the rotor. It should be noted that the harmonics excited by the DC bias current only exist in the flux regulating process. When flux regulating is not needed, the DC bias current $I_d$ is zero, and harmonics in Equation (15) do not exist in this case.

3.3. No Load Flux Linkage

From Equations (13) and (15), we can find that the second item in these two equations has the same PPN and rotating speed, which means the second harmonic group in Equation (13) can be adjusted by the DC bias current. The total excitation flux can be obtained by summing up Equations (13) and (15), as given in Equation (16).

$$\begin{array}{l}B\left(\theta ,t\right)=B_{PM}\left(\theta ,t\right)+B_f\left(\theta ,t\right)\\ ={\displaystyle \sum _{n=1}^{\infty }{B}_{PMn}\cos \left(n{p}_r\theta -n{p}_r\left({\Omega }_{r}t+{\theta }_0\right)\right)}+{\displaystyle \sum _{v=1}^{\infty }{B}_{fv}\cos \left(v\frac{N_s}{2}\theta \right)}\\ +{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{v=1}^{\infty }\left(B_{PMnv}+B_{fnv}\right)}\cos \left(\left(n{p}_r\pm v\frac{N_s}{2}\right)\theta -n{p}_r\left({\Omega }_{r}t+{\theta }_0\right)\right)}\end{array}$$

(16)

The no load flux linkage of sub-phase one ${\Psi }_1\left(t\right)$ and sub-phase two ${\Psi }_2\left(t\right)$ can be calculated as given in Equations (17) and (18), respectively.

$$\begin{array}{l}{\Psi }_1\left(t\right)=r_g{l}_s{\displaystyle \underset{\theta c-\frac{b_{so}}{2}}{\overset{{\theta }_c+\frac{b_{so}}{2}}{\int }}B\left(\theta ,t\right)d\theta }-r_g{l}_s{\displaystyle \underset{{\theta }_c-\frac{b_{so}}{2}+\frac{\pi }{6}}{\overset{{\theta }_c+\frac{b_{so}}{2}+\frac{\pi }{6}}{\int }}B\left(\theta ,t\right)d\theta }\\ =4r_g{l}_s\left\{\begin{array}{l}{\displaystyle \sum _{n=1}^{\infty }\frac{B_{PMn}}{n{p}_r}\sin \left(n{p}_r\frac{bso}{2}\right)\sin \left(n{p}_r\frac{\pi }{12}\right)\sin \left(n{p}_r\left({\theta }_c+\frac{\pi }{12}\right)-n{p}_r\left({\Omega }_{r}t+{\theta }_0\right)\right)}\\ +{\displaystyle \sum _{v=1}^{\infty }\frac{2B_{fv}}{v{N}_s}\sin \left(v{N}_s\frac{bso}{4}\right)\sin \left(v{N}_s\frac{\pi }{24}\right)\sin \left(v\frac{N_s}{2}\left({\theta }_c+\frac{\pi }{12}\right)\right)}\\ +{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{v=1}^{\infty }\frac{B_{PMnv}+B_{fnv}}{n{p}_r\pm v\frac{N_s}{2}}\sin \left(\left(n{p}_r\pm v\frac{N_s}{2}\right)\frac{bso}{2}\right)}\sin \left(\left(n{p}_r\pm v\frac{N_s}{2}\right)\frac{\pi }{12}\right)\sin \left(\left(n{p}_r\pm v\frac{N_s}{2}\right)\left({\theta }_c+\frac{\pi }{12}\right)-n{p}_r\left({\Omega }_{r}t+{\theta }_0\right)\right)}\end{array}\right\}\end{array}$$

(17)

$$\begin{array}{l}{\Psi }_2\left(t\right)=-r_g{l}_s{\displaystyle \underset{{\theta }_c-\frac{b_{so}}{2}+\pi }{\overset{{\theta }_c+\frac{b_{so}}{2}+\pi }{\int }}B\left(\theta ,t\right)d\theta }+r_g{l}_s{\displaystyle \underset{{\theta }_c-\frac{b_{so}}{2}+\frac{7\pi }{6}}{\overset{{\theta }_c+\frac{b_{so}}{2}+\frac{7\pi }{6}}{\int }}B\left(\theta ,t\right)d\theta }\\ =4r_g{l}_s\left\{\begin{array}{l}{\displaystyle \sum _{n=1}^{\infty }\frac{B_{PMn}}{n{p}_r}\sin \left(n{p}_r\frac{bso}{2}\right)\sin \left(n{p}_r\frac{\pi }{12}\right)\sin \left(n{p}_r\left({\theta }_c+\frac{\pi }{12}\right)-n{p}_r\left({\Omega }_{r}t+{\theta }_0\right)\right)}\\ -{\displaystyle \sum _{v=1}^{\infty }\frac{2B_{fv}}{v{N}_s}\sin \left(v{N}_s\frac{bso}{4}\right)\sin \left(v{N}_s\frac{\pi }{24}\right)\sin \left(v\frac{N_s}{2}\left({\theta }_c+\frac{\pi }{12}\right)\right)}\\ +{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{v=1}^{\infty }\frac{B_{PMnv}+B_{fnv}}{n{p}_r\pm v\frac{N_s}{2}}\sin \left(\left(n{p}_r\pm v\frac{N_s}{2}\right)\frac{bso}{2}\right)}\sin \left(\left(n{p}_r\pm v\frac{N_s}{2}\right)\frac{\pi }{12}\right)\sin \left(\left(n{p}_r\pm v\frac{N_s}{2}\right)\left({\theta }_c+\frac{\pi }{12}\right)-n{p}_r\left({\Omega }_{r}t+{\theta }_0\right)\right)}\end{array}\right\}\end{array}$$

(18)

where $r_g$ is the air-gap radius, $l_s$ and ${\theta }_c$ refer to the stack length and coil initial position, respectively. One can see that the no-load flux linkage has three components, the first and third items are rotating components, which vary with the time. The second item is the DC bias component. It should be noted that the DC bias components of the flux linkage in sub-phase one and sub-phase two have opposing direction.

3.4. Back EMF

The back-EMF can be calculated from the derivation of open-circuit flux linkage. Since the derivation of a constant is zero, the DC bias component in the flux linkage does not influence back-EMF, therefore the back-EMF of the two sub-phases is equal, as given in Equation (19).

$$\begin{array}{l}{e}_1\left(t\right)=e_2\left(t\right)=-\frac{d{\Psi }_1\left(t\right)}{dt}\\ =4r_g{l}_s\left\{\begin{array}{l}{\displaystyle \sum _{n=1}^{\infty }{B}_{PMn}{\Omega }_r\sin \left(n{p}_r\frac{bso}{2}\right)\sin \left(n{p}_r\frac{\pi }{12}\right)\cos \left(n{p}_r\left({\theta }_c+\frac{\pi }{12}\right)-n{p}_r\left({\Omega }_{r}t+{\theta }_0\right)\right)}\\ +{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{v=1}^{\infty }\frac{B_{PMnv}+B_{fnv}}{n{p}_r\pm v\frac{N_s}{2}}n{p}_r{\Omega }_r\sin \left(\left(n{p}_r\pm v\frac{N_s}{2}\right)\frac{bso}{2}\right)}\sin \left(\left(n{p}_r\pm v\frac{N_s}{2}\right)\frac{\pi }{12}\right)\cos \left(\left(n{p}_r\pm v\frac{N_s}{2}\right)\left({\theta }_c+\frac{\pi }{12}\right)-n{p}_r\left({\Omega }_{r}t+{\theta }_0\right)\right)}\end{array}\right\}\end{array}$$

(19)

One can find that the back EMF has two parts, in which the first one is generated only by the rotor PMs, and the second one is produced by the DC bias current and rotor PMs simultaneously. Therefore, by controlling the DC bias current, the second item of the back EMF can be regulated effectively.

4. Optimization and Finite Element Analysis

4.1. Design Optimization

Before investigating the electromagnetic performances, an optimization method coupled TS-FEM is used to conduct design optimization. Generally, the machine in traction vehicle should have: (1) High torque density to fulfill the requirements during start-up and climbing; (2) Low torque ripple to reduce the vibration and noise; (3) High efficiency to reduce power consumption and increase the mileage range. Therefore, three objectives are considered during optimization, which are the average electromagnetic torque $f_1$, torque ripple $f_2$, and efficiency $f_3$. The optimization problem is expressed as

$$\min \left\{-f_1\left(x\right),f_2\left(x\right),-f_3\left(x\right)\right\},x\in F$$

(20)

In which $x$ and $F$ refer to the geometric parameters and their constraints.

The flowchart of the optimization process is shown in Figure 2, in which the optimization algorithm and finite element analysis are directly coupled and the whole process is automatic. The armature current density is 8 A/mm² and DC bias current is not applied. The optimization algorithm randomly generates the initial values of the optimized parameters within their ranges, which is labeled as the current solution x and a series of neighborhood solutions x₁, x₂,…, x_p are generated around x. These solutions are automatically passed to the Maxwell software. Maxwell conducts a finite element calculation and returns the torque, torque ripple, and efficiency to the optimization algorithm for fitness evaluation and the optimal solution within the neighborhood is chosen. The optimal solution is labeled as the new current solution x*, and the optimization algorithm generates a new neighborhood around this optimal solution and starts a new circulation. The Tabu search algorithm is investigated in [31] and multi-level optimization of electrical machines is reported in [32,33]. Although the electromagnetic performances can be influenced by many factors, only structural parameters are optimized in this paper, as given in Table 1. The optimization is conducted on a prototype with 11 rotor pole-pairs and 12 stator slots. Since the DC bias current is not a fixed value, it can be changed from zero to the maximum value which corresponds to the maximum current density. Therefore, there is no need to optimize the DC bias current.

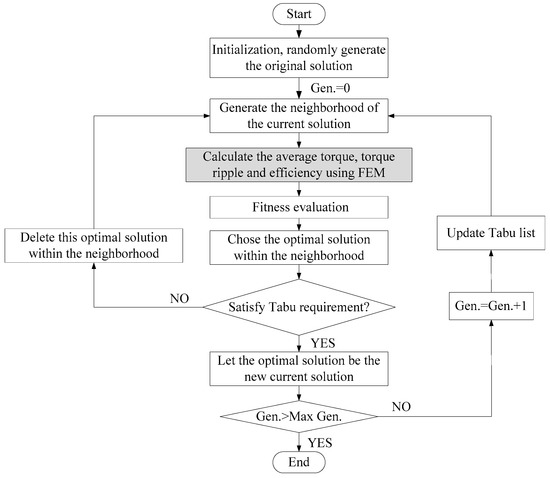
Figure 2. Flowchart of the optimization process.

Table 1. Optimized parameters and their limits. DCF-HEM: DC-coil-free-hybrid excited machines; PM: permanent magnet.

Parameters	DCF-HEM
	Upper Limit	Lower Limit
Inner diameter of stator (mm)	64	55
Rotor PM ratio	80%	30%
Thickness of rotor PM (mm)	5	2
Width of stator teeth (mm)	8	5
Height difference of stator teeth (mm)	5	2

The optimization results of average torque and efficiency are given in Figure 3. One can find that when the output torque becomes larger, the machine efficiency tends to increase. Therefore, when the proposed DCF-HEM is designed with a large output torque, high efficiency can also be achieved. Figure 4 shows the optimization results of average torque and torque ripple. One can see that the torque ripple varies disorderly when the average torque increases, and no clear regularity can be found between the change of average torque and torque ripple. The three-objective Pareto results are given in Figure 5.

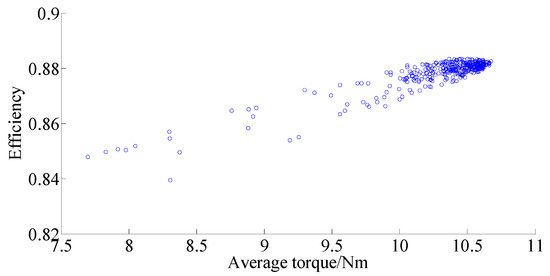
Figure 3. Optimization results of average torque and efficiency.

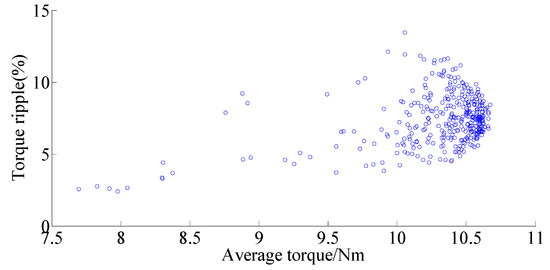
Figure 4. Optimization results of average torque and torque ripple.

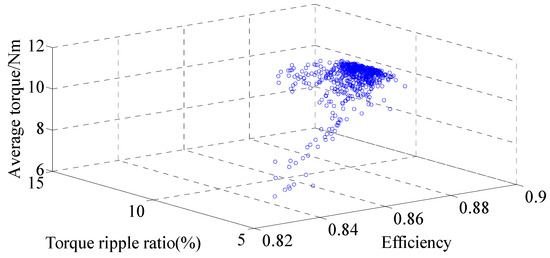
Figure 5. Three-objective Pareto results.

With the results of multi-objective optimization, a single objective optimization is conducted to maximize the output torque. The constraints are that the efficiency should be greater than 0.88 and the torque ripple lower than 10%. The objective function is given as

$$\{\begin{array}{l}\min \left\{-f_1\left(x\right)\right\}\\ f_2\left(x\right)\le 10\%,f_3\left(x\right)\ge 0.88\end{array}$$

(21)

Figure 6 shows the results of single objective optimization, in which the total iterative number is 30. One can see that the optimization process can converge within 20 iterations, which illustrates high efficiency of the optimization algorithm. The final design parameters are listed in Table 2.

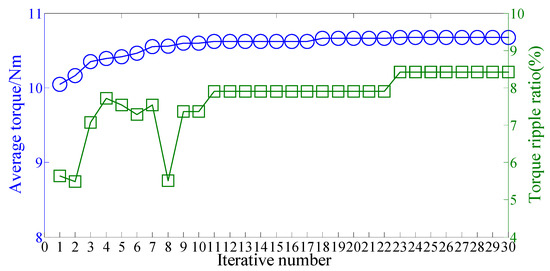
Figure 6. Results of single-objective optimization.

Table 2. Design parameters.

Parameters	Initial Value	Optimized Value
Outer diameter of stator (mm)	90
Inner diameter of stator (mm)	56	58.8
Outer diameter of rotor (mm)	55	57.8
Inner diameter of rotor (mm)	30
Stack length (mm)	80
Air-gap length (mm)	0.5
Stator teeth width (mm)	6.4	5.8
Height difference of stator teeth (mm)	3.2	2.7
PPN of armature winding	5
PPN of field winding	6
PPN of rotor PMs	11
Rotor PM ratio (%)	60	50
Rotor PM thickness (mm)	3.5	4.3
Number of phases	3
Number of stator slots	12
Relative permeability of NdFeB	1.05
Remanence of NdFeB (T)	1.2

4.2. Finite Element Analysis

FEM is used to simulate the electromagnetic performances of DCF-HEM. Firstly, the no-load flux density in the air-gap when applied with different DC bias currents iscalculated and given in Figure 7, as well as the harmonic spectrums. The 10 A, 0 A, and −10 A are the values of the DC bias current. One can see that the air-gap flux can be efficiently adjusted by the DC bias current. The results in Figure 7 show a good match with the mathematical derivation given in Equation (16). Harmonic with 11 pole-pairs is the fundamental component of the rotor PM field, which corresponds to the first item of Equation (16) and cannot be controlled by the DC bias current as given in Figure 7. Harmonic with six pole-pairs is only excited by the DC bias current, which corresponds to the second item of Equation (16). And harmonic with five pole-pairs is generated by both the rotor PM and DC bias current, which corresponds to the third item of Equation (16) and can be regulated by controlling the DC bias current.

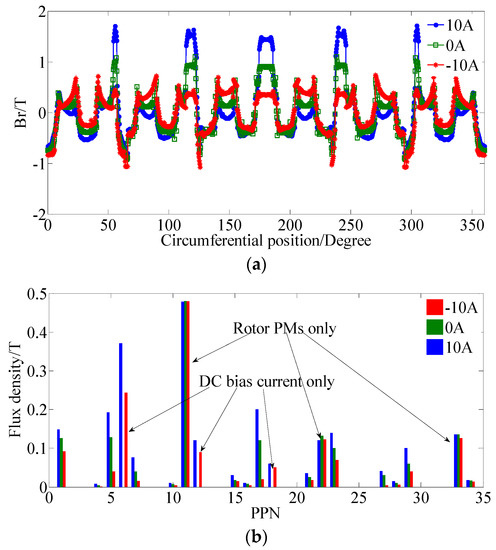
Figure 7. No-load air-gap flux density distributions and harmonics. (a) Flux density distributions. (b) Harmonics.

Figure 8 shows the no-load flux linkage waveforms when the machine speed is 800 r/min. The flux linkage waveforms of the two sub-phases are investigated separately. One can see that the flux linkage of the two sub-phases are synchronous but with opposite DC bias components. The peak-peak value of flux linkage increases when the DC bias current is positive, which corresponds to the flux strengthening stage. When applied with negative DC bias current, the peak-peak value of the flux linkage decreases, which corresponds to the flux weakening process. In a traditional synchronous machine, flux linkage has no DC bias component. However, in our proposed machine, the rotor permanent magnet field can generate a stationary harmonic with six pole-pairs caused by the flux modulating effect. This 6-pole-pair harmonic will produce DC bias flux linkage and share the same magnetic path as the DC bias current.

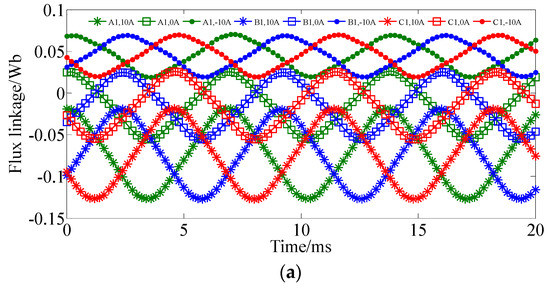
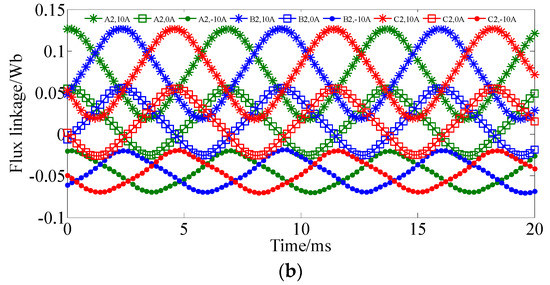
Figure 8. No load flux linkage waveforms. (a) Sub-phase one. (b) Sub-phase two.

Figure 9 gives the back-EMF waveforms when the machine speed is 800 r/min, the corresponding machine frequency is 147 Hz. One can see that the back EMF can be strengthened and weakened efficiently by the DC bias current. It should be noted that the DC bias component in the flux linkage has no influence on the back EMF because the differential of DC bias flux linkage is zero and the EMF is determined by the variation of the flux linkage. Although sub-phase one and sub-phase two have opposite DC bias flux linkage components, their back EMF waveforms are coincident.

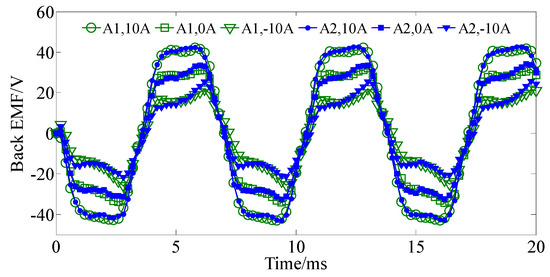
Figure 9. Back EMF waveforms.

The stationary torque is calculated and given in Figure 10, when the armature current density is 8 A/mm². Again, we can see that the output torque can be adjusted by controlling the DC bias current. For the driving machine in electric vehicles, the maximum current density can be around 22 A/mm² when a liquid cooling system is used. However, this maximum current density can only be applied for a very short period since huge heat will be generated by the large copper loss. Definitely, copper loss and temperature will increase when the current density is 22 A/mm², and the efficiency will be reduced. The output torque and torque per PM volume (T/PMV) of the proposed DCF-HEM are given in Figure 11. In this case, no DC bias current is applied and the winding current only has an AC component which is used to generate electromagnetic torque. The maximum T/PMV reaches 594 kN·m/m³ when the armature current density is 22 A/mm². The electromagnetic performances of the proposed DCF-HEM are summarized in Table 3.

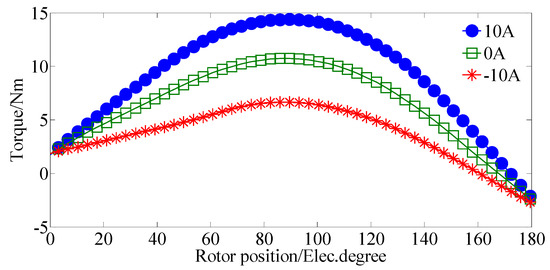
Figure 10. Stationary torque waveforms.

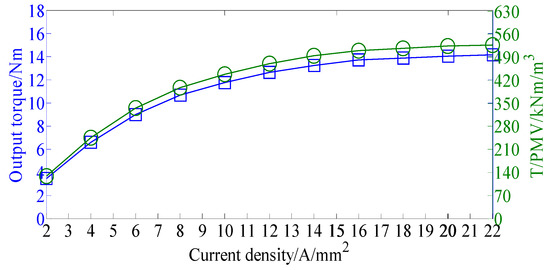
Figure 11. Output torque and T/PMV when applied with different current densities.

Table 3. Electromagnetic performances.

Items	Initial Value	Optimized Value
Rated power (W)	745	896
Rated speed (r/min)	800
Rated torque (N·m)	8.9	10.7
Peak torque (N·m)	11.9	14.1
PM usage (cm3)	22.64	26.8
Torque density (kN·m/m3)	23.6	28
T/PMV (kN·m/m3)	526	594

5. Experimental Validation

The prototype of the proposed DCF-HEM was manufactured with the same parameters as given in Table 1. Figure 12 shows the experimental test bench. All the coils are brought out and connected outside the machine. The windings of the two sub-phases are connected separately, and each sub-phase is controlled by a converter. A 1.5 kW servo machine connected to a Siemens 1212C PLC controller (SIMENS, München, Germany) is used to provide adjustable load torque. Torque sensor is used to test the electromagnetic torque, and an oscilloscope is used to display the tested waveforms.

Figure 12. Test bench of the proposed DCF-HEM.

First, the back-EMF waveforms when the machine speed is 800 r/min are measured, as given in Figure 13. Since each phase has two sub-phases, the back EMF waveforms of both sub-phase windings are measured. A good match between the measured results and the simulated ones can be observed. Figure 14 shows the stationary torque waveforms, when the machine is applied with 8 A RMS AC current without DC bias. The corresponding current density is 8 A/mm² since the cross-sectional area of the stator coil is 1 mm². Again, there is good agreement between the results of the experimental tests and simulation. The measured torque density is 21 kNm/m³ innatural cooling conditions.

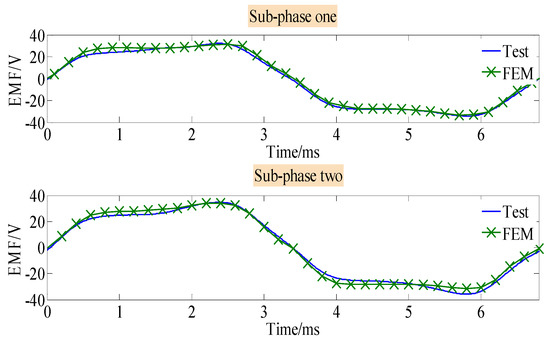
Figure 13. Back EMF waveforms.

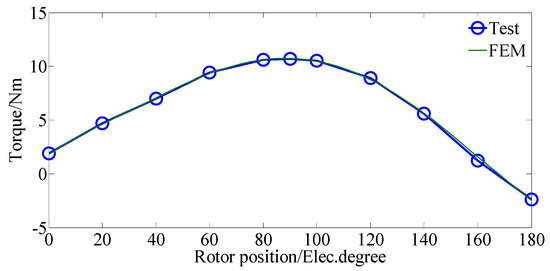
Figure 14. Stationary torque waveforms.

Figure 15 shows the transient waveforms of the phase current, electromagnet torque, and rotating speed when the proposed machine starts up from the stationary condition to 200 r/min. The load torque is 10 N·m, which is provided by the servo machine. Although the mechanical characteristics were not investigated, it can be observed from Figure 15 that the proposed DCF-HEM can reach steady state condition within 200 ms, which shows good dynamic performances. The efficiency map of the proposed machine over the whole operating region was investigated, and compared with the efficiency when using external DC field current control as used in traditional hybrid excited machines, as given in Figure 16. It can be seen that the proposed DCF-HEM can achieve both higher torque and a wider flux weakening range. It should be noted that there is a tradeoff between the torque density and flux weakening range. If we reduce the permanent magnet excitation, the flux weakening capability can be improved but the torque density will be reduced.

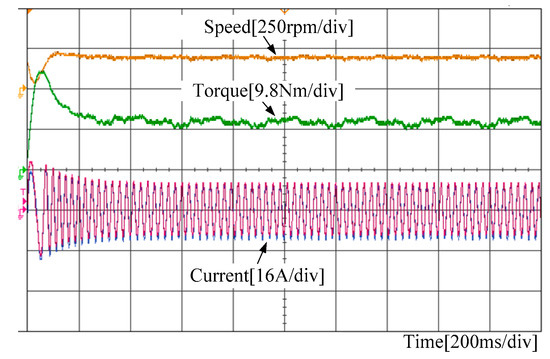
Figure 15. Measured transient waveforms during start-up process.

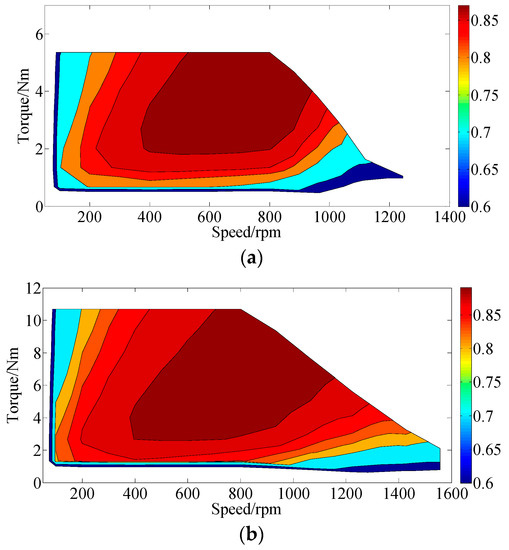
Figure 16. Efficiency maps. (a) External DC field current control. (b) DC bias current control.

6. Conclusions

A novel DCF-HEM with PM-iron consequent-pole rotor is proposed in this paper. DC coils in traditional HEMs are eliminated in the proposed design, and DC bias current is injected into the excitation to achieve flux regulation. Compared with traditional HEMs, the proposed DCF-HEM can be designed with a higher torque capability and a wider flux regulating range. The proposed machine has good potential in electric traction applications.