Fuzzy Stochastic Unit Commitment Model with Wind Power and Demand Response under Conditional Value-At-Risk Assessment

Abstract

With the increasing penetration of wind power and demand response integrated into the grid, the combined uncertainties from wind power and demand response have been a challenging concern for system operators. It is necessary to develop an approach to accommodate the combined uncertainties in the source side and load side. In this paper, the fuzzy stochastic conditional value-at-risk criterions are proposed as the risk measure of the combination of both wind power uncertainty and demand response uncertainty. To improve the computational tractability without sacrificing the accuracy, the fuzzy stochastic chance-constrained goal programming is proposed to transfer the fuzzy stochastic conditional value-at-risk to a deterministic equivalent. The operational risk of forecast error under fuzzy stochastic conditional value-at-risk assessment is represented by the shortage of reserve resource, which can be further divided into the load-shedding risk and the wind curtailment risk. To identify different priority levels for the different objective functions, the three-stage day-ahead unit commitment model is proposed through preemptive goal programming, in which the reliability requirement has the priority over the economic operation. Finally, a case simulation is performed on the IEEE 39-bus system to verify the effectiveness and efficiency of the proposed model.

1. Introduction

Energy is essential for economic development and domestic activities [1]. With the worldwide depletion of fossil energy and greenhouse gas emission, wind power as a major renewable energy has increasingly attracted attention [2,3]. However, because of the volatile and intermittent nature of wind power availability, the integration of wind power has brought challenges to the operation scheduling [4,5]. To accommodate wind power fluctuations in the dispatch, a sufficient flexibility of the system has to be reserved. Traditionally, the reserve capacities are scheduled by a deterministic and fixed ratio of the load [6], which is usually unsuitable for accommodating the forecast error of wind power and even amplifies the risk of load shedding.

To enable a comprehensive and flexible consideration of the uncertainty of wind power, significant studies have been performed through the stochastic optimization. The scenario-based method generates a variety of wind power scenarios on the basis of the given probability distribution of wind speed or wind power [7,8]. To improve the solution efficiency of the optimization model, scenario reduction techniques were introduced at the expense of the accuracy [9]. To utilize the statistical information of the uncertain variables, the chance-constrained programming (CCP) was introduced to solve the unit commitment (UC) model [10,11]. To improve the flexibility of generation scheduling, the decision is allowed to violate the constraints within the predefined confidence interval. Wang et al. [12] proposed stochastic chance-constrained goal programming (CCGP) by the combination of CCP and goal programming to achieve the best trade-off between the reserve cost and the risk level. In robust methods, the optimal solution is immune to the probability distribution and can be generated within the given bound, which is usually solved by using dual programming and Bender’s decomposition techniques [13,14]. The concept of uncertainty budget was introduced to mitigate the overconservatism of solution [15]. To carry on the risk assessment of stochastic wind power, the risk-based UC model usually introduces the concepts of operational risks of the power system [16,17]. Zhang and Giannakis [18] introduced the value-at-risk (VaR) and the conditional value-at-risk (CVaR) as the risk measures of load shedding and wind curtailment. Albeit VaR is a widely accepted measure to evaluate risk, it is unable to comply with the subadditivity and the consistency axioms. To overcome these drawbacks of VaR, CVaR was proposed as an adjustable risk measure, and the stochastic CVaR cold be solved by an additional linear programming.

Integrated into the power system as dispatchable resources, demand response (DR) programs have the potential to accommodate the uncertainty of wind power, and the traditional DR is dispatched as deterministic consumer behaviors [19]. However, due to the change in consumption behaviors, lack of policy attention, and other arbitrary factors, the actual response under DR is uncertain [20]. The impact of the combined uncertainties from DR and wind power has been amplified by the deepening of the integration of wind power and DR. Wang et al. [21] generated a variety of wind power scenarios and price elastic load (PEL) by Monte Carlo simulation, and CCP was introduced to formulate the risk constraint. Zhao et al. [22] proposed a multistage, robust optimization model considering the combined uncertainties of wind power and PEL on the basis of the interval programming and robust programming. Yang et al. [23] elaborated the probabilistic DR behaviors under an imprecise price elasticity demand curve.

The majority of the current researches focuses on coping with the single uncertainty in source side and demand side, which is inadequate to capture the full range of the combined uncertainties from wind power and DR. Meanwhile, most of the existing risk assessments based on CVaR have been performed on the basis of the probability distribution. Wang et al. [24] presented a distributional robust model on the basis of the concept of CVaR to generate the required reserve, considering the probability distribution of wind power forecast error. Paterakis et al. [25] developed the reserve valuation framework based on CVaR and obtained the stochastic wind power scenarios on the basis of historical data. Asensio and Contreras [26] established the two-stage UC model, including the CVaR assessment in isolated systems, and took the uncertainty of stochastic energy resources into consideration. Previous related works were done to evaluate the operational risk under a stochastic environment, which were unable to tackle the complicated uncertainties. Furthermore, the traditional CVaR had to be calculated by adding an additional linear programming, which aggravated the structural complexity of the optimization model. The computational burden of the model is still of concern when applied to practical implementations.

To develop a tool to accommodate both wind power uncertainty and DR uncertainty, in this paper, fuzzy stochastic conditional value-at-risk (FSCVaR) criterions are proposed as the risk measure of the combined uncertainties. To generate an efficient solution, the fuzzy stochastic chance-constrained goal programming (FSCCGP) is introduced to transform the traditional FSCCGP into a deterministic equivalent. In addition, the stochastic wind power and fuzzy PEL are considered, and FSCVaR is formulated by the shortage-of-reserve resource. Considering the system reliability requirements and economic goals, the three-stage UC model based on preemptive goal programming (PGP) is proposed.

The proposed FSCVaR based on FSCCGP is an adjustable risk assessment in comparison with other related risk approaches. More specifically, the main contribution of this paper is threefold:

(1)

The formulation of FSCVaR assessment can accommodate complicated uncertainties. Thus, the operational risk, considering stochastic wind power and fuzzy PEL, is evaluated by FSCVaR.

(2)

The FSCCGP is introduced to transfer the traditional FSCCGP to a deterministic equivalent, which mitigates the complexity of the UC model and contributes to high solution efficiency and transparency.

(3)

The PGP is proposed to consider the priorities of different goals and generate the tradeoff between reliability requirements and economic goals.

The remaining part of this paper is organized as follows. In Section 2, the stochastic CVaR and the fuzzy CVaR are introduced, and the FSCCGP is proposed to transform the FSCVaR into a deterministic equivalent. In Section 3, the uncertain factors of the power system are taken into consideration, and the shortage-of-reserve capacities are formulated by FSCVaR. In Section 4, a three-stage UC model considering the combined uncertainty of wind power and DR is proposed, and the PGP is presented to identify different priority levels of the objective functions. In Section 5, a case study on the IEEE 39-bus system is performed, and the associated computational results are examined. In Section 6, a summary of our discussions and contributions is presented.

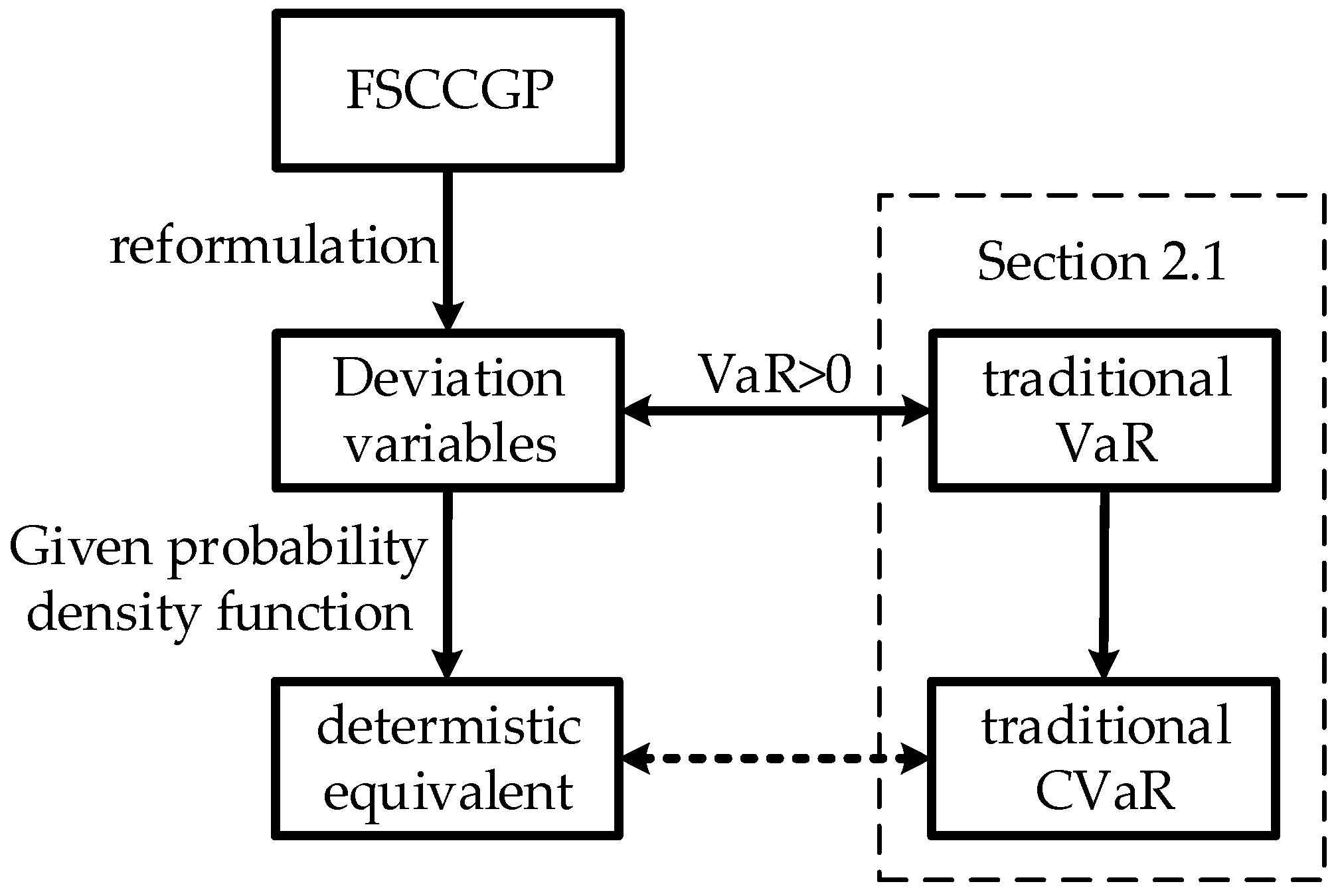
2. The FSCVaR Based on FSCCGP

2.1. FSCVaR Theory

As widely accepted risk measures, VaR and CVaR have been traditionally utilized to hedge the investment risk in the portfolio of financial instruments. VaR represents the maximum potential loss, ensuring that the total loss of the financial asset suffers with the specified probability level. However, the discontinuous distribution of VaR may aggravate the hurdles of computational complexities. From the theoretical point of view, VaR lacks convexity and subadditivity, which makes VaR inadequate to evaluate the coherent risk of general loss distribution.

As an adjustable risk measure derived from VaR, CVaR represents the conditional mean of investment loss beyond VaR. CVaR complies with consistent axiom and convexity, which provides an appropriate approach to measure the inherent risk effectively. Given the confidence level $\beta$, VaR and CVaR in the stochastic environment are formulated, respectively, as follows:

$$RVa{r}_{\beta }(x)=\min \left\{\alpha \in R：\phi \left(f(x,\xi ),\alpha \right)\ge \beta \right\}$$

(1)

$$RCVa{r}_{\beta }(x)=\frac{1}{1-\beta }{\displaystyle {\int }_{f\left(x,\xi \right)\ge RVa{r}_{\beta }(x)}f\left(x,\xi \right)\rho \left(\xi \right)d\xi }$$

(2)

where, $RVa{r}_{\beta }$ is the stochastic VaR with the predefined confidence level $\beta$, $RCVa{r}_{\beta }$ is the stochastic CVaR with the predefined confidence level $\beta$, $x\in X$ is the decision vector in the portfolio optimization, $\xi$ is the stochastic vector, $\rho \left(\xi \right)$ is the probability density function of $\xi$, $f(x,\xi )$ is the stochastic loss function, and $\phi \left(f(x,\xi ),\alpha \right)$ is the distribution probability of $f(x,\xi )$ not exceeding the threshold $\alpha$, which is formulated as follows:

$$\phi \left(f(x,\xi ),\alpha \right)={\displaystyle {\int }_{f(x,\xi )\le \alpha }\rho \left(\xi \right)d\xi }$$

(3)

The stochastic CVaR criterion is employed to assess the probabilistic risk in the majority of current researches. However, since the combined uncertainties in the source side and demand side are taken into consideration in this paper, it is necessary to develop a coherent risk measure in the fuzzy environment.

The fuzzy VaR and CVaR assessment under the given confidence level $\beta$ are formulated, respectively, as follows [27]:

$$FVa{r}_{\beta }(x)=\min \left\{\alpha \in R：Cr\left(f(x,\mu ),\alpha \right)\ge \beta \right\}$$

(4)

$$FCVa{r}_{\beta }(x)=\frac{1}{1-\beta }{\displaystyle {\int }_{\beta }^{1}FVa{r}_{\beta }\left(r\right)}dr$$

(5)

where, $FVa{r}_{\beta }$ is the fuzzy VaR within the predefined confidence level $\beta$, $FCVa{r}_{\beta }$ is the fuzzy CVaR within the predefined confidence level $\beta$, $\mu$ is the fuzzy vector in the uncertain environment, $f\left(x,\mu \right)$ is the fuzzy loss function, and $C_r\left(f\left(x,\mu \right),\alpha \right)$ is the credibility probability of $f\left(x,\mu \right)$ not exceeding the threshold $\alpha$.

Traditionally, the optimization problem including VaR is computationally intractable. To circumvent this problem, the original problem can be transformed into a linear programming problem by adding auxiliary variables [18], which provides an approach to calculate the stochastic CVaR. Nevertheless, the complexity of the optimization model is intensified by an additional linear programming, and the optimization process mandates the application of a numerical optimizer. Moreover, the method is unable to effectively formulate a fuzzy CVaR in the fuzzy environment. In order to propose the risk measure in the source side and demand side, CCGP is utilized to formulate the FSCVaR criterion in this paper.

2.2. The Deterministic Equivalent of FSCVaR by CCGP

To obtain the deterministic equivalent of FSCVaR, it is necessary to introduce the CCGP to transform the traditional CVaR into the corresponding deterministic form. The transformation sequence of FSCVaR is shown in Figure 1.

Traditional CCP allows the decision to violate the chance constraints, but the probability of constraint violation has to cover the predefined risk level. It is not easy to comply with multiple chance constraints at the same time, which results in the recurrence of nondominated solutions. To overcome the drawbacks of CCP, CCGP is proposed to identify different priority levels of multiple chance constraints [28]. The stochastic CCGP can be formulated as follows:

$$\{\begin{array}{l}\min u_i{d}_i^{+}+v_i{d}_i^{-}\\ s.t.\\ \mathrm{Pr}\{g_i(x,\overrightarrow{\xi })-b_i\le d_i^{+}\}\ge {\beta }_i^{+}\\ \mathrm{Pr}\{b_i-g_i(x,\overrightarrow{\xi })\le d_i^{-}\}\ge {\beta }_i^{-}\\ d_i^{+},d_i^{-}\ge 0,\end{array}$$

(6)

where, ${\beta }_i^{+}$ and ${\beta }_i^{-}$ are the predefined confidence levels which are given by the decision maker, $b_i$ is the goal value of the function $g_i$, $d_i^{+}$ and $d_i^{-}$ are the positive deviation and the negative deviation of the target value $b_i$, respectively, $u_i$ and $v_i$ are the weight factors corresponding to the positive deviation and the negative deviation, respectively. The positive deviation and the negative deviation can be analytically reformulated as follows:

$$\{\begin{array}{l}{d}_i^{+}=\min \{d\vee 0|\mathrm{Pr}\left\{g_i(x,\overrightarrow{\xi })-b_i\le d_i^{+}\right\}\ge {\beta }_i^{+}\}\\ d_i^{-}=\min \{d\vee 0|\mathrm{Pr}\left\{b_i-g_i(x,\overrightarrow{\xi })\le d_i^{-}\right\}\ge {\beta }_i^{-}\}\end{array}$$

(7)

Noting that $P_r(f(x_i,\overrightarrow{\xi })-b_i\le d)=\phi (x,d)$, Equation (7) can be transformed into VaR in a similar form, as follows:

$$\{\begin{array}{l}{d}_i^{+}=RVa{r}_{\beta }^{+}(x)\vee 0\\ d_i^{-}=RVa{r}_{\beta }^{-}(x)\vee 0\end{array}$$

(8)

It is noteworthy that the operational risk takes a non-negative value in the power system. In contrast to previous works, stochastic VaR can be transformed to the deviation of CCGP without sacrificing the accuracy. The existing researches indicate that if the chance constraints can be reformulated according to the Equation (9) [28], whereby the stochastic variables can be separated from the function and the stochastic vector can be represented by a variable $\xi$, given that $\varphi$ is the probability density function of $\xi$, the deviation of CCGP can be transferred to a deterministic equivalent, as follows:

$$\{\begin{array}{l}\mathrm{Pr}\{h\left(x\right)-\xi -b_i\le d_i^{+}\}\ge {\beta }_i^{+}\\ \mathrm{Pr}\{b_i-h\left(x\right)+\xi \le d_i^{-}\}\ge {\beta }_i^{-}\end{array},where{g}_i\left(x,\xi \right)=h\left(x\right)-\xi$$

(9)

$$\{\begin{array}{l}{d}_i^{+}=\left[h_i\left(x\right)-b_i-{\varphi }^{-1}\left(1-{\beta }_i^{+}\right)\right]\vee 0\\ d_i^{-}=\left[b_i-h_i\left(x\right)+{\varphi }^{-1}\left({\beta }_i^{-}\right)\right]\vee 0\end{array}$$

(10)

Leveraging on the Equation (10), random CVaR(RCVaR) can be equivalently transformed into a deterministic equivalent, as follows:

$$\{\begin{array}{l}RCVa{r}_{\beta }^{+}(x)=h(x)-\frac{1}{1-{\beta }_i^{+}}{\displaystyle {\int }_{{\varphi }^{-1}\left(0\right)}^{{\varphi }^{-1}\left(1-{\beta }_i^{+}\right)}\xi \rho \left(\xi \right)d\xi }\\ RCVa{r}_{\beta }^{-}(x)=\frac{1}{1-{\beta }_i^{-}}{\displaystyle {\int }_{{\varphi }^{-1}\left({\beta }_i^{-}\right)}^{{\varphi }^{-1}\left(1\right)}\xi \rho \left(\xi \right)d\xi }-h(x)\end{array}$$

(11)

Similar to the deterministic equivalent of stochastic CVaR, given that $\psi$ is the credibility distribution function of $\mu$, fuzzy CVaR(FCVAR) can be formulated by implementing CCGP, as follows:

$$\begin{array}{l}FCVa{r}_{\beta }^{+}(x)=h(x)-\frac{1}{1-{\beta }_i^{+}}{\displaystyle {\int }_{{\beta }_i^{+}}^1{\psi }^{-1}\left(\mu \right)d\mu }\\ FCVa{r}_{\beta }^{-}(x)=\frac{1}{1-{\beta }_i^{-}}{\displaystyle {\int }_{{\beta }_i^{-}}^1{\psi }^{-1}\left(\mu \right)d\mu }-h(x)\end{array}$$

(12)

In sum, FSCVaR, which comprises stochastic CVaR and fuzzy CVaR, can be determined as the risk measure in the complicated uncertainty environment. Compared with existing works, CVaR can be directly transferred to the deterministic equivalent by introducing the deviation of CCGP, which can drastically improve the solution efficiency.

3. The Uncertainty Factors in the Grid and the Corresponding Reserve Constraints

With the increasing integration of the wind power and flexible demands, the combined uncertainties in the source side and demand side have to be considered in the generation scheduling. More specifically, the combined uncertainties contain the stochasticity of the wind power and the fuzziness of PEL.

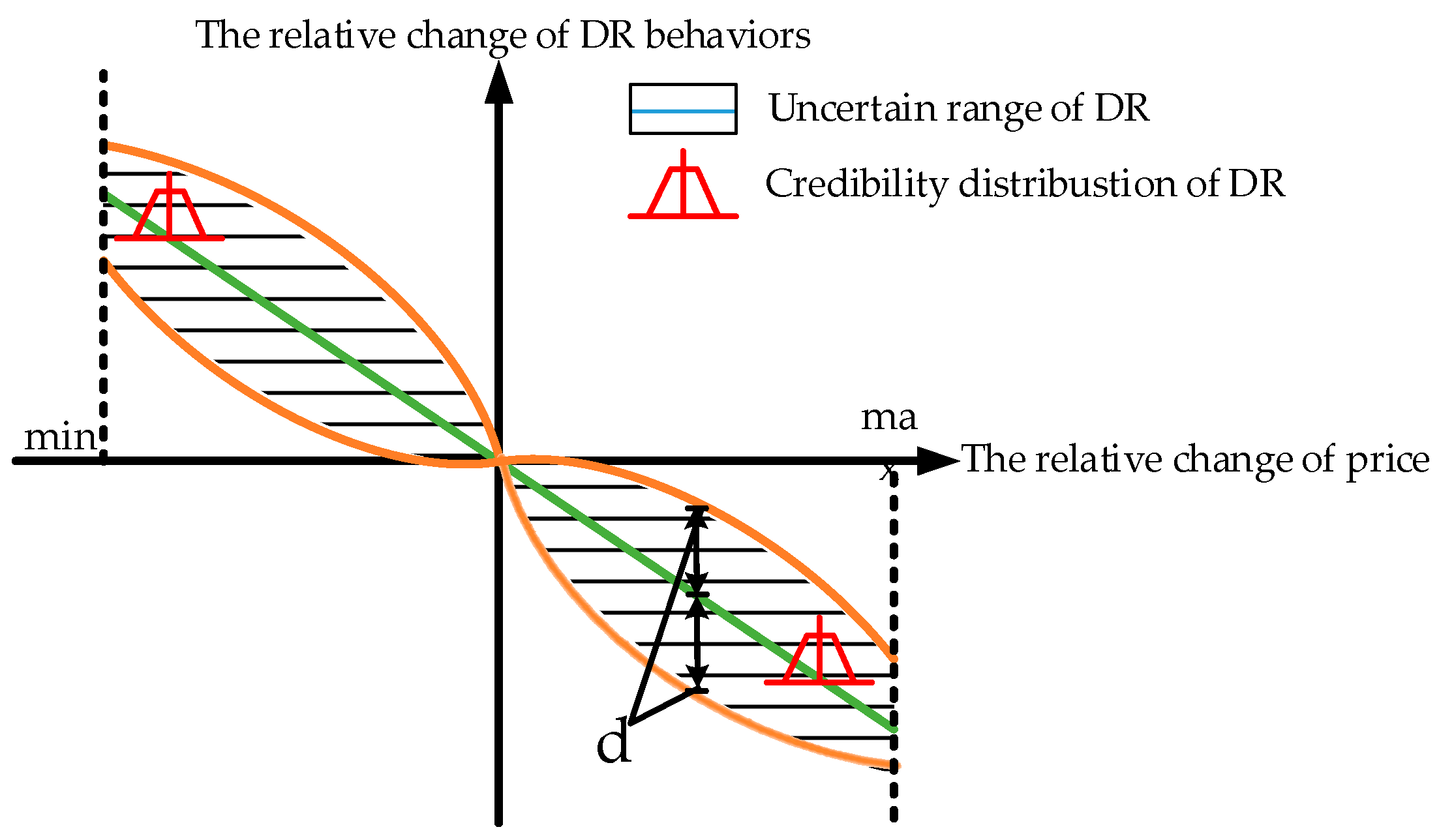
3.1. The Uncertainty from Wind Power and DR

3.1.1. The Fuzziness of DR

DR is mainly divided in two categories: price DR and incentive DR. The consumer behaviors under incentive DR are scheduled by signing contracts with the consumers. With the unaffordable punishment applied in case of a breach of contract, most consumers are motivated to adhere to predefined response behaviors, which can be approximately considered as the deterministic loads. In comparison with incentive DR, the consumer behaviors of price DR vary with different prices. Moreover, arbitrary factors have a remarkable impact on the consumer behaviors. More specifically, because of the willingness of consumer behaviors, ignore policies and communication delays, the actual response from the customers of PEL is uncertain in nature, as Figure 2 shown. With the increase of the relative change of the price, the response from consumers has a tendency to decrease. Because of the imprecise price elastic response curve, the fuzzy characteristics of consumer behaviors are exposed. To mathematically characterize the uncertainty of DR, the concept of self–elastic is employed to formulate the response behavior, as follows:

$$\Delta L^t={\lambda }_{ep}^t{\epsilon }_{tt}{L}^t$$

(13)

where $\Delta L^t$ is the demand response amount of PEL, ${\lambda }_{ep}^t$ is the relative change in the price, ${\epsilon }_{tt}$ is self-elastic coefficient, $L^t$ is the forecast load without PEL.

The fuzzy error of the demand response amount can be formulated as follows:

$${\widetilde{\Delta L_{\mu }}}^t={\mu }_{ep}{\lambda }_{ep}^t{\epsilon }_{tt}\Delta L^t$$

(14)

where ${\widetilde{\Delta L_{\mu }}}^t$ is the forecast error of the demand response amount of PEL and ${\mu }_{ep}$ is the forecast error of the relative change of the demand response amount, which is formulated by triangle fuzzy number.

$${\mu }_{ep}=（-d_{\lambda },0,d_{\lambda })$$

(15)

where $d_{\lambda }$ is the threshold of the forecast error of PEL.

3.1.2. The Stochasticity of Wind Power

With the influence of height, climate, and other natural factors, the actual output of wind power is stochastic and volatile [29,30]. The prediction error of wind power adheres to a normal distribution, and the mean of the distribution is set to zero:

$$\xi \sim N\left(0,\sigma \right)$$

(16)

where $\xi$ is the prediction error of wind power and $\sigma$ is the variance of the prediction error of wind power, which can be calculated by using the proposed method, as follows [31]:

$$\xi \sim N(0,\frac{1}{5}{P}_W^t+\frac{1}{50}{W}_s)$$

(17)

where $P_W^t$ is the forecast wind power and $W_s$ is the total installed capacity of wind power.

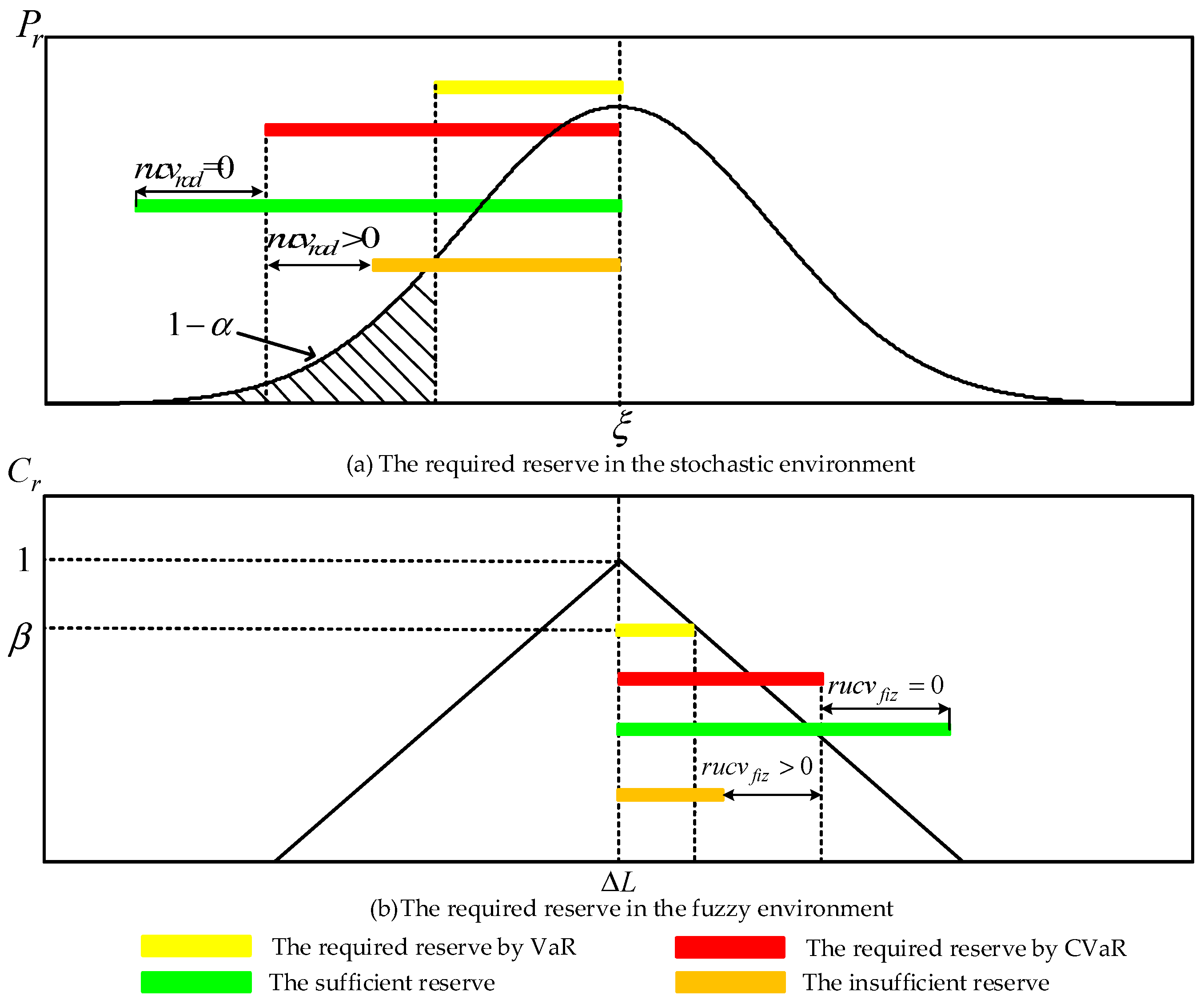
3.2. FSCVaR Based on System Reserve Shortage

To eliminate the forecast error in the source side and demand side, sufficient capacities have to be reserved in unit commitment and dispatch. On the basis of the discussion in the Section 2.2 and Section 3.1 , system reserve constraints can be formulated by fuzzy stochastic CCP:

$$\{\begin{array}{l}Ch\left({\displaystyle \sum _{i=1}^n{P}_{up,i}^t}\ge {\widetilde{\Delta L_{\mu }}}^t-\xi \right)\left({\alpha }_1\right)\ge {\beta }_1\\ Ch\left({\displaystyle \sum _{i=1}^n{P}_{dw,i}^t}\ge \xi -{\widetilde{\Delta L_{\mu }}}^t\right)\left({\alpha }_2\right)\ge {\beta }_2\end{array}$$

(18)

where ${\alpha }_1$, ${\alpha }_2$, ${\beta }_1$, and ${\beta }_2$ are the confidence levels given by the decision maker, and $P_{up,i}^t$ and $P_{dw,i}^t$ are the upward reserve and the downward reserve of the thermal unit, respectively. Based on the mathematical transformation in the Section 2.2, the reserve shortage can be rationally modelled by CCGP by the Equation (19), which refers to the deviation between the actual reserve capacity and the required reserve to cover the given risk level. In the terms of risk measure, the reserve shortage reflects the VaR of the scheduling under the given risk level:

$$\{\begin{array}{l}{d}_{up}^t=\left[{\mu }^{-1}(2-2{\beta }_1)-{\varphi }^{-1}\left(1-{\alpha }_1\right)-{\displaystyle \sum _{i=1}^n{P}_{up,i}^t}\right]\vee 0\\ d_{dw}^t=\left[-{\displaystyle \sum _{i=1}^n{P}_{dw,i}^t}+{\varphi }^{-1}\left({\alpha }_2\right)-{\mu }^{-1}(2-2{\beta }_2)\right]\vee 0\end{array}$$

(19)

To provide an intuitive way to distinguish the fuzzy CVaR from the stochastic CVaR, the upward reserve and downward reserve are divided by two independent reserves, respectively.

$$\begin{array}{l}{P}_{up,i}^t=P_{urad,i}^t+P_{ufuz,i}^t\\ P_{dw,i}^t=P_{drad,i}^t+P_{dfuz,i}^t\end{array}$$

(20)

where $P_{urad,i}^t$ and $P_{drad,i}^t$ are the upward reserve and downward reserve for stochastic forecast error of wind power, respectively, and $P_{ufuz,i}^t$ and $P_{dfuz,i}^t$ are the upward reserve and downward reserve for fuzzy forecast error of DR, respectively. According to the Equation (20), the original VaR can be further divided by fuzzy VaR and stochastic VaR as follows:

$$\{\begin{array}{l}{d}_{urad}^t=\left[-{\varphi }^{-1}\left(1-{\alpha }_1\right)-{\displaystyle \sum _{i=1}^n{P}_{urad,i}^t}\right]\vee 0\\ d_{drad}^t=\left[-{\displaystyle \sum _{i=1}^n{P}_{drad,i}^t}+{\varphi }^{-1}\left({\alpha }_2\right)\right]\vee 0\\ d_{ufuz}^t=\left[{\mu }^{-1}(2-2{\beta }_1)-{\displaystyle \sum _{i=1}^n{P}_{ufuz,i}^t}\right]\vee 0\\ d_{dfuz}^t=\left[-{\mu }^{-1}(2-2{\beta }_2)-{\displaystyle \sum _{i=1}^n{P}_{dfuz,i}^t}\right]\vee 0\end{array}$$

(21)

where $d_{urad}^t$ and $d_{drad}^t$ are the upward reserve shortage and downward reserve shortage of the stochastic forecast error, respectively, $d_{ufuz}^t$ and $d_{dfuz}^t$ are the upward reserve shortage and downward reserve shortage of the fuzzy forecast error, respectively. In accordance with Equations (11) and (12) in the Section 2.2, FSCVaR, formulated by the deviation of CCGP, is transformed into the deterministic equivalent:

$$\{\begin{array}{l}rucva{r}_{rad}(x)=\frac{{\sigma }^2}{\left(1-\beta \right)}\rho \left({\varphi }^{-1}\left(1-\beta \right)\right)-{\displaystyle \sum _{i=1}^n{P}_{urad,i}^t}\\ rdcva{r}_{rad}(x)=\frac{{\sigma }^2}{\left(1-\beta \right)}\rho \left({\varphi }^{-1}\left(1-\beta \right)\right)-{\displaystyle \sum _{i=1}^n{P}_{drad,i}^t}\\ rucva{r}_{fuz}(x)=\left(1-\beta \right)0+\beta d-{\displaystyle \sum _{i=1}^n{P}_{ufuz,i}^t}\\ rdcva{r}_{fuz}(x)=\left(1-\beta \right)0+\beta d-{\displaystyle \sum _{i=1}^n{P}_{dfuz,i}^t}\end{array}$$

(22)

where $rucva{r}_{rad}(x)$ and $rdcva{r}_{rad}(x)$ are CVaR represented by the upward reserve shortage and downward reserve shortage of the stochastic forecast error, respectively, and $rucva{r}_{fuz}(x)$ and $rdcva{r}_{fuz}(x)$ are CVaR represented by the upward reserve shortage and downward reserve shortage of the fuzzy prediction error, respectively. To shed light on the essential concept and practical implementation of CVaR, CVaR represented by the upward reserve is taken as an example, as shown in Figure 3. When the actual wind power is inferior to the forecasted wind power and the upward reserve is unable to handle the prediction error, $rucva{r}_{rad}(x)>0$. This indicates that the risk of load shedding exceeds the given value. When the actual reserve is sufficient to satisfy the reserve requirement, $rucva{r}_{rad}(x)=0$, which means that the risk of load shedding is inferior to the given value. When the actual response from the consumers exceeds the prediction of the demand response amount, $rucva{r}_{fiz}(x)>0$. This means that the underlying risk of load shedding is beyond the predefined risk level, which is similar to the situation of $rucva{r}_{rad}(x)$. Corresponding to the risk of insufficient positive reserve, $rdcva{r}_{rad}(x)$ and $rdcva{r}_{fiz}(x)$ indicate the risk of wind curtailment resulting from insufficient downward reserve.

4. The Three-Stage UC Model Based on PGP

To adequately consider the fuzzy stochastic characteristics of the source side and demand side, the combined uncertainties of wind power and PEL are considered in the UC model. Meanwhile, the FSCVaR criterions are modeled by FSCCGP as the risk measure in a complicated uncertainty environment.

4.1. The Objective Functions of the Model

There is usually a conflict between the system reliability and the economic objectives, which requires scheduling a plan to achieve the best trade-off between stability requirements and the economic operation.

According to Section 3.2, the system reliability goal in the UC model is formed by a deterministic CVaR criterion, as follows:

$$\min \left(rucva{r}_{rad}+rdcva{r}_{rad}(x)+rucva{r}_{fuz}(x)+rdcva{r}_{fuz}(x)\right)$$

(23)

The economic goal is to minimize the operating cost, as follows:

$$\min C_{total}=C_{fc}+C_{res}+C_{su}$$

(24)

where $C_{total}$, $C_{fc}$, $C_{res}$, and $C_{su}$ are the operational cost, fuel cost, reserve cost, and start-up cost, respectively.

4.2. Constraints of the UC Model

• Power balance constraint:

  $${\displaystyle \sum _{i=1}^{N_G}{P}_{G,i}^t}{v}_{i,t}+{\displaystyle \sum _{j=1}^{N_W}{P}_{Wf,j}^t}=L^t-\Delta L^t$$

  (25)

  where $P_{G,i}^t$ is the output of thermal unit and $v_i^t$ is the on-off status of the thermal unit.
• Unit reserve constraints

  $$\{\begin{array}{l}{P}_{G,i}^t+P_{up,i}^t\le P_{G\max ,i}{v}_{i,t}\\ P_{G,i}^t-P_{dw,i}^t\ge P_{G\min ,i}{v}_{i,t}\end{array}$$

  (26)

  where $P_{G\max ,i}$ and $P_{G\min ,i}$ are the maximum output and the minimum output of the thermal unit, respectively.
• Ramping constraints:

  $$\{\begin{array}{l}{P}_{G,i}^t+P_{up,i}^t\le P_{G\max ,i}{v}_{i,t}\\ P_{G,i}^t-P_{dw,i}^t\ge P_{G\min ,i}{v}_{i,t}\end{array}$$

  (27)

  where $P_{G\max ,i}$ and $P_{G\min ,i}$ are the maximum output and the minimum output of the thermal unit, respectively.
• Minimum shut-up and shut-down time constraints:

  $$\{\begin{array}{l}\left(v_{i,t-1}-v_{i,t}\right)\left(T_{on,i,t-1}-T_{on,i}\right)\ge 0\\ \left(v_{i,t}-v_{i,t-1}\right)\left(T_{off,i,t-1}-T_{off,i}\right)\ge 0\end{array}$$

  (28)

  where $T_{on,i}$ and $T_{off,i}$ are the minimum shut-up time and the minimum shut-down time, respectively.

4.3. The Three-Stage UC Model Based on PGP

The objective functions of system reliability contain the shortage of the upward reserve capacity and of the downward reserve capacity, of which, the shortage of the upward reserve has priority over the latter. This is mainly attributed to the fact that the risk of the load shedding is more unaffordable than the risk of the wind curtailment. Meanwhile, in concordance with the essential requirements in the thermal generation unit commitment, the system reliability has the priority over the economical objective. To identify the different priority levels of the different functions, PGP is introduced in this paper. In the PGP, the objective functions are ordered one on top of another in accordance with the corresponding rank of every goal [32]. Firstly, the goal with the highest priority is optimized in the original feasible region, and the feasible region of the lower stage is updated dynamically based on the optimal solution of the upper stage.

The objective function of the first stage is to minimize the shortage of the upward reserve, aiming at substantially mitigating the risk of load shedding:

$$\min rucva{r}_{rad}(x)+rucva{r}_{fuz}(x)$$

(29)

The objective function of the second stage is to minimize the shortage of the downward reserve, which is combined with the objective function of the first stage to meet the reliability requirement. On the basis of the PGP theory, because of the priority of the load shedding risk over the wind curtailment, the additional constraint based on the optimal solution of the first stage is established in the second stage:

$$\{\begin{array}{l}\min rdcva{r}_{rad}(x)+rdcva{r}_{fuz}(x)\\ rucva{r}_{rad}+rucva{r}_{fuz}(x)\le Z_1\end{array}$$

(30)

where $Z_1$ is the optimal solution of the first stage.

The objective function of the third stage is that the operational cost fulfill the economic goals in the UC model. Because of the priority of the safety requirement over the economical demand, the additional constraints based on the optimal solution of the first stage and the second stage are established in the last stage:

$$\{\begin{array}{l}\min C_{total}=C_{fc}+C_{res}+C_{su}\\ rucva{r}_{rad}(x)+rucva{r}_{fuz}(x)\le Z_1\\ rdcva{r}_{rad}(x)+rdcva{r}_{fuz}(x)\le Z_2\end{array}$$

(31)

where $Z_2$ is the optimal solution of the second stage.

In sum, every stage of the UC model based on PGP needs to hold the original constraints which are contained in Equations (25)–(28). Meanwhile, the additional constraints based on the optimal schedules of the former stages have to be satisfied in the every stage.

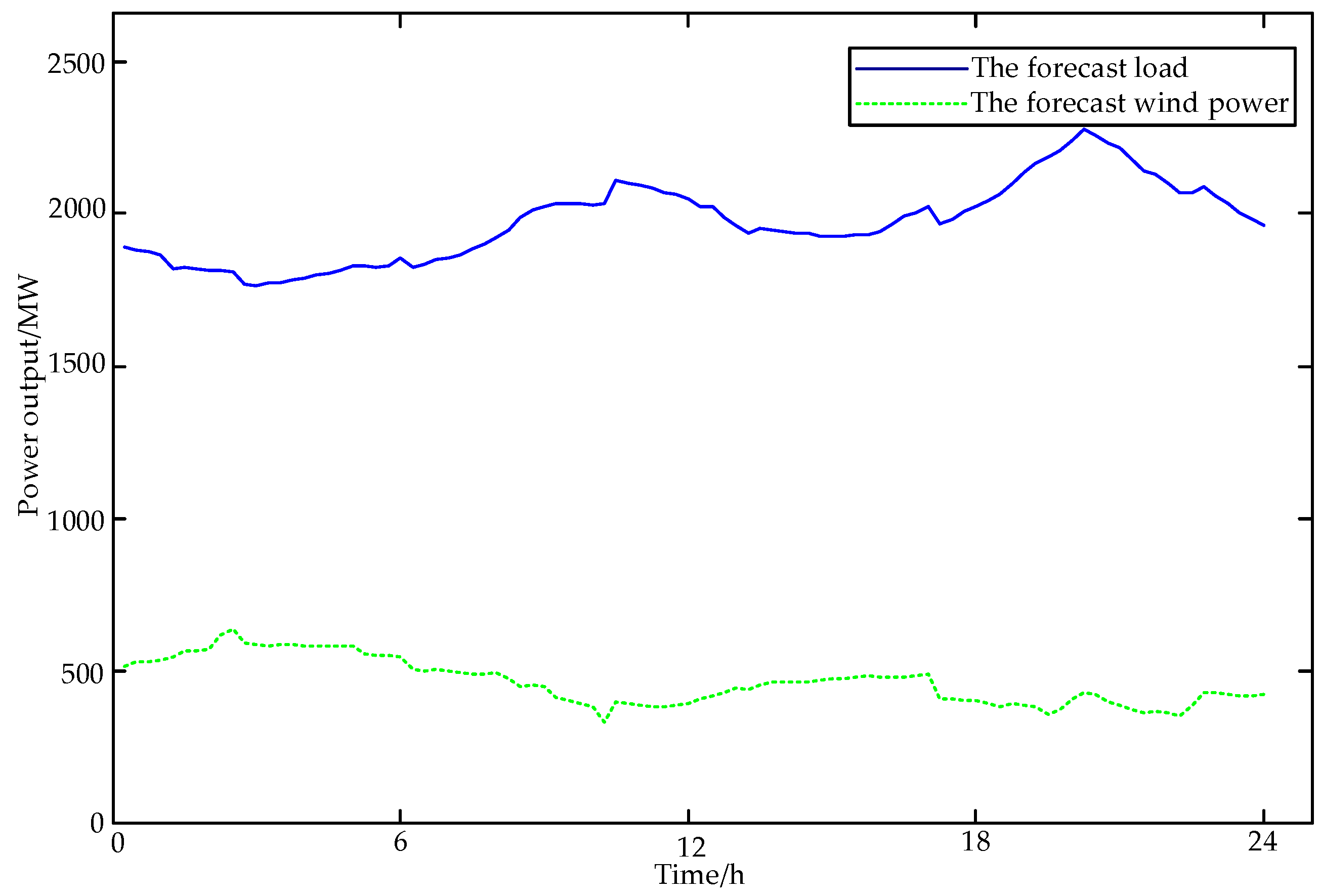
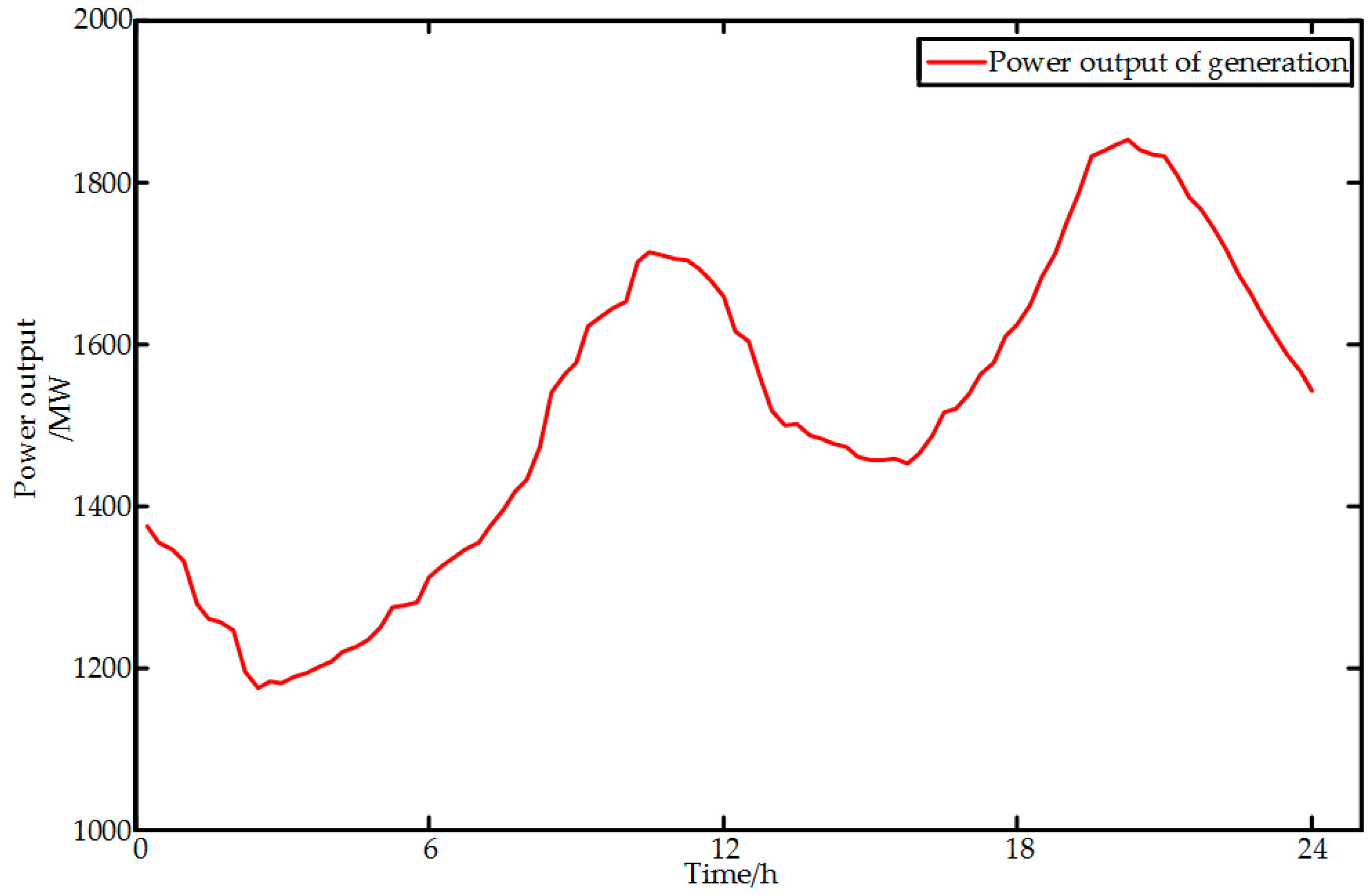
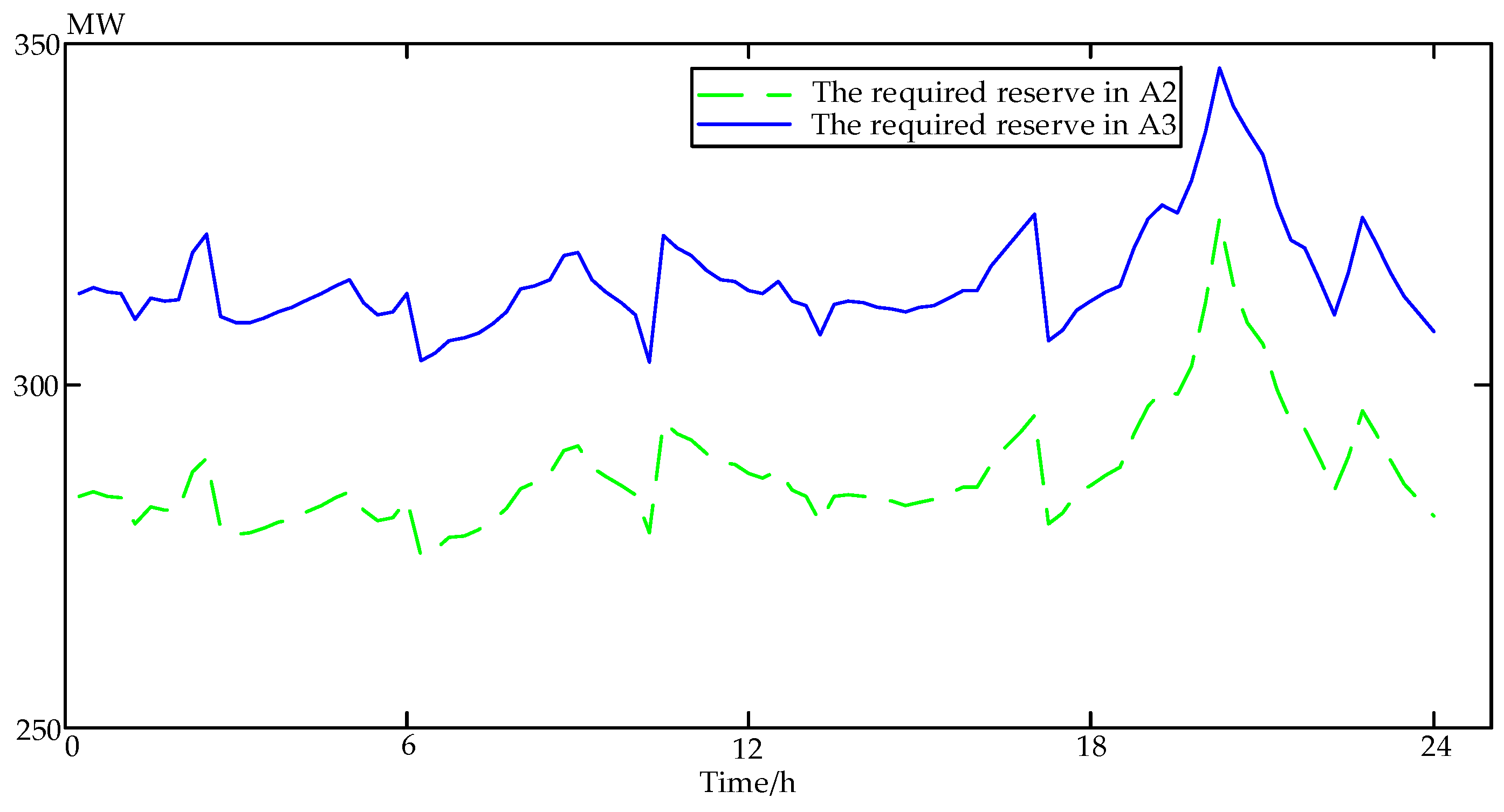
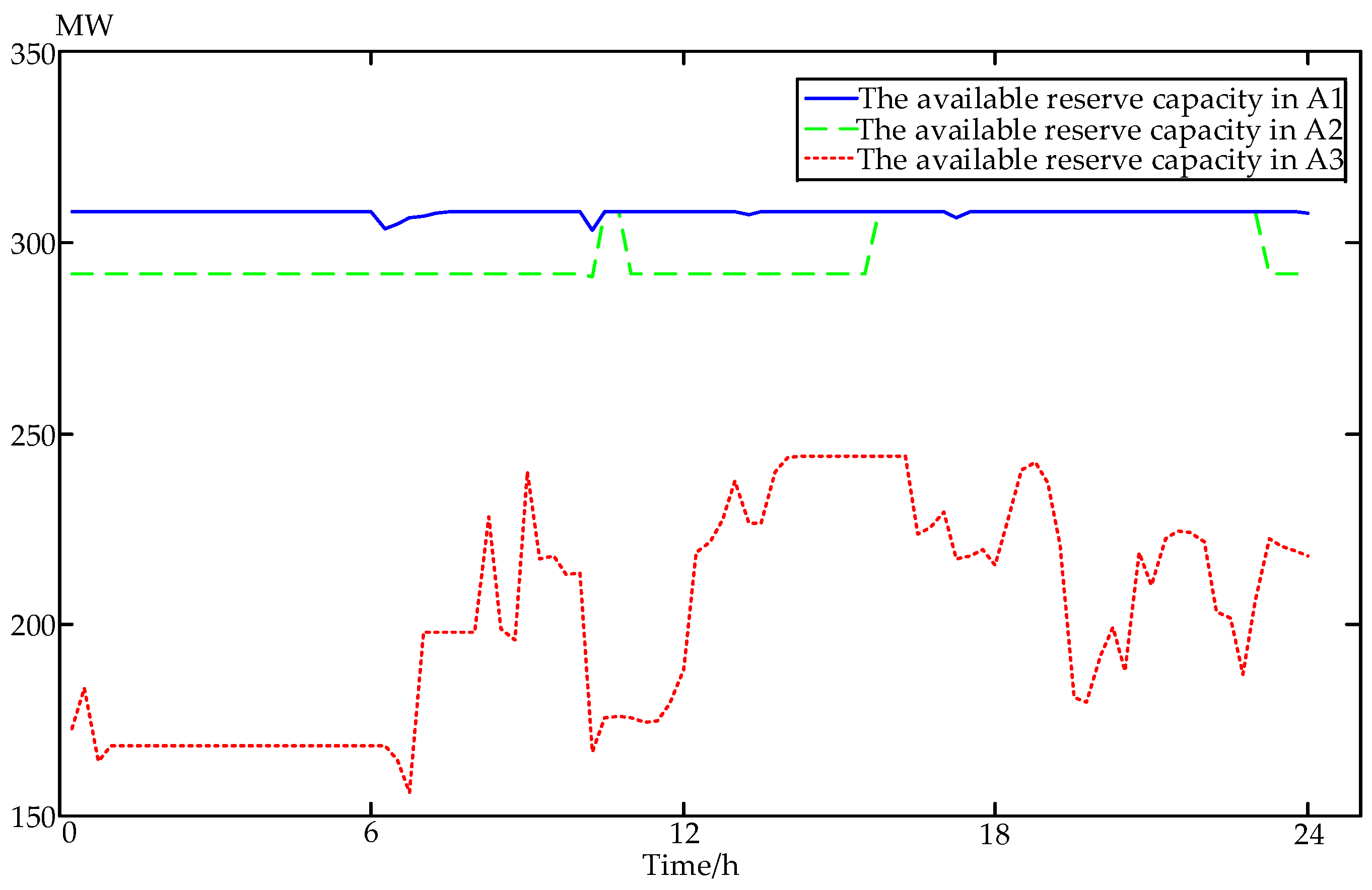
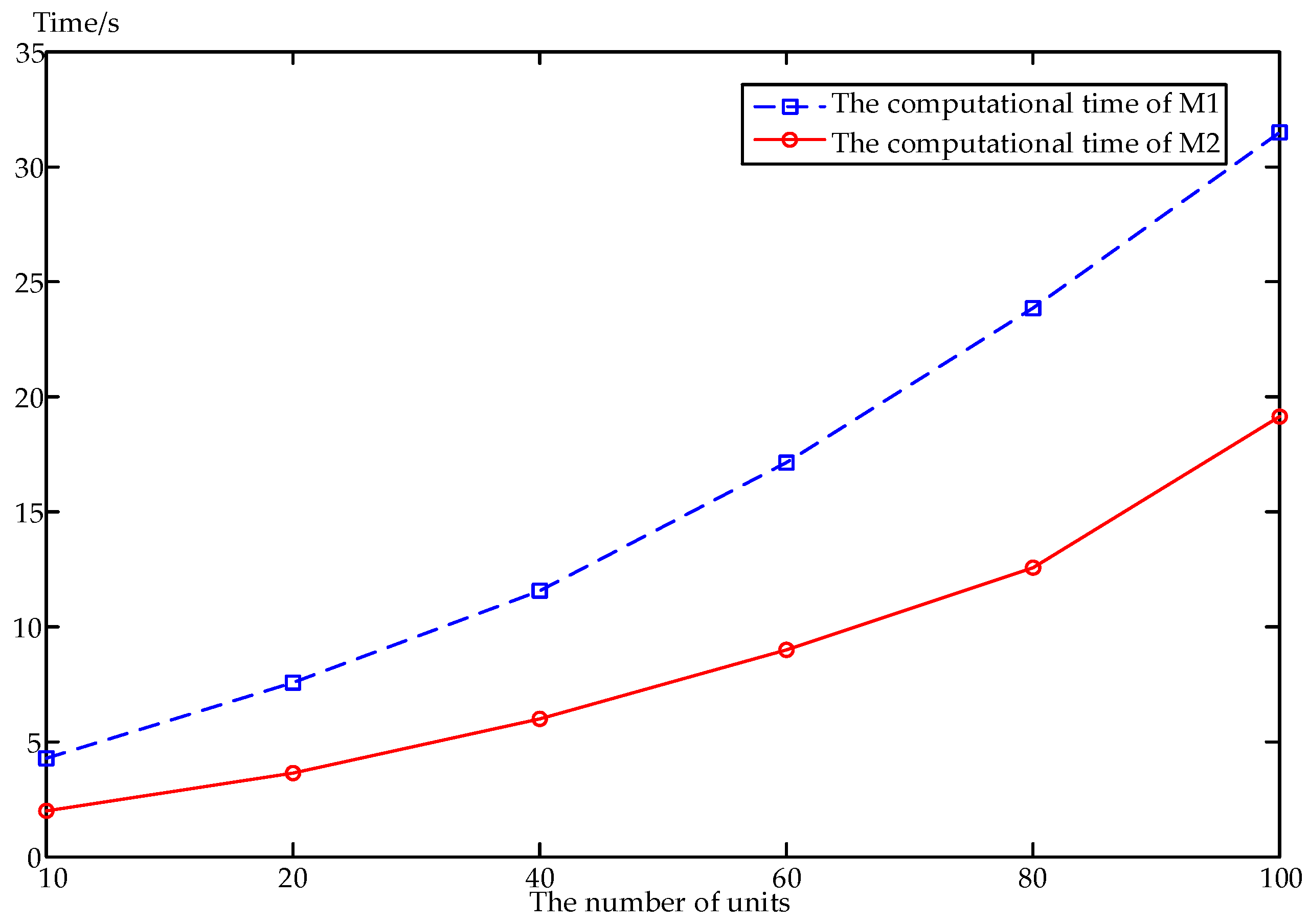
5. Case Sudy

For the sake of the risk assessment of the combined uncertainties in the source side and demand side, an illustrative case is studied, represented by the IEEE 39-bus system with 10 generators. The forecasted wind power and forecasted system load are shown in Figure 4. The self-elastic coefficient ${\epsilon }_{tt}$ is −0.15, and the threshold of the forecast error of PEL, $d_{\lambda }$, is 0.4. The data related to the IEEE 39-bus system with 10 generators is shown in [33]. The reserve cost is assumed to be 50% of the fuel cost of the corresponding units, and the confidence level in the reserve is ${\alpha }_1={\alpha }_2={\beta }_1={\beta }_2=0.95$. The power output of generation is shown in Figure 5.

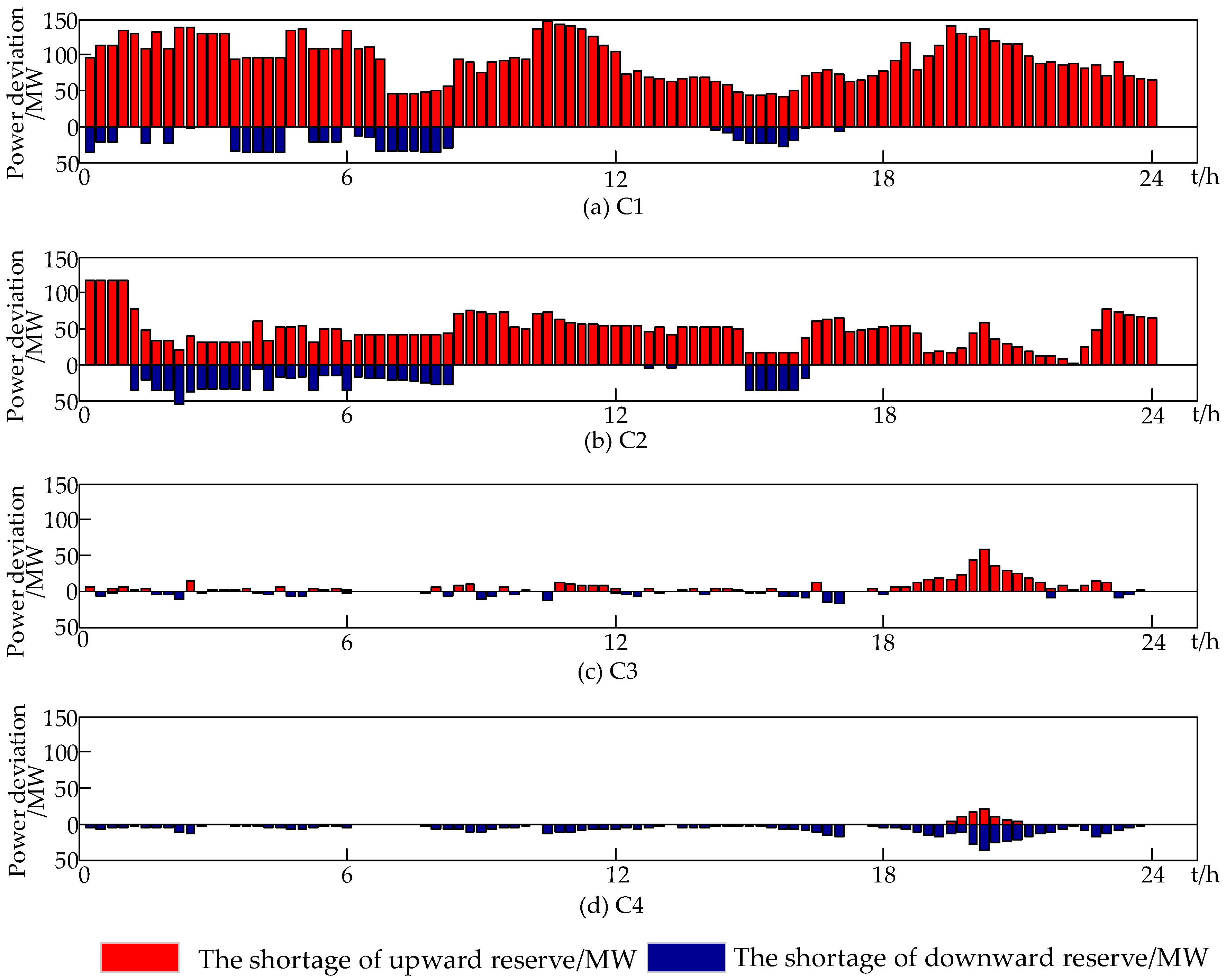
5.1. Risk Criterions Analysis

In order to explore the impact of the risk measure on the UC scheduling, we compare three cases in the test and analyze the corresponding available reserve capacities:

A1: the one-stage UC model is established to optimize the operation cost without the reliability requirements. The objective function of the UC model is modeled according to the Equation (24).

A2: the three-stage UC model is established, by which the VaR is determined as the risk measure of the UC model. The objective functions of the first stage and second stage in Section 4.3 are replaced by the corresponding VaR form;

A3: the three-stage UC model proposed in Section 4.3 is established, by which the CVaR is determined as the risk measure of the UC model.

The minimum reserve required for the given risk level is shown in Figure 6, and the available reserve capacities of the different cases is illustrated in Figure 7.

As Figure 7 shows, lower reserve capacities are provided in A1 than in A2 and A3. The reason lies in the fact that the operation cost is determined as the only objective of A1 and the reliability requirement is ignored. In order to generate the economic optimal solution of A1, the units with more economic parameters have the priority, to generate more power output. Thus, the available reserve capacities provided by the units are limited, which substantially reduces the system flexibility. As Figure 6 shows, because of the difference of risk measure between A2 and A3, the required reserves for covering the given risk in the A2 are smaller than those in A3, and higher required reserves occur with higher available reserve capacities. This is mainly attributed to the fact that VaR describes the greatest risk under the given confidence level and is unable to effectively handle the combined uncertainties in the extreme scenarios. Compared with VaR, CVaR is competent enough to measure the tail risk. Consequently, the maximization of the available reserve capacities is catered to cope with the risk of complicated uncertainty in A3.

5.2. Computational Performance

In order to verify the solution efficiency of the CVaR criterion proposed in this paper, two methods are adopted to optimize the three-stage UC model in different scales of the simulation cases.

M1: the linear programming method is introduced to solve the CVaR [18]. The discrete scenario number Ns in the linear programming method is 1000.

M2: the method proposed in this paper is introduced to transform CVaR into a deterministic equivalent.

The computational efficiency of the two approaches is shown in Figure 8.

As Figure 8 shows, CVaR in M2 is much more computationally efficient than M1. As the system scale escalates, there is a tendency of the calculation time to increase in two cases. Nevertheless, in terms of changing trends, there is a significant difference between M1 and M2. The solution time in M1 increases sharply, but M2 rises relatively gently. This is mainly attributed to the reason that the traditional CVaR is calculated by adding auxiliary variables and an additional linear programming. In M1, the optimization model in every stage needs an additional solution of the linear programming, which intensifies the computational burden and structure complexity of the UC model. In M2, the CVaR is transformed into the deterministic form by the application of CCGP, and no additional variables need to be introduced. The result reveals that the computational efficiency can be increased drastically by the application of the proposed approach.

5.3. The Analysis of the Priorities of the Objective Goals

In order to elaborate a hierarchical relationship between different objective functions in the UC model, four cases are simulated and analyzed to verify the influence of the priorities of different goals on the optimization model. The shortage of the system reserves is shown in Figure 9:

C1: multiple objectives are translated to a single objective with the weight factors [23], and the weight factors of the reserve shortage goals are 20.

C2: multiple objectives are translated to a single objective with the weight factors [23], and the weight factors of the reserve shortage goals are 50.

C3: the PGP method is employed to establish a two-stage UC model, and the objective function of each stage is formulated as Equations (23) and (24), respectively.

C4: the PGP method is employed to establish a three-stage UC model, and the objective function of each stage is formulated as Equations (29)–(31), respectively.

As Figure 9 shows, the total amount of the reserve shortage in C1 is notably larger than in C2. This indicates that a high weight of the reliability goals incurs into a low reserve shortage risk, and the weight coefficients of the objective functions have a remarkable impact on the schedule. Meanwhile, the total amount of the reserve shortage in C1 and C2 is remarkably higher than that in C3 and C4. Since there is no clear priority between system reliability and economic goals in C1 and C2, the reserve requirement is not fulfilled preferentially, and the scheduling is too rash and risky to tackle the complicated uncertainties from wind power and PEL. PGP is employed to identify the priority levels of the different goals in C3 and C4, and the minimization of the shortage risk is catered. Albeit there is no difference in the total amount of the system reserve shortage, the shortage of the upward reserve in C3 is notably lower than the shortage in C4. Recall that the upward reserve shortage and the downward reserve shortage represent the load shedding risk and wind curtailment risk in the Section 3.2, respectively. The load shedding risk in C3 has a more significant impact on the schedule than in C4. Moreover, there is a frequent change from the upward reserve shortage to the downward reserve shortage, which indicates that the complexity for generation scheduling has been amplified. In comparison with the former cases, the schedule in C4 identifies different priority levels for every objective function by introducing the PGP. The reliability requirement of the power system has the priority over the economic goals, and the minimization of the upward reserve is catered in the first stage.

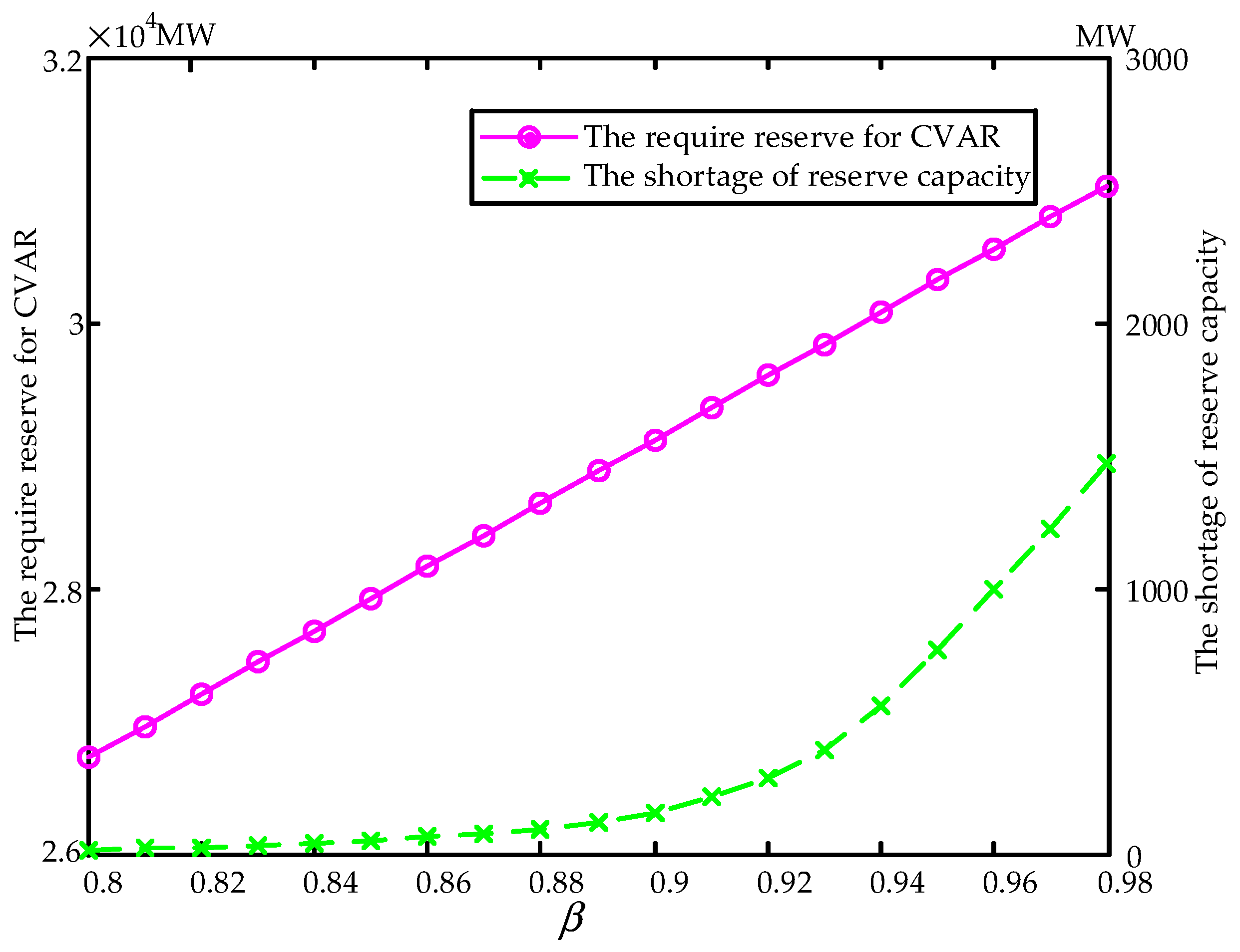
5.4. Sensitive Analysis

In order to investigate the tendency of the reserve capacity under different reliability requirements, the confidence level is varied from 0.8 to 0.98, and a variety of scenarios are optimized. The results of the confidence level $\alpha$ and $\beta$ are shown in Figure 10 and Figure 11, respectively.

As Figure 10 and Figure 11 show, with the increase of the confidence level, the minimum required reserve for covering the risk level increases, which intensifies the shortage risk of the reserve capacity. When the confidence level is inferior to 0.94, the shortage risk of the system reserve is relatively small. This is mainly attributed to the fact that the total amount of the required reserve is affordable, and the system flexibility can be reserved by the system to cope with the combined uncertainties from wind power and DR. When the confidence level is greater than 0.94, the reserve deviation risk is increasingly stressing. This is mainly due to the reason that the minimum required reserve has gradually approached and even exceeded the largest available reserve capacity. Consequently, the forecasted error is not fully accommodated by the available reserve capacity, and the reserve deviation risk increases sharply. In addition, the tendency to increase of the required reserve under the confidence level $\beta$ is approximately linear, mainly due to the fuzzy characteristic of the DR uncertainty.

6. Conclusions

To evaluate the underlying risk of the combined uncertainties from wind power and DR, fuzzy stochastic conditional value-at-risk criterions are established by introducing the fuzzy stochastic chance-constrained goal programming. To satisfy the different requirements with different priorities, the three-stage unit commitment model is established by preemptive goal programming to generate the best trade-off between system reliability and economical goal. The main contributions of this work are summarized as follows:

(1)

Compared with the value-at-risk, the unit commitment model based on the conditional value-at-risk amplifies the required reserves to cater the minimization of the complicated uncertainty. The results of the risk criterions experiment indicate that the unit commitment model with conditional value-at-risk as the risk assessment can hedge against the operational risk and meet the system reliability requirement.

(2)

In comparison with the traditional linear programming to solve the CVaR, CVaR can be transferred to a deterministic equivalent by introducing CCGP in the proposed model. High solution efficiency and transparency have been ensured, which is supported by the simulation results of the computational performance.

(3)

The reserve capacities of the scheduling vary with the different priorities of the different objective functions. In the proposed unit commitment model based on preemptive goal programming, the load shedding risk is minimized preferentially, and the system reliability has the priority over the economic goal, which is supported by the analysis of the priorities of the objective goals.

In future work, we plan to study the real-time dispatch considering the combined uncertainties of wind power and demand response. We also want to conduct a comparison of risk assessment between unit commitment and real-time dispatch. Another interesting direction for future research is the potential consideration of more uncertain resources in the power system.