Quantifying the Nonlinear Dynamic Behavior of the DC-DC Converter via Permutation Entropy
Abstract
:1. Introduction
1.1. Background
1.2. Formulation of the Problem of Interest for This Investigation
1.3. Literature Survey
1.4. Scope and Contribution of This Study
1.5. Organization of the Paper
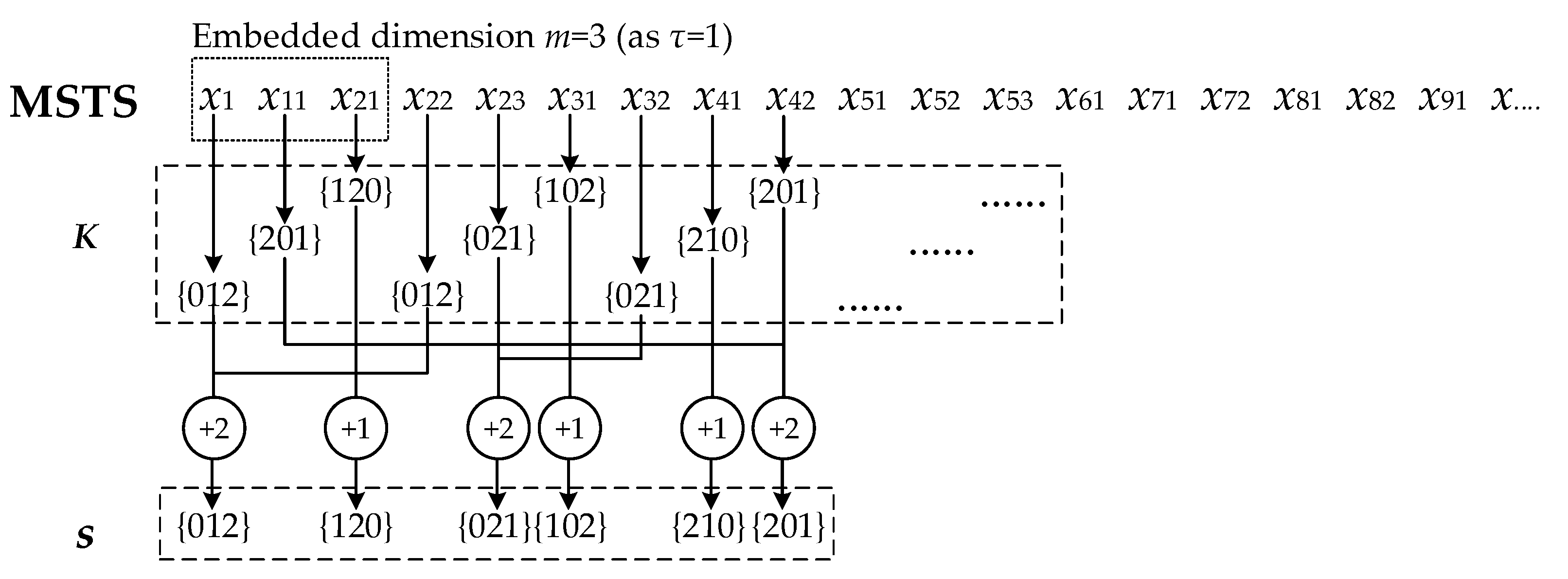
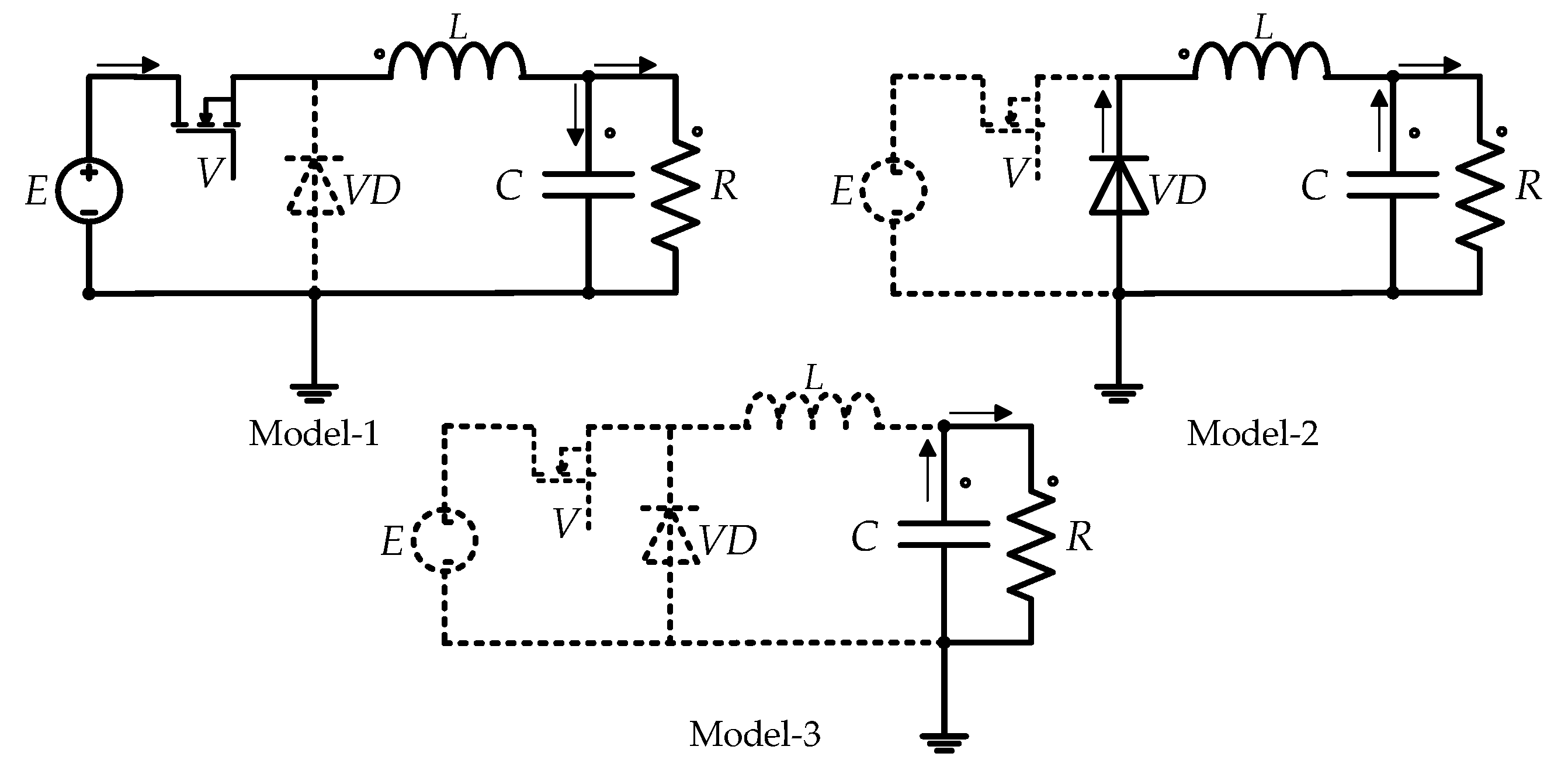
2. MSTS of the Modeled Converter
3. Permutation Entropy
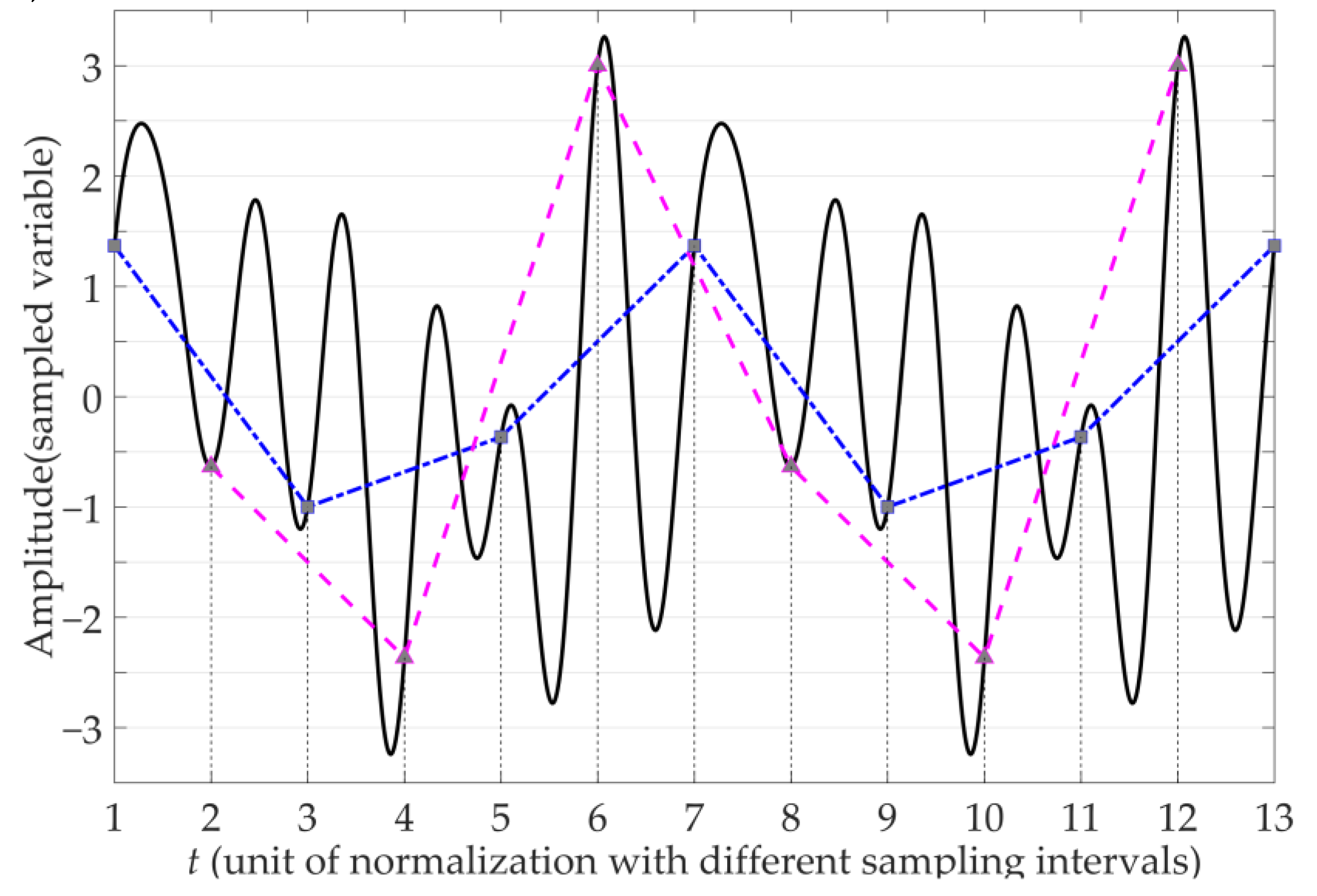
3.1. Phase Space Reconstruction Theory
3.2. Symbol Permutation Method
4. Combination of MSTS and Permutation Entropy
- (1)
- Assuming the signal is random, such as white noise, permutation entropy is expected to be close to the maximum value . Considering that there are at least two operation modes in period-1, the recurring number of the MSTS is greater than or equal to 2. Hence, the minimum value of PE is .
- (2)
- When the system does not enter the chaotic state by changing m, the acquired permutation entropy remains uniform. This means that increasing or decreasing m as appropriate does not affect the value of the permutation entropy.
- (3)
- DCM and CCM can be further divided into different working patterns according to the different switching numbers of modes. Border collision occurs when the working pattern combination changes. The complexity of the systems in DCM working patterns is usually greater than that of the CCM working pattern. Therefore, the more DCM patterns the system contains, the higher the value of the permutation entropy. After entering chaos, the permutation sequence K shows a certain disorder. Because the chaotic motion is pseudo-random, the permutation entropy obtained in the chaotic state is not able to reach the maximum value.
5. Application Example
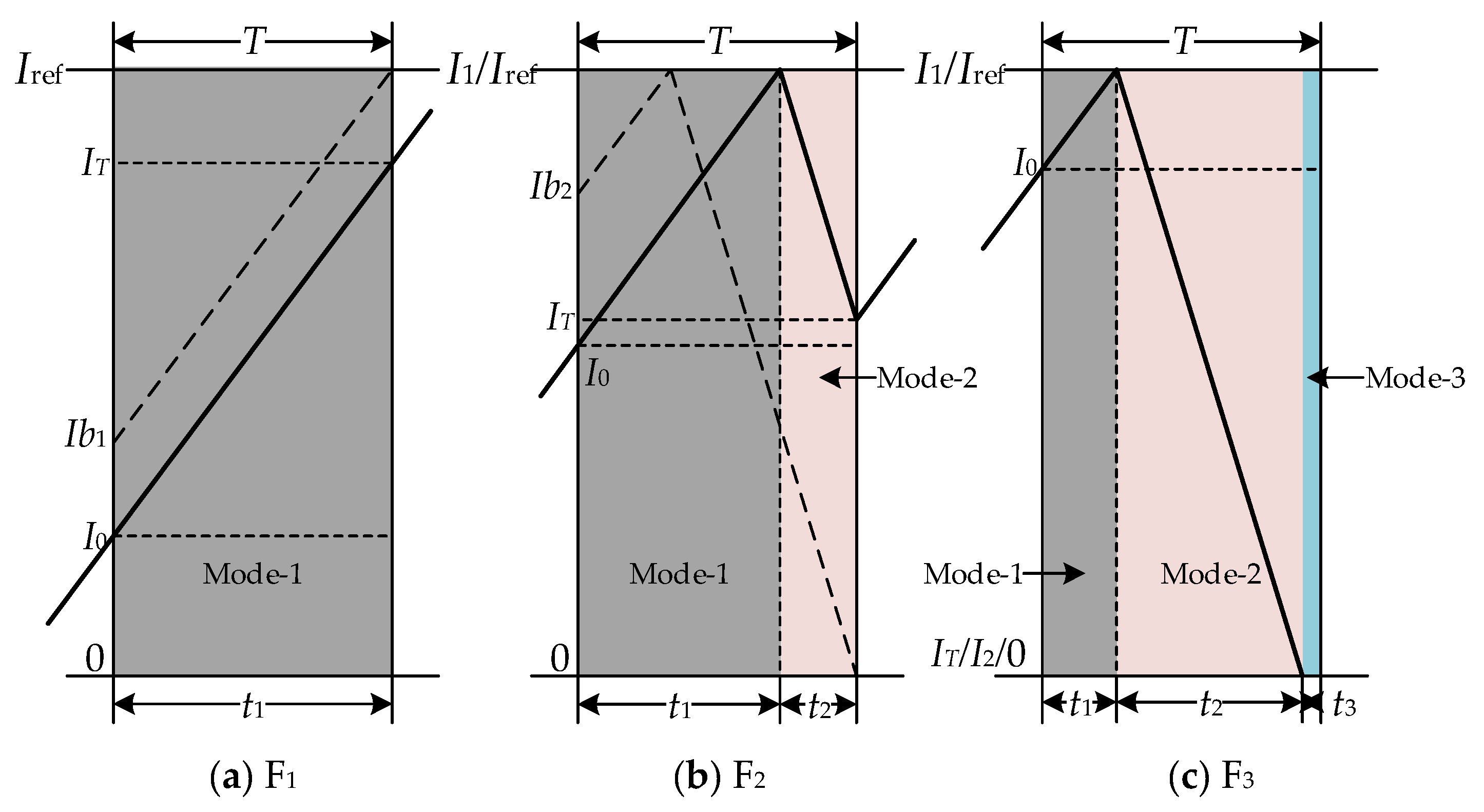
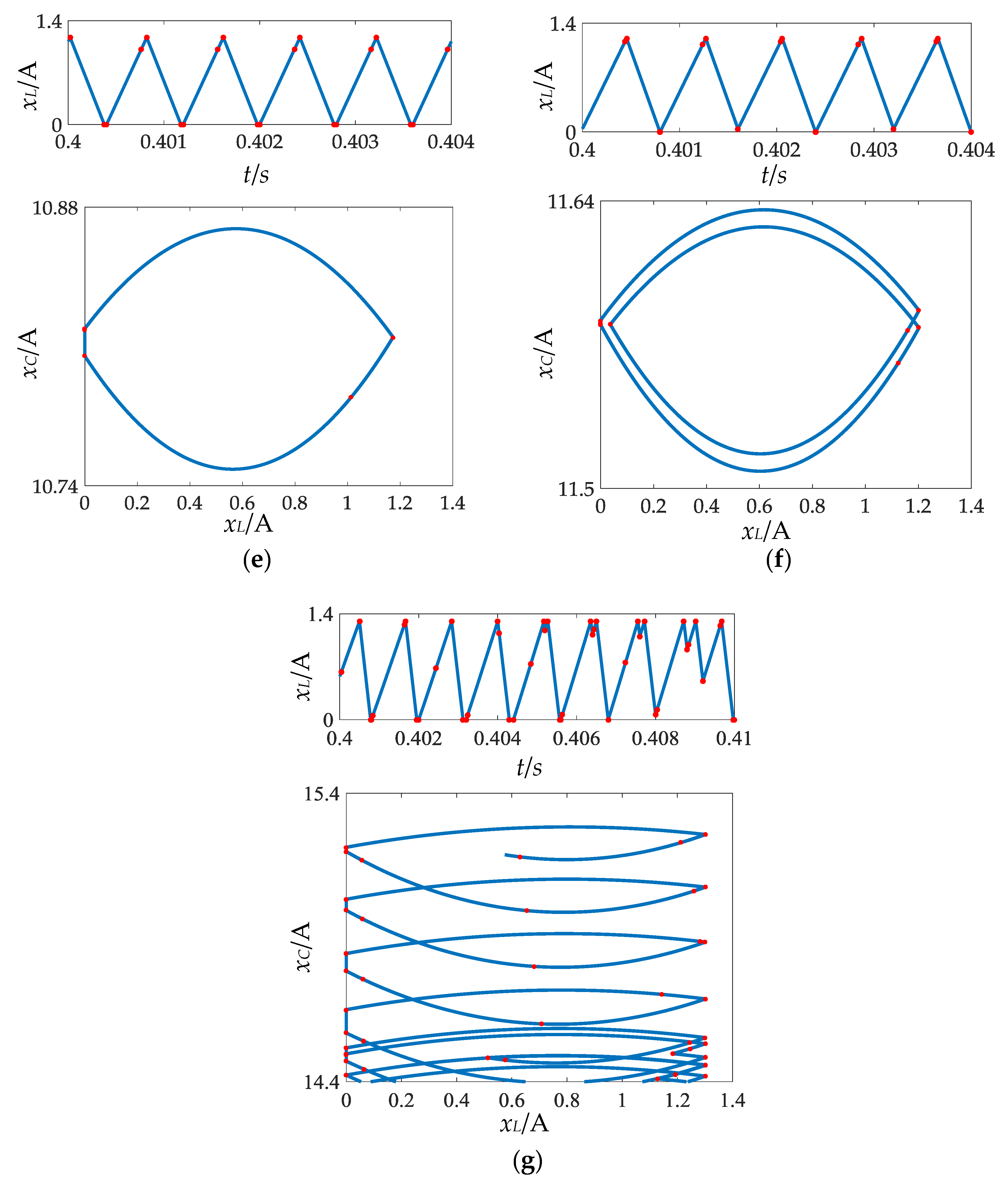
- As Iref ∈ [0.1200,0.2778], the system works in the F3 pattern of period-1. In this pattern, there are three modes in each period of the system, which means the system is in the DCM state. Then, the first border collision bifurcation occurs in the system at Iref = 0.2779 A. Because the inductor current in the steady state collides with Ib2, the operating mode changes and the working patterns of the converter system change from F3 to F2.
- During Iref ∈[0.2779,0.8295], the system still works in the period-1 state, but the operating mode is F2. At this time, the system has two modes in each period. When Iref = 0.8296, the system generates period doubling bifurcation and enters period-2. Since there is no border collision bifurcation, the working patterns are extended to F2F2.
- When Iref ∈[0.8296,1.1946], the system works in period-2. We found that two bounder collisions of the system occur in this area because the inductance current of the system collides with the borderline of Ib2 and Ib1 at Iref = 0.9007 and Iref = 1.1578 A, respectively. Hence, the operating pattern of the converter system changes from F2F2 at Iref ∈[0.8296,0.9006] to F2F3 at Iref ∈[0.9007,1.1577] and to F1F3 at Iref ∈[1.1578,1.1946]. From the entropy value of three period-2 orbits shown in Figure 7, the permutation entropy value of period-2 is greater than the corresponding entropy value of any working pattern in the entirety of period-1. The sample entropy, used for assessing the complexity of the time sequence shown in Figure 9, is the negative logarithm of the probability of if two sets of simultaneous data points of length m have a distance smaller than r, then two sets of simultaneous data points of length m + 1 also have a distance smaller than r [28]. However, with the change in sample entropy, we could not find the bifurcation information of the system under period-1 and period-2 states.
- As Iref ∈[1.1947,1.2624], the system works in the period-4 state with the working pattern F1F2F1F3, and there are seven modes in this state. Then, the fifth time border collision bifurcation of a fixed point and Ib1 curve collision occur once more in the system at Iref = 1.2625 A. At this time, LLE shown in Figure 10 is greater than 0 and the mode switching shows disorder, which means that the system is beginning enter the chaotic state. When Iref ≥ 1.2625 A, a number of border collisions occur in the chaotic state, as depicted in Figure 7. Then, the value of permutation entropy is no longer stable, exhibiting similar characteristics to the LLE, and its corresponding value is greater than any period. The characteristics described are consistent with Bandt C et al. [20].
6. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tse, C.K.; Di Bernardo, M. Complex Behavior in Switching Power Converters. Proc. IEEE 2002, 90. [Google Scholar] [CrossRef]
- Rodriguez, E.; El Aroudi, A.; Guinjoan, F.; Alarcon, E. A Ripple-Based Design-Oriented Approach for Predicting Fast-Scale Instability in DC-DC Switching Power Supplies. IEEE Trans. Circuit Syst. I Reg. Papers 2012, 59, 215–227. [Google Scholar] [CrossRef]
- Zhou, S.; Zhou, G.; Wang, Y.; Liu, X.; Xu, S. Bifurcation analysis and operation region estimation of current-mode-controlled SIDO boost converter. IET Power Electron. 2017, 10, 846–853. [Google Scholar] [CrossRef]
- Fossas, E.; Olivar, G. Study of chaos in the buck converter. IEEE Trans. Circuit Syst. I Fundam. Theory Appl. 1996, 43, 13–25. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Tang, C.; Dai, X.; Hu, A.; Nguang, S. Bifurcation Phenomena Studies of a Voltage Controlled Buck-Inverter Cascade System. Energies 2017, 10, 708. [Google Scholar] [CrossRef]
- Dai, D.; Tse, C.K.; Ma, X. Symbolic analysis of switching systems: Application to bifurcation analysis of DC/DC switching converters. IEEE Trans. Circuit Syst. I Reg. Papers 2005, 52, 1632–1643. [Google Scholar] [CrossRef]
- Han, M. Prediction Theory and Method of Chaotic Time Series, 1st ed.; China Water Power Press: Beijing, China, 2007; pp. 36–61. ISBN 978-7-5084-4534-2. [Google Scholar]
- Yan, D.; Wang, W.; Chen, Q. Nonlinear Modeling and Dynamic Analyses of the Hydro–Turbine Governing System in the Load Shedding Transient Regime. Energies 2018, 11, 1244. [Google Scholar] [CrossRef]
- Iu, H.H.C.; Tse, C.K. A study of synchronization in chaotic autonomous Cuk DC/DC converters. IEEE Trans. Circuit Syst. I: Fundam. Theory Appl. 2000, 47, 913–918. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Wang, Y. Study on the Stability and Entropy Complexity of an Energy-Saving and Emission-Reduction Model with Two Delays. Entropy-Switz. 2016, 18, 371. [Google Scholar] [CrossRef]
- Khalil, H.K. NONLINEAR SYSTEMS, 2nd ed.; Prentice-Hall, Inc.: New Jersey, NJ, USA, 1996; ISBN 0-13-P8U24-8. [Google Scholar]
- Wang, X.; Zhang, B.; Qiu, D. The Quantitative Characterization of Symbolic Series of a Boost Converter. IEEE Trans. Power Electron. 2011, 26, 2101–2105. [Google Scholar] [CrossRef]
- Li, N.; Pan, W.; Xiang, S.; Zhao, Q.; Zhang, L.; Mu, P. Quantifying the Complexity of the Chaotic Intensity of an External-Cavity Semiconductor Laser via Sample Entropy. IEEE J. Quantum Electron. 2014, 50, 1–8. [Google Scholar] [CrossRef]
- Liu, J.; Xu, H. Nonlinear Dynamic Research of Buck Converter Based on Multiscale Entropy. In Proceedings of the 2015 Fifth International Conference on Instrumentation and Measurement, Computer, Communication and Control, Qinhuangdao, China, 18–20 September 2015. [Google Scholar] [CrossRef]
- Zhao, M.; Xu, G. Feature extraction of power transformer vibration signals based on empirical wavelet transform and multiscale entropy. IET Sci. Meas. Technol. 2018, 12, 63–71. [Google Scholar] [CrossRef]
- Xiao, M.; Wei, H.; Xu, Y.; Wu, H.; Sun, C. Combination of R-R Interval and Crest Time in Assessing Complexity Using Multiscale Cross-Approximate Entropy in Normal and Diabetic Subjects. Entropy 2018, 20, 497. [Google Scholar] [CrossRef]
- Ray, A. Symbolic dynamic analysis of complex systems for anomaly detection. Signal Process. 2004, 84, 1115–1130. [Google Scholar] [CrossRef]
- Xie, F.; Zhang, B.; Yang, R.; Qiu, D. Quantifying the Complexity of DC-DC Switching Converters by Joint Entropy. IEEE Trans. Circuits Syst. II 2014, 61, 579–583. [Google Scholar] [CrossRef]
- Zhang, B.; Qu, Y. The Precise Discrete Mapping of Voltage-Fed DCM Boost Converter and Its Bifurcation and Chaos. Trans. China Electrotech. Soc. 2002, 17, 43–47. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88. [Google Scholar] [CrossRef] [PubMed]
- El-mezyani, T.; Wilson, R.; Sattler, M.; Srivastava, S.K.; Edrington, C.S.; Cartes, D.A. Quantification of complexity of power electronics based systems. IET Electr. Syst. Trans. 2012, 2, 211. [Google Scholar] [CrossRef]
- Gray, R.M. Entropy and Information Theory, 2nd ed.; Springer Science & Business Media: New York, NY, USA, 2011; ISBN 978-1-4419-7969-8. [Google Scholar]
- Zunino, L.; Rosso, O.A.; Soriano, M.C. Characterizing the Hyperchaotic Dynamics of a Semiconductor Laser Subject to Optical Feedback Via Permutation Entropy. IEEE J. Select. Topics Quantum Electron. 2011, 17, 1250–1257. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Villecco, F.; Li, M.; Song, W. Multi-Scale Permutation Entropy Based on Improved LMD and HMM for Rolling Bearing Diagnosis. Entropy 2017, 19, 176. [Google Scholar] [CrossRef]
- Packard, N.H.; Crutchfield, J.P.; Farmer, J.D.; Shaw, R.S. Geometry from a time series. Phys. Rev. Lett. 1980, 45, 712–716. [Google Scholar] [CrossRef]
- Stark, J.; Broomhead, D.S.; Davies, M.E.; Huke, J. Takens embedding theorems for forced and stochastic systems. Nonlinear Anal. Theory Methods Appl. 1997, 30, 5303–5314. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, L. PWM DC—Study on Nonlinear Dynamics Behavior in PWM Switched—Capacitor DC-DC Converter. Acta Electron. Sinica 2008, 36, 266–270. [Google Scholar]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278. [Google Scholar] [CrossRef] [PubMed]


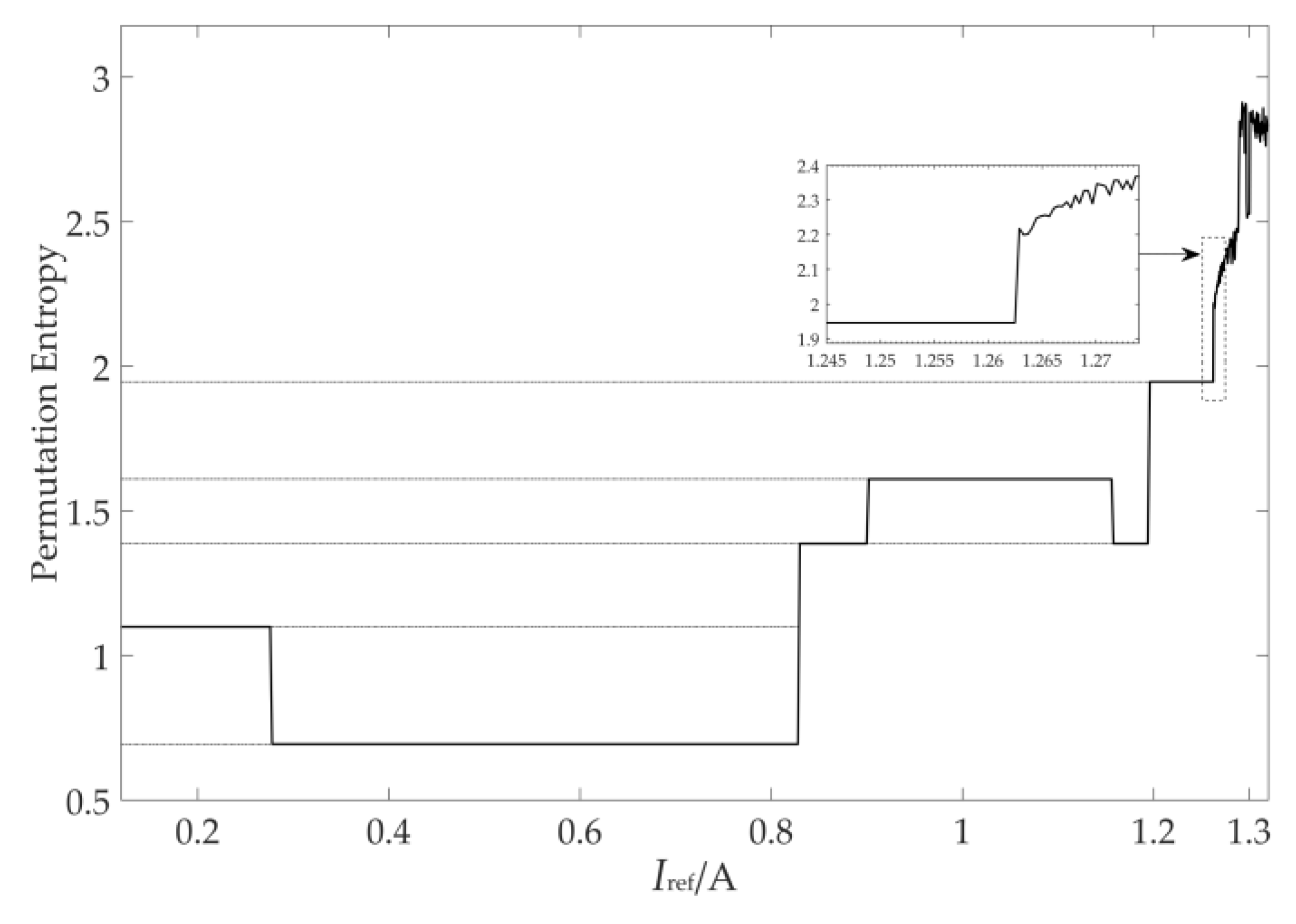
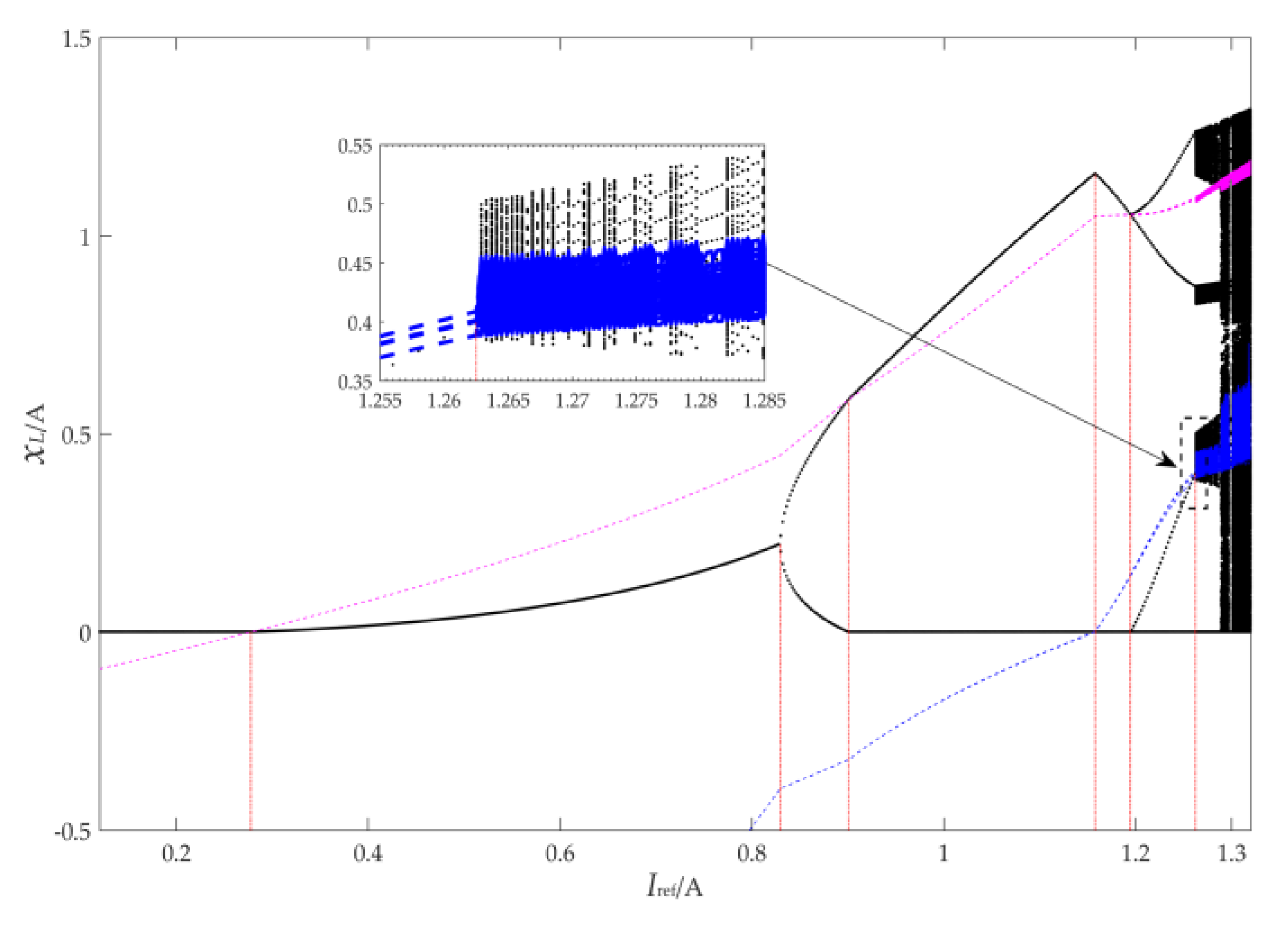

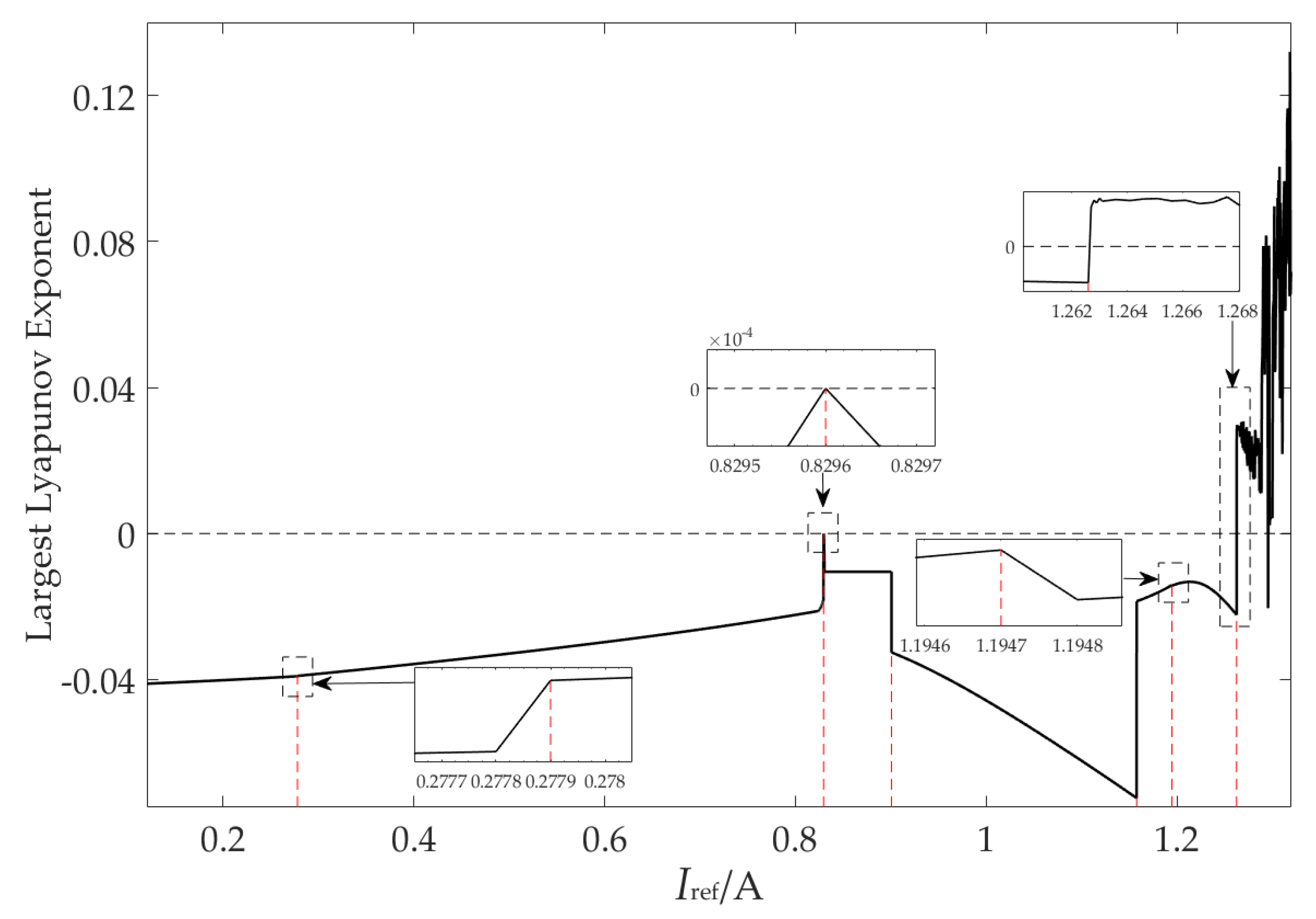
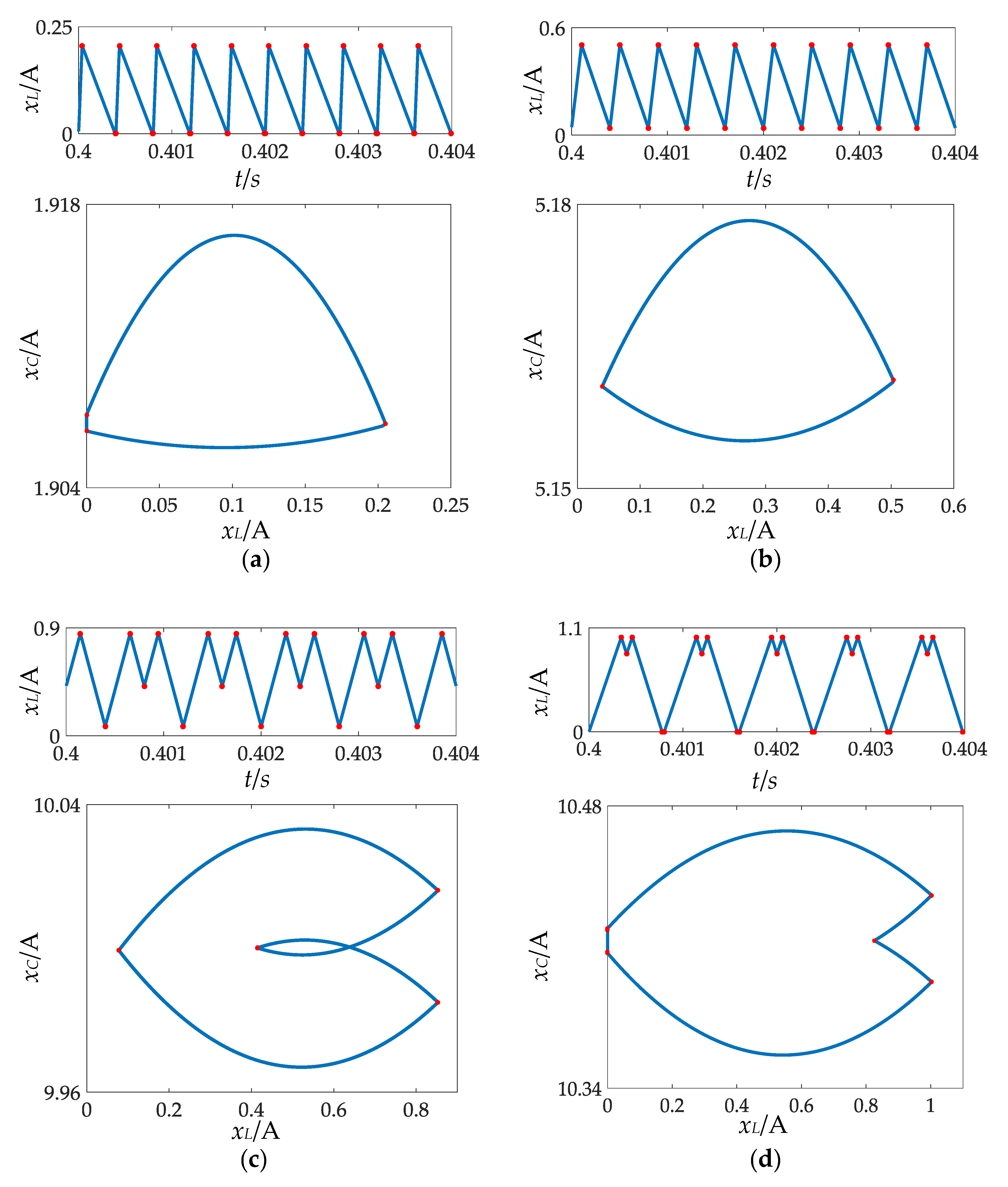

| Iref/A | S | MSTS-PE | State |
|---|---|---|---|
| [0.1200,0.2778] | ({1203},{0231},{0231})∞ | 1.0986 | Period-1 |
| [0.2779,0.8295] | ({1203},{0213})∞ | 0.6931 | Period-1 |
| [0.8296,0.9006] | ({3102},{2013},{1302},{0213})∞ | 1.3863 | Period-2 |
| [0.9007,1.1577] | ({3102},{2301},{1203},{0132},{0213})∞ | 1.6094 | Period-2 |
| [1.1578,1.1946] | ({2301},{1230},{0123},{0312})∞ | 1.3863 | Period-2 |
| [1.1947,1.2624] | ({2031},{1203},{3012},{2301},{1230},{0123},{0312})∞ | 1.9459 | Period-4 |
| [1.2625,1.3200] | No period: ({…}, …) | >2.2 | Chaos |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Z.; Xie, F.; Zhang, B.; Qiu, D. Quantifying the Nonlinear Dynamic Behavior of the DC-DC Converter via Permutation Entropy. Energies 2018, 11, 2747. https://doi.org/10.3390/en11102747
Luo Z, Xie F, Zhang B, Qiu D. Quantifying the Nonlinear Dynamic Behavior of the DC-DC Converter via Permutation Entropy. Energies. 2018; 11(10):2747. https://doi.org/10.3390/en11102747
Chicago/Turabian StyleLuo, Zhenxiong, Fan Xie, Bo Zhang, and Dongyuan Qiu. 2018. "Quantifying the Nonlinear Dynamic Behavior of the DC-DC Converter via Permutation Entropy" Energies 11, no. 10: 2747. https://doi.org/10.3390/en11102747
APA StyleLuo, Z., Xie, F., Zhang, B., & Qiu, D. (2018). Quantifying the Nonlinear Dynamic Behavior of the DC-DC Converter via Permutation Entropy. Energies, 11(10), 2747. https://doi.org/10.3390/en11102747




