Performance Analysis of Conjugate Gradient Algorithms Applied to the Neuro-Fuzzy Feedback Linearization-Based Adaptive Control Paradigm for Multiple HVDC Links in AC/DC Power System
Abstract
:1. Introduction
- Implementation of the SD algorithm and six CG methods for online optimization of ANFFBLC parameters.
- Evaluation and comparison of damping performance of the SD algorithm and six CG methods along with conventional and non-conventional control schemes.
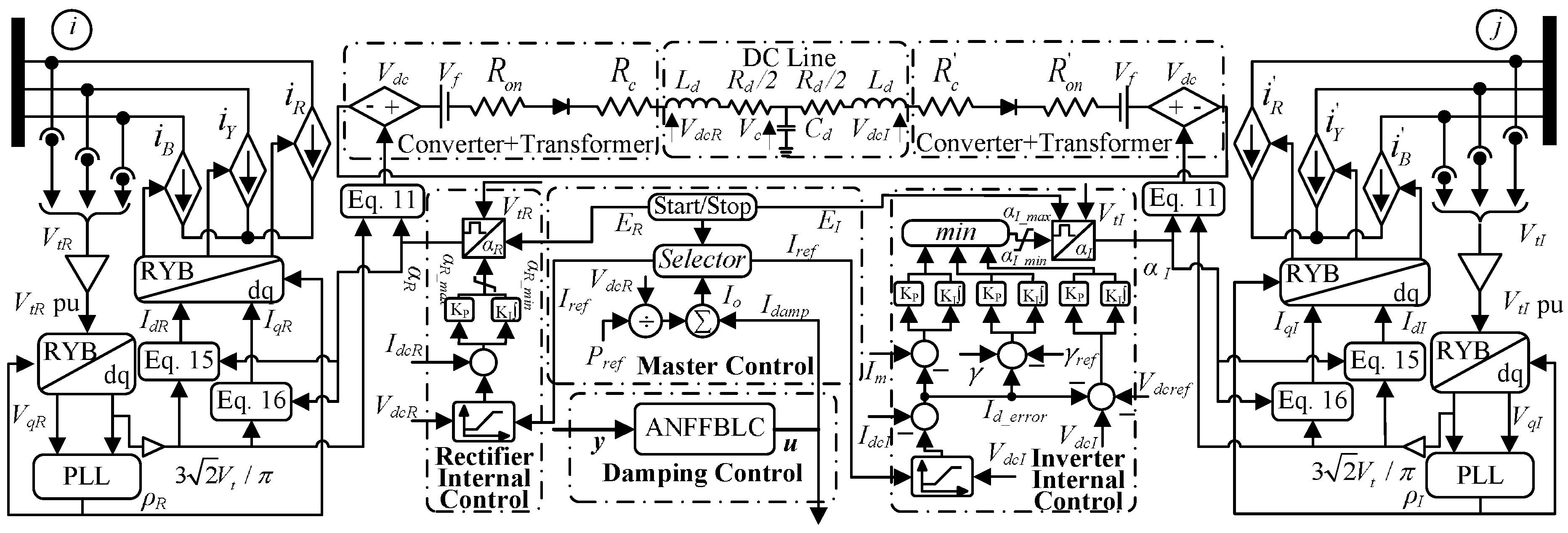
2. AC/DC Power System Model Description
2.1. Power System Components Modeling
- is the field voltage.
- is the transient voltage in the d/q-axis.
- is the armature current in the d/q-axis.
- are synchronous, transient and sub-transient reactances in the d/q-axis, respectively.
- is the armature leakage reactance.
- is the transient time constants of the d/q-axis.
- is the sub-transient time constants of the d/q-axis.
- is the d-axis flux linkage of the damper winding.
- is the q-axis flux linkage of the damper winding.
- H is the inertia constant.
- is the generator electrical power.
- is the generator mechanical power.
- is the generator rotor angle.
- is the generator rotor speed.
2.2. HVDC Dynamics
2.2.1. LCC-HVDC Converter Modeling
2.2.2. DC Transmission System
2.2.3. LCC-HVDC Control
3. Closed-Loop Control System Design
3.1. Feedback Linearization Control
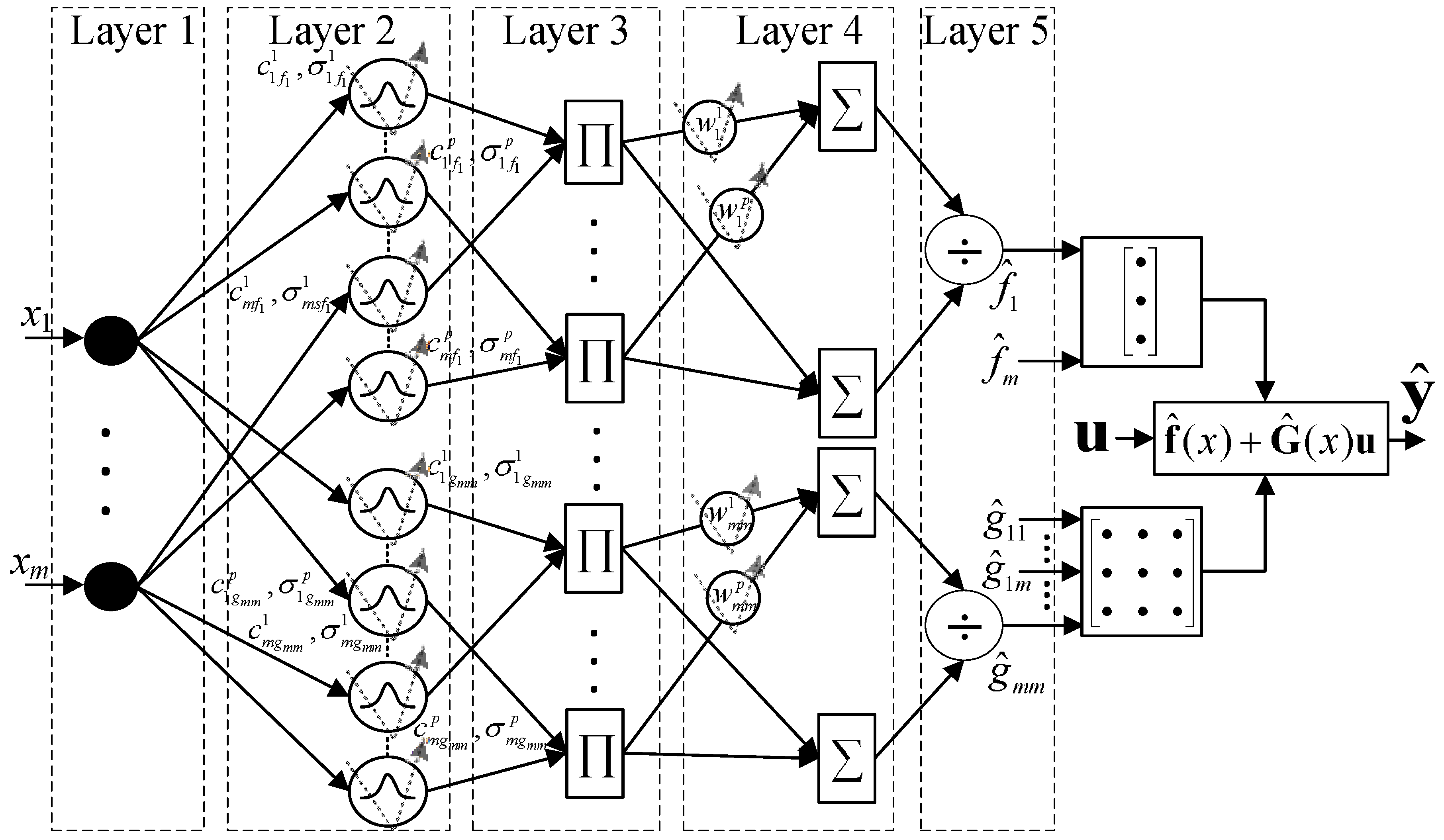
3.2. Adaptive Neuro-Fuzzy Identification
- Rule : If is and is and ⋯ and is , Then is
- Rule : If is and is and ⋯ and is , Then is
Conjugate Gradient Algorithm for Parameter Optimization
- Fletcher and Reeves (FR) presented the first nonlinear CG algorithm with update choice for the CG coefficient, , given as [43]:
- Polak-Ribière and Polayk (PRP) proposed a CG method that updated the CG coefficient, , using the following formula [44].
- The CG algorithm suggested by Fletcher (CD) has a strong convergence property, and the coefficient, , is updated using [45]:
- The effect of inexact linear search was considered by Liu and Storey (LS) to develop a generalized CG scheme with coefficient updated as [46]:
- In [47], a CG algorithm was presented by Dai and Yuan (DY) with a sufficient descent property. The CG coefficient, , is updated as:
- A modified CG algorithm is proposed by Hager and Zhang (HZ) that has a more complicated update formula [48]. The CG coefficient, , is updated as:
3.3. nLMS-Based Self-Tuning of FBLC Coefficients
3.4. Computational Steps for Closed-Loop Control System
- The wide area measurement system transmits the actual speed of generators, , to HVDC control.
- Speed deviations of the generators w.r.t. the swing machine are computed as plant output, , where and .
- ANFFBLC captures the nonlinear dynamics, and , of the power system using as explained in Section 3.2. The parameters of ANFIS of ANFFBLC are instantaneously optimized through the CG algorithm to minimize the identification error defined in Equation (44).
- At the same instant, the online estimation generates the appropriate input . The coefficients, , are optimized through the nLMS algorithm to minimize the tracking error of Equation (31).
- ANFFBLC generates the appropriate control law, that is based on identified functions and and optimized as given in Equation (38).
- The ANFFBLC output constitutes and for master controls of HVDC Link 1 and Link 2, respectively. The modulates the current order for HVDC link using Equation (23).
- At each pole control, the current order generates the corresponding ignition delay angle, , that controls the power flow through the HVDC system
- During normal operation, , and power flow through the HVDC system is set to a pre-specified value. During perturbed operating conditions, the generators oscillate against each other at a speed different from the set value. The speed deviations are detected by ANFFBLC, and the appropriate damping signal is generated for each HVDC system. The precise power flow control through the HVDC link improves the damping of power oscillations present in the system and improves its stability.
4. Simulation Results and Discussion
- Low-frequency oscillations: Observation of over-shoot and settling time for modes with oscillations of generators to against the reference generator i.e., .
- Performance indexes: The two used indexes for quantitative measures are Integral of Time-weighted Squared Error (ITSE) and Integral of Time-weighted Absolute Error (ITAE) [50]. For performance indexes, the error is calculated as .
4.1. Scenario # 1
4.2. Scenario # 2
4.3. Scenario # 3
4.4. Performance Comparison of CG Algorithms
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Klein, M.; Rogers, G.J.; Kundur, P. A fundamental study of inter-area oscillations in power systems. IEEE Trans. Power Syst. 1991, 6, 914–921. [Google Scholar] [CrossRef]
- Sitnikov, V.; Povh, D.; Retzmann, D.; Teltsch, E. Solutions for large power system interconnections. In Proceedings of the Cigré Conference, Saint Petersburg, Russia, 17–19 September 2003. [Google Scholar]
- Rogers, G. Power System Oscillations; Springer: New York, NY, USA, 2012; pp. 7–22. [Google Scholar]
- Setreus, J.; Bertling, L. Introduction to HVDC technology for reliable electrical power systems. In Proceedings of the 10th IEEE International Conference on Probabilistic Methods Applied to Power Systems, Rincon, PR, USA, 25–29 May 2008; pp. 1–8. [Google Scholar]
- Harnefors, L.; Johansson, N.; Zhang, L.; Berggren, B. Interarea oscillation damping using active-power modulation of multiterminal HVDC transmissions. IEEE Trans. Power Syst. 2014, 29, 2529–2538. [Google Scholar] [CrossRef]
- Daryabak, M.; Filizadeh, S.; Jatskevich, J.; Davoudi, A.; Saeedifard, M.; Sood, V.K.; Martinez, J.A.; Aliprantis, D.; Cano, J.; Mehrizi-Sani, A. Modeling of LCC-HVDC systems using dynamic phasors. IEEE Trans. Power Deliv. 2014, 29, 1989–1998. [Google Scholar] [CrossRef]
- Li, R.; Bozhko, S.; Asher, G. Frequency control design for offshore wind farm grid with LCC-HVDC link connection. IEEE Trans. Power Electron. 2008, 23, 1085–1092. [Google Scholar] [CrossRef]
- MESSINA. Damping of low-frequency interarea oscillations using HVDC modulation and SVC voltage support. Electr. Power Compon. Syst. 2003, 31, 389–402. [Google Scholar]
- Badran, S.M.; Choudhry, M.A. Design of modulation controllers for AC/DC power systems. IEEE Trans. Power Syst. 1993, 8, 1490–1496. [Google Scholar] [CrossRef]
- Pipelzadeh, Y.; Chaudhuri, B.; Green, T.C. Coordinated damping control through multiple HVDC systems: A decentralized approach. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 24–29 July 2011; pp. 1–8. [Google Scholar]
- Mao, X.; Yao, Z.; Lin, G.; Wu, X. Researches on coordinated control strategy for inter-area oscillations in AC/DC hybrid grid with multi-infeed HVDC. In Proceedings of the 2005 IEEE/PES Transmission and Distribution Conference and Exhibition: Asia and Pacific, Dalian, China, 18 August 2005; pp. 1–6. [Google Scholar]
- Rahman, H.L.; Khan, B.H. Stability improvement of power system by simultaneous AC-DC power transmission. Electr. Power Syst. Res. 2008, 78, 756–764. [Google Scholar] [CrossRef]
- Hammons, J.; Yeo, R.L.; Gwee, C.L.; Kacejko, P.A. Enhancement of power system transient response by control of HVDC converter power. Electr. Mach. Power Syst. 2000, 28, 219–241. [Google Scholar]
- Cai, H.; Qu, Z.; Gan, D. A nonlinear robust HVDC control for a parallel AC/DC power system. Comput. Electr. Eng. 2003, 29, 135–150. [Google Scholar] [CrossRef]
- Mc Namara, P.; Negenborn, R.R.; De Schutter, B.; Lightbody, G. Optimal coordination of a multiple HVDC link system using centralized and distributed control. IEEE Tran. Control Syst. Technol. 2013, 21, 302–314. [Google Scholar] [CrossRef]
- Preece, R.; Milanovic, J.V.; Almutairi, A.M.; Marjanovic, O. Damping of inter-area oscillations in mixed AC/DC networks using WAMS based supplementary controller. IEEE Trans. Power Syst. 2013, 28, 1160–1169. [Google Scholar] [CrossRef]
- Lascu, C.; Jafarzadeh, S.; Fadali, M.S.; Blaabjerg, F. Direct torque control with feedback linearization for induction motor drives. IEEE Trans. Power Electron. 2017, 32, 2072–2080. [Google Scholar] [CrossRef]
- Khan, L.; Lo, K.L. Hybrid micro-GA based FLCs for TCSC and UPFC in a multi-machine environment. Electr. Power Syst. Res. 2006, 76, 832–843. [Google Scholar] [CrossRef]
- Song, G.; Song, G.; Longman, R.W.; Mukherjee, R. Integrated sliding-mode adaptive-robust control. IEE Proc. Control Theory Appl. 1999, 146, 341–347. [Google Scholar] [CrossRef]
- Eriksson, R.; Knazkins, V.; Söder, L. Coordinated control of multiple HVDC links using input–output exact linearization. Electr. Power Syst. Res. 2010, 80, 1406–1412. [Google Scholar] [CrossRef]
- Lee, D.; Kim, H.J.; Sastry, S. Feedback linearization vs. adaptive sliding mode control for a quadrotor helicopter. Inter. J. Control Autom. Syst. 2009, 7, 419–428. [Google Scholar] [CrossRef]
- Malik, O.P. Adaptive control of synchronous machine excitation. In Microprocessor-Based Control Systems; Sinha, N.K., Ed.; Springer: Dordrecht, The Netherlands, 1986; pp. 61–79. [Google Scholar]
- Yeşildirek, A.; Lewis, F.L. Feedback linearization using neural networks. Automatica 1995, 31, 1659–1664. [Google Scholar] [CrossRef]
- Arif, J.; Ray, S.; Chaudhuri, B. MIMO feedback linearization control for power systems. Int. J. Electr. Power Energy Syst. 2013, 45, 87–97. [Google Scholar] [CrossRef]
- Khan, L.; Ahmed, N.; Lozano, C. GA neuro-fuzzy damping control system for UPFC to enhance power system transient stability. In Proceedings of the 7th International Multi Topic Conference (INMIC 2003), Islamabad, Pakistan, 8–9 December 2003; pp. 276–282. [Google Scholar]
- Mitra, S.; Hayashi, Y. Neuro-fuzzy rule generation: Survey in soft computing framework. IEEE Trans. Neural Netw. 2000, 11, 748–768. [Google Scholar] [CrossRef] [PubMed]
- Azar, A.T. Adaptive Neuro-Fuzzy Systems. In Fuzzy Systems; Azar, A.T., Ed.; IN-TECH: Vienna, Austria, 2010; pp. 85–110. [Google Scholar]
- Shi, M.; Mizumoto, M. Some considerations on conventional neuro-fuzzy learning algorithms by gradient descent method. Fuzzy Sets Syst. 2000, 112, 51–63. [Google Scholar] [CrossRef]
- Shewchuk, J.R. An Introduction to the Conjugate Gradient Method without the Agonizing Pain; Carnegie Mellon University: Pittsburgh, PA, USA, 1994. [Google Scholar]
- Saini, L.M.; Soni, M.K. Artificial neural network-based peak load forecasting using conjugate gradient methods. IEEE Trans. Power Syst. 2002, 17, 907–912. [Google Scholar] [CrossRef]
- Liang, N.Y.; Huang, G.B.; Saratchandran, P.; Sundararajan, N. A fast and accurate online sequential learning algorithm for feedforward networks. IEEE Trans. Neural Netw. 2006, 17, 1411–1423. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, S.; Khan, L. Adaptive feedback linearization based HVDC damping control paradigm for power system stability enhancement. In Proceedings of the IEEE 2016 International Conference on Emerging Technologies (ICET), Islamabad, Pakistan, 18–19 October 2016; pp. 1–6. [Google Scholar]
- Marino, R.; Tomei, P. Robust stabilization of feedback linearizable time-varying uncertain nonlinear systems. Automatica 1993, 29, 181–189. [Google Scholar] [CrossRef]
- Slock, D.T. On the convergence behavior of the LMS and the normalized LMS algorithms. IEEE Trans. Signal Process. 1993, 41, 2811–2825. [Google Scholar] [CrossRef]
- Ahmad, S.; Khan, L. A self-tuning NeuroFuzzy feedback linearization-based damping control strategy for multiple HVDC links. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 913–938. [Google Scholar] [CrossRef]
- Sauer, P.W.; Pai, M.A. Power System Dynamics and Stability, 1st ed.; Pearson Education: Dehli, India, 1998. [Google Scholar]
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Kundur, P. Power System Stability and Control, 3rd ed.; McGraw-Hill: New York, NY, USA, 1994; pp. 463–580. [Google Scholar]
- Arrillaga, J.; Liu, Y.H.; Watson, N.R. Flexible Power Transmission: The HVDC Options; John Wiley & Sons Ltd.: Chichester, UK, 2007. [Google Scholar]
- Slotine, J.J.; Li, W. Applied Nonlinear Control; Prentice-Hall: Englewood Cliffs, NJ, USA, 1991; pp. 207–271. [Google Scholar]
- Labiod, S.; Boucherit, M.S.; Guerra, T.M. Adaptive fuzzy control of a class of MIMO nonlinear systems. Fuzzy Sets Syst. 2005, 151, 59–77. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006; pp. 101–134. [Google Scholar]
- Fletcher, R.; Reeves, C.M. Function minimization by conjugate gradients. Comput. J. 1964, 7, 149–154. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, W.; Li, D.H. A descent modified Polak-Ribière-Polyak conjugate gradient method and its global convergence. IMA J. Numerical Anal. 2006, 26, 629–640. [Google Scholar] [CrossRef]
- Fletcher, R. Practical Methods of Optimization, 2nd ed.; John Wiley & Sons Ltd.: Chichester, UK, 1987; pp. 80–94. [Google Scholar]
- Liu, Y.; Storey, C. Efficient generalized conjugate gradient algorithms, part 1: Theory. J. Optim. Theory Appl. 1991, 69, 129–137. [Google Scholar] [CrossRef]
- Dai, Y.H.; Yuan, Y. A nonlinear conjugate gradient method with a strong global convergence property. SIAM J. Optim. 1999, 10, 177–182. [Google Scholar] [CrossRef]
- Hager, W.W.; Zhang, H. A new conjugate gradient method with guaranteed descent and an efficient line search. SIAM J. Optim. 2005, 16, 170–192. [Google Scholar] [CrossRef]
- Ahmad, S.; Khan, L. Adaptive feedback linearization control for power oscillations damping in AC/DC power system. In Proceedings of the IEEE 13th International Conference on Frontiers of Information Technology (FIT), Islamabad, Pakistan, 14–16 December 2015; pp. 199–204. [Google Scholar]
- Solihin, M.I.; Tack, L.F.; Kean, M.L. Tuning of PID controller using particle swarm optimization (PSO). Int. J. Adv. Sci. Eng. Inf. Technol. 2011, 1, 458–461. [Google Scholar] [CrossRef]
- Ali, S.; Khan, M.H.; Raja, A.A. TCSC based online adaptive control for improving damping in multimachine power system. In Proceedings of the IEEE International Conference on Energy Systems and Policies (ICESP), Islamabad, Pakistan, 24–26 November 2014; pp. 1–5. [Google Scholar]
- Powell, M.J. Restart procedures for the conjugate gradient method. Math. Program. 1977, 12, 241–254. [Google Scholar] [CrossRef]
- Dai, Y.; Han, J.; Liu, G.; Sun, D.; Yin, H.; Yuan, Y.X. Convergence properties of nonlinear conjugate gradient methods. SIAM J. Optim. 2000, 10, 345–358. [Google Scholar] [CrossRef]
- Hager, W.W.; Zhang, H. A survey of nonlinear conjugate gradient methods. Pac. J. Optim. 2006, 2, 35–58. [Google Scholar]







| Scenario | Performance | %Age Improvement AdapPID, DirINF and ANFFBLC w.r.t. PID | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Index | AdapPID | DirINF | SD | FR | CD | DY | PRP | LS | HZ | |
| 1 | ITAE | 16 | 21 | 31 | 33 | 33 | 35 | 35 | 35 | 36 |
| ITSE | 24 | 33 | 47 | 50 | 51 | 51 | 53 | 54 | 55 | |
| 2 | ITAE | 9 | 20 | 28 | 28 | 30 | 31 | 32 | 33 | 37 |
| ITSE | 12 | 23 | 46 | 47 | 50 | 52 | 53 | 54 | 58 | |
| 3 | ITAE | 2 | 13 | 23 | 26 | 31 | 32 | 32 | 33 | 35 |
| ITSE | 8 | 29 | 39 | 44 | 54 | 54 | 56 | 56 | 61 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, S.; Khan, L. Performance Analysis of Conjugate Gradient Algorithms Applied to the Neuro-Fuzzy Feedback Linearization-Based Adaptive Control Paradigm for Multiple HVDC Links in AC/DC Power System. Energies 2017, 10, 819. https://doi.org/10.3390/en10060819
Ahmad S, Khan L. Performance Analysis of Conjugate Gradient Algorithms Applied to the Neuro-Fuzzy Feedback Linearization-Based Adaptive Control Paradigm for Multiple HVDC Links in AC/DC Power System. Energies. 2017; 10(6):819. https://doi.org/10.3390/en10060819
Chicago/Turabian StyleAhmad, Saghir, and Laiq Khan. 2017. "Performance Analysis of Conjugate Gradient Algorithms Applied to the Neuro-Fuzzy Feedback Linearization-Based Adaptive Control Paradigm for Multiple HVDC Links in AC/DC Power System" Energies 10, no. 6: 819. https://doi.org/10.3390/en10060819





