Conserving Capital by Adjusting Deltas for Gamma in the Presence of Skewness

Abstract

An argument for adjusting Black Scholes implied call deltas downwards for a gamma exposure in a left skewed market is presented. It is shown that when the objective for the hedge is the conservation of capital ignoring the gamma for the delta position is expensive. The gamma adjustment factor in the static case is just a function of the risk neutral distribution. In the dynamic case one may precompute at the date of trade initiation a matrix of delta levels as a function of the underlying for the life of the trade and subsequently one just has to look up the matrix for the hedge. Also constructed are matrices for the capital reserve, the profit, leverage and rate of return remaining in the trade as a function of the spot at a future date in the life of the trade. The concepts of profit, capital, leverage and return are as described in Carr, Madan and Vicente Alvarez (2010). The dynamic computations constitute an application of the theory of nonlinear expectations as described in Cohen and Elliott (2010).

1 INTRODUCTION

We shall show that in the interests of conserving capital in markets where delta hedging leaves one exposed to residual risk one may wish to adjust one’s delta position in line with position’s gamma. When markets are complete as in the case of a diffusion for the underlying risk, the risk in a position’s gamma is perfectly compensated by the theta and the resulting local cash flow is transformed into a riskless exposure. More generally, in the presence of numerous jump possibilities, for all levels of theta, a long delta position is exposed in left skewed markets to losses of down moves in proportion to the position gamma. Inorder to reduce the capital cost of these exposures one may wish to reduce the delta in line with the gamma. Similarly, a short delta position is induced to tilt the delta to a higher short position to access downside gains thereby conserving capital. These intuitions will be made precise and verified here. The result is the recommendation of a gamma adjustment to delta hedging that responds to the underlying volatility and the market skew.

We first work in a static single period context defining capital, profits, leverage and returns as in Carr, Madan and Vicente Alvarez (2010) and show how capital conservation strategies lead to gamma adjustments for the delta. The static model presented builds on the theory of two price markets developed in Cherny and Madan (2010) that gave us operational procedures for determining bid and ask prices. These prices are by construction concave and convex functionals on the space of bounded random variables and hence they are nonlinear. We go on to employ the fast developing theory of nonlinear expectations (Peng (2004), Rosazza Gianin (2006), Delbaen, Peng, Rosazza Gianin (2010), Jobert and Rogers (2008), Cohen and Elliott (2010)) to construct dynamically consistent sequences of bid and ask prices that result in dynamic gamma adjusted delta hedging strategies. These are implemented and compared to delta hedging at the Black Scholes implied volatility when the underlying risk is that of a Lévy process. Significant levels of capital conservation are seen to result from the use of a gamma adjustment.

The outline of the rest of the paper is as follows. Section 2 briefly presents the static concepts of profit, capital, leverage and return. Section 3 investigates in the static context the benefits of the proposed gamma adjustment. Section 4 discusses the use of nonlinear expectations in a multiperiod context. Section 5 develops dynamic hedging for capital conservation. These are implemented on a one year out of the money call and put option and the results are reported. Section 6 concludes.

2 THE ONE PERIOD MODEL

We begin with the model of a market as a counterparty as described in Cherny and Madan (2010). The market is modeled by describing the bounded random variables the market will accept at zero cost to it. In keeping with classical finance where market participants may trade arbitrary sizes with the market, it is observed that this set of random variables acceptable to the market at zero cost must be a convex cone that contains the nonnegative random variables. As a result (Artzner, Delbaen, Eber and Heath (1999)) one may associate with each such set a convex set of probability measures $ℳ$ equivalent to the original measure P such that X is acceptable to the market at zero cost if and only if

The set $ℳ$ is referred to as test scenarios in Carr, Geman and Madan (2001) and supporting measures in Cherny and Madan (2009, 2010). Related literature includes Jaschke and Küchler (2001), and Černý and Hodges (2000). With a view to keeping the set of acceptable risks strictly smaller than those acceptable in classical finance we suppose, as in Cherny and Madan (2010) that the base or reference measure P is a risk neutral measure and further that P ∈ $ℳ$.

Cherny and Madan (2010) show that for an unhedged risk X to be acceptable to the market the cost of selling X to the market is the bid price b(X) where

Similarly the market sells the cash flow X and takes the opposite position −X for the ask price a(X) where

In the presence of zero cost hedging assets, where $\mathscr{H}$ denotes the set of zero cost cash flows to the hedging assets, one defines the risk neutral measures $ℛ$ as all measures Q equivalent to P for which E^Q[H] = 0, all H ∈ $\mathscr{H}$. The bid and ask prices respectively b_h(X), a_h(X) for the hedged cash flow are respectively

One observes that the hedged bid is higher and the ask is lower with a correspondingly narrower spread.

The optimal hedges for the ask price, H and the bid price H are defined by

Models defining acceptable cash flows in terms of their distribution functions F(x) were introduced in Cherny and Madan (2010) following Kusuoka (2001) using concave distortions for Ψ(u) a concave distribution function on the unit interval by defining X as acceptable just if

The set of supporting measures $ℳ$ is identified in Cherny (2006) as all measures Q equivalent to P whose density Z satisfies

It is shown in Cherny and Madan (2010) that if we focus on approving distribution functions F(x) or equivalently their inverses G(u) then the supporting measures have densities Z(u) on the unit interval with H(u) ≤ Ψ(u) where H′ = Z. It is shown in Cherny and Madan (2010) that in terms of distortions one may write the unhedged bid and ask prices as

Carr, Madan and Vicente Alvarez (2010) express these prices in terms of the inverse distribution function with median, F(m) = 1/2 as

(1)

(2)

For hedges H ∈ $\mathscr{H}$ with hedged distribution functions F_H (X) the distribution function for X − H the bid and ask prices are

(3)

(4)

The distortion used in Cherny and Madan (2009, 2010) and Carr, Madan and Vicente Alvarez (2010) is minmaxvar defined by

We shall continue to use this distortion here.

Given explicitly computable expressions (3) and (4) for the bid and ask prices in the presence of hedges Carr, Madan and Vicente Alvarez (2010) employ these to define the up front profit on a trade, the capital reserve to be taken on the trade and hence the return of the trade. In addition measuring the scale as the expectation of the absolute deviation from the median, leverage is defined as the ratio of the scale to the capital. The upfront profit is defined as the difference between the mid quote and the risk neutral expectation and for options it is observed that this is generally positive. The capital reserve is defined as the cost of going in and out of the trade with the market and hence paying the spread between the ask and bid prices. It is observed from expressions (1) and (2) that the profit π and capital κ are given by

where H is antisymmetric about 1/2 and is zero at 0, 1/2 and 1, while K is symmetric about 1/2 and specifically

The return ρ is just π/κ while the leverage λ = scale/κ where the scale is given by

3 GAMMA ADJUSTED DELTAS IN LEFT SKEWED MARKETS

We consider here the hedging of quadratic exposures with a view to minimizing the capital charge for the residual risk exposure. Suppose the target cash flow c(S) to be hedged over a time interval of size h is quadratic in the stock price with

Consider a hedge position ζ in the stock with a residual cash flow of

Suppose the underlying stock price motion x = S − S₀ has distribution F(x) and the objective is to minimize the capital required defined by the difference between the ask and bid prices computed using the concave distortion Ψ. To evaluate this capital we need to determine the distribution function of the residual cash flow as both the bid and ask prices are functions of this distribution function. Let C denote the residual cash flow.

The probability F_C(v) that C ≤ v is the probability that

The minimum cash flow occurs at

and is equal to

Hence

For we solve for x the equation

with

and the probability that C ≤ v equals the probability that S − S₀ lies between the two solutions. We then have that

We define

and write

The lower bound is now

Now −C ≤ γη²/2 and the distribution function for −C is Pr (−C ≤ v) and

for v < γη²/2 we have that

It follows that the ask price is

and the bid price is

Hence the capital is

Now we make the change of variable

to observe that

For the optimal value for η we just need to minimize the expression for unit γ or we need to minimize

and this expression just depends on the underlying stock price distribution. One may therefore determine the optimal η from the risk neutral distribution of the stock and then we hedge with gamma adjustment using the delta position

ζ = δ − ηγ.

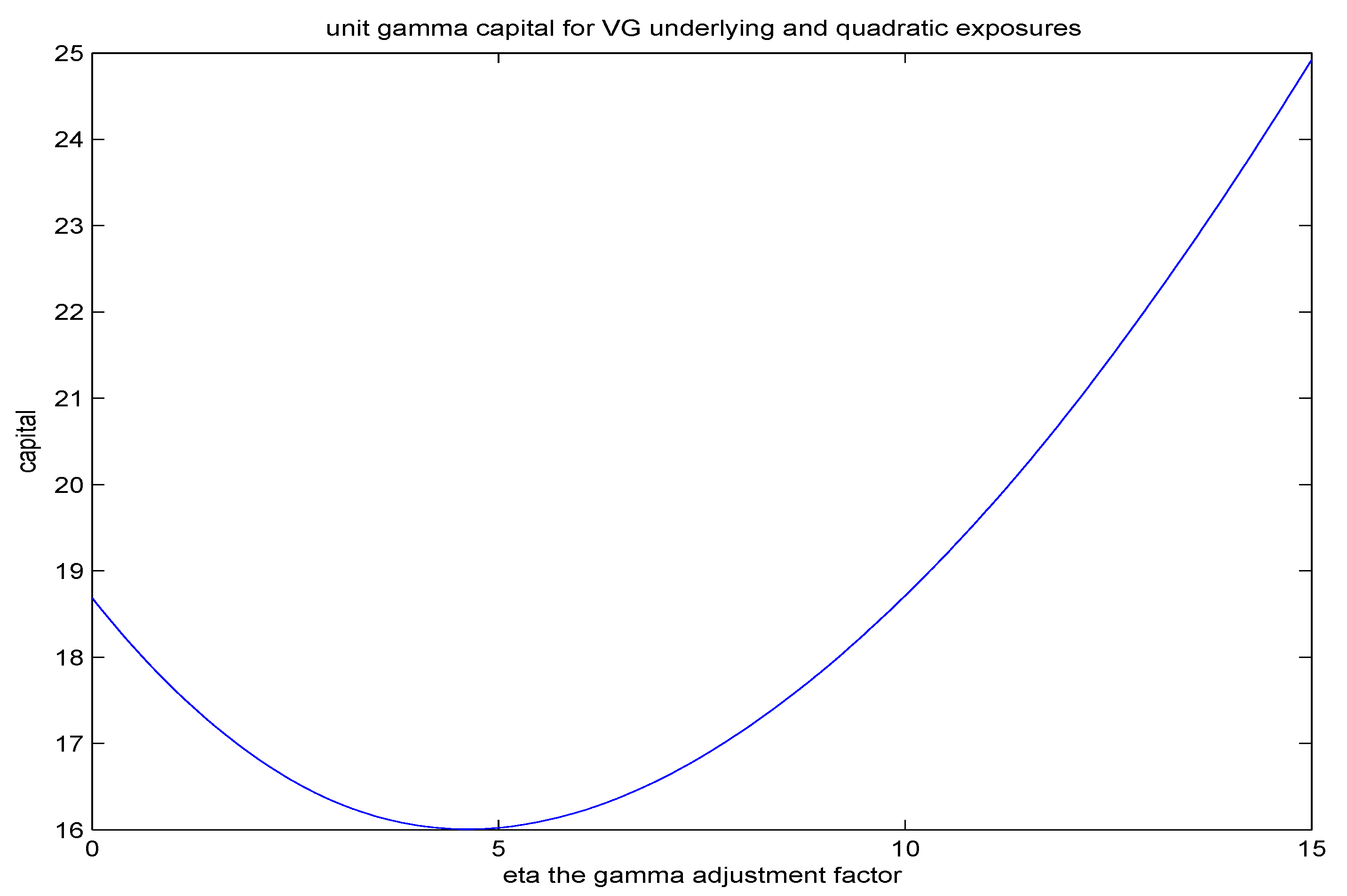
We illustrate the function Λ as a function of η for the variance gamma model (Madan and Seneta (1990), Madan Carr and Chang (1998)) calibrated to options on the SPX on July 15 2010. For weekly monitoring with VG parameters .2196, .3317, −.3596 we graph in Figure (1) the unit gamma capital as a function of the adjustment factor η. The minimum in this case occurs at η = 4.6071.

We observe from this section the basic intuition underlying the gamma adjustment for delta hedging when markets are skewed downwards. Residual risks even if they are symmetric are not symmetrically priced and since the downside exposure is more expensive, the optimal delta should be adjusted downwards in the presence of of some gamma risk. We now take up issues of dynamic hedging in incomplete markets.

4 A MULTI PERIOD MODEL

We now consider dynamic models for capital and the implementation of hedges that minimize the capital required to hold the remaining risk or uncertainty that is yet to be resolved in a trade. This requires a dynamic definition of bid and ask prices from which we will get our dynamic definition of capital. The hedges are then chosen to successively minimize this dynamically constructed measure of capital. With a view to understanding dynamically consistent sequences of bid and ask prices we consider a discrete time multiperiod model with dates t = {0, 1, 2, … , T}. For our construction of dynamically consistent sequences of bid and ask prices we follow Cohen and Elliott (2010). We therefore suppose the underlying risk is that of a finite state Markov chain X_t, for X₀ = 0 and t = 1, 2, …, T with

X_t ∈ {e₁, e₂, · · ·e_N},

where e_i is the i^th row of an N dimensional identity matrix. Without loss generality one may identify the states of any finite state Markov process with the unit vectors of N dimensional space. Let be a filtered probability space, where is the completion of the sigma algebra generated by the process X up to time t.

One may then defined a martingale difference process M_t implicitly by

The process M_t represents the conditional local risk in the underlying risk process. We shall construct our dynamically consistent sequence of bid and ask prices as nonlinear expectations using Theorem 6.1 of Cohen and Elliott (2010) as solutions of a backward stochastic difference equation for a suitably chosen driver F(ω, t, Y, Z). For a continuous time analysis one has to involve backward stochastic differential equations El Karoui and Huang (1997), Cohen and Elliott (2010b).

Since even in a static context bid prices are concave functionals and ask prices are convex functionals of the random variables being priced these valuations cannot be represented by expectation operators traditionally used as valuation operators. In the context of discrete time Markov chains Cohen and Elliott (2010) have defined dynamically consistent translation invariant nonlinear expectation operators defined on the family of subsets . Our dynamic bid and ask prices will be examples of such operators.

For completeness we recall the definition of an –consistent nonlinear expectation for . A system of operators

is an –consistent nonlinear expectation for if it satisfies the following properties:

• For componentwise, then

  componentwise, with for each i,

  only if
• for any –measurable Q.
• for any s ≤ t
• For any

Furthermore the system of operators is dynamically translation invariant if for any and any ,

Such dynamically consistent translation invariant nonlinear expectations may be constructed from solutions of Backward Stochastic Difference Equations. These are equations to be solved simultaneously for processes Y, Z where Y_t is the nonlinear expectation and the pair (Y, Z) satisfy

for a suitably chosen adapted map called the driver and for Q an valued measurable terminal random variable. We shall work in this paper generally with the case K = 1. For all t, (Y_t, Z_t) are measurable.

For a translation invariant nonlinear expectation the driver F must be independent of Y and must satisfy the normalisation condition F(ω, t, Y_t, 0) = 0. Additionally to ensure the existence of a solution the driver must satisfy the following two conditions.

(i) For any Y, if ( for all t), then = for all t.

(ii) For any Z, for all t, the map is a bijection from , up to equality

Finally drivers used in constructing nonlinear expectations must be balanced. A driver is said to be balanced if it satisfies the following two conditions, for each t, and any Q¹,Q² ∈ and two solutions (Y¹, Z¹) and (Y ², Z²)

(iii) for all i; the i^th component of F; given by e_iF satisfies

with equality only if

(iv) if

then

We shall use different drivers for our dynamically consistent bid and ask price sequences that we denote by F_b, F_a respectively.

For the bid price construction we define

where

While for the ask price we define

It is clear that the normalisation condition F_u(ω, t, Y_t, 0) = 0 for u = a, b is satisfied.

For the existence of a solution and condition (i) we observe that if then and so they have the same one step ahead distribution functions and so both

Condition (ii) is clearly satisfied as F_u, u = a, b are independent of Y. Finally we wish to check that the driver is balanced. For this consider two solutions (Y¹, Z¹) and (Y², Z²) to the backward stochastic difference equations and we consider first condition (iii) We wish to show that

Now we may define and and we observe that b(X) > x₁ and b(Y) < y_N where x₁ is the worst outcome for X and y_N is the best outcome for Y. It follows that b(X) − b(Y) > x₁ − y_N the worst outcome for X − Y. Hence condition (iii) holds. A similar argument works for F_a. Condition (iv) follows as F is independent of Y.

Hence one may obtain dynamically consistent sequences of bid and ask prices as nonlinear expectations by solving the backward stochastic difference equations associated with these drivers. In fact we have for that

where

Taking t conditional expectations we see that

(5)

(6)

(7)

(8)

for the bid process and similarly for the ask process

(9)

(10)

(11)

(12)

The equations (5),(6),(7). and (8) constitute our recursion for the bid price sequence, while (9),(10),(11). and (12) form the recursion for the sequence of ask prices. We observe from equations (8) and (12) that one may make the computations even when we do not have a finite state Markov chain and do not identify the process for and we just use the recursions to compute the values for and in our applications this is what we will do.

We now consider this recursion in a two period setting to help fine tune the details of the procedure. Consider then a risk A₂ representing an asset with uncertainty resolved at time 2. We shall compare treating the two periods as a single period and computing the bid price in a single step, with what is obtained on employing a two step iteration for two periods of unit length. For simplicity we suppose that A₂ evolves as a Lévy martingale so that

where X₁, X₂ are independent draws from a single zero mean Lévy process at unit time.

If we apply our procedure for the two periods in one step we obtain for the bid price

where we use for b(X) the distorted expectation of the zero mean random variable X. We know that b(A₂ − A₀) < 0 and hence that B < A₀.

Now consider the computation in two steps of one period. This will give at time 1 the value

and we know from the stationarity of the law for the increment,

that

It follows that

Going one more time step we get

Now

and hence we get that

We get a better bid price going in one step compared to the two short steps of one period. However if we think of the penalty b(A₂ − A₀) as a capital charge then this is a charge for two periods while the two one step charges are for one period. The correct comparison is then between

It is now possible that

making the one step procedure the one with the higher bid. These considerations suggest that we take the timing factor into account in defining the penalty. Note further that the continuous time penalty is in the form

For a time step of h we revise our recursion to

(13)

(14)

for the bid process and similarly for the ask process

(15)

(16)

5 DYNAMIC HEDGING FOR CAPITAL CONSERVATION

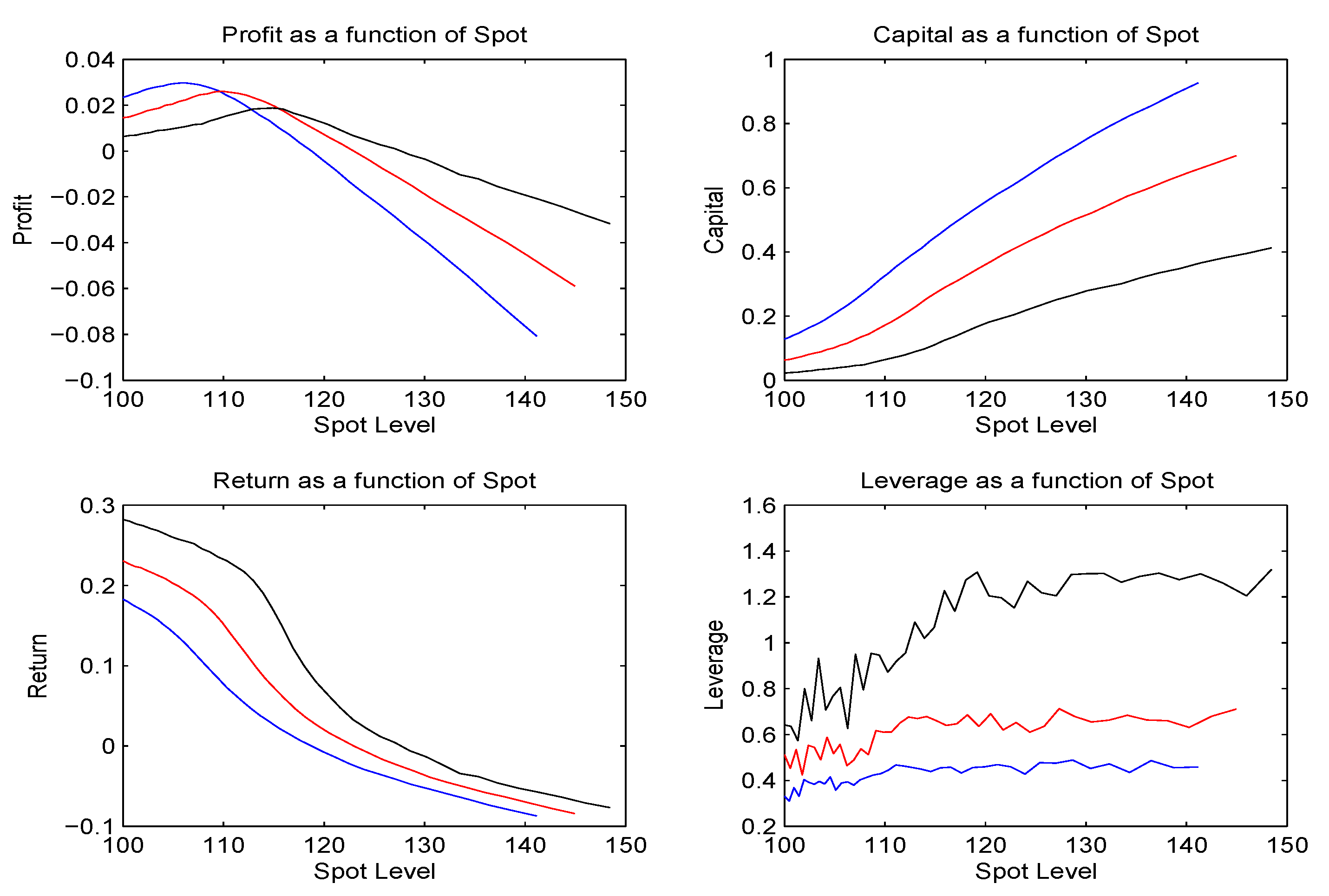
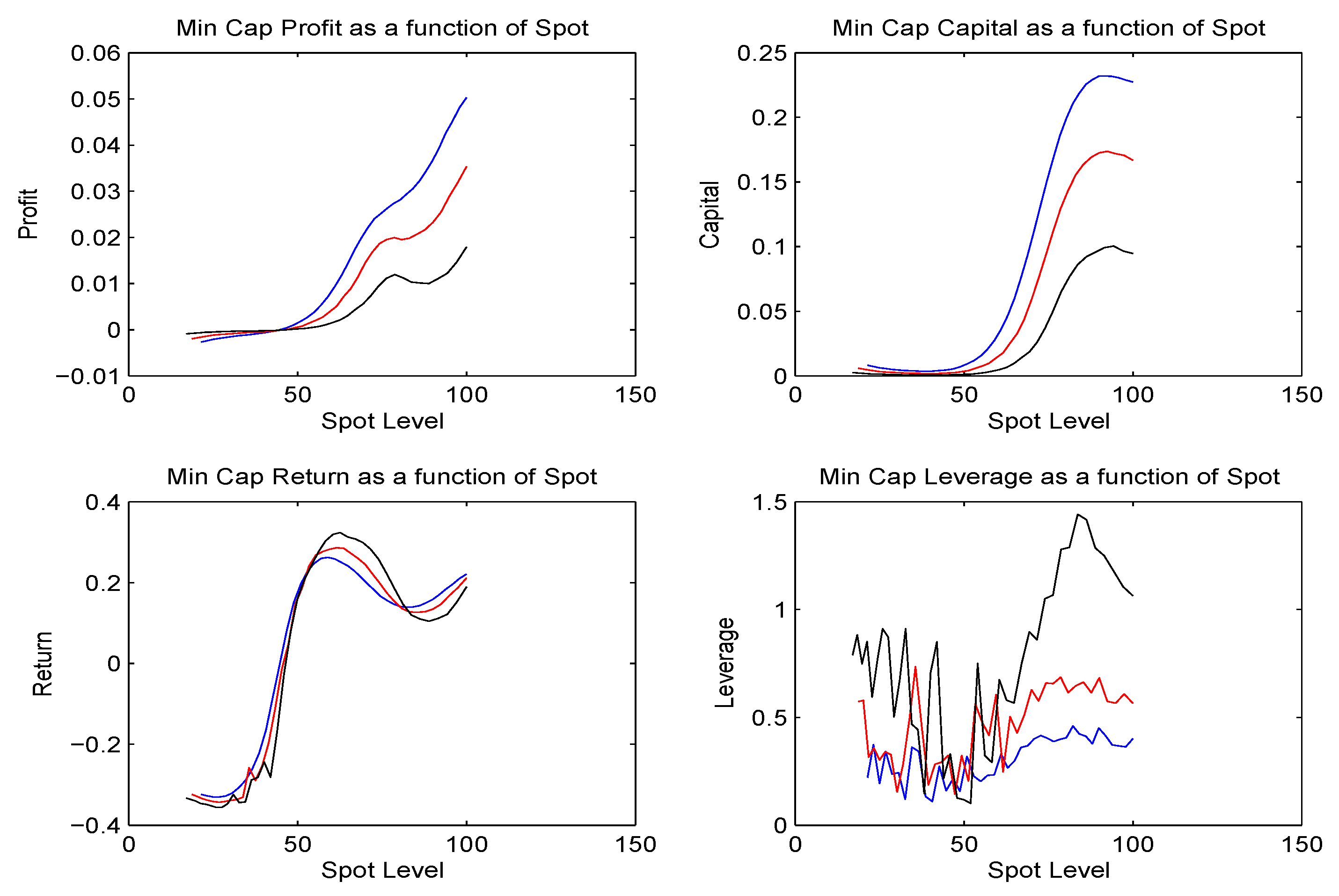
Given that the bid and ask price processes are nonlinear expectations we have that both the profit and the capital are nonlinear expectations. We now take for the stock an underlying exponential Lévy process with a given risk neutral law. For our time step we shall work with one week and then we report on dynamic hedging where each week the hedge position is chosen to minimize the capital reserve to be held against the remaining uncertainty yet to be resolved. We shall also report on the Black Scholes deltas computed at the implied volatility and the capital reserves to be held against such a hedging strategy. We shall observe that hedging at Black Scholes implied volatilities is considerably more expensive than the minimum capital hedge. We shall hedge a one year 120 call and a one year 80 put and in each case we compute the profit the capital, the rate of return and the leverage as a function of the level of the spot at week’s end. We present graphs of these functions at the end of 3, 6, and 9 months along with the bid, ask, mid, and risk neutral prices initially and the asscoiated profit capital, return and leverage all computed using our dynamically consistent recursion. In addition we present graphs for the minimum capital delta as a function of the spot price also at 3, 6 and 9 months.

The initial spot price is 100 the interest rate is 0.0379 the dividend yield is 0.0229 and the stock price dynamics calibrated to one year SPX options on July 15 2010 are given by the variance gamma process with σ = 0.2397, ν = 2.2765 and θ = −0.2109. The V G process is

where W(t) is a standard Brownian motion and g(t) is an independent gamma process with mean rate unity and variance ν. The stock price porcess is then given by

For each of 52 week ends we determine a nonuniform grid between the lower and upper stock price with a probability of a tenth of a percent of being outside this interval. The grid is constructed with 100 levels for the stock price at each week end. The grid construction is based on the procedure described in Mijatović and Pistorius (2010). We know the payoff at week 52 and all prices, bid, ask and risk neutral equal this payoff at week 52. For each week end from week 51 to week 1 we work back recursively computing the bid, ask and risk neutral expectation at each grid point by simulating the process forward for one week and then computing the required expactations and distorted expectations. The distortion used is minmaxvar and the stress level is 0.25. At each grid point we numerically solve an optimization problem to minimize the capital reserve and determine the delta position in the stock for this grid point. The final output consists of three matrices of size 51 by 100 that contain the bid, ask and risk neutral expectation at each grid point when there is no hedge. In the presence of an optimized delta hedge we have one more matrix and this is capital minimizing delta if the stock is at the particular grid level at the particular week end. Finally we simulate for one week the stock from the initial start level of 100 to compute the initial bid, ask and risk neutral price. We then get the initial profit capital, return and leverage. The one step ahead bid, ask and risk neutral values in the simulation are interpolated from the stored grid point values as we work back through the recursion. The results for the unhedged and minimum capital hedges are presented in two subsections.

5.1 Unhedged Results

We first report on the initial values of the variables of interest for the 80 put and the 120 call in the absence of any dynamic hedging. The variables of interest are the bid, ask, the mid price, rne the risk neutral expectation, scale the expected absolute deviation from the median, prf the profit cap the capital reserve,ret the return and lev the leverage provided. These are presented in

Table 1. Initial Unhedged Values

Variable	80 Put	120 Call
bid	5.0738	1.6162
ask	5.5572	1.8419
mid	5.3155	1.7291
rne	5.1966	1.6988
scale	0.1259	0.0670
prf	0.1189	0.0303
cap	0.4834	0.2256
ret	0.2460	0.1343
lev	0.2605	0.2971

.

We next present in Figure (2) and Figure (3) graphs of the profit, capital, return and leverage at 3, 6 and 9 months as a function of the level of the spot price.

5.2 Minimum capital hedge results

We report in this subsection on the results of implementing at each week end, a delta position that minimizes the post hedge reserve capital charge for the remaining uncertainty. Again we first present the results on the variables of interest at the initial date in

Table 2. Minimum Capital Delta Hedge

Variable	80 Put	120 Call
bid	4.6723	1.5221
ask	4.9465	1.6834
mid	4.8094	1.6028
rne	4.7471	1.5644
scale	0.0681	0.0476
prf	0.0623	0.0384
cap	0.2741	0.1613
ret	0.2273	0.2382
lev	0.2485	0.2948

.

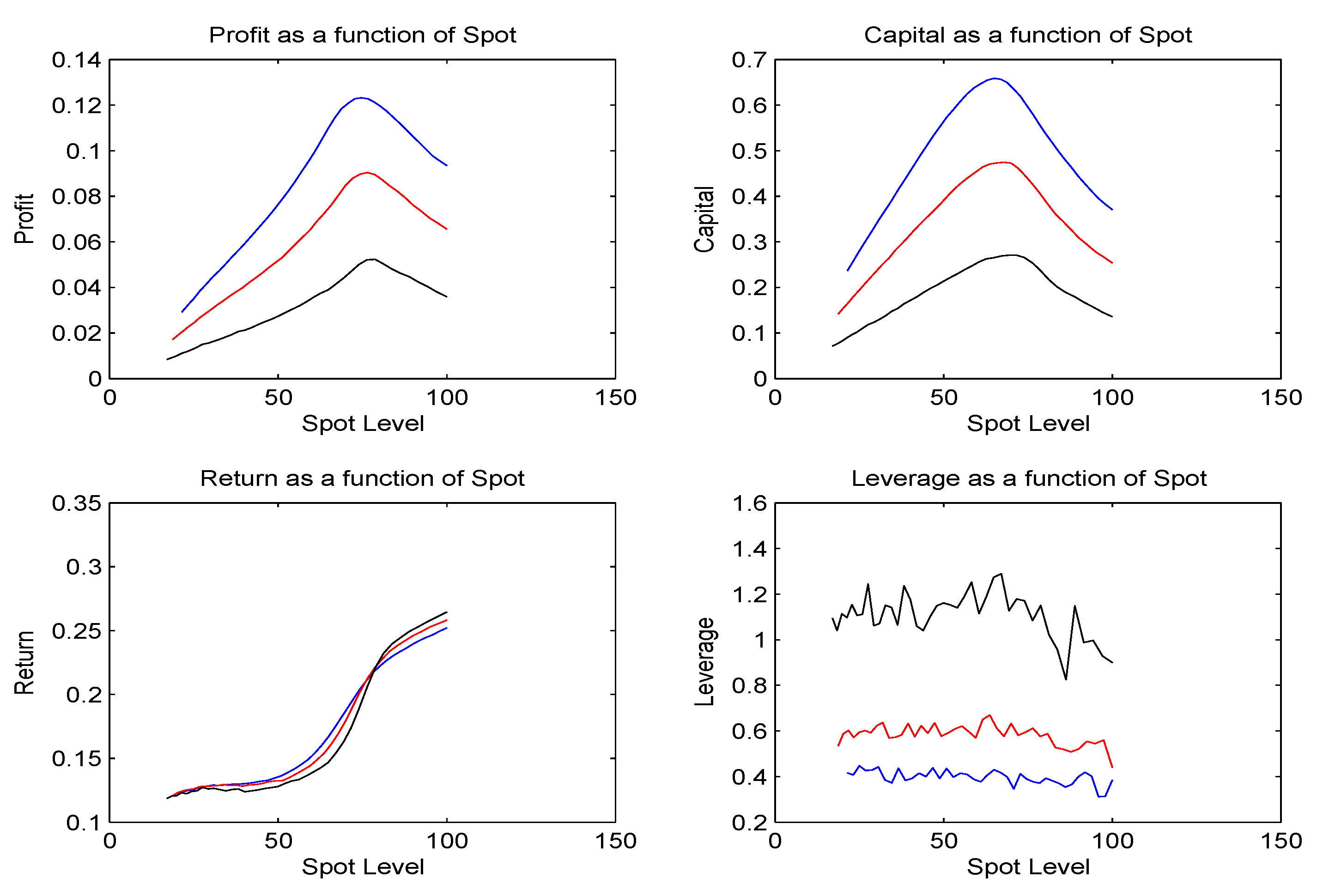
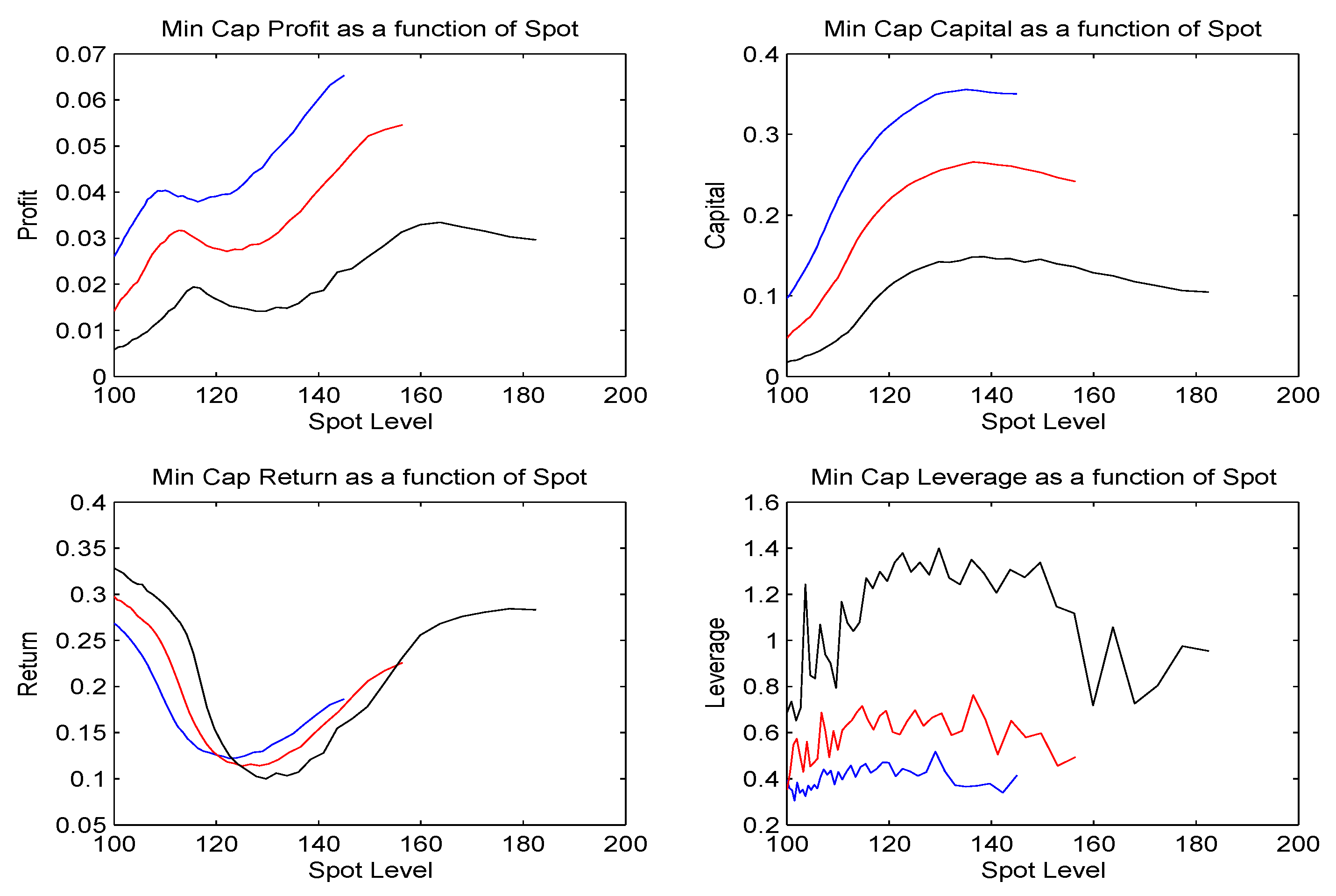
We present in Figure (4) and Figure (5) the profit, capital, return and leverage at 3, 6 and 9 months for the 120 one year Call and the 80 one year Put as functions of the level of the spot.

Additionally we present a graph for the delta positions taken in Figure (6) and Figure (7) to hedge the remaining risk with a view to minimizing reserve capital charges.

We also computed the dynamic levels of profit, capital, return and leverage for both the 120 one year call and 80 one year put using Black Scholes deltas computed at the implied volatility. The Black Scholes call deltas were considerably higher and the put deltas were lower in absolute value than what is observed under the optimal minimum capital hedge. We report in

Table 3. Black Scholes Delta Hedge

Variable	80 Put	120 Call
bid	3.8532	2.3318
ask	4.8601	3.8047
mid	4.3566	3.0683
rne	4.3386	2.9177
scale	0.1478	0.0904
prf	0.0180	0.1506
cap	1.0069	1.4728
ret	0.0179	0.1023
lev	0.1468	0.0641

the initial values for hedging at Black Scholes implied.

We observe that the capital levels are sufficiently higher for the Black Scholes delta hedge.

6 CONCLUSION

We present first in the static case and then in the dynamic case the argument for adjusting Black Scholes implied call deltas downwards for a gamma exposure in a left skewed market when the objective for the hedge is the conservation of capital. For similar reasons the absolute value of put deltas should be increased to accomodate the costs imposed on residual risks by the market skewness. The gamma adjustment factor in the static case is shown to be just a function of the risk neutral distribution that can be calibrated from the option surface. This could be periodically adjusted as skewness levels are observed to move around. In the dynamic case one may precompute at the date of trade initiation a matrix of delta levels as a function of the underlying for the life of the trade and subsequently one just has to look up the matrix for the hedge. Additionally the matrix could be periodically recalibrated. Also constructed are matrices for the capital reserve, the profit, leverage and rate of return remaining in the trade as a function of the spot at a future date in the life of the trade. These could be periodically recalibrated using the procedures outlined. The concepts of profit, capital, leverage and return are as described in Carr, Madan and Vicente Alvarez (2010).

The dynamic computations constitute an application of the theory of nonlinear expectations as described in Cohen and Elliott (2010) for a finite state stochastic difference equation framework. Bid and ask prices are computed as nonlinear expectations using a penalty driver for the periodic risk that comes from our static model. The dynamic implementation could be speeded up on employing the static adjustment factors as approximations where by one estimates gamma exposures by regression or the use of the Black Scholes gamma.