1. Introduction
The concept of capital structure arbitrage is well understood. Using Merton’s model of firm value [
1], mispricing between the equity and debt of a company can be sought. Several studies have now been published [
2,
3,
4,
5,
6,
7,
8]. As first explained by Zeitsch and Birchall [
9], Merton models are most sensitive to volatility. Stamicar and Finger [
10] showed the potential for exploiting that sensitivity by calibrating the CreditGrades model [
11] to equity implied volatility in place of historic volatility. The results produced model implied Credit Default Swap (CDS) spreads that closely matched the actual traded five-year CDS. Other studies [
12,
13,
14] have subsequently been published that agree with the findings in [
10] for a broad cross-section of credits. More generally, quantifying credit risk through structural models has also been investigated by Eom, Helwege and Huang [
15], Huang and Zhou [
16], as well as Huang and Huang [
17].
Within arbitrage studies, the calculation of asset volatility has not been consistently treated. Yu [
2] calibrated to a 1000-day historic volatility. Similarly, Balazs and Imbierowicz [
3] employed historic volatilities. Baljum and Larson [
4] calibrated the capital structure to a one-month, at-the-money put implied volatility. Wojtowicz [
5] computed the daily market implied volatility by solving for the model CDS premium that replicated the actual market CDS spread before taking a 100-day moving average of the resulting volatilities. Ju et al. [
6] adopted a volatility curve applied to a 1000-day historic volatility to introduce calibration flexibility. Huang and Luo [
7] employed call option implied volatilities that underwent a least square error minimization.
The question naturally arises as to what is the optimal volatility to calibrate the Merton model to? Similarly, what technique should be used to calibrate it? Any moving average will reduce the sensitivity to volatility (or corrupt the risk-neutral calibration), thereby reducing the ability to reproduce the CDS and trade efficiently. All of the studies mentioned above, except for [
6], employed the CreditGrades model [
11], where the default barrier is held constant with random jumps introduced by assuming that the recovery rate follows a log-normal distribution. Calibrating such an approach is problematic as data are scarce. Secondly, it weakens the risk-neutral calibration as the data are historic; again, reducing the market responsiveness. There is also no justification for employing this model over, say, the commercially-available and widely-used Moody’s KMV [
18], nor other models, such as Leland and Toft [
19] or Geske and Johnson [
20,
21].
The aim of this study is to eliminate the use of historic data, thereby improving the model’s responsiveness. To achieve this, calibration to deep out-of-the money put volatilities will be proposed using a basic Merton model. A new technique is then used to explicitly derive the default barrier. The methodology requires solving for the default threshold numerically, point by point, as the asset value where the market capitalization of the company asymptotes to zero. This naturally maintains the risk neutrality. The desire is to improve the responsiveness of the default probability calculation. It is well documented that Merton models often fail to replicate the outright magnitude of the CDS spread. With the enhancements outlined here, it will be shown that very close agreement between the traded CDS and the synthetic CDS is consistently possible. As first mentioned in [
18], historically, the credit risk of financial institutions has been difficult to model. This has led to such companies being excluded from studies [
2,
5,
7,
13,
18,
22]. That limitation is overcome here due to the focus on modeling the volatility.
The close agreement that results between the synthetic CDS and the traded contract forms the basis for the approach to identify capital structure arbitrage opportunities. Divergence between the synthetic and the traded CDS can still occur, as sentiment may differ between the equity and credit markets for a given company. Trading a corporate’s equity against its debt is the basic technique of capital structure arbitrage. However, all studies published to date only consider delta-hedging or trading the underlying equity itself against the CDS. As outlined in [
9], the sensitivity to volatility, or vega, can be several orders of magnitude greater than the delta. Here, we shall show that the main driver of the arbitrage strategy should be to trade the CDS against the equity implied volatility; not the stock itself. In fact, the equity or delta hedge is largely ineffectual when compared to the vega hedge. This result is new. We then illustrate a volatility hedging technique with several case studies to show the effectiveness of focusing the hedging strategy on the implied volatility. This is then extended and back tested across all applicable CDS.
As summarized in
Table 1, 830 credits are covered with data from January 2004 until December 2011. The companies are spread across all industries and geographies. This encompasses the universe of CDS contracts where an active equity option market also exists. It includes the liquid pre-Lehman market, the Lehman default itself and the subsequent European debt crisis.
The volatility hedging strategy will be run against all 830 obligors across the entire time period. Summary statistics of the performance of the strategy, across the full universe of credits under consideration, are then presented.
In
Section 2, an outline of the model is given. In particular, the risk-neutral calibration of the default barrier is defined.
Section 3 provides the motivation for calibrating the model to deep out-of-the-money put volatilities. The output from the model is then shown in
Section 4. The methodology to exploit volatility-based capital structure arbitrage is then given in
Section 5. This includes several case studies to explicitly illustrate the technique. Using the approach across all of the credits from
Table 1,
Section 6 then shows the results of back testing the approach from 2006 until the end of 2011.
Section 7 summarizes the results.
2. Model Description
In this study, the aim is to maximize the responsiveness of the model to the asset volatility. The derivation used here draws directly on [
1,
18] with limited use of [
11]. The crucial difference from all other models is the ability to calibrate risk-neutrally, thereby eliminating the need for historic data; most notably for calculating the default barrier.
Following [
1], assume two classes of securities, namely equity and debt. The equity pays no dividends, and the bond is due to be repaid at time
T. Define
as the value of the assets and
as the asset volatility. In the Merton framework, the firm’s assets follow the geometric Brownian motion:
where
r is the asset drift due to risk-neutral interest rate dynamics and
is a standard, risk neutrally calibrated, Wiener process. The traded securities are
S, the observed value of a company’s market capitalization (or share price), and a defaultable corporate bond
B, with maturity
T. The payment to shareholders at time
t is given by:
Market capitalization is therefore given by the standard Black–Scholes formulation,
, as:
where:
and
N(…) is the Gaussian distribution. The default time within the model is calculated as the first hitting time for the default barrier. This is defined as:
where
is the instantaneous default point for the bond at time
t.
Equity is a market observable. Total liabilities are obtained directly from an issuer’s balance sheet. The remaining unknowns are then the value of the firm’s assets and the asset volatility. Returning to (2), assume that an equity volatility exists; we then have that:
On the other hand, applying Ito’s lemma to (2) gives:
Equating (5) and (6), we find that:
There are two boundary conditions that
must satisfy, namely:
and when
, assume that:
Likewise,
These conditions represent the behavior of
near default and when well capitalized. To the first order, (8) gives:
The simplest expression that will then satisfy (8) and (9) is:
Substituting (10) into (7) yields:
Equation (11) is the basic representation of the asset volatility as derived in CreditGrades [
11]. However, CreditGrades subsequently holds the default barrier constant and models the recovery as a historically-calibrated log-normal variable. In fact, this is not needed. Equation (8) already defines the default barrier. The boundary condition (8) should also hold in the limit or:
For senior unsecured debt, the market standard assumption for loss given default, or LGD, is 60%. As an initial estimate for the default point, take:
Substitute (13) into (11). Equation (12) can now be solved numerically by seeking an updated
, such that:
where
i = 1, 2, …. Equations (11) and (14) are then iterated for
until convergence is achieved. To solve (14), the Brent–Dekker algorithm is used [
23,
24]. The methodology is typically employed to solve for the root of a function using a combination of bisection, secant and inverse quadratic interpolation. However, as
is a non-negative, monotonically-increasing function, solving for a root of
is not strictly possible. Instead, a tolerance is defined to represent the limit in (12). The Brent–Dekker solver then seeks a solution to within that tolerance. Here, the algorithm searches for the value of
, where the market capitalization drops by 99%, or in effect to within an accuracy of 1%. The advantage of this approach is that at any given time, the exact liabilities and the relationship to the default point cannot be known. However, using the option curve to determine
allows calibration to the market and captures the latest sentiment, thereby minimizing arbitrary intervention. Consequently, the default point will move day on day, and it is risk-neutrally calibrated. This approach to implying the default point is new.
Following [
18], the probability of default is the probability that the issuer’s assets will be less than the book value of the issuer’s liabilities when the debt matures. That is:
where
is the probability of default at time
t;
was given by (1) and was calculated in
in (14). From (1), we have that:
and
was defined in (11). Substituting (16) into (15) gives:
Now,
. Thus, we can define the default probability in terms of the cumulative normal distribution as:
Within the credit market, CDS liquidity is concentrated on the five-year, senior unsecured contract. Other maturities do trade, most notably from three to 10 years, but the majority of markets will be made for the on-the-run five-year tenor. As per [
25], the CDS fair-value is obtained by equating the premiums paid by the protection buyer versus any contingent payout from a credit event paid by the protection seller. Consequently,
where
is the discount factor to the
i-th day and
is the associated default probability. In practice,
is implied from the quoted CDS. Here, the aim is to replicate the CDS by defining
using (17). Hence, substituting (17) into (18) produces the synthetic CDS. The
,
i = 1 …
n, then form the synthetic CDS time series. Any CDS contract requires a constant LGD assumption. As an initial estimate, LGD = 60%, which is the market default. However, the LGD represents a degree of freedom that can be calibrated to reduce the pricing error between the synthetic CDS and the traded contract. Here, the LGD is scaled to minimize, on average, the magnitude of the synthetic versus the traded five-year CDS. The LGD is calibrated once, where 0 < LGD <1, and then held constant. Yu [
2] employed a similar technique by calibrating to minimize the sum of squared errors of the first 10 days of the time series. Given that the aim is to model the liquid five-year CDS, the maturity of the model,
T, is also set to five years.
3. Model Calibration
Here, Equation (11) will be calibrated to a one-month 10-delta put implied volatility. The justification is both theoretical and motivated by market observables. Following Merton [
1], define the debt-holder’s payoff as
. Then:
and
B were defined in Equations (1) and (2), respectively.
is the value of a put option with the same characteristics as (3). Hence, debt-holders are long the face value of the bond and have sold a put option on the assets of the company. In theory, if the debt-holders bought back the put in (19), they would be hedged against default risk. In practice, this can only be achieved by buying CDS protection. Consequently, CDS can be thought of as a proxy for a put option on the assets of the firm. The value of the put option will vary depending on the value of the company’s equity. Large declines in the market capitalization will increase the value of the put option. The best indicator of such a decline will be the deep out-of-the money put implied volatilities.
If market sentiment turns against any issuer, low delta puts will attract interest as a relatively inexpensive hedge. If the share price weakens, then such a position will quickly increase in value. Generally, increased open interest in such low delta strikes will quickly skew the implied volatility versus higher strikes, as the volatility seller will demand a higher premium for the risk. There are also other considerations. For example, stocks do typically report earnings on a quarterly basis. There is a danger that this can push option implied volatility higher ahead of earnings announcements, especially for deep out-of-the-money put options. In general, this is not an issue, and a simple robustness check could be employed to correct for this, if desired.
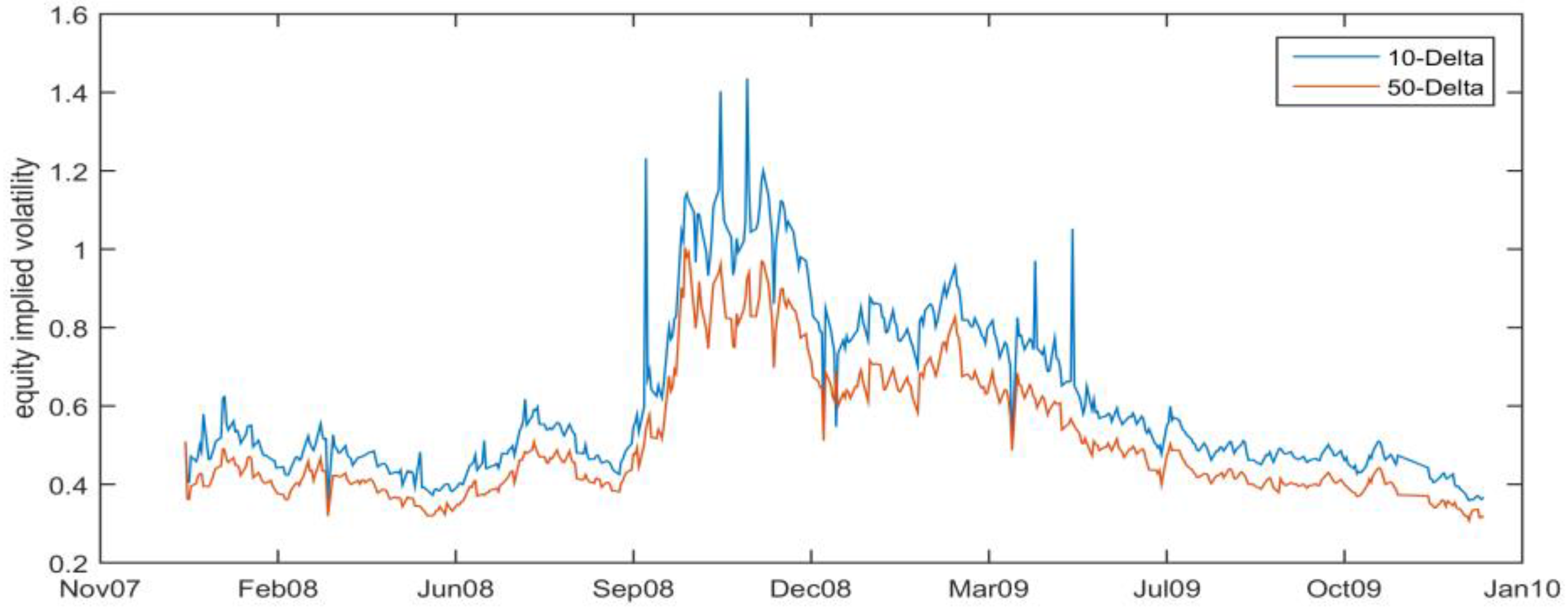
In
Figure 1, the average 10-delta and 50-delta one-month put implied volatility is plotted through 2008 and 2009 for the companies listed in
Table 1. In early 2008, the differential between the 10-delta and 50-delta put volatility was approximately four volatility points. By the last quarter of 2008, that difference was as large as 20. The peak difference of 60 volatility points occurred in September 2008 when Lehman defaulted. Only in late 2009 did the differential reduce back to four volatility points. The fact that the low delta volatilities can trade significantly higher and over a greater range of values than at-the-money volatilities will increase the variability and responsiveness of the default probability in (17). This will subsequently also be reflected in the calculation of the synthetic CDS. Using the lowest strike possible, or 10-delta, should therefore be the calibration choice. All volatility data were sourced from Bloomberg. The Bloomberg data series for the one-month maturity is the deepest. There are data for the three-month maturity, but they are not as consistent. Beyond three months, Bloomberg has no reliable data; hence the use of the one-month 10-delta put volatility. This reflects the general open interest that can be seen in the market.
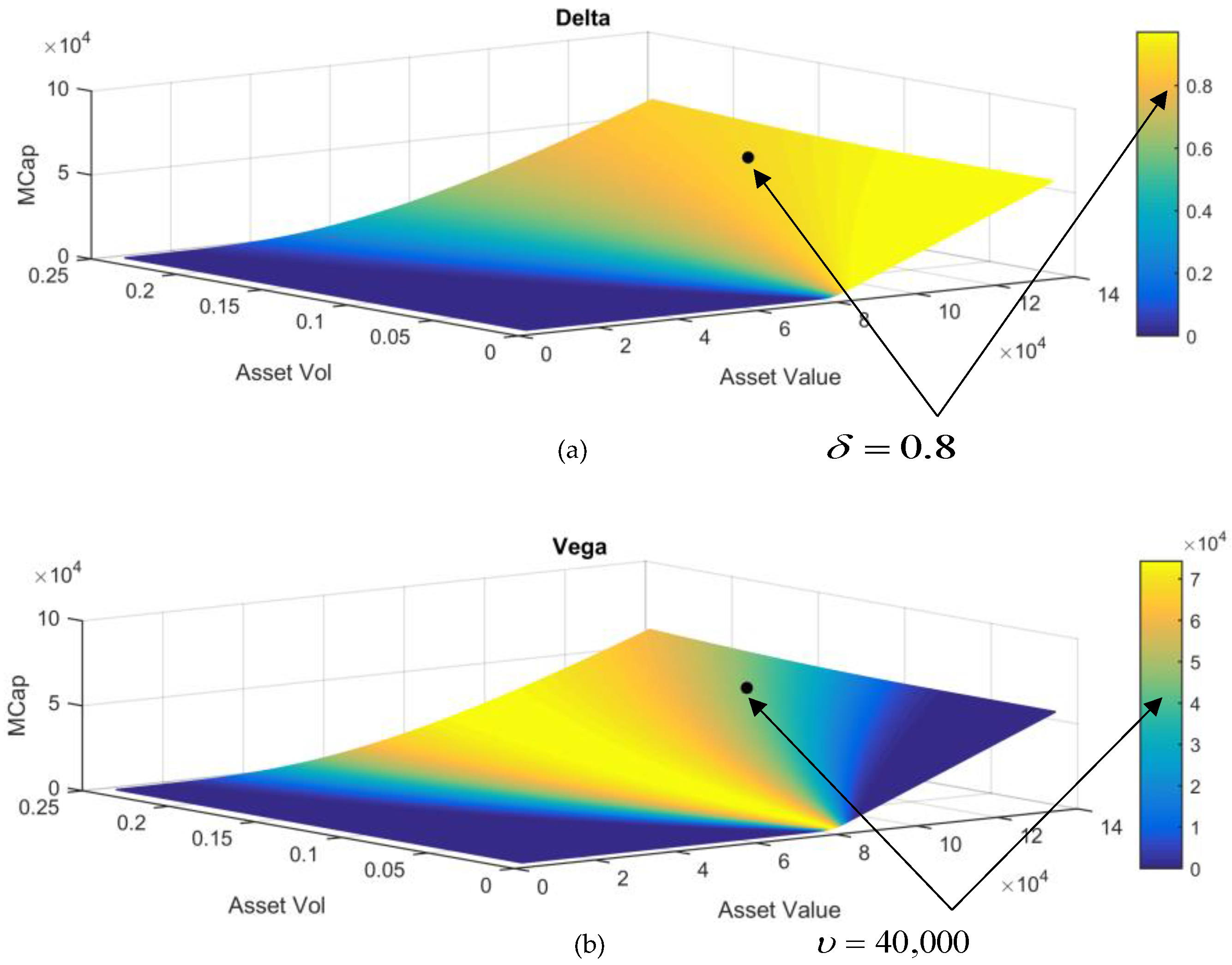
The choice of the implied volatility is crucial. Consider
Figure 2. It shows the sensitivity for Bay Moteren Werke, or BMW, as the market capitalization moves against the underlying asset price and against the asset volatility.
The point on each surface shows the equity-liabilities relationship as of late 2011. The color of each plot represents the magnitude of each sensitivity. The value of each sensitivity can be ascertained by matching the color of the region where the point is located to the scale next to each chart. Reading off the charts, we can see that delta = 0.8 and vega = 40,000.In other words, the sensitivity to asset volatility is five orders of magnitude greater than the sensitivity to asset value. The difference in the magnitude of the sensitivities holds across all combinations of asset value and asset volatility.
The relative magnitudes of delta and vega are an observation that holds for all issuers.
Table 2 shows the breakdown of delta and vega, in late 2011, by industry and geography, for the credits from
Table 1. Putting aside the one credit from Africa, all names show at least a differential of four orders of magnitude between delta and vega. The largest discrepancy is for financials, which shows a difference of six orders of magnitude. The heavy model dependence on volatility is a key reason that financial institutions have not performed well historically in Merton models. Financials are often excluded from analyses [
2,
5,
7,
13,
18,
22], as their capital structures have posed challenges. This will be exacerbated if the model is not fully calibrated risk neutrally to the most sensitive volatility, i.e., the 10-delta put. Another observation is that financials with large asset values (in excess of USD200 billion can skew the results in
Table 2. For example, removing China Construction Bank and Mizuho Corporate Bank from the Asian cohort sees the vega drop from 63,935 to 12,477. There is a similar effect in Europe, although the magnitude is also affected by the Eurodollar exchange rate in late 2011. Hence, volatility is the single most important parameter in a structural model.
4. Model Output
To illustrate the model’s performance, the output for four different credits from Europe, Asia and North America are shown in
Figure 3,
Figure 4,
Figure 5 and
Figure 6. The companies in question are BMW, which continues the calibration exercise from the previous section, Boeing Co., Hutchison Whampoa and Hartford Financial Services. Here, the choice of a financial institution is deliberate. As discussed in the previous section, such companies historically have proven difficult to calibrate in the Merton framework. However, as given in
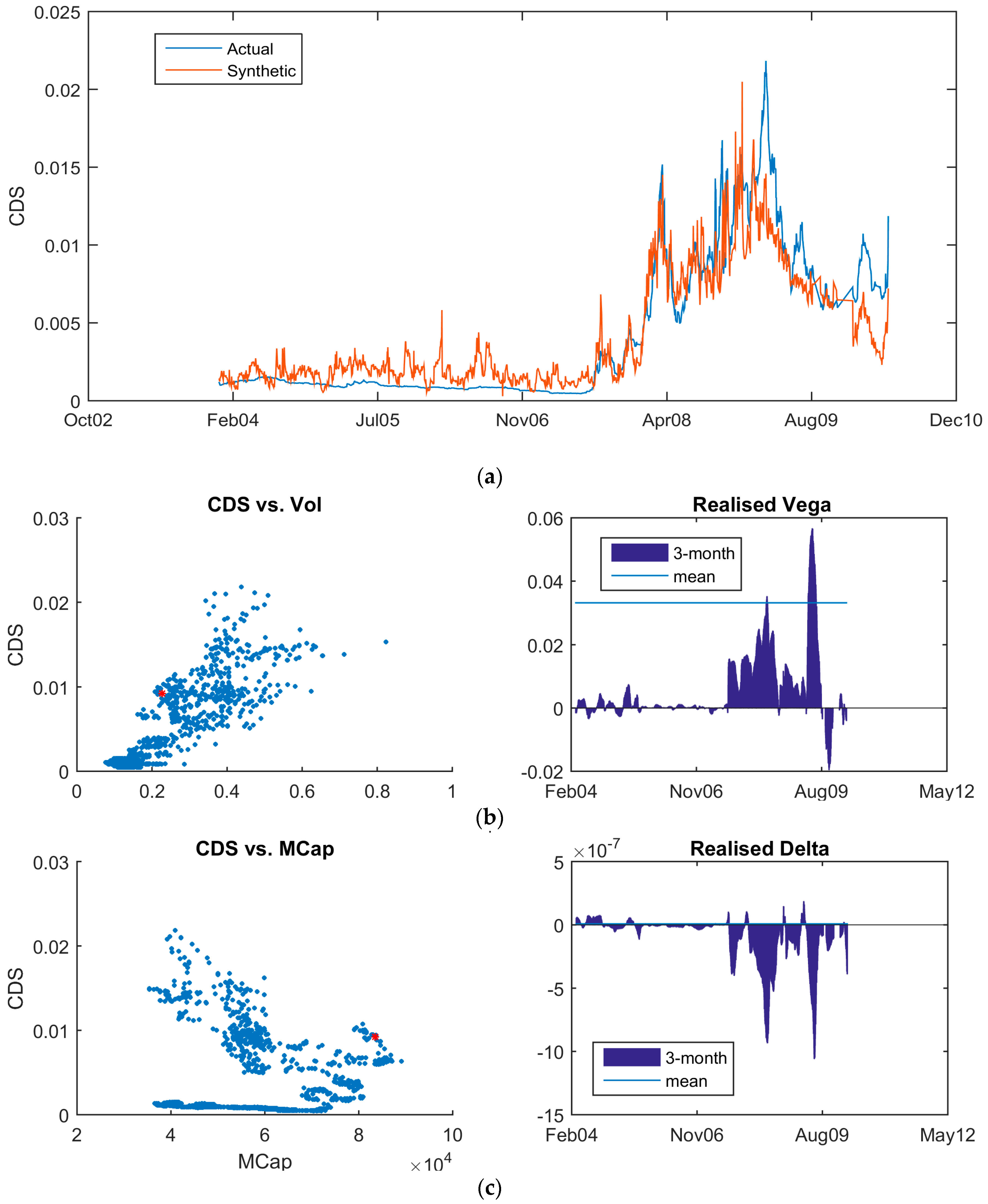
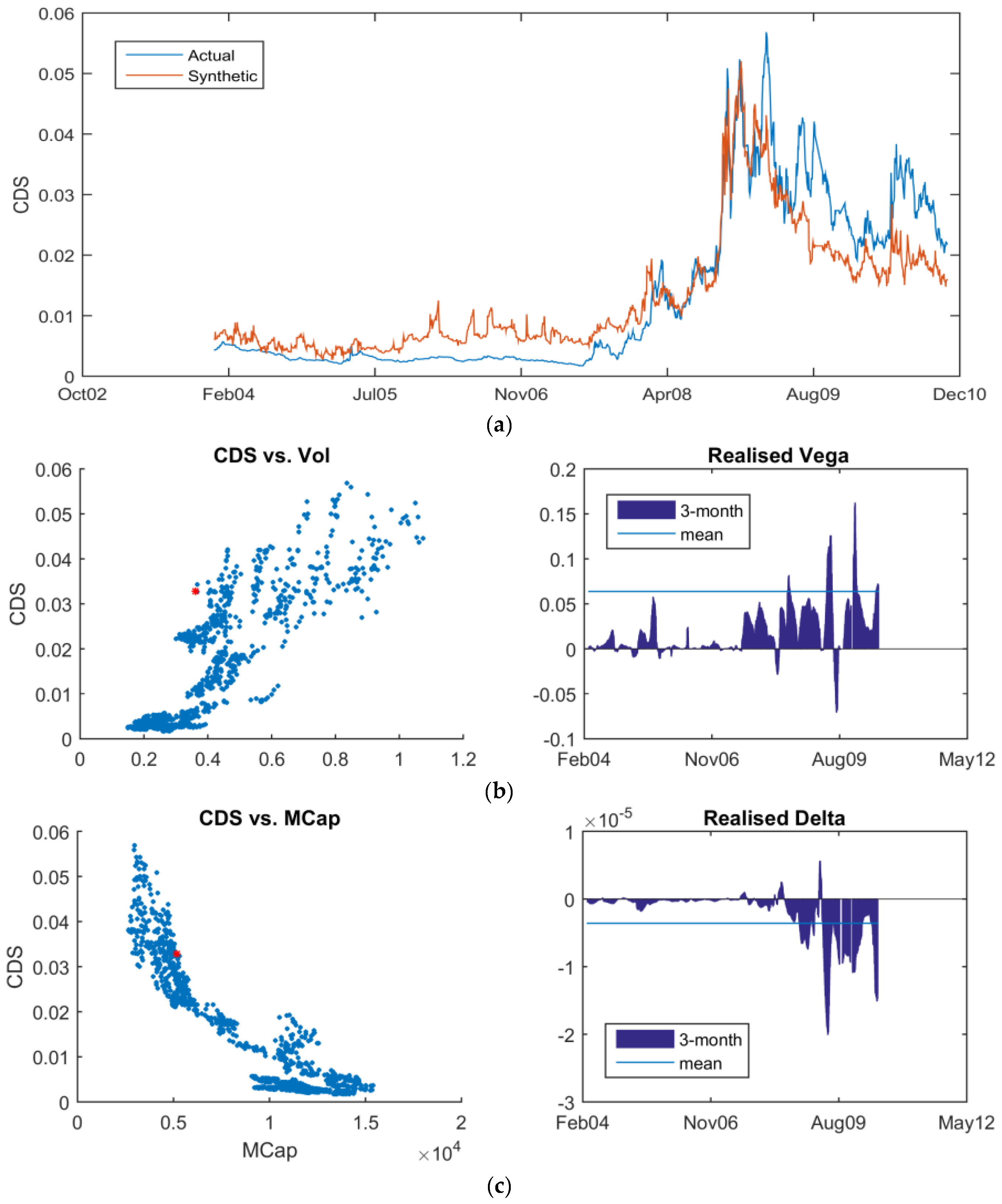
Table 1, financials represent the largest percentage of credits that are applicable to this approach. Hence, removing them significantly decreases the analysis opportunities. Here, financial institutions are not excluded. With the risk-neutral model formulation derived earlier, the modelling limitations are overcome, and good agreement between the synthetic CDS and the traded five-year contract can be achieved. The ability for the model to replicate financial CDS is also new.
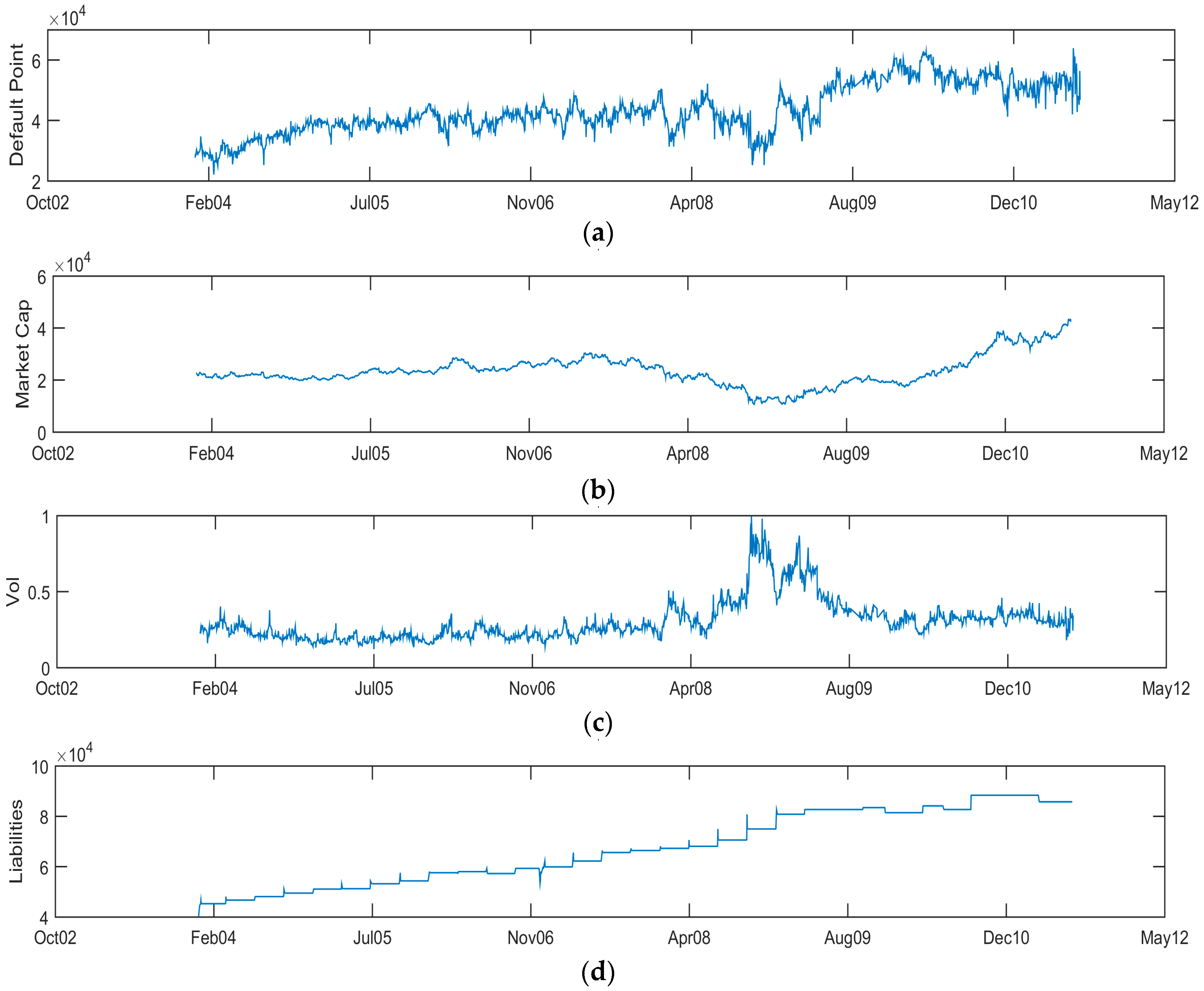
For the default barrier calculation, in
Figure 3, the default point for BMW is calculated using Equation (14) and plotted against the company’s market capitalization, asset volatility and liabilities through time. The charts show that the default point responds generally linearly versus the market capitalization and liabilities. The spike in asset volatility corresponding to the Lehman default significantly reduced the default barrier. In isolation, a lower default barrier would be interpreted as a reduction in default risk. In effect, the rise in volatility is interpreted by the Merton model as an increase in the potential for the asset value of the company to grow, or the ability of the company to trade its way to higher profits. This needs to be coupled with the decrease in market capitalization and the increase in leverage leading into 2008 to produce a higher default probability. Similarly, in
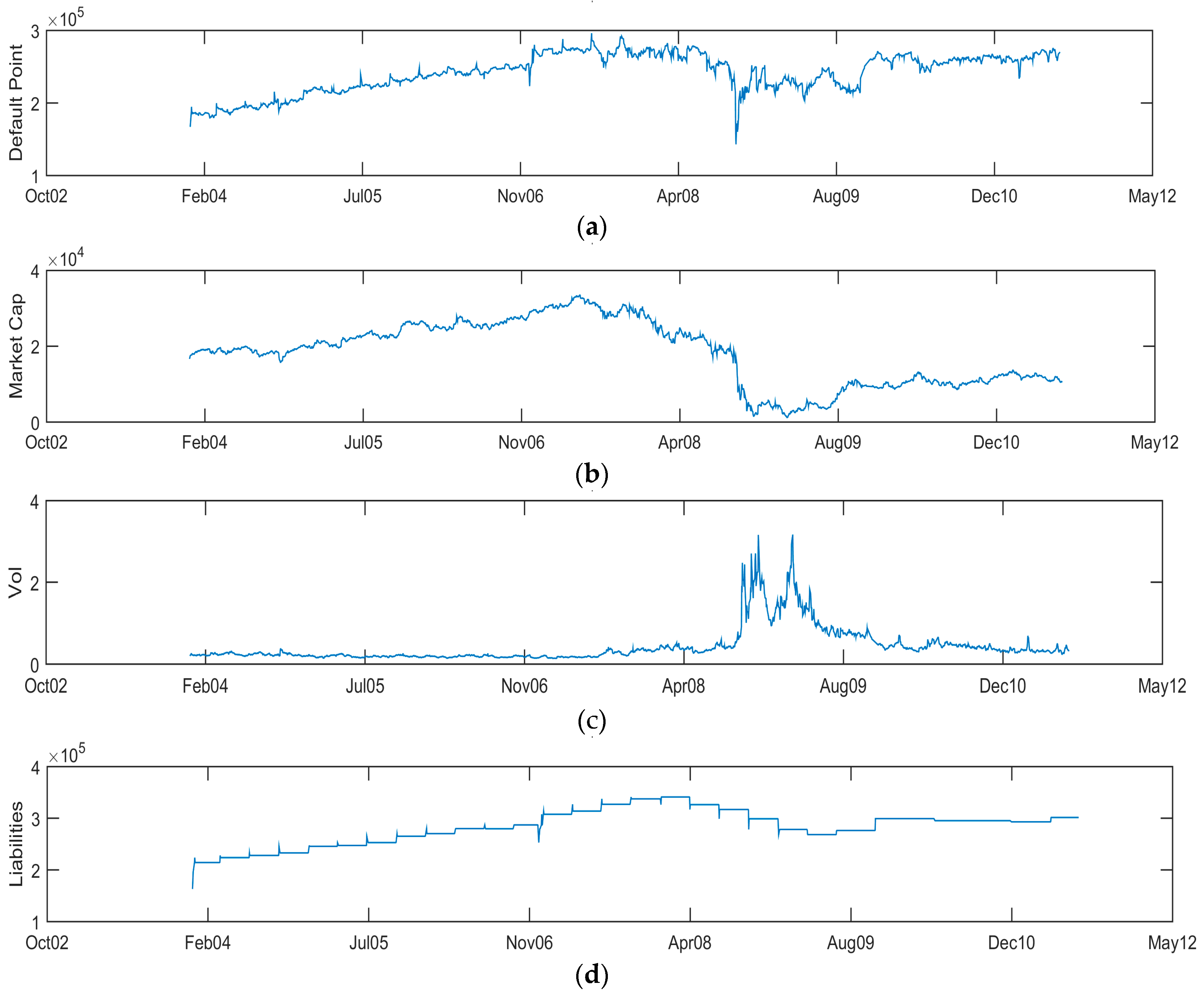
Figure 4, the default barrier for Hartford Financial Services is plotted. There is a sharp decrease in the default barrier corresponding to the Lehman default. The increasing leverage prior to 2008 and the post-Lehman equity sell-off coupled with the rise in implied volatility produce a substantial move in the default point. Again, the net non-linear effect is an increase in the default probability. Specifying the default barrier independently using historic data, such as in [
11], cannot produce this market responsiveness. This directly contributes to the ability to accurately model financial institutions. For completeness,
Figure 5 shows the default barrier for Hutchison Whampoa and Boeing Co.
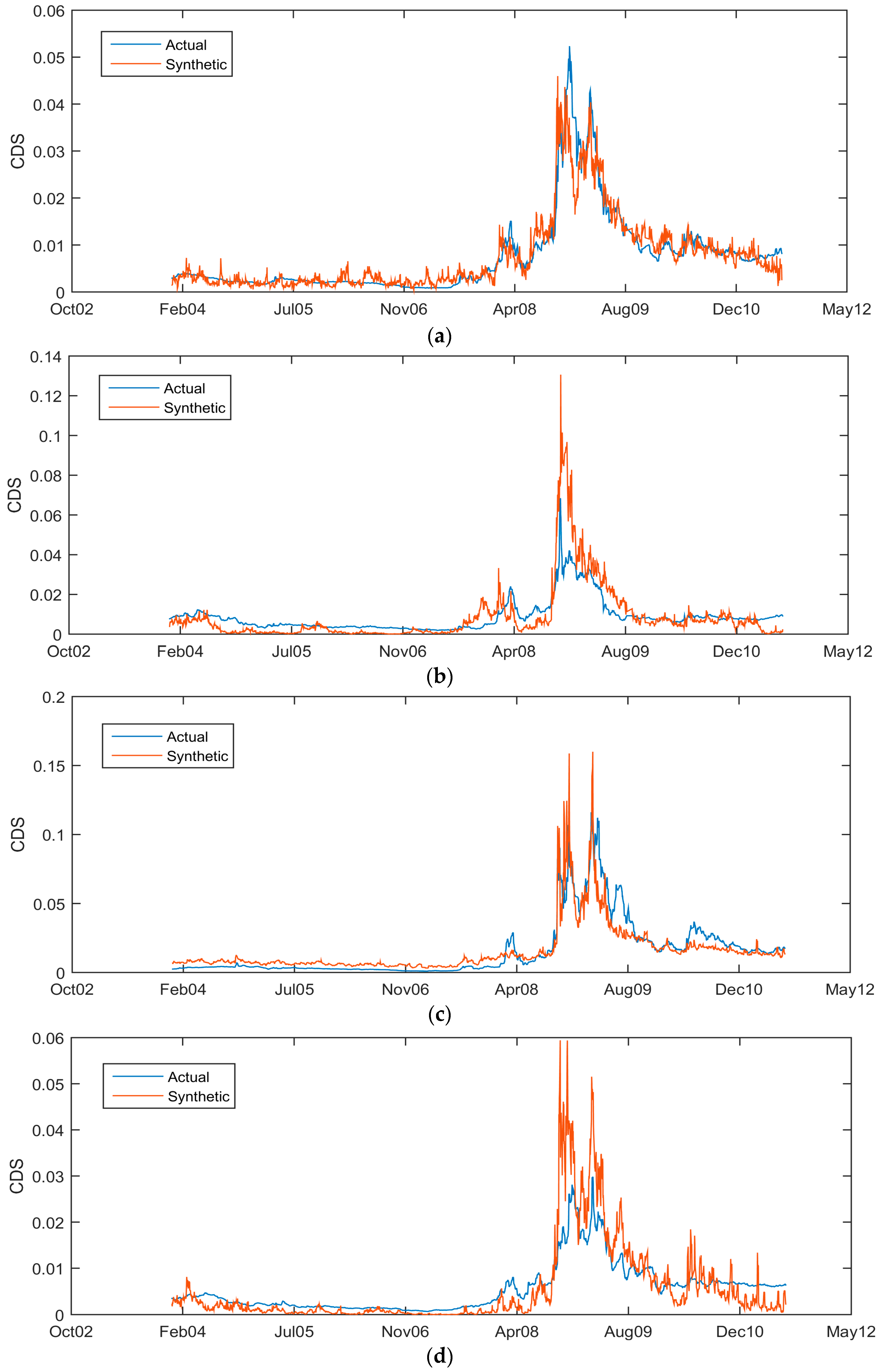
In
Figure 6, the synthetic CDS, calculated using (17) is plotted against the actual five-year, senior unsecured, CDS spread. For all four corporates, there is close agreement between the synthetic CDS and the traded contract; including the financial institution in
Figure 6c. Both the shape and the outright magnitudes of the spreads are comparable. This indicates that both the equity and debt markets are pricing efficiently. The close agreement between the Merton model and the traded CDS agrees with the findings of Stimcar and Finger [
10], as well as Huang and Luo [
7]. Both studies employed model variants of [
11].
From a capital structure perspective, the key is to look for divergence between the synthetic and traded CDS. There is evidence of this separation in
Figure 6c for Hartford Financial Services in mid-2009 and again in late 2010. The synthetic CDS led the traded CDS by tightening faster in both instances. Theoretically, as the least secured creditors, equity markets should react faster than debt investors, thereby creating the trading opportunities as shown. That is the case for Hartford Financial. However, post-Lehman, this is no longer the case. Rather than seeing the traded CDS converge to the synthetic CDS, the opposite can occur. Consequently, it is necessary to trade the capital structure completely to hedge this effect by either buying or selling volatility on the underlying stock against the CDS as required.
5. Capital Structure Arbitrage
All arbitrage studies to date [
2,
3,
4,
5,
6,
7,
8] have employed a strategy of trading the CDS against the underlying equity itself using a hedge ratio that is derived in closed form from the model. In effect, the authors use:
where S was defined in (2) and CDS is the synthetic CDS calculated using (18). As shown in
Figure 6, the synthetic CDS is not smooth. Both [
7,
10] show similar behavior. The implication is that the calculation of (20) will contain noise, and the hedge ratio will vary significantly, even alternating between positive and negative values. One answer is to adopt a dynamic hedging strategy to adjust the delta hedge, which Huang and Luo explore in [
7].
None of the authors of [
2,
3,
4,
5,
6,
7,
8] consider basing the trading strategy on the implied volatility. There is no justification for this approach apart from the fact that the delta hedge was derived in CreditGrades [
11], which is the predominant capital structure model used in studies. Furthermore, CreditGrades uses a 1000-day moving average historical volatility. Such a calibration will drastically reduce the responsiveness to the volatility as the daily updates to the asset volatility only have a small incremental effect. Hence, volatility hedging will not appear to be as relevant. Nevertheless, there has been some treatment of the relationship between CDS and equity option implied volatilities in the literature. Carr and Wu [
26] documented the co-movement of corporate CDS with implied volatilities and their skews. They also investigated the co-movement of sovereign CDS with currency option implied volatilities and skews [
27]. The difference is that the two were not linked through a structural model, but rather through a reduced form model that assumes that the equity (currency) price jumps to zero (or a sizable amount) upon the arrival of a default. In [
28], Carr and Wu also established a direct link between American deep out-of-the-money puts and credit protection. Similarly, Cremers, Driessen, Maenhout and Weinbaum [
29] documented the relationship between CDS and equity options. Cremers, Driessen and Maenhout [
30] did consider a structural model, and showed how option-implied jump risk premium can help to address the gap between theory and practice in terms of the outright CDS spread level.
As shown in
Table 3, there is no significant difference in the correlation between the CDS and the implied volatility, nor the CDS with the market capitalization. Hence, there is no empirical reason to favor one sensitivity over the other.
The question is whether there is any justification for using an alternative to (20).
Table 2 indicated that the asset volatility was the key variable, not the stock price. Hence, the theoretical differential in the sensitivities suggests that the implied volatility should be considered.
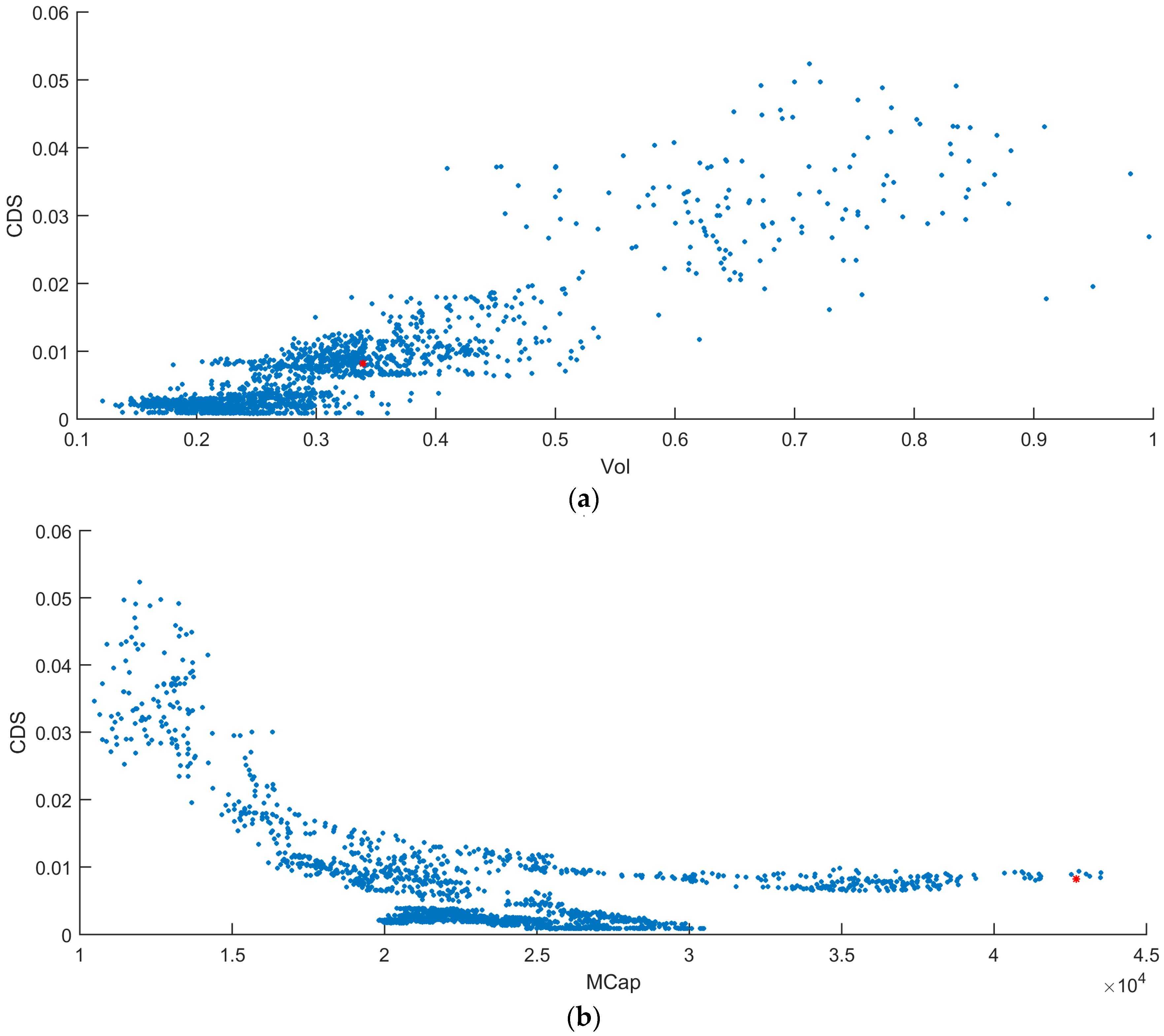
Returning to BMW, consider
Figure 7. Here, the five-year CDS is plotted against both the 10-delta implied equity volatility and against the market capitalization. The plots span the entire time series from 2004 to the end of 2011. What is immediately apparent is that movement in the implied volatility corresponds to movement in the CDS, whereas large moves in the market capitalization do not necessarily move the CDS. In fact, the BMW market capitalization drops from EUR45 billion (BN) to 15 BN without an appreciable move in the CDS. Large CDS moves only occur when the market capitalization drops below EUR15 BN. The difficulty of capturing stock moves against the CDS has also been reported in [
31,
32]. In effect, the realized movements in the market are reflecting the relative magnitudes of the delta and vega from
Table 2.
In
Table 4, empirical hedge ratios are calculated by regressing the CDS against the 10-delta put implied volatility and then against market capitalization for the entire cohort of 830 credits across the time series. Without fail, the CDS is significantly more sensitive to movements in the implied volatility than the market capitalization. In fact,
Table 4 contradicts the delta-hedging strategy. The basic delta-hedging strategy used in [
2,
3,
4,
5,
6,
7,
8] is to either sell protection on the CDS and short the stock or to buy protection on the CDS and buy the stock. If anything, the findings of
Table 4 contradict this approach. The delta-hedge in all cases is negative. Selling CDS protection and shorting the stock will, on average, always result in a loss on the equity leg.
Taking this a step further, the empirical delta is calculated per USD 1 million (MN) equivalent in market capitalization. What this implies is that for a delta-hedging strategy to be effective, hedges equaling a substantial part of the total market capitalization need to be held. For example, the delta hedge ratio for North America indicates that, on average, to hedge an 8-bp move in the CDS, USD 100 MN in equity needs to be held. In practice, such positions are impossible to execute in the market either from the sheer volume of shares required or the amount of capital needing to be held to execute it. Trading the volatility offers a more effective hedge where the trader can ‘get set’, and it also captures the main responsiveness seen in the market.
To reflect both the theoretical and empirical sensitivity, the main hedging tool to be used here is:
where
is the 10-delta implied put volatility and
CDS is the traded five-year contract. Furthermore, to reflect the noise inherent in the analytic calculation of (21), the hedge ratios will be calculated empirically. The model itself will only be used to signal arbitrage opportunities. To illustrate the debt-equity arbitrage, three case studies will be presented: Anadarko Petroleum Corporation (APC), Commonwealth Bank of Australia (CBA) and Peugeot SA (PEUGF), as representative examples of the approach.
5.1. Anadarko Petroleum
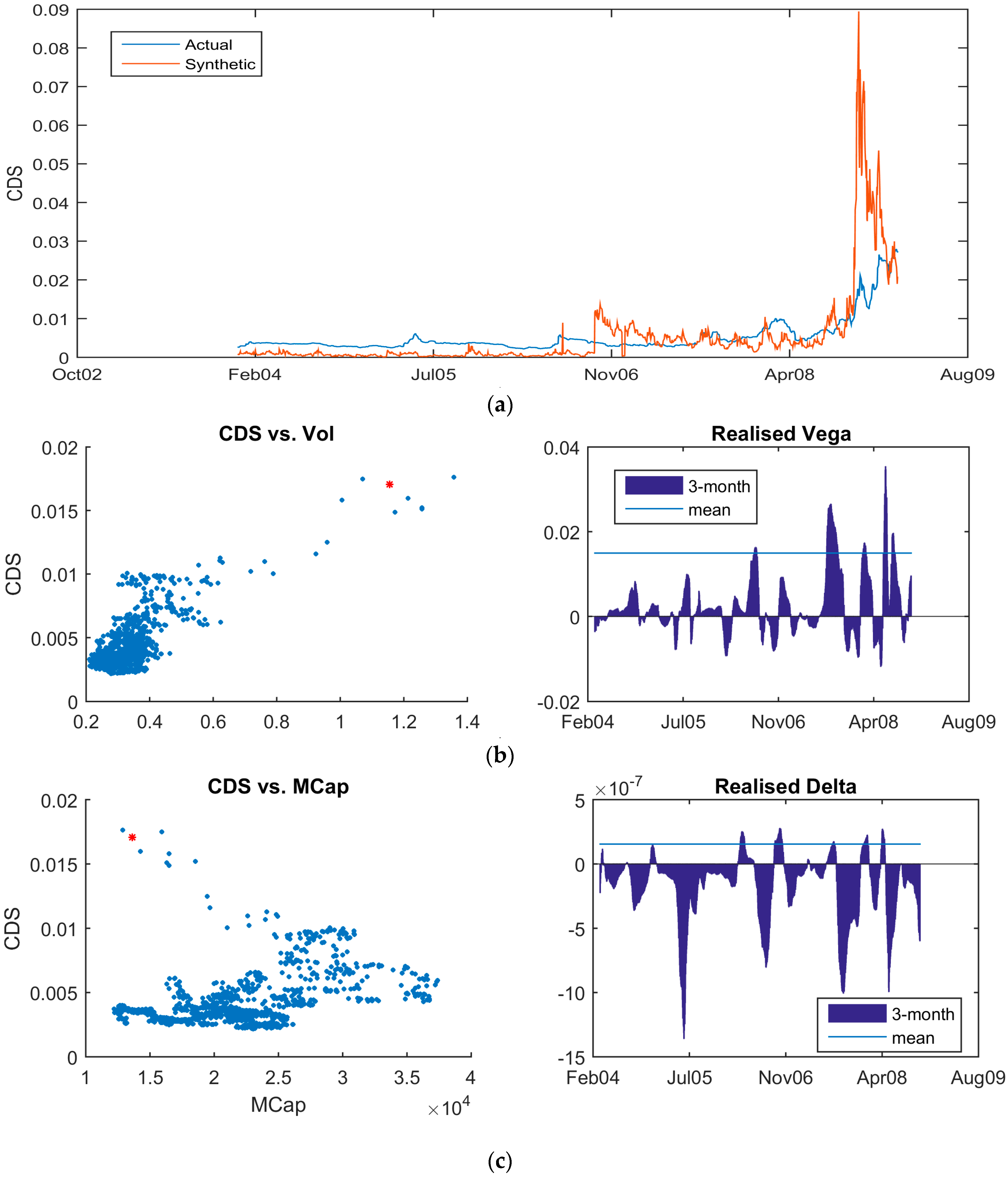
As shown in
Figure 8a, following the Lehman default, there was a capital structure misalignment for APC in October 2008. The synthetic CDS had widened substantially further than the traded five-year CDS. This indicates that the implied volatility is rich versus the CDS. Exploiting this requires selling puts on the equity itself versus buying protection on the CDS.
In
Figure 8b,c, the five-year traded CDS is plotted against the 10-delta implied equity put volatility and against the market capitalization. Equations (20) and (21) are then derived empirically by regressing the CDS against each variable. There are two calculations each for Equations (20) and (21). One is calculated on a 90-day rolling window. The other is across the entire dataset and is intended as the mean hedge ratio for executing trades. The rolling window is used for monitoring the stability of the hedge. The assumption is that the misalignment will return to the long-run mean, thereby making that the hedge of choice. However, the hedge efficiency will depend on the overall consistency of the relationship between the two market variables. If there is a substantial deviation between the mean hedge ratio and the current market, then the trade can be reassessed. As mentioned previously, there is no intention to theoretically derive the hedge ratio. Despite the close agreement between the synthetic and traded CDS, the synthetic CDS is not ‘smooth’. This will introduce non-trivial noise into any theoretical calculation. From
Figure 8b, the empirical hedge ratio for APC varies across the time series with an average ratio of:
where
vol = 1%. In the second half of 2008, both the rolling three-month numerical hedge and the long-term average are of comparable magnitude, thereby making (22) viable. Take a standard five-year CDS contract with a notional of USD10 million. Define the dollar value sensitivity of the trade to a 1 basis point (bp) move in the CDS curve as the DV01. Using the standard CDS model [
25], a quick calculation for APC shows that:
Multiplying (22) by (23) gives:
For late October 2008, seek liquid option contracts with the longest maturity profile. To satisfy this, choose the APC 25 January 2009 puts at 30.62. Note that the option is close to at-the-money. The choice of strike was dictated by liquid available maturities and strikes following the Lehman default. A quick calculation shows that:
where
is the dollar value of a single contract to a one-point volatility shift. Each contract contains 100 options, which produces the following hedge:
The full strategy is then:
The revenue from selling the puts is USD1,200,000. From
Figure 8a, the synthetic and traded five-year CDS had re-converged by mid-February 2009. In fact, the five-year CDS had widened from 152 bp to 239 bp. The APC 1 M ATM vol dropped from 120.25% to 60.75%. The equity price rallied from USD30 to USD40. Hence, the P&L equals:
Hence, a net profit of USD 1,550,000 results. This is an example where both legs converge and are profitable. In the next case study, the volatility position will provide a hedge against loss on the CDS leg.
5.2. Commonwealth Bank
Now, consider CBA. As shown
Figure 9a, the synthetic CDS and the traded five-year CDS were misaligned in March 2010. From
Figure 9b,
per USD10 MN contract notional. With a more stable post-Lehman market, seek to trade low delta options. Hence, take the 25-delta CBA 25 June 2010 puts at 53 where:
which leads to the arbitrage hedge:
and 0.935 is the foreign exchange spot rate for the AUD. The trading strategy, executed in mid-April, is then:
Following
Figure 9a, in May 2010, there was civil unrest in Greece. This led to a sell-off in risky assets. Hence, by the end of the first week of May 2010, the five-year CDS referencing CBA had widened to 118 bps. The CBA 25-delta volatility had increased from 16.5% to 31.3%, producing the following P&L:
CDS: USD200,000 loss.
Equity options: USD300,000 profit.
Net P&L: USD100,000 profit.
CBA is an important case study because it shows the effectiveness of the vega hedge. If the trader only sold protection on the CDS, then the spread widening in May 2010 would have resulted in a significant loss. Executing the volatility hedge offset that loss and resulted in a net profit from the convergence in the capital structure. Likewise, delta hedging would have been ineffectual. From March to May 2010, the underlying CBA share price only moved from AUD 55.6 in mid-march to 53 in the first week of May. As per [
2,
3,
4,
5,
6,
7,
8], selling CDS protection requires shorting the stock as the hedge. In that case, the loss would have only been minimally offset by the movement in the share price.
Figure 9c confirms the general low sensitivity of the CDS to the share price.
5.3. Peugeot SA
During 2010, arbitrage opportunities in the French auto-makers, Peugeot and Renault, developed due to rating downgrades from S&P and Moody’s. Both companies saw their ratings drop to sub-investment grade. This led the CDS market wider despite a relatively stable equity market. As shown in
Figure 10a, the synthetic CDS and the traded five-year CDS were misaligned for the second time in June 2010. Calculating the empirical hedge ratio gives:
per USD10 MN contract notional.
Figure 10b shows a strong agreement between the three-month and mean hedge ratios. With such a large delta, there is a need to cheapen the volatility hedge as much as possible. This is done by extending the maturity and decreasing the delta.
Consider the PEUGF 25 September Puts at 16; effectively a three-month 10-delta option. Hence:
which leads to the arbitrage hedge:
where 1.22 is the FX spot rate for the EUR.
The trading strategy, executed in early June, is then:
Sell USD10 MN protection on PEUGF at 344 bp.
Buy 12,000 contracts of PEUGF 25 September Puts at 16 with delta exchange.
Following
Figure 10a, both the actual traded five-year CDS and the synthetic CDS continued to tighten until converging in November 2010. The actual CDS tightened from 344 bps to 213 bps. The share price increased from 20.27 to 28.46. Likewise, volatility decreased by 10 points. Hence, the options expired worthless. The resulting P&L was then:
CDS: USD600,000 profit.
Equity options: EUR330,000 loss.
Net P&L: USD270,000 profit.
Here, the vega hedge was not required and expired worthless. That loss was offset by the gain in the CDS. However, the importance of hedging with a (relatively) inexpensive low-delta position was crucial to protecting against any volatility spike while keeping the overall cost of the volatility hedge low, so as not to erode the P&L from the CDS position. Note that the delta-hedging strategy of selling protection on the CDS and shorting the stock would have resulted in a loss on the equity leg. In fact, as shown in
Figure 10c, the relationship between the CDS and the equity is consistently negative.
6. Back Testing
The previous section outlined the basic capital structure arbitrage technique required to trade the five-year CDS against the equity implied volatility. Here, that process is automated to identify capital structure misalignments across the time series of all 830 applicable CDS from 2004 until the end of 2011. Define the L-2 distance function,
D, as:
The data from 2004 and 2005 are used to initially calibrate the model and to calculate the L-2 distance. Call this the historic differential. Similarly calculate the L-2 distance for the current trading month,
. That is then calculated from January 2006 onwards. Likewise,
D is updated to the preceding month. Define the signal strength as the ratio of the current differential divided by the historic differential,
Order the output firstly by the smallest L-2 distance to the largest, then by the magnitude of the signal strength. A high signal strength, coupled with a low L-2 distance, indicates that the synthetic CDS has deviated from the traded CDS based on the historical average. This is then an indicator of a capital structure misalignment. Given the relative positions of the synthetic and traded CDS, the arbitrage strategy is executed. Define a trade that buys CDS protection and sells volatility as “short” the credit (or “buying” protection on the CDS). Likewise, define a trade that sells CDS protection and buys volatility, as being “long” the credit (or “selling” protection on the CDS).
Positions matching the top 10 signals are traded with an equal CDS trade notional of USD10 million versus appropriate vega hedges determined from the empirical hedge ratio. All CDS positions were actively quoted in the market at the time of trading in a size of USD10 MN, including during the Lehman default. Trades were held until the synthetic CDS converged with the traded contract or a maximum holding period of six months was reached. If a position was closed out, a new trade was executed based on the strongest untraded signal given by (24). The daily P&L is shown in
Figure 11a. For the period from January 2006 to December 2011, we find:
Percentage of winning trades: 70%.
Percentage of losing trades: 30%.
Percentage of re-converging trades: 80%.
Maximum consecutive winners: 19.
Maximum consecutive losers: four.
Average trade length: three months.
Number of long trades: 139.
Number of short trades: 145.
Percentage of the universe traded: 12%.
Average annual return: USD14 MN.
Largest drawdown: USD1.2 MN.
An immediate observation is that only a small percentage of the available companies was actually traded. Recall that the arbitrage strategy seeks explicit misalignment in the capital structure as measured by the differential between the synthetic CDS and the actual five-year CDS; or L-2 distance. Moreover, the dislocation should be significant versus the historic differential. At any point in time, most corporates do not display any misalignment. Hence, the strategy is very selective. In general, profitable days outnumber the losses. Furthermore, the magnitude of the losses is smaller than the size of the profits. This is an indication of the effectiveness of the vega hedge. Actual market quotes, incorporating bid-offers, were used to calculate the P&L. Hence, accurate transaction costs are included in the calculations. Given that the strategy was driven by the implied volatility, in both the sensitivity of the model and the trading strategy, that can be seen in the resulting P&L. Before the Lehman default, outright levels of volatility in the market were low. This is reflected in the low P&L. The period of highest volatility, 2008 to 2009, yields the highest returns. Other periods are commensurate.
The strategy is market neutral. In
Figure 11b, trades are evenly split between buy and sell positions. The model tends to detect buy protection signals in a weakening market and sell protection opportunities when CDS spreads are tightening. The selection criteria favored credits with lower L-2 distances, i.e., corporates where the synthetic and traded CDS were historically tightly coupled. Consequently, the percentage of positions where the capital structure re-aligned was high. Only a small number of trades exceeded the six-month holding period.
7. Conclusions
All previous capital structure arbitrage studies have focused on trading the CDS against the underlying equity itself. The importance of the equity volatility in the arbitrage strategy has been largely ignored. Here, a deep out-of-the-money put volatility was used to calibrate the structural model. Then, by using a fully risk-neutral calibration, to derive the default barrier, very exact matches can be achieved between the synthetic CDS and the traded CDS contract. Misalignment between the synthetic and traded CDS will still occur when credit and equity markets diverge in opinion on the quality of an obligor; hence the arbitrage opportunities. By basing the trading strategy on the relationship between the implied volatility and the CDS, and deriving the hedge ratio empirically, an effective convergence strategy can be executed. The strategy required hedging the risk due to movement in the implied volatility, not the underlying stock.
Going forward, detecting the dislocations in the market remains challenging. The mechanism for signal generation used in this study was relatively straightforward and exploited the breakdown in the close agreement between the synthetic and traded CDS. That was adequate here, as only positions in the top 10 signals were held. Likewise, aspects such as timing the trades were not considered. For example, selling protection into a deteriorating credit may result in short-term losses as the CDS widens and the capital structure misalignment develops in the market. The equity options traded also contained significant gamma. The P&L may be enhanced by trading the movement in the underlying stock and adjusting the vega hedge. Weighting the trading towards credits with stronger signal strength is another possibility worth investigating. Improving the automation of the trading strategy itself also remains an area for obvious research.