Estimation of Effective Day Length at Any Light Intensity Using Solar Radiation Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. BSRN Data
2.2. Definition of Effective Day Length
2.3. Data Analysis
2.4. Model Validation
3. Results
3.1. Relationships between Monthly Average of Effective Day Length and Other Climatic Elements
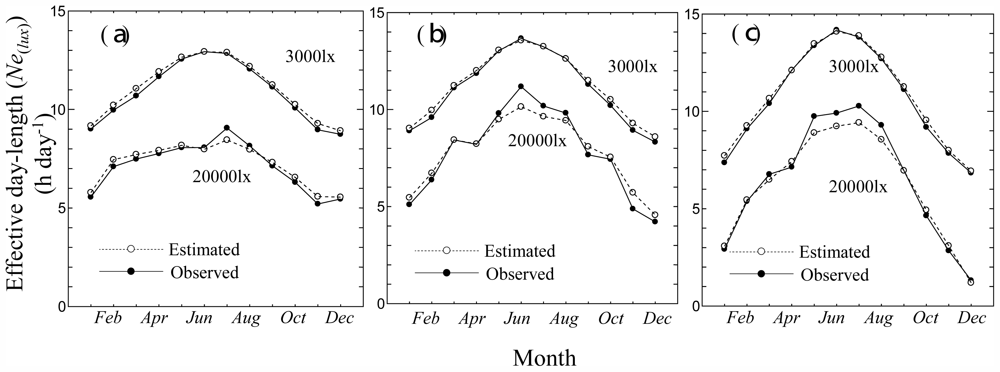
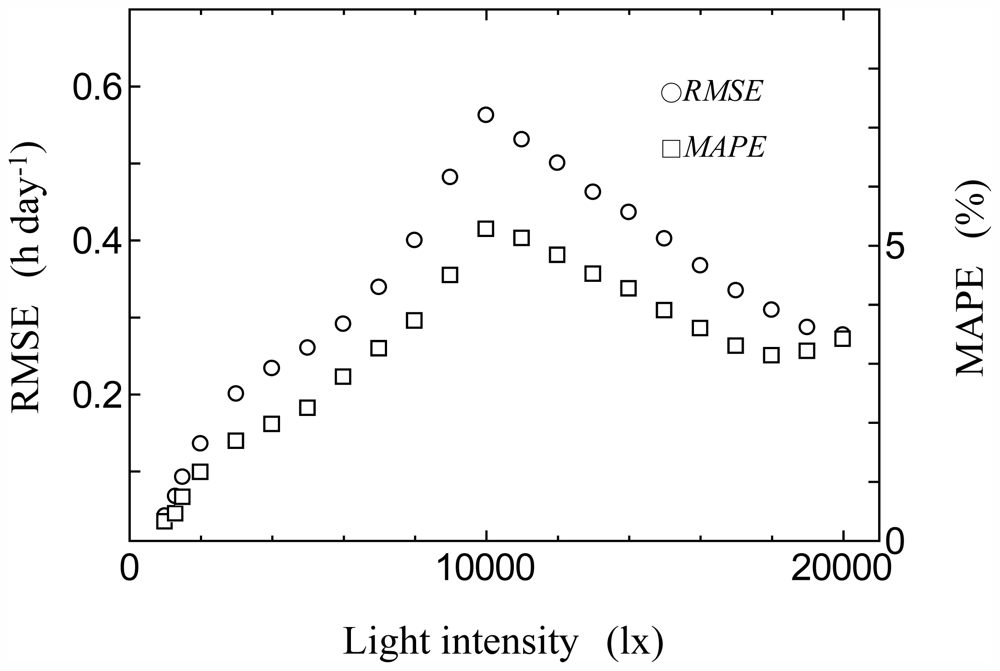
3.2. Consistency Check
4. Discussion
References and Notes
- Boivin, D.B.; Duffy, J.F.; Kronauer, R.E.; Czeisler, C.A. Dose-response relationships for resetting of human circadian clock by light. Nature 1996, 379, 540–542. [Google Scholar]
- Brainard, G.C.; Hanifin, J.P.; Greeson, J.M.; Byrne, B.; Glickman, G.; Gerner, E.; Rollag, M.D. Action spectrum for melatonin regulation in humans: Evidence for a novel circadian photoreceptor. J. Neurosci 2001, 21, 6405–6412. [Google Scholar]
- Gooley, J.J.; Rajaratnam, S.M.; Brainard, G.C.; Kronauer, R.E.; Czeisler, C.A.; Lockley, S.W. Spectral responses of the human circadian system depend on the irradiance and duration of exposure to light. Sci. Transl. Med 2010, 2, 31–33. [Google Scholar]
- Thapan, K.; Arendt, J.; Skene, D.J. An action spectrum for melatonin suppression: Evidence for a novel non-rod, non-cone photoreceptor system in humans. J. Physiol 2001, 535, 261–267. [Google Scholar]
- McClung, C.R. Plant circadian rhythms. Plant Cell 2006, 18, 792–803. [Google Scholar]
- Bray, M.S.; Young, M.E. Circadian rhythms in the development of obesity: Potential role for the circadian clock within the adipocyte. Obes. Rev 2007, 2, 169–181. [Google Scholar]
- Borisenkov, M.F.; Bazhenov, S.M. Seasonal patterns of breast tumor growth in Far North residents. Vopr. Onkol 2005, 51, 708–711. [Google Scholar]
- Oh, E.Y.; Ansell, C.; Nawaz, H.; Yang, C.H.; Wood, P.A.; Hrushesky, W.J. Global breast cancer seasonality. Breast Cancer Res. Treat 2010, 123, 233–243. [Google Scholar]
- Reiter, R.J.; Tan, D.X.; Erren, T.C.; Fuentes-Broto, L.; Paredes, S.D. Light-mediated perturbations of circadian timing and cancer risk: A mechanistic analysis. Integr. Cancer Ther 2009, 8, 354–360. [Google Scholar]
- Yang, X.; Wood, P.A.; Ansell, C.M.; Quiton, D.F.; Oh, E.Y.; Du-Quiton, J.; Hrushesky, W.J. The circadian clock gene Per1 suppresses cancer cell proliferation and tumor growth at specific times of day. Chronobiol. Int 2009, 7, 1323–1339. [Google Scholar]
- Kegel, M.; Dam, H.; Ali, F.; Bjerregaard, P. The prevalence of seasonal affective disorder (SAD) in Greenland is related to latitude. Nord. J. Psychiatry 2009, 63, 331–335. [Google Scholar]
- Monteleone, P.; Martiadis, V.; Maj, M. Circadian rhythms and treatment implications in depression. Prog. Neuropsychopharmacol. Biol. Psychiatry 2011, 35, 1569–1574. [Google Scholar]
- Magnusson, A.; Partonen, T. The diagnosis, symptomatology, and epidemiology of seasonal affective disorder. CNS Spectr 2005, 10, 625–634. [Google Scholar]
- World Radiation Monitoring Center, Baseline Surface Radiation Network (BSRN) Database Website. Available online: http://www.bsrn.awi.de/en/home/ accessed on 1 October 2011.
- Igawa, N.; Nakamura, H.; Goto, K.; Shimosaki, S. A method for the estimation of the solar illuminance based upon the solar irradiance. J. Arch. Environ. Eng 1999, 256, 17–24. [Google Scholar]
- Igawa, N. An examination of the luminous efficacy of daylight. 6th Lux Pacifica 2009, 1, 43–48. [Google Scholar]
- Darula, S.; Kittler, R.; Kambezidis, H.; Bartzokas, A. Guidelines for More Realistic Daylight Exterior Conditions in Energy Conscious Design. Computer Adaptation and Examples, SK-GR 013/1998; Institute of Construction and Archirecture (ICA), Slovak Academy of Sciences (SAS): Bratislava, Slovak Republic; National Observatory of Athens (NOA), Institute of Environmental Research and Sustainable Development: Athens, Greece, 2000. [Google Scholar]
- Vaulx-en-Velin Station Database Website. Available online: http://idmp.entpe.fr/vaulx/mesfr.htm accessed on 1 October 2011.
- R Foundation for Statistical Computing Website. Available online: http://www.r-project.org accessed on 1 October 2011.
- Sack, R.L.; Auckley, D.; Auger, R.R.; Carskadon, M.A.; Wright, K.P.; Vitiello, M.V.; Zhdanova, I.V. Circadian rhythm sleep disorders: Part I, basic principles, shift work and jet lag disorders. Sleep 2007, 30, 1460–1483. [Google Scholar]
- Cole, R.J.; Kripke, D.F.; Wisbey, J.; Mason, W.J.; Gruen, W.; Hauri, P.J.; Juarez, S. Seasonal variation in human illumination exposure at two different latitudes. J. Biol. Rhythms 1995, 10, 324–334. [Google Scholar]
- Hebert, M.; Dumont, M.; Paquet, J. Seasonal and diurnal patterns of human illumination under natural conditions. Chronobiol. Int 1998, 15, 59–70. [Google Scholar]
- Chegaar, M.; Lamri, A.; Chibani, A. Estimating global solar radiation using sunshine hours. Rev. Energ. Ren 1998, 1, 7–11. [Google Scholar]
- Paltineanu, Cr.; Mihailescu, I.F.; Torica, V.; Albu, A.N. Correlation between sunshine duration and global solar radiation in south-eastern Romania. Int. Agrophysics 2002, 16, 139–145. [Google Scholar]
- Yang, Q.; Tsukamoto, O. Estimation of daily solar radiation from sunshine duration in Ningxia region, China. Okayama Univ. Earth Sci. Rep 2009, 15, 79–86. [Google Scholar]





| Observation Points | Position | Number of Observed Months | |||||
|---|---|---|---|---|---|---|---|
| Lat. | Lon. | 2004 | 2005 | 2006 | 2007 | ||
| 1 | Alice Springs | −23.8 | 133.9 | 12 | 12 | 12 | 12 |
| 2 | Bondville | 40.1 | −88.4 | 12 | 12 | 12 | 12 |
| 3 | Boulder Surfrad | 40.1 | −105.2 | 12 | 12 | 11 | 12 |
| 4 | Carpentras | 44.1 | 5.1 | 12 | 12 | 11 | 12 |
| 5 | Cocos Island | − 12.2 | 96.8 | - | - | - | 11 |
| 6 | Darwin | −12.4 | 130.9 | 6 | 9 | 7 | 7 |
| 7 | Desert Rock | 36.6 | −116.0 | 12 | 12 | 12 | 12 |
| 8 | Fort Peck | 48.3 | −105.1 | 12 | 12 | 12 | 12 |
| 9 | Goodwin Creek | 34.3 | −89.9 | 10 | 12 | 12 | 12 |
| 10 | Lauder | −45.1 | 169.7 | 12 | 12 | 12 | 12 |
| 11 | Momote | −2.1 | 147.4 | - | 1 | 2 | 1 |
| 12 | Nauru Island | −0.5 | 166.9 | - | - | 3 | 3 |
| 13 | Rock Springs | 40.7 | −77.9 | 11 | 12 | 12 | 12 |
| 14 | Sede Boqer | 30.0 | 34.0 | 2 | 3 | 10 | 11 |
| 15 | Sioux Falls | 43.7 | −96.6 | 12 | 12 | 12 | 11 |
| 16 | São Martinho da Serra | − 29.4 | − 53.8 | - | - | - | 12 |
| 17 | Tamanrasset | 22.8 | 5.5 | 12 | 12 | 12 | 12 |
| 18 | Xianghe | 39.8 | 116.7 | - | 2 | 10 | 8 |
| Observation Points | Position | Observed Year | ||
|---|---|---|---|---|
| Lat. | Lon. | |||
| 1 | Tateno (Japan) | 36.1 | 14.3 | 2008 |
| 2 | Chesapeake Light (USA) | 36.9 | −75.7 | 2008 |
| 3 | Payerne (Switzerland) | 46.8 | 6.9 | 2008 |
| 4 | Vaulx-en-Velin (France) | 45.8 | 4.9 | 2008–2010 |
© 2011 by the authors; licensee MDPI, Basel, Switzerland This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yokoya, M.; Shimizu, H. Estimation of Effective Day Length at Any Light Intensity Using Solar Radiation Data. Int. J. Environ. Res. Public Health 2011, 8, 4272-4283. https://doi.org/10.3390/ijerph8114272
Yokoya M, Shimizu H. Estimation of Effective Day Length at Any Light Intensity Using Solar Radiation Data. International Journal of Environmental Research and Public Health. 2011; 8(11):4272-4283. https://doi.org/10.3390/ijerph8114272
Chicago/Turabian StyleYokoya, Masana, and Hideyasu Shimizu. 2011. "Estimation of Effective Day Length at Any Light Intensity Using Solar Radiation Data" International Journal of Environmental Research and Public Health 8, no. 11: 4272-4283. https://doi.org/10.3390/ijerph8114272




