Indirect Virus Transmission via Fomites Can Counteract Lock-Down Effectiveness
Abstract
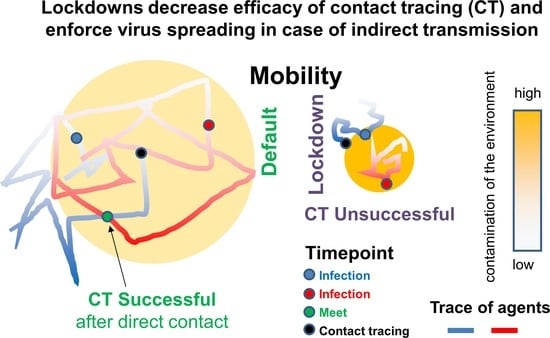
:Highlights
- Contact tracing (CT) alone can control epidemic spreading
- CT efficacy changes under mobility lockdowns (LDs)
- A small fraction of indirect transmission can impede disease control
- Detailed knowledge regarding transmission routes is crucial to determine efficient non-pharmaceutical intervention strategies
- Reduction of indirect transmission via fomites becomes particular important in the course of mobility LDs
Abstract
1. Introduction
2. Methods
| Parameter | Symbol | Value | Comment |
|---|---|---|---|
| duration of the exposed state | TE = 1/α | 2 days | [23], 2 days |
| incubation time | TN | 5 days | [25], 4.75 days |
| minimal time of infectious state | TI | 5 days | [26], TN − TE + 2 days |
| fraction of asymptotic cases | FA | 1/2, 2/3,…, 5/6 | serological studies, see text |
| agent return time | tret | 12 h | [22], 12 and 24 h |
| time step | Δt | 3.6 min | tret/200 |
| maximum step size: reference LD20 | rmax | 3.0 m 0.6 m | average distance from base position after tret: ~30 m ~6 m |
| contact/infection radius | rin | 4 m | set |
| rate of direct transmission rate of indirect transmission | βdi βin | 0.2/day 0.2/day | transmission rate close to βex (±10%, Figure S1) set |
| number of interaction points contamination rate per agent virus load half-life-time | M aL dL | 8450 100/tret 15 h | set set transmission rate close to βex (±10%) |
| recovery rate after TI | γ | 0.05/day | recovery rate ≈ γex (Figure S1) |
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brauner, J.M.; Mindermann, S.; Sharma, M.; Johnston, D.; Salvatier, J.; Gavenčiak, T.; Stephenson, A.B.; Chindelevitch, L.; Gal, Y.; Kulveit, J.; et al. Inferring the effectiveness of government interventions against COVID-19. Science 2021, 371, eabd9338. [Google Scholar] [CrossRef] [PubMed]
- Harvey, A.P.; Fuhrmeister, E.R.; Cantrell, M.E.; Pitol, A.K.; Swarthout, J.M.; Powers, J.E.; Nadimpalli, M.L.; Julian, T.R.; Pickering, A.J. Longitudinal Monitoring of SARS-CoV-2 RNA on High-Touch Surfaces in a Community Setting. Environ. Sci. Technol. Lett. 2021, 8, 168–175. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wu, J.; Smith, L.M.; Li, X.; Yancey, O.; Franzblau, A.; Dvonch, J.T.; Xi, C.; Neitzel, R.L. Monitoring SARS-CoV-2 in air and on surfaces and estimating infection risk in buildings and buses on a university campus. J. Expo. Sci. Environ. Epidemiol. 2022, 27, 751–758. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Rao, J.; Kang, Y.; Liang, Y.; Kruse, J.; Dopfer, D.; Sethi, A.K.; Mandujano Reyes, J.F.; Yandell, B.S.; Patz, J.A. Association of Mobile Phone Location Data Indications of Travel and Stay-at-Home Mandates With COVID-19 Infection Rates in the US. JAMA Netw. Open 2020, 3, e2020485. [Google Scholar] [CrossRef]
- Otter, J.A.; Donskey, C.; Yezli, S.; Douthwaite, S.; Goldenberg, S.D.; Weber, D.J. Transmission of SARS and MERS coronaviruses and influenza virus in healthcare settings: The possible role of dry surface contamination. J. Hosp. Infect. 2016, 92, 235–250. [Google Scholar] [CrossRef] [Green Version]
- Marquès, M.; Domingo, J.L. Contamination of inert surfaces by SARS-CoV-2: Persistence, stability and infectivity. A review. Environ. Res. 2021, 193, 110559. [Google Scholar] [CrossRef]
- Bueckert, M.; Gupta, R.; Gupta, A.; Garg, M.; Mazumder, A. Infectivity of SARS-CoV-2 and Other Coronaviruses on Dry Surfaces: Potential for Indirect Transmission. Materials 2020, 13, 5211. [Google Scholar] [CrossRef]
- Kasloff, S.B.; Leung, A.; Strong, J.E.; Funk, D.; Cutts, T. Stability of SARS-CoV-2 on critical personal protective equipment. Sci. Rep. 2021, 11, 984. [Google Scholar] [CrossRef]
- Ratnesar-Shumate, S.; Williams, G.; Green, B.; Krause, M.; Holland, B.; Wood, S.; Bohannon, J.; Boydston, J.; Freeburger, D.; Hooper, I.; et al. Simulated Sunlight Rapidly Inactivates SARS-CoV-2 on Surfaces. J. Infect. Dis. 2020, 222, 214–222. [Google Scholar] [CrossRef]
- Xie, C.; Zhao, H.; Li, K.; Zhang, Z.; Lu, X.; Peng, H.; Wang, D.; Chen, J.; Zhang, X.; Wu, D.; et al. The evidence of indirect transmission of SARS-CoV-2 reported in Guangzhou, China. BMC Public Health 2020, 20, 1202. [Google Scholar] [CrossRef]
- Meiksin, A. Dynamics of COVID-19 transmission including indirect transmission mechanisms: A mathematical analysis. Epidemiol. Infect. 2020, 148, e257. [Google Scholar] [CrossRef] [PubMed]
- Bilinski, A.; Mostashari, F.; Salomon, J.A. Modeling CT Strategies for COVID-19 in the Context of Relaxed Physical Distancing Measures. JAMA Netw. Open 2020, 3, e2019217. [Google Scholar] [CrossRef]
- Peak, C.M.; Kahn, R.; Grad, Y.H.; Childs, L.M.; Li, R.; Lipsitch, M.; Buckee, C.O. Individual quarantine versus active monitoring of contacts for the mitigation of COVID-19: A modelling study. Lancet Infect. Dis. 2020, 20, 1025–1033. [Google Scholar] [CrossRef]
- Hellewell, J.; Abbott, S.; Gimma, A.; Bosse, N.I.; Jarvis, C.I.; Russell, T.W.; Munday, J.D.; Kucharski, A.J.; Edmunds, W.J.; Centre for the Mathematical Modelling of Infectious Diseases COVID-19 Working Group; et al. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Glob. Health 2020, 8, e488–e496. [Google Scholar] [CrossRef] [Green Version]
- Ullah, S.; Khan, M.A. Modeling the impact of non-pharmaceutical interventions on the dynamics of novel coronavirus with optimal control analysis with a case study. Chaos Solitons Fractals 2020, 139, 110075. [Google Scholar] [CrossRef] [PubMed]
- Almagor, J.; Picascia, S. Exploring the effectiveness of a COVID-19 CT app using an agent-based model. Sci. Rep. 2020, 10, 22235. [Google Scholar] [CrossRef] [PubMed]
- Aleta, A.; Martín-Corral, D.; YPiontti, A.P.; Ajelli, M.; Litvinova, M.; Chinazzi, M.; Dean, N.E.; Halloran, M.E.; Longini, I.M., Jr.; Merler, S.; et al. Modelling the impact of testing, CT and household quarantine on second waves of COVID-19. Nat. Hum. Behav. 2020, 4, 964–971. [Google Scholar] [CrossRef]
- Wesley, C.L.; Allen, L.J.S.; Langlais, M. Models for the spread and persistence of hantavirus infection in rodents with direct and indirect transmission. Math. Biosci. Eng. 2010, 7, 195–211. [Google Scholar]
- Ganguly, N.; Krueger, T.; Mukherjee, A.; Saha, S. Epidemic spreading through direct and indirect interactions. Phys. Rev. E Stat. Nonlin. Soft Matter. Phys. 2014, 90, 032808. [Google Scholar] [CrossRef]
- Loeffler-Wirth, H.; Schmidt, M.; Binder, H. COVID-19 Transmission Trajectories-Monitoring the Pandemic in the Worldwide Context. Viruses 2020, 12, 777. [Google Scholar] [CrossRef]
- Taghizadeh, L.; Karimi, A.; Heitzinger, C. Uncertainty quantification in epidemiological models for the COVID-19 pandemic. Comput. Biol. Med. 2020, 125, 104011. [Google Scholar] [CrossRef] [PubMed]
- González, M.C.; Hidalgo, C.A.; Barabási, A.L. Understanding individual human mobility patterns. Nature 2008, 453, 779–782. [Google Scholar] [CrossRef] [PubMed]
- Byrne, A.W.; McEvoy, D.; Collins, A.B.; Hunt, K.; Casey, M.; Barber, A.; Butler, F.; Griffin, J.; Lane, E.A.; McAloon, C.; et al. Inferred duration of infectious period of SARS-CoV-2: Rapid scoping review and analysis of available evidence for asymptomatic and symptomatic COVID-19 cases. BMJ Open 2020, 10, e039856. [Google Scholar] [CrossRef] [PubMed]
- Elias, C.; Sekri, A.; Leblanc, P.; Cucherat, M.; Vanhems, P. The incubation period of COVID-19: A meta-analysis. Int. J. Infect. Dis. 2021, 104, 708–710. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Pahlavan, A.A.; Mendez, S.; Abkarian, M.; Stone, H.A. Towards improved social distancing guidelines: Space and time dependence of virus transmission from speech-driven aerosol transport between two individuals. Phys. Rev. Fluids 2020, 5, 122501. [Google Scholar] [CrossRef]
- Beigel, J.H.; Tomashek, K.M.; Dodd, L.E.; Mehta, A.K.; Zingman, B.S.; Kalil, A.C.; Osinusi, A.; Nayak, S.; Lane, H.C.; ACTT-1 Study Group Members; et al. Remdesivir for the Treatment of COVID-19—Final Report. N. Engl. J. Med. 2020, 383, 1813–1826. [Google Scholar] [CrossRef]
- Santos-Hövener, C.; Neuhauser, H.K.; Rosario, A.S.; Busch, M.; Schlaud, M.; Hoffmann, R.; Gößwald, A.; Koschollek, C.; Hoebel, J.; Allen, J.; et al. Serology- and PCR-based cumulative incidence of SARS-CoV-2 infection in adults in a successfully contained early hotspot (CoMoLo study), Germany, May to June 2020. Euro Surveill 2020, 25, 2001752. [Google Scholar] [CrossRef]
- Streeck, H.; Schulte, B.; Kümmerer, B.M.; Richter, E.; Höller, T.; Fuhrmann, C.; Bartok, E.; Dolscheid-Pommerich, R.; Berger, M.; Wessendorf, L.; et al. Infection fatality rate of SARS-CoV2 in a super-spreading event in Germany. Nat. Commun. 2020, 11, 5829. [Google Scholar] [CrossRef]
- Böhning, D.; Rocchetti, I.; Maruotti, A.; Holling, H. Estimating the undetected infections in the COVID-19 outbreak by harnessing capture-recapture methods. Int. J. Infect. Dis. 2020, 97, 197–201. [Google Scholar] [CrossRef]
- Li, Y.; Yao, L.; Li, J.; Chen, L.; Song, Y.; Cai, Z.; Yang, C. Stability issues of RT-PCR testing of SARS-CoV-2 for hospitalized patients clinically diagnosed with COVID-19. J. Med. Virol. 2020, 92, 903–908. [Google Scholar] [CrossRef] [Green Version]
- Afzal, A. Molecular diagnostic technologies for COVID-19: Limitations and challenges. J. Adv. Res. 2020, 26, 149–159. [Google Scholar] [CrossRef] [PubMed]
- Kortela, E.; Kirjavainen, V.; Ahava, M.J.; Jokiranta, S.T.; But, A.; Lindahl, A.; Jääskeläinen, A.E.; Jääskeläinen, A.J.; Järvinen, A.; Jokela, P.; et al. Real-life clinical sensitivity of SARS-CoV-2 RT-PCR test in symptomatic patients. PLoS ONE 2021, 16, e0251661. [Google Scholar] [CrossRef] [PubMed]
- Feng, Z. Final and peak epidemic sizes for SEIR models with quarantine and isolation. Math. Biosci. Eng. 2007, 4, 675–686. [Google Scholar] [PubMed]
- Oraby, T.; Tyshenko, M.G.; Maldonado, J.C.; Vatcheva, K.; Elsaadany, S.; Alali, W.Q.; Longenecker, J.C.; Al-Zoughool, M. Modeling the effect of lockdown timing as a COVID-19 control measure in countries with differing social contacts. Sci. Rep. 2021, 11, 3354. [Google Scholar] [CrossRef]
- Zhang, J.; Litvinova, M.; Liang, Y.; Zheng, W.; Shi, H.; Vespignani, A.; Viboud, C.; Ajelli, M.; Yu, H. The impact of relaxing interventions on human contact patterns and SARS-CoV-2 transmission in China. Sci. Adv. 2021, 7, eabe2584. [Google Scholar] [CrossRef]
- Saracci, R. Prevention in COVID-19 time: From failure to future. J. Epidemiol. Community Health 2020, 74, 689–691. [Google Scholar]
- Sommerstein, R.; Fux, C.A.; Vuichard-Gysin, D.; Abbas, M.; Marschall, J.; Balmelli, C.; Troillet, N.; Harbarth, S.; Schlegel, M.; Widmer, A.; et al. Risk of SARS-CoV-2 transmission by aerosols, the rational use of masks, and protection of healthcare workers from COVID-19. Antimicrob. Resist Infect. Control 2020, 9, 100. [Google Scholar] [CrossRef]
- Goldberg, Y.; Mandel, M.; Bar-On, Y.M.; Bodenheimer, O.; Freedman, L.; Haas, E.J.; Milo, R.; Alroy-Preis, S.; Ash, N.; Huppert, A. Waning Immunity after the BNT162b2 Vaccine in Israel. N. Engl. J. Med. 2021, 385, e85. [Google Scholar] [CrossRef]
- Atifa, A.; Khan, M.A.; Iskakova, K.; Al-Duais, F.S.; Ahmad, I. Mathematical modeling and analysis of the SARS-CoV-2 disease with reinfection. Comput. Biol. Chem. 2022, 98, 107678. [Google Scholar] [CrossRef]
- Gavish, N.; Yaari, R.; Huppert, A.; Katriel, G. Population-level implications of the Israeli booster campaign to curtail COVID-19 resurgence. Sci. Transl. Med. 2022, 14, eabn9836. [Google Scholar] [CrossRef]
- Kasper, M.R.; Geibe, J.R.; Sears, C.L.; Riegodedios, A.J.; Luse, T.; Von Thun, A.M.; McGinnis, M.B.; Olson, N.; Houskamp, D.; Fenequito, R.; et al. An Outbreak of COVID-19 on an Aircraft Carrier. N. Engl. J. Med. 2020, 383, 2417–2426. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.P.; Wong, Z.S.; Wang, L.; Thanh, T.T.; Van Nguyen, H.; Gilmour, S. Rapid impact assessments of COVID-19 control measures against the Delta variant and short-term projections of new confirmed cases in Vietnam. J. Glob. Health 2021, 11, 03118. [Google Scholar] [CrossRef] [PubMed]
- Wan, B.; Zhang, X.; Luo, D.; Zhang, T.; Chen, X.; Yao, Y.; Zhao, X.; Lei, L.; Liu, C.; Zhao, W.; et al. On-site analysis of COVID-19 on the surfaces in wards. Sci Total Environ. 2021, 753, 141758. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Tian, H.; Zhang, L.; Zhang, M.; Guo, D.; Wu, W.; Zhang, X.; Kan, G.L.; Jia, L.; Huo, D.; et al. Reduction of secondary transmission of SARS-CoV-2 in households by face mask use, disinfection and social distancing: A cohort study in Beijing, China. BMJ Glob. Health 2020, 5, e002794. [Google Scholar] [CrossRef]
- Lewis, D. COVID-19 rarely spreads through surfaces. So why are we still deep cleaning? Nature 2021, 590, 26–28. [Google Scholar] [CrossRef]
- Pastorino, B.; Touret, F.; Gilles, M.; de Lamballerie, X.; Charrel, R.N. Prolonged Infectivity of SARS-CoV-2 in Fomites. Emerg. Infect. Dis. 2020, 26, 2256–2257. [Google Scholar] [CrossRef]
- Beamer, P.I.; Plotkin, K.R.; Gerba, C.P.; Sifuentes, L.Y.; Koenig, D.W.; Reynolds, K.A. Modeling of human viruses on hands and risk of infection in an office workplace using micro-activity data. J. Occup. Environ. Hyg. 2015, 12, 266–275. [Google Scholar] [CrossRef]
- Teslya, A.; Pham, T.M.; Godijk, N.G.; Kretzschmar, M.E.; Bootsma, M.C.J.; Rozhnova, G. Impact of self-imposed prevention measures and short-term government-imposed social distancing on mitigating and delaying a COVID-19 epidemic: A modelling study. PLoS Med. 2020, 17, e1003166. [Google Scholar] [CrossRef]
- Le Bert, N.; Tan, A.T.; Kunasegaran, K.; Tham, C.Y.L.; Hafezi, M.; Chia, A.; Chng, M.H.Y.; Lin, M.; Tan, N.; Linster, M.; et al. SARS-CoV-2-specific T cell immunity in cases of COVID-19 and SARS, and uninfected controls. Nature 2020, 584, 457–462. [Google Scholar] [CrossRef]
- Grifoni, A.; Weiskopf, D.; Ramirez, S.I.; Mateus, J.; Dan, J.M.; Moderbacher, C.R.; Rawlings, S.A.; Sutherland, A.; Premkumar, L.; Jadi, R.S.; et al. Targets of T Cell Responses to SARS-CoV-2 Coronavirus in Humans with COVID-19 Disease and Unexposed Individuals. Cell 2020, 181, 1489–1501. [Google Scholar] [CrossRef]
- Tartof, S.Y.; Slezak, J.M.; Fischer, H.; Hong, V.; Ackerson, B.K.; Ranasinghe, O.N.; Frankland, T.B.; Ogun, O.A.; Zamparo, J.M.; Gray, S.; et al. Effectiveness of mRNA BNT162b2 COVID-19 vaccine up to 6 months in a large integrated health system in the USA: A retrospective cohort study. Lancet 2021, 398, 1407–1416. [Google Scholar] [CrossRef]
- Long, Q.X.; Tang, X.J.; Shi, Q.L.; Li, Q.; Deng, H.J.; Yuan, J.; Hu, J.L.; Xu, W.; Zhang, Y.; Lv, F.J.; et al. Clinical and immunological assessment of asymptomatic SARS-CoV-2 infections. Nat. Med. 2020, 26, 1200–1204. [Google Scholar] [CrossRef] [PubMed]
- Kissler, S.M.; Fauver, J.R.; Mack, C.; Tai, C.G.; Breban, M.I.; Watkins, A.E.; Samant, R.M.; Anderson, D.J.; Metti, J.; Khullar, G.; et al. Viral Dynamics of SARS-CoV-2 Variants in Vaccinated and Unvaccinated Persons. N. Engl. J. Med. 2021, 385, 2489–2491. [Google Scholar] [CrossRef] [PubMed]
- Rippinger, C.; Bicher, M.; Urach, C. Evaluation of undetected cases during the COVID-19 epidemic in Austria. BMC Infect. Dis. 2021, 21, 70. [Google Scholar] [CrossRef] [PubMed]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thalheim, T.; Krüger, T.; Galle, J. Indirect Virus Transmission via Fomites Can Counteract Lock-Down Effectiveness. Int. J. Environ. Res. Public Health 2022, 19, 14011. https://doi.org/10.3390/ijerph192114011
Thalheim T, Krüger T, Galle J. Indirect Virus Transmission via Fomites Can Counteract Lock-Down Effectiveness. International Journal of Environmental Research and Public Health. 2022; 19(21):14011. https://doi.org/10.3390/ijerph192114011
Chicago/Turabian StyleThalheim, Torsten, Tyll Krüger, and Jörg Galle. 2022. "Indirect Virus Transmission via Fomites Can Counteract Lock-Down Effectiveness" International Journal of Environmental Research and Public Health 19, no. 21: 14011. https://doi.org/10.3390/ijerph192114011