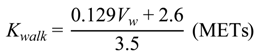Gait Recognition and Walking Exercise Intensity Estimation
Abstract
:1. Introduction
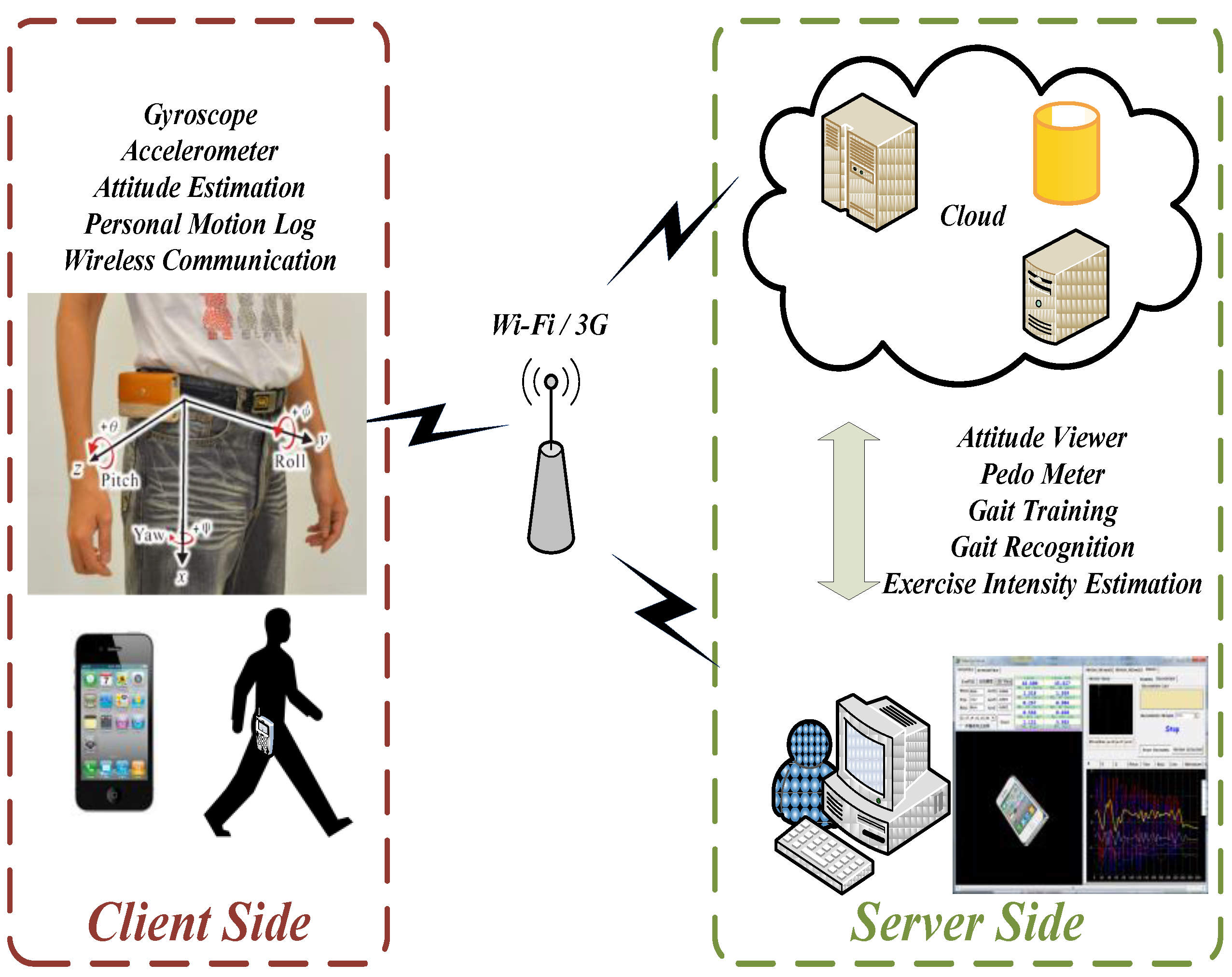
2. System Architecture and Design


3. Methodology and Principles of Analysis
3.1.Attitude Recognition
3.1.1. Attitude Representation
3.1.2. Introduction to the αβ Filter

3.2. Gait Training and Recognition
3.2.1. Preprocessing the Gait Vector
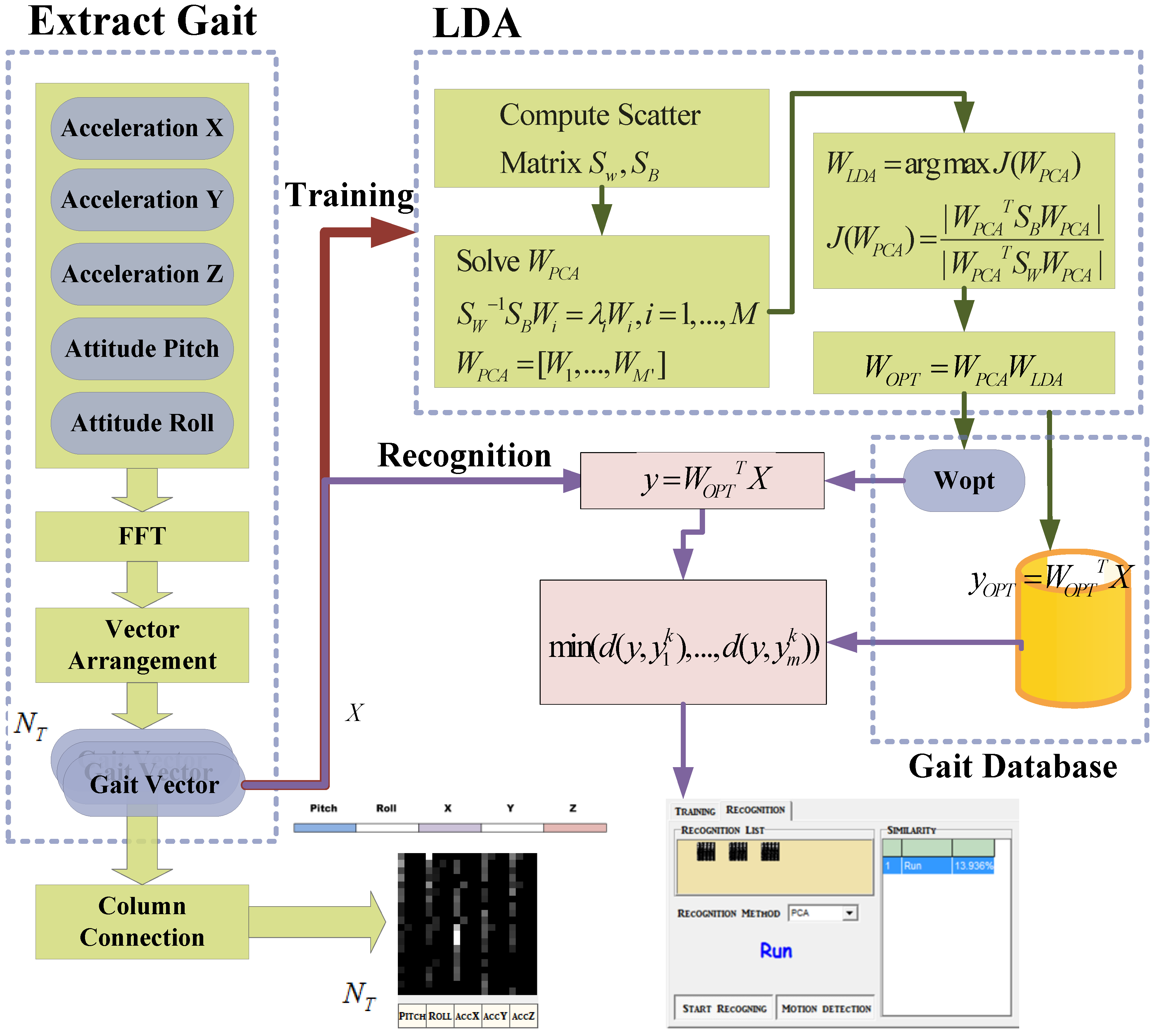
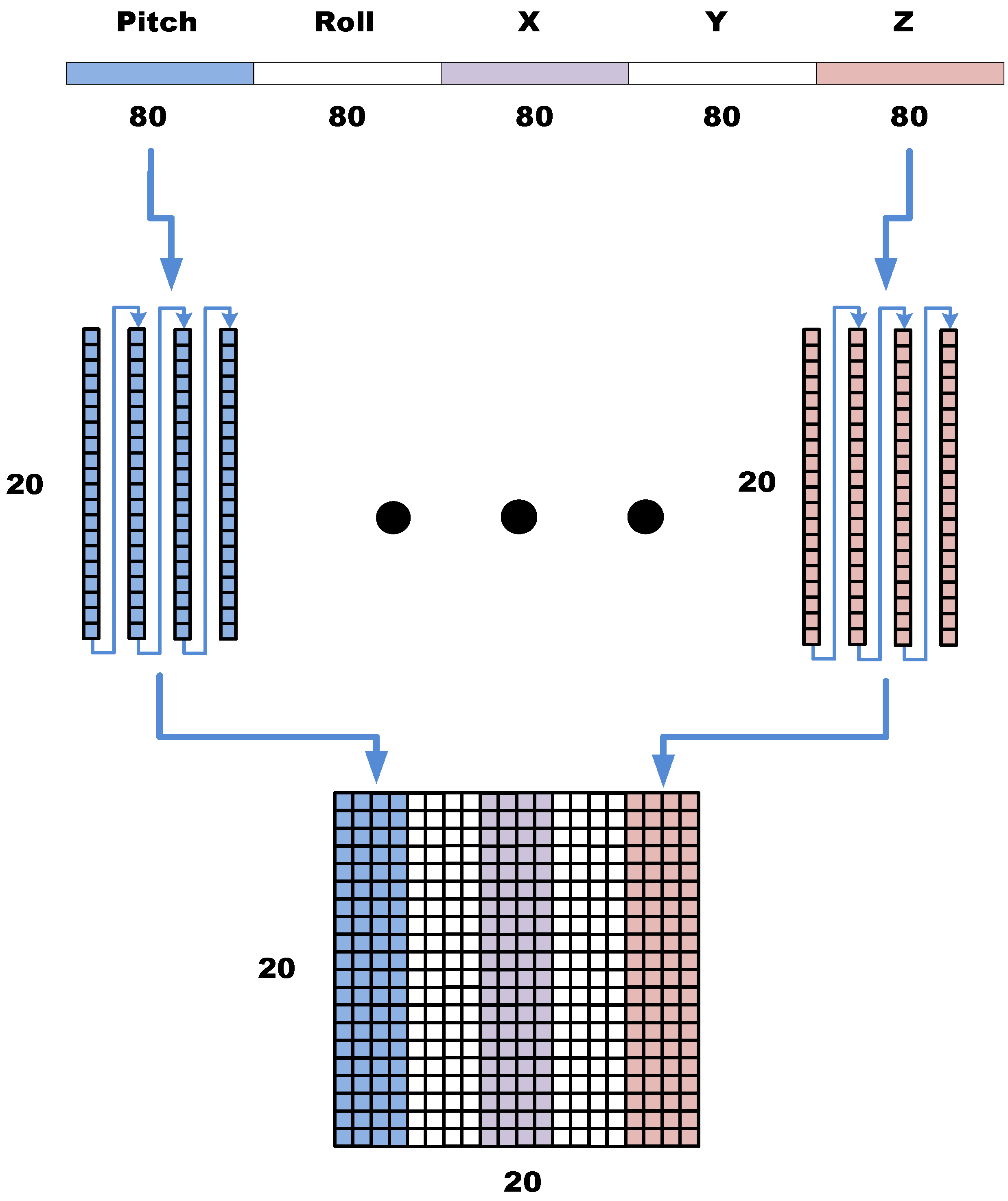

3.2.2. Decision Methods Used for Gait Recognition
3.3. Number of Steps and Period of Strides
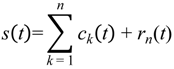
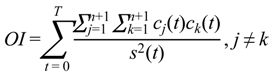
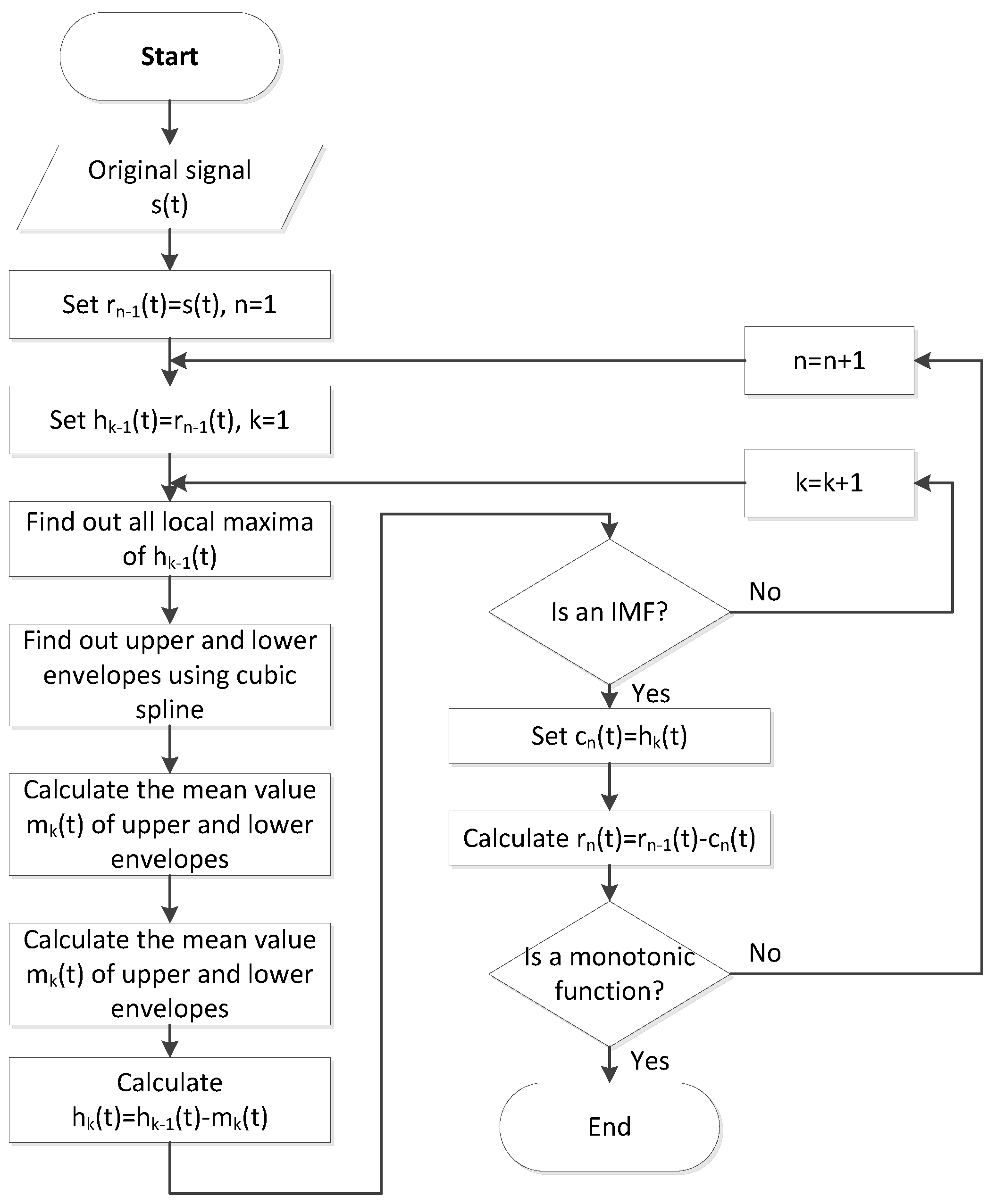
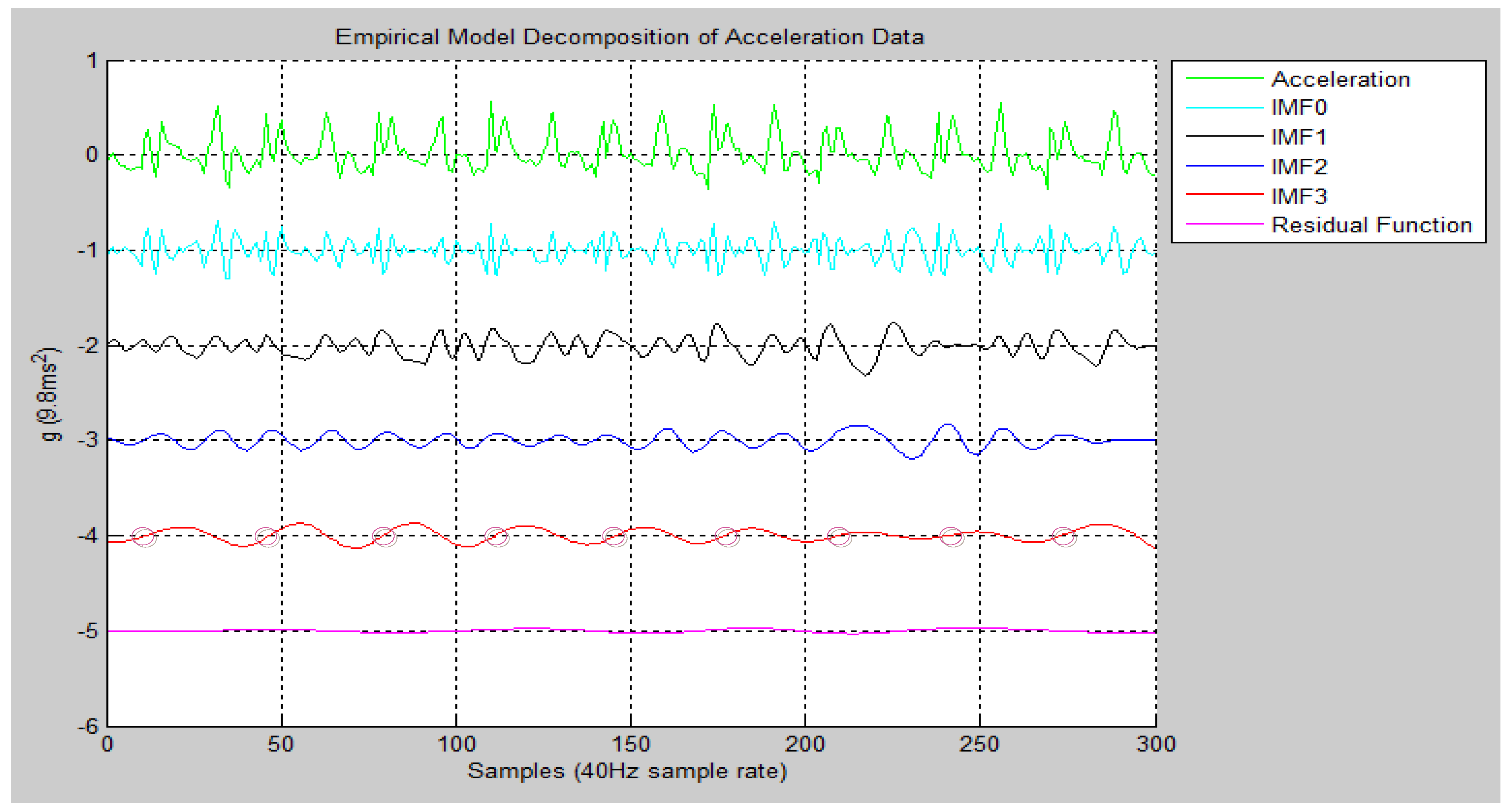
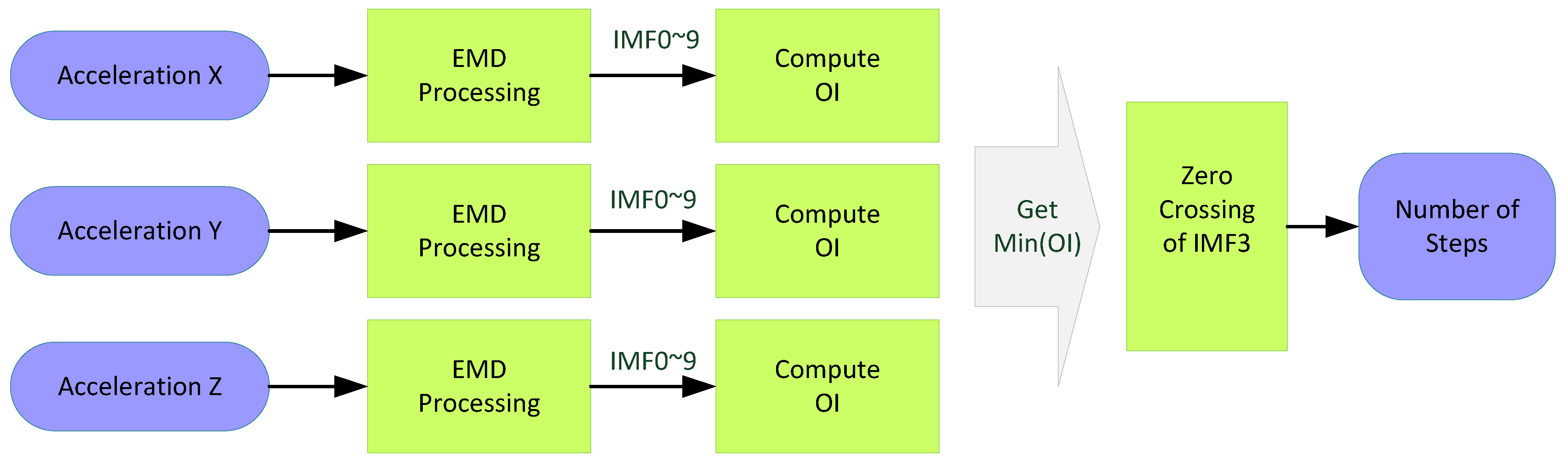
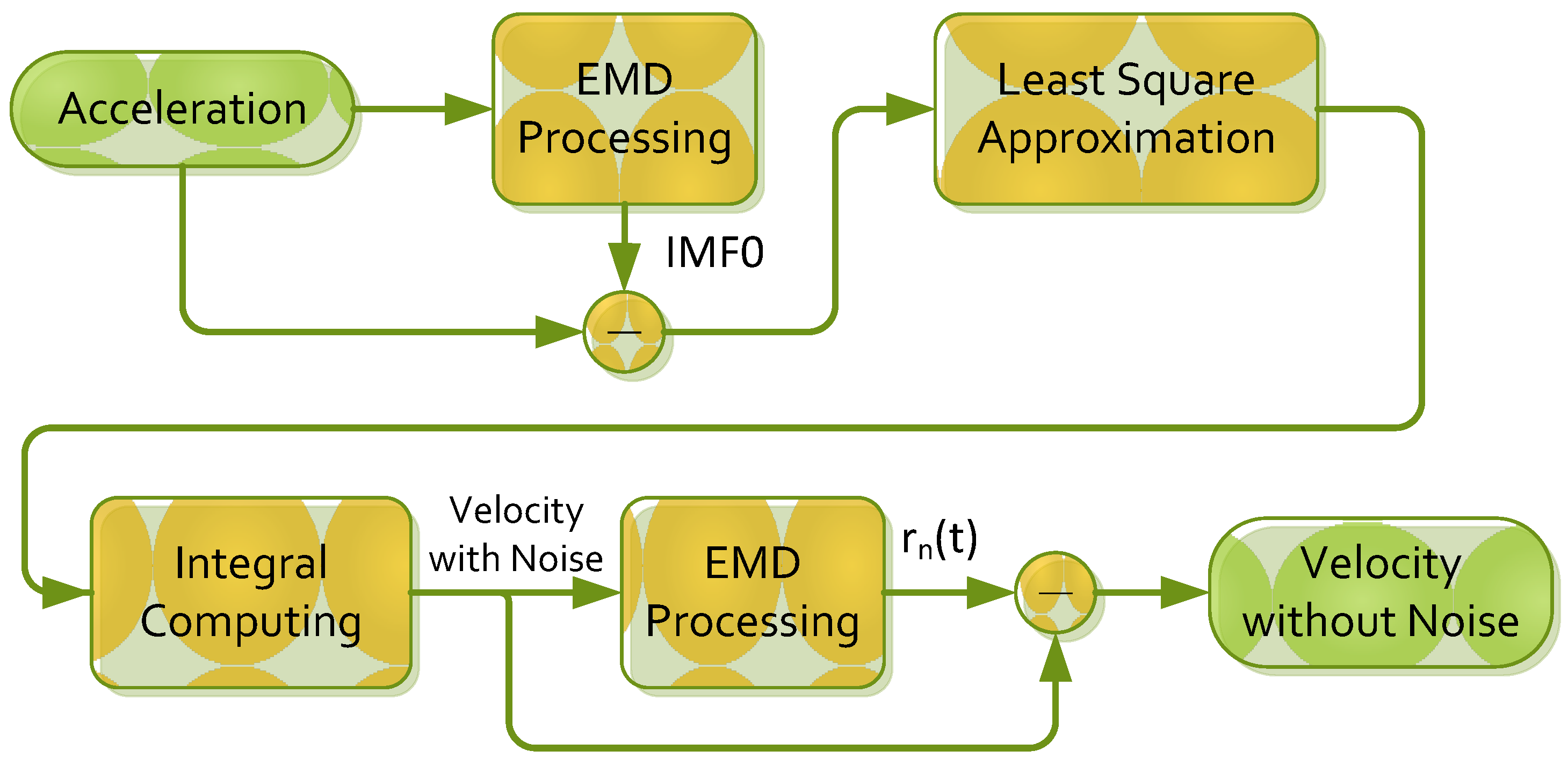
3.4. Estimation of Exercise Intensity
Q = S2f2 + (S1 + 1 + N) f + ba
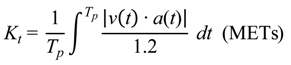
4. Experimental Results and Discussion
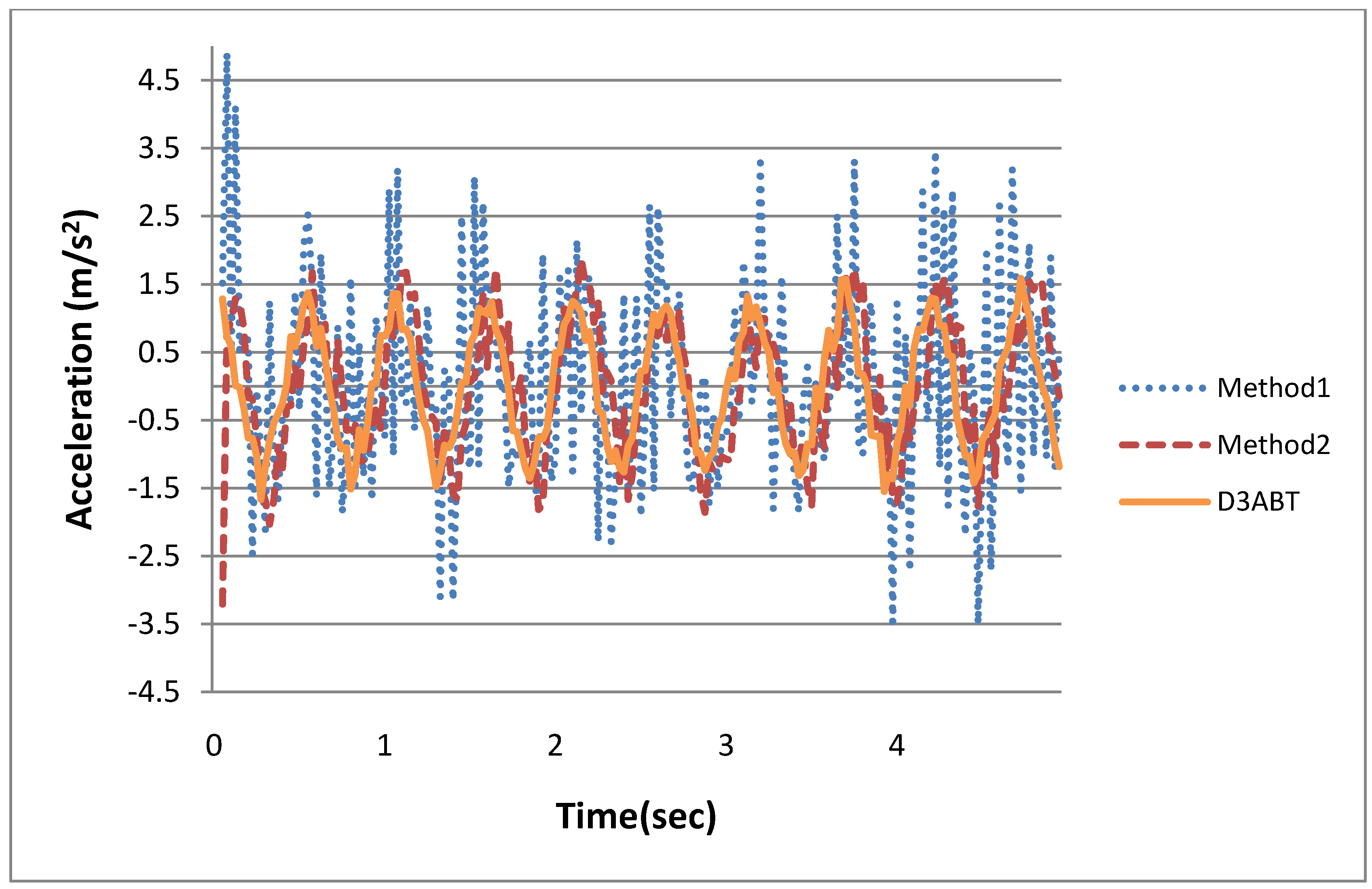
4.1. Algorithm Verification
| Gender | Male | Female |
|---|---|---|
| Subjects | 5 | 5 |
| Age | 30 ± 4 | 26.5 ± 3.5 |
| Height | 172 ± 9 cm | 155 ± 5 cm |
| Body Weight | 75 ± 10 Kg | 47.5 ± 6.5 Kg |
| Leg Length | 101 ± 9 cm | 87.5 ± 2.5 cm |


4.2. Experiments on the Number and Frequency of Steps
(steps counted by the participants) %
| Gender | Male | Female | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Subject | Subject1 | Subject2 | Subject3 | Subject4 | Subject5 | Subject6 | Subject7 | Subject8 | Subject9 | Subject10 | |
| Walking Speed | Normal | 98.75% | 91.67% | 96.67% | 91.89% | 96.05% | 96.77% | 96.77% | 100.0% | 96.00% | 96.00% |
| Normal | 96.25% | 97.22% | 100.0% | 92.11% | 93.75% | 98.92% | 98.92% | 96.20% | 95.89% | 90.91% | |
| Normal | 94.29% | 95.71% | 90.00% | 94.81% | 95.31% | 94.68% | 94.68% | 95.95% | 96.00% | 86.84% | |
| Normal | 96.30% | 98.41% | 93.44% | 96.05% | 100.0% | 94.57% | 94.57% | 97.37% | 100.0% | 91.89% | |
| Normal | 97.22% | 92.06% | 93.44% | 97.33% | 92.19% | 93.26% | 93.26% | 93.42% | 97.30% | 89.04% | |
| Normal | 98.75% | 89.29% | 96.72% | 94.81% | 90.63% | 97.75% | 97.75% | 97.40% | 94.03% | 96.00% | |
| Fast | 92.86% | 91.07% | 100.0% | 96.05% | 91.38% | 90.00% | 90.00% | 95.31% | 95.65% | 97.06% | |
| Very Fast | 98.86% | 93.02% | 98.39% | 97.33% | 85.19% | 88.24% | 88.24% | 88.33% | 83.33% | 93.33% | |
| Slow | 95.12% | 98.46% | 96.72% | 100.0% | 97.10% | 95.79% | 95.79% | 91.14% | 93.83% | 92.11% | |
| Very Slow | 97.56% | 100.0% | 98.36% | 95.65% | 98.61% | 98.92% | 98.92% | 98.77% | 78.02% | 98.82% | |
| Average Accuracy | 96.60% | 94.69% | 96.37% | 95.60% | 94.02% | 94.89% | 94.89% | 95.39% | 93.01% | 93.20% | |
| Gender Accuracy | 95.46% | 94.28% | |||||||||
| Overall Accuracy | 94.87% | ||||||||||
| >95% | 90~95% | <90% | |||||||||
4.3. Gait Recognition Experiments

| Subjects | Percentage of Training Data (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | |
| Subject 1 | 78.02% | 88.65% | 95.60% | 97.10% | 97.80% | 98.50% | 99.50% | 100.00% | 100.00% |
| Subject 2 | 75.07% | 85.93% | 92.98% | 94.48% | 94.30% | 96.07% | 96.45% | 96.95% | 98.24% |
| Subject 3 | 74.91% | 84.67% | 93.57% | 95.07% | 96.67% | 97.93% | 96.30% | 96.80% | 98.47% |
| Subject 4 | 75.03% | 86.05% | 92.03% | 93.53% | 96.95% | 98.02% | 95.85% | 96.35% | 98.89% |
| Subject 5 | 75.75% | 87.06% | 92.29% | 93.79% | 93.42% | 97.09% | 97.30% | 97.80% | 96.96% |
| Subject 6 | 75.24% | 85.90% | 91.58% | 93.08% | 94.06% | 96.94% | 94.96% | 95.46% | 100.00% |
| Subject 7 | 75.89% | 85.56% | 94.50% | 96.00% | 95.31% | 94.38% | 96.91% | 97.41% | 99.53% |
| Subject 8 | 76.66% | 87.65% | 93.53% | 95.03% | 94.75% | 95.11% | 96.56% | 97.06% | 99.03% |
| Subject 9 | 74.93% | 85.39% | 90.83% | 92.33% | 95.00% | 96.54% | 97.87% | 98.37% | 99.88% |
| Subject 10 | 76.51% | 88.03% | 93.09% | 94.59% | 93.53% | 94.40% | 96.66% | 97.16% | 99.46% |
| Average Recognition Rate(%) | 75.80% | 86.49% | 93.00% | 94.50% | 95.18% | 96.50% | 96.84% | 97.34% | 99.05% |
| Worst Recognition Rate(%) | 74.91% | 84.67% | 90.83% | 92.33% | 93.42% | 94.38% | 94.96% | 95.46% | 96.96% |
| Best Recognition Rate(%) | 78.02% | 88.65% | 95.60% | 97.10% | 97.80% | 98.50% | 99.50% | 100.00% | 100.00% |
4.4. Exercise Intensity Experiments
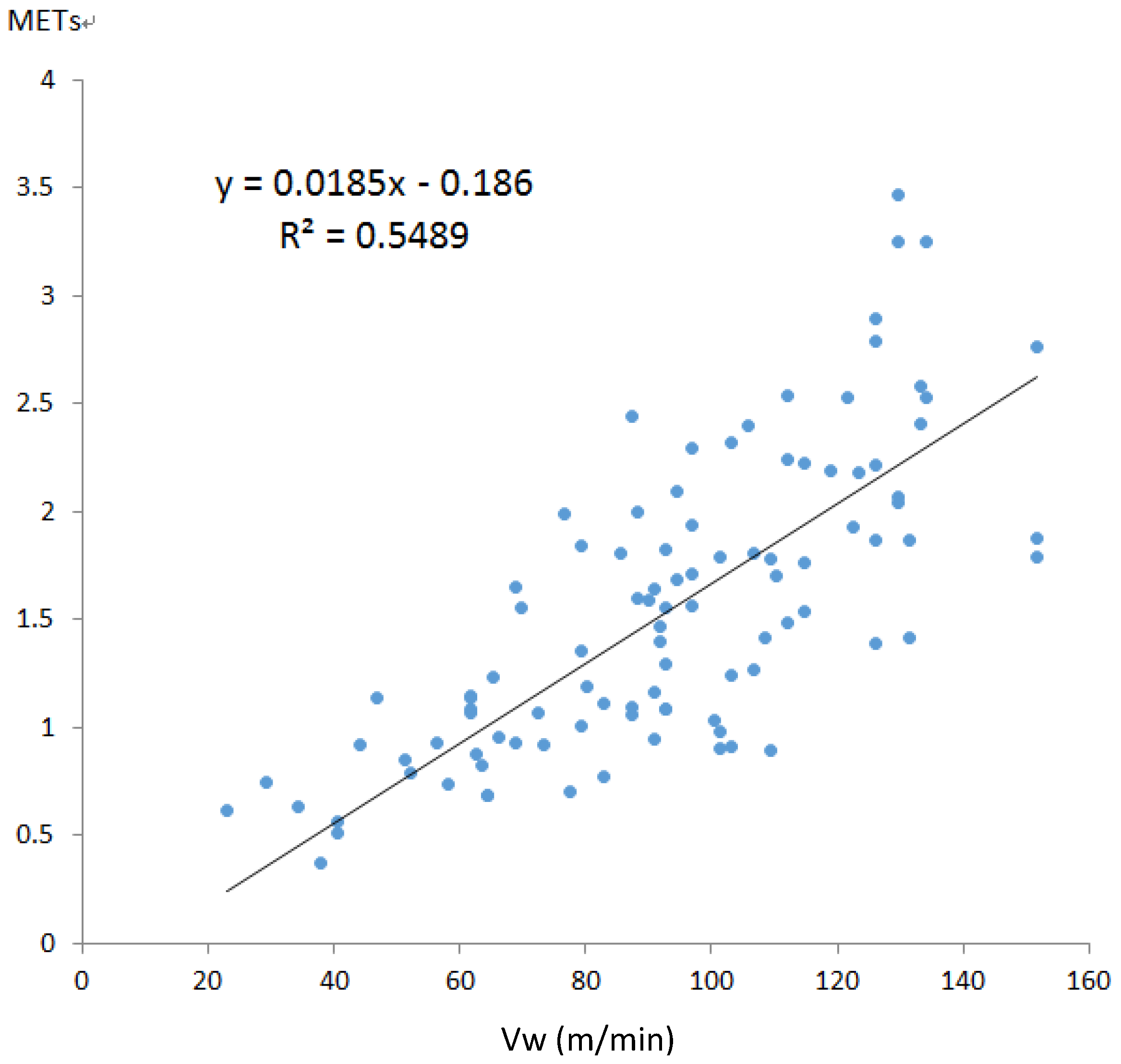

4.5. Discussion
 is the walking exercise intensity calculated by substituting Vw into (12). The values |Error| and
is the walking exercise intensity calculated by substituting Vw into (12). The values |Error| and  are the absolute values of Kwalk − Kwalk and
are the absolute values of Kwalk − Kwalk and  − Kwalk , respectively. Because the exercise intensity ranged from 0.9 to 15 [25], the average absolute error was defined as 100% × |Error| / (15 − 0.9). Table 4 indicates that the proposed algorithm increased the coefficients of determination of the regression equation from 0.55 to 0.81, and the regression equation exhibited an average error rate as low as 2.4%, which is superior to that obtained by duplicating the method of Kurihara (4%). These statistics verified that, compared with Kurihara’s method (13), the formula developed in this study, Formula (12), is more suitable for calculating the work done by inertia in the estimation of exercise intensity.
− Kwalk , respectively. Because the exercise intensity ranged from 0.9 to 15 [25], the average absolute error was defined as 100% × |Error| / (15 − 0.9). Table 4 indicates that the proposed algorithm increased the coefficients of determination of the regression equation from 0.55 to 0.81, and the regression equation exhibited an average error rate as low as 2.4%, which is superior to that obtained by duplicating the method of Kurihara (4%). These statistics verified that, compared with Kurihara’s method (13), the formula developed in this study, Formula (12), is more suitable for calculating the work done by inertia in the estimation of exercise intensity. | ACSM [6] | Reduplicated Y. Kurihara’s Work | The Proposed Sysem | |||||
|---|---|---|---|---|---|---|---|
| Vw (m/min) | Kwalk (METs) | Kwalk (METs) | |Error| (METs) | Error percentage (%) |  (METs) (METs) |  (METs) (METs) | Error percentage (%) |
| 53.6 | 2 | 3 | 1 | 7.1% | 2.6 | 0.6 | 4.3% |
| 67 | 3 | 3.5 | 0.5 | 3.5% | 3.1 | 0.1 | 0.7% |
| 80.5 | 3.3 | 4 | 0.7 | 5.0% | 3.6 | 0.3 | 2.1% |
| 93.9 | 3.8 | 4.5 | 0.7 | 5.0% | 4.1 | 0.3 | 2.1% |
| 107.3 | 5 | 5 | 0 | 0.0% | 4.6 | 0.4 | 2.8% |
| Mean | 0.6 | 4% | 0.4 | 2.4% | |||
| Standard Deviation | 0.3 | 2.4% | 0.2 | 1.2% | |||
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Centers for Disease Control and Prevention (CDC). Obesity: Halting the Epidemic by Making Health Easier at a Glance 2011. Available online: http://www.cdc.gov/chronicdisease/resources/publications/AAG/obesity.htm (accessed on 30 December 2013).
- Karvonen, M.; Kentala, M.; Mustala, O. The effects of training on heart rate: A longitudinal study. Ann. Med. Exp. Biol. Fenn. 1957, 35, 307–315. [Google Scholar]
- Jette, M.; Sidney, K.; Bluemchen, G. Metabolic equivalents (METs) in exercise testing, exercise prescription, and evaluation of functional capacity. Clin. Cardiol. 1990, 13, 555–565. [Google Scholar] [CrossRef]
- Ainsworth, B.E.; Haskell, W.L.; Whitt, M.C.; Irwin, M.L.; Swartz, A.M.; Strath, S.J.; O’Brien, W.L. Compendium of physical activities: An update of activity codes and MET intensities. Med. Sci. Sports Exerc. 2000, 32, 498–504. [Google Scholar] [CrossRef]
- Ainsworth, B.E.; Haskell, W.L.; Whitt, M.C.; Irwin, M.L.; Swartz, A.M.; Strath, S.J.; O’Brien, W.L. Compendium of Physical Activities: A second update of codes and MET values. Med. Sci. Sports Exerc. 2011, 43, 1575–1581. [Google Scholar] [CrossRef]
- Williams, L.; Wilkins, P. ACSM’s Guidelines for Exercise Testing and Prescription, 6th ed.; ACSM: Indianapolis, IN, USA, 2000. [Google Scholar]
- Mathie, M.J.; Celler, B.G.; Lovell, N.H.; Coster, A.C.F. Classification of basic daily movements using a triaxal accelerometer. Med. Biol. Eng. Comput. 2004, 42, 679–687. [Google Scholar] [CrossRef]
- Huynh, T.; Schiele, B. Towards Less Supervision in Activity Recognition from Wearable Sensors. In Proceedings of the Tenth IEEE International Symposium on Wearable Computers, Montreux, Switzerland, 11–14 October 2006; pp. 3–10.
- Zhang, T.; Wang, J.; Xu, L.; Liu, P. Fall Detection by Wearable Sensor and One-class SVM Algorithm. In Lecture Notes in Control and Information Sciences: Intelligent Computing in Signal Processing and Pattern Recognition; Huang, D.S., Li, K., Irwin, G.W., Eds.; Springer-Verlag: Berlin, Germany, 2006; Volume 345, pp. 858–863. [Google Scholar]
- Long, X.; Yin, B.; Aarts, R.M. Single-accelerometer-based daily physical activity classification. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; pp. 6107–6110.
- Pober, D.M.; Staudenmayer, J.; Raphael, C.; Freedson, P.S. Development of novel techniques to classify physical activity mode using accelerometers. Med. Sci. Sports Exerc. 2006, 38, 1626–1634. [Google Scholar] [CrossRef]
- Chen, Y.P.; Yang, J.Y.; Liou, S.N.; Lee, G.Y.; Wang, J.S. Online classifier construction algorithm for human activity detection. Appl. Math. Comput. 2008, 205, 849–860. [Google Scholar] [CrossRef]
- Kurihara, Y.; Watanabe, K.; Yoneyama, M. Estimation of walking exercise intensity using 3-D acceleration sensor. IEEE Trans. Syst. Man Cybern. B 2012, 42, 495–500. [Google Scholar] [CrossRef]
- Apple Inc. Core Motion Framework Reference. Available online: https://developer.apple.com/library/ios/documentation/CoreMotion/Reference/CoreMotion_Reference/_index.html (accessed on 30 December 2013).
- Godfrey, A.; Conway, R.; Meagher, D.; Ólaighin, G. Direct measurement of human movement by accelerometry. Med. Eng. Phys. 2008, 30, 1364–1386. [Google Scholar] [CrossRef]
- Mannini, A.; Sabatini, A.M. Machine learning methods for classifying human physical activity from on-body accelerometers. Sensors 2010, 10, 1154–1175. [Google Scholar] [CrossRef]
- Won, S.H.P.; Golnaraghi, F.A. Triaxial Accelerometer Calibration Method Using a Mathematical Model. IEEE Trans. Instrum. Meas. 2010, 59, 2144–2153. [Google Scholar] [CrossRef]
- Peng, J.L.; Su, J.P. Design and Implementation of a High-Precision 6-DOF Inertial Measurement Unit for Unmanned Vehicles. Master Thesis, Institute of Electrical Engineering, National Yunlin University of Science and Technology, Yunlin, Taiwan, July 2007; pp. 58–60. [Google Scholar]
- Carpenter, M.G.; Frank, J.S.; Silcher, C.P.; Peysar, G.W. The influence of postural threat on the control of upright stance. Exp. Brain Res. 2001, 138, 210–218. [Google Scholar] [CrossRef]
- Analog Devices Inc. Fast Fourier Transforms. Available online: http://www.analog.com/static/imported-files/seminars_webcasts/MixedSignal_Sect5.pdf (accessed on 30 December 2013).
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis. In Proceedings of the Royal Society on Mathematical, Physical and Engineering Sciences, London, UK, 8 March 1998; Volume 454, pp. 903–995.
- Syed, Z.F.; Aggarwal, P; Goodall, C.; Niu, X.; El-Sheimy, N. A new multi-position calibration method for MEMS inertial navigation systems. Meas. Sci. Technol. 2007, 18, 1897. [Google Scholar] [CrossRef]
- Leica Geosystems. Leica Disto™ D3ABT. Available online: http://www.leica-geosystems.com/en/Leica-DISTO-D3a-BT_81303.htm (accessed on 30 December 2013).
- Waters, R.L. Energy-speed relationship of walking, standard tables. J. Orthop. Res. 1988, 6, 215–222. [Google Scholar] [CrossRef]
- Ministry of Health, Labour and Welfare (Japan). Movement Criterion for Health Care (2005)—Body Activity, Movement, and Physical Strength. Available online: http://www.mhlw.go.jp/shingi/2006/02/dl/s0223-6d.pdf (accessed on 30 December 2013).
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lin, B.-S.; Liu, Y.-T.; Yu, C.; Jan, G.E.; Hsiao, B.-T. Gait Recognition and Walking Exercise Intensity Estimation. Int. J. Environ. Res. Public Health 2014, 11, 3822-3844. https://doi.org/10.3390/ijerph110403822
Lin B-S, Liu Y-T, Yu C, Jan GE, Hsiao B-T. Gait Recognition and Walking Exercise Intensity Estimation. International Journal of Environmental Research and Public Health. 2014; 11(4):3822-3844. https://doi.org/10.3390/ijerph110403822
Chicago/Turabian StyleLin, Bor-Shing, Yu-Ting Liu, Chu Yu, Gene Eu Jan, and Bo-Tang Hsiao. 2014. "Gait Recognition and Walking Exercise Intensity Estimation" International Journal of Environmental Research and Public Health 11, no. 4: 3822-3844. https://doi.org/10.3390/ijerph110403822