Modeling and Preventive Measures of Hand, Foot and Mouth Disease (HFMD) in China
Abstract
:1. Introduction
2. Methods
2.1. Data
| Mouth/Year | 2009 | 2010 | 2011 | 2012 |
|---|---|---|---|---|
| January | – – | 37,567 | 32,179 | 50,758 |
| February | – – | 23,862 | 10,609 | 40,505 |
| March | 54,713 | 77,756 | 34,709 | 99,052 |
| April | 212,435 | 248,609 | 99,819 | 237,478 |
| May | 169,073 | 354,347 | 230,460 | 462,116 |
| June | 178,680 | 343,100 | 303,594 | 381,626 |
| July | 162,060 | 261,263 | 253,442 | 248,739 |
| August | 99,897 | 119,096 | 132,154 | 118,333 |
| September | 85,504 | 101,654 | 120,802 | 135,974 |
| October | 76,948 | 87,612 | 122,491 | 146,392 |
| November | 61,918 | 79,591 | 152,768 | 150,264 |
| December | 47,817 | 60,879 | 126,679 | 127,205 |
2.2. Model Analysis
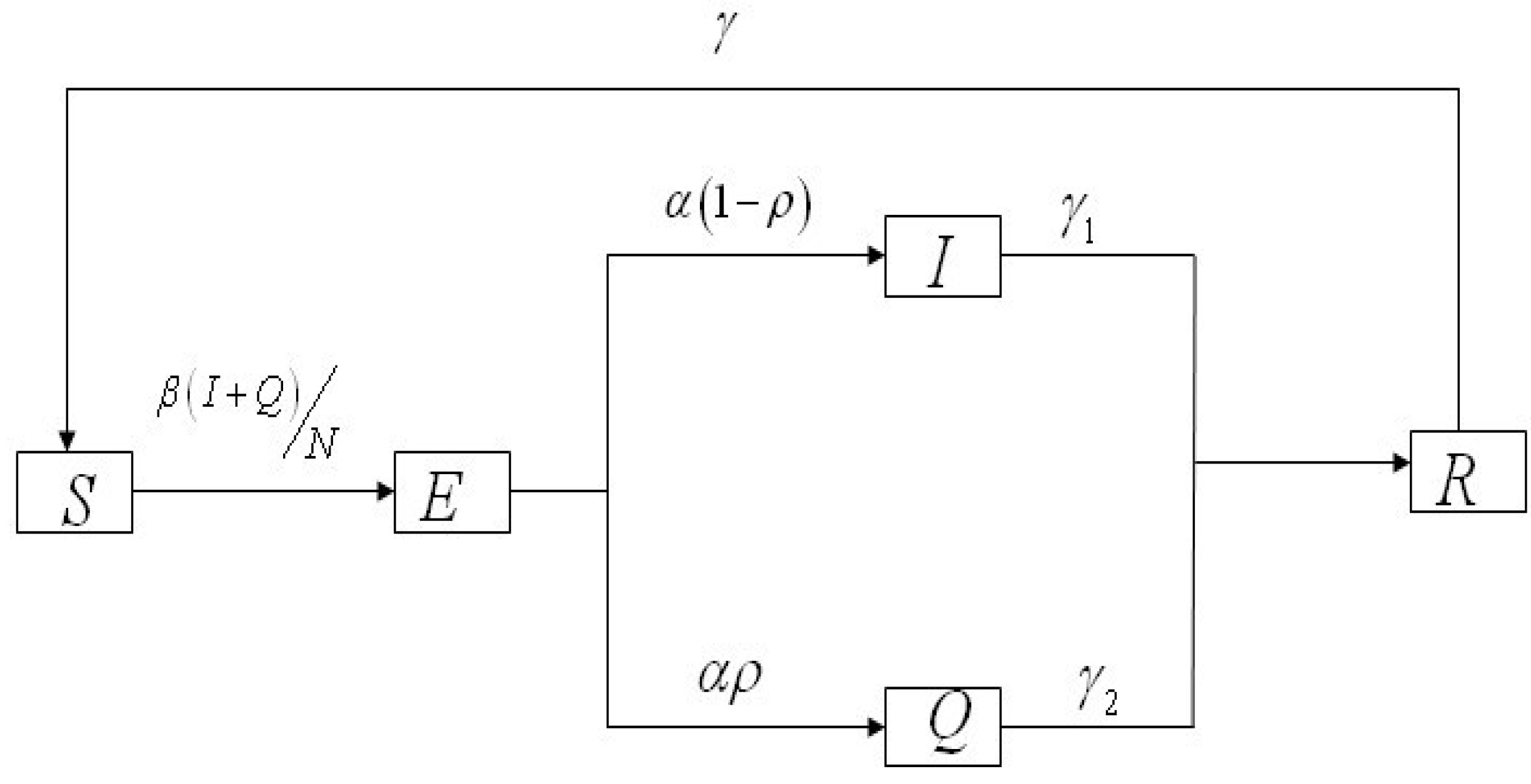
2.3. Parameters and Model Hypothesis
2.4. Model Formulation
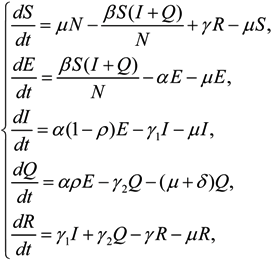
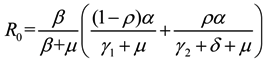
3. Results
3.1. Parameter Estimation
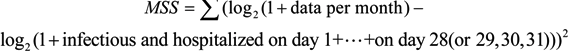
| Parameter Interval and R0 | Source | 2009 | 2010 | 2011 | 2012 |
|---|---|---|---|---|---|
| β in [0.0001,50] | MSS | 1.0252 | 0.5575 | 0.5149 | 0.7738 |
| γ1 in [0.1,1] | MSS | 0.9419 | 0.5136 | 0.4744 | 0.7348 |
| γ2 in [0.1,1] | MSS | 0.4034 | 0.2251 | 0.3080 | 0.2013 |
| α in [0.0001,1] | MSS | 0.3907 | 1 | 1 | 1 |
| ρ in [0.01,1] | MSS | 0.01 | 0.01 | 0.01 | 0.01 |
| γ in [0.0001,1] | MSS | 0.0089 | 0.0072 | 0.0126 | 0.0111 |
| S(0) | Fixed | 1.4 × 108 | 1.4×108 | 1.4 × 108 | 1.4 × 108 |
| E(0)in [1.8 × 104,1.4 × 107] | MSS | 2.4029 × 105 | 2.0430 × 104 | 1.8290 × 104 | 1.9790 × 104 |
| I(0)in [1.8 × 103,1.8 × 105] | MSS | 1.9469 × 103 | 1.8001 × 103 | 1.8 × 103 | 1.8001 × 103 |
| Q(0) | Fixed | 1,765 | 1,212 | 1,038 | 1,673 |
| R(0) | Fixed | 0 | 0 | 0 | 0 |
| R0 | Calculated | 1.1028 | 1.0993 | 1.0911 | 1.0809 |
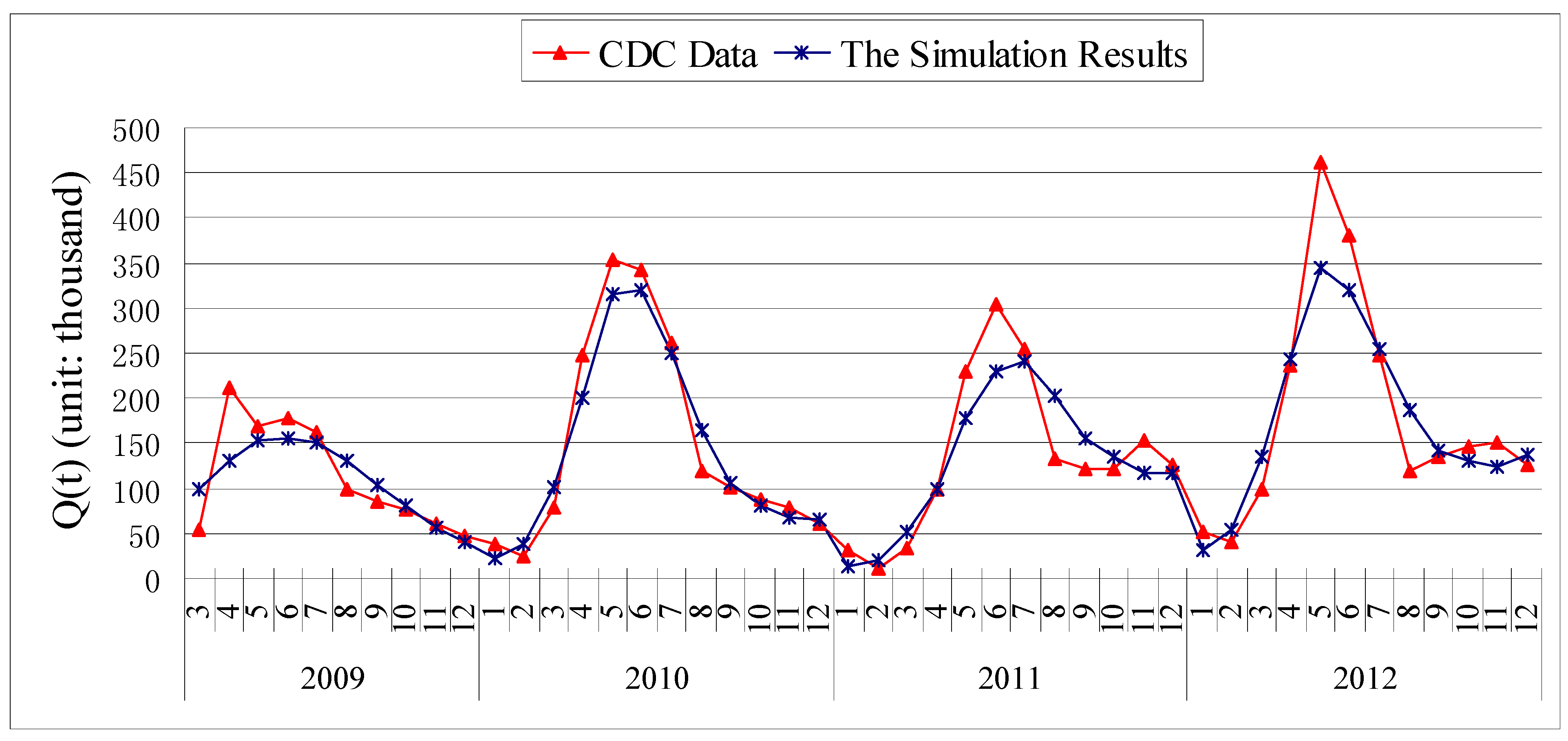
3.2. Chi-Square Test of Goodness of Fit
| 2009 | 2010 | 2011 | 2012 | |
|---|---|---|---|---|
| Chi-square value | 0.0525 | 0.1094 | 0.257 | 0.1012 |
| υ * | 1 | 3 | 3 | 3 |
| AV * | 3.841 | 7.815 | 7.815 | 7.815 |
3.3. Sensitivity Analysis
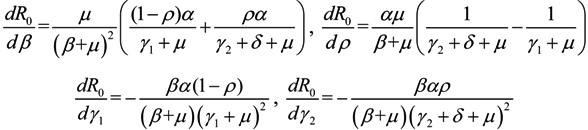
 ,
,  ,
,  and
and  , we can see that R0 decreases as β decreases, R0 decreases as γ1 or γ2 increases, and the impact of ρ on R0 depends on the values of γ1 and γ2. In theory, if we can control some parameters such that R0 < 1, then the disease will die out. On this basis we shall put forward detail preventive strategies of HFMD in the following section.
, we can see that R0 decreases as β decreases, R0 decreases as γ1 or γ2 increases, and the impact of ρ on R0 depends on the values of γ1 and γ2. In theory, if we can control some parameters such that R0 < 1, then the disease will die out. On this basis we shall put forward detail preventive strategies of HFMD in the following section.4. Discussion and Conclusions
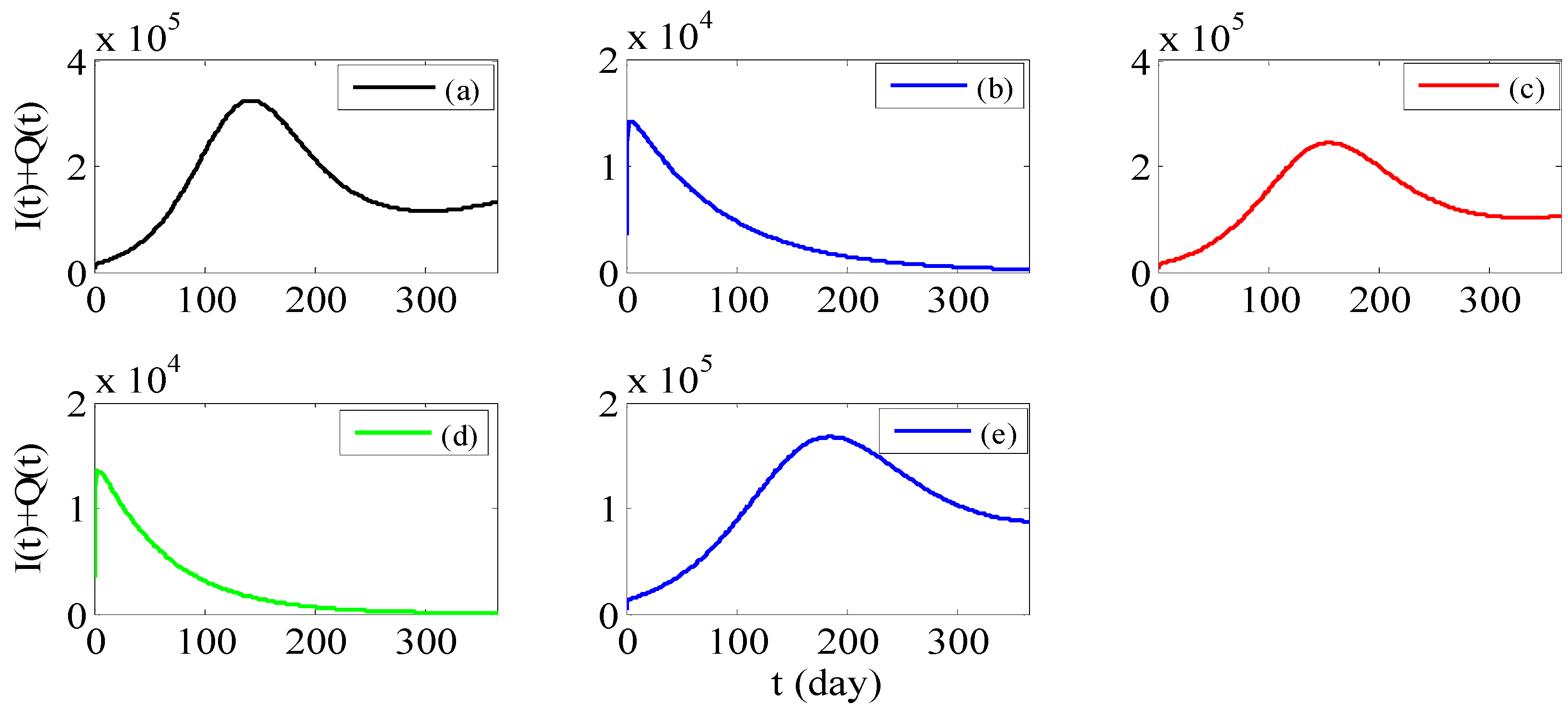
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, J.L. Threshold dynamics for a HFMD epidemic model with periodic transmission rate. Nonlinear Dyn. 2011, 64, 89–95. [Google Scholar] [CrossRef]
- Ma, Y.J.; Liu, M.X.; Hou, Q.; Zhao, J.Q. Modeling seasonal HFMD with the recessive infection in Shandong, China. Math. Biosci. Eng. 2013, 10, 1159–1171. [Google Scholar] [CrossRef]
- Schmidt, N.J.; Lennette, E.H.; Ho, H.H. An apparently new enterovirus isolated from patients with disease of the central nervous system. J. Infect. Dis. 1974, 129, 304–309. [Google Scholar]
- Blomberg, J.; Lycke, E.; Ahlfors, K.; Johnsson, T.; Wolontis, S.; von Zeipel, G. New enterovirus type associated with epidemic of aseptic meningitis and/or hand, foot, and mouth disease. Lancet 1974, 2. [Google Scholar] [CrossRef]
- Shindarov, L.M.; Chumakov, M.P.; Voroshilova, M.K.; Bojinov, S.; Vasilenko, S.M.; Iordanov, I.; Kirov, I.D.; Kamenov, E.; Leshchinskaya, E.V.; Mitov, G.; et al. Epidemiological, clinical and pathomorphological characteristics of epidemic poliomyelitis-like disease caused by enterovirus 71. J. Hyg. Epidemiol. Microbiol. Immunol. 1979, 23, 284–295. [Google Scholar]
- Ishimaru, Y.; Nakano, S.; Yamaoka, K.; Takami, S. Outbreaks of hand, foot, and mouth disease by enterovirus 71: High incidence of complication disorders of central nervous system. Arch. Dis. Child. 1980, 55, 583–588. [Google Scholar] [CrossRef]
- Nagy, G.; Takatsy, S.; Kukan, E.; Mihaly, I.; Domok, I. Virological diagnosis of enterovirus type 71 infective: Experiences gained during an epidemic of acute CNS diseases in Hungary in 1978. Arch. Virol. 1982, 71, 217–227. [Google Scholar] [CrossRef]
- Gilbert, G.L.; Dickson, K.E.; Waters, M.J.; Kennett, M.L.; Land, S.A.; Sneddon, M. Outbreak of enterovirus 71 infection in Victoria, Australia, with a high incidence of neurologic involvement. Pediatr. Infect. Dis. J. 1988, 7, 484–488. [Google Scholar] [CrossRef]
- Alexander, J.P.; Baden, L.; Pallansch, M.A.; Anderson, L.J. Enterovirus 71 infections and neurologic disease—United States, 1977–1991. J. Infect. Dis. 1994, 169, 905–908. [Google Scholar]
- Da Silva, E.E.; Winkler, M.T.; Pallansch, M.A. Role of enterovirus 71 in acute flaccid paralysis after the eradication of poliovirus in Brazil. Emerg. Infect. Dis. 1996, 2, 231–233. [Google Scholar] [CrossRef]
- Chan, L.G.; Parashar, U.D.; Lye, M.S.; Ong, F.G.L.; Zaki, S.R.; Alexander, J.P.; Ho, K.K.; Han, L.L.; Pallansch, M.A.; Suleiman, A.B.; et al. Deaths of children during an outbreak of hand, foot, and mouth disease in Sarawak, Malaysia: Clinical and pathological characteristics of the disease. Clin. Infect. Dis. 2000, 31, 678–683. [Google Scholar] [CrossRef]
- Chang, L.Y.; Huang, Y.C.; Lin, T.Y. Fulminant neurogenic pulmonary oedema with hand, foot and mouth disease. Lancet 1998, 352, 367–368. [Google Scholar] [CrossRef]
- Wu, T.N.; Tsai, S.F.; Li, S.F.; Lee, T.F.; Huang, T.M.; Wang, M.L.; Hsu, K.H.; Shen, C.Y. Sentinel surveillance of enterovirus 71, Taiwan, 1998. Emerg. Infect. Dis. 1998, 5, 458–460. [Google Scholar]
- Chang, L.Y.; Lin, T.Y.; Hsu, K.H.; Huang, Y.C.; Lin, K.L.; Hsueh, C.; Shih, S.R.; Ning, H.C.; Hwang, M.S.; Wang, H.S.; et al. Clinical features and risk factors of pulmonary oedema after enterovirus-71-related hand, foot, and mouth disease. Lancet. 1999, 354, 1682–1686. [Google Scholar] [CrossRef]
- Ho, M.; Chen, E.R.; Hsu, K.H.; Twu, S.J.; Shih, S.R. An epidemic of enterovirus 71 infection in Taiwan. N. Engl. J. Med. 1999, 341, 929–935. [Google Scholar] [CrossRef]
- Dolin, R. Enterovirus 71-emerging infections and emerging questions. N. Engl. J. Med. 1999, 341, 984–985. [Google Scholar] [CrossRef]
- China on Alert as Virus Spreads. Available online: http://news.bbc.co.uk/1/hi/world/asia-pacific/7381741.stm (accessed on 11 January 2013).
- China Reports 537 Deaths from Hand-foot-mouth Disease This Year. Available online: http://news.xinhuanet.com/english2010/china/2010–06/24/c_13367598.htm (accessed on 11 January 2013).
- Tiing, F.C.S.; Labadin, J. A simple deterministic model for the spread of hand, foot and mouth disease (HFMD) in Sarawak. In Proceedings of Second Asia International Conference on Modeling and Simulation, Kuala Lumpur, Malaysia, 13–15 May 2008.
- Su, X.R.; Liu, S. Age-structured HFMD model with isolation. Sci. Tech. Eng. 2009, 9, 5311–5315. (in Chinese). [Google Scholar]
- The Chinese Center for Disease Control and Prevention. Available online: http://www.chinacdc.cn/tjsj/ (accessed on 11 January 2013).
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Zhang, X.A.; Zhao, Y.D.; Neumann, A.U. Partial immunity and vaccination for influenza. J. Comput. Biol. 2010, 17, 1689–1696. [Google Scholar] [CrossRef]
- Snedecor, G.W.; Cochran, W.G. Statistical Methods, 8th ed.; Iowa State University Press: Ames, IA, USA, 1989; pp. 178–196. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, Y.; Zhang, J.; Zhang, X. Modeling and Preventive Measures of Hand, Foot and Mouth Disease (HFMD) in China. Int. J. Environ. Res. Public Health 2014, 11, 3108-3117. https://doi.org/10.3390/ijerph110303108
Li Y, Zhang J, Zhang X. Modeling and Preventive Measures of Hand, Foot and Mouth Disease (HFMD) in China. International Journal of Environmental Research and Public Health. 2014; 11(3):3108-3117. https://doi.org/10.3390/ijerph110303108
Chicago/Turabian StyleLi, Yong, Jinhui Zhang, and Xinan Zhang. 2014. "Modeling and Preventive Measures of Hand, Foot and Mouth Disease (HFMD) in China" International Journal of Environmental Research and Public Health 11, no. 3: 3108-3117. https://doi.org/10.3390/ijerph110303108




