Assessing and Mapping Spatial Associations among Oral Cancer Mortality Rates, Concentrations of Heavy Metals in Soil, and Land Use Types Based on Multiple Scale Data
Abstract
:1. Introduction
2. Experimental Section
2.1. Data Collection

2.2. Area-to-point Poisson Kriging
2.3. Cluster Analysis
2.4. Kruskal-Wallis Test for Comparing Mean Mortality Rates for All Land Use Types
3. Results
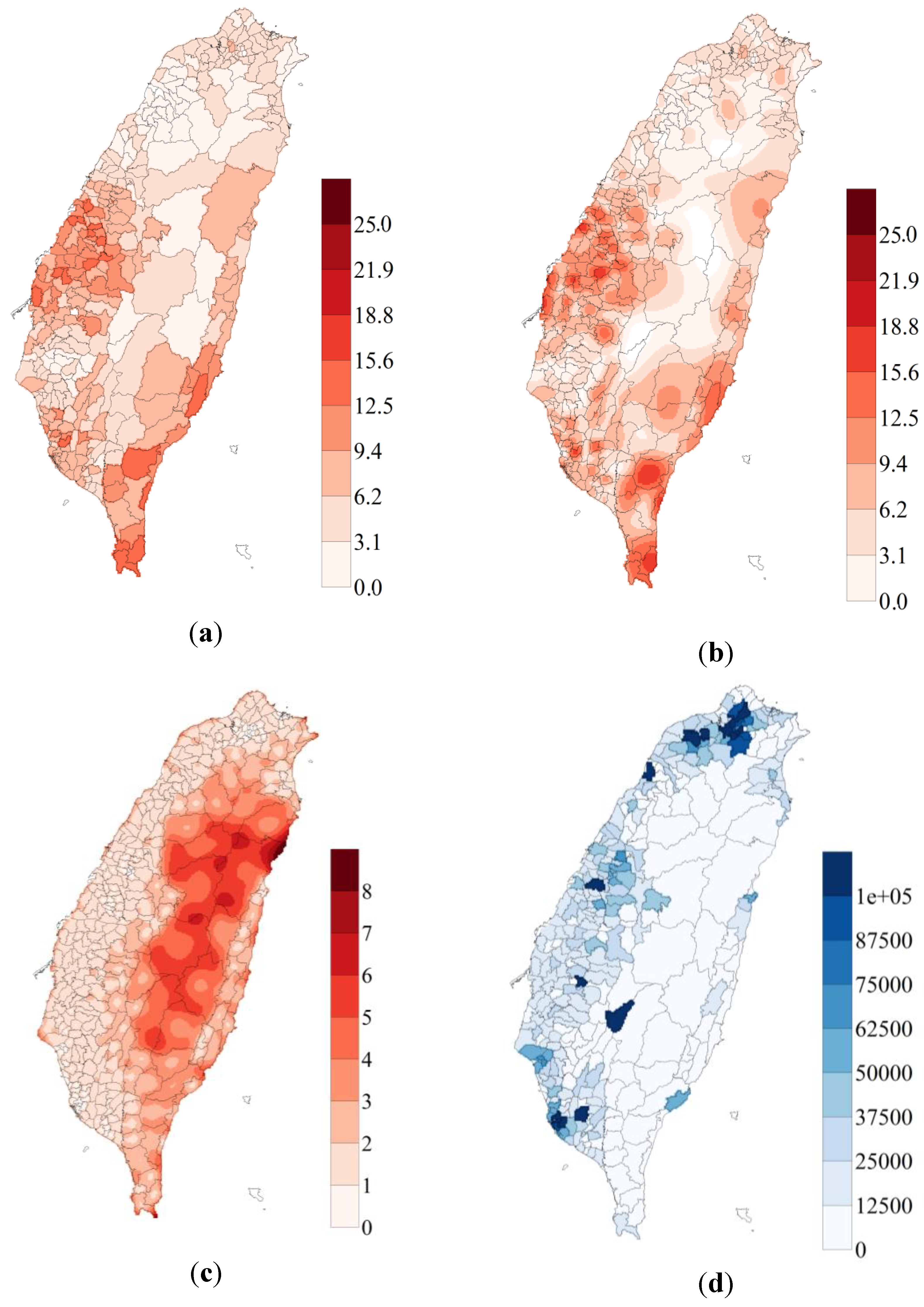
3.1. Downscaled Spatial Distribution and Variance in OC Mortality Rate

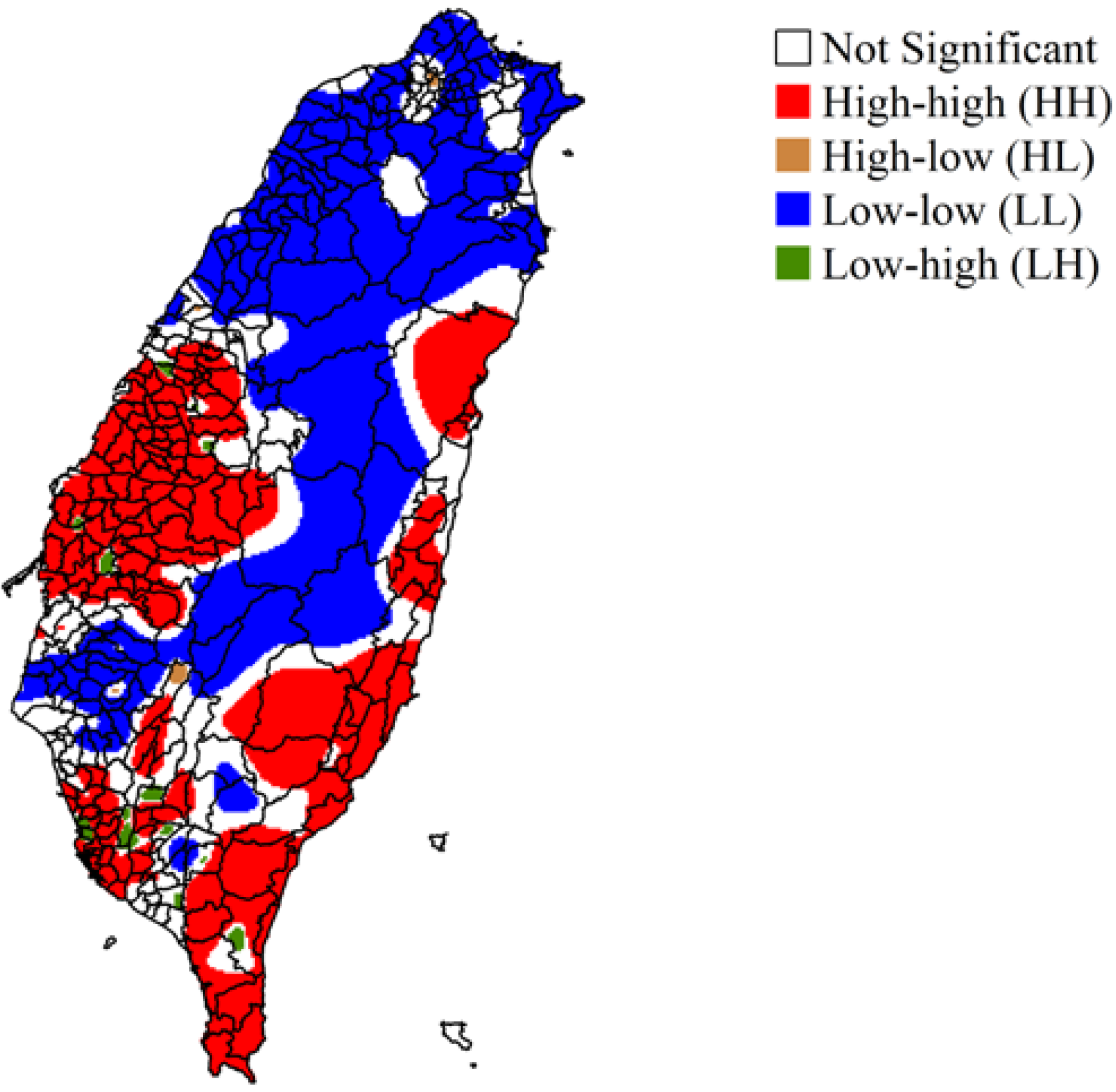
3.2. Estimated Spatial Distribution of OC Mortality Rate and Local Moran Statistics
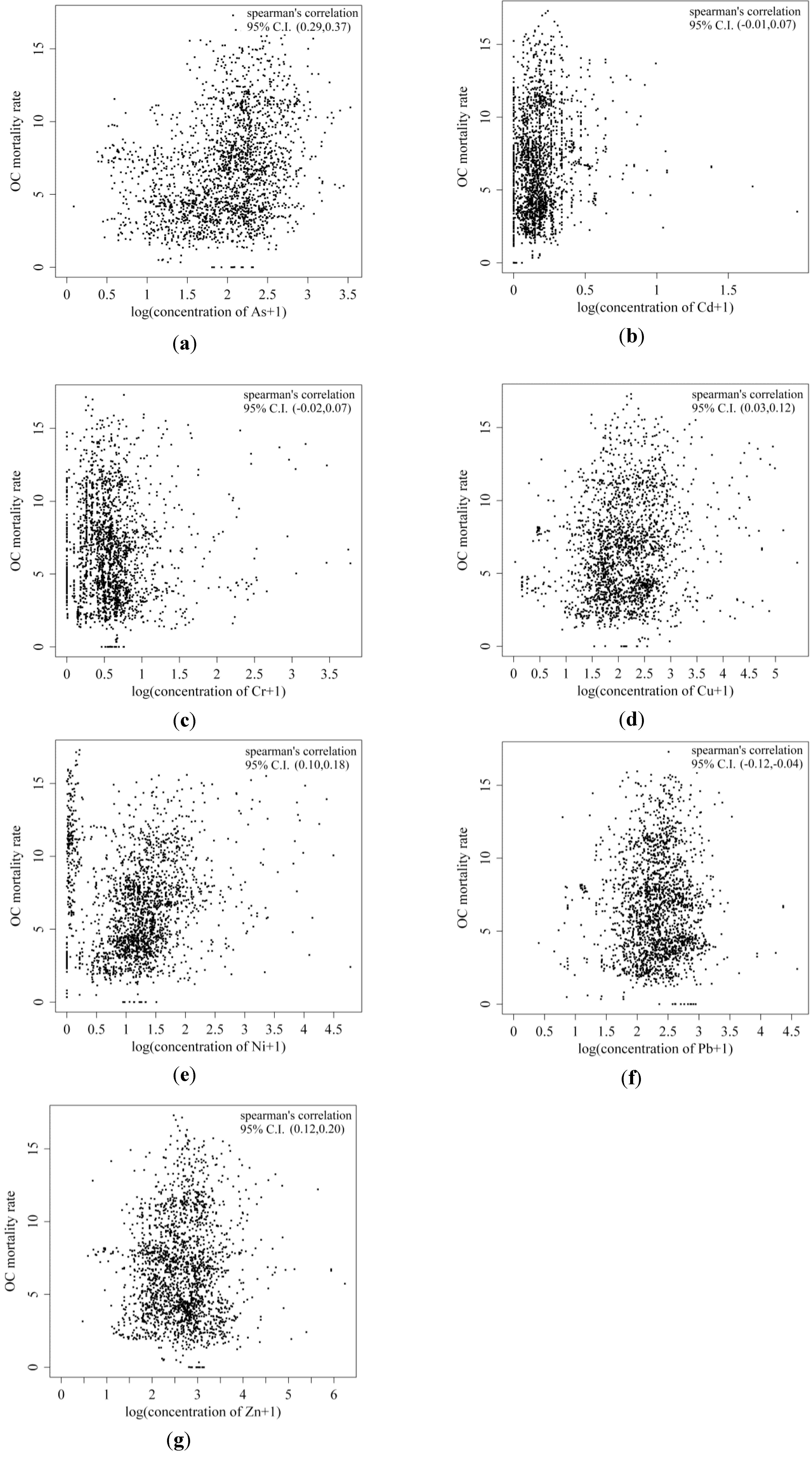
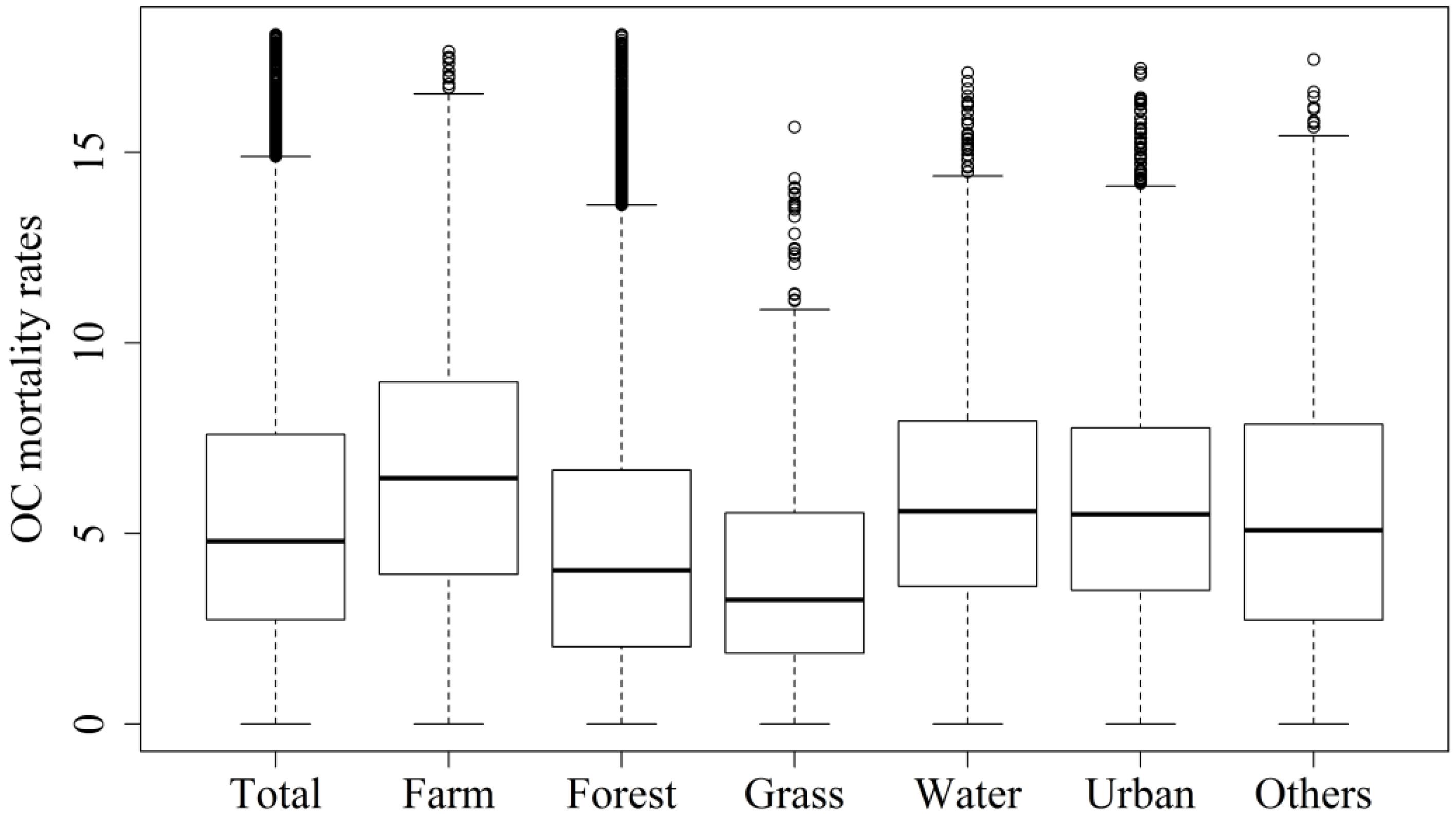
3.3. Correlation between Land-use and OC Mortality Rate
| Land type | Hotspot (%) |
|---|---|
| Farm | 46.4 |
| Forest | 25.8 |
| Grass | 19.3 |
| Water | 36.2 |
| Urban | 37.4 |
| Others | 41.4 |
| Entire area | 32.5 |
3.4. p-field Simulation of OC Mortality Rate

4. Discussion
4.1. Analysis of Variograms and the Relationship between OC and Heavy Metals
4.2. Analysis of OC Mortality Patterns
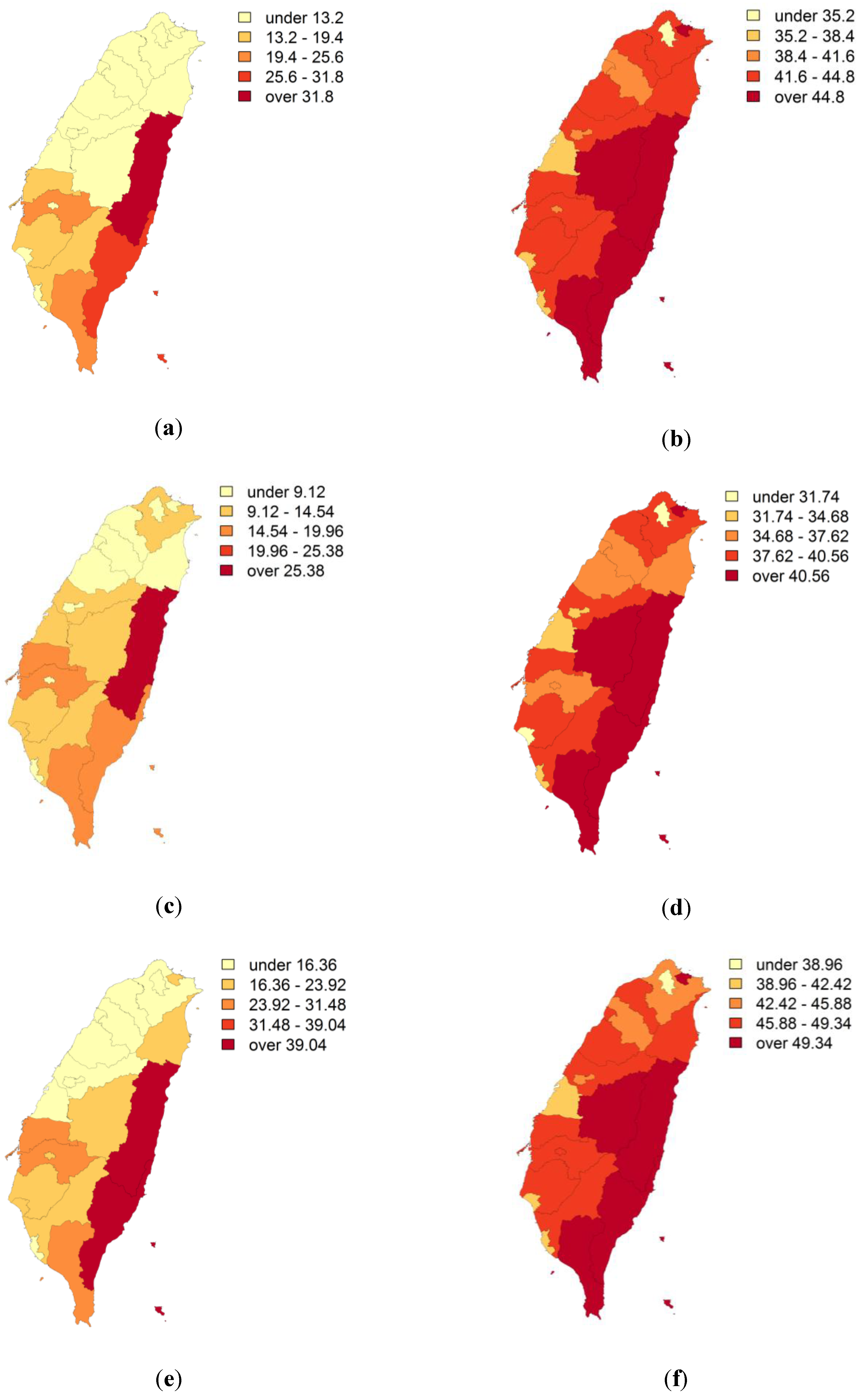
4.3. p-field Simulation of OC Mortality Rate
4.4. Spatial Patterns of OC Mortality in Different Land Use Types
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Su, C.-C.; Lin, Y.-Y.; Chang, T.-K.; Chiang, C.-T.; Chung, J.-A.; Hsu, Y.-Y.; Lian, I.-B. Incidence of oral cancer in relation to nickel and arsenic concentrations in farm soils of patients’ residential areas in Taiwan. BMC Public Health 2010, 10. [Google Scholar] [CrossRef]
- Su, C.-C.; Tsai, K.-Y.; Hsu, Y.-Y.; Lin, Y.-Y.; Lian, I.-B. Chronic exposure to heavy metals and risk of oral cancer in Taiwanese males. Oral Oncol. 2010, 46, 586–590. [Google Scholar] [CrossRef]
- Chiang, C.-T.; Lian, I.-B.; Su, C.-C.; Tsai, K.-Y.; Lin, Y.-P.; Chang, T.-K. Spatiotemporal trends in oral cancer mortality and potential risks associated with heavy metal content in Taiwan soil. Int. J. Environ. Res. Public Health 2010, 7, 3916–3928. [Google Scholar] [CrossRef]
- Chiang, C.-T.; Hwang, Y.-H.; Su, C.-C.; Tsai, K.-Y.; Lian, I.-B.; Yuan, T.-H.; Chang, T.-K. Elucidating the underlying causes of oral cancer through spatial clustering in high-risk areas of Taiwan with a distinct gender ratio of incidence. Geospat. Health 2010, 4, 231–242. [Google Scholar]
- Wei, B.; Jia, X.; Ye, B.; Yu, J.; Zhang, B.; Zhang, X.; Lu, R.; Dong, T.; Yang, L. Impacts of land use on spatial distribution of mortality rates of cancers caused by naturally occurring asbestos. J. Expo. Sci. Environ. Epidemiol. 2012, 22, 516–521. [Google Scholar] [CrossRef]
- Liu, X.; Song, Q.; Tang, Y.; Li, W.; Xu, J.; Wu, J.; Wang, F.; Brookes, P.C. Human health risk assessment of heavy metals in soil–vegetable system: A multi-medium analysis. Sci. Total Environ. 2013, 463, 530–540. [Google Scholar]
- Poggio, L.; Vrščaj, B.; Schulin, R.; Hepperle, E.; Ajmone Marsan, F. Metals pollution and human bioaccessibility of topsoils in Grugliasco (Italy). Environ. Pollut. 2009, 157, 680–689. [Google Scholar] [CrossRef]
- Luo, X.-S.; Ding, J.; Xu, B.; Wang, Y.-J.; Li, H.-B.; Yu, S. Incorporating bioaccessibility into human health risk assessments of heavy metals in urban park soils. Sci. Total Environ. 2012, 424, 88–96. [Google Scholar] [CrossRef]
- Xia, X.; Chen, X.; Liu, R.; Liu, H. Heavy metals in urban soils with various types of land use in Beijing, China. J. Hazard. Mater. 2011, 186, 2043–2050. [Google Scholar] [CrossRef]
- Wang, M.; Markert, B.; Chen, W.; Peng, C.; Ouyang, Z. Identification of heavy metal pollutants using multivariate analysis and effects of land uses on their accumulation in urban soils in Beijing, China. Environ. Monit. Assess. 2012, 184, 5889–5897. [Google Scholar] [CrossRef]
- Yuan, T.-H.; Lian, I.-B.; Tsai, K.-Y.; Chang, T.-K.; Chiang, C.-T.; Su, C.-C.; Hwang, Y.-H. Possible association between nickel and chromium and oral cancer: A case-control study in Central Taiwan. Sci. Total Environ. 2011, 409, 1046–1052. [Google Scholar] [CrossRef]
- Goovaerts, P. Application of Geostatistics in Cancer Studies. In Geoenv VII–Geostatistics for Environmental Applications; Springer: Berlin, Germany, 2010; pp. 107–119. [Google Scholar]
- Goovaerts, P. Geostatistical analysis of county-level lung cancer mortality rates in the Southeastern United States. Geogr. Anal. 2010, 42, 32–52. [Google Scholar] [CrossRef]
- Bonyah, E.; Munyakazi, L.; Nsowah-Nuamah, N.; Asong, D.; Saeed, I. Application of area to point kriging to breast cancer incidence in the Ashanti region of Ghana. Int. J. Med. Med. Sci. 2013, 5, 68–75. [Google Scholar]
- Goovaerts, P. Geostatistical analysis of disease data: Accounting for spatial support and population density in the isopleth mapping of cancer mortality risk using area-to-point Poisson kriging. Int. J. Health Geogr. 2006, 5. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical Analysis of Health Data: State-of-the-Art and Perspectives. In Geoenv VI–Geostatistics for Environmental Applications; Springer: Berlin, Germany, 2008; pp. 3–22. [Google Scholar]
- Shao, C.; Mueller, U.; Cross, J. Area-to-point Poison Kriging Analysis for Lung Cancer Incidence in Perth Areas. In Proceedings of the 18th World IMACS/MODSIM Congress, Cairns, Australia, 13–17 July 2009; pp. 13–17.
- Goovaerts, P. Geostatistical analysis of health data with different levels of spatial aggregation. Spat. Spatiotemporal Epidemiol. 2012, 3, 83–92. [Google Scholar] [CrossRef]
- Bonyah, E. Application of area to point kriging to Buruli ulcer incidence in Ashanti and Brong Ahafo regions of Ghana. Geoinform. Geostat. Overview 2013. [Google Scholar] [CrossRef]
- Goovaerts, P. Medical geography: A promising field of application for geostatistics. Mathem. Geosci. 2009, 41, 243–264. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistical analysis of disease data: Visualization and propagation of spatial uncertainty in cancer mortality risk using Poisson kriging and p-field simulation. Int. J. Health Geogr. 2006, 5. [Google Scholar] [CrossRef] [Green Version]
- Kerry, R.; Goovaerts, P.; Haining, R.P.; Ceccato, V. Applying geostatistical analysis to crime data: Car-related thefts in the Baltic States. Geogr. Anal. 2010, 42, 53–77. [Google Scholar] [CrossRef]
- Goovaerts, P. Accounting for rate instability and spatial patterns in the boundary analysis of cancer mortality maps. Environ. Ecol. Stat. 2008, 15, 421–446. [Google Scholar] [CrossRef]
- Goovaerts, P.; Jacquez, G.M. Detection of temporal changes in the spatial distribution of cancer rates using local Moran’s I and geostatistically simulated spatial neutral models. J. Geogr. Syst. 2005, 7, 137–159. [Google Scholar]
- Goovaerts, P.; Jacquez, G. Accounting for regional background and population size in the detection of spatial clusters and outliers using geostatistical filtering and spatial neutral models: The case of lung cancer in Long Island, New York. Int. J. Health Geogr. 2004, 3. [Google Scholar] [CrossRef] [Green Version]
- Oliver, M.A.; Webster, R. Kriging: A method of interpolation for geographical information systems. Int. J. Geogr. Inform. Syst. 1990, 4, 313–332. [Google Scholar]
- Anselin, L. Local indicators of spatial association—Lisa. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Taylor, R. Interpretation of the correlation coefficient: A basic review. J. Diag. Med. Sonogr. 1990, 6, 35–39. [Google Scholar] [CrossRef]
- Lin, Y.-P.; Teng, T.-P.; Chang, T.-K. Multivariate analysis of soil heavy metal pollution and landscape pattern in Changhua County in Taiwan. Landsc. Urban Plann. 2002, 62, 19–35. [Google Scholar] [CrossRef]
- Lin, Y.-P.; Chang, T.-K.; Shih, C.-W.; Tseng, C.-H. Factorial and indicator kriging methods using a geographic information system to delineate spatial variation and pollution sources of soil heavy metals. Environ. Geol. 2002, 42, 900–909. [Google Scholar] [CrossRef]
- Lin, Y.-P.; Chang, T.-K.; Teng, T.-P. Characterization of soil lead by comparing sequential gaussian simulation, simulated annealing simulation and kriging methods. Environ. Geo. 2001, 41, 189–199. [Google Scholar] [CrossRef]
- Lopez-Abente, G. Risk of cancer mortality in Spanish towns lying in the vicinity of pollutant industries. ISRN Oncol. 2012. [Google Scholar] [CrossRef]
- Blot, W.J.; Fraumeni, J.F. Geographic patterns of lung cancer: Industrial correlations. Am. J. Epidemiol. 1976, 103, 539–550. [Google Scholar]
- Boffetta, P. Epidemiology of environmental and occupational cancer. Oncogene 2004, 23, 6392–6403. [Google Scholar] [CrossRef]
- Chiang, C.-T.; Chang, T.-K.; Hwang, Y.-H.; Su, C.-C.; Tsai, K.-Y.; Yuan, T.-H.; Lian, I.-B. A critical exploration of blood and environmental chromium concentration among oral cancer patients in an oral cancer prevalent area of Taiwan. Environ. Geochem. Health 2011, 33, 469–476. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lin, W.-C.; Lin, Y.-P.; Wang, Y.-C.; Chang, T.-K.; Chiang, L.-C. Assessing and Mapping Spatial Associations among Oral Cancer Mortality Rates, Concentrations of Heavy Metals in Soil, and Land Use Types Based on Multiple Scale Data. Int. J. Environ. Res. Public Health 2014, 11, 2148-2168. https://doi.org/10.3390/ijerph110202148
Lin W-C, Lin Y-P, Wang Y-C, Chang T-K, Chiang L-C. Assessing and Mapping Spatial Associations among Oral Cancer Mortality Rates, Concentrations of Heavy Metals in Soil, and Land Use Types Based on Multiple Scale Data. International Journal of Environmental Research and Public Health. 2014; 11(2):2148-2168. https://doi.org/10.3390/ijerph110202148
Chicago/Turabian StyleLin, Wei-Chih, Yu-Pin Lin, Yung-Chieh Wang, Tsun-Kuo Chang, and Li-Chi Chiang. 2014. "Assessing and Mapping Spatial Associations among Oral Cancer Mortality Rates, Concentrations of Heavy Metals in Soil, and Land Use Types Based on Multiple Scale Data" International Journal of Environmental Research and Public Health 11, no. 2: 2148-2168. https://doi.org/10.3390/ijerph110202148





